Arctan-Gravity Model
Abstract
:1. Introduction
2. The Model
2.1. Constant Curvature Solutions
3. The Scalar-Tensor Form

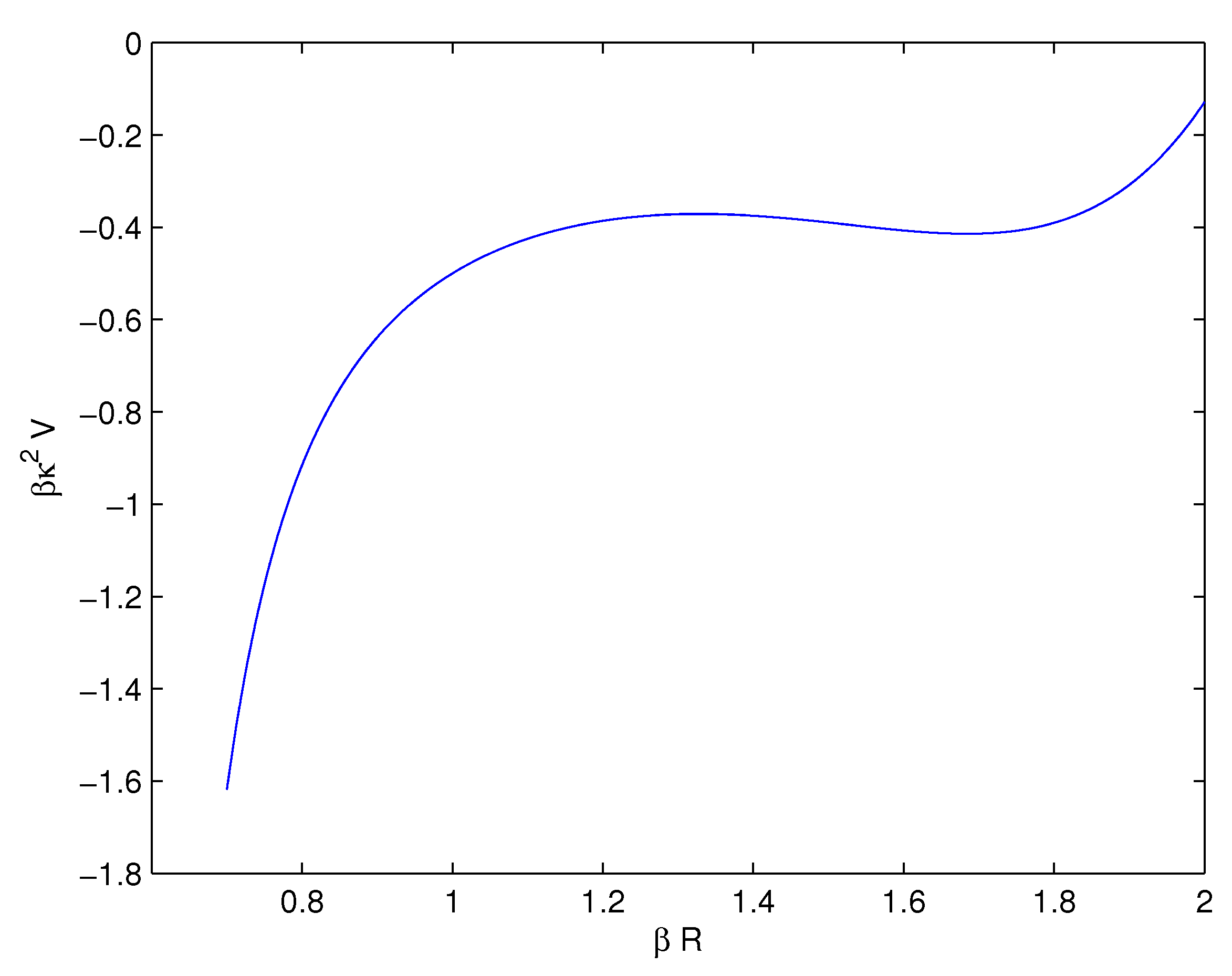
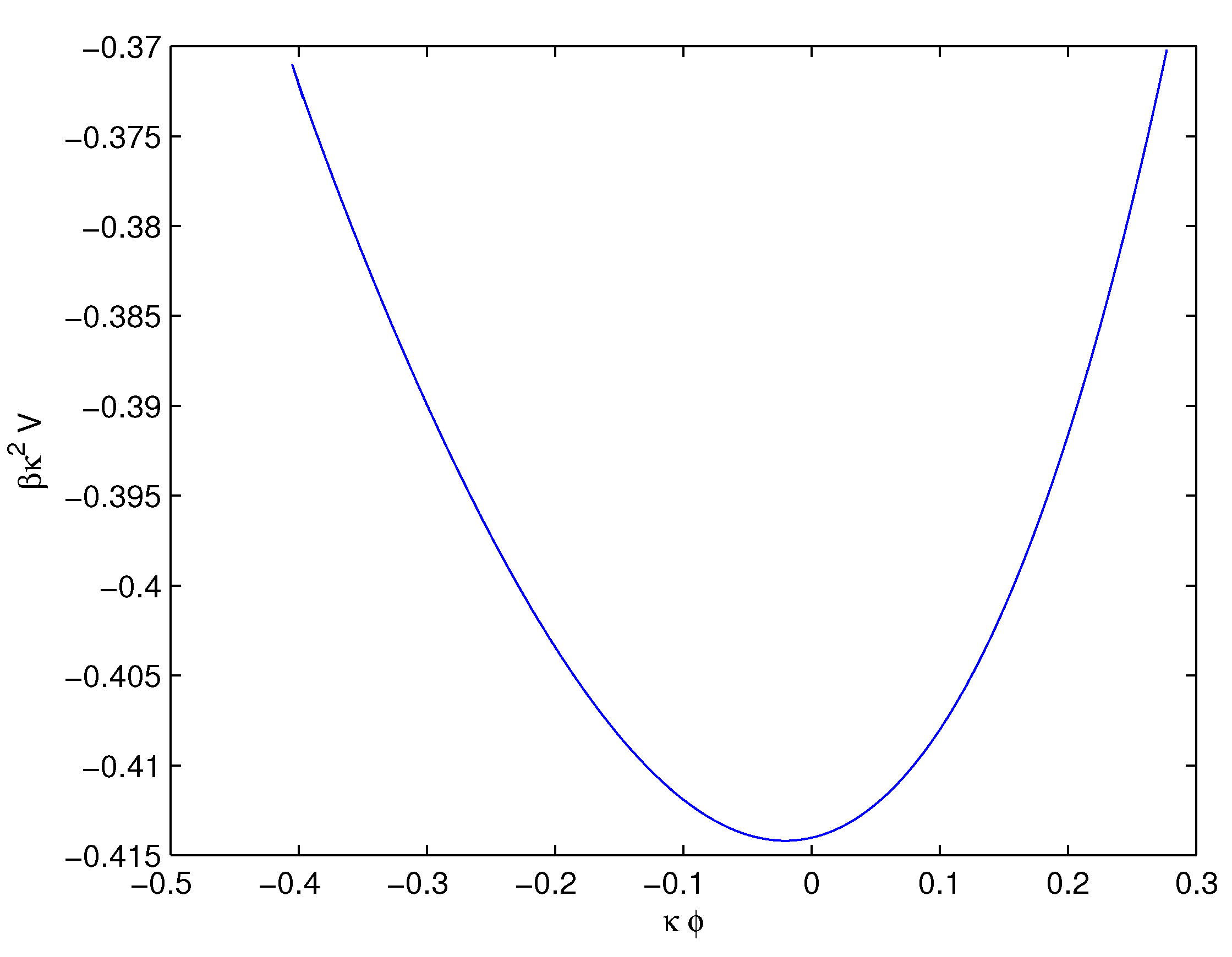
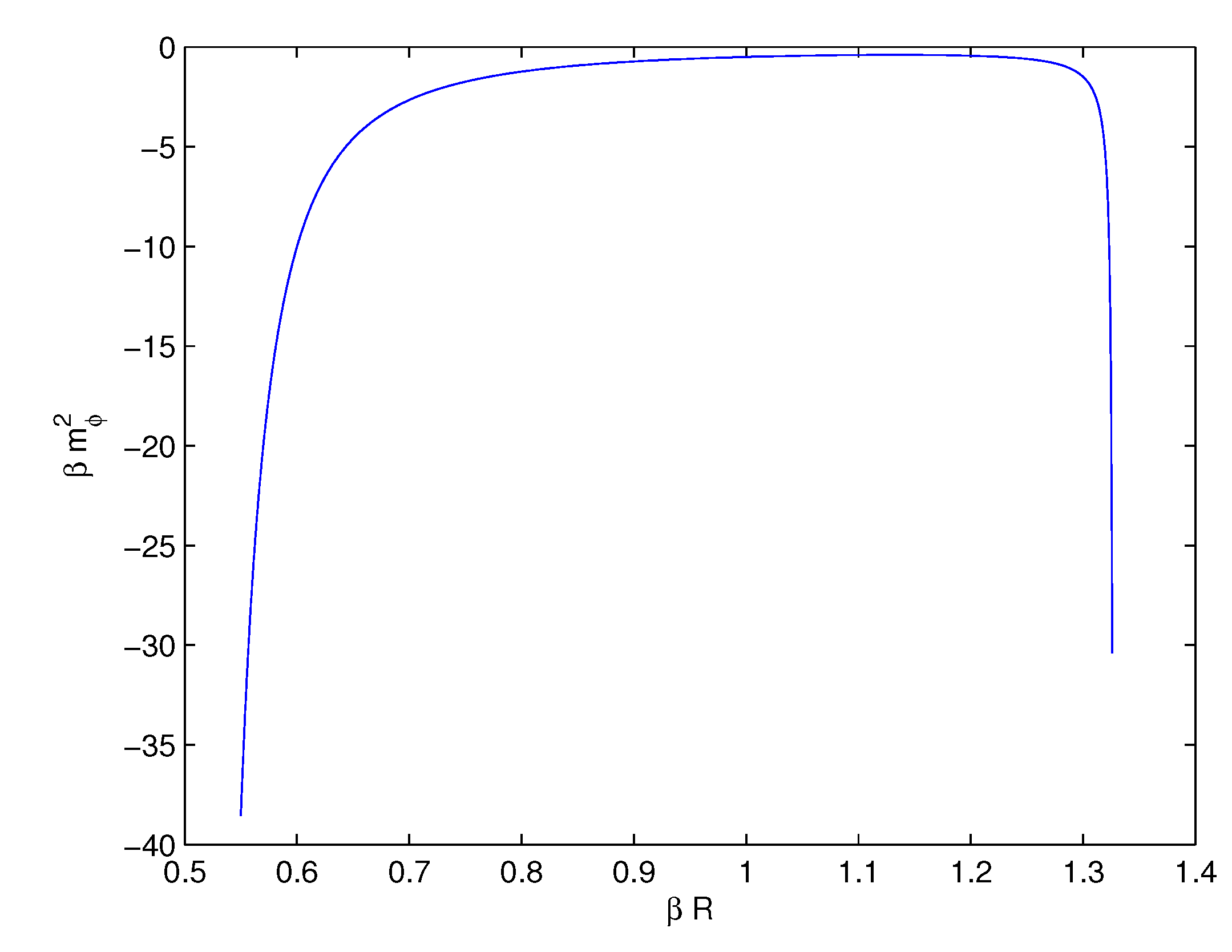
4. Cosmological Parameters
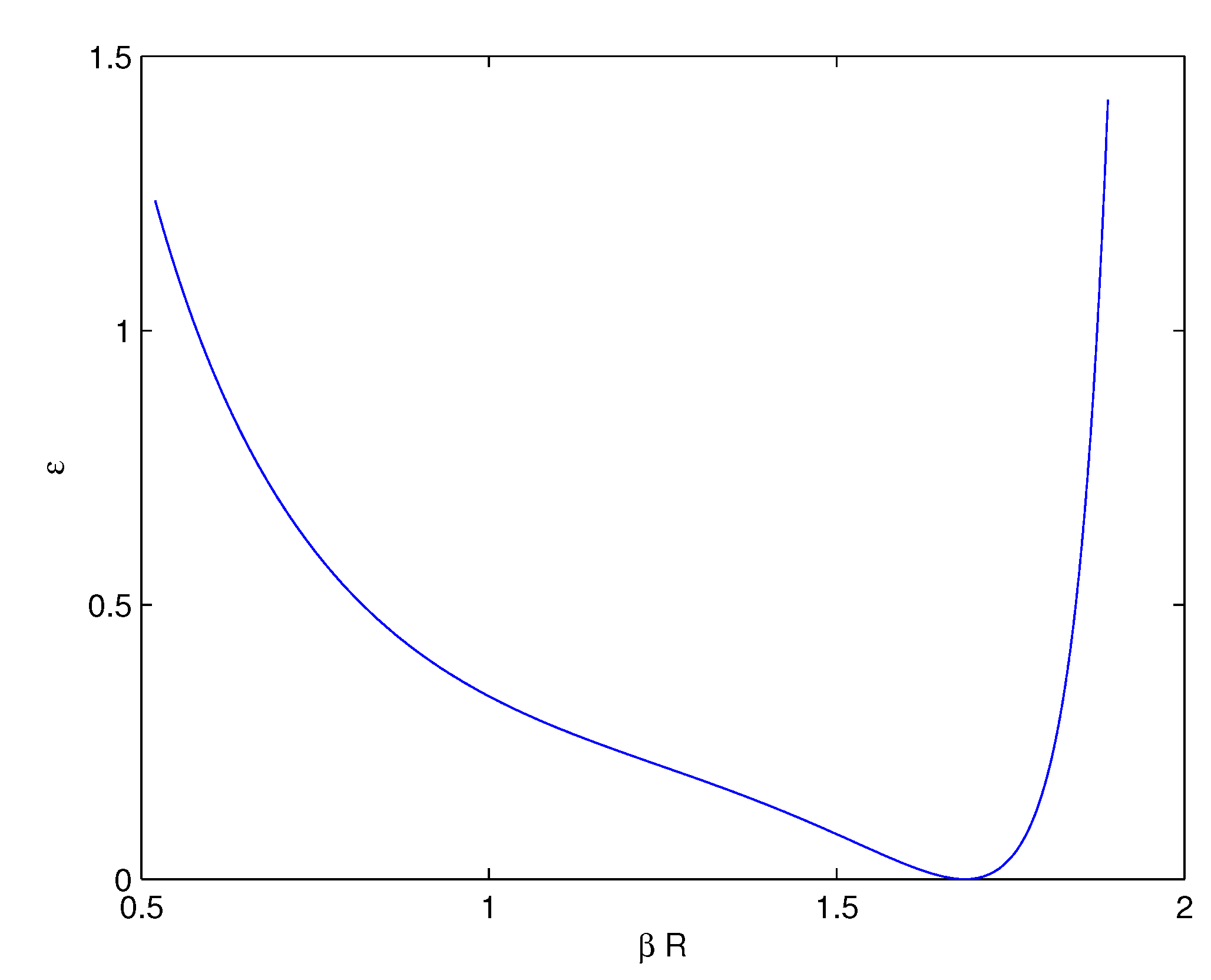
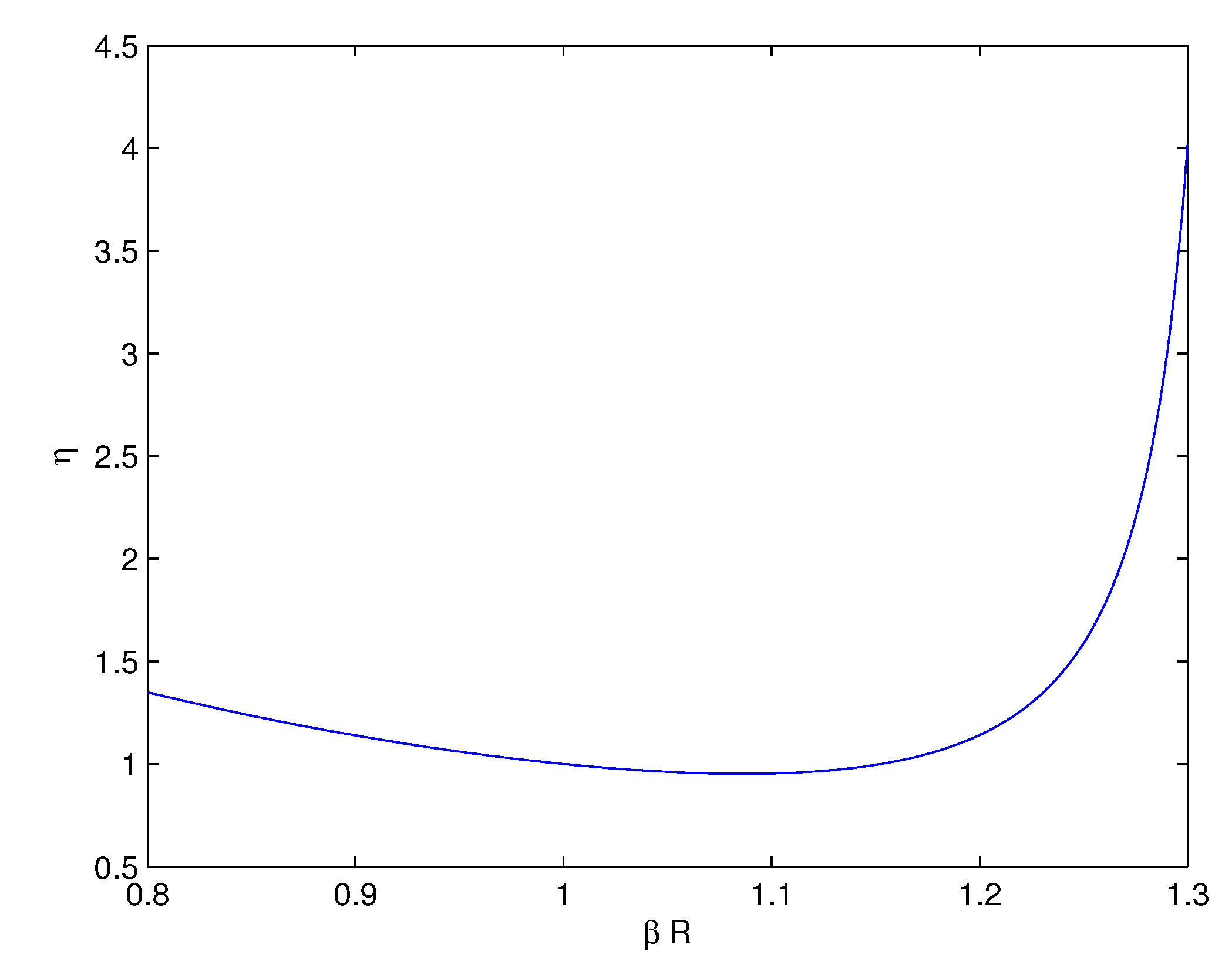
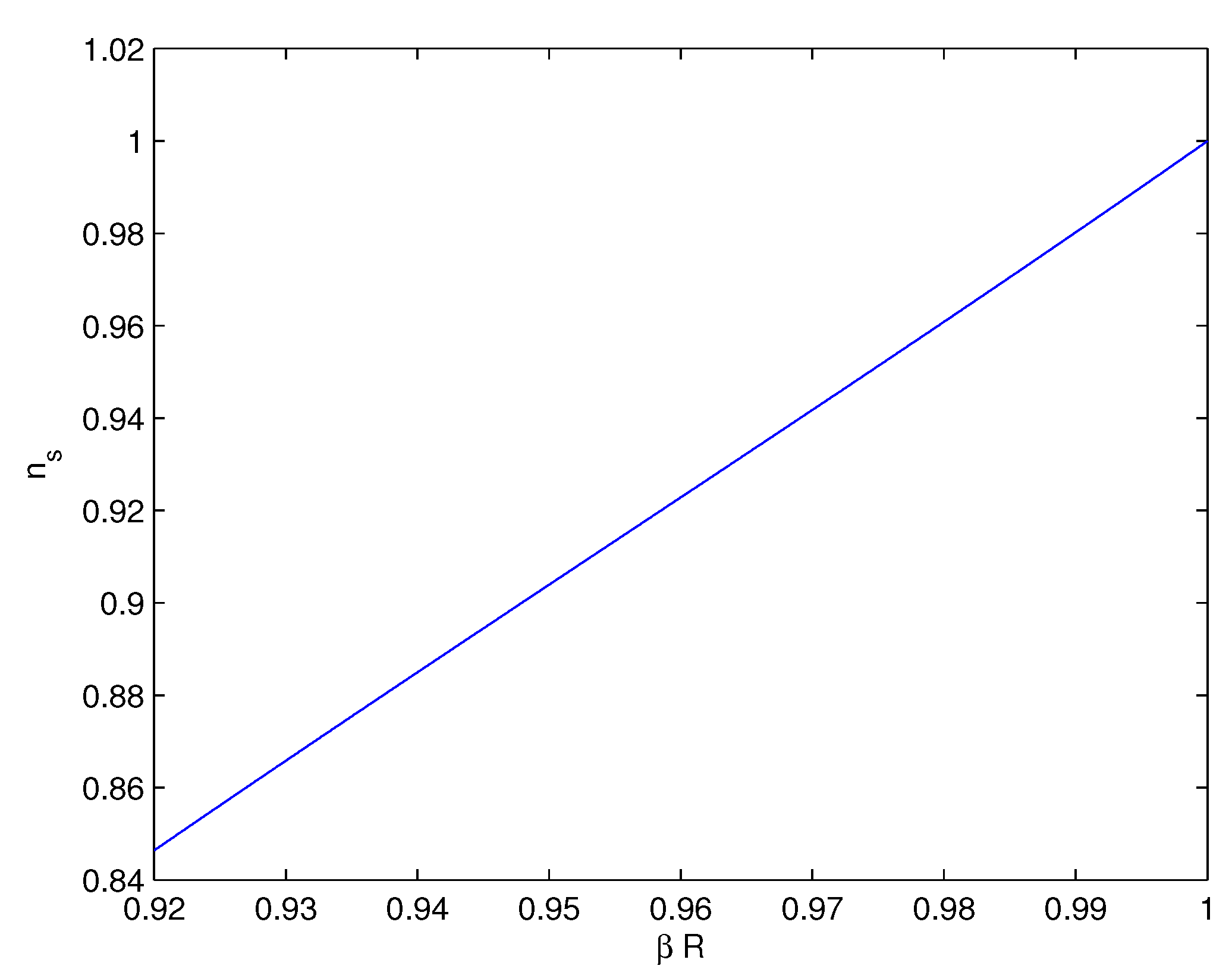
5. Conclusions
Conflicts of Interest
References
- Frieman, J.A.; Turner, M.S.; Huterer, D. Dark Energy and the Accelerating Universe. Annu. Rev. Astron. Astrophys. 2008, 46, 385–432. [Google Scholar] [CrossRef]
- Linde, A.D. Particle Physics and Inflationary Cosmology; Harwood Academic Publishers: Chur, Switzerland, 1992. [Google Scholar]
- Capozziello, S.; Faraoni, V. Beyond Einstein Gravity: A Survey of Gravitational Theories for Cosmology and Astrophysics; Springer: New York, NY, USA, 2011. [Google Scholar]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rep. 2011, 505, 59–144. [Google Scholar] [CrossRef]
- Starobinsky, A.A. A New Type of Isotropic Cosmological Models Without Singularity. Phys. Lett. B 1980, 91, 99–102. [Google Scholar] [CrossRef]
- Hu, W.; Sawicki, I. Models of f(R) Cosmic Acceleration that Evade Solar-System Tests. Phys. Rev. D 2007, 76, 064004. [Google Scholar] [CrossRef]
- Appleby, S.A.; Battye, R.A. Do consistent F(R) models mimic General Relativity plus? Phys. Lett. B 2007, 654, 7–12. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Disappearing cosmological constant in f(R) gravity. JETP Lett. 2007, 86, 157–163. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unifying inflation with ΛCDM epoch in modified f(R) gravity consistent with Solar System tests. Phys. Lett. B 2007, 657, 238. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified f(R) gravity unifying Rm inflation with ΛCDM epoch. Phys. Rev. D 2008, 77, 026007. [Google Scholar] [CrossRef]
- Cognola, G.; Elizalde, E.; Nojiri, S.; Odintsov, S.D.; Sebastiani, L.; Zerbini, S. A Class of viable modified f(R) gravities describing inflation and the onset of accelerated expansion. Phys. Rev. D 2008, 77, 046009. [Google Scholar] [CrossRef]
- Deser, S.; Gibbons, G.W. Born-Infeld-Einstein actions? Class. Quant. Grav. 1998, 15, L35–L39. [Google Scholar] [CrossRef]
- Kruglov, S.I. Born-Infeld-like modified gravity. Int. J. Theor. Phys. 2013, 52, 2477–2484. [Google Scholar] [CrossRef]
- Kruglov, S.I. On exponential modified gravity. Int. J. Mod. Phys. A 2013, 28, 1350119. [Google Scholar] [CrossRef]
- Kruglov, S.I. Modified arctan-gravity model mimicking a cosmological constant. Phys. Rev. D 2014, 89, 064004. [Google Scholar] [CrossRef]
- Sebastiani, L.; Cognola, G.; Myrzakulov, R.; Odintsov, S. D.; Zerbini, S. Nearly Starobinsky inflation from modified gravity. Phys. Rev. D 2014, 89, 023518. [Google Scholar] [CrossRef]
- Bamba, K; Nojiri, S.; Odintsov, S.D.; Diego, S.-G. Inflationary universe from perfect fluid and F(R) gravity and its comparison with observational data. Phys. Rev. D 2014, 90, 124061. [Google Scholar]
- Cognola, G.; Elizalde, E.; Nojiri, S.; Odintsov, S.D.; Zerbini, S. One-loop f(R) gravity in de Sitter universe. J. Cosmo. Astropart. Phys. 2005, 2005, 010. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified gravity with negative and positive powers of the curvature: Unification of the inflation and of the cosmic acceleration. Phys. Rev. D 2003, 68, 123512. [Google Scholar] [CrossRef]
- Carroll, S.M.; Duvvuri, V.; Trodden, M.; Turner, M.S. Is cosmic speed - up due to new gravitational physics? Phys. Rev. D 2004, 70, 043528. [Google Scholar] [CrossRef]
- Amendola, L.; Gannouji, R.; Polarski, D.; Tsujikawa, S. Conditions for the cosmological viability of f(R) dark energy models. Phys. Rev. D 2007, 75, 083504. [Google Scholar] [CrossRef]
- Linder, E.V. Exponential Gravity. Phys. Rev. D 2009, 80, 123528. [Google Scholar] [CrossRef]
- Bañados, M.; Ferreira, P.G. Eddington’s theory of gravity and its progeny. Phys. Rev. Lett. 2010, 105, 011101, Erratum-ibid. 2014, 113, 119901. [Google Scholar] [CrossRef]
- Pani, P.; Cardoso, V.; Delsate, T. Compact stars in Eddington inspired gravity. Phys. Rev. Lett. 2011, 107, 031101. [Google Scholar] [CrossRef] [PubMed]
- Barrow, J.D.; Ottewill, A.C. The Stability of General Relativistic Cosmological Theory. J. Phys. A 1983, 16, 2757. [Google Scholar] [CrossRef]
- Magnano, G.; Sokolowski, L.M. On physical equivalence between nonlinear gravity theories and a general relativistic selfgravitating scalar field. Phys. Rev. D 1994, 50, 5039–5059. [Google Scholar] [CrossRef]
- Müller, V.; Schmidt, H.J.; Starobinsky, A.A. The Stability of the De Sitter Space-time in Fourth Order Gravity. Phys. Lett. B 1988, 202, 198. [Google Scholar] [CrossRef]
- Liddle, A.R.; Lyth, D.H. Cosmological Inflation and Large-Scale Structure; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Ade, P.A.R.; Aghanim, N.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; et al. (Planck Collaboration, 2013). Planck 2013 results. XVI. Cosmological parameters. Astron. Astrophys. 2014, 571, A16. [Google Scholar]
- Stelle, K.S. Renormalization of Higher Derivative Quantum Gravity. Phys. Rev. D 1977, 16, 953. [Google Scholar] [CrossRef]
- Buchbinder, I.L.; Odintsov, S.D.; Shapiro, I.L. Effective Action in Quantum Gravity; IOP Publishing Ltd: Bristol, UK, 1992. [Google Scholar]
- Ade, P.A.R.; Aghanim, N.; Ahmed, Z.; Aikin, R.W.; Alexander, K.D.; Arnaud, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barkats, D.; et al. Joint Analysis of BICEP2/Keck Array and Planck Data. Phys. Rev. Lett. 2015, 114, 101301. [Google Scholar] [CrossRef] [PubMed]
- Linde, A.D. Inflationary Cosmology. Lect. Notes Phys. 2008, 738, 1–54. [Google Scholar]
© 2015 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kruglov, S.I. Arctan-Gravity Model. Universe 2015, 1, 82-91. https://doi.org/10.3390/universe1010082
Kruglov SI. Arctan-Gravity Model. Universe. 2015; 1(1):82-91. https://doi.org/10.3390/universe1010082
Chicago/Turabian StyleKruglov, Sergey I. 2015. "Arctan-Gravity Model" Universe 1, no. 1: 82-91. https://doi.org/10.3390/universe1010082
APA StyleKruglov, S. I. (2015). Arctan-Gravity Model. Universe, 1(1), 82-91. https://doi.org/10.3390/universe1010082





