A Computational Framework for High-Throughput Isotopic Natural Abundance Correction of Omics-Level Ultra-High Resolution FT-MS Datasets
Abstract
:1. Introduction
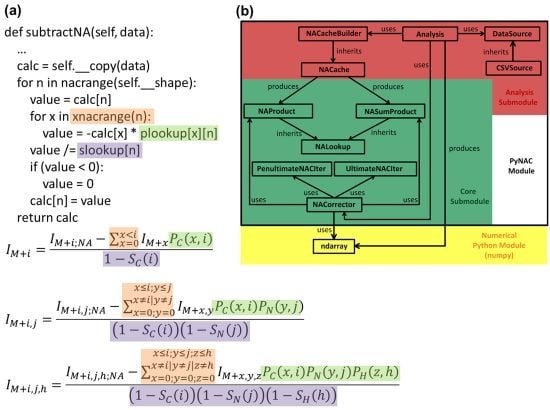
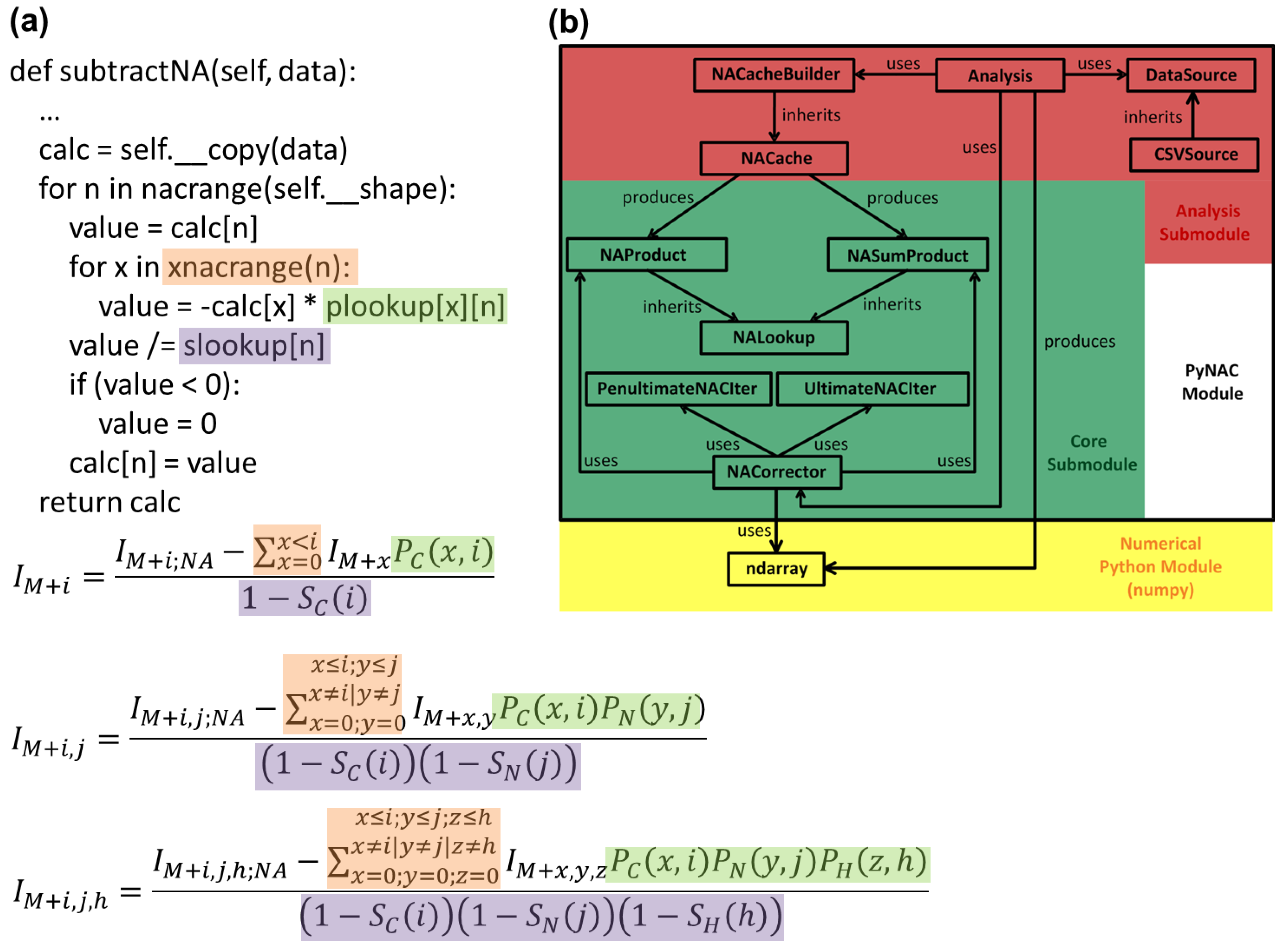
2. Methodology for Peak Correction



3. Software Design and Methods
3.1. Language and Library Choices
3.2. Data Flow
3.3. P and S Caching
3.4. Correction Algorithm, Constructors, and Modularity
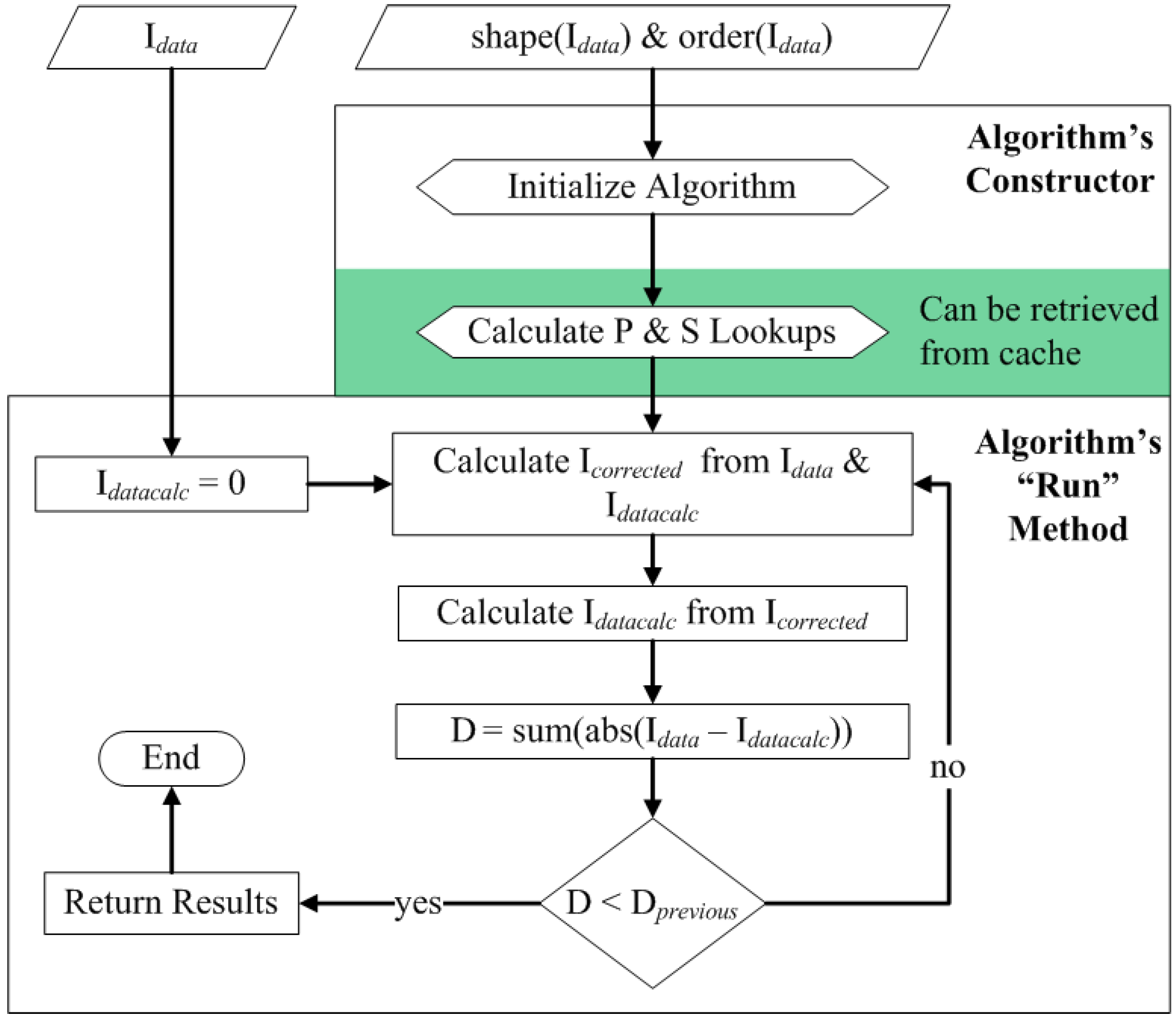
3.5. Quality Control
3.6. Implementations of Binomial Terms
3.7. Cell Culture and FT-ICR-MS
4. Results and Discussion
4.1. Validation of the Algorithm
| 13C Count a | Intensity b | Python (New) c | Perl (Old) d | Difference |
|---|---|---|---|---|
| 5 | 187.9 | 214.81 | 214.81 | 2.27 × 10−10 |
| 6 | 60.5 | 39.81 | 39.81 | 1.79 × 10−11 |
| 7 | 109.8 | 116.15 | 116.15 | 1.78 × 10−10 |
| 8 | 418.4 | 449.36 | 449.36 | 3.58 × 10−10 |
| 9 | 23.1 | 0 | 0 | 0 |
| 10 | 165 | 176.39 | 176.39 | 3.68 × 10−10 |
| 11 | 1438 | 1,523.77 | 1,523.77 | 2.63× 10−9 |
| 12 | 1,215.9 | 1,183.78 | 1,183.78 | 3.59 × 10−9 |
| 13 | 4,235.8 | 4,360.57 | 4,360.57 | 3.63 × 10−9 |
| 14 | 1,562.5 | 1,420.73 | 1,420.73 | 2.17 × 10−9 |
| 15 | 1,253.9 | 1,231.68 | 1,231.68 | 4.81 × 10−9 |
| 16 | 175.8 | 149.9 | 149.9 | 4.44 × 10−10 |
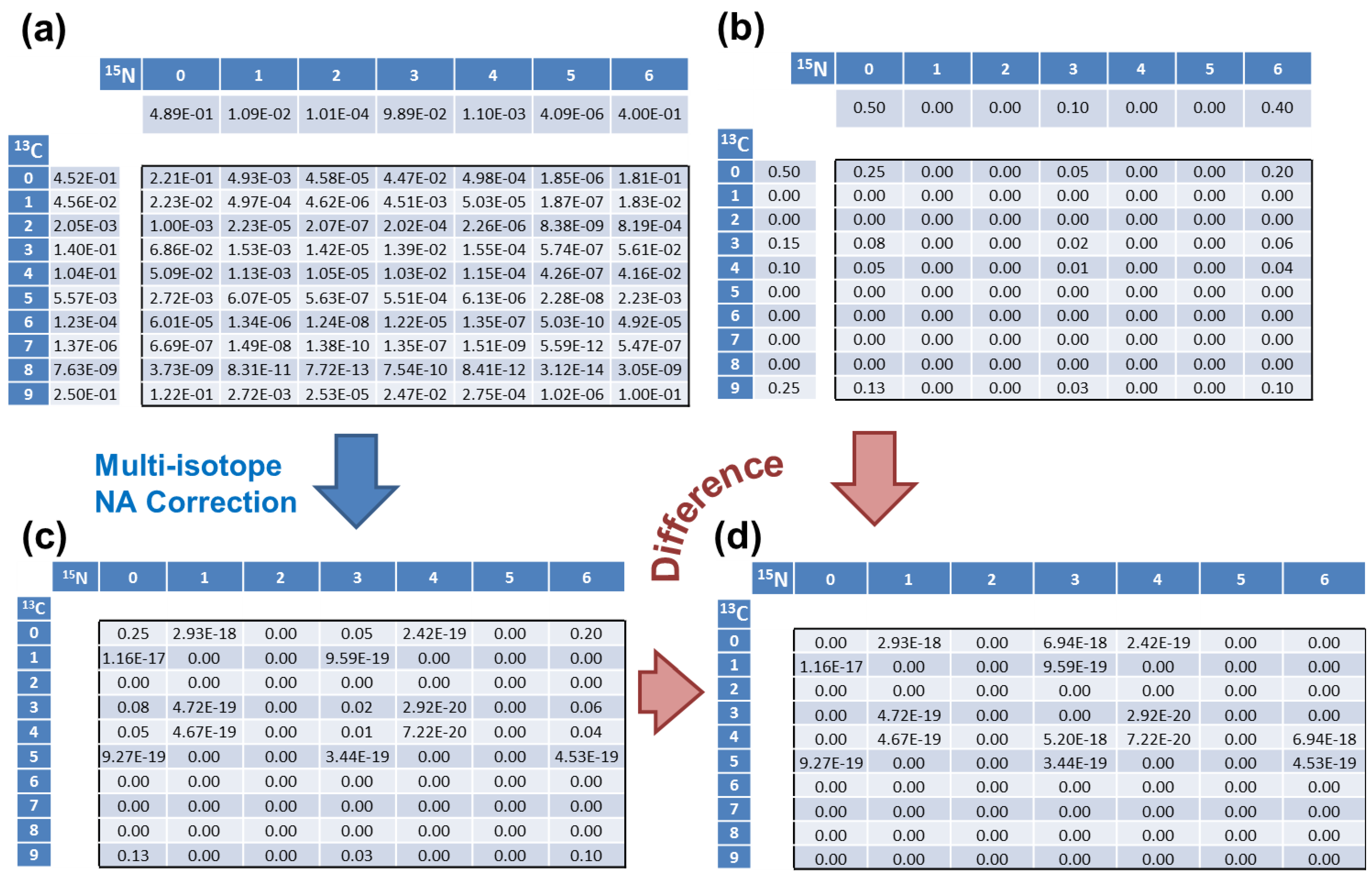
| 13C Count | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Simulated | 0.5 | 0 | 0 | 0.15 | 0.1 | 0 | 0 | 0 | 0 | 0.25 |
| addNA | 0.4523 | 0.0456 | 0.0020 | 0.1403 | 0.1040 | 0.0056 | 1.2 × 10−4 | 1.4 × 10−6 | 7.6 × 10−9 | 0.25 |
| 15N Count | 0 | 1 | 2 | 3 | 4 | 5 | 6 | - | - | - |
| Simulated | 0.5 | 0 | 0 | 0.1 | 0 | 0 | 0.4 | - | - | - |
| addNA | 0.4890 | 0.0109 | 0.0001 | 0.0989 | 0.0011 | 4 × 10−6 | 0.4 | - | - | - |
4.2. Numerical Analysis of Interleaving Method
| org | comb | comb2 | choose | logReal | |
|---|---|---|---|---|---|
| org | 0 | −2.36 × 10−16 | −5.67 × 10−14 | −2.36 × 10−16 | −2.36 × 10−15 |
| comb | - | - | −5.66 × 10−14 | 0 | −2.25 × 10−15 |
| comb2 | - | - | - | 5.66 × 10−14 | 5.48 × 10−14 |
| choose | - | - | - | - | −2.25 × 10−15 |
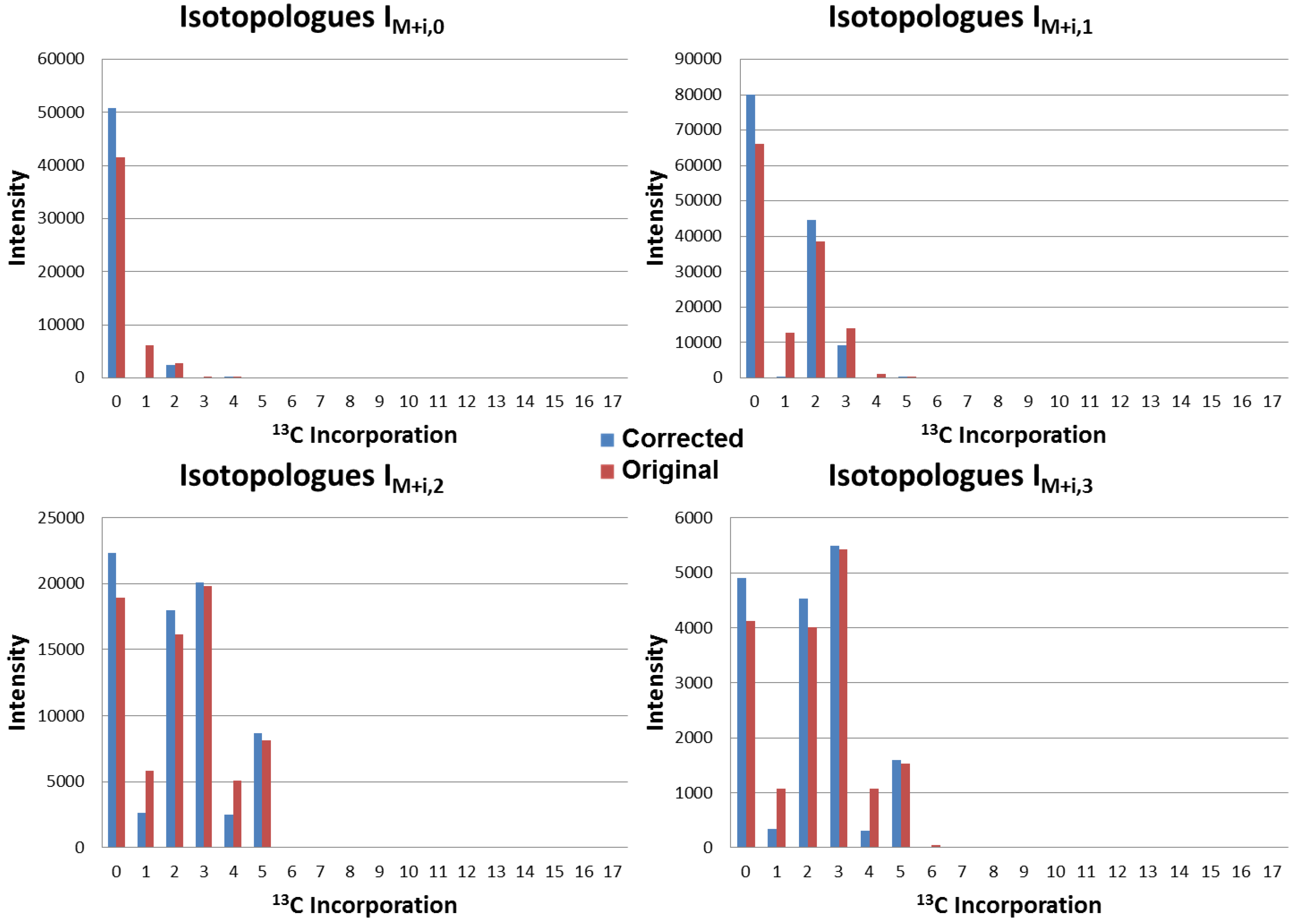
4.3. Application to Observed Isotopologues of UDP-GlcNAc
4.4. Running Time
5. Conclusions
Software Availability
Acknowledgments
Conflicts of Interest
References
- Rittenberg, D.; Schoenheimer, R. Deuterium as an indicator in the study of intermediary metabolism. J. Biol. Chem. 1937, 121, 235. [Google Scholar]
- Schoenheimer, R.; Rittenberg, D. The study of intermediary metabolism of animals with the aid of isotopes. Physiol. Rev. 1940, 20, 218. [Google Scholar]
- Schoenheimer, R.; Rittenberg, D. Deuterium as an indicator in the study of intermediary metabolism. J. Biol. Chem. 1935, 111, 163. [Google Scholar]
- Boros, L.G.; Brackett, D.J.; Harrigan, G.G. Metabolic biomarker and kinase drug target discovery in cancer using stable isotope-based dynamic metabolic profiling (SIDMAP). Curr. Cancer Drug Tar. 2003, 3, 445–453. [Google Scholar] [CrossRef]
- Fan, T.W.; Lane, A.N.; Higashi, R.M.; Farag, M.A.; Gao, H.; Bousamra, M.; Miller, D.M. Altered regulation of metabolic pathways in human lung cancer discerned by (13)C stable isotope-resolved metabolomics (SIRM). Mol. Cancer 2009, 8, 41. [Google Scholar] [CrossRef]
- Lane, A.N.; Fan, T.W.M.; Xie, Z.; Moseley, H.N.B.; Higashi, R.M. Isotopomer analysis of lipid biosynthesis by high resolution mass spectrometry and NMR. Anal. Chim. Acta 2009, 651, 201–208. [Google Scholar] [CrossRef]
- Moseley, H.N. Correcting for the effects of natural abundance in stable isotope resolved metabolomics experiments involving ultra-high resolution mass spectrometry. BMC Bioinformatics 2010, 11, 139. [Google Scholar] [CrossRef]
- Pingitore, F.; Tang, Y.J.; Kruppa, G.H.; Keasling, J.D. Analysis of amino acid isotopomers using FT-ICR MS. Anal. Chem. 2007, 79, 2483–2490. [Google Scholar] [CrossRef]
- Moseley, H.N.; Lane, A.N.; Belshoff, A.C.; Higashi, R.M.; Fan, T.W. A novel deconvolution method for modeling UDP-N-acetyl-D-glucosamine biosynthetic pathways based on (13)C mass isotopologue profiles under non-steady-state conditions. BMC Biol. 2011, 9, 37. [Google Scholar] [CrossRef]
- Dauner, M.; Sauer, U. GC-MS Analysis of amino acids rapidly provides rich information for isotopomer balancing. Biotechnol. Progr. 2000, 16, 642–649. [Google Scholar] [CrossRef]
- Fischer, E.; Sauer, U. Metabolic flux profiling of Escherichia coli mutants in central carbon metabolism using GC-MS. Eur. J. Biochem. 2003, 270, 880–891. [Google Scholar] [CrossRef]
- Hellerstein, M.K.; Neese, R.A. Mass isotopomer distribution analysis at eight years: Theoretical, analytic, and experimental considerations. Am. J. Physiol.—Endoc. M. 1999, 276, E1146–E1170. [Google Scholar]
- Lee, W.N.P.; Byerley, L.O.; Bergner, E.A.; Edmond, J. Mass isotopomer analysis: Theoretical and practical considerations. Biol. Mass Spectrom. 1991, 20, 451–458. [Google Scholar] [CrossRef]
- Snider, R. Efficient calculation of exact mass isotopic distributions. JASMS 2007, 18, 1511–1515. [Google Scholar]
- Van Winden, W.; Wittmann, C.; Heinzle, E.; Heijnen, J. Correcting mass isotopomer distributions for naturally occurring isotopes. Biotechnol. Bioeng. 2002, 80, 477–479. [Google Scholar] [CrossRef]
- Wahl, S.A.; Dauner, M.; Wiechert, W. New tools for mass isotopomer data evaluation in 13C flux analysis: Mass isotope correction, data consistency checking, and precursor relationships. Biotechnol. Bioeng. 2004, 85, 259–268. [Google Scholar] [CrossRef]
- Zhang, X.; Hines, W.; Adamec, J.; Asara, J.; Naylor, S.; Regnier, F. An automated method for the analysis of stable isotope labeling data in proteomics. JASMS 2005, 16, 1181–1191. [Google Scholar]
- Fernandez, C.A.; Des Rosiers, C.; Previs, S.F.; David, F.; Brunengraber, H. Correction of 13C mass isotopomer distributions for natural stable isotope abundance. J. Mass Spectrom. 1996, 31, 255–262. [Google Scholar] [CrossRef]
- Rockwood, A.L.; Haimi, P. Efficient calculation of accurate masses of isotopic peaks. JASMS 2006, 17, 415–419. [Google Scholar]
- Rockwood, A.L.; van Orden, S.L. Ultrahigh-speed calculation of isotope distributions. Anal. Chem. 1996, 68, 2027–2030. [Google Scholar] [CrossRef]
- Yergey, J.A. A general approach to calculating isotopic distributions for mass spectrometry. Int. J. Mass Spectrom. Ion Phys. 1983, 52, 337–349. [Google Scholar] [CrossRef]
- Rossum, G.V. The Python Programming Language. Available online: http://www.python.org/ (accessed on 21 July 2013).
- Sanner, M.F. Python: A programming language for software integration and development. J. Mol. Graph. Model. 1999, 17, 57–61. [Google Scholar]
- Oliphant, T.E. A Guide to NumPy; Trelgol Publishing: Spanish Fork, UT, USA, 2006; Volume 1, pp. 1–371. [Google Scholar]
- Gamma, E. Design Patterns: Elements of Reusable Object-Oriented Software; Addison-Wesley Professional: Boston, MA, USA, 1995; pp. 1–416. [Google Scholar]
- Moseley, H.N.B. Error analysis and propagation in metabolomics data analysis. Comp. Struct Biotech. J. 2013, 4, e201301006. [Google Scholar]
- Moseley Bioinformatics Laboratory Software Repository for download. Available online: http://bioinformatics.cesb.uky.edu/bin/view/Main/SoftwareDevelopment/ (accessed on 21 July 2013).
Supplementary Files
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Carreer, W.J.; Flight, R.M.; Moseley, H.N.B. A Computational Framework for High-Throughput Isotopic Natural Abundance Correction of Omics-Level Ultra-High Resolution FT-MS Datasets. Metabolites 2013, 3, 853-866. https://doi.org/10.3390/metabo3040853
Carreer WJ, Flight RM, Moseley HNB. A Computational Framework for High-Throughput Isotopic Natural Abundance Correction of Omics-Level Ultra-High Resolution FT-MS Datasets. Metabolites. 2013; 3(4):853-866. https://doi.org/10.3390/metabo3040853
Chicago/Turabian StyleCarreer, William J., Robert M. Flight, and Hunter N. B. Moseley. 2013. "A Computational Framework for High-Throughput Isotopic Natural Abundance Correction of Omics-Level Ultra-High Resolution FT-MS Datasets" Metabolites 3, no. 4: 853-866. https://doi.org/10.3390/metabo3040853
APA StyleCarreer, W. J., Flight, R. M., & Moseley, H. N. B. (2013). A Computational Framework for High-Throughput Isotopic Natural Abundance Correction of Omics-Level Ultra-High Resolution FT-MS Datasets. Metabolites, 3(4), 853-866. https://doi.org/10.3390/metabo3040853