Theoretical Analysis of the Built-in Metabolic Pathway Effect on the Metabolism of Erythrocyte-Bioreactors That Neutralize Ammonium
Abstract
1. Introduction
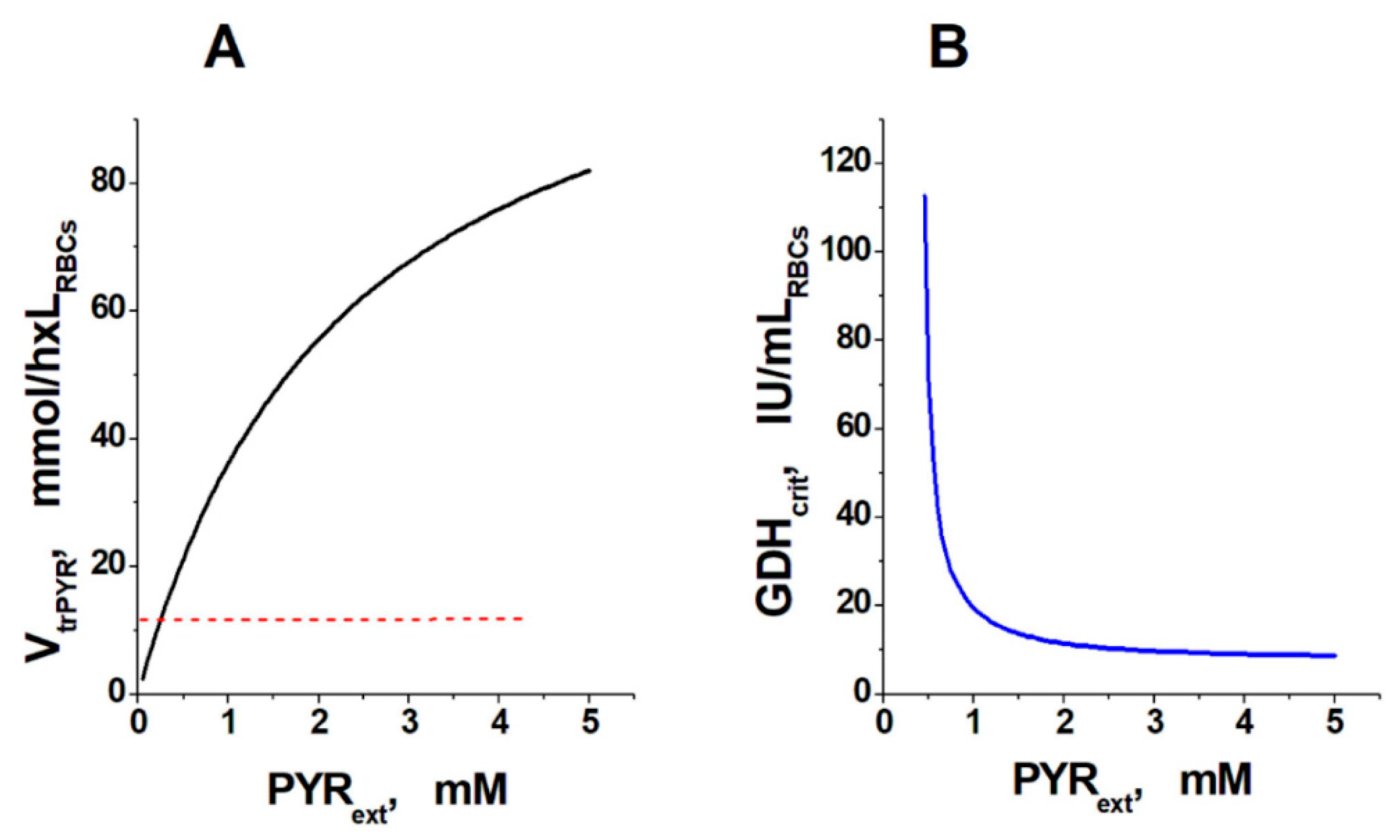
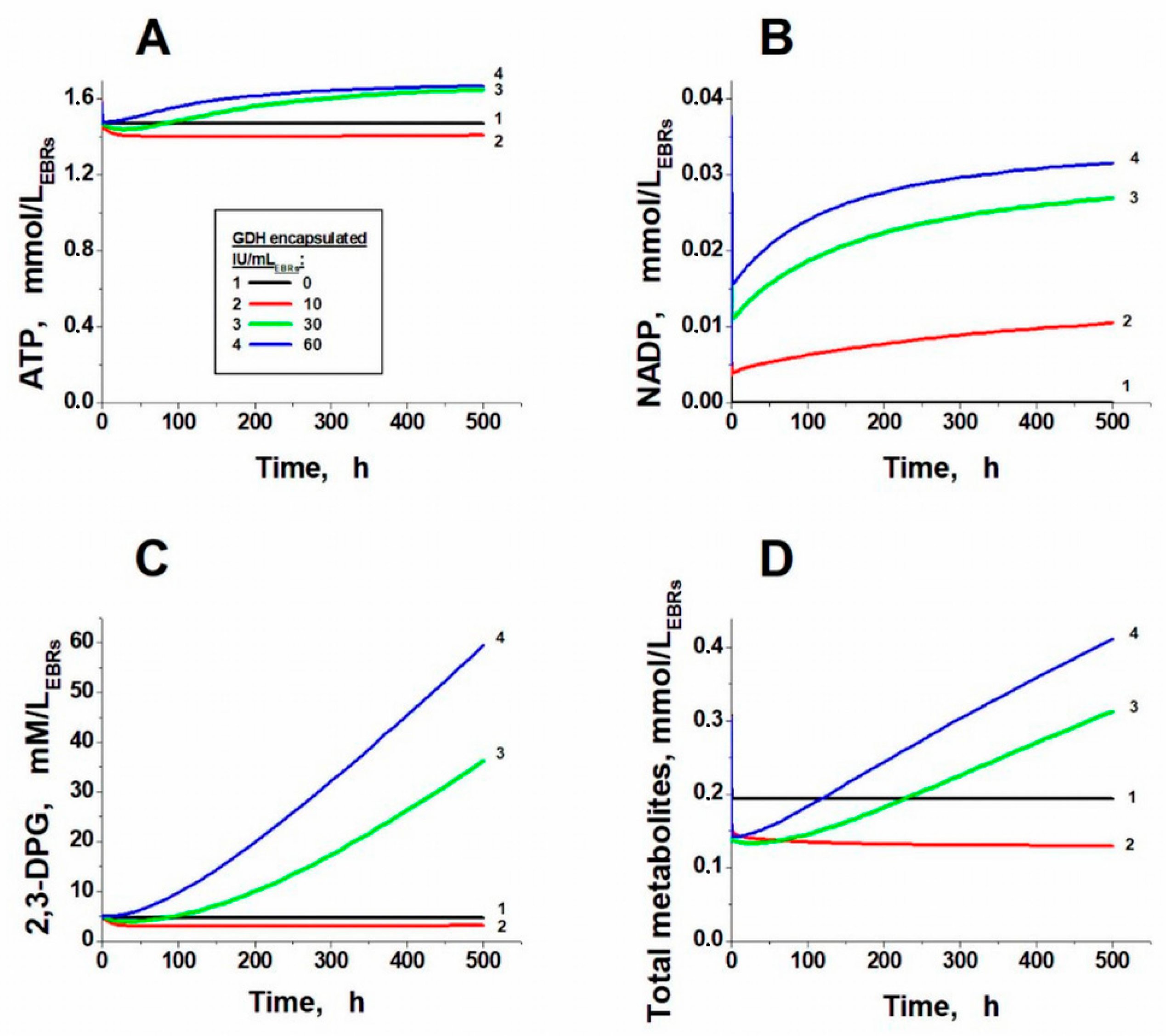
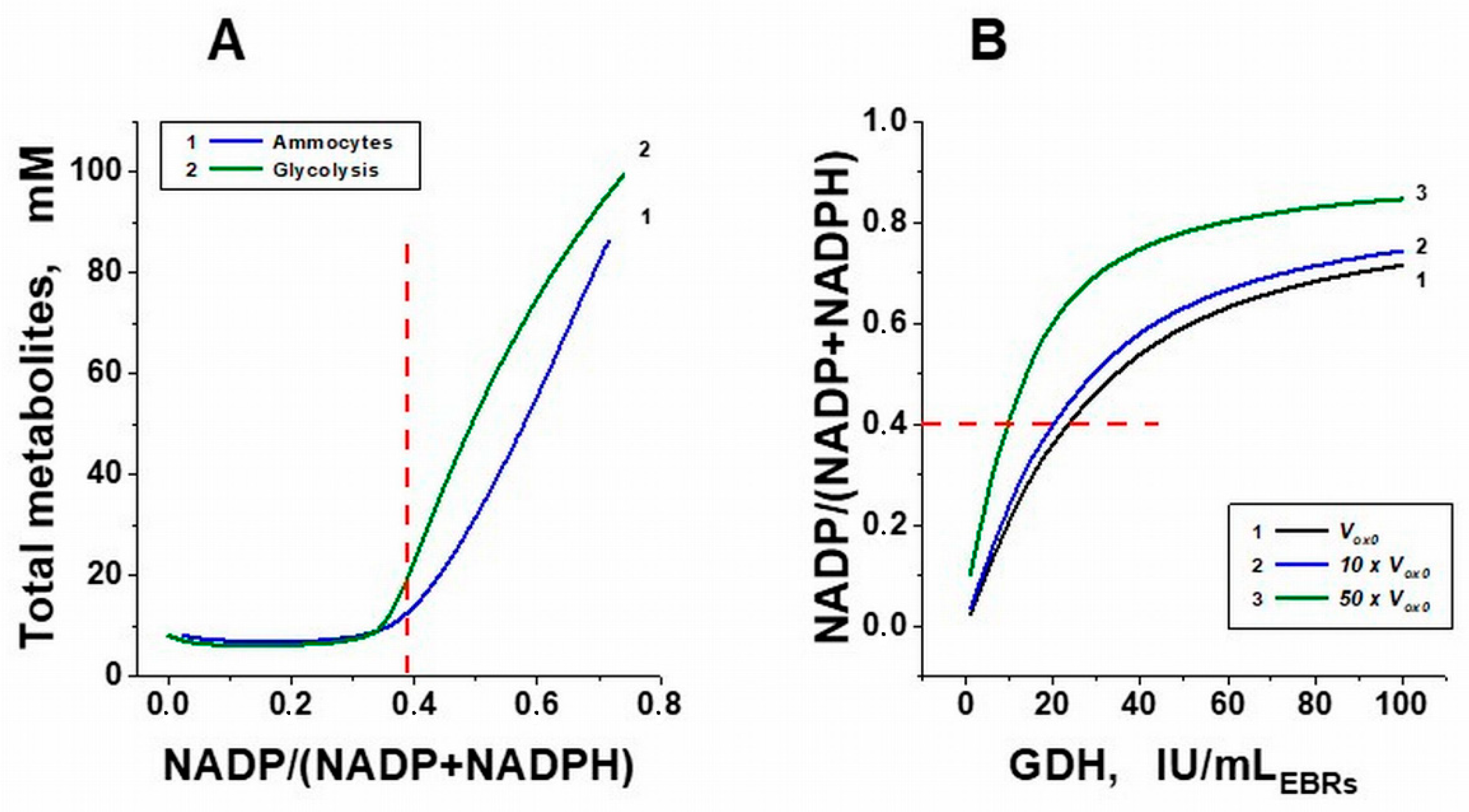
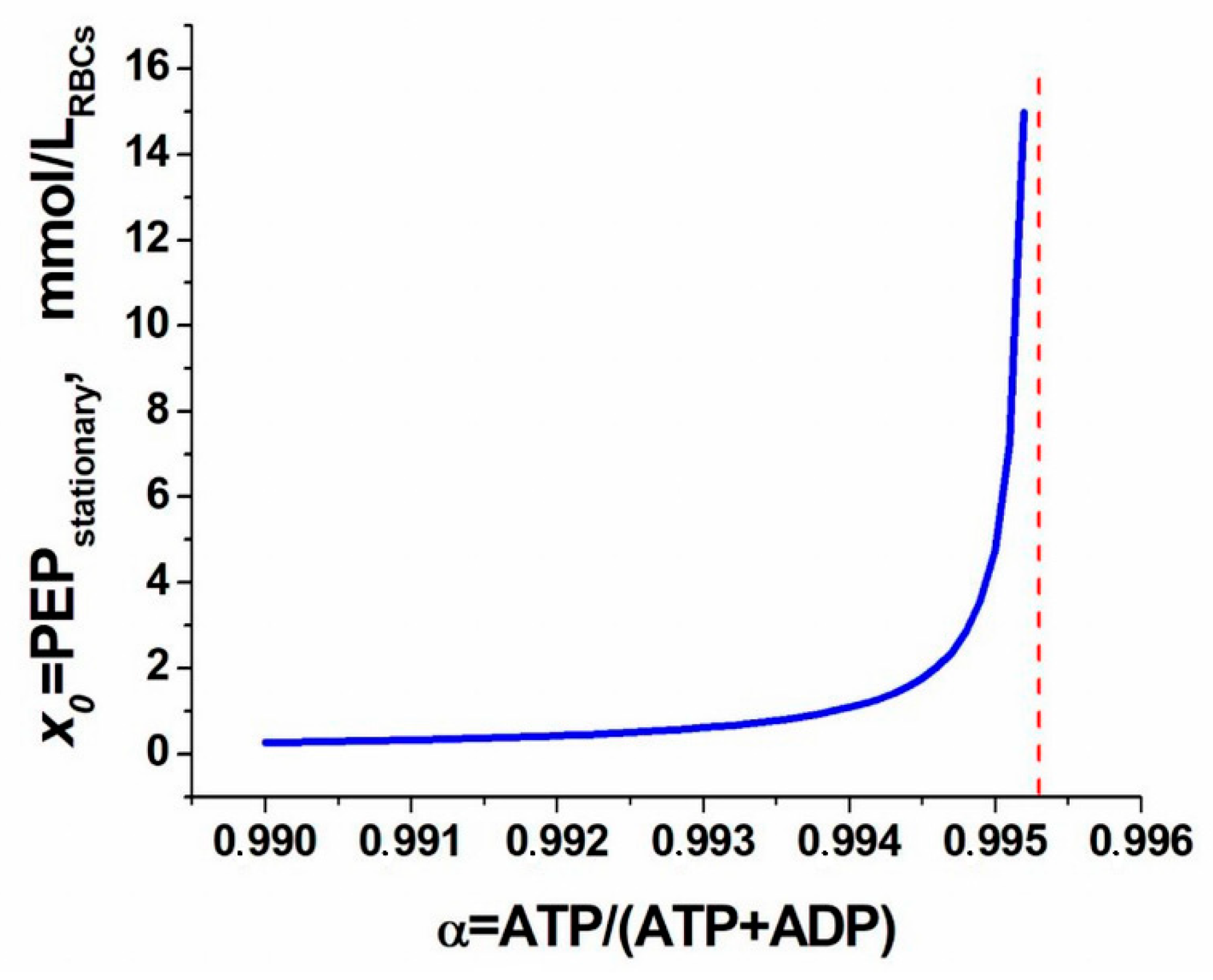
2. Results and Discussion
3. Methods
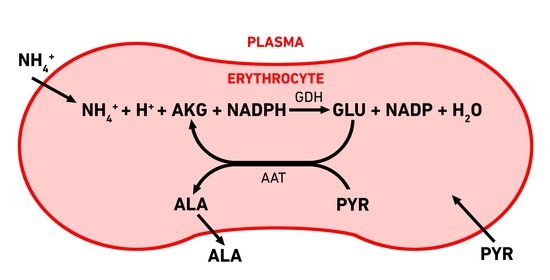
3.1. Erythrocyte-Bioreactors for Ammonium Removing
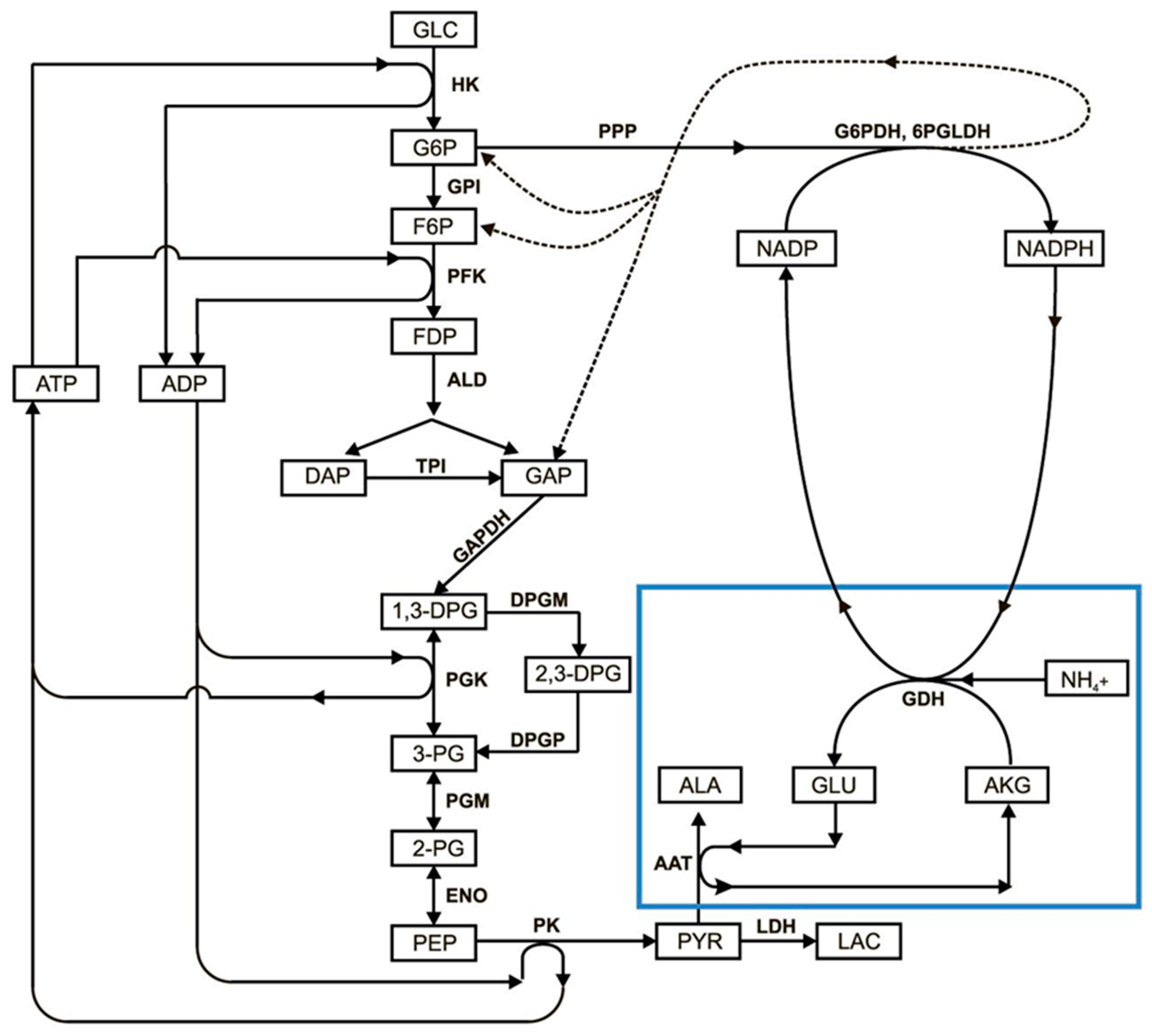
3.2. Mathematical Model of EBR Neutralizing Ammonium
- The rate of the hexokinase reaction was considered independent of the glucose concentration;
- The erythrocyte membrane was considered impermeable to all the substances under consideration, except for lactate, pyruvate, α-ketoglutarate, alanine, and ammonium ions;
- The rate of transport of all metabolites penetrating the membrane, except for lactate and pyruvate, was considered proportional to the gradient of their concentrations on both sides of the membrane:where KA is the permeability coefficient for metabolite A, and [A]int and [A]ext are the concentration of A in the cell and in the plasma, respectively.VtrA = KA × ([A]int − [A]ext),
- 4.
- The transport of ammonium was considered fast enough that its concentrations in plasma and cells remained in equilibrium at any time;
- 5.
- Pools of adenylates, erythrocyte volume, and rate of NADPH oxidation in oxidative metabolism were considered constant;
- 6.
- The pentose phosphate pathway is represented by a single G6PDH reaction, since it is the rate-limiting reaction in the PPP.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Deegan, P.B.; Cox, T.M. Imiglucerase in the treatment of Gaucher disease: A history and perspective. Drug Des. Dev. Ther. 2012, 6, 81–106. [Google Scholar] [CrossRef][Green Version]
- Rytting, M.E. Role of L-asparaginase in acute lymphoblastic leukemia: Focus on adult patients. Blood Lymphat. Cancer Targets Ther. 2012, 2, 117–124. [Google Scholar] [CrossRef][Green Version]
- Hout, H.; Reuser, A.J.; Vulto, A.G.; Loonen, M.C.; Cromme, D.A.; Ploeg, A.T. Recombinant human α-glucosidase from rabbit milk in Pompe patients. Lancet 2000, 356, 397–398. [Google Scholar] [CrossRef]
- Koleva, L.D.; Bovt, E.A.; Ataullakhanov, F.I.; Sinauridze, E.I. Erythrocytes as carriers: From drug delivery to biosensors. Pharmaceutics 2020, 12, 276. [Google Scholar] [CrossRef]
- Bax, B.E. Erythrocytes as carriers of therapeutic enzymes. Pharmaceutics 2020, 12, 435. [Google Scholar] [CrossRef]
- Alexandrovich, Y.G.; Kosenko, E.A.; Sinauridze, E.I.; Obydennyi, S.I.; Kireev, I.I.; Ataullakhanov, F.I.; Kaminsky, Y.G. Rapid elimination of blood alcohol using erythrocytes: Mathematical modeling and in vitro study. Biomed. Res. Int. 2017, 2017. [Google Scholar] [CrossRef]
- Lizano, C.; Sanz, S.; Luque, J.; Pinilla, M. In vitro study of alcohol dehydrogenase and acetaldehyde dehydrogenase encapsulated into human erythrocytes by an electroporation procedure. Biochim. Biophys. Acta Gen. Subj. 1998, 1425, 328–336. [Google Scholar] [CrossRef]
- Magnani, M.; Fazi, A.; Mangani, F.; Rossi, L.; Mancini, U. Methanol detoxification by enzyme-loaded erythrocytes. Biotechnol. Appl. Biochem. 1993, 18, 217–226. [Google Scholar] [CrossRef]
- Muthuvel, A.; Rajamani, R.; Manikandan, S.; Sheeladevi, R. Detoxification of formate by formate dehydrogenase-loaded erythrocytes and carbicarb in folate-deficient methanol-intoxicated rats. Clin. Chim. Acta 2006, 367, 162–169. [Google Scholar] [CrossRef]
- Sanz, S.; Lizano, C.; Luque, J.; Pinilla, M. In vitro and in vivo study of glutamate dehydrogenase encapsulated into mouse erythrocytes by a hypotonic dialysis procedure. Life Sci. 1999, 65, 2781–2789. [Google Scholar] [CrossRef]
- Kosenko, E.A.; Venediktova, N.I.; Kudryavtsev, A.A.; Ataullakhanov, F.I.; Kaminsky, Y.G.; Felipo, V.; Montoliu, C. Encapsulation of glutamine synthetase in mouse erythrocytes: A new procedure for ammonia detoxification. Biochem. Cell Biol. 2008, 86, 469–476. [Google Scholar] [CrossRef] [PubMed]
- Protasov, E.S.; Borsakova, D.V.; Alexandrovich, Y.G.; Korotkov, A.V.; Kosenko, E.A.; Butylin, A.A.; Ataullakhanov, F.I.; Sinauridze, E.I. Erythrocytes as bioreactors to decrease excess ammonium concentration in blood. Sci. Rep. 2019, 9, 1455. [Google Scholar] [CrossRef] [PubMed]
- Baruchel, A.; Bertrand, Y.; Thomas, X.; Blin, N.; Tavernier, E.; Ducassou, S.; Vey, N.; Gandemer, V.; Cacheux, V.; Mazingue, F.; et al. Updated clinical activity of GRASPA versus native l-asparaginase in combination with cooprall regimen in phase 3 randomized trial in patients with relapsed acute lymphoblastic leukemia. (NCT01518517). Blood 2015, 126, 3723. [Google Scholar] [CrossRef]
- Kravtzoff, R.; Desbois, I.; Lamagnere, J.P.; Muh, J.P.; Valat, C.; Chassaigne, M.; Colombat, P.; Ropars, C. Improved pharmacodynamics of L-asparaginase-loaded in human red blood cells. Eur. J. Clin. Pharmacol. 1996, 49, 465–470. [Google Scholar] [CrossRef] [PubMed]
- Sinauridze, E.I.; Vitvitsky, V.M.; Pichugin, A.V.; Zhabotinsky, A.M.; Ataullakhanov, F.I. A new chemotherapeutic agent: L-asparaginase entrapped in red blood cells. Adv. Exp. Med. Biol. 1992, 326, 203–206. [Google Scholar] [CrossRef]
- Loach, J.R.; Ihler, G.M. A dialysis procedure for loading erythrocytes with enzymes and lipids. Biochim. Biophys. Acta Gen. Subj. 1977, 496, 136–145. [Google Scholar] [CrossRef]
- Adriaenssens, K.; Karcher, D.; Lowenthal, A.; Terheggen, H.G. Use of enzyme-loaded erythrocytes in in-vitro correction of arginase-deficient erythrocytes in familial hyperargininemia. Clin. Chem. 1976, 22, 323–326. [Google Scholar] [CrossRef]
- Bax, B.E.; Levene, M.; Bain, M.D.; Fairbanks, L.D.; Filosto, M.; Kalkan Uçar, S.; Klopstock, T.; Kornblum, C.; Mandel, H.; Rahman, S.; et al. Erythrocyte encapsulated thymidine phosphorylase for the treatment of patients with Mitochondrial Neurogastrointestinal Encephalomyopathy: Study protocol for a multi-centre, multiple dose, open label trial. J. Clin. Med. 2019, 8, 1096. [Google Scholar] [CrossRef]
- Auron, A.; Brophy, P.D. Hyperammonemia in review: Pathophysiology, diagnosis, and treatment. Pediatr. Nephrol. 2012, 27, 207–222. [Google Scholar] [CrossRef]
- Venediktova, N.I.; Kosenko, E.A.; Kaminsky, Y.G. Studies on ammocytes: Development, metabolic characteristics, and detoxication of ammonium. Bull. Exp. Biol. Med. 2008, 146, 730–732. [Google Scholar] [CrossRef]
- Sanz, S.; Lizano, C.; Garín, M.I.; Luque, J.; Pinilla, M. Biochemical properties of alcohol dehydrogenase and glutamate dehydrogenase encapsulated into human erythrocytes by a hypotonic-dialysis procedure. In Erythrocytes as Drug Carriers in Medicine; Sprandel, U., Way, J.L., Eds.; Springer Science + Business Media: Berlin, Germany, 1997; pp. 101–108. ISBN 978-1-4899-0046-3. [Google Scholar]
- Sanz, S.; Pinilla, M.; Garin, M.; Tipton, K.F.; Luque, J. The influence of enzyme concentration on the encapsulation of glutamate dehydrogenase and alcohol dehydrogenase in red blood cells. Biotechnol. Appl. Biochem. 1995, 22, 223–231. [Google Scholar] [PubMed]
- Martinov, M.V.; Plotnikov, A.G.; Vitvitsky, V.M.; Ataullakhanov, F.I. Deficiencies of glycolytic enzymes as a possible cause of hemolytic anemia. Biochim. Biophys. Acta Gen. Subj. 2000, 1474, 75–87. [Google Scholar] [CrossRef]
- Ataullakhanov, F.I.; Buravtsev, V.N.; Zhabotinskii, A.M.; Norina, S.B.; Pichugin, A.V.; Erlikh, L.I. Interaction of Embden-Meyerhof pathway and hexose monophosphate shunt in erythrocytes. Biokhimia 1981, 46, 723–731. [Google Scholar]
- Sass, M.D. Utilization of alpha-ketoglutarate by red blood cells for glutathione synthesis. Nature 1963, 200, 1209–1210. [Google Scholar] [CrossRef] [PubMed]
- Young, J.D.; Jones, S.E.M.; Ellory, J.C. Amino acid transport in human and in sheep erythrocytes. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1980, 209, 355–375. [Google Scholar] [CrossRef]
- Halestrap, A.P. Transport of pyruvate and lactate into human erythrocytes. Evidence for the involvement of the chloride carrier and a chloride-independent carrier. Biochem. J. 1976, 156, 193–207. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Protasov, E.; Koleva, L.; Bovt, E.; Ataullakhanov, F.I.; Sinauridze, E. Theoretical Analysis of the Built-in Metabolic Pathway Effect on the Metabolism of Erythrocyte-Bioreactors That Neutralize Ammonium. Metabolites 2021, 11, 36. https://doi.org/10.3390/metabo11010036
Protasov E, Koleva L, Bovt E, Ataullakhanov FI, Sinauridze E. Theoretical Analysis of the Built-in Metabolic Pathway Effect on the Metabolism of Erythrocyte-Bioreactors That Neutralize Ammonium. Metabolites. 2021; 11(1):36. https://doi.org/10.3390/metabo11010036
Chicago/Turabian StyleProtasov, Evgeniy, Larisa Koleva, Elizaveta Bovt, Fazoil I. Ataullakhanov, and Elena Sinauridze. 2021. "Theoretical Analysis of the Built-in Metabolic Pathway Effect on the Metabolism of Erythrocyte-Bioreactors That Neutralize Ammonium" Metabolites 11, no. 1: 36. https://doi.org/10.3390/metabo11010036
APA StyleProtasov, E., Koleva, L., Bovt, E., Ataullakhanov, F. I., & Sinauridze, E. (2021). Theoretical Analysis of the Built-in Metabolic Pathway Effect on the Metabolism of Erythrocyte-Bioreactors That Neutralize Ammonium. Metabolites, 11(1), 36. https://doi.org/10.3390/metabo11010036