Operational Decision Model with Carbon Cap Allocation and Carbon Trading Price
Abstract
:1. Introduction
2. Literature Review
2.1. Production and Operational Model
2.2. Carbon Cap and Trade
3. Model
- In the second stage, each entity makes its own production decision considering the carbon cap allocated for each entity from the first stage. Moreover, the carbon price for purchasing and selling carbon permit are determined interdependently by the carbon supply and demand mechanism through the carbon market.
- In the first stage, each entity’s carbon cap is allocated at the cost per unit carbon cap.
3.1. The Second Stage
3.2. The First Stage
- Each entity would purchase/sell the carbon permit with the carbon cap and trade comparing the operational decision without the carbon cap and trade.
- Each entity would emit more/less carbon than without the carbon cap and trade.
- Each entity’s cap can be higher/lower with the carbon cap and trade than its carbon emission without the carbon cap and trade.
4. Analytical Results
- 1.
- The total amount of carbon emission with the carbon cap and trade market is less than without carbon cap and trade market, if
- 2.
- Otherwise, the total amount of carbon emission with the carbon cap and trade market is larger than without carbon cap and trade market.
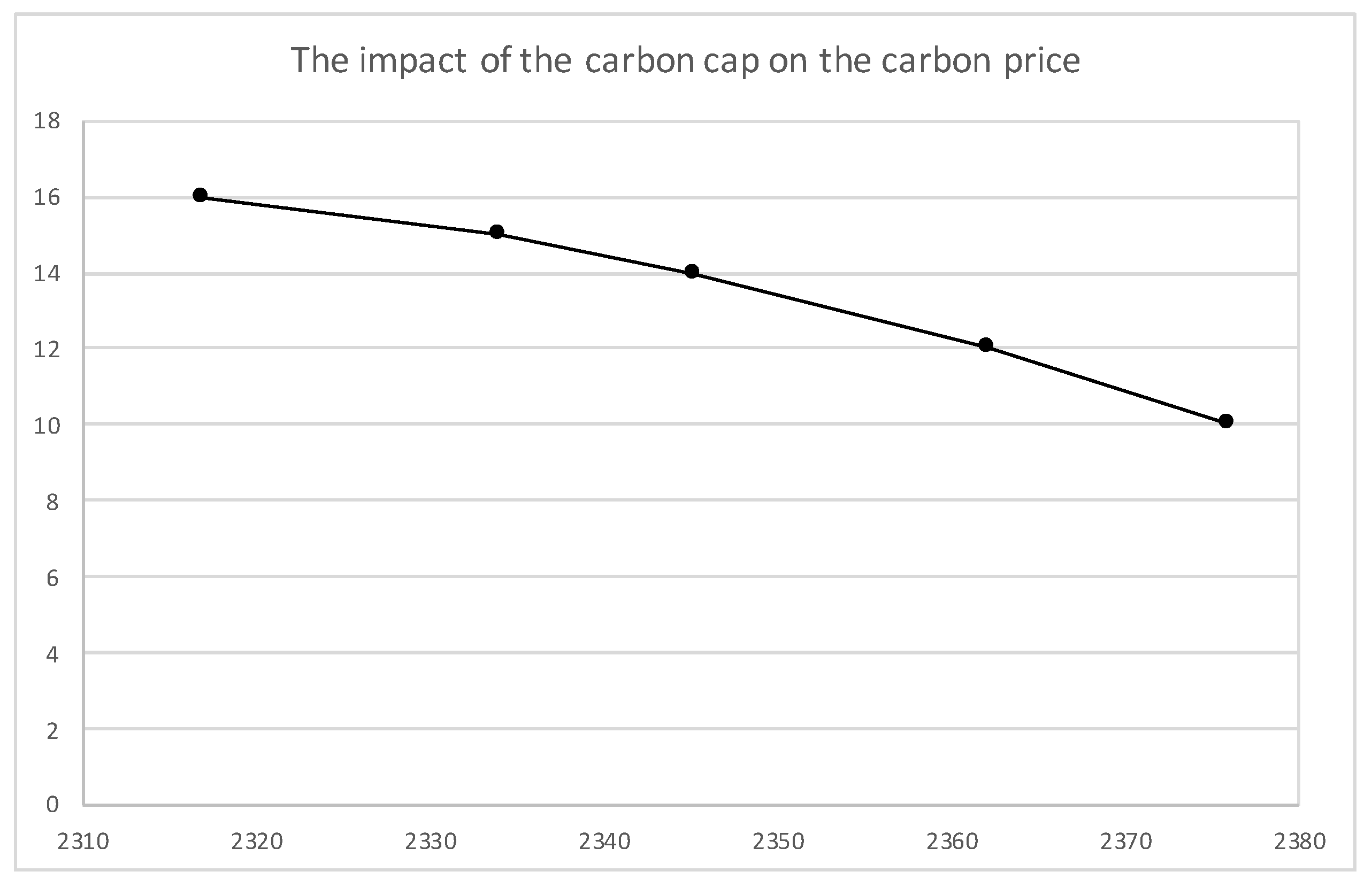
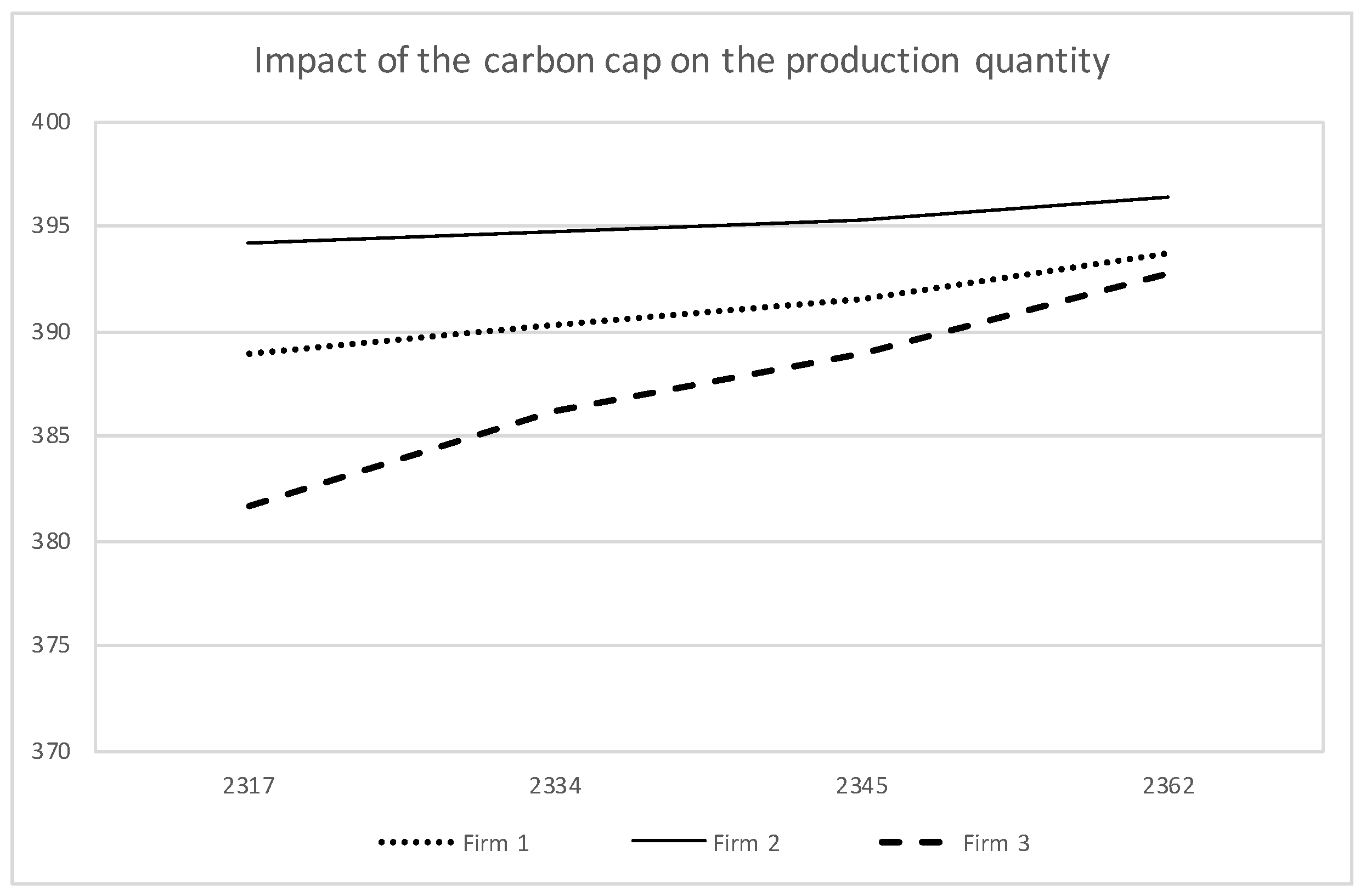
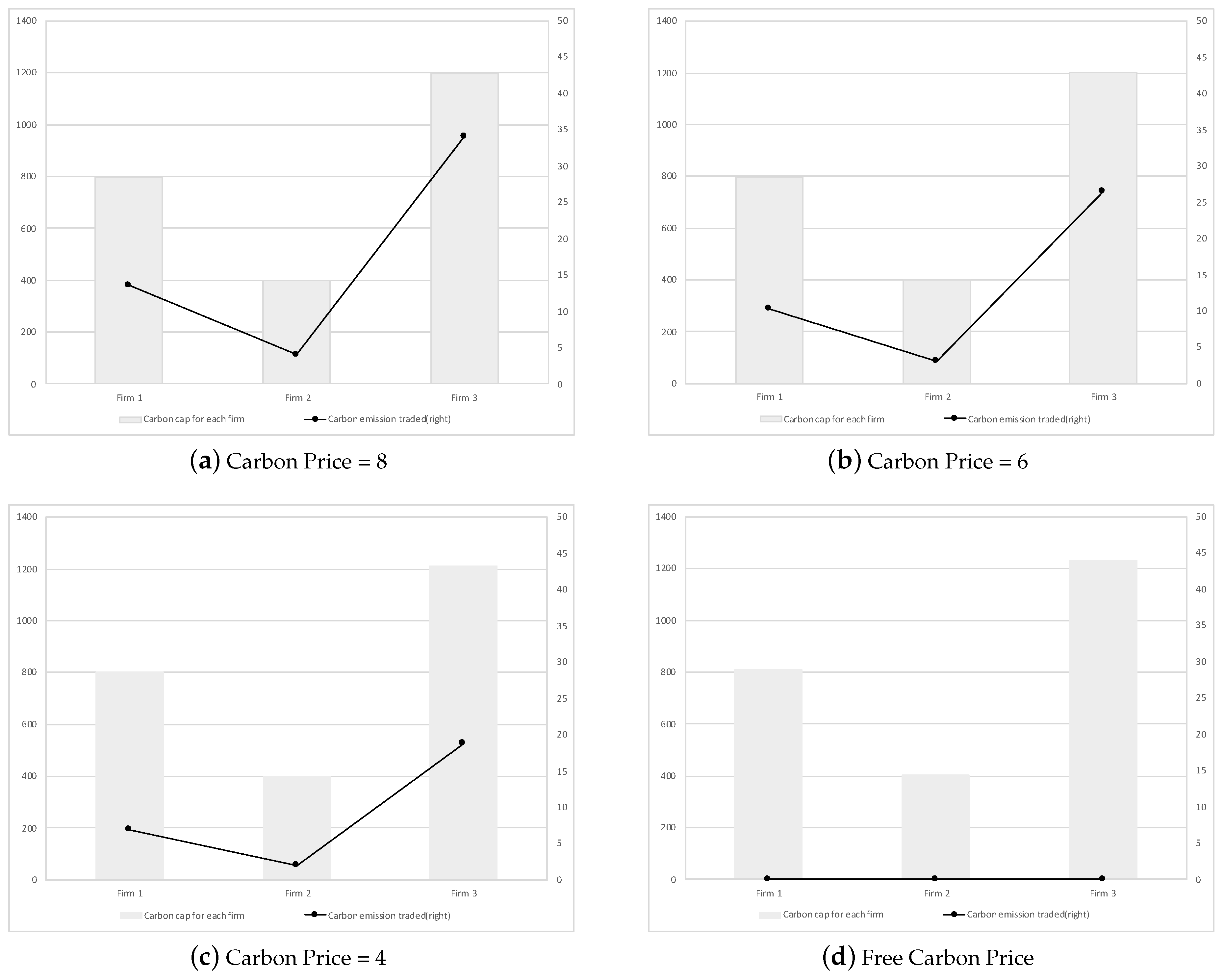
5. Numerical Example
6. Conclusions
- In the first stage, each entity’s carbon cap is allocated by considering its profit objective together with its production decisions and the interdependently determined carbon price.
- In the second stage, each entity makes its own production decision with the carbon cap decided in the first stage and the carbon trading price are determined interdependently by the carbon supply and demand mechanism through the carbon market.
Funding
Acknowledgments
Conflicts of Interest
References
- Tsao, Y.C.; Lee, P.L.; Chen, C.H.; Liao, Z.W. Sustainable newsvendor models under trade credit. J. Clean. Prod. 2017, 141, 1478–1491. [Google Scholar] [CrossRef]
- Gottlieb, J.W. International emissions trading. Strateg. Plan. Energy Environ. 2001, 20, 15–25. [Google Scholar] [CrossRef]
- Walker, H.; Seuring, S.; Sarkis, J.; Klassen, R. Sustainable operations management: Recent trends and future directions. Int. J. Oper. Prod. Manag. 2014, 34. [Google Scholar] [CrossRef]
- Letmathe, P.; Balakrishnan, N. Environmental considerations on the optimal product mix. Eur. J. Oper. Res. 2005, 167, 398–412. [Google Scholar] [CrossRef]
- Hua, G.; Cheng, T.; Wang, S. Managing carbon footprints in inventory management. Int. J. Prod. Econ. 2011, 132, 178–185. [Google Scholar] [CrossRef]
- Chen, X.; Benjaafar, S.; Elomri, A. The carbon-constrained EOQ. Oper. Res. Lett. 2013, 41, 172–179. [Google Scholar] [CrossRef]
- Caro, F.; Corbett, C.J.; Tan, T.; Zuidwijk, R. Double counting in supply chain carbon footprinting. Manuf. Serv. Oper. Manag. 2013, 15, 545–558. [Google Scholar] [CrossRef]
- Cachon, G.P. Retail store density and the cost of greenhouse gas emissions. Manag. Sci. 2014, 60, 1907–1925. [Google Scholar] [CrossRef]
- Granot, D.; Granot, F.; Sosic, G. Allocation of Greenhouse Gas Emissions in Supply Chains. Available online: https://pdfs.semanticscholar.org/2c1c/90268ae4288f3b7cdf1d614c16744a1da1d6.pdf (accessed on 20 February 2019).
- Du, S.; Ma, F.; Fu, Z.; Zhu, L.; Zhang, J. Game-theoretic analysis for an emission-dependent supply chain in a ‘cap-and-trade’system. Ann. Oper. Res. 2015, 228, 135–149. [Google Scholar] [CrossRef]
- Hovelaque, V.; Bironneau, L. The carbon-constrained EOQ model with carbon emission dependent demand. Int. J. Prod. Econ. 2015, 164, 285–291. [Google Scholar] [CrossRef]
- Kim, S.; Lee, J.; Park, M. Mathematical Modeling for Risk Averse Firm Facing Loss Averse Customer’s Stochastic Uncertaintya. Math. Probl. Eng. 2017, 2017, 6810415. [Google Scholar] [CrossRef]
- Lee, J.; Lee, M.L.; Park, M. A Newsboy Model with Quick Response under Sustainable Carbon Cap-N-Trade. Sustainability 2018, 10, 1410. [Google Scholar] [CrossRef]
- Song, J.; Leng, M. Analysis of the single-period problem under carbon emissions policies. In Handbook of Newsvendor Problems; Springer Publishing: New York, NY, USA, 2012; pp. 297–313. [Google Scholar]
- Rosič, H.; Jammernegg, W. The economic and environmental performance of dual sourcing: A newsvendor approach. Int. J. Prod. Econ. 2013, 143, 109–119. [Google Scholar] [CrossRef]
- Chen, X.; Wang, X.; Kumar, V.; Kumar, N. Low carbon warehouse management under cap-and-trade policy. J. Clean. Prod. 2016, 139, 894–904. [Google Scholar] [CrossRef]
- Cramton, P.; Kerr, S. Tradeable carbon permit auctions: How and why to auction not grandfather. Energy Policy 2002, 30, 333–345. [Google Scholar] [CrossRef]
- Böhringer, C.; Lange, A. On the design of optimal grandfathering schemes for emission allowances. Eur. Econ. Rev. 2005, 49, 2041–2055. [Google Scholar] [CrossRef]
- Benjaafar, S.; Li, Y.; Daskin, M. Carbon footprint and the management of supply chains: Insights from simple models. IEEE Trans. Autom. Sci. Eng. 2013, 10, 99–116. [Google Scholar] [CrossRef]
- Hong, K.; Jung, H.; Park, M. Predicting European carbon emission price movements. Carbon Manag. 2017, 8, 33–44. [Google Scholar] [CrossRef]
- An, J.; Lee, J. A Newsvendor Non-Cooperative Game for Efficient Allocation of Carbon Emissions. Sustainability 2018, 10, 154. [Google Scholar] [CrossRef]
- Yun, J.; Won, D.; Park, K. Dynamics from open innovation to evolutionary change. J. Open Innov. Technol. Mark. Complex. 2016, 2, 7. [Google Scholar] [CrossRef]
- Yun, J.J.; Won, D.; Park, K. Entrepreneurial cyclical dynamics of open innovation. J. Evol. Econ. 2018, 28, 1151–1174. [Google Scholar] [CrossRef]
- Chaabane, A.; Ramudhin, A.; Paquet, M. Design of sustainable supply chains under the emission trading scheme. Int. J. Prod. Econ. 2012, 135, 37–49. [Google Scholar] [CrossRef]
- Zhou, P.; Wang, M. Carbon dioxide emissions allocation: A review. Ecol. Econ. 2016, 125, 47–59. [Google Scholar] [CrossRef]
- Tang, L.; Wu, J.; Yu, L.; Bao, Q. Carbon allowance auction design of China’s emissions trading scheme: A multi-agent-based approach. Energy Policy 2017, 102, 30–40. [Google Scholar] [CrossRef]
| Conditions | [10,11] | [4,5,6,7,8,13,21] | [5,6,9,18,19,24] | [17,19,20,25] | Our Study |
|---|---|---|---|---|---|
| Uncertain Demand | √ | √ | |||
| Production/Operation Decision | √ | √ | √ | √ | |
| Interdependency of Operational decision, Carbon Cap and Price | √ | ||||
| Carbon Trade | √ | √ | √ | √ | √ |
| Entity | ||||
|---|---|---|---|---|
| 1 | $100 | $60 | $40 | 2 |
| 2 | $120 | $90 | $70 | 1 |
| 3 | $110 | $60 | $50 | 3 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J. Operational Decision Model with Carbon Cap Allocation and Carbon Trading Price. J. Open Innov. Technol. Mark. Complex. 2019, 5, 11. https://doi.org/10.3390/joitmc5010011
Lee J. Operational Decision Model with Carbon Cap Allocation and Carbon Trading Price. Journal of Open Innovation: Technology, Market, and Complexity. 2019; 5(1):11. https://doi.org/10.3390/joitmc5010011
Chicago/Turabian StyleLee, Jinpyo. 2019. "Operational Decision Model with Carbon Cap Allocation and Carbon Trading Price" Journal of Open Innovation: Technology, Market, and Complexity 5, no. 1: 11. https://doi.org/10.3390/joitmc5010011
APA StyleLee, J. (2019). Operational Decision Model with Carbon Cap Allocation and Carbon Trading Price. Journal of Open Innovation: Technology, Market, and Complexity, 5(1), 11. https://doi.org/10.3390/joitmc5010011





