BESTIE: Broadcast Encryption Scheme for Tiny IoT Equipment

Abstract

In public key broadcast encryption, anyone can securely transmit a message to a group of receivers such that privileged users can decrypt it. The three important parameters of the broadcast encryption scheme are the length of the ciphertext, the size of private/public key, and the performance of encryption/decryption. It is suggested to decrease them as much as possible; however, it turns out that decreasing one increases the other in most schemes. This paper proposes a new broadcast encryption scheme for tiny Internet of Things (IoT) equipment (BESTIE), minimizing the private key size in each user. In the proposed scheme, the private key size is $O\left(\log n\right)$, the public key size is $O\left(\log n\right)$, the encryption time per subset is $O\left(\log n\right)$, the decryption time is $O\left(\log n\right)$, and the ciphertext text size is $O\left(r\right)$, where n denotes the maximum number of users, and r indicates the number of revoked users. The proposed scheme is the first subset difference-based broadcast encryption scheme to reduce the private key size $O\left(\log n\right)$ without sacrificing the other parameters. We prove that our proposed scheme is secure under q-Simplified Multi-Exponent Bilinear Diffie-Hellman (q-SMEBDH) in the standard model.

1. Introduction

In a modern Internet of Things (IoT) infrastructure, the number of total devices tend to increase on a large scale, while the size of individual equipment become smaller. When dealing with secure communications for a massive number of resource-constrained devices, it is important not only to support flexible access control but also to minimize transmission costs and device computation/storage overhead. Broadcast encryption is the fundamental cryptographic primitive to uphold secure communication to any group of privileged devices.

1.1. Broadcast Encryption

In the Broadcast encryption (BE) scheme, anyone can securely transmit a message to a group of receivers such that privileged users can decrypt it. In BE protocol, the transmission consists of $(S,Hdr,C{T}_{sk})$: the S is a group (subset) of users, $Hdr$ is a header which contains the encryption of session key $sk$, and $C{T}_{sk}$ is the ciphertext of message encrypted with the key $sk$. When receiving the following transmission, a user first extracts (or decrypts) the session key $sk$ from $Hdr$; then, he/she uses the following symmetric key $sk$ for the decryption of $C{T}_{sk}$. If the user is not covered in S, this indicates that the user is revoked and should not be able to extract the key from $Hdr$. Moreover, the system should guarantee that, even if all the revoked users collude, it should be impossible to learn any information about the $sk$ in the $Hdr$. The header is considered a real ciphertext in a BE field of research, since it holds the security of transmissions.

In BE systems, the main competitive issue was reducing the number of subsets to cut down the ciphertext header size. The subset group S works as an encryption unit in most BE schemes and privileged users are determined by multiple subsets. In this case, the header should include all of the corresponding encryptions of $sk$. To be more concrete, suppose we have subsets of $S_1,\cdots ,S_n$; then, the header $\left\{Hdr\right\}$ is a vector that consists of $Hd{r}_1,\cdots ,Hd{r}_n$. Namely, the header size is strictly linear to the number of subsets, which clarifies that the number of subsets needs to be minimized.

Many schemes have been proposed [1,2,3,4,5] in different representations with the purpose of reducing the number of subsets, i.e., the header size in BE. In particular, subset difference schemes [1,6] have been received a lot of attention and adopted practically from DVD and Blu-ray disc standards (AACS) to Pay-TV systems since SD schemes provide appropriate parameters of key size, execution time, and ciphertext size. Hence, this paper concentrates on the SD-based approach.

By varying the SD framework, Lin’s group proposed an interval coverage [2] which achieves a comparable header size to the SD approach. Moreover, Kim et al. [3] devised a combinatorial subset difference (CSD), which extends the SD to be more general and expressive. Figure 1 shows an example to visualize each representation. The SD represents a subset with a subtraction (difference) of two subtrees, which is from a binary tree constructed with users mapped as leaf nodes. As an example, in Figure 1a, the SD representation $(1,7)$ covers privileged users $4,5,6$. The interval representation lets a subset denote a range of privileged users. In the example of Figure 1b, $(4,6)$ can cover the privileged users $4,5,6$. The SD representation is likely to cover more users since subtrees provide more flexible depth compared to the fixed range of interval representation. However, SD has a limitation: it is bound to the tree hierarchy. When converting the binary tree to the bitwise representation $(0,1,*)$ by translating the left edge as 0 and the right edge as 1 (Figure 1c), the wildcard (*) cannot be placed before the bit. The reason for this is that each bit is decided from top to bottom due to the hierarchy, thus an unfixed bit (*) can only exist when its parent is fixed. The SD and interval schemes, therefore, show analogous results in terms of header sizes; the SD scheme shows a header size of $4r$, and the interval scheme shows a header size of $3r$ in the worst case, where r is the number of revoked users. Note that it is hard to decide which scheme has a smaller header size, if not fixed in the worst cases.

Similar to SD, the CSD also represents a subset with a subtraction of two sets, but each subset is no longer a subtree; it is a label of binary bits which is a generalized expansion of the subset difference. In the example of Figure 1c, the CSD subset $(**,*1)$ can cover the privileged users $00,10$. Note that the representation $*1$ is impossible to visualize in the tree figure, since the tree is bound to the hierarchy. The CSD has removed the limitation of hierarchy that lies in the subset difference, and it can cover both the SD and the interval representation with a bit label. It is the most generalized form of subset construction that can cover all existing representations. The CSD cuts the header size down to $2r$, even in the worst case, and shows that it can always cover users with less (or at least the same) subsets than SD representations.

The public key broadcast encryption scheme for the CSD representation [3] has shown that BE can be applied efficiently to the secure multicast in IoT systems. Since the CSD can represent the generalized binary bits, it can cover the bit string of IP addresses for devices in an IoT system network. The experiments in Reference [3] show that the CSD scheme is practical and appropriate for IoT multicasts within a large scale of devices.

1.2. BE for Tiny Equipment

While the number of IoT equipment increases, the size of the equipment itself decreases. In current IoT infrastructures, devices are likely to have no more than a few kilobytes of secure on-chip storage. Note that the key should not be stored in the off-chip flash storage (which could be larger), since they are exposed to the public and commonly extractable [7]. In this setting, the keys of BE should be short enough to be stored in the small-sized memory of tiny IoT equipment. To justify the usage of BE in various IoT systems with tiny devices, we list some specific application examples:

• Secure multicast: The research of Reference [3] already justified the usage of BE for secure multicast. To be more specific, an IoT system manager may want to broadcast and distribute secure messages to the devices by using the subset difference of IPv6 address bit string. Current IoT equipment commonly utilize chips that have 4 KB to 128 KB of non-volatile memory (EEPROM or on-chip flash). Some devices tend to use trusted platform module (TPM) chips that can store and manage keys securely, and the TPM key storage also has a size of no more than 16 KB. (ATmega 128 microprocessor has 128 KB flash and 4 KB EEPROM, and Atmel TPM series provide 16 KB of non-volatile key storage [8]).
• Engine control unit (ECU) firmware management: The engine control unit (ECU) of a vehicle is known to have a key storage for its code and data encryption. In time-to-time firmware updates, the system needs to set privileged devices either to guarantee customized firmwares for different vehicles or to revoke the disclosed keys that are often used by other vendors. BE can provide an appropriate environment for the large scale of ECU firmware encryption management. The non-volatile on-chip memory of the ECU usually has a size of no more than 12 KB.

Unfortunately, none of the existing BE schemes are capable of satisfying the requirement of small sized keys in a setting with a massive number of devices. There were some noticeable works that focus on the key size of BE, like Reference [6]. In Reference [6], the authors proposed a scheme that reduces the private key (SK) size from $O\left({\log }^{3}n\right)$ to $O\left({\log }^{2}n\right)$, compared to the original $SD$-based schemes [4]. Interval scheme [2] also shows a same order of $O\left({\log }^{2}n\right)$ for the SK size, while maintaining the same transmission complexity as [4,6]. The size complexity $O\left({\log }^{2}n\right)$, however, is not small enough to be practically applied for tiny IoT devices. In the secure multicast example, the current IPv6 standard considers $2^{128}$ users. Therefore, in the secure multicast for random devices, the system should provide a full spectrum of representations for the 128-bit address combinations. The ECU firmware case is also similar; the vehicle ECU has its own ID which usually consists of distinct 32 to 128 bits [9]. This leads the private key to grow larger than 40 KB for 32 bits or 640 KB for 128 bits, which cannot be stored in the small on-chip storage of 12 KB in ECU. In fact, it is an open problem to reduce the private key size to $O\left(\log n\right)$ in the SD-based BE approach. This should be achieved with a reasonable cost; Goodrich [10] proposed a symmetric BE with the SK size of $O\left(\log n\right)$, but the computation cost is $O\left(n\right)$ which is beyond practical (see

Table 1. Comparison of costs between SD-based public-key Broadcast encryption (BE). ref. n = the number of total users, and r = the number of revoked users.

	BESTIE	LKLP’14	Lin’10	DF’02	NNL’01	GST’04
	(Ours)	[6]	[2]	[4]	[11]	[10]
PK Size	$O\left(\log n\right)$	$O\left(1\right)$	$O\left(\log n\right)$	$O\left(\log n\right)$	N/A	N/A
SK Size	$O\left(\log n\right)$	$O\left({\log }^{2}n\right)$	$O\left({\log }^{2}n\right)$	$O\left({\log }^{3}n\right)$	$O\left({\log }^{2}n\right)$	$O\left(\log n\right)$
CT Size	$O\left(r\right)$	$O\left(r\right)$	$O\left(r\right)$	$O\left(r\right)$	$O\left(r\right)$	$O\left(kr\right)$
Enc Time	$O\left(r\right)$	$O\left(r\right)$	$O\left(r\right)$	$O\left(r\log n\right)$	$O\left(r\log n\right)$	$O\left(kr\log \right(n/k\left)\right)$
Dec Time	$O\left(\log n\right)$	$O\left(1\right)$	$O\left(\log n\right)$	$O\left(\log n\right)$	$O\left(\log n\right)$	$O\left(n^{1/k}\right)$
Enc type	Asymmetric	Asymmetric	Asymmetric	Asymmetric	Symmetric	Symmetric
Assumption	$q-SMEBDH$	$q-SMEBDH$	$q-BDHE$	$q-BDHI$	One-way func.	One-way func.
ROM	No	Yes	No	No	No	No

for details).

1.3. BESTIE with Short-Key

In this paper, we propose BESTIE, a new broadcast encryption scheme which has a short key size for tiny IoT equipment. The proposed BESTIE has a key size of $O\left(\log n\right)$, which exceeds the current boundary of the key size $O\left({\log }^{2}n\right)$ among the existing subset difference-based broadcast encryptions. By applying BESTIE in the 128-bit ID systems, we can obtain a 7 KB private key (SK), which can be easily stored in the secure on-chip memory of tiny IoT equipment. Moreover, the BESTIE does not sacrifice any other factor, such as execution (encryption/decryption) times or header sizes.

The main idea to reduce the key size in the proposed scheme is to share the same random value for every key, while different random values are applied for each key in the existing subset difference-based approaches. In the original CSD scheme [3], as well as most subset difference-based schemes, $O\left(l\right)$ size key is required for each bit in the ID, i.e., given a private key $SK=(S{K}_{I{D}_1},\cdots ,S{K}_{I{D}_l})$, each element $S{K}_{I{D}_i}$ contains a primary key and $O\left(l\right)$ size auxiliary key for the other bit positions to build a decryption key, where l denotes the bit-length or $\log n$ (for total n users). In the existing schemes, each auxiliary key should contain an independent random value; otherwise, a combination of keys may generate an unauthorized decryption key. The proposed BESTIE devises a novel and secure way to reuse the $O\left(l\right)$ auxiliary key for all primary keys. As a result, the BESTIE requires $O\left(\log n\right)$ size key. The detailed construction is available in Section 4.

Another interesting feature is that, unlike most existing schemes, BESTIE does not demand a public key (PK) for the decryption. Other schemes, such as SD [6] or interval schemes [2], reconstruct the corresponding decryption key from the PK, as well as the SK in the decryption phase, and thus need to maintain the PK in the device storage or receive the PK from the communication. On the other hand, since the decryption in BESTIE relies on the computation with the secret key SK only, there is no need to store the PK in the device. This indicates that BESTIE has an advantage in the PK storage and/or PK transmission overhead.

1.4. Contributions

We formally summarize the contributions of our BESTIE as follows:

• Theoretical advance: The proposed BESTIE resolves a challenging problem to reduce the private key size to $O\left(\log n\right)$ in the SD-based BE approach, without sacrificing any other efficiency. Moreover, BESTIE is compatible with even CSD, which is more expressive, and is thus more compact than SD.
• Practicality: The BESTIE is applicable to large scale IoT systems ($2^{128}$ devices) with a reasonable performance; it requires only 7 KB private key size while the private key size is more than 600 KB in the other existing SD-based approaches.
• Implementation: We implement the proposed protocol on the Intel Edison 500 Mhz IoT device. The implementation result can be directly utilized for various IoT applications, such as secure multicast and ECU firmware updates.
• Security: We prove that the BESTIE is collusion resistant and IND-sID-CPA-secure under the l-Simplified Multi-Exponent Bilinear Diffie-Hellman (l-SMEBDH) assumption (without the random oracle model). We also provide an IND-sID-CCA-secure version of the scheme.

Section 2 organizes related works. Section 3 describes a required background and definitions. We present the construction and the security proof of our proposed BESTIE in Section 4 and extend it to the CCA-secure scheme in Section 5. Section 6 analyzes experimental results. In Section 7, we draw a conclusion.

2. Related Work

The broadcast encryption (BE) is a traditional cryptographic method, and there have been a variety of researches with different features [1,4,5,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25]. Known also as a revocation schemes, BE can provide efficient revocation of individual users, while letting the privileged users remain available to decrypt the broadcasted transmission. The listed categories below are the various viewpoints in BE, and every existing BE scheme has its own feature due to the different purposes.

• Stateful vs. stateless: There are two types of BE schemes, which are stateful schemes [24,26,27] and stateless schemes [1,10,22]. In the stateful BE scheme, the key exchange occurs more than once. On the other hand, the stateless BE scheme allows the key exchange only once in the initial setup. Stateful schemes can be useful in a setting that can allow users to interact after the initial setup. However, in real practice, such as Pay-TV systems or IoT networks, once the devices are deployed, it becomes a big burden to update all keys synchronously.
• Symmetric vs. asymmetric: The BE can be also categorized as a symmetric BE [10,25] and asymmetric BE. In the symmetric BE, only a trusted user who has a symmetric key can encrypt and broadcast the message to the receivers. An asymmetric BE, known as a public key broadcast encryption (PKBE), enables any user to broadcast the encrypted information.

It is clear that a stateful BE scheme and a symmetric BE scheme have more limitations in terms of its usage; this paper proposes a stateless public key (asymmetric) BE scheme. For a more practical use, most optimizations of BE schemes are focused on reducing header or key sizes.

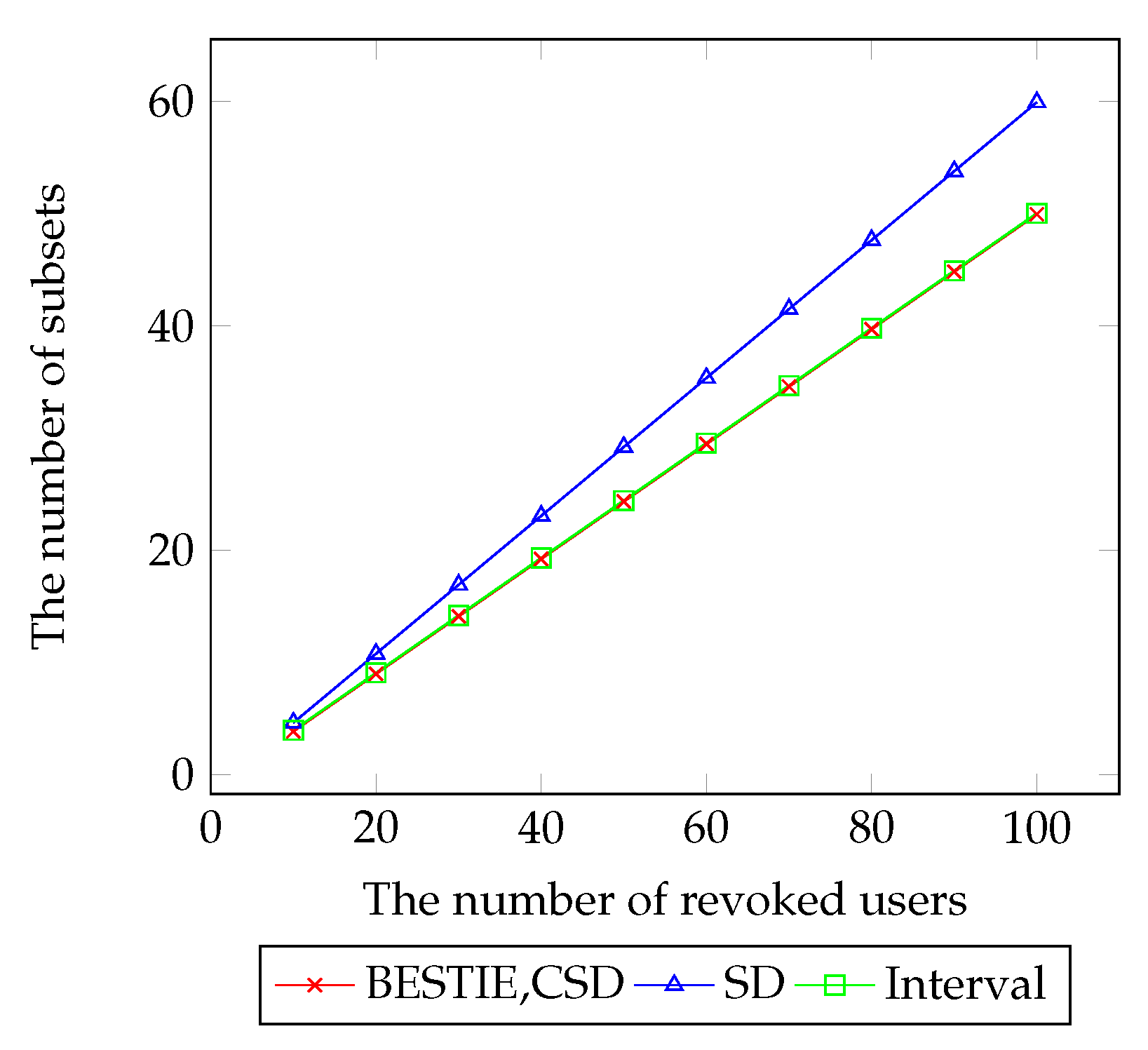
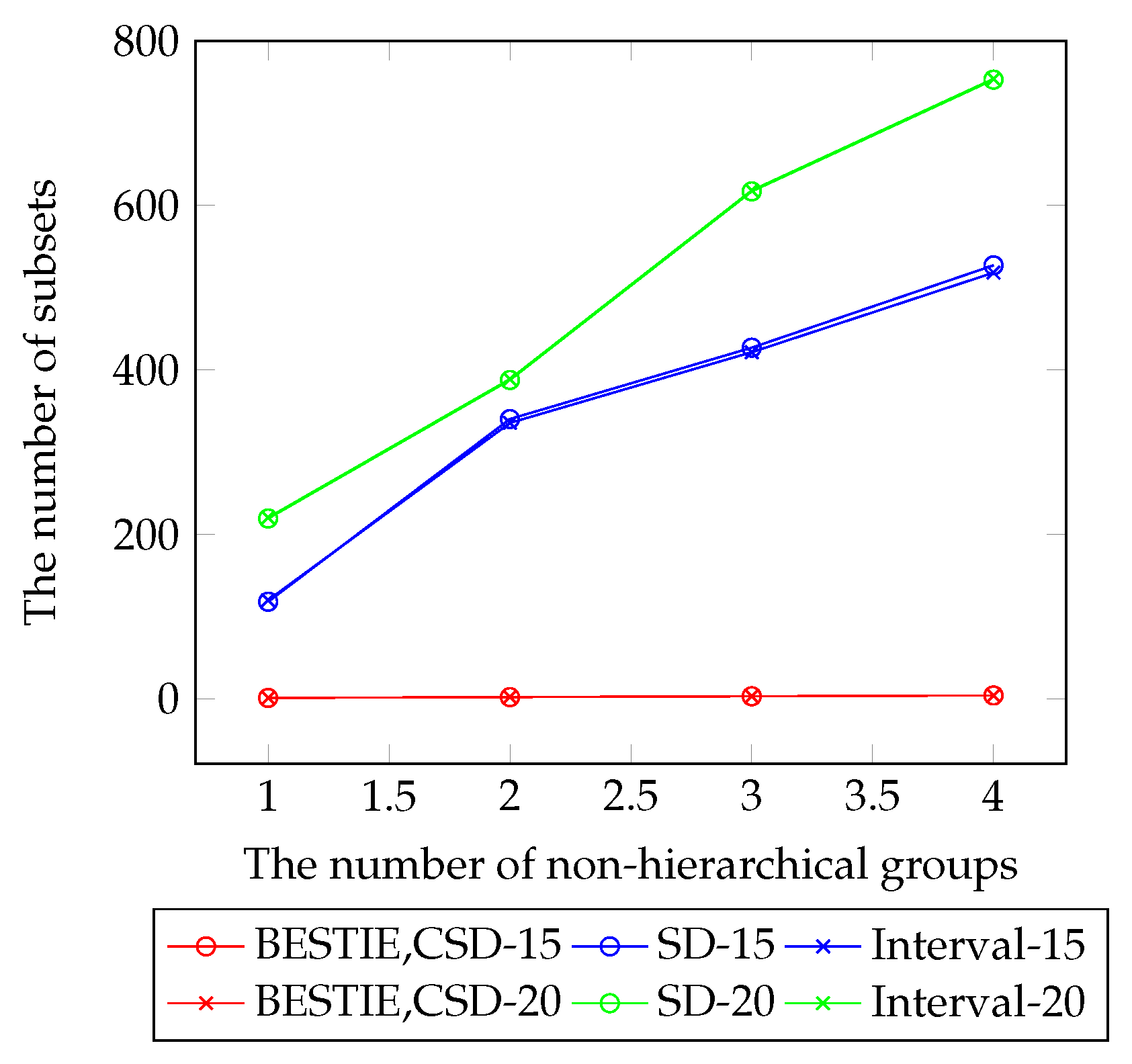
• lHeader size: The main objective of the BE research was to reduce the header size, which decides the transmission overhead. Since the header size relies on the number of subsets, there were many works that proposed subset construction/representation methods [2,10,11,22]. The most common representations were the complete subtree (CS) [11], the subset difference (SD) [11], and the interval encryption [2]. The CS method covers users with root nodes of subtrees. The SD method covers users with a subtraction of two subtrees. The interval encryption covers users with ranges of privileged users. Recently, the work of Reference [3] proposed a combinatorial subset difference (CSD), which covers users with a subtraction of two non-hierarchical bit-labels. The SD scheme has a header size of $4r$, the interval scheme has a header size of $3r$, and the CSD scheme has a header size of $2r$, each for the worst cases when r is the number of revoked users.
• Key size: Some works have focused on reducing the PK/SK size of BE, although there usually is a trade-off between the size and the encryption/decryption time. The work of Reference [6] has succeeded on reducing the SK size to the order of $O\left({\log }^{2}n\right)$ in the subset difference. The interval scheme also obtained an order of $O\left({\log }^{2}n\right)$ for the SK size. Until now, even a symmetric key BE (which is limited, but more generally efficient) has a boundary of $O\left({\log }^{2}n\right)$ for the size of SK.

2.1. SD-Based BE

Among the existing BE schemes, our main focus is on the SD-based methods (e.g., SD, interval, CSD), which achieves the header size of $O\left(r\right)$. In methods that do not use SD, the header size is impractical since it depends on the number of total users n instead of the number of revocation r. For instance, Boneh et al. [5] proposed a notable scheme which covers the users as groups of indices; their general construction gains the header size of $O\left(\sqrt{n}\right)$ (PK size: $O\left(\sqrt{n}\right)$, SK size: $O\left(1\right)$, encryption time: $O\left(n\right)$, decryption time: $O\left(\sqrt{n}\right)$). However, in general practice, the revocation tends to remain small while the total user grows large in various applications: the number of revocation r is much smaller than the $\sqrt{n}$.

Table 1 shows the order of costs in SD-based BE schemes that achieve the header (CT) size of $O\left(r\right)$, where n is the number of total users, and r is the number of revoked users. NNL’01 [11] is the original SD scheme which is a symmetric key BE. DF’02 [4] proposed a transformation technique that converts a symmetric key BE to public key BE by utilizing hierarchical identity-based encryption (HIBE); the shown results are obtained by applying the BBG-HIBE [20] scheme to the NNL’01. (DF’02 [4] states $O\left(1\right)$ PK size and $O\left({\log }^{2}n\right)$ SK size, but it refers to the HIBE keys; remind that the BBG-HIBE key has $O\left(\log n\right)$ elements). Lin’10 [2] refers to the interval encryption, which is similar to the SD in a way that the users are represented in a binary tree; the secret key size is $O\left({\log }^{2}n\right)$. LKLP’14 [6] proposes a more efficient SD scheme with utilizing the random oracle, which also achieves the secret key size of $O\left({\log }^{2}n\right)$. GST’04 [10] is a symmetric key BE which focuses on the $O\left(\log n\right)$ SK size. However, it sacrifices the decryption time to $O\left(n\right)$, or increase CT size and encryption time by a given constant k to mitigate the decryption time. Compared with all existing SD-based BE schemes, BESTIE is the first approach to obtain a $O\left(\log n\right)$ SK size while providing overall decent performance. Moreover, since BESTIE does not sacrifice any other factors, it retains a small CT size, a small PK size, and fast encryption/decryption performance.

2.2. Attribute-Based Encryption

From a high-level perspective, BE can be considered as a special case of attribute-based encryption (ABE) [28,29,30,31]; if we let each bitwise ID be an attribute and define subset inclusion as an access policy of ciphertext-policy ABE (CP-ABE), it can provide the same functionality of BE. However, as most general cases are not as efficient as special cases, ABE cannot achieve time and size costs comparable to BE. For instance, in the CP-ABE with constant-size ciphertext [31], the key size grows linear to the number of attributes. Since the access policy requires a bitwise representation of the ID and subsets, the key size roughly grows to $O\left(2^n\right)$, which is beyond practical.

3. Preliminaries

In this section, we provide backgrounds and preliminary definitions. Section 3.1 describes the basic definition of public key broadcast encryption (PKBE). Section 3.2 defines the formal security model for our proposed system. Section 3.3 gives a remark for the mathematical background about bilinear maps and pairings in elliptic curve groups. In Section 3.4, we describe the cryptographic assumption which our system is based on. Section 3.5 gives a summary for the combinatorial subset difference, which is a subset cover method our system adopts.

3.1. Public Key Broadcast Encryption

In a public key broadcast encryption (PKBE) system, the original message m is commonly encrypted to $C_K$, which is often called the broadcast body, with a simple symmetric key algorithm (e.g., AES block cipher). Then, the symmetric key M is encrypted with the PKBE encryption, so that the legitimate receivers can obtain the symmetric key M and use it for the symmetric decryption of $C_K$ to obtain m. In the following decryption of BE systems, the symmetric key M is considered as a message; the symmetric key encryption/decryption process (i.e., m, $C_K$) is common and often omitted in BE schemes.

The PKBE encryption is required for each subset, and the header (or the broadcast ciphertext) $Hdr$ for each subset is collected into a vector $\left\{Hdr\right\}={\left\{(S_i,Hd{r}_{S_i})\right\}}_{i=1}^w$ where w is the number of total subsets. A legitimate user decrypts the message by looking for the $Hd{r}_{S_i}$ corresponding to the subset $S_i$ where it belongs to, obtaining M from $Hd{r}_{S_i}$ with the PKBE decryption, and finally decrypting the message m from the broadcast body $C_K$. Formally, a PKBE system $\mathsf{\Pi }$ consists of four algorithms:

$\mathsf{Setup}(l,\lambda )$

takes user’s ID bit-length l and session key length $\lambda$ as inputs. It outputs public parameters $PK$ and a master key $MK$.

$\mathsf{KeyGen}(ID,MK,PK)$

takes user’s l-bit $ID$, master key $MK$, and public key $PK$ as inputs. It outputs a private key set $S{K}_{ID}$.

$\mathsf{Encrypt}(S,PK,M)$

takes a subset S, and a public key $PK$ and a message M as inputs. It outputs a broadcast ciphertext $Hd{r}_S$ for the subset S.

$\mathsf{Decrypt}(S,ID,S{K}_{ID},Hd{r}_S)$

takes a subset S, a user id $ID\in {\{0,1\}}^l$, private key $S{K}_{ID}$ for user $ID$, and a header $Hd{r}_S$ as inputs. If $ID\in S$, then it outputs message M.

The system is correct if every user in S can get the message M. Namely, for all S and all $ID\in S$, if $(PK,MK)\leftarrow \mathsf{Setup}(l,\lambda )$, $S{K}_{ID}\leftarrow \mathsf{KeyGen}(ID,MK,PK)$, and $Hd{r}_S$←$\mathsf{Encrypt}$$(S,PK,M)$ then $\mathsf{Decrypt}$$(S,ID,S{K}_{ID},Hd{r}_S)$ extracts M.

3.2. Security Model

In this section, we describe a selective semantic security (IND-sID-CPA) and a selective CCA-security (IND-sID-CCA) for broadcast encryption as in Reference [3,5]. Depending on whether the number of challenged sets is represented as a single subset or as multiple subsets, we separate security notions as a single-set security and a multi-set security. Consequently, the single-set security implies a multi-set security as shown in Reference [3].

The single-set security is defined as a following game between an adversary $\mathcal{A}$ and a challenger $\mathcal{C}$. Both $\mathcal{C}$ and $\mathcal{A}$ are given l and $\lambda$, the user ID length and the key length, respectively, as inputs. Note that the collusion resistance is straightforward, since the secret keys for all users (except the selected target) are distributed before the challenge.

Init: 

Algorithm $\mathcal{A}$ outputs a set $S^{*}$ of users to attack.

Setup: 

The challenger $\mathcal{C}$ performs $\mathsf{Setup}(l,\lambda )$ to obtain a public key $PK$ and a master key $MK$.

KeyGen: 

The challenger $\mathcal{C}$ runs $\mathsf{KeyGen}(ID,MK,PK)$ to obtain private keys $S{K}_{0^l}$, ⋯, $S{K}_{1^l}$. $\mathcal{C}$ then provides $\mathcal{A}$ with the public key $PK$ and all private keys $S{K}_{ID}$ for $ID\notin S^{*}$.

Phase 1: 

(optional for CCA) Attacker $\mathcal{A}$ adaptively issues decryption queries $q_1,\cdots ,q_d$ where a decryption query consists of the triple $(S,ID,Hd{r}_S)$ with $S\subseteq S^{*}$ and $ID\in S$. $\mathcal{C}$ responds with $\mathsf{Decrypt}(S,ID,S{K}_{ID},Hd{r}_S)$.

Challenge: 

For the challenge, algorithm $\mathcal{A}$ outputs two messages $M_0$ and $M_1$. $\mathcal{C}$ picks $\xi \in \{0,1\}$, encrypts the message $M_{\xi }$ by running $\mathsf{Encrypt}(S^{*},PK,M_{\xi })$ to obtain $Hd{r}_S^{*}$, and gives $Hd{r}_S^{*}$ to the attacker $\mathcal{A}$.

Phase 2: 

(optional for CCA) Attacker $\mathcal{A}$ continues to adaptively issue decryption queries $q_{d+1}$, ⋯, $q_D$ where a decryption query consists of $(S,ID,Hd{r}_S)$ with $S\subseteq S^{*}$ and $ID\in S$. The only constraint is that $Hd{r}_S\ne Hd{r}_S^{*}$. $\mathcal{C}$ responds as in query phase 1.

Guess: 

Attacker $\mathcal{A}$ produces its guess ${\xi }^{\prime }\in \{0,1\}$ for $\xi$ and wins the game if $\xi ={\xi }^{\prime }$.

Let ${\mathsf{AdvSSBr}}_{\mathcal{A},\mathsf{\Pi }}(l,\lambda )$ be the advantage that $\mathcal{A}$ wins the above game.

Definition 1. 

A public key broadcast encryption Π is $(t,ϵ,l,\lambda )$-single-set-CPA secure if for every t-time adversary $\mathcal{A}$ we have that $|{\mathsf{AdvSSBr}}_{\mathcal{A},\mathsf{\Pi }}$$(l,\lambda )$−$1/2|<$ϵ.

Definition 2. 

A public key broadcast encryption Π is $(t,ϵ,l,\lambda ,d,D)$-single-set-CCA secure if $|{\mathsf{AdvSSBr}}_{\mathcal{A},\mathsf{\Pi }}$$(l,\lambda )$−$1/2|<$ϵ for every t-time adversary $\mathcal{A}$ with at most D decryption queries.

The multi-set security game is defined similar to the single-set security game, except the challenged set is given as multiple subsets.

Init: 

Algorithm $\mathcal{A}$ outputs a set $S^{*}=\{S_1^{*},\cdots ,S_w^{*}\}$ of users to attack.

Setup: 

The challenger $\mathcal{C}$ executes $\mathsf{Setup}(l,\lambda )$ to obtain a public key $PK$ and a master key $MK$.

KeyGen: 

The challenger $\mathcal{C}$ runs $\mathsf{KeyGen}(ID,MK,PK)$ to obtain private keys $S{K}_{0^l}$, ⋯, $S{K}_{1^l}$. $\mathcal{C}$ gives $\mathcal{A}$ all private keys $S{K}_{ID}$ for $ID\notin S_i^{*}$ where $i=1,\cdots ,w$.

Phase 1: 

(optional for CCA) Attacker $\mathcal{A}$ adaptively issues decryption queries $q_1,\cdots ,q_d$ where a decryption query consists of the triple $(S,ID,Hd{r}_S)$ with $S\subseteq S^{*}$ and $ID\in S$. $\mathcal{C}$ responds with $\mathsf{Decrypt}(S,ID,S{K}_{ID},Hd{r}_S)$.

Challenge: 

For the challenge, algorithm $\mathcal{A}$ outputs two messages $M_0$ and $M_1$. $\mathcal{C}$ picks $\xi \in \{0,1\}$, encrypts the message $M_{\xi }$ by running $\mathsf{Encrypt}(S_i^{*},PK,M_{\xi })$ to obtain $Hd{r}_{S_i}^{*}$ for $i=1,\cdots ,w$, and gives all $Hd{r}_{S_i}^{*}$ to the attacker $\mathcal{A}$.

Phase 2: 

(optional for CCA) Attacker $\mathcal{A}$ continues to adaptively issue decryption queries $q_{d+1}$, ⋯, $q_D$ where a decryption query consists of $(S,ID,Hd{r}_S)$ with $S\subseteq S^{*}$ and $ID\in S$. The only constraint is that $Hd{r}_{S_i}\ne Hd{r}_{S_i}^{*}$. $\mathcal{C}$ responds as in query phase 1.

Guess: 

Attacker $\mathcal{A}$ provides its guess ${\xi }^{\prime }\in \{0,1\}$ for $\xi$ and wins the game if $\xi ={\xi }^{\prime }$.

Let ${\mathsf{AdvMSBr}}_{\mathcal{A},\mathsf{\Pi }}(l,\lambda )$ be the advantage that $\mathcal{A}$ wins the above game.

Definition 3. 

A public key broadcast encryption Π is $(t,ϵ,l,\lambda )$-multi-set-CPA secure if $|{\mathsf{AdvMSBr}}_{\mathcal{A},\mathsf{\Pi }}(l,\lambda )-1/2|<ϵ$ for every t-time adversary $\mathcal{A}$.

Definition 4. 

A public key broadcast encryption Π is $(t,ϵ,l,\lambda ,d,D)$-multi-set-CCA secure if for every t-time adversary $\mathcal{A}$ with at most D decryption queries we have that $|{\mathsf{AdvMSBr}}_{\mathcal{A},\mathsf{\Pi }}(l,\lambda )-1/2|<ϵ$.

In Reference [3], it is shown that the single-set security implies the multi-set security.

Theorem 1

([3]). Suppose the public key broadcast encryption Π is $(t,ϵ,l,\lambda )$-single-set-CPA secure ($(t,ϵ,l,\lambda ,d,D)$-single-set-CCA secure). Then, public key broadcast encryption Π is $(t,{ϵ}^{\prime },l,\lambda )$-multi-set-CPA secure ($(t,{ϵ}^{\prime },l,\lambda ,d,D)$-multi-set-CCA secure) for ${ϵ}^{\prime }<ϵ*w$, where w is the number of subsets.

3.3. Bilinear Groups

We briefly examine bilinear maps and bilinear map groups. We adopt the following notation [32,33,34].

• ${\mathbb{G}}_1$, ${\mathbb{G}}_2$ and ${\mathbb{G}}_T$ are (multiplicative) cyclic groups of prime order p.
• $g_1$ and $g_2$ are generators of ${\mathbb{G}}_1$ and ${\mathbb{G}}_2$, respectively.
• $e:{\mathbb{G}}_1\times {\mathbb{G}}_2\to {\mathbb{G}}_T$ denotes a bilinear map.

Let ${\mathbb{G}}_1$, ${\mathbb{G}}_2$, and ${\mathbb{G}}_T$ be groups as above. A bilinear map is a map $e:{\mathbb{G}}_1\times {\mathbb{G}}_2\to {\mathbb{G}}_{\mathbb{T}}$ with satisfying the following properties:

• Bilinear: for all $u\in {\mathbb{G}}_1$, $v\in {\mathbb{G}}_2$ and $a,b\in {\mathbb{Z}}_p$, we have $e(u^a,v^b)=e{(u,v)}^{ab}$
• Non-degenerate: $e(g_1,g_2)\ne 1$.

We say that ${\mathbb{G}}_1$ and ${\mathbb{G}}_2$ are bilinear groups if the group action in ${\mathbb{G}}_1$ and ${\mathbb{G}}_2$ can be computed efficiently and there exist a group ${\mathbb{G}}_T$ and an efficiently computable bilinear map $e:{\mathbb{G}}_1\times {\mathbb{G}}_2\to {\mathbb{G}}_T$ as above.

3.4. Computational Complexity Assumptions

The security of our system is based on a complexity assumption called q-simplified multi exponent bilinear Diffie-Hellman (q-SMEBDH) assumption. The q-SMEBDH assumption was originally introduced in Reference [6], but without formal analysis on the hardness of the assumption. In this paper, we formally show that the q-SMEBDH is a weaker assumption than the q-bilinear Diffie-Hellman exponent known as q-BDHE, by reducing q-SMEBDH to the q-BDHE.

Assumption 1. 

(q-Simplified Multi-Exponent Bilinear Diffie-Hellman, q-SMEBDH). Let $(p,{\mathbb{G}}_1,{\mathbb{G}}_2,{\mathbb{G}}_T,e)$ describe the bilinear group of prime order p with the security parameter λ. Let $g_1$ and $g_2$ be generators of ${\mathbb{G}}_1$ and ${\mathbb{G}}_2$, respectively. The q-SMEBDH assumption is that, if the challenge tuples $P=((p,{\mathbb{G}}_1,{\mathbb{G}}_2,{\mathbb{G}}_T,e),$$g_1,g_2,g_1^c,g_2^c,$${\{g_1^{a_i},g_2^{a_i},g_1^{b/a_i},g_2^{b/a_i}\}}_{1\le i\le q},$ ${\{g_1^{b{a}_i/a_j},g_2^{b{a}_i/a_j}\}}_{1\le i,j,i\ne j,\le q})$ and T are given, no PPT algorithm $\mathcal{B}$ can distinguish $T=T_0=e{(g_1,g_2)}^{bc}$ from $T=T_1=e{(g_1,g_2)}^d$ with more than a negligible advantage. The advantage of $\mathcal{B}$ is defined as $Ad{v}_{\mathcal{B}}^{q-SMEBDH}\left(\lambda \right)$ = $Pr[\mathcal{B}(P,T_0)=0]-Pr[\mathcal{B}(P,T_1)=0]$, where the probability is taken over the random choice of $a_1,\dots ,a_l,b,c,d\in {\mathbb{Z}}_p$.

We prove that the q-SMEBDH is weaker than the well-known q bilinear Diffie-Hellman exponent assumption (q-BDHE). The (decisional) q-BDHE problem is stated as follows [5,20,35,36]: given a vector of elements,

$$\begin{array}{c}(g_1,h_1,{\{g_1^{{\alpha }^i}\}}_{i\in \left[2q\right],i\ne q+1},g_2,h_2,\hfill \\ \hfill {\{g_2^{{\alpha }^i}\}}_{i\in \left[2q\right],i\ne q+1})\in {\mathbb{G}}_1^{2q+1}\times {\mathbb{G}}_2^{2q+1}\end{array}$$

as input, it should be hard to distinguish $e{(g_1,h_2)}^{{\alpha }^{q+1}}$ ( = $e{(h_1,g_2)}^{{\alpha }^{q+1}}$ ) from random where ${\log }_{g_1}{h}_1={\log }_{g_2}{h}_2$.

Lemma 1. 

If there is an adversary $\mathcal{A}$ which solves a q-SMEBDH problem with ϵ advantage in time τ, then there is an adversary which solves a q-BDHE problem with ϵ advantage in time $\tau +q^2$.

Proof. 

We will reduce a q-BDHE problem to a q-SMEBDH problem. Assume that $(g^{\prime }{}_1,{\{g^{\prime }{{}_1}^{{\alpha }^i}\}}_{i\in \left[2q\right],i\ne q+1},g_2^{\prime },h,{\{g^{\prime }{{}_2}^{{\alpha }^i}\}}_{i\in \left[2q\right],i\ne q+1})$ is given. To reduce it to q-SMEBDH, choose random exponents $v_1,\cdots ,v_q\in {\mathbb{Z}}_p$. Let $a_i={\alpha }^i·v_i$. Let $b={\alpha }^{q+1}$.

$$\begin{array}{ccc}\hfill & g_1^{a_i}=g^{\prime }{{}_1}^{{\alpha }^i{v}_i}.\hfill & \hfill g_2^{a_i}=g^{\prime }{{}_2}^{{\alpha }^i{v}_i}.\\ \hfill & g_1^{b/a_i}=g^{\prime }{{}_1}^{{\alpha }^{q+1-i}{v}_i^{-1}}.\hfill & \hfill g_2^{b/a_i}=g^{\prime }{{}_2}^{{\alpha }^{q+1-i}{v}_i^{-1}}.\\ \hfill & g_1^{b{a}_j/a_i}=g^{\prime }{{}_1}^{{\alpha }^{q+1+j-i}{v}_j{v}_i^{-1}}.\hfill & \hfill g_2^{b{a}_j/a_i}=g^{\prime }{{}_2}^{{\alpha }^{q+1+j-i}{v}_j{v}_i^{-1}}.\end{array}$$

Note that, since $i\ne j$, $q+1+j-i\ne q+1$ and $2\le q+1+j-i\le 2q$. Let $g_1^c=h_1$ and $g_2^c=h_2$.

If, for a given q-SMEBDH, there is an adversary $\mathcal{A}$ which decides whether $T=e(g_1^b,g_2^c)$ with $ϵ$ advantage, then using $\mathcal{A}$, we can decide whether $T=e{(g_1,h_2)}^{{\alpha }^{q+1}}$ with $ϵ$ advantage since $e{(g_1,h_2)}^{{\alpha }^{q+1}}$ = $e{(g_1,g_2^c)}^b$.  □

3.5. Combinatorial Subset Difference

The subset cover representation method of our system is based on the combinatorial subset difference (CSD) proposed in Reference [3]. The CSD uses a more general, thus, more compact representation method which is extended from the subset difference (SD). The subset difference is the most common representation method in the broadcast encryption (BE) in literature, which denotes a subset with a difference of two subtrees. To be more specific, the SD method constructs a binary tree by mapping the users to the leaf nodes, and represents the subset of privileged users by subtracting the two complete subtrees denoted as the root node of each subtree (i.e., $(CL,RL)$, where $CL$ is a covered set, and $RL$ is a revoked set).

CSD [3] is a more universal type of representation method that consists of a subtraction of two non-hierarchical labels. It is similar to the SD method, but $CL$ and $RL$ are no longer subtrees; labels are bit-strings which consist of $\{0,1,*\}$, where a wildcard * includes both 0 and 1. CSD is a more generalized expression compared to the SD and includes all possible SD combinations. The number of subsets in CSD is always smaller than that of SD, or at least the same. The header sizes in CSD are $2r$ in the worst case, while they are $4r$ in the SD in the worst case (r = the number of revoked users).

A secure and efficient BE construction compatible with CSD is more challenging than a construction based on SD. Since the key structure is not bound to the tree structure anymore, there are more representation cases that a privileged user has to decrypt using its key. Thus, the BE scheme with CSD may cause key size growth to cover additional cases and is even harder to reduce the key size. In this paper, we propose the first BE scheme, which minimizes the key size to be logarithmic and is compatible with even CSD, as well as SD.

4. Proposed Broadcast Encryption Scheme

In this section, we propose BESTIE, a broadcast encryption scheme applicable to tiny IoT equipment and prove its security. In Section 4.1, we describe our intuitions of how to compress the key size. We construct our proposed BE scheme in Section 4.2, analyze the complexity in Section 4.3, and prove its security in Section 4.4.

4.1. Main Idea

Before the formal description, we informally elaborate a sketch of the idea that lies behind the BESTIE. The main contribution of the BESTIE is to compress the private key size from $O\left({\log }^{2}n\right)$ to $O\left(\log n\right)$.

As mentioned in Section 1, most subset difference-based schemes require $O\left(l\right)$ size key for each bit in the ID. i.e., given a private key $SK=(S{K}_{I{D}_1},\cdots ,S{K}_{I{D}_l})$, each element $S{K}_{I{D}_i}$ contains a primary key, and $O\left(l\right)$ size auxiliary key. In the existing schemes, each auxiliary key should contain an independent random value; otherwise, a combination of keys may generate an unauthorized decryption key.

In Reference [3], the CSD subset is represented as $(CL,RL)$ where $CL$ is a covered set and $RL$ is a revoked set and a user with an ID should be able to construct its decryption key only if it belongs to the covered set but NOT to the revoked set, i.e., $ID\in CL$ and $ID\in \neg RL$. The combination of key elements derives a decryption key. However, the combination should be performed in a restricted way to prevent from generating any unauthorized decryption key. To ensure that the combination generates only legitimate keys, the scheme has the auxiliary keys with different random exponents $r_i$ for each primary key. The resulting $SK$ for the user with $ID=I{D}_1\cdots I{D}_l$ in the CSD is summarized as follows.

$$\begin{array}{cc}\hfill S{K}_{I{D}_i}& =\left\{g^{\alpha }{(\cdots k_{i,{\overline{ID}}_i})}^{r_i}\right\}\hfill \\ \hfill & \cup \{k_{j,0}^{r_i},k_{j,1}^{r_i}|j\ne i,j\in [1,l]\},\hfill \end{array}$$

(1)

where sets $\left\{g^{\alpha }{(\cdots k_{i,{\overline{ID}}_i})}^{r_i}\right\}$ and $\{k_{j,0}^{r_i},k_{j,1}^{r_i}|j\ne i,j\in [1,l]\}$ include a primary key and auxiliary keys, respectively.

Thus, the key size becomes $O\left({\log }^{2}n\right)$, since $i\in [1,l]$. (i.e., $O\left(\log n\right)$ per combination ×$\log n$ combinations). Existing subset difference-based BE schemes [2,6] have the similar approach. Hence, the known lower key size bound has been $O\left({\log }^{2}n\right)$.

In our approach, we detach $k_{i,{\overline{ID}}_i}$ from the primary key $g^{\alpha }{(\cdots k_{i,{\overline{ID}}_i})}^{r_i}$ of $S{K}_{I{D}_i}$ in Equation (1) by splitting the master key $\alpha$ into a pair ($\alpha -{\alpha }_w$, ${\alpha }_w$), and apply the same random r to the auxiliary keys as follows:

$$\begin{array}{cc}\hfill S{K}_{ID}& =\left\{g^{\alpha -{\alpha }_w}{(\cdots )}^r\right\}\hfill \\ \hfill & \cup \{g^{{\alpha }_w}{k}_{j,{\overline{ID}}_j}^r,k_{j,I{D}_j}^r|j\in [1,l]\}.\hfill \end{array}$$

(2)

Now, the key is divided into two parts such that a decryption key can be constructed only if both conditions $ID\in CL$ and $ID\in \neg RL$ are satisfied. Note that, if at least a single bit in ID is different from $RL$ (i.e., $ID\notin RL$), then $g^{{\alpha }_w}$ and $g^{\alpha -{\alpha }_w}$ can be combined, outputting the decryption key $g^{\alpha }$.

The full construction is more complex, and we describe it in the next section.

4.2. Construction

In this section, we describe the formal construction of the proposed BESTIE, which is a public key broadcast encryption scheme. As defined in Section 3.1, the public key broadcast encryption can allow any user (or device) to broadcast messages. When the system begins, each user is grouped into a specific subset. To broadcast the message, the broadcaster needs to run encryption for each subset to obtain subset header.

Figure 2 visualizes the overall workflow of the public key broadcast encryption. The manager runs the setup to initiate the system, publishes the public key $PK$, and keeps the master secret key $MK$. Then, by using $MK$, the manager runs key generation for each device and provides corresponding secret keys $S{K}_{ID}$. When a device wants to broadcast a message, it runs encryption for each subset to obtain corresponding header, and gathers all headers to broadcast the vector of headers. When a device receives the headers, it searches the header for its own subset, and runs decryption with the header and its own secret key to obtain the message.

In the following construction, we denote $I{D}_i$, $C{L}_i$, and $R{L}_i$ the ith bit of a bit-string $ID$, $CL$, and $RL$, respectively. In addition, we denote $H\left(ID\right)$ = $h_0{\prod }_{i=1}^l{h}_{i,I{D}_i}$, $K\left(ID\right)$ = $k_0{\prod }_{i=1}^l{k}_{i,I{D}_i}$, $h_{i,*}=h_{i,0}·h_{i,1}$ and $k_{i,*}=1$.

Setup($l,\lambda$):

This algorithm first generates the bilinear groups ${\mathbb{G}}_1$, ${\mathbb{G}}_2$ of prime order p of bit size $\theta \left(\lambda \right)$. It selects random elements $g_1\in {\mathbb{G}}_1$ and $g_2\in {\mathbb{G}}_2$. It selects a random exponent $\alpha \in {\mathbb{Z}}_p$. It chooses $O\left(l\right)$ random group elements $h_0,h_{1,0},h_{1,1},\cdots ,h_{l,0}$, $h_{l,1},k_0,k_{1,0},k_{1,1},$$\cdots ,k_{l,0},k_{l,1}\in {\mathbb{G}}_1$. It outputs a master key $MK=g_1^{\alpha }$ and a public key as

$$\begin{array}{c}\hfill PK=((p,{\mathbb{G}}_1,{\mathbb{G}}_2,{\mathbb{G}}_T,e),g,h_0,h_{1,0},h_{1,1},\cdots ,h_{l,0},h_{l,1},\hfill \\ \hfill k_0,k_{1,0},k_{1,1},\cdots ,k_{l,0},k_{l,1},\mathsf{\Omega }=e{(g_1,g_2)}^{\alpha }).\hfill \end{array}$$

KeyGen($ID,MK,PK$):

This algorithm takes as input $ID=I{D}_1\cdots I{D}_l$, the master key $MK$, and the public key $PK$. It chooses random exponents ${\alpha }_w$ and $r\in {\mathbb{Z}}_p$ and outputs a private key $S{K}_{ID}$ as

$$\begin{array}{cc}\hfill S{K}_{ID}=(& x_0,x_1,\cdots ,x_l,y_0,y_1\cdots ,y_{2l},z)\hfill \\ \hfill =(& g_1^{\alpha -{\alpha }_w}H{\left(ID\right)}^r,h_{1,{\overline{ID}}_1}^r,\cdots ,h_{l,{\overline{ID}}_l}^r,\hfill \\ \hfill & k_0^r,g_1^{{\alpha }_w}{k}_{1,{\overline{ID}}_1}^r,k_{1,I{D}_1}^r,\cdots ,g_1^{{\alpha }_w}{k}_{l,{\overline{ID}}_l}^r,k_{l,I{D}_l}^r,g_2^r).\hfill \end{array}$$

Encrypt($S,PK,M$):

This algorithm takes S = ($CL$,$RL$) = ($C{L}_1\cdots C{L}_l$, $R{L}_1\cdots R{L}_l$) as input labels, the public key $PK$, and a message $M\in {\mathbb{G}}_T$ as inputs. It selects a random exponent $t\in {\mathbb{Z}}_p$ and outputs a ciphertext by implicitly including $S=(CL,RL)$ as

$$\begin{array}{c}\hfill Hd{r}_S=\{C_0={\mathsf{\Omega }}^t·M,C_1=g_2^t,C_2=H{\left(CL\right)}^t,C_3=K{\left(RL\right)}^t\}.\end{array}$$

Decrypt($S,ID,S{K}_{ID},Hd{r}_S$):

This algorithm takes a subset $S=(CL,RL)$, a user’s $ID$, a private key $S{K}_{ID}$, and a ciphertext $Hd{r}_S$ for S as inputs. Let $P=\left\{i\right|I{D}_i\ne R{L}_i\wedge R{L}_i\ne *\}$ and $Q=\left\{i\right|I{D}_i=R{L}_i\wedge R{L}_i\ne *\}$. Let d denote the number of bits, which, in $ID$, are different from $RL$ or $d=\left|P\right|$.

If $d>0$, it parses $S{K}_{ID}=(x_0,x_1,\cdots ,x_l,y_0,y_1\cdots ,y_{2l},z)$.

Then, it computes

$$\begin{array}{cc}\hfill & x^{\prime }=x_0\prod _{C{L}_i=*}{x}_i\hfill \\ \hfill & y^{\prime }={(y_0\prod _{i\in P}{y}_{2i-1}\prod _{i\in Q}{y}_{2i})}^{d^{-1}}\hfill \end{array}$$

and outputs a message as

$$\begin{array}{c}\hfill M=C_0·e{(x^{\prime }·y^{\prime },C_1)}^{-1}·e(C_2·C_3^{d^{-1}},z).\end{array}$$

Otherwise, it outputs ⊥.

The correctness is verified by the following equation.

$$\begin{array}{cc}\hfill x^{\prime }& =x_0\prod _{C{L}_i=*}{x}_i=g_1^{\alpha -{\alpha }_w}{(h_0\prod _{i=1}^l{h}_{i,I{D}_i})}^r·\prod _{C{L}_i=*}{h}_{i,\overline{I{D}_i}}^r\hfill \\ \hfill & =g_1^{\alpha -{\alpha }_w}{(h_0\prod _{C{L}_i\ne *}{h}_{i,I{D}_i}\prod _{C{L}_i=*}{h}_{i,*})}^r=g_1^{\alpha -{\alpha }_w}H{\left(CL\right)}^r\hfill \\ \hfill y^{\prime }& ={(y_0\prod _{i\in P}{y}_{2i-1}\prod _{i\in Q}{y}_{2i})}^{d^{-1}}\hfill \\ \hfill & ={(k_0^r{g}_1^{{\alpha }_{w}d}\prod _{R{L}_i\ne *}{k}_{i,R{L}_i}^r)}^{d^{-1}}\hfill \\ \hfill & =g_1^{{\alpha }_w}{(k_0\prod _{R{L}_i\ne *}{k}_{i,R{L}_i})}^{r{d}^{-1}}=g_1^{{\alpha }_w}K{\left(RL\right)}^{r{d}^{-1}}.\hfill \end{array}$$

Since $x^{\prime }=g_1^{\alpha -{\alpha }_w}H{\left(CL\right)}^r$, $y^{\prime }$ = $g_1^{{\alpha }_w}K{\left(RL\right)}^{r{d}^{-1}}$, and $x^{\prime }·y^{\prime }$ = $g_1^{\alpha }H{\left(CL\right)}^{r}K{\left(RL\right)}^{r{d}^{-1}}$,

$$\begin{array}{cc}\hfill \frac{e(x^{\prime }·y^{\prime },C_1)}{e(C_2·C_3^{d^{-1}},z)}& =\frac{e(g_1^{\alpha }H{\left(CL\right)}^{r}K{\left(RL\right)}^{r{d}^{-1}},g_2^t)}{e(H{\left(CL\right)}^{t}K{\left(RL\right)}^{t{d}^{-1}},g_2^r)}\hfill \\ \hfill & =e{(g_1,g_2)}^{\alpha t}={\mathsf{\Omega }}^t.\hfill \end{array}$$

4.3. Complexity Analysis

In this section, we analyze the complexity of the key sizes and the execution time of the proposed public key broadcast encryption scheme. The main complexity relies on the parameter l, which is the number of bits for total users n (or $\log n$).

For the key sizes, the public key size requires four fixed elements $g,h_0,k_0,\mathsf{\Omega }$ and l elements $h_{i,0},h_{i,1},k_{i,0},k_{i,1}$, which is total $2l+4$ elements where the default element size is 20 bytes. The secret key requires total $2l+3$ elements where the default element size is 20 bytes, which reduces the order to $O\left(l\right)$ or $O\left(\log n\right)$. The header size for a single subset requires four fixed elements, which is constant-size.

For the execution time, the encryption time for a single subset requires four elliptic curve computations, which is almost negligible as $O\left(1\right)$. Since the number of subsets depend on the subset representation, the complexity is determined by the number of subsets in the CSD, which is $O\left(r\right)$. The decryption time requires $O\left(l\right)$ computations, which is $O\left(\log n\right)$ for n total users.

4.4. Security Proof

Theorem 2. 

Let ${\mathbb{G}}_1$ and ${\mathbb{G}}_2$ be bilinear groups of prime order p. Suppose the (decision) $(t,ϵ,4q)$-SMEBDH assumption holds in ${\mathbb{G}}_1\times {\mathbb{G}}_2$. Then, the proposed public key broadcast encryption system is $(t^{\prime },ϵ,q,\lambda )$ semantically secure for arbitrary q, and $t^{\prime }<t+O\left(\mathbf{e}{q}^2\right)$, where $\mathit{e}$ is the maximum time for an exponentiation in ${\mathbb{G}}_1$ and ${\mathbb{G}}_2$.

Proof. 

Suppose $\mathcal{A}$ has advantage $ϵ$ in attacking the proposed public key broadcast encryption system. Using $\mathcal{A}$, we construct an algorithm $\mathcal{B}$ that solves the (decision) $4q$-SMEBDH problem.

For generators $g_1\in {\mathbb{G}}_1$ and $g_2\in {\mathbb{G}}_2$, and $b\in {\mathbb{Z}}_p$, algorithm $\mathcal{B}$ is given as input random tuples $P=((p,{\mathbb{G}}_1,{\mathbb{G}}_2,{\mathbb{G}}_T,e),$$g_1$, $g_2$, ${\{g_1^{a_i},g_2^{a_i},g_1^{b/a_i},g_2^{b/a_i}\}}_{1\le i\le 4q}$, ${\{g_1^{b{a}_i/a_j},g_2^{b{a}_i/a_j}\}}_{1\le i,j,i\ne j,\le 4q},$$g_1^c$, $g_2^c)$ and T that is either sampled from $P_{SMEBDH}$ (where $T=e{(g_1,g_2)}^{bc}$) or from $R_{SMEBDH}$ (where T is uniform and independent in ${\mathbb{G}}_T$ ). Algorithm $\mathcal{B}$’s goal is to output 1 when the input tuple T is sampled from $P_{SMEBDH}$ and 0 otherwise. Note that we let $l=q$ in this proof. Algorithm $\mathcal{B}$ interacts with $\mathcal{A}$ in a selective subset game as follows:

Init:

The game begins with $\mathcal{A}$ outputting a subset $S^{*}=(C{L}^{*},R{L}^{*})$ to attack where $C{L}^{*}$, $R{L}^{*}\in {\{0,1,*\}}^l$.

Setup:

To generate the public key, algorithm $\mathcal{B}$ chooses random exponents ${\gamma }_1$, ${\gamma }_2$, $v_1,\cdots v_{4l}$$\in {\mathbb{Z}}_p$, and sets $h_{i,j}=g_1^{a_{2i-1+j}}·g_1^{v_{2i-1+j}}$, $k_{i,j}=g_1^{a_{2l+2i-1+j}}·g_1^{v_{2l+2i-1+j}}$ for $i\in \{1,\cdots ,l\}$ and $j\in \{0,1\}$, $h_0={\left({\prod }_{i=1}^l{h}_{i,C{L}_i^{*}}\right)}^{-1}·g_1^{{\gamma }_1}$ and $k_0={\left({\prod }_{i=1}^l{k}_{i,R{L}_i^{*}}\right)}^{-1}·g_1^{{\gamma }_2}$. Let $\alpha =b$.

KeyGen:

To generate a private key $S{K}_{ID}$ for user $ID$$\in {\{0,1\}}^l$, algorithm $\mathcal{B}$ considers the following three cases.

(i)

$ID\notin C{L}^{*}$:

Algorithm $\mathcal{B}$ chooses random exponents $r^{\prime }$ and ${\alpha }_w$$\in {\mathbb{Z}}_p$ and sets $r=\frac{-b}{a_{2j-1+I{D}_j}}+r^{\prime }$ where $I{D}_j\ne C{L}_j^{*}$.

Algorithm $\mathcal{B}$ can easily compute $g_1^{v_{i}r}$,

since $g_1^{v_{i}r}$=$g_1^{\frac{-b}{a_{2j-1+I{D}_j}}·v_i}·g_1^{v_i{r}^{\prime }}$.

Algorithm $\mathcal{B}$ computes $x_0$ as follows:

$$\begin{array}{cc}\hfill & \prod _{i=1}^l{h}_{i,I{D}_i}^r=\prod _{i=1}^l{(g_1^{a_{2i-1+I{D}_i}})}^{\frac{-b}{a_{2j-1+I{D}_j}}+r^{\prime }}·g_1^{v_{2i-1+I{D}_i}r}\hfill \\ \hfill & =\prod _{i=1,i\ne j}^l{g}_1^{-b·\frac{a_{2i-1+I{D}_i}}{a_{2j-1+I{D}_j}}}·g_1^{-b}·\prod _{i=1}^l{(g_1^{a_{2i-1+I{D}_i}})}^{r^{\prime }}·g_1^{v_{2i-1+I{D}_i}r}.\hfill \end{array}$$

$$\begin{array}{cc}\hfill h_0^r& ={({(\prod _{i=1}^l{h}_{i,C{L}_i^{*}})}^{-1}·g_1^{{\gamma }_1})}^r\hfill \\ \hfill & ={(\prod _{i=1}^l{g}_1^{-a_{2i-1+C{L}_i^{*}}}·g_1^{{\gamma }_1})}^{\frac{-b}{a_{2j-1+I{D}_j}}+r^{\prime }}·g_1^{-v_{2i-1+C{L}_i^{*}}r}\hfill \\ \hfill & =\prod _{i=1}^l{g}_1^{b·\frac{a_{2i-1+C{L}_i^{*}}}{a_{2j-1+I{D}_j}}}·g_1^{\frac{-b}{a_{2j-1+I{D}_j}}{\gamma }_1}·g_1^{-v_{2i-1+C{L}_i^{*}}r}·h_0^{r^{\prime }}.\hfill \end{array}$$

$$\begin{array}{cc}\hfill & x_0=g_1^{\alpha -{\alpha }_w}H{\left(ID\right)}^r=g_1^{b-{\alpha }_w}·h_0^r·\prod _{i=1}^l{h}_{i,I{D}_i}^r\hfill \\ \hfill & =g_1^{b-{\alpha }_w}\prod _{i=1}^l{g}_1^{b·\frac{a_{2i-1+C{L}_i^{*}}}{a_{2j-1+I{D}_j}}}·g_1^{\frac{-b}{a_{2j-1+I{D}_j}}{\gamma }_1}·g_1^{-v_{2i-1+C{L}_i^{*}}r}·h_0^{r^{\prime }}\hfill \\ \hfill & ·\prod _{i=1,i\ne j}^l{g}_1^{-b\frac{a_{2i-1+I{D}_i}}{a_{2j-1+I{D}_j}}}·g_1^{-b}·\prod _{i=1}^l{(g_1^{a_{2i-1+I{D}_i}})}^{r^{\prime }}·g_1^{v_{2i-1+I{D}_i}r}\hfill \\ \hfill & =g_1^{-{\alpha }_w}\prod _{i=1}^l{g}_1^{b·\frac{a_{2i-1+C{L}_i^{*}}}{a_{2j-1+I{D}_j}}}·g_1^{\frac{-b}{a_{2j-1+I{D}_j}}{\gamma }_1}·h_0^{r^{\prime }}·\prod _{i=1,i\ne j}^l{g}_1^{-b·\frac{a_{2i-1+I{D}_i}}{a_{2j-1+I{D}_j}}}\hfill \\ \hfill & ·\prod _{i=1}^l{(g_1^{a_{2i-1+I{D}_i}})}^{r^{\prime }}·g_1^{-v_{2i-1+C{L}_i^{*}}r}·g_1^{v_{2i-1+I{D}_i}r}.\hfill \end{array}$$

Algorithm $\mathcal{B}$ computes $x_i$, $y_0$, $y_i$, and z as follows:

$$\begin{array}{cc}\hfill x_i& =h_{i,\overline{I{D}_i}}^r=g_1^{a_{2i-1+\overline{I{D}_i}}·(\frac{-b}{a_{2j-1+I{D}_j}}+r^{\prime })}·g_1^{v_{2i-1+\overline{I{D}_i}}r}\hfill \\ \hfill & =g_1^{-b·\frac{a_{2i-1+\overline{I{D}_i}}}{a_{2j-1+I{D}_j}}}·{(g_1^{a_{2i-1+\overline{I{D}_i}}})}^{r^{\prime }}·g_1^{v_{2i-1+\overline{I{D}_i}}r}.\hfill \end{array}$$

$$\begin{array}{cc}\hfill y_0& =k_0^r={({(\prod _{i=1}^l{k}_{i,R{L}_i^{*}})}^{-1}·g_1^{{\gamma }_2})}^{\frac{-b}{a_{2j-1+I{D}_j}}+r^{\prime }}\hfill \\ \hfill & =\prod _{i=1}^l{g}_1^{b·\frac{a_{2l+2i-1+R{L}_i^{*}}}{a_{2j-1+I{D}_j}}}·g_1^{{\gamma }_2·\frac{-b}{a_{2j-1+I{D}_j}}}·k_0^{r^{\prime }}·g_1^{-v_{2l+2i-1+R{L}_i^{*}}r}\hfill \end{array}$$

$$\begin{array}{cc}\hfill y_{2i-1}& =g_1^{{\alpha }_w}{k}_{i,\overline{I{D}_i}}^r=g_1^{{\alpha }_w}·g_1^{-b·\frac{a_{2l+2i-1+\overline{I{D}_i}}}{a_{2j-1+I{D}_j}}}·{(g_1^{a_{2l+2i-1+\overline{I{D}_i}}})}^{r^{\prime }}·g_1^{v_{2l+2i-1+\overline{I{D}_i}}r}.\hfill \end{array}$$

$$\begin{array}{cc}\hfill y_{2i}& =k_{i,I{D}_i}^r=g_1^{-b·\frac{a_{2l+2i-1+I{D}_i}}{a_{2j-1+I{D}_j}}}·{(g_1^{a_{2l+2i-1+I{D}_i}})}^{r^{\prime }}·g_1^{v_{2l+2i-1+I{D}_i}r}.\hfill \end{array}$$

$$\begin{array}{cc}\hfill z& =g_2^r=g_2^{\frac{-b}{a_{2j-1+I{D}_j}}+r^{\prime }}=g_2^{\frac{-b}{a_{2j-1+I{D}_j}}}·g_2^{r^{\prime }}.\hfill \end{array}$$

(ii)

$ID\in C{L}^{*}$ and $ID\in R{L}^{*}$ :

Algorithm $\mathcal{B}$ selects random exponents $r^{\prime }$ and u$\in {\mathbb{Z}}_p$ and sets $r={\sum }_{j=1}^l\frac{-b}{a_{2l+2j-1+\overline{I{D}_j}}}+r^{\prime }$. It sets ${\alpha }_w=b-u$.

Algorithm $\mathcal{B}$ can compute $g^{v_{i}r}$, since $g_1^{v_{i}r}=g_1^{{\sum }_{j=1}^l\frac{-b}{a_{2l+2j-1+\overline{I{D}_j}}}·v_i}·g_1^{v_i{r}^{\prime }}$.

Algorithm $\mathcal{B}$ computes $x_0$ as follows:

$$\begin{array}{cc}\hfill \prod _{i=1}^l{h}_{i,I{D}_i}^r=& \prod _{i=1}^l{(g_1^{a_{2i-1+I{D}_i}})}^{{\sum }_{j=1}^l\frac{-b}{a_{2l+2j-1+\overline{I{D}_j}}}+r^{\prime }}·g_1^{v_{2i-1+I{D}_i}r}\hfill \\ \hfill =& \prod _{i=1}^l\prod _{j=1}^l{g}_1^{-b·\frac{a_{2i-1+I{D}_i}}{a_{2l+2j-1+\overline{I{D}_j}}}}·\prod _{i=1}^l{(g_1^{a_{2i-1+I{D}_i}})}^{r^{\prime }}·g_1^{v_{2i-1+I{D}_i}r}.\hfill \end{array}$$

$$\begin{array}{cc}\hfill h_0^r=& {({(\prod _{i=1}^l{h}_{i,C{L}_i^{*}})}^{-1}·g_1^{{\gamma }_1})}^r\hfill \\ \hfill =& {(\prod _{i=1}^l{g}_1^{-a_{2i-1+C{L}_i^{*}}}·g_1^{{\gamma }_1})}^{{\sum }_{j=1}^l\frac{-b}{a_{2l+2j-1+\overline{I{D}_j}}}+r^{\prime }}·\prod _{i=1}^l{g}_1^{-v_{2i-1+C{L}_i^{*}}r}\hfill \\ \hfill =& \prod _{i=1}^l\prod _{j=1}^l{g}_1^{b\frac{a_{2i-1+C{L}_i^{*}}}{a_{2l+2j-1+\overline{I{D}_j}}}}·\prod _{j=1}^l{g}_1^{\frac{-b}{a_{2l+2j-1+\overline{I{D}_j}}}{\gamma }_1}·h_0^{r^{\prime }}·\prod _{i=1}^l{g}_1^{-v_{2i-1+C{L}_i^{*}}r}.\hfill \end{array}$$

$$\begin{array}{cc}\hfill x_0& =g_1^{\alpha -{\alpha }_w}H{\left(ID\right)}^r=g_1^u{h}_0^r\prod _{i=1}^l{h}_{i,I{D}_i}^r.\hfill \end{array}$$

Algorithm $\mathcal{B}$ computes $x_i$, $y_0$, $y_i$, and z as follows:

$$\begin{array}{cc}\hfill x_i& =h_{i,\overline{I{D}_i}}^r\hfill \\ \hfill & =g_1^{a_{2i-1+\overline{I{D}_i}}·({\sum }_{j=1}^l\frac{-b}{a_{2l+2j-1+\overline{I{D}_j}}}+r^{\prime })}·g_1^{v_{2i-1+\overline{I{D}_i}}r}\hfill \\ \hfill & =\prod _{j=1}^l{g}_1^{-b·\frac{a_{2i-1+\overline{I{D}_i}}}{a_{2l+2j-1+\overline{I{D}_j}}}}·{(g_1^{a_{2i-1+\overline{I{D}_i}}})}^{r^{\prime }}·g_1^{v_{2i-1+\overline{I{D}_i}}r}.\hfill \end{array}$$

$$\begin{array}{cc}\hfill y_0& =k_0^r={({(\prod _{i=1}^l{k}_{i,R{L}_i^{*}})}^{-1}·g_1^{{\gamma }_2})}^{{\sum }_{j=1}^l\frac{-b}{a_{2l+2j-1+\overline{I{D}_j}}}+r^{\prime }}\hfill \\ \hfill & =\prod _{i=1}^l\prod _{j=1}^l{g}_1^{b·\frac{a_{2l+2i-1+R{L}_i^{*}}}{a_{2l+2j-1+\overline{I{D}_j}}}}·\prod _{j=1}^l{g}_1^{\frac{-b}{a_{2l+2j-1+\overline{I{D}_j}}}·{\gamma }_2}·k_0^{r^{\prime }}·\prod _{i=1}^l{g}_1^{-v_{2i-1+R{L}_i^{*}}r}.\hfill \end{array}$$

Note that $R{L}_i^{*}=I{D}_i$ if $R{L}_i^{*}\ne *$.

If $R{L}_i^{*}=*$ then $a_{2l+2i-1+R{L}_i^{*}}=0$ since $k_{i,*}=1$.

$$\begin{array}{cc}\hfill y_{2i-1}& =g_1^{{\alpha }_w}·k_{i,I{D}_i}^r\hfill \\ \hfill & =g^{b-u}·g_1^{{\sum }_{j=1}^l-b·\frac{a_{2l+2i-1+\overline{I{D}_i}}}{a_{2l+2j-1+\overline{I{D}_j}}}}·{(g_1^{a_{2l+2i-1+\overline{I{D}_i}}})}^{r^{\prime }}·g_1^{v_{2l+2i-1+\overline{I{D}_i}}r}\hfill \\ \hfill & =g_1^{b-u}\prod _{j=1,j\ne i}^l{g}_1^{-b·\frac{a_{2l+2i-1+\overline{I{D}_i}}}{a_{2l+2j-1+\overline{I{D}_j}}}}·g_1^{-b}·{(g_1^{a_{2l+2i-1+\overline{I{D}_i}}})}^{r^{\prime }}·g_1^{v_{2l+2i-1+\overline{I{D}_i}}r}\hfill \\ \hfill & =g_1^{-u}\prod _{j=1,j\ne i}^l{g}_1^{-b·\frac{a_{2l+2j-1+\overline{I{D}_j}}}{a_{2l+2j-1+\overline{I{D}_j}}}}·{(g_1^{a_{2l+2i-1+\overline{I{D}_i}}})}^{r^{\prime }}·g_1^{v_{2l+2i-1+\overline{I{D}_i}}r}.\hfill \end{array}$$

$$\begin{array}{cc}\hfill y_{2i}& =k_{i,I{D}_i}^r=g_1^{{\sum }_{j=1}^l-b·\frac{a_{2l+2i-1+I{D}_i}}{a_{2l+2j-1+\overline{I{D}_j}}}}·{(g_1^{a_{2l+2i-1+I{D}_i}})}^{r^{\prime }}·g_1^{v_{2l+2i-1+I{D}_i}r}\hfill \end{array}$$

$$\begin{array}{c}\hfill z=g_2^r=g_2^{{\sum }_{j=1}^l\frac{-b}{a_{2l+2j-1+\overline{I{D}_j}}}+r^{\prime }}=\prod _{j=1}^l{g}_2^{\frac{-b}{a_{2l+2j-1+\overline{I{D}_j}}}}·g_2^{r^{\prime }}.\end{array}$$

(iii)

$ID\in C{L}^{*}$ and $ID\notin R{L}^{*}$:

Algorithm $\mathcal{B}$ does not require the $S{K}_{ID}$, since $ID\in S^{*}$.

Challenge:

Algorithm $\mathcal{A}$ submits challenge labels $(C{L}^{\prime },R{L}^{\prime })$ and two messages $M_0^{*}$, $M_1^{*}$. If $(C{L}^{\prime }\ne C{L}^{*})\vee (R{L}^{\prime }\ne R{L}^{*})$, then Algorithm $\mathcal{B}$ aborts the simulation since it failed to guess the challenge labels. Otherwise, $\mathcal{B}$ flips a random coin $\xi \in \{0,1\}$ internally. $\mathcal{B}$ implicitly sets $t=c$ and creates a challenge ciphertext as

$$\begin{array}{c}\hfill (C_0,C_1,C_2,C_3)=(T·M_{\xi }^{*},g_2^c,{\left(g_1^c\right)}^{{\gamma }_1},{\left(g_1^c\right)}^{{\gamma }_2}).\end{array}$$

Guess:

Finally, $\mathcal{A}$ outputs a guess ${\xi }^{\prime }\in \{0,1\}$. Algorithm $\mathcal{B}$ concludes its own game by producing a guess as follows. If $\xi ={\xi }^{\prime }$ then $\mathcal{B}$ outputs 1 meaning $T=e{(g_1,g_2)}^{bc}$. Otherwise, it outputs 0 meaning that T is random in ${\mathbb{G}}_T$.

To complete the proof, we show that public keys, private keys, and the challenge ciphertext are correctly distributed. The public keys are correctly distributed since new random elements $v_i$ are chosen from ${\mathbb{Z}}_p$. The private keys are correctly distributed as shown in the query phase. The challenge ciphertext is correctly distributed since it satisfies the following equation:

$$\begin{array}{cc}\hfill C_0& =e{(g_1,g_2)}^{\alpha t}{M}_{\xi }^{*}=e{(g_1,g_2)}^{bc}{M}_{\xi }^{*},\hfill \\ \hfill C_1& =g_2^t=g_2^c,\hfill \\ \hfill C_2^{t^{-1}}& =H\left(C{L}^{*}\right)=h_0\prod _{i=1}^l{h}_{i,C{L}_i^{*}}\hfill \\ \hfill & ={(\prod _{i=1}^l{h}_{i,C{L}_i^{*}})}^{-1}{g}_1^{{\gamma }_1}\prod _{i=1}^l{h}_{i,C{L}_i^{*}}=g_1^{{\gamma }_1},\hfill \\ \hfill C_3^{t^{-1}}& =K\left(R{L}^{*}\right)=k_0\prod _{i=1}^l{k}_{i,R{L}_i^{*}}\hfill \\ \hfill & ={(\prod _{i=1}^l{k}_{i,R{L}_i^{*}})}^{-1}{g}_1^{{\gamma }_2}\prod _{i=1}^l{k}_{i,R{L}_i^{*}}=g_1^{{\gamma }_2}.\hfill \end{array}$$

When the input tuple is sampled from $P_{SMEBDH}$ (where $T=e{(g_1,g_2)}^{bc}$), then $\mathcal{A}$’s view is identical to its view in a real attack game, and, therefore, $\mathcal{A}$ satisfies $\left|Pr\right[\xi ={\xi }^{\prime }]-1/2|\ge ϵ$. When the input tuple is sampled from $R_{SMEBDH}$ (where T is uniform in ${\mathbb{G}}_T$), then $Pr[\xi ={\xi }^{\prime }]=1/2$. Therefore, with $g_1$ uniform in ${\mathbb{G}}_1$, $g_2$ uniform in ${\mathbb{G}}_2$, b and c uniform in ${\mathbb{Z}}_p$, and T uniform in ${\mathbb{G}}_T$, we have that

$$\begin{array}{cc}\hfill |Pr[B(P,e{(g_1,g_2)}^{bc})=0]& -Pr\left[B\right(P,T)=0]|\hfill \\ \hfill & \ge \left|\right(1/2+ϵ)-1/2|=ϵ\hfill \end{array}$$

as required, which completes the proof of the theorem. □

5. CCA-Secure Broadcast Encryption

In this section, we extend our proposed BESTIE to the chosen-cipertext-secure broadcast encryption, similar to Reference [3,37] by attaching an unforgeable one-time signature scheme to the semantically secure PKBE scheme. To utilize the CCA extension in Reference [3,37], we require our broadcast encryption to support general IDs such that wildcards (*) can be used in IDs for key generation. Thus, we first describe a general ID scheme as a building block. Then, we represent a CCA-secure scheme with a complexity analysis and security proof.

5.1. General ID Scheme

In this section, we explain a general ID scheme as described in Reference [3], which can include wildcards (*) in the IDs for key generation. Similar to Section 4.2, we denote $I{D}_i$, $C{L}_i$, and $R{L}_i$ the ith bit of bit-strings $ID$, $CL$, and $RL$, respectively. In addition, we denote $H\left(ID\right)$ = $h_0{\prod }_{i=1}^l{h}_{i,I{D}_i}$, $K\left(ID\right)$ = $k_0{\prod }_{i=1}^l{k}_{i,I{D}_i}$, $h_{i,*}=h_{i,0}·h_{i,1}$ and $k_{i,*}=1$.

Setup($l,\lambda$): The setup is equivalent to the main scheme in Section 4.2.

$$\begin{array}{cc}\hfill MK& =g_1^{\alpha },\hfill \\ \hfill PK=& ((p,{\mathbb{G}}_1,{\mathbb{G}}_2,{\mathbb{G}}_T,e),g,h_0,h_{1,0},h_{1,1},\cdots ,h_{l,0},h_{l,1},\hfill \\ \hfill & k_0,k_{1,0},k_{1,1},\cdots ,k_{l,0},k_{l,1},\mathsf{\Omega }=e{(g_1,g_2)}^{\alpha }).\hfill \end{array}$$

KeyGen($ID,MK,PK$): Private key generation is similar to the main scheme, except for the wildcards (*). We set $h_{i,*}=1$ and populate $h_{i,0}^r$ and $h_{i,1}^r$ for $h_{i,\overline{*}}^r$. Similarly, the interpretation of $k_{i,*}$ covers both $k_{i,0}$ and $k_{i,1}$. Therefore, if $I{D}_i=*$, $S{K}_{ID}$ includes both ${g_1}^{{\alpha }_w}{k}_{i,0}^r$ and ${g_1}^{{\alpha }_w}{k}_{i,1}^r$, as well as $h_{i,0}^r$ and $h_{i,1}^r$. The key generation is summarized as follows:

$$\begin{array}{cc}\hfill S{K}_{ID}=(& x_0,x_1,\cdots ,x_l,y_0,y_1,\cdots ,y_{2l},z),where\hfill \\ \hfill & x_0=g_1^{\alpha -{\alpha }_w}H{\left(ID\right)}^r,\hfill \\ \hfill & x_i=h_{i,{\overline{ID}}_i}^r(1\le i\le l)\hfill \\ \hfill & y_0=k_0^r\hfill \\ \hfill & \left\{\begin{array}{cc}\hfill & y_{2i-1}=g_1^{{\alpha }_w}{k}_{i,{\overline{ID}}_i}^r\hfill \\ \hfill & y_{2i}=k_{i,I{D}_i}^r\hfill \end{array}\right\}(1\le i\le l),ifI{D}_i\ne *\hfill \\ \hfill & \left\{\begin{array}{cc}\hfill & y_{2i-1}=g_1^{{\alpha }_w}{k}_{i,0}^r\hfill \\ \hfill & y_{2i}=g_1^{{\alpha }_w}{k}_{i,1}^r\hfill \end{array}\right\}(1\le i\le l),ifI{D}_i=*\hfill \\ \hfill & z=g_2^r.\hfill \end{array}$$

Encrypt($S,PK,M$): The encryption is equivalent to the main scheme in Section 4.2.

$$\begin{array}{c}\hfill Hd{r}_S=\{C_0={\mathsf{\Omega }}^t·M,C_1=g_2^t,C_2=H{\left(CL\right)}^t,C_3=K{\left(RL\right)}^t\}.\end{array}$$

Decrypt($S,ID,S{K}_{ID},Hd{r}_S$): Similar to the decryption in Section 4.2, for $I{D}_i\ne *$, let $P=\left\{i\right|I{D}_i\ne *\wedge I{D}_i\ne R{L}_i\wedge R{L}_i\ne *\}$ and $Q=\left\{i\right|I{D}_i\ne *\wedge I{D}_i=R{L}_i\wedge R{L}_i\ne *\}$. We define new sets for wildcards as $P^{*}=\{I{D}_i=*\wedge R{L}_i=1\}$ and $Q^{*}=\{I{D}_i=*\wedge R{L}_i=0\}$.

Then, let $d=\left|P\right|+|P^{*}|+|Q^{*}|$, where $\left|P\right|$ denotes the number of bits which in $ID$ are different from $RL$, and $|P^{*}|+|Q^{*}|$ indicates the number of * in $ID$.

If $d>0$, it parses $S{K}_{ID}=(x_0,x_1,\cdots ,x_l,y_0,y_1\cdots ,y_{2l},z)$.

Then, it computes

$$\begin{array}{cc}\hfill x^{\prime }=& x_0·\prod _{C{L}_i=*\wedge I{D}_i\ne *}{x}_i·\prod _{C{L}_i\ne *\wedge I{D}_i=*}{h}_{i,C{L}_i}^r·\prod _{C{L}_i=*\wedge I{D}_i=*}{h}_{i,0}^r{h}_{i,1}^r\hfill \\ \hfill y^{\prime }=& {(y_0·\prod _{i\in P\cup P^{*}}{y}_{2i-1}·\prod _{i\in Q\cup Q^{*}}{y}_{2i})}^{d^{-1}}\hfill \end{array}$$

and outputs a message as

$$\begin{array}{c}\hfill M=C_0·e{(x^{\prime }·y^{\prime },C_1)}^{-1}·e(C_2·C_3^{d^{-1}},z).\end{array}$$

Otherwise, it outputs ⊥.

5.2. CCA-Secure Scheme

In the following notation, a vector $V=(v_1,\cdots ,v_n)$ is interchangeably presented as $v_1\cdots v_n$. With vectors $V=(v_1,\cdots ,v_n)$ and $V^{\prime }=(v_1^{\prime },\cdots ,v_m^{\prime })$, we denote the concatenation of V and $V^{\prime }$ or $V\left|\right|V^{\prime }=(v_1,\cdots ,v_n,v_1^{\prime },\cdots ,v_m^{\prime })$.

We extend our semantically secure broadcast encryption scheme using a similar technique presented in Reference [3,37] to attain the chosen ciphertext security. We can construct an l-level public key broadcast encryption system $\mathsf{\Pi }=(\mathsf{Setup},\mathsf{KeyGen},\mathsf{Encrypt},\mathsf{Decrypt})$ secure against chosen-ciphertext attacks using the $(l+z)$-level ${\mathsf{\Pi }}^{\prime }=({\mathsf{Setup}}^{\prime },{\mathsf{KeyGen}}^{\prime },{\mathsf{Encrypt}}^{\prime },{\mathsf{Decrypt}}^{\prime })$ semantically secure broadcast encryption scheme with a strong one-time signature scheme $(SigKeyGen,Sign,Verify)$ with verification keys which are mapped to ${\{0,1\}}^z$. The main idea is that $ID=(b_1,\cdots ,b_l)\in {\{1,0,*\}}^l$ in $\mathsf{\Pi }$ is transformed to $I{D}^{\prime }=ID\left|\right|{*}^z=(b_1,\cdots ,b_l,*,\cdots ,*)\in {\{1,0,*\}}^{l+z}$ in ${\mathsf{\Pi }}^{\prime }$. Therefore, the secret key $S{K}_{ID}$ for $ID$ in $\mathsf{\Pi }$ becomes the secret key $S{K}_{I{D}^{\prime }}$ in ${\mathsf{\Pi }}^{\prime }$. When encrypting a message M for the $ID$ in $\mathsf{\Pi }$, the sender constructs a z-bit verification key $V_{sig}=(e_1,\cdots ,e_z)\in {\{0,1\}}^z$ and then encrypts M to the $I{D}^{\prime }=ID\left|\right|V_{sig}$ using ${\mathsf{\Pi }}^{\prime }$.

For more detail, l-level $\mathsf{\Pi }$ is built using $(l+z)$-level ${\mathsf{\Pi }}^{\prime }$ and a one-time signature scheme as the following:

Setup($l,\lambda$): Let $2^l$ be the maximum number of users and $lambda$ be the session key length. Assume that the signature verification key space is ${\{0,1\}}^z$.

Perform a semantically secure broadcast encryption scheme ${\mathsf{\Pi }}^{\prime }$ to generate the public key $PK$ and master secret key $MK$, and output $PK$ and $MK$.

$$\begin{array}{cc}\hfill & PK,MK\leftarrow {\mathsf{Setup}}^{\prime }(l+z).\hfill \end{array}$$

KeyGen($ID,MK,PK$): To generate a private key $S{K}_{ID}$ for an identity $ID=b_1\cdots b_l$ utilizing the master secret key, encode $ID$ to $I{D}^{\prime }=ID\left|\right|\underset{z}{\overset{**\cdots *}{︸}}$. The key generation algorithm in ${\mathsf{KeyGen}}^{\prime }$ of ${\mathsf{\Pi }}^{\prime }$ generates the secret key $S{K}_{I{D}^{\prime }}^{\prime }$.

Let $S{K}_{ID}=S{K}_{I{D}^{\prime }}^{\prime }=(S{K}_{I{D}^{\prime },1}^{\prime },\cdots ,S{K}_{I{D}^{\prime },l+z}^{\prime })$ and output ${\left\{S{K}_{ID}\right\}}_{ID\in {\{0,1\}}^l}$.

$$\begin{array}{cc}\hfill & {\left\{S{K}_{I{D}^{\prime }}^{\prime }\right\}}_{I{D}^{\prime }\in {\{0,1\}}^{l+z}}\leftarrow {\mathsf{KeyGen}}^{\prime }(I{D}^{\prime },MK,PK).\hfill \end{array}$$

Encrypt($S,PK,M$): Perform $SigKeyGen\left(1^z\right)$ algorithm to get a signature signing key $K_{sig}$ and a verification key $V_{sig}$. Assume that $V_{sig}=e_1\cdots e_z$. For a given $S=\left(CL\right||V_{sig},RL|\left|V_{sig}\right)$, run ${\mathsf{Encrypt}}^{\prime }$ to obtain header $Hd{r}_S$ and sign the header as

$$\begin{array}{cc}\hfill Hd{r}_S& \leftarrow {\mathsf{Encrypt}}^{\prime }(S,PK,M)\hfill \\ \hfill \sigma & \leftarrow Sign(Hd{r}_S,K_{sig})\hfill \end{array}$$

and output the tuple $Hdr$ as $(Hd{r}_S,\sigma ,V_{sig})$.

Decrypt($S,ID,S{K}_{ID},Hdr$):

Parse $Hdr=((C_0,C_1,C_2,C_3),\sigma ,V_{sig})$.

• Verify if $\sigma$ is valid against $(C_0,C_1,C_2,C_3)$ under the key $V_{sig}$. If invalid, output ⊥.
• Otherwise, encode $ID$ to $I{D}^{\prime }=ID\left|\right|\underset{z}{\overset{**\cdots *}{︸}}$, execute
  ${\mathsf{Decrypt}}^{\prime }$($S,I{D}^{\prime },S{K}_{ID},Hdr)$ and output the message M.

Correctness can be shown with a similar computation to the one in Section 4. It is noted that the user key size is enlarged from $O\left(l\right)$ to $O(l+z)$, and the header size increases by the size of a signature and a verification key.

5.3. Complexity Analysis

In this section, we analyze the complexity of the key sizes and the execution time of the proposed public key broadcast encryption scheme. The general complexity is increased from l to $l+z$ where z is a bit-length of the one-time signature verification key, since the CCA-secure extension requires z additional depth from the original scheme.

For the key sizes, the public key size requires $2(l+z)+4$ elements, and the secret key size requires $2(l+z)+3$ elements. The header size is 5 fixed elements, since the CCA-secure header requires one-time signature in addition to the original header.

The encryption additionally requires one-time signature singing time and the decryption additionally requires one-time signature verifying time. However, one-time signature processing time is very fast and negligible: the execution times remain almost the same as the original CPA-secure scheme.

5.4. Security Proof

Theorem 3. 

Let $\mathbb{G}$ be a bilinear group of prime order p. For any integer l, the public key broadcast encryption system Π is $(t,{ϵ}_1+{ϵ}_2,l,\lambda ,D)$ CCA-secure if the public key broadcast encryption system ${\mathsf{\Pi }}^{\prime }$ is $(t^{\prime },{ϵ}_1,l+z,\lambda ,0)$ semantically secure in $\mathbb{G}$ and the signature scheme is $(t^{\prime \prime },{ϵ}_2,z,1)$ strongly existentially unforgeable. Moreover, $t<t^{\prime }-(2(l+z)\mathit{a}+2\mathit{p})·D-t_s$, where $\mathit{a}$ is point addition time, $\mathit{p}$ is pairing time, and $t_s$ presents the sum of $SigKeyGen$, $Sign$ and $Verify$ computation time.

Proof. 

Assume that there exists a t-time adversary $\mathcal{A}$ such that $|AdvB{r}_{\mathcal{A},\mathsf{\Pi }}-1/2|>{ϵ}_1+{ϵ}_2$. We construct an algorithm $\mathcal{B}$ that has advantage $|AdvB{r}_{B,{\mathsf{\Pi }}^{\prime }}-1/2|>{ϵ}_1$ in $\mathbb{G}$. Algorithm $\mathcal{B}$ proceeds as following.

Init: Algorithm $\mathcal{B}$ performs $\mathcal{A}$ and receives set $S^{*}$ in which users $\mathcal{A}$ challenges on. $\mathcal{B}$ executes the $SigKeyGen$ algorithm to obtain a signature signing key $K_{sig}^{*}$ and a verification key $V_{sig}^{*}\in {\{0,1\}}^z$. Let $V_{sig}^{*}=e_1\cdots e_z$; then, $\mathcal{B}$ builds $S^{**}$ = $\left\{U\right|\left|V_{sig}^{*}\right|U\in S^{*}\}$ and outputs it.

Setup:$\mathcal{B}$ gets the public key $PK$ of ${\mathsf{\Pi }}^{\prime }$ from challenger $\mathcal{C}$.

KeyGen:$\mathcal{B}$ obtains secret keys $S{K}_{I{D}^{\prime }}$ for revoked $I{D}^{\prime }\notin S^{**}$ from challenger $\mathcal{C}$. Note that $I{D}^{\prime }\notin S^{**}$ iff $\forall X\in S^{**}$, $\exists i$, $I{D}_i^{\prime }\ne X_i\wedge X_i\ne *$, and $I{D}^{\prime }\in S^{**}$ iff $\exists X\in S^{**}$, $\forall i$, $I{D}_i^{\prime }=X_i\vee X_i=*$.

Since ${\mathsf{\Pi }}^{\prime }$ can generate secret keys using *, $I{D}^{\prime }$ can be classified into the following two forms:

• $I{D}^{\prime }=ID\left|\right|\underset{z}{\overset{**\cdots *}{︸}}$ for $ID\notin S^{*}$
• $I{D}^{\prime }=ID\left|\right|\underset{k-1}{\overset{**\cdots *}{︸}}{\overline{e}}_k\underset{z-k}{\overset{**\cdots *}{︸}}$ for $ID\in S^{*}$ and $k\in \{1,\cdots ,z\}$.

Algorithm $\mathcal{B}$ responds with $PK$ and secret keys $S{K}_{I{D}^{\prime }}^{\prime }$ of the first type of $I{D}^{\prime }$. Note that the secret key $S{K}_{ID}=S{K}_{I{D}^{\prime }}^{\prime }$ where $I{D}^{\prime }=ID\left|\right|\underset{z}{\overset{**\cdots *}{︸}}$. The secret keys $S{K}_{I{D}^{\prime }}^{\prime }$ of the second type of $I{D}^{\prime }$ are used to respond to the decryption queries of $\mathcal{A}$ as following.

Phase 1: Algorithm $\mathcal{A}$ issues decryption queries.

Let $(ID,S,Hdr)$ be a decryption query where $S\subseteq S^{*}$ and $ID\in S$. Let $Hdr=(Hd{r}_S,\sigma ,V_{sig})$. Algorithm $\mathcal{B}$ responds as following:

• Perform $Verify$ to check the signature $\sigma$ against $Hd{r}_S=(C_0,C_1,C_2,C_3)$ with verification key $V_{sig}$. If the signature is invalid, then $\mathcal{B}$ returns ⊥.
• If $V_{sig}=V_{sig}^{*}$, then a forge event happens, and algorithm $\mathcal{B}$ outputs a random bit $b\stackrel{\$}{\leftarrow }\{0,1\}$ and aborts the simulation.
• Otherwise, $\mathcal{B}$ decrypts the header using the second type of secret keys.

Let $V=\underset{k-1}{\overset{**\cdots *}{︸}}{\overline{e}}_k\underset{z-k}{\overset{**\cdots *}{︸}}$, where $k\in \{1,\cdots ,z\}$. Using $S{K}_{ID\left|\right|V}$, B can obtain $M\leftarrow {\mathsf{Decrypt}}^{\prime }(S,ID,S{K}_{ID\left|\right|V},Hd{r}_S)$ since $V_{sig}$ is covered by V.

Challenge: When $\mathcal{A}$ outputs $M_0$ and $M_1$ for the challenge, $\mathcal{B}$ bypasses them to $\mathcal{C}$ and gets the challenge $Hd{r}_S^{*}$. To generate a challenge for $\mathcal{A}$, $\mathcal{B}$ calculates $Hd{r}^{*}$ as the following:

$$\begin{array}{c}{\sigma }^{*}\leftarrow Sign(Hd{r}_S^{*},K_{sig}^{*})\hfill \\ Hd{r}^{*}\leftarrow (Hd{r}_S^{*},{\sigma }^{*},V_{sig}^{*}).\hfill \end{array}$$

$\mathcal{B}$ replies with $Hd{r}^{*}$ to $\mathcal{A}$.

Phase 2: Same as in query phase 1.

Guess: Algorithm $\mathcal{A}$ outputs a guess $b\in \{0,1\}$. Then, $\mathcal{B}$ outputs 1 if $b=b^{\prime }$, or outputs 0 otherwise.

Notice that algorithm $\mathcal{B}$ can simulate all queries to run $\mathcal{A}$, $\mathcal{B}$’s success probability as the following:

$$\begin{array}{c}|AdvB{r}_{B,{\mathsf{\Pi }}^{\prime }}-\frac{1}{2}|\ge |AdvB{r}_{\mathcal{A},\mathsf{\Pi }}-\frac{1}{2}|-Pr\left[\mathit{forge}\right]\hfill \\ >({ϵ}_1+{ϵ}_2)-Pr\left[\mathit{forge}\right].\hfill \end{array}$$

It is required to compute the probability of $\mathcal{B}$ aborting the simulation as a result of a forge to conclude the proof of Theorem 3. We argue that $Pr\left[\mathit{forge}\right]<{ϵ}_2$. Otherwise one can utilize $\mathcal{A}$ to forge signatures with a probability of at least ${ϵ}_2$. Shortly, we can build another simulator that knows the private key, but receives $K_{sig}^{*}$ as a challenge in an existential forgery game. In the above experiment, $\mathcal{A}$ aborts by submitting a query that includes an existential forgery under $K_{sig}^{*}$ on some ciphertexts. Our simulator can use this forgery to win the existential forgery game. During the game the adversary makes only one chosen message query to generate the signature for the challenge ciphertext. Hence, $Pr\left[\mathit{forge}\right]<{ϵ}_2$. It now follows that $\mathcal{B}$’s advantage is at least ${ϵ}_1$, as required.  □

6. Experiment

In this section, we show and compare the implementation results by constructing the BESTIE protocol on the real IoT system, which can let many useful IoT applications, such as secure multicast, be available. We present the experimental results in terms of three main factors—the ciphertext header size, the execution time, and the key size—in the proposed scheme (BESTIE) and existing PKBE schemes. We programmed and tested the BESTIE and other schemes on the Intel Edison board environment with a 32-bit 500 Mhz processor, which is commonly utilized as a small IoT device. We performed real encryption protocols based on ublinux 3.10.17 system and pairing-based cryptography (PBC) library (element type set as type F, or $f_{param}$, which is size-friendly), from setup to encryption/decryption, and measured the time and size of parameter results.

The number of subsets define the ciphertext header sizes in broadcast encryptions. Figure 3 and Figure 4 compares the number of subsets in the BESTIE, CSD [3], SD [4], and interval schemes [2]. Note that the header sizes are equivalent in BESTIE and CSD since they share the same CSD representation method. In Figure 3, the y axis represents the number of subsets as varying the number of randomly chosen revoked users (x axis) varies. The number of total users is $2^{128}$. The result shows that the number of subsets is strictly linear to the number of revoked users. In Figure 4, instead of a random revocation, we vary the number of randomly chosen secure multicast subsets. Secure multicast subsets are non-hierarchical subsets that include wildcards (*) in the middle of covering labels (e.g., $1**01-10**1$). BESTIE,CSD-15, SD-15, and Interval-15 indicate $2^{15}$ total users. BESTIE, CSD-20, SD-20, and Interval-20 indicate $2^{20}$ total users. Since the CSD representation supports a non-hierarchical representation (* can be placed anywhere), it can cover the non-hierarchical example within a single CSD subset; the number of subsets in BESTIE and CSD is identical to the number of non-hierarchical groups. However, the number of subsets in the SD and interval schemes is large since they only support hierarchical representations.

Figure 5 represents the encryption time in the BESTIE, CSD, and interval schemes by measuring the time of encrypting a fixed message with using each protocol. The y-axis represents the encryption time measured in seconds, and the x-axis represents the bit-length of users. The SD scheme follows the encryption of Reference [20], thus it requires point exponentiation for the increasing bit-length. In the figure, the encryption time in SD increases dramatically when the bit-length gets longer. The results show that, other than the SD scheme, the encryption time remains similar, and BESTIE shows the best encryption performance among the BE schemes.

Figure 6 represents the decryption time in the BESTIE, CSD, and interval schemes, by measuring the time of decrypting a fixed message with using each protocol. Since the decryption is generally performed in a slow IoT (or embedded) system, the decryption performance should be improved. Since the decryption algorithm mostly performs multiplication of secret keys with constant number of pairings and exponentiations in BESTIE and CSD, the decryption time does not increase as the number of users increases. On the other hand, since the interval scheme performs key derivation using a public parameter for decryption, the decryption time is proportional to the depth of users. Hence, BESTIE and CSD are IoT-friendly PKBE schemes in decryption.

Table 2. Key size of BESTIE, CSD, SD, and interval schemes.

	$\mathbf{Depth}$	BESTIE	CSD	SD(HIBE)	Interval
	$\left(\mathbf{bits}\right)$	(Ours)	[3]	[4,20]	[2]
PK size
$\left(KB\right)$	8 bit	0.66	0.66	0.20	0.39
	16 bit	1.29	1.29	0.35	0.70
	32 bit	2.54	2.54	0.66	1.33
	64 bit	5.04	5.04	1.29	2.58
	128 bit	10.04	10.04	2.54	5.08
SK size
$\left(KB\right)$	8bit	0.53	3.79	10.04	2.58
	16 bit	1.00	15.04	80.04	10.08
	32 bit	1.93	60.04	640.04	40.08
	64 bit	3.81	240.04	5120.04	160.08
	128 bit	7.56	960.04	40960.04	640.08

shows the public key and secret key size in the bestie, CSD, SD, and interval schemes. When the number of users is $2^{128}$, BESTIE requires 7.56 KB of SK storage, while CSD, SD, and interval schemes require 960 KB, 40,960 KB, and 640 KB, respectively. Overall, the encryption and decryption performance results show that the BESTIE achieves the fastest encryption and decryption time both less than 200 ms; it indicates that the performance overhead is not an issue in the IoT implementation. The main issue is the secret key size: The key storage sizes in most resource-constrained devices are less than 8 KB. The key size results show that the BESTIE achieves the smallest key size due to the smaller order of $O\left(\log n\right)$, which is the only available result for the restricted key storages in IoT devices.

7. Conclusions

This paper proposes a broadcast encryption scheme for tiny IoT equipment (BESTIE) that reduces the key size suitable for a large scale IoT systems. The proposed BESTIE is a public key broadcast encryption scheme for the combinatorial subset difference (CSD) representation. BESTIE has the most efficient ciphertext header size, which is $2r$ in the worst case, where r is the number of revoked users. Most importantly, BESTIE is the first scheme to reduce a key size to $O\left(\log n\right)$ from $O\left({\log }^{2}n\right)$, which was the minimal key size in existing subset difference-based approaches, without sacrificing any other factor.

The experimental results show that the BESTIE has the best performance in key generation, encryption, and decryption. Furthermore, in BESTIE the SK size is no more than 7 KB, even for the IPv6 128 bit settings (or $2^{128}$ devices). We prove that the proposed BESTIE is secure under q-Simplified Multi-Exponent Bilinear Diffie-Hellman (q-SMEBDH) assumption without the random oracle model.