Low-Complexity Multi-User Parameterized Beamforming in Massive MIMO Systems
Abstract
1. Introduction
2. System Model
3. Proposed Beamforming Scheme
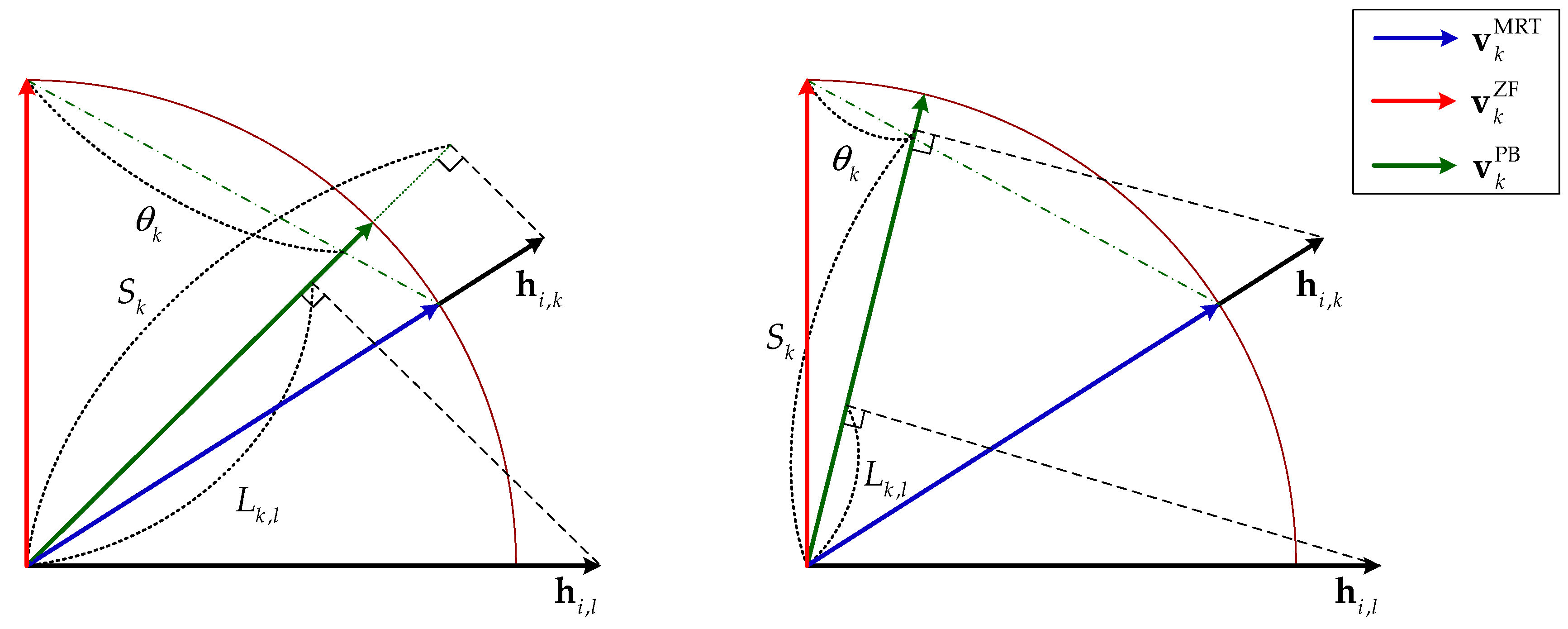
3.1. Proposed Multi-User Parameterized Beamforming (MUPB)
3.2. Computational Complexity
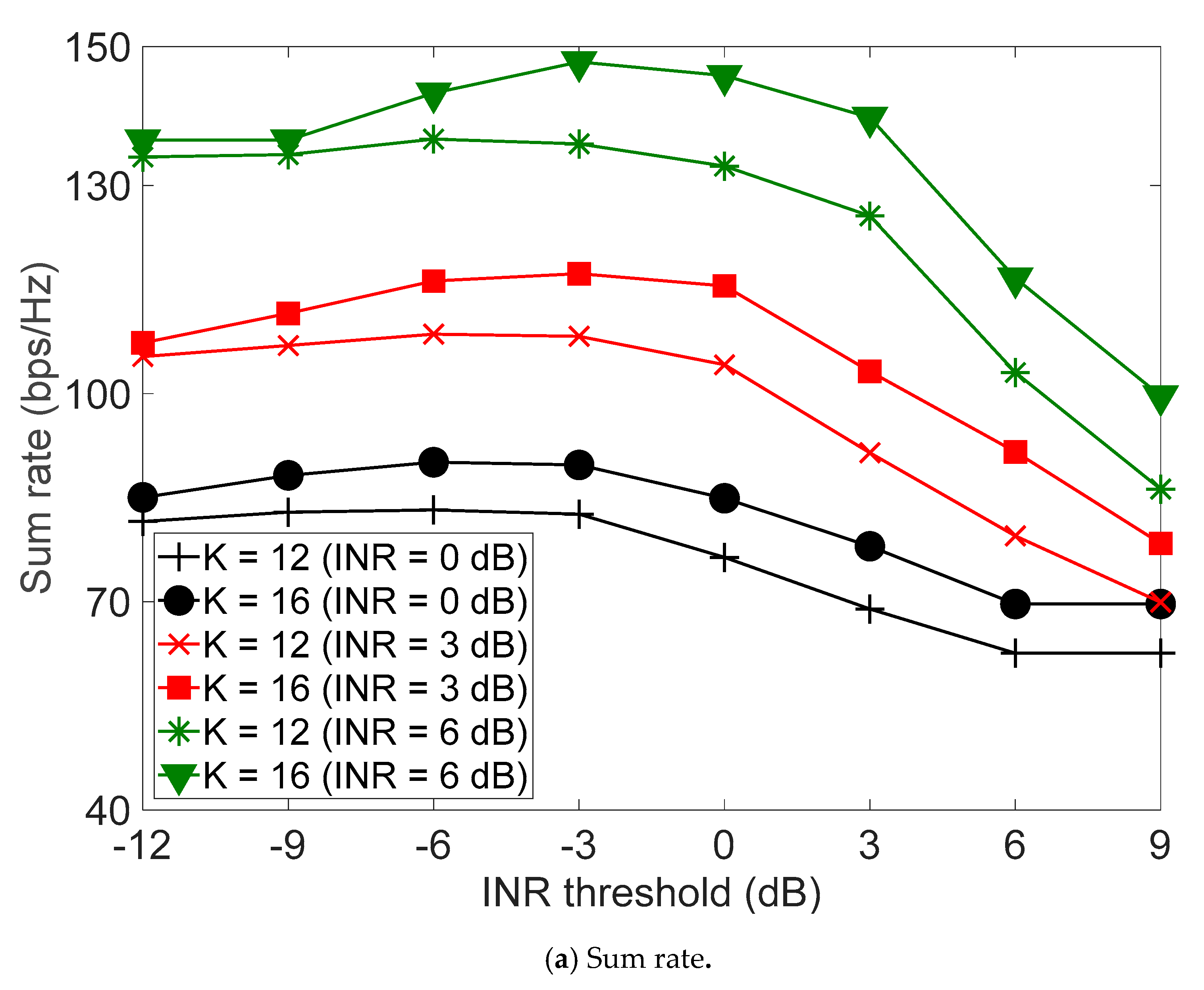
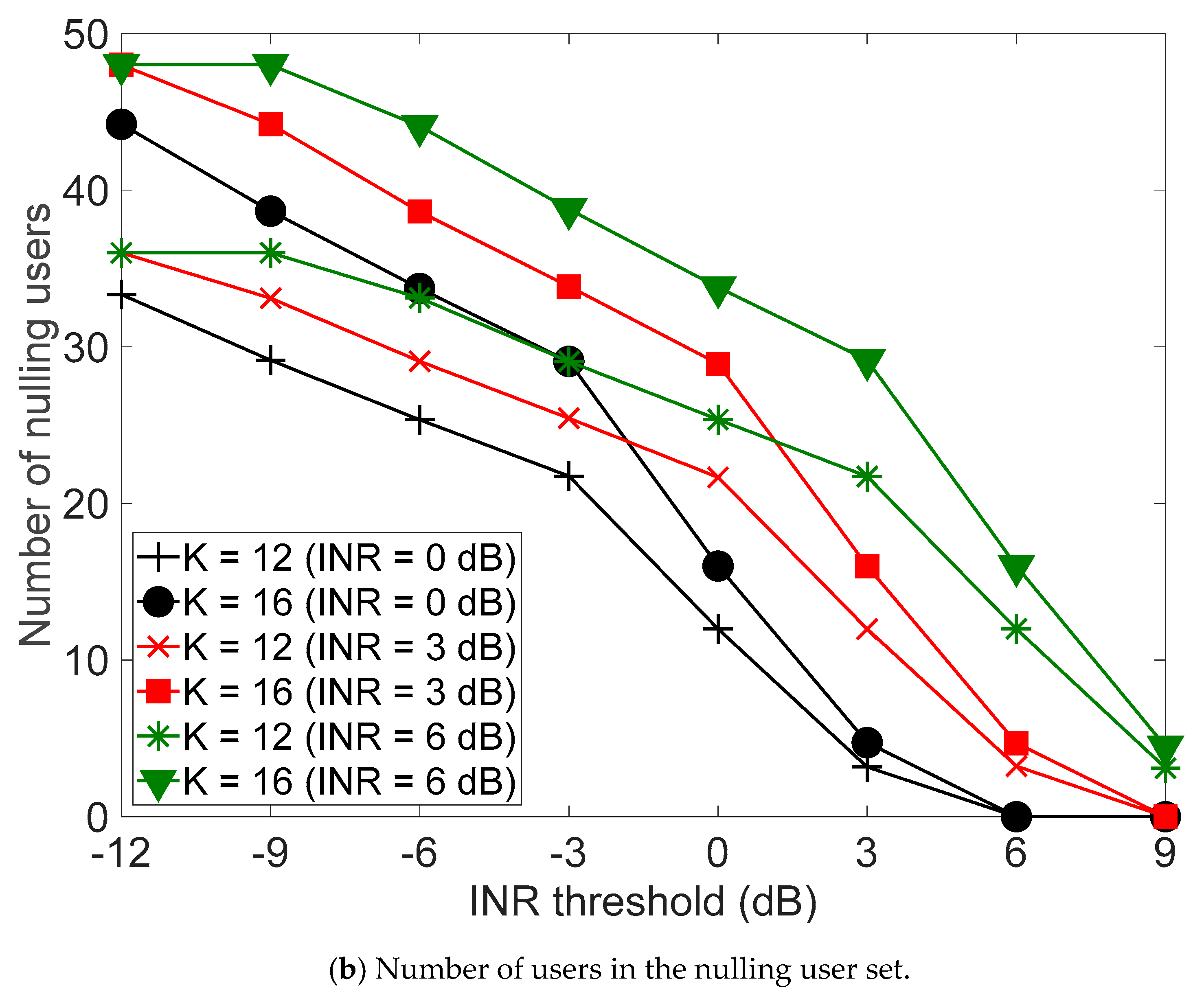
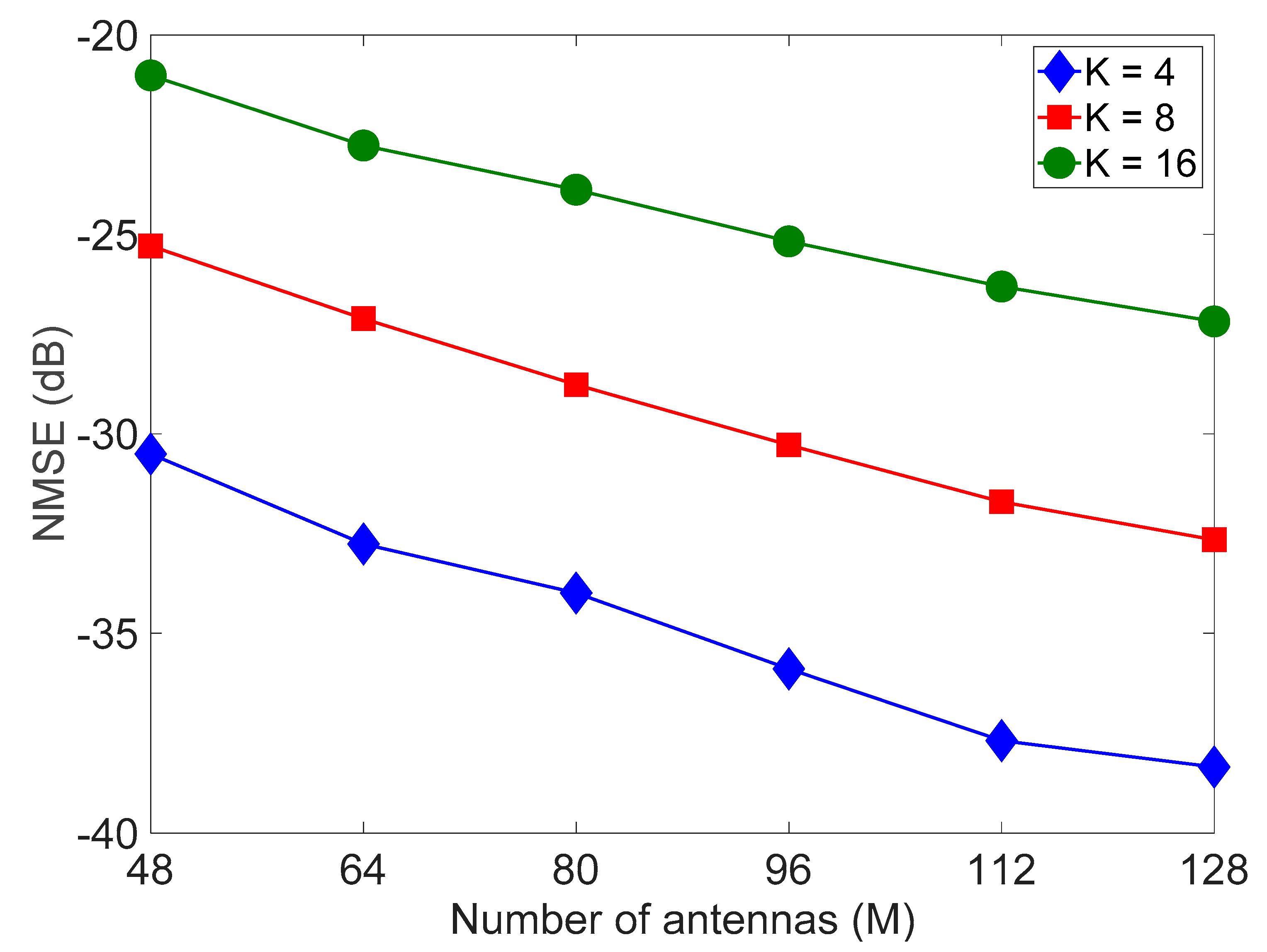
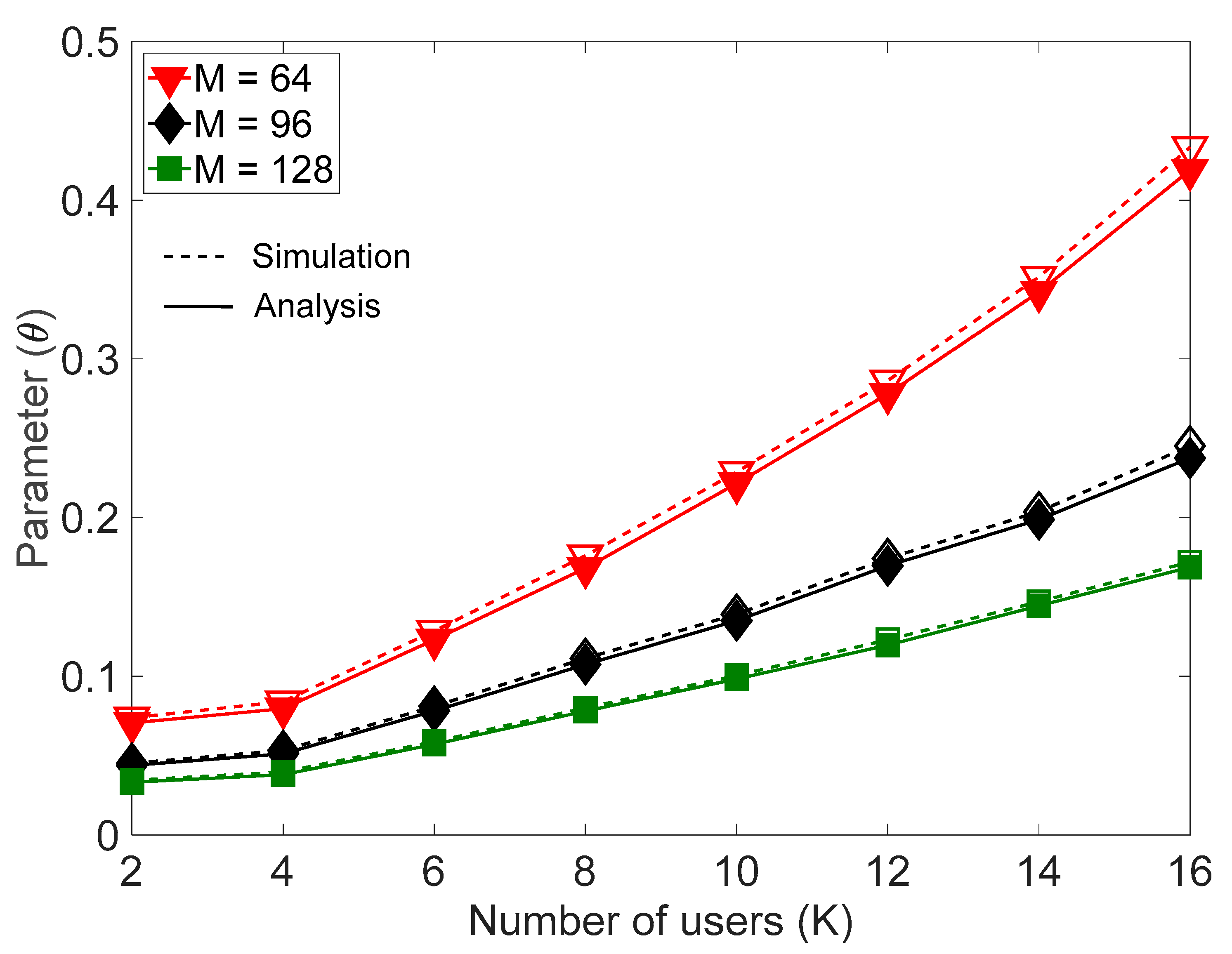
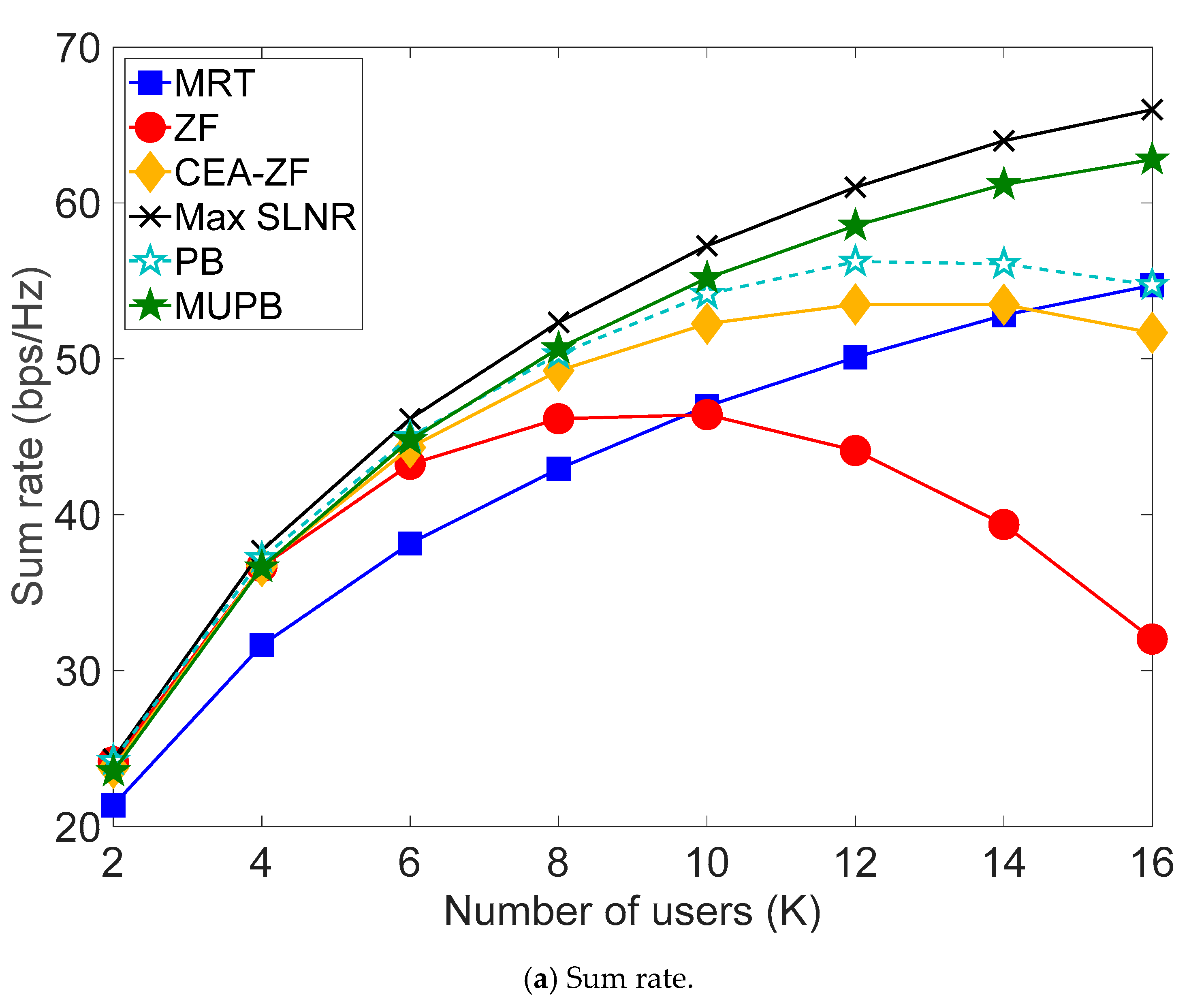
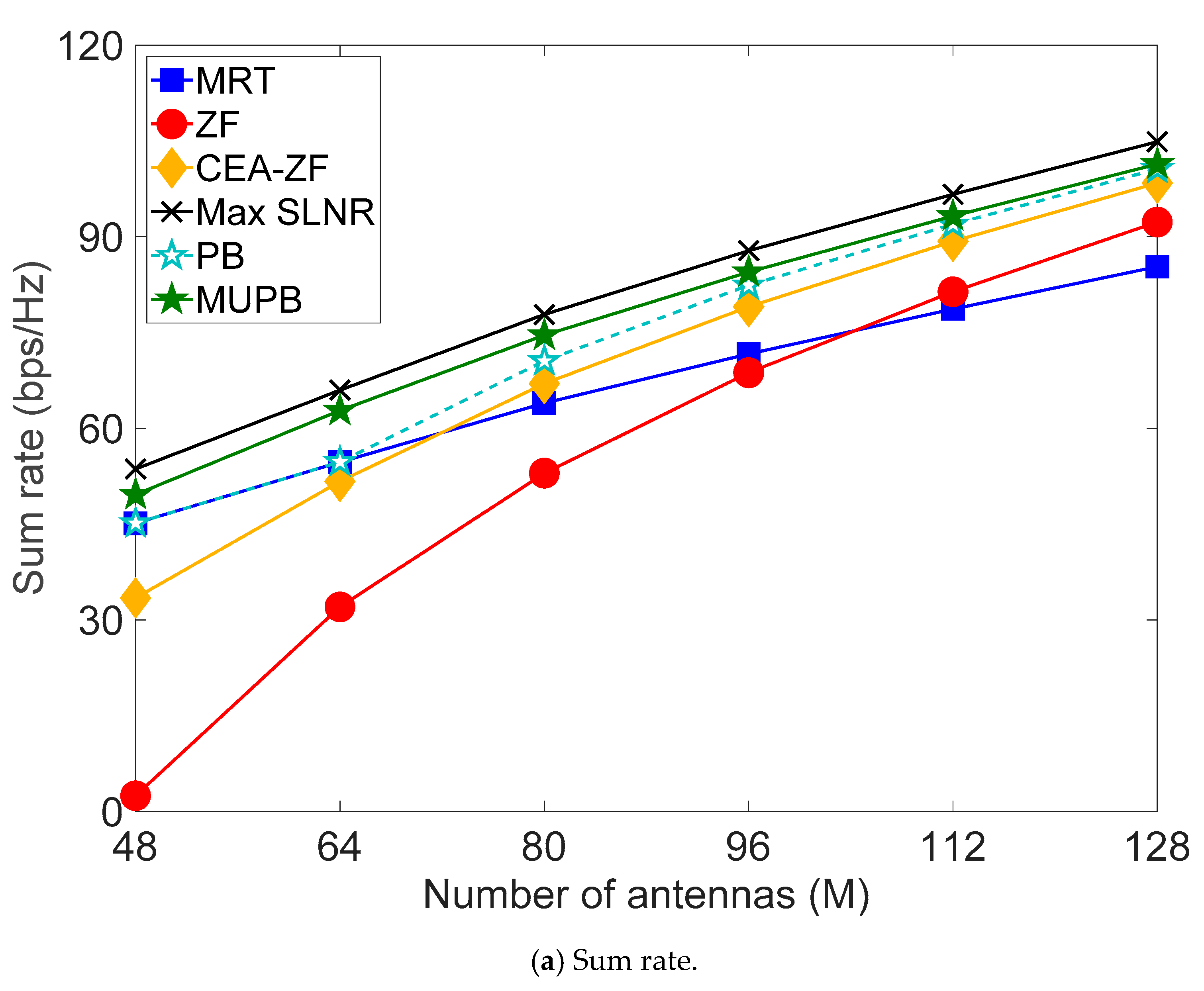
4. Performance Verification
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Yang, P.; Xiao, Y.; Xiao, M.; Li, S. 6G wireless communications: Vision and potential techniques. IEEE Netw. 2019, 33, 70–75. [Google Scholar] [CrossRef]
- Maruta, K.; Falcone, F. Massive MIMO systems: Present and future. Electronics 2020, 9, 385. [Google Scholar] [CrossRef]
- Viswanathan, H.; Mogensen, P.E. Communications in the 6G era. IEEE Access 2020, 8, 57063–57074. [Google Scholar] [CrossRef]
- Marzetta, T.L. Noncooperative cellular wireless with unlimited numbers of base station antennas. IEEE Trans. Wirel. Commun. 2010, 9, 3590–3600. [Google Scholar] [CrossRef]
- Rusek, F.; Persson, D.; Lau, B.K.; Larsson, E.G.; Marzetta, T.L.; Edfors, O.; Tufvesson, F. Scaling up MIMO: Opportunities and challenges with very large arrays. IEEE Trans. Signal Process. Mag. 2013, 30, 40–60. [Google Scholar] [CrossRef]
- Wong, K.; Pan, Z. Array gain and diversity order of multiuser MISO antenna systems. Int. J. Wirel. Inf. Netw. 2008, 15, 82–89. [Google Scholar] [CrossRef]
- Moon, S.H.; Lee, C.; Lee, S.R.; Lee, I. Joint user scheduling and adaptive intercell interference cancelation for MISO downlink cellular systems. IEEE Trans. Veh. Technol. 2013, 62, 172–181. [Google Scholar] [CrossRef]
- Lu, L.; Li, G.Y.; Swindlehurst, A.L.; Ashikhmin, A.; Zhang, R. An overview of massive MIMO: Benefits and challenges. IEEE J. Sel. Top. Signal Process. 2014, 8, 742–758. [Google Scholar] [CrossRef]
- Prabhu, H.; Rodrigues, J.; Edfors, O.; Rusek, F. Approximative matrix inverse computations for very-large MIMO and applications to linear pre-coding systems. In Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC), Shanghai, China, 7–10 April 2013; pp. 2710–2715. [Google Scholar]
- Kammoun, A.; Müller, A.; Björnson, E.; Debbah, M. Linear precoding based on polynomial expansion: Large-scale multi-cell MIMO systems. IEEE J. Sel. Top. Signal Process. 2014, 8, 861–875. [Google Scholar] [CrossRef]
- Man, Y.; Li, Z.; Yan, F.; Xing, S.; Shen, L. Massive MIMO pre-coding algorithm based on truncated Kapteyn series expansion. In Proceedings of the IEEE International Conference on Communication Systems (ICCS), Shenzhen, China, 14–16 December 2016; pp. 1–5. [Google Scholar]
- Lee, K.; Chen, C. An eigen-based approach for enhancing matrix inversion approximation in massive MIMO systems. IEEE Trans. Veh. Techol. 2017, 66, 5483–5487. [Google Scholar]
- Gao, X.; Dai, L.; Zhang, J.; Han, S.; I, C.L. Capacity-approaching linear precoding with low-complexity for large-scale MIMO systems. In Proceedings of the IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015; pp. 1577–1582. [Google Scholar]
- Xie, T.; Dai, L.; Gao, X.; Dai, X.; Zhao, Y. Low-complexity SSOR-based precoding for massive MIMO systems. IEEE Commun. Lett. 2016, 20, 744–747. [Google Scholar] [CrossRef]
- Man, Y.; Zhang, C.; Li, Z.; Yan, F.; Xing, S.; Shen, L. Massive MIMO precoding algorithm based on improved Newton iteration. In Proceedings of the IEEE 85th Vehicular Technology Conference (VTC Spring), Sydney, Australia, 4–7 June 2017; pp. 1–5. [Google Scholar]
- Minango, J.; Almeida, C. A low-complexity linear precoding algorithm based on Jacobi method for massive MIMO systems. In Proceedings of the IEEE 87th Vehicular Technology Conference (VTC Spring), Porto, Portugal, 3–6 June 2018; pp. 1–5. [Google Scholar]
- Liu, Y.; Liu, J.; Wu, Q.; Zhang, Y.; Jin, M. A near-optimal iterative linear precoding with low complexity for massive MIMO systems. IEEE Commun. Lett. 2019, 23, 1105–1108. [Google Scholar] [CrossRef]
- Lee, C.; Moon, S.H.; Lee, S.R.; Lee, I. Adaptive beamforming selection methods for inter-cell interference cancellation in multicell multiuser systems. In Proceedings of the IEEE International Conference on Communications (ICC), Budapest, Hungary, 9–13 June 2013; pp. 5684–5688. [Google Scholar]
- Yang, H.H.; Geraci, G.; Quek, T.Q.S.; Andrews, J.G. Cell-edge-aware precoding for downlink massive MIMO cellular networks. IEEE Trans. Signal Process. 2017, 65, 3344–3358. [Google Scholar] [CrossRef]
- Venturino, L.; Prasad, N.; Wang, X. Coordinated linear beamforming in downlink multicell wireless networks. IEEE Trans. Wirel. Commun. 2010, 9, 1451–1461. [Google Scholar] [CrossRef]
- Garzás, J.J.E.; Hong, M.; Garcia, A.; García-Armada, A. Interference pricing mechanism for downlink multicell coordinated beamforming. IEEE Trans. Commun. 2014, 62, 1871–1883. [Google Scholar] [CrossRef]
- Sadek, M.; Tarighat, A.; Sayed, A.H. A leakage-based precoding scheme for downlink multi-user MIMO channels. IEEE Trans. Wirel. Commun. 2007, 6, 1711–1721. [Google Scholar] [CrossRef]
- Boukhedimi, I.; Kammoun, A.; Alouini, M. Coordinated SLNR based precoding in large-scale heterogeneous networks. IEEE J. Sel. Top. Signal Process. 2017, 11, 534–548. [Google Scholar] [CrossRef]
- Jorswieck, E.; Larsson, E.; Danev, D. Complete characterization of the Pareto boundary for the MISO interference channel. IEEE Trans. Signal Process. 2008, 56, 5292–5296. [Google Scholar] [CrossRef]
- Mochaourab, R.; Jorswieck, E. Optimal beamforming in interference networks with perfect local channel information. IEEE Trans. Signal Process. 2011, 59, 1128–1141. [Google Scholar] [CrossRef]
- Couillet, R.; Debbah, M. Random Matrix Methods for Wireless Communications, 1st ed.; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Ngo, H.; Larsson, E.; Marzetta, T.L. Energy and spectral efficiency of very large multiuser MIMO systems. IEEE Trans. Commun. 2013, 61, 1436–1449. [Google Scholar]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Hunger, R. Floating Point Operations in Matrix-Vector Calculus; Technical Report; Munich University of Technology: Munich, Germany, 2007. [Google Scholar]
- He, S.; Huang, Y.; Yang, L.; Ottersten, B. Coordinated multicell multiuser precoding for maximizing weighted sum energy efficiency. IEEE Trans. Signal Process. 2014, 62, 741–751. [Google Scholar] [CrossRef]
- Horn, R.; Johnson, C. Matrix Analysis; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Parkvall, S.; Dahlman, E.; Furuskär, A.; Jading, Y.; Olsson, M.; Wänstedt, S.; Zangi, K. LTE-Advanced—Evolving LTE towards IMT-Advanced. In Proceedings of the IEEE 68th Vehicular Technology Conference, Calgary, AB, Canada, 21–24 September 2008; pp. 1–5. [Google Scholar]
- Pan, C.; Ren, H.; Elkashlan, M.; Nallanathan, A.; Hanzo, L. The non-coherent ultra-dense C-RAN is capable of outperforming its coherent counterpart at a limited fronthaul capacity. IEEE J. Sel. Areas Commun. 2018, 36, 2549–2560. [Google Scholar] [CrossRef]
- Rose, H.E. Linear Algebra: A Pure Mathematical Approach; Birkhaüser: Basel, Switzerland, 2002. [Google Scholar]



| Scheme | Computational Complexity |
|---|---|
| MRT | |
| ZF | |
| CEA-ZF | |
| Max SLNR | |
| PB | |
| MUPB |
| Simulation Parameters | Value |
|---|---|
| Number of BSs B | 3 |
| Cell radius | 300 m |
| Cell center radius | 200 m |
| Path loss | , where is the distance between BS i and user k in km |
| Maximum transmit power | 30 dBm |
| Power allocation | |
| Noise power | −92 dBm |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, G.-W.; Lee, Y.-H. Low-Complexity Multi-User Parameterized Beamforming in Massive MIMO Systems. Electronics 2020, 9, 882. https://doi.org/10.3390/electronics9060882
Jung G-W, Lee Y-H. Low-Complexity Multi-User Parameterized Beamforming in Massive MIMO Systems. Electronics. 2020; 9(6):882. https://doi.org/10.3390/electronics9060882
Chicago/Turabian StyleJung, Geon-Woong, and Yong-Hwan Lee. 2020. "Low-Complexity Multi-User Parameterized Beamforming in Massive MIMO Systems" Electronics 9, no. 6: 882. https://doi.org/10.3390/electronics9060882
APA StyleJung, G.-W., & Lee, Y.-H. (2020). Low-Complexity Multi-User Parameterized Beamforming in Massive MIMO Systems. Electronics, 9(6), 882. https://doi.org/10.3390/electronics9060882





