Abstract
In this paper, the emergence of multistable behavior through the use of fractional-order-derivatives in a Piece-Wise Linear (PWL) multi-scroll generator is presented. Using the integration-order as a bifurcation parameter, the stability in the system is modified in such a form that produces a basin of attraction segmentation, creating many stable states as scrolls are generated in the integer-order system. The results here presented reproduce the same phenomenon reported in systems with integer-order derivatives, where the multistable regimen is obtained through a parameter variation. The multistable behavior reported is also validated through electronic simulation. The presented results are not only applicable in engineering fields, but they also enrich the analysis and the understanding of the implications of using fractional integration orders, boosting the development of further and better studies.
1. Introduction
Several nonlinear dynamical systems present the coexistence of stable states, or attractors, for a given set of parameters. This type of behavior is known as multistability, a phenomenon where the system presents more than one possible final state conditioned only by the initial conditions with which the system is evaluated. This type of behavior can be found in almost any area of science, such as electronics [1], optics [2,3], mechanics [4] and economics, among others [5]. It is due to its vast field of appearance, and potential technological applications, that the study and control of multistable systems is one of the favorite topics in the analysis of nonlinear systems.
Nonlinear dynamical systems are related, in most cases, by the presence of strange attractors in its phase spaces, as the multi-scroll systems. This kind of system has positioned itself as one of the favorite topics in the scientific community, sustaining its interest in the endless number of applications and possible technological developments that multi-scroll systems present. Without loss of generality, the generation of systems with multi-scrolls is based on the implementation of Piece-Wise Linear (PWL) systems, and the induction of multiple equilibrium points to dissipative systems [6,7,8,9,10,11]. Besides, this type of complex system is characterized by presenting a hierarchical structure, where both continuous and discrete dynamics coexist, generating decision-making systems. These types of systems are also known as hybrid systems [12,13,14].
The study and characterization of nonlinear systems have been mostly addressed using integer-derivative operators. However, the use of operators, both derivative and integrative, of non-integer-order has received attention in recent years. The uses of this type of operators give the name to the fractional calculation, having numerous examples of its application in the area of nonlinear systems [15,16,17]. One of the main differences between classical calculus (integer-order) and fractional-order-calculus, is based on the ability to model memory and hereditary properties in fractional systems.
The appearance of multistable states in integer-order multi-scroll systems has been reported in several ways, that is, through the eigenspectra variation in a PWL system [18], or by applying some control techniques that generate the coexistence of several monostable attractors [19]. In fractional-order systems, the multistability phenomenon has also been reported [20,21,22,23], where such investigations range from systems without equilibrium points, systems based on memristors, and systems capable of presenting a family of attractors with the coexistence of bistable attractors. Furthermore, some interesting insights were provided by Reference [24], where the stability results in linear time-invariant fractional-order systems involving Caputo derivatives are presented. In Reference [24], the authors discuss the system behavior ( matrix) when its eigenvalues are on the boundary of the stable region, presenting singular points in the solutions, such as cusp and multiple-points in the solution trajectories.
Motivated by the results above mentioned, this work presents numerical analysis from a fractional-order multi-scroll system, where the appearance of generalized multistability, as defined in Reference [25], is achieved when the system is close to being stable through the fractional-integration-order. The results here presented have the aim of validating the theory developed for linear time-invariant fractional-order systems and the self-intersecting trajectories. The results about multistability in a multi-scroll fractional order system here reported, for first time to the author’s knowledge, show a behavior also observed in an integer-order system where the multistability is achieved through an eigenspectra variation, inferring that the modification of the vector field in an integer-order system is equivalent to the use of fractional-order derivatives.
The rest of the work is organized as follows—the second section describes the basic concepts of the multi-scroll generator system studied, as well as the basis of fractional calculus. The numerical results of the implemented methodology for the obtention of multistability are shown in Section 3. The discussion of results is presented in Section 4. The main conclusions of the work are explained at the end of the paper.
2. Material and Methods
2.1. Fractional Calculus Preliminaries
Fractional-order derivatives are just generalizations of the integer-order ones. Nevertheless, it is possible to find several definitions of fractional calculus in literature [26,27], being the Riemann-Liouville and the Caputo definitions the most commonly used. The Caputo derivative of fractional-order q of the function is defined as follows:
with , and is the Gamma function, defined in Equation (2).
In contrast with integer-order systems, the local stability in fractional-order systems depends on the derivative order (q), and creates a whole region of stability shown in Figure 1 [28]. Its worth to mention that the stability of an equilibrium point can be controlled employing a fractional-order modification. Considering a general k-dimensional fractional-order system as the described in Equation (3), with eigenvalues, it is possible to define the stability of the system through its eigenvalues analysis and classify it. Consider the system defined by:
where A is a lineal operator defined in , the stability of Equation (3) is defined as [26]:
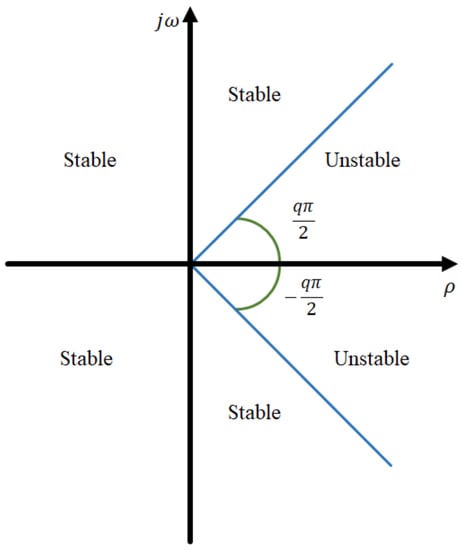
Figure 1.
Stability region of a fractional-order linear time-invariant system with order .
- Stable, if and only if .
- Asymptotically stable, if and only if . In this case, the solution as .
- Unstable, if and only if , for at least one eigenvalue.
2.2. Multiscroll Chaotic System
As a special case of chaotic systems, the jerk equation, which can be expressed in several ways [29,30], is commonly applied in multi-scroll generators, because it can be expressed on the canonical controllable form [31,32]. By considering a system based on the jerk equation, Equation (4) [30,33,34,35,36], which fulfils all the conditions to be called a Unstable Dissipative System type I [14,18], that is, for the control parameter , with eigenvalues , and the sum of its components is . Its worth to mention that the eigenvaqlues are obtained through the linearization of system Equation (4), and solving the characteristic polynomial .
where is the Caputo fractional-order operator, and indicates the variable where the fractional operator is applied. The control parameter is a constant that defines the eigenvalues of the system, being, in this case, [33]. The function represents the commutation law (non-linear function), whose purpose is to control the visit in the different domains in the system, is achieved through the coexistence of a large number of one-spiral unstable trajectories, described in Equation (5). Then, it is possible to generate an attractor with multiple scrolls using a commutation law, in this case, a Piece-Wise Linear (PWL) function. The PWL function () induces as many switching surfaces (commutation surfaces) as desired, and thus guarantee the generation of the same number of scrolls as space divisions.
The equilibrium point location of the system shown in Equation (4), and the use of the nonlinear function described in Equation (5), is easy to obtain by solving the equation , where A represents the linear operator in the system, and B the nonlinearity. Using the parameter , the system eigenvalues are defined as hyperbolic-saddle-node points, that is, the system is consistent with the Unstable Dissipative System type I (UDS I); where the integer-order dynamic is shown in Figure 2.
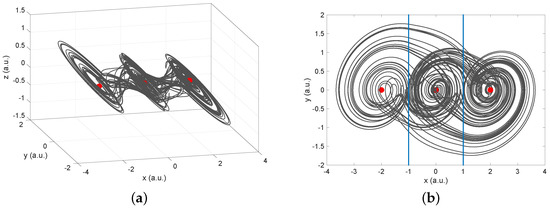
Figure 2.
Dynamical behavior for Equation (4) with Equation (5), solved for an integer-order. The system presents a Maximum Lyapunov Exponente (MLE), MLE = 0.4347. (a) Projection on the plane, and (b) in the plane. Attractor generated for . The Equilibrium Points (EP) are depicted in red. The switching surfaces (commutation surfaces) correspond to the vertical blue lines (SW) in (b).
The system described by Equation (4) is numerically analyzed through the use of the Adams-Bashforth-Moulton (ABM) method [37]. The algorithm is a generalization of the classical ABM integrator that is well known in the resolution of first-order switching systems problems [28,38]. Solving the system of coupled fractional-differential equations for the integration-order vector , the system response is drawn in Figure 2, where the equilibrium points are also depicted.
The interest is to have unstable dynamics, thus the system presented in Equation (4) is restricted to have at least one eigenvalue in the unstable region, that is, Equation (4) is unstable if and only if for at least one of its eigenvalues . Since , and the eigenvalues are . Since , the critical-integration order is defined as (Section 2.1), and by substitution is obtained the critical-integration-order .
Considering the stability limitations for fractional-order systems, the system described for Equation (4) has a critic integration-order at , where all the eigenvalues will be located in the stable region (Figure 1). Accordingly to the fractional-calculus theory [28], if the system is analyzed with integration orders , the dynamics of the system will be annihilated, turning each equilibrium point into a focus attractor.
The fractional-order system described in Equation (4), is analyzed for a fixed control parameter , associated with the nonlinear function described by Equation (5), an integration size , where the integration order will be the same in the three-state variables. A bifurcation diagram of fractional-order vs local maximum in the x state variable is calculated (Figure 3), where it is possible to observe qualitative changes in the system dynamics, region delimited by red solid lines. Such changes in the temporal series boost to develop a more detailed study in the system behavior, where the multistable phenomenon is present, which will be described in the following section.
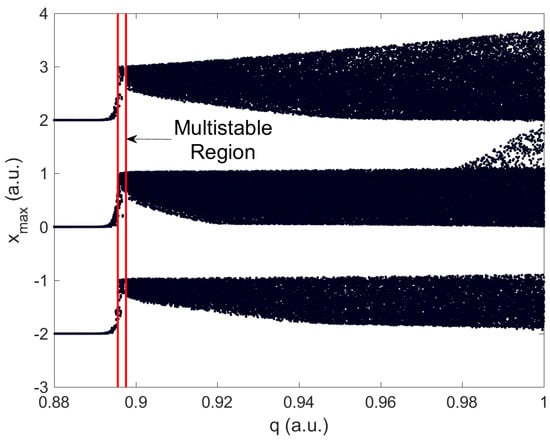
Figure 3.
Numerical bifurcation diagram of the system under integration-order variation, where the region delimited by red lines corresponds to multistable behavior. The integration order is varied in the range , with .
In Figure 3, three different kinds of behaviors are generated by the system, a fixed point dynamic for , multistable behavior for , and monostable multiscroll behavior for . To validates the behaviors exhibited, the Maximum Lyapunov Exponent (MLE) from the time series, as defined in Reference [39], was calculated and following shown:
- Fixed point behavior, MLE = 0.
- Multistable single scroll, , MLE = 0.0144.
- Monostable multi-scroll, , MLE = 0.4347.
3. Results
With the temporal series used to construct the bifurcation diagram shown in Figure 3, an analysis of the number of scrolls generated is developed by estimating around which fixed point the trajectory generated lives. In Figure 4a, the number of scrolls obtained by the use of an integration-order minor than one is depicted. For better visualization, the results for are omitted since the system does not modify the number of scrolls generated until that integration-order value.
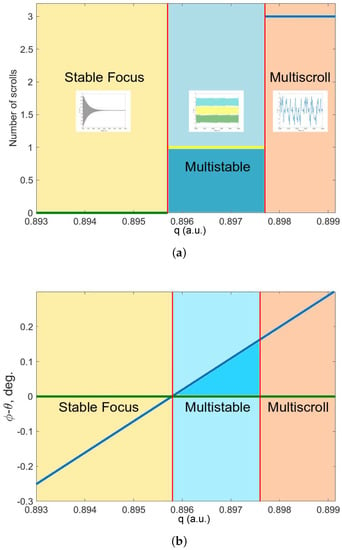
Figure 4.
(a) The number of scrolls generated for each integration order. In the inset, the associated temporal behavior its shown. (b) The angle difference () between the integration order and the critical integration order, is shown. The multistable region is delimited by the integration-order values . The colors in the figure delimited the three different behaviors in the fractional-order-system: The monostable dynamics (orange area), the coexistence of attractors (blue region), and the fixed point behavior (yellow area).
For values , Figure 4a shows a constant behavior in zero (green line/yellow area), indicating that the system response converges to a fixed point. This result validates the fractional-order equilibrium point stability mentioned in former sections (Figure 1). The blue section corresponds to the multistable region, where the system is capable to generate a single scroll in each domain (yellow line). The single-scroll is stable along time, it means, that the single scroll dynamic is present for . The orange region indicates that the system keeps generating the natural monostable attractor with 3-scrolls (blue line).
To better understand the state transitions in the system, the angle difference between the critic integration order () and each of the integration orders analyzed is measured and shown in Figure 4b. This means that for an integer order corresponds an angle ( for ), and the critical integration order has a constant angle of (as defined in the third case of the fixed points stability in fractional-order systems, Section 2.1), being the difference plotted as a diagonal blue line in Figure 4b. In Figure 4b, it is also possible to see that the multistable region exists for , which corresponds to an integration-order range of values . As in Figure 4a, the color areas indicate the different possible states that the system can present by using fractional-order. In both figures, the abscissa axis represents the different integration orders analyzed. The associated results for are omitted for better visualization since there is no other state transition in that value range.
To show the multistable states obtained in the system, the attractors generated for an integration-order are calculated, where the only modification between them are the initial conditions. In Figure 5 the three possible states are presented. Notice that the equilibrium point location has not been changed, is the equilibrium point the center of each of the three monostable states.
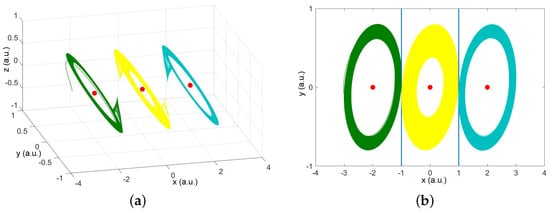
Figure 5.
Multistable attractors obtained for and initial conditions: (Green), (Yellow), and (Cyan). (a) in phase space, and (b) projection in plane.
Electronic Validation
The use of specialized simulation software to analyze chaotic systems has increased in recent years, and given the precision that this type of software offers, these results have been adopted as experimental validations [13,40,41]. In this sense, the elecronic results shown in this work are based on obtaining time series from the simulation of electronic circuits in the Multisim development platform.
The electronic implementation of the system described by Equation (4), is based on the properties of analogous calculus [13], implemented through operational amplifiers. The electronic circuit that resembles a fractional-order capacitor, is called fractance. The circuit shown in Figure 6a corresponds to the linear operator of the analyzed model. The implemented nonlinear function (), corresponds to a PWL function based on operational amplifiers, also called a Saturated Non-Lineal Function (SNLF), for the generation of a 3-scrolls attractor, as reported in [42], shown in Figure 6b.
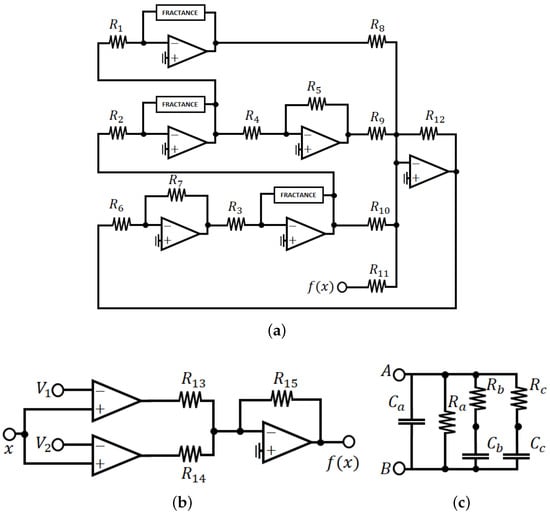
The closest value, implemented in a fractance, to those found in the previous section to obtain multistable states () corresponds to , which considering the electronics tolerances produce a shifting in the fractance order. Considering this, the implementation of a fractance of order is carried out as defined in Reference [43], which is shown in Figure 6c. All operational amplifiers shown in Figure 6 correspond to TL082 circuits, with a voltage supply V. The electronic components used in Figure 6, and the voltages used to build in the PWL function, are described in Table 1.

Table 1.
Electronic components used in the implementation of Figure 6.
In order to prove the multistable behavior, described in former sections, an analogical simulation is developed, where the system described by Equation (4) is analyzed with the use of a nonlinear function of three levels, with an integration order in each state variable. The results, shown in Figure 7, validates the theory previously developed. The integer-order dynamics is obtained by substituting the fractances by 10 nF capacitors, and changing for 10 k resistors.
4. Discussion
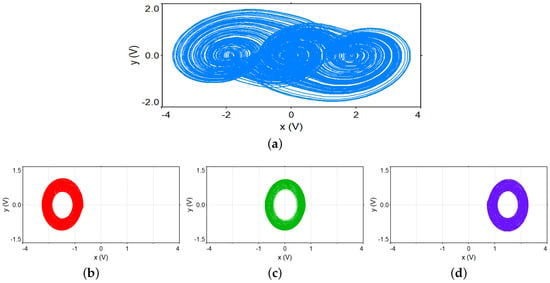
From the attractors shown in Figure 5, it is possible to say that the system presents a multistable behavior for specific initial conditions. To validate that the system presents a multistable behavior, the associated basin of attraction is calculated with the integration order , the same value used in Figure 5. The colors in the basin of attraction (Figure 8) correspond to the attractor colors of Figure 5.
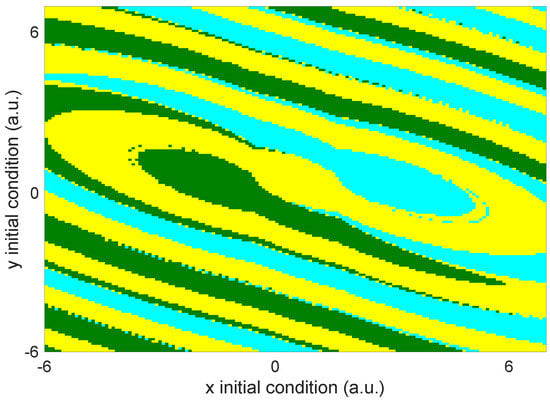
The basin of attraction displayed in Figure 8 validates that the system presents the coexistence of three single-scroll attractors. The location of each possible state is defined by the commutation law, where each attractor surrounds its equilibrium point. In comparison, the multistable states present a decree in their amplitudes. It is worth to remark that, according to the fractional calculus theory, the multistable dynamic has only been achieved by employing the modification in the local stability of each equilibrium point, where the eigenvalues of the system remain without any change.
Additionally, it is possible to extend this result to any number of stable final states by the addition of domains to commutation law, Equation (5). To validate this, consider the generation of an attractor with 9-scrolls as the one shown in Figure 9a, with value . The integer-order dynamics generate a 9-scroll attractor with eight switching surfaces, where each equilibrium point corresponds to the center of each scroll. Since the linear operator is the same one as described in Equation (4), the stability analysis indicates a critical integration order . When the system shown in Figure 9 is analyzed for an integration order , the emerge of 9-multistable states is arise, displayed in Figure 10a,b, where each possible state corresponds to each of the domains in the system. Notice that, also, in this case, the center of each scroll is the same equilibrium point, where the location of them has not been changed. The corresponding basin of attraction is calculated, and depicted, in Figure 10c, where the colors in the basin are related to the colors in the corresponding attractors shown in Figure 10a,b.
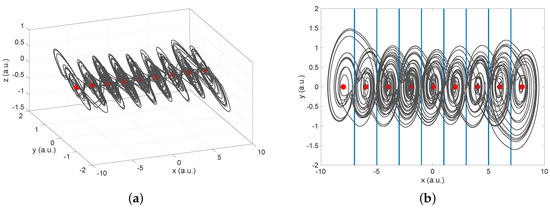
Figure 9.
Dynamical behavior for Equation (4) with a 9-level PWL, solved for an integer-order. The system presents a Maximum Lyapunov Exponent (MLE), MLE = 0.3953. (a) Projection on the plane, and (b) in the plane. Attractor generated for . The Equilibrium Points (EP) are depicted in red. The switching surfaces (commutation surfaces) correspond to the vertical blue lines (SW).
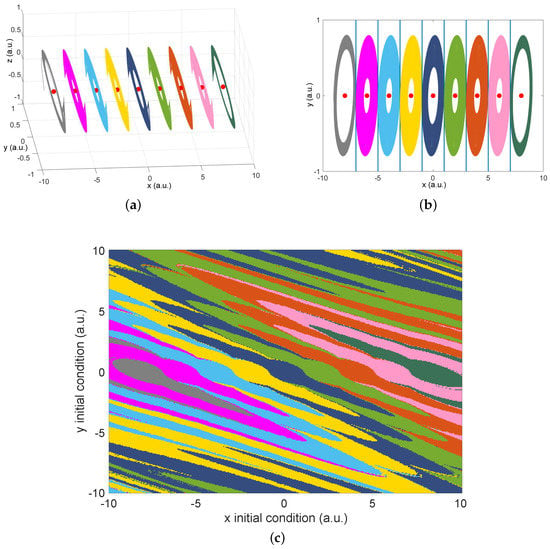
Figure 10.
Multistable attractors generated by Equation (4) with an 9-level PWL for ; (a) in phase space, and (b) in plane. The system presents a Maximum Lyapunov Exponent (MLE), MLE = 0.0144. The Equilibrium Points (EP) are depicted in red. The switching surfaces (plateaus, commutation surfaces) correspond to the vertical blue lines (SW) in (b). (c) Basin of attraction section from attractors shown in (a,b), for , and an initial condition in the third state variable . The colors in the figure, are related to the colors in the attractors from Figure 10a,b.
Even this kind of behavior has not been reported in fractional-order systems, presents similar results to those presented in an integer-order system. In Reference [18], the authors report the generation of a multistable system based on the jerk equation, where such behavior is achieved through a bifurcation parameter modification which correlates directly with the direction, and location, of the stable and unstable manifolds associated to system eigenvectors. Such eigenspectra variation reaches critical eigenvalues for which the system becomes almost stable, a region where the coexistence of several single-scroll attractors is generated, in a similar way that it is found the multistable behavior shown in this paper when the linear operator is close to becoming stable through the use of fractional-order-derivatives.
5. Conclusions
In this work, a new approach to the generation of multistable behaviors in a multi-scroll system has been reported, through the use of the integration-order as a system parameter, that is, a 3-scroll attractor became into a 3 possible single-scroll multistable states. It is possible to extend this result to any number of final stable states by the addition of domains to commutation law. Using the integration order as a bifurcation parameter, the local stability in the system is modified in such form that produces a basin of attraction segmentation, creating as many stable states as scrolls generate the integer-order system. The results reproduce, to a great extent, a similar phenomenon reported in integer-order systems, in which multistability is obtained through the eigenspectra variation.
Since the multistable behavior obtained in the system reproduces the same behavior obtained in an integer-order system, these results infer that the modification of the vector field employing fractional derivatives could be associated with the parameters of the vector field of an integer-order system. These kinds of results are very interesting and a boost to developing further studies in the vector field behavior of fractional-order systems and its correlation with the entire-order vector field. The results here presented are not only applicable in engineering fields, but they also enrich the analysis and understanding of the implications of using fractional integration orders. The corresponding analogical implementation, in order to compare the presented results, is proposed as future work.
Author Contributions
J.L.E.-M.: Writing—Original Draft, Writing—Review & Editing, Methodology, Software, Validation, Data Curation, Visualization. G.H.-C.: Supervision, Writing—Review & Editing, Conceptualization, Resources, Project administration. R.J.-R.: Formal analysis, Funding acquisition, Writing—Review & Editing. J.H.G.-L.: Formal analysis, Funding acquisition, Writing—Review & Editing. V.A.: Formal analysis, Funding acquisition, Writing—Review & Editing. B.B.C.-Q.: Investigation, Writing—Review & Editing. H.E.G.-V.: Supervision, Writing—Review & Editing, Conceptualization, Resources, Project administration. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
J.L.E.-M. acknowledges CONACYT for the financial support (National Fellowship CVU-706850, No. 582124) and the University of Guadalajara, CULagos (Mexico). H.E.G.-V. acknowledges to PRODEP for the support (project 252787) to the realization of a post-doctoral stay at the University of Guadalajara, CULagos. G.H.-C. acknowledges to the University of Guadalajara for the support (project 241596) to the realization of the sabbatical stay at St. Mary’s University, and E.C.C. for fruitful discussions. The authors acknowledge the financial support from the University of Guadalajara under the projects “Research Laboratory Equipment for Academic Groups in Optoelectronics from CULAGOS”, and R-0138/2016, Agreement RG/019/2016-UdeG, RC/075/2018, Agreement RG/006/2018, UDG, Mexico.
Conflicts of Interest
The authors certify that they have NO affiliations with or involvement in any organization or entity with any financial interest (such as honoraria; educational grants; participation in speakers’ bureaus; membership, employment, consultancies, stock ownership, or other equity interest; and expert testimony or patent-licensing arrangements), or non-financial interest (such as personal or professional relationships, affiliations, knowledge or beliefs) in the subject matter or materials discussed in this manuscript.
References
- Maurer, J.; Libchaber, A. Effect of the Prandtl number on the onset of turbulence in liquid 4He. J. Phys. Lett. 1980, 41, 515–518. [Google Scholar] [CrossRef]
- Huerta-Cuellar, G.; Pisarchik, A.N.; Barmenkov, Y.O. Experimental characterization of hopping dynamics in a multistable fiber laser. Phys. Rev. E 2008, 78, 035202. [Google Scholar] [CrossRef] [PubMed]
- Sevilla-Escoboza, R.; Huerta-Cuéllar, G.; Jaimes-Reátegui, R.; García-López, J.; Medel-Ruiz, C.; Castañeda, C.E.; López-Mancilla, D.; Pisarchik, A.N. Error-feedback control of multistability. J. Frankl. Inst. 2017, 354, 7346–7358. [Google Scholar] [CrossRef]
- Thompson, J.M.T.; Stewart, H.B. Nonlinear Dynamics and Chaos; John Wiley & Sons: Chichester, West Sussex, UK, 2002. [Google Scholar]
- Pisarchik, A.N.; Feudel, U. Control of multistability. Phys. Rep. 2014, 540, 167–218. [Google Scholar] [CrossRef]
- Escalante-González, R.; Gilardi-Velázquez, H.; Campos-Cantón, E. A class of Chua-like systems with only two saddle-foci of different type. IFAC-PapersOnLine 2018, 51, 156–161. [Google Scholar] [CrossRef]
- Suykens, J.A.K.; Huang, A. A family of n-scroll attractors from a generalized Chua’s circuit. Arch. Elektron. Ubertragungstechnik 1997, 51, 131–137. [Google Scholar]
- Campos-Cantón, E.; Campos-Cantón, I.; González Salas, J.; Cruz Ordaz, F. A parameterized family of single-double-triple-scroll chaotic oscillations. Rev. Mex. De Física 2008, 54, 411–415. [Google Scholar]
- Li, G.; Chen, X. Constructing piecewise linear chaotic system based on the heteroclinic Shil’nikov theorem. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 194–203. [Google Scholar] [CrossRef]
- Wu, T.; Wang, L.; Yang, X.S. Chaos generator design with piecewise affine systems. Nonlinear Dyn. 2016, 84, 817–832. [Google Scholar] [CrossRef]
- Wang, L.; Yang, X.S. Heteroclinic cycles in a class of 3-dimensional piecewise affine systems. Nonlinear Anal. Hybrid Syst. 2017, 23, 44–60. [Google Scholar] [CrossRef]
- Goebel, R.; Sanfelice, R.G.; Teel, A.R. Hybrid dynamical systems. IEEE Control Syst. Mag. 2009, 29, 28–93. [Google Scholar] [CrossRef]
- Ontañón-García, L.; Campos-Cantón, E.; Femat, R. Analog electronic implementation of a class of hybrid dissipative dynamical system. Int. J. Bifurc. Chaos 2016, 26, 1650018. [Google Scholar] [CrossRef]
- Echenausía-Monroy, J.L.; Huerta-Cuéllar, G. A novel approach to generate attractors with a high number of scrolls. Nonlinear Anal. Hybrid Syst. 2020, 35, 100822. [Google Scholar] [CrossRef]
- Petráš, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Freeborn, T.J.; Maundy, B.; Elwakil, A.S. Measurement of supercapacitor fractional-order model parameters from voltage-excited step response. IEEE J. Emerg. Sel. Top. Circuits Syst. 2013, 3, 367–376. [Google Scholar] [CrossRef]
- Elwakil, A.S. Fractional-order circuits and systems: An emerging interdisciplinary research area. IEEE Circuits Syst. Mag. 2010, 10, 40–50. [Google Scholar] [CrossRef]
- Gilardi-Velázquez, H.E.; Ontañón-García, L.J.; Hurtado-Rodriguez, D.G.; Campos-Cantón, E. Multistability in piecewise linear systems versus eigenspectra variation and round function. Int. J. Bifurc. Chaos 2017, 27, 1730031. [Google Scholar] [CrossRef]
- Ontañón-García, L.; Campos-Cantón, E. Widening of the basins of attraction of a multistable switching dynamical system with the location of symmetric equilibria. Nonlinear Anal. Hybrid Syst. 2017, 26, 38–47. [Google Scholar] [CrossRef]
- Pham, V.T.; Kingni, S.T.; Volos, C.; Jafari, S.; Kapitaniak, T. A simple three-dimensional fractional-order chaotic system without equilibrium: Dynamics, circuitry implementation, chaos control and synchronization. AEU-Int. J. Electron. Commun. 2017, 78, 220–227. [Google Scholar] [CrossRef]
- Xu, Y.; Sun, K.; He, S.; Zhang, L. Dynamics of a fractional-order simplified unified system based on the Adomian decomposition method. Eur. Phys. J. Plus 2016, 131, 186. [Google Scholar] [CrossRef]
- Munoz-Pacheco, J.M.; Zambrano-Serrano, E.; Volos, C.; Jafari, S.; Kengne, J.; Rajagopal, K. A new fractional-order chaotic system with different families of hidden and self-excited attractors. Entropy 2018, 20, 564. [Google Scholar] [CrossRef]
- Zhou, C.; Li, Z.; Xie, F. Coexisting attractors, crisis route to chaos in a novel 4D fractional-order system and variable-order circuit implementation. Eur. Phys. J. Plus 2019, 134, 73. [Google Scholar] [CrossRef]
- Bhalekar, S.; Patil, M. Singular points in the solution trajectories of fractional order dynamical systems. Chaos: Interdiscip. J. Nonlinear Sci. 2018, 28, 113123. [Google Scholar] [CrossRef] [PubMed]
- Anzo-Hernández, A.; Gilardi-Velázquez, H.E.; Campos-Cantón, E. On multistability behavior of unstable dissipative systems. Chaos: Interdiscip. J. Nonlinear Sci. 2018, 28, 033613. [Google Scholar] [CrossRef] [PubMed]
- Diethelm, K. The Analysis of Fractional Differential Equations: An Application-Oriented Exposition Using Differential Operators of Caputo Type; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: San Diego, CA, USA, 1998; Volume 198. [Google Scholar]
- Zambrano-Serrano, E.; Campos-Cantón, E.; Muñoz-Pacheco, J.M. Strange attractors generated by a fractional order switching system and its topological horseshoe. Nonlinear Dyn. 2016, 83, 1629–1641. [Google Scholar] [CrossRef]
- Sprott, J.C. Some simple chaotic flows. Phys. Rev. E 1994, 50, R647. [Google Scholar] [CrossRef] [PubMed]
- Chiu, R.; López-Mancilla, D.; Castañeda, C.E.; Orozco-López, O.; Villafaña-Rauda, E.; Sevilla-Escoboza, R. Design and implementation of a jerk circuit using a hybrid analog–digital system. Chaos Solitons Fractals 2019, 119, 255–262. [Google Scholar] [CrossRef]
- Glover, K.; Willems, J. Parametrizations of linear dynamical systems: Canonical forms and identifiability. IEEE Trans. Autom. Control 1974, 19, 640–646. [Google Scholar] [CrossRef]
- Denham, M. Canonical forms for the identification of multivariable linear systems. IEEE Trans. Autom. Control 1974, 19, 646–656. [Google Scholar] [CrossRef]
- Echenausía-Monroy, J.L.; García-López, J.H.; Jaimes-Reátegui, R.; López-Mancilla, D.; Huerta-Cuellar, G. Family of bistable attractors contained in an unstable dissipative switching system associated to a SNLF. Complexity 2018, 2018. [Google Scholar] [CrossRef]
- Campos-Cantón, E.; Barajas-Ramírez, J.G.; Solis-Perales, G.; Femat, R. Multiscroll attractors by switching systems. Chaos: Interdiscip. J. Nonlinear Sci. 2010, 20, 013116. [Google Scholar] [CrossRef]
- Campos-Cantón, E.; Femat, R.; Chen, G. Attractors generated from switching unstable dissipative systems. Chaos: Interdiscip. J. Nonlinear Sci. 2012, 22, 033121. [Google Scholar] [CrossRef] [PubMed]
- Campos-Cantón, E. Chaotic attractors based on unstable dissipative systems via third-order differential equation. Int. J. Mod. Phys. C 2016, 27, 1650008. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J.; Freed, A.D. A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 2002, 29, 3–22. [Google Scholar] [CrossRef]
- Gilardi-Velázquez, H.; Campos-Cantón, E. Nonclassical point of view of the Brownian motion generation via fractional deterministic model. Int. J. Mod. Phys. C 2018, 29, 1850020. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D: Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Hammouch, Z.; Mekkaoui, T. Circuit design and simulation for the fractional-order chaotic behavior in a new dynamical system. Complex Intell. Syst. 2018, 4, 251–260. [Google Scholar] [CrossRef]
- Chen, D.; Liu, C.; Wu, C.; Liu, Y.; Ma, X.; You, Y. A new fractional-order chaotic system and its synchronization with circuit simulation. Circuits Syst. Signal Process. 2012, 31, 1599–1613. [Google Scholar] [CrossRef]
- Lu, J.; Yu, S.; Leung, H.; Chen, G. Experimental verification of multidirectional multiscroll chaotic attractors. IEEE Trans. Circuits Syst. I Regul. Pap. 2006, 53, 149–165. [Google Scholar] [CrossRef]
- Zambrano-Serrano, E.; Muñoz-Pacheco, J.M.; Campos-Cantón, E. Circuit synthesis of an incommensurate fractional order multi-scroll PWL chaotic system. In Proceedings of the 2017 6th International Conference on Modern Circuits and Systems Technologies (MOCAST), Thessaloniki, Greece, 4–6 May 2017; pp. 1–4. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).