Performance Analysis of Interference-Aware Multi-Packet Reception Networks
Abstract
1. Introduction
- The assumption of an innovative operation mode, where the transmission of the MPR nodes depends on the level of interference sensed by the receiver;
- The derivation of the sensing threshold to parameterize the carrier sense scheme at the receiver, which is used by the receiver to signal that the multiple MPR nodes can initiate the transmission. The sensing threshold takes into account the spatial distribution of the nodes, fading conditions and a circular spatial sensing region centered at the receiver;
- The characterization of the uplink throughput achieved when no interferers are sensed in the carrier sensing region of the receiver and multiple MPR nodes simultaneously transmit;
- A detailed study of the upper bound of the conditional throughput achieved by the wireless network that takes into account the carrier sense duration and the interference of other ongoing communications located outside the carrier sensing region.
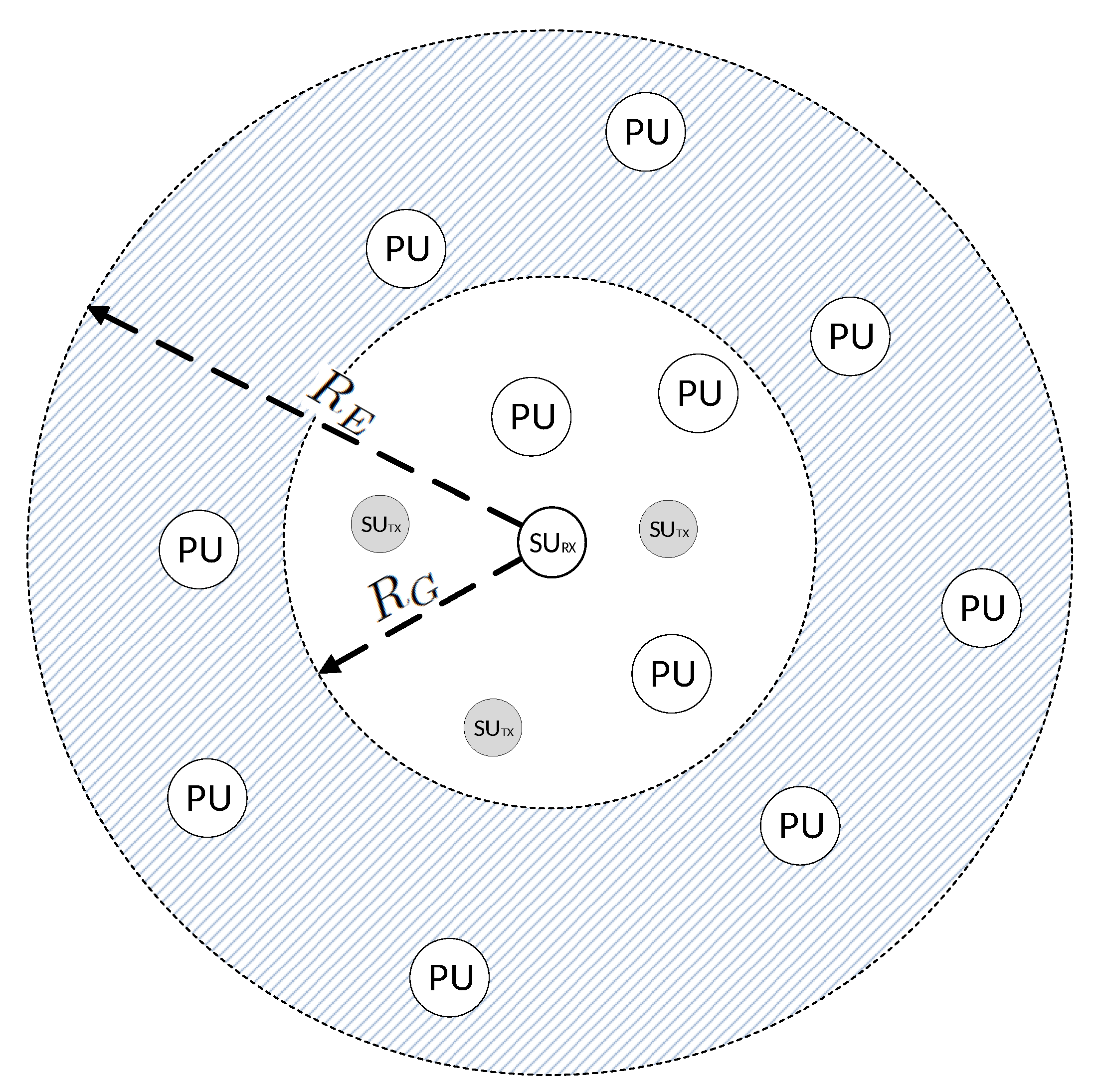
2. System Description
3. Amplitude and Power of the Aggregate Interference
3.1. Power Signals of Secondary Network
3.2. Power and Envelope Signals of Primary Network
3.3. Noise Power Characterization
4. MPR-based PHY-layer Performance Characterization
4.1. Spectrum Sensing Performance Characterization
4.2. Capture Performance Characterization
4.3. Conditional Throughput
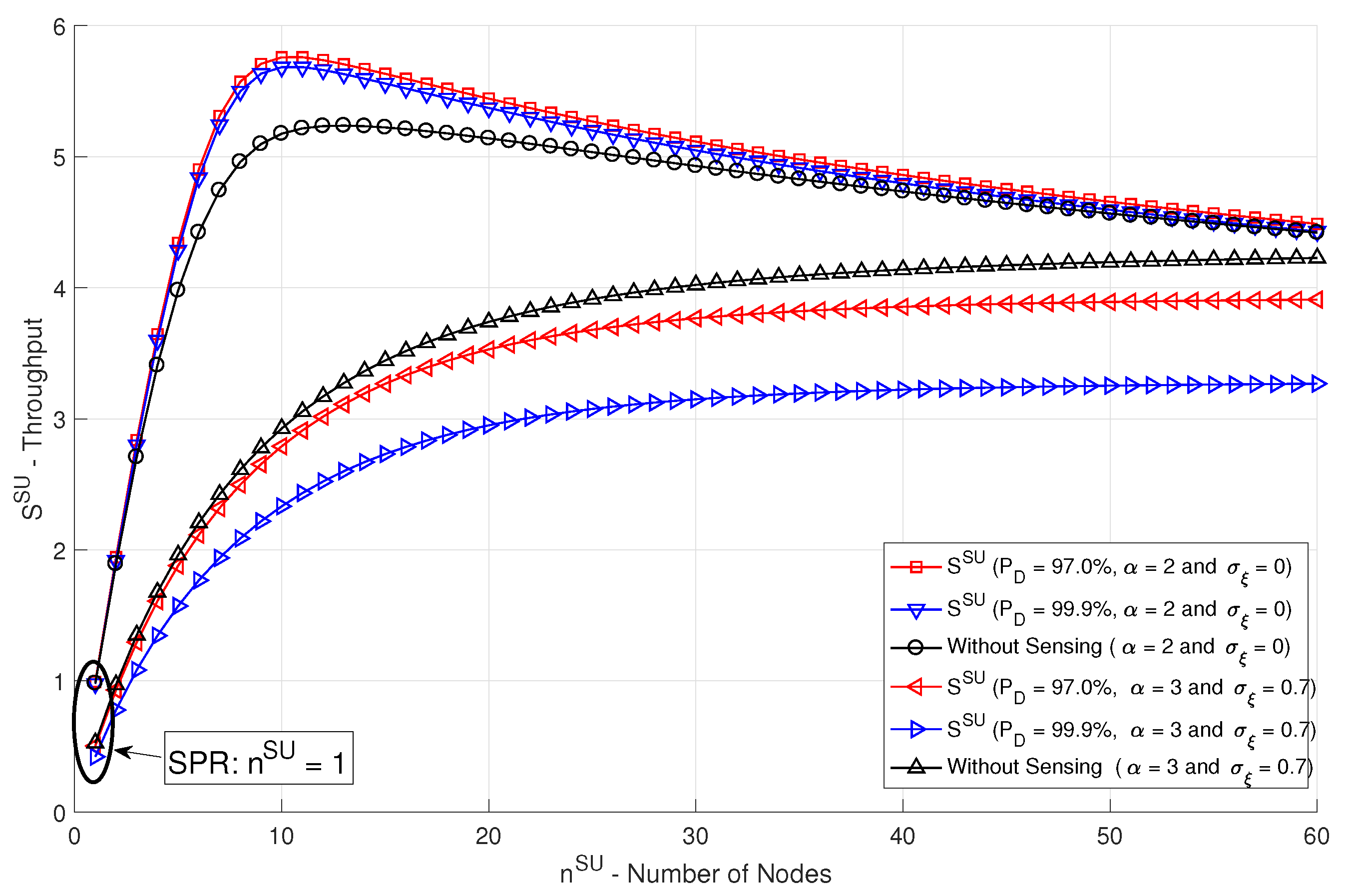
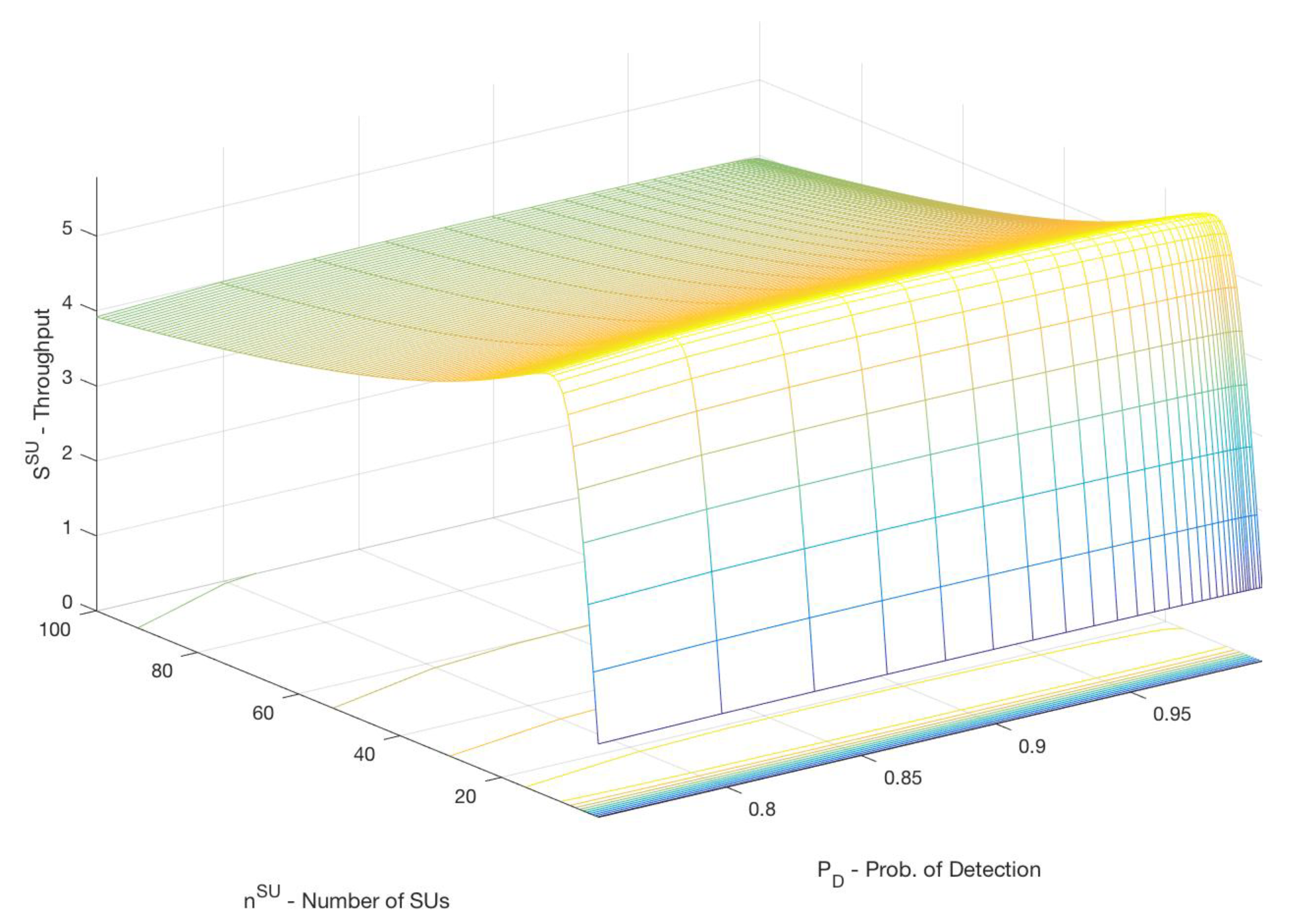
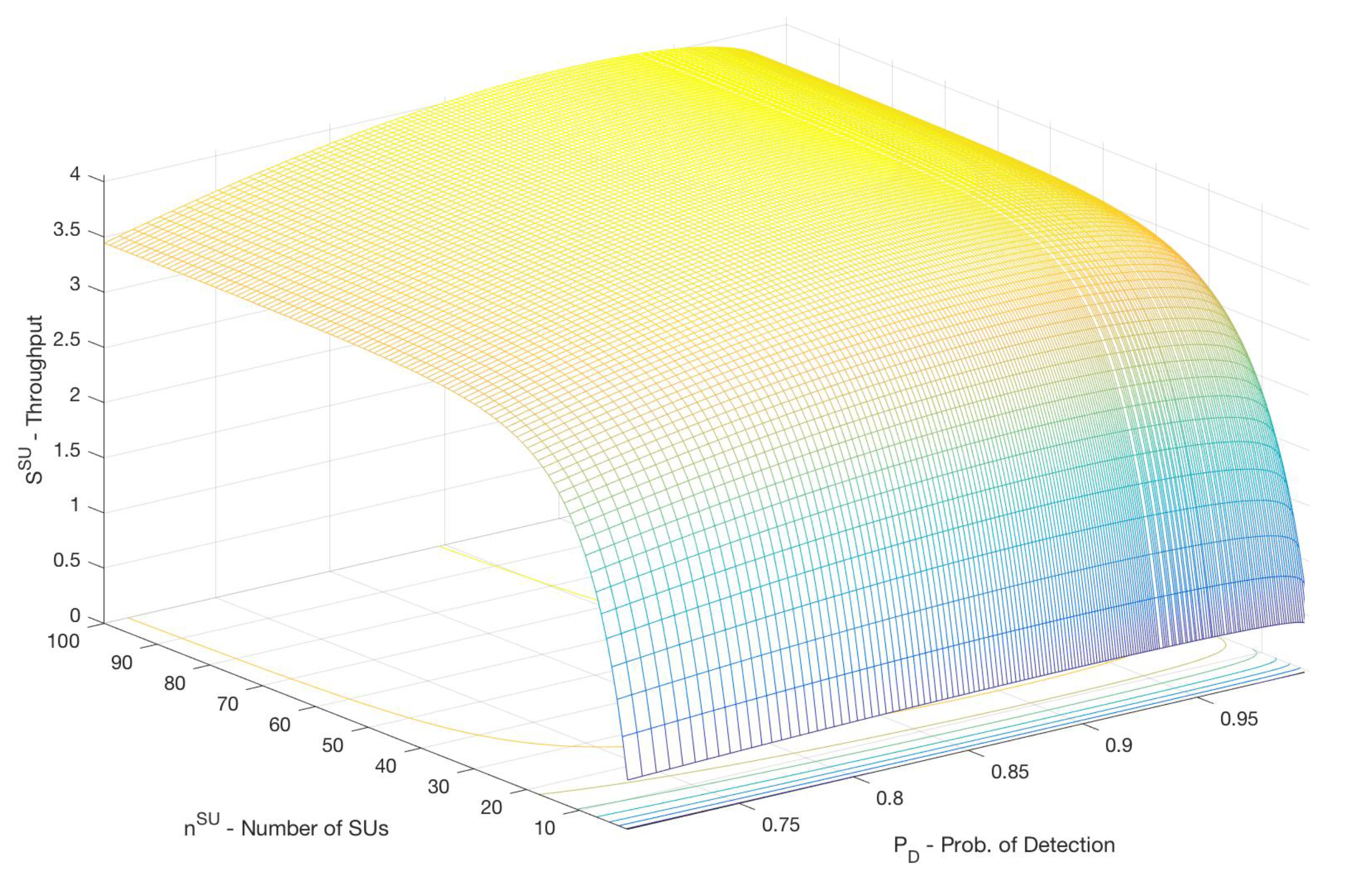
5. Performance Results and Discussion
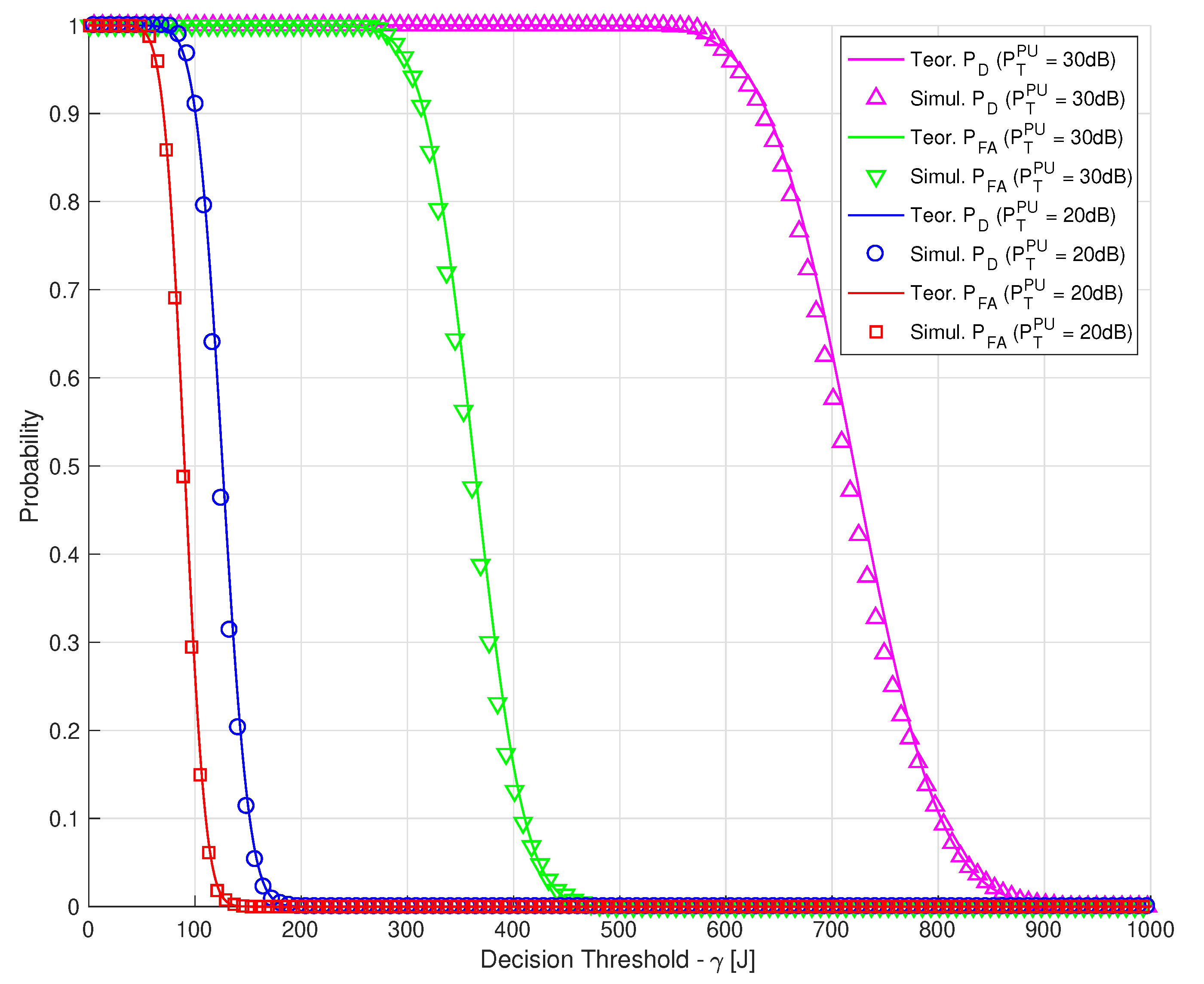
5.1. Validation of the EBS Performance
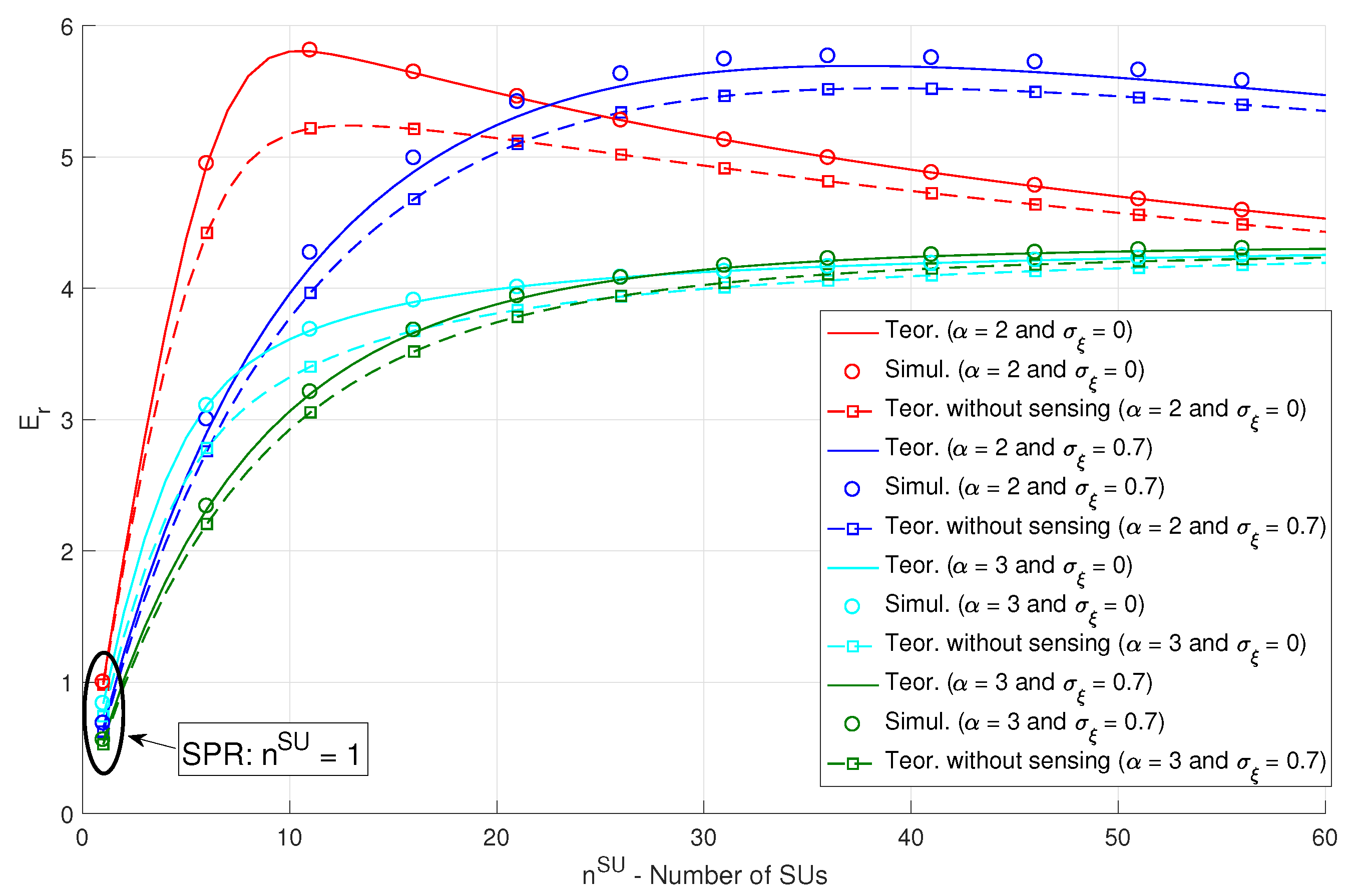
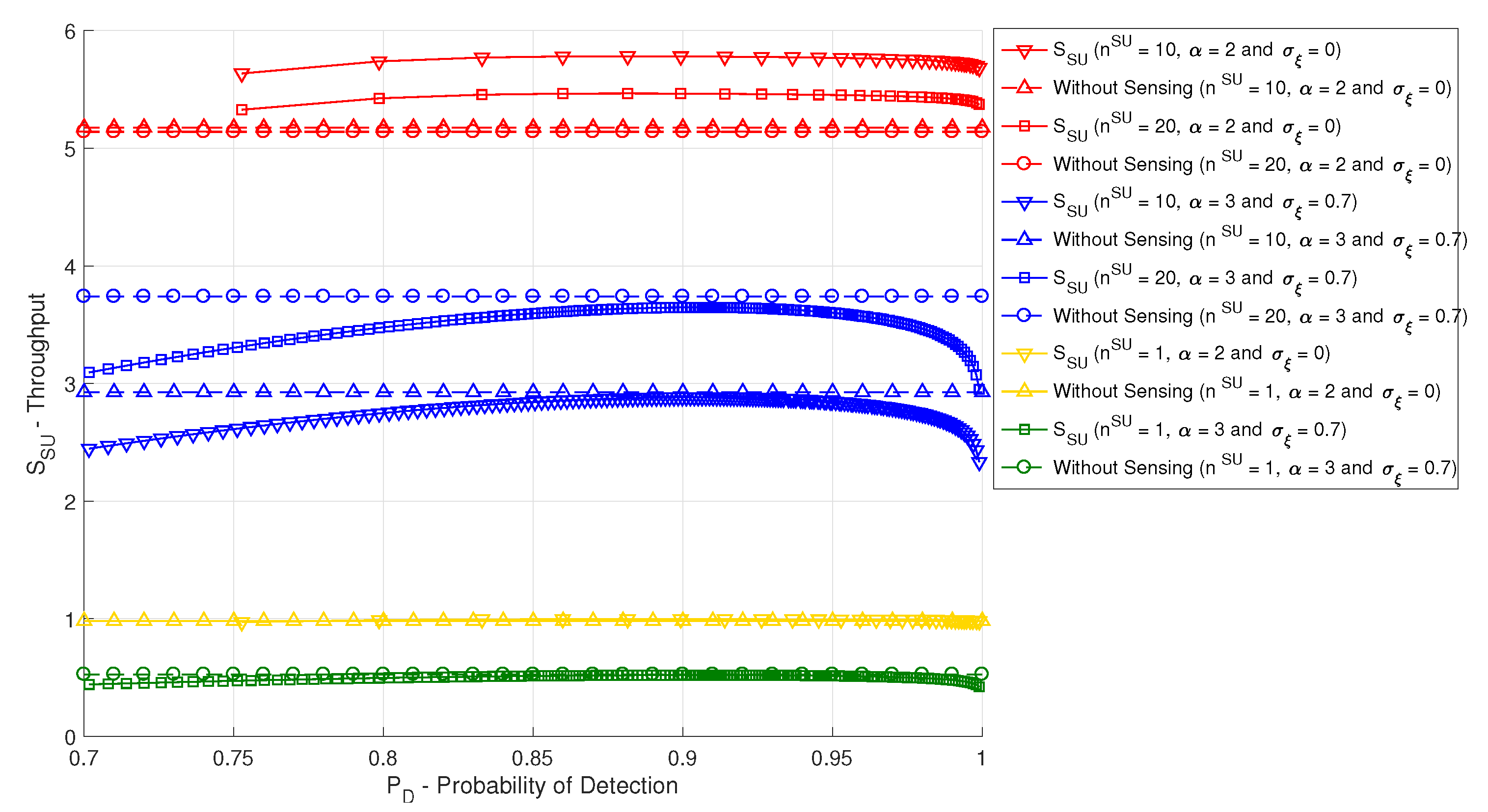
5.2. Decentralized Wireless Network Performance in Shared Channels
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AWGN | Additive White Gaussian Noise |
| CF | Characteristic Function |
| CLT | Central Limit Theorem |
| CSMA | Carrier-Sense Multiple Access |
| EBS | Energy-based Sensing |
| IoT | Internet of Things |
| M2M | Machine-to-Machine |
| MGF | Moment-Generating Function |
| MPR | Multi-Packet Reception |
| Probability Density Function | |
| PU | Primary User |
| RV | Random Variable |
| SINR | Signal-to-Interference-plus-Noise Ratio |
| SNR | Signal-to-Noise Ratio |
| SPR | Single-Packet Reception |
| SU | Secondary User |
References
- Rajandekar, A.; Sikdar, B. A Survey of MAC Layer Issues and Protocols for Machine-to-Machine Communications. IEEE Internet Things J. 2015, 2, 175–186. [Google Scholar] [CrossRef]
- Gupta, P.; Kumar, P. The capacity of wireless networks. IEEE Trans. Inf. Theory 2000, 46, 388–404. [Google Scholar] [CrossRef]
- Zhang, Y.; Gong, A.; Lo, Y.; Li, J.; Shu, F.; Wong, W.S. Generalized p-Persistent CSMA for Asynchronous Multiple-Packet Reception. IEEE Trans. Commun. 2019, 67, 6966–6979. [Google Scholar] [CrossRef]
- Zhang, Y.; Lo, Y.; Shu, F.; Li, J. Achieving Maximum Reliability in Deadline-Constrained Random Access With Multiple-Packet Reception. IEEE Trans. Veh. Technol. 2019, 68, 5997–6008. [Google Scholar] [CrossRef]
- Sadjadpour, H.; Wang, Z.; Garcia-Luna-Aceves, J. The capacity of wireless ad hoc networks with multi-packet reception. IEEE Trans. Commun. 2010, 58, 600–610. [Google Scholar] [CrossRef]
- MacKenzie, R.; O’Farrell, T. Throughput and Delay Analysis for p-Persistent CSMA with Heterogeneous Traffic. IEEE Trans. Commun. 2010, 58, 2881–2891. [Google Scholar] [CrossRef]
- Dai, L. Toward a Coherent Theory of CSMA and Aloha. IEEE Trans. Wirel. Commun. 2013, 12, 3428–3444. [Google Scholar] [CrossRef]
- Sun, X.; Dai, L. To Sense or Not To Sense: A Comparative Study of CSMA With Aloha. IEEE Trans. Commun. 2019, 67, 7587–7603. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Zheng, P.X.; Liew, S.C. How Does Multiple-Packet Reception Capability Scale the Performance of Wireless Local Area Networks? IEEE Trans. Mob. Comput. 2009, 8, 923–935. [Google Scholar] [CrossRef]
- Jin, H.; Seo, J.; Leung, V.C.M. Cooperative Pseudo-Bayesian Backoff Algorithms for Unsaturated CSMA Systems with Multi-Packet Reception. IEEE Trans. Mob. Comput. 2015, 14, 302–315. [Google Scholar] [CrossRef]
- Wang, H.; Fapojuwo, A.O. A Survey of Enabling Technologies of Low Power and Long Range Machine-to-Machine Communications. IEEE Commun. Surv. Tutor. 2017, 19, 2621–2639. [Google Scholar] [CrossRef]
- Bae, Y.H.; Choi, B.D.; Alfa, A.S. Achieving Maximum Throughput in Random Access Protocols with Multipacket Reception. IEEE Trans. Mob. Comput. 2014, 13, 497–511. [Google Scholar] [CrossRef]
- Chan, D.S.; Berger, T.; Tong, L. Carrier Sense Multiple Access Communications on Multipacket Reception Channels: Theory and Applications to IEEE 802.11 Wireless Networks. IEEE Trans. Commun. 2013, 61, 266–278. [Google Scholar] [CrossRef]
- Chen, C.; Hou, S.; Wu, S. A Novel Analytical Model for Asynchronous Multi-Packet Reception MAC Protocol. IEEE Commun. Lett. 2017, 21, 1289–1292. [Google Scholar] [CrossRef]
- Stefanović, C.; Paolini, E.; Liva, G. Asymptotic Performance of Coded Slotted ALOHA With Multipacket Reception. IEEE Commun. Lett. 2018, 22, 105–108. [Google Scholar] [CrossRef]
- Choi, J. On Simultaneous Multipacket Channel Estimation and Reception in Random Access for MTC Under Frequency-Selective Fading. IEEE Trans. Commun. 2018, 66, 5360–5369. [Google Scholar] [CrossRef]
- Zhao, L.; Chi, X.; Qian, L.; Chen, W. Analysis on Latency-Bounded Reliability for Adaptive Grant-Free Access With Multipackets Reception (MPR) in URLLCs. IEEE Commun. Lett. 2019, 23, 892–895. [Google Scholar] [CrossRef]
- Furtado, A.; Irio, L.; Oliveira, R.; Bernardo, L.; Dinis, R. Spectrum Sensing Performance in Cognitive Radio Networks With Multiple Primary Users. IEEE Trans. Veh. Technol. 2016, 65, 1564–1574. [Google Scholar] [CrossRef]
- Stüber, G.L. Principles of Mobile Communication, 2nd ed.; Springer: Boston, MA, USA, 2001. [Google Scholar]
- Al-Ahmadi, S.; Yanikomeroglu, H. On the approximation of the generalized-K distribution by a gamma distribution for modeling composite fading channels. IEEE Trans. Wirel. Commun. 2010, 9, 706–713. [Google Scholar] [CrossRef]
- Irio, L.; Furtado, A.; Oliveira, R.; Bernardo, L.; Dinis, R. Interference Characterization in Random Waypoint Mobile Networks. IEEE Trans. Wirel. Commun. 2018, 17, 7340–7351. [Google Scholar] [CrossRef]
- Tang, H. Some physical layer issues of wide-band cognitive radio systems. In Proceedings of the First IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks, 2005, DySPAN 2005, Baltimore, MD, USA, 8–11 November 2005; pp. 151–159. [Google Scholar]
- Ghasemi, A.; Sousa, E. Optimization of Spectrum Sensing for Opportunistic Spectrum Access in Cognitive Radio Networks. In Proceedings of the 2007 4th IEEE Consumer Communications and Networking Conference, Las Vegas, NV, USA, 11–13 January 2007; pp. 1022–1026. [Google Scholar] [CrossRef]
- Luis, M.; Furtado, A.; Oliveira, R.; Dinis, R.; Bernardo, L. Towards a Realistic Primary Users’ Behavior in Single Transceiver Cognitive Networks. IEEE Commun. Lett. 2013, 17, 309–312. [Google Scholar] [CrossRef]
- Kostylev, V. Energy detection of a signal with random amplitude. In Proceedings of the IEEE International Conference on Communications, ICC 2002, New York, NY, USA, 28 April–2 May 2002; Volume 3, pp. 1606–1610. [Google Scholar] [CrossRef]
- Furtado, A.; Oliveira, R.; Dinis, R.; Bernardo, L. Successful Packet Reception Analysis in Multi-Packet Reception Wireless Systems. IEEE Commun. Lett. 2016, 20, 2498–2501. [Google Scholar] [CrossRef]
| Parameter | Value |
|---|---|
| Channel bandwidth (W) | 100 kHz |
| Sampling Rate | 5 s |
| Frame duration () | 10 ms |
| Transmission Power ( and ) | 30 dB |
| PUs access probability () | |
| PUs spatial density () | |
| sense radius | 30 m |
| PUs outer radius | 500 m |
| AWGN variance () | 1 (0 dB) |
| Capture threshold (b) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Furtado, A.; Oliveira, R.; Bernardo, L.; Dinis, R. Performance Analysis of Interference-Aware Multi-Packet Reception Networks. Electronics 2020, 9, 665. https://doi.org/10.3390/electronics9040665
Furtado A, Oliveira R, Bernardo L, Dinis R. Performance Analysis of Interference-Aware Multi-Packet Reception Networks. Electronics. 2020; 9(4):665. https://doi.org/10.3390/electronics9040665
Chicago/Turabian StyleFurtado, Antonio, Rodolfo Oliveira, Luis Bernardo, and Rui Dinis. 2020. "Performance Analysis of Interference-Aware Multi-Packet Reception Networks" Electronics 9, no. 4: 665. https://doi.org/10.3390/electronics9040665
APA StyleFurtado, A., Oliveira, R., Bernardo, L., & Dinis, R. (2020). Performance Analysis of Interference-Aware Multi-Packet Reception Networks. Electronics, 9(4), 665. https://doi.org/10.3390/electronics9040665






