WhatsTrust: A Trust Management System for WhatsApp
Abstract
1. Introduction
- A trust management system for one of the most popular social networking applications with high security risks, WhatsApp, which has not been targeted by any other previous work.
- A new approach to calculate a user’s reputation in a way that marginalizes the harm of collectively malicious users.
- A well-controlled experimental framework for evaluating the proposed approach.
2. Literature Review
3. System Model
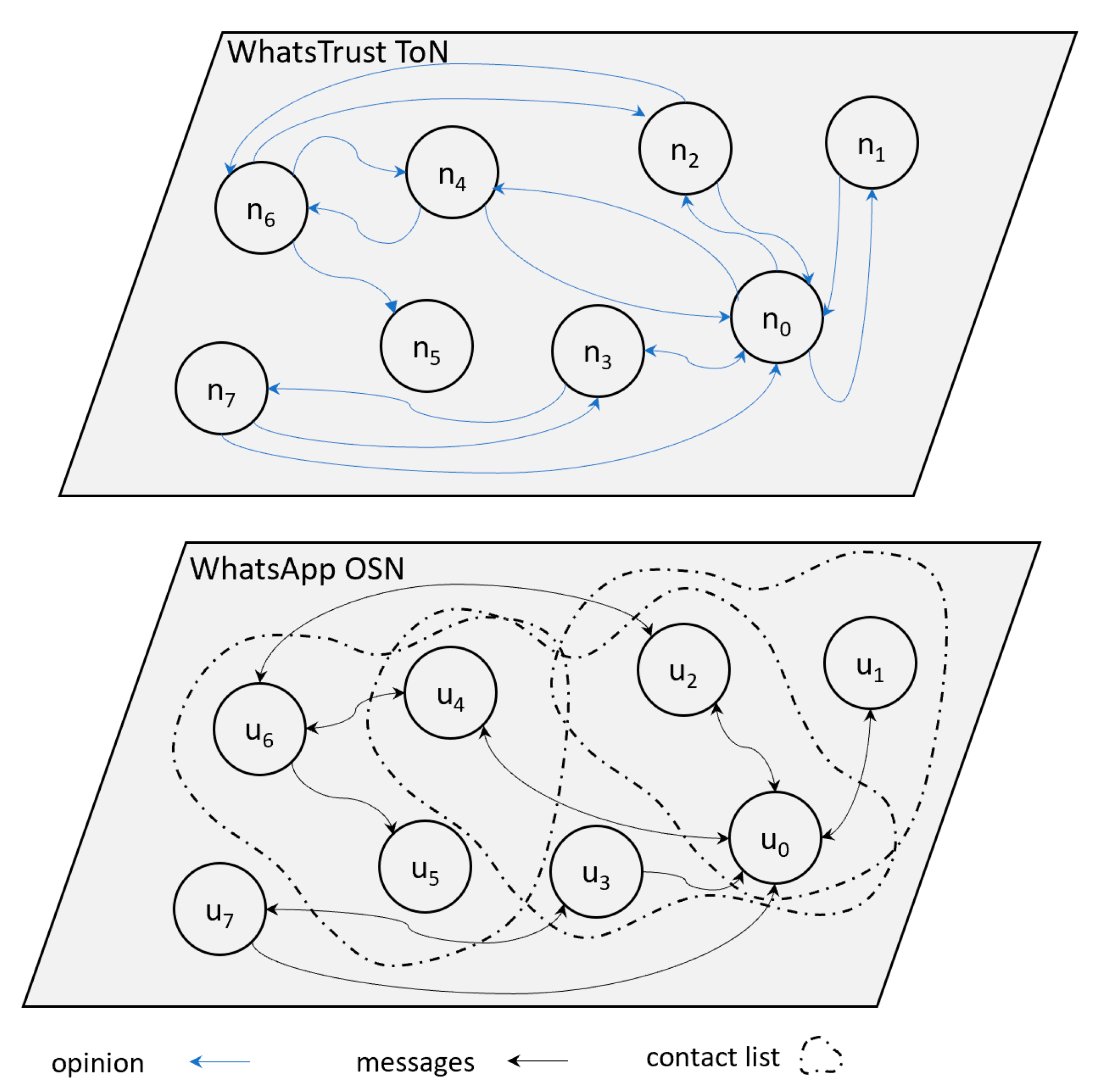
3.1. Network Model
3.2. User Models
- Good nodes: these are nodes that provide valid content and fair ratings about other nodes.
- Malicious nodes: these are nodes that intend to harm other nodes and distort their reputation. WhatsTrust considers two types of malicious nodes.
- Naive malicious nodes: these are malicious nodes that work individually to deliver invalid contents and unfair ratings to other nodes.
- Collectively malicious nodes: these are malicious nodes that form groups to distribute invalid contents and harm other nodes. A collectively malicious node gives positive ratings to the nodes within its group, to raise their reputations, and unfair negative ratings to all other nodes to distort their reputations.
3.3. Relationship Models
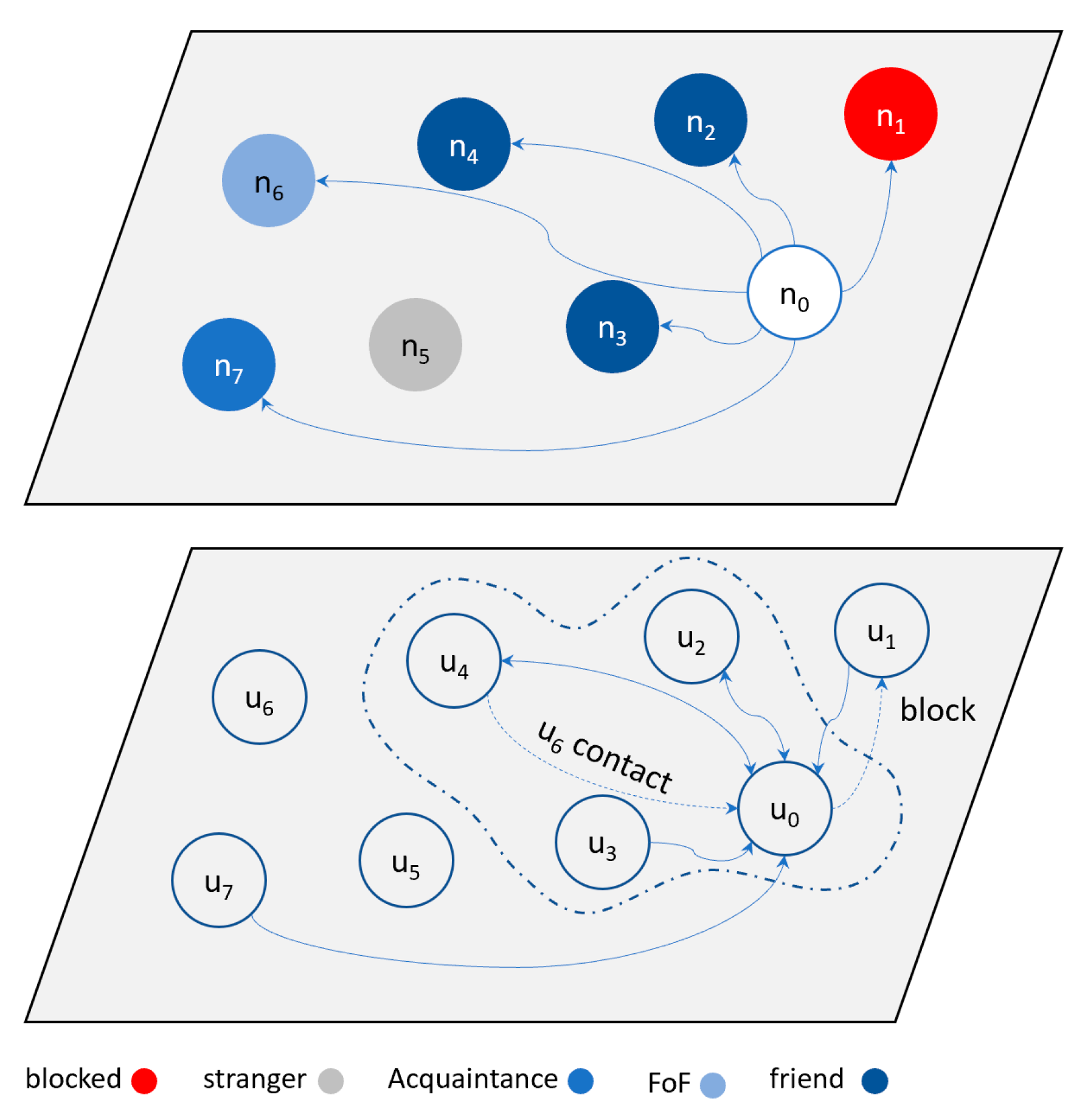
- Friend: a node n0 considers another node ni (e.g., n2, n3, and n4) a friend if ni’s mobile phone number (ID number) exists in n0’s contact list.
- Acquaintance: A node n0 considers another node (e.g., n7) an acquaintance if n7 exists in n0’s local trust list but is not in the contact list. Acquaintances may also include group members.
- Friend of a friend (FoF): A node n0 considers another node (e.g., n6) a FoF if n6 does not exist in n0’s local trust list or contact list, but exists in his friends’ contact list. As explained in Section 4.2.1, when a node n0 receives a message from n6 for the first time, n0 checks with his friends (e.g., n4) if n6 is in their contact list. If so, n0 considers n6 to be a FoF.
- Blocked: a node n0 may block another node (e.g., n1), which prevents node n1 from sending messages to n0.
- Stranger: In all other cases, a node n0 considers other nodes (e.g., n5) to be strangers. This indicates that n5 is not in n0’s contact list or local trust list, nor is he in his friends’ contact lists.
3.4. Message-Exchange Models
- Message-sending models:
- A user may send a message to another user (one to one).
- A user may send a message to a group of users using group chat (one to many). WhatsApp has a maximum group size of 256 users.
- A user may broadcast a message to all contacts (one to all).
- A user may send a message m1 to request a reply message. When the recipient replies, m1 is considered a request.
- Message-receiving models:
- A user may not receive a message from a friend or any other user on the network unless the user is blocked.
- Once a user opens a received message, the following actions may be taken:
- Reply by responding to the message in a private chat with a user or a group chat with multiple users.
- Forward the message to a friend, an acquaintance, or a group of users. Forwarded messages are labeled, which allows receiving users to identify whether the message is written by the sender.
- Copy the content of a message and paste it in an outgoing message.
- Delete a received message.
- Star a received message by marking it with a star.
3.5. Rating Model
- Positive rating: WhatsTrust considers the following actions of a user who received a message (recipient) to be positive, and hence, assign the user who sends the message (sender) a positive rating.
- The recipient user adds the sender to his contacts.
- The recipient replies to the sender’s message.
- The recipient stars the message received from the sender.
- Negative rating: WhatsTrust considers the following actions of a recipient to be negative, and hence, assigns the sender a negative rating.
- The recipient blocks the sender.
- The recipient reports the sender.
4. WhatsTrust Algorithm Design
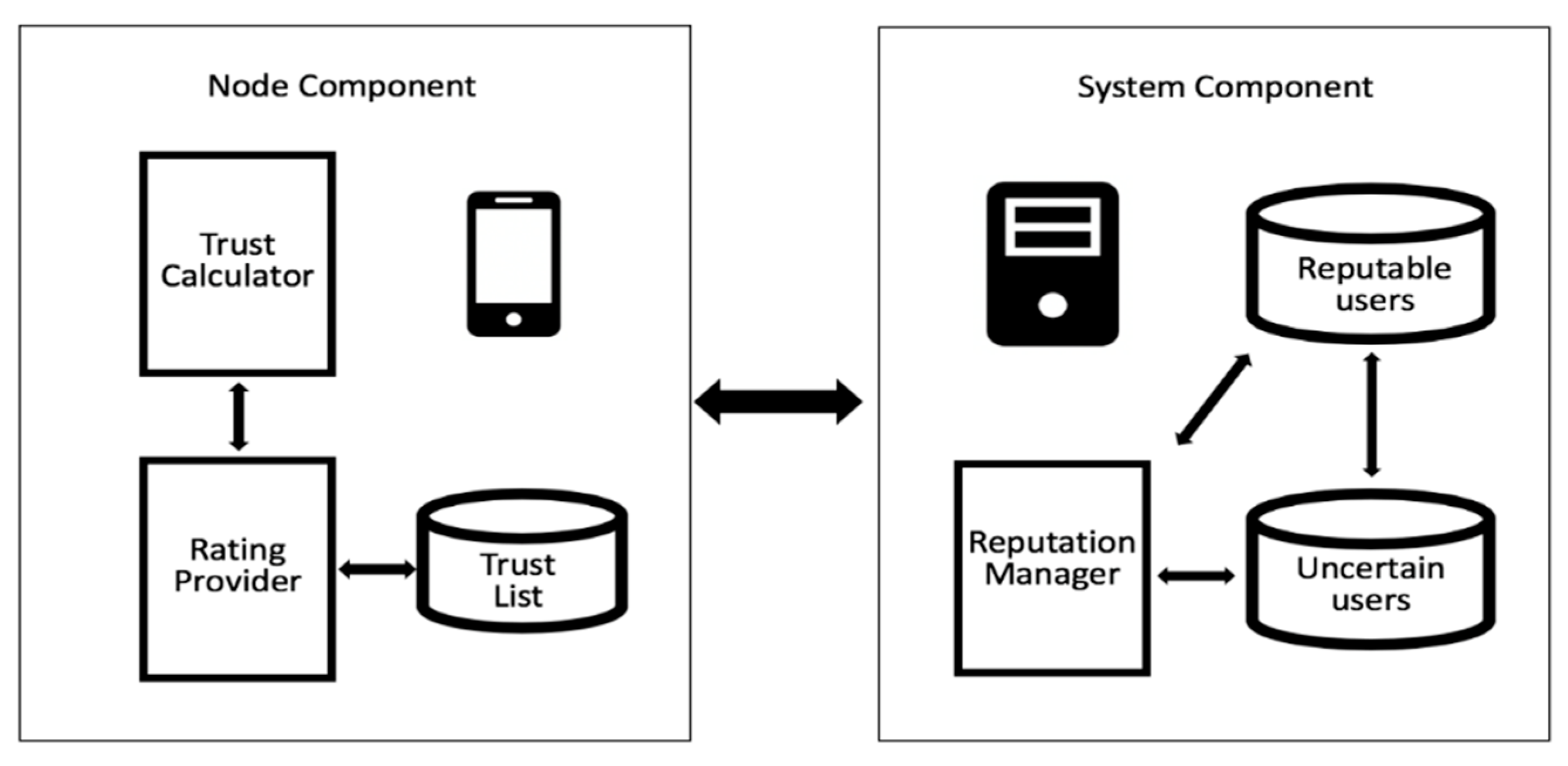
4.1. System Architecture
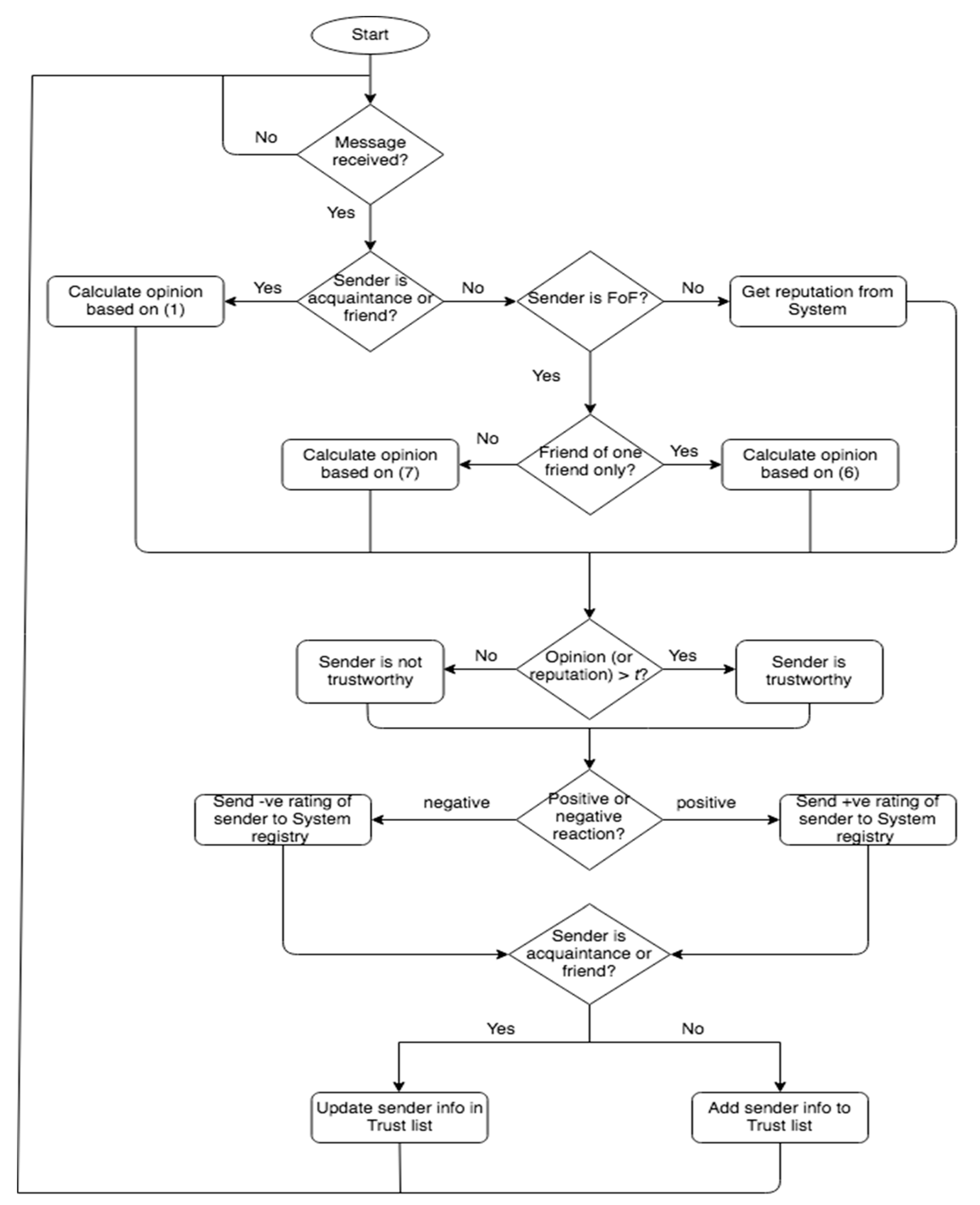
4.2. How the Algorithm Works
4.2.1. Node Algorithm
4.2.2. System Algorithm
5. Evaluation Methodology
5.1. Evaluation Framework
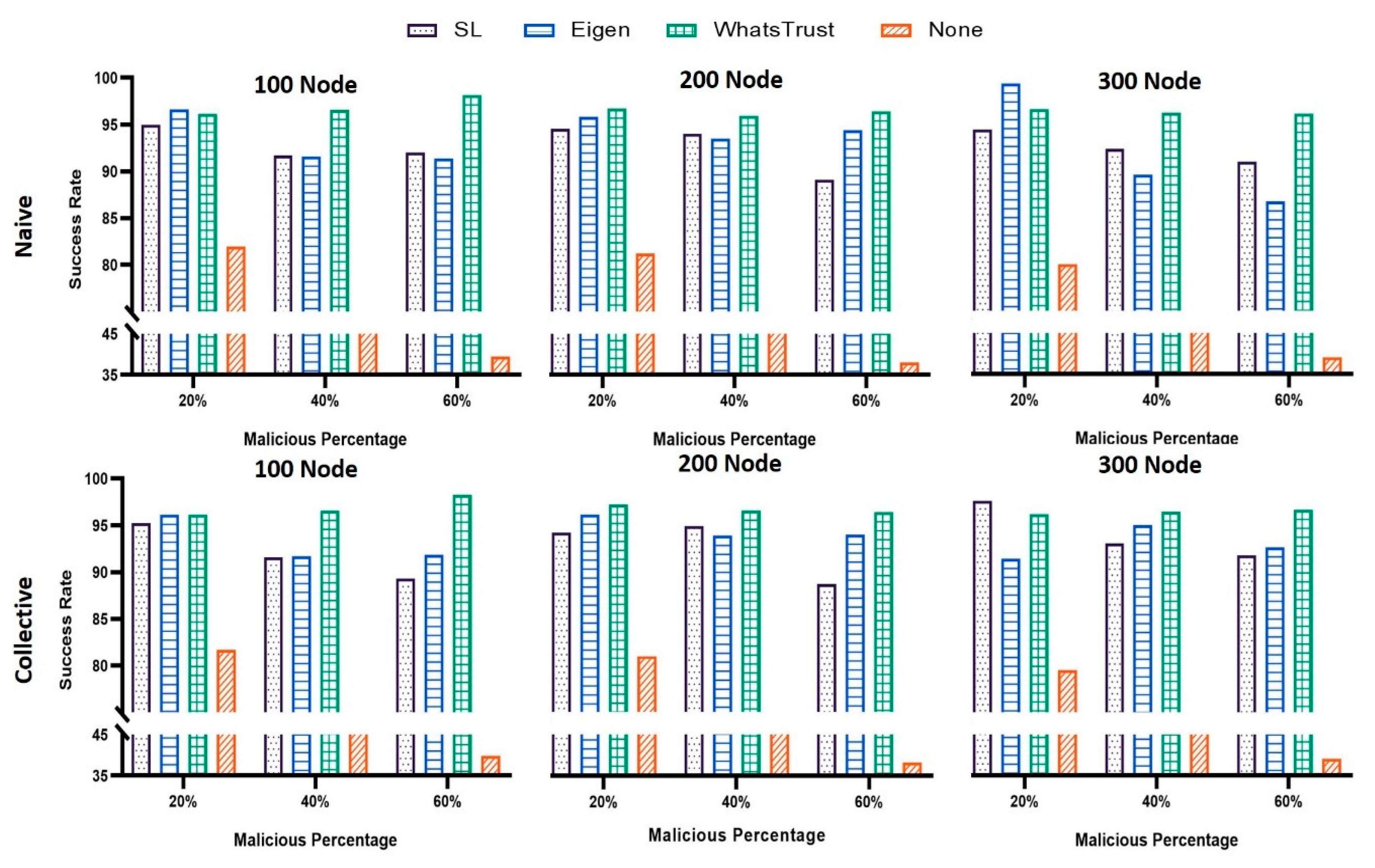
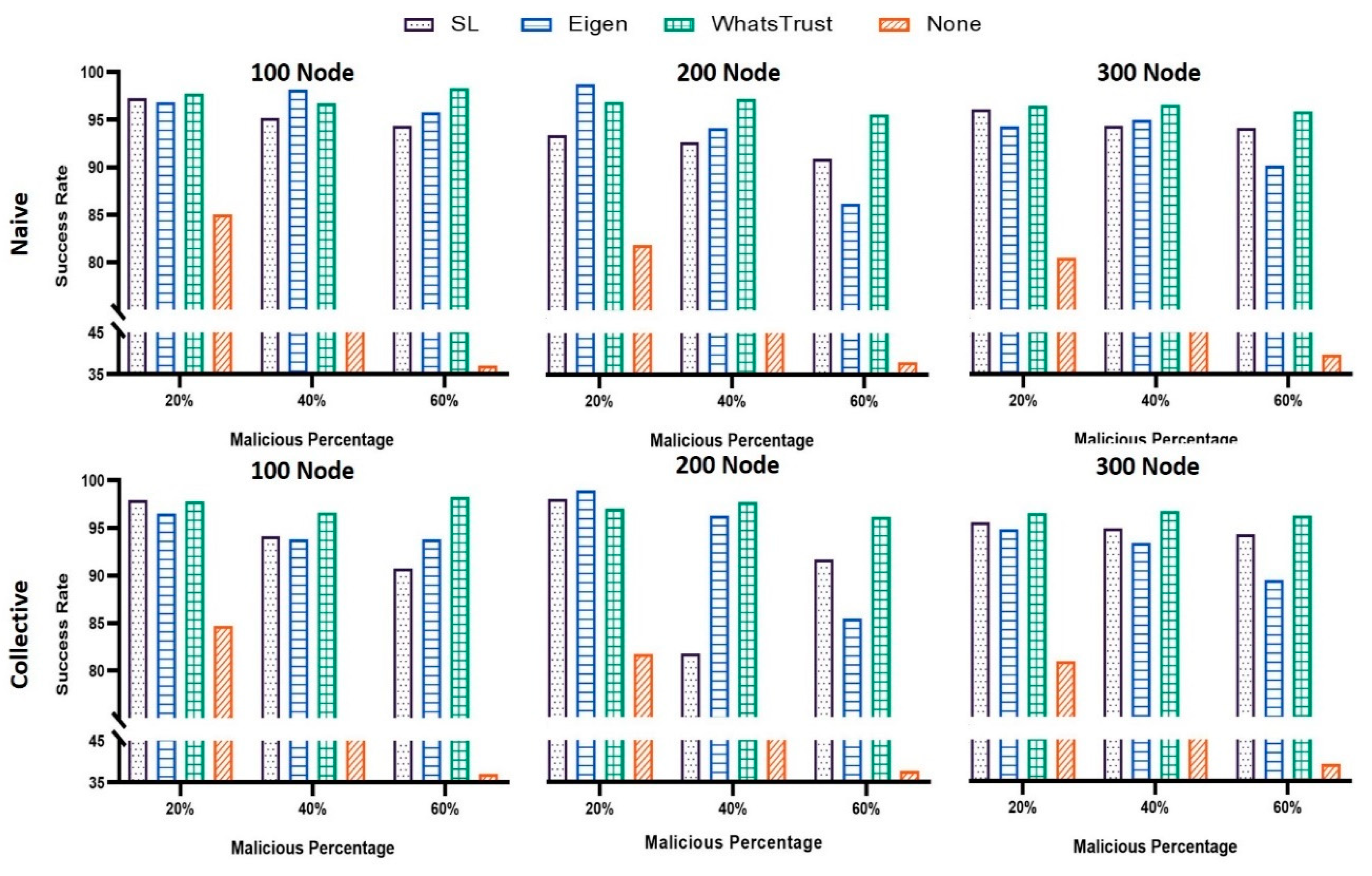
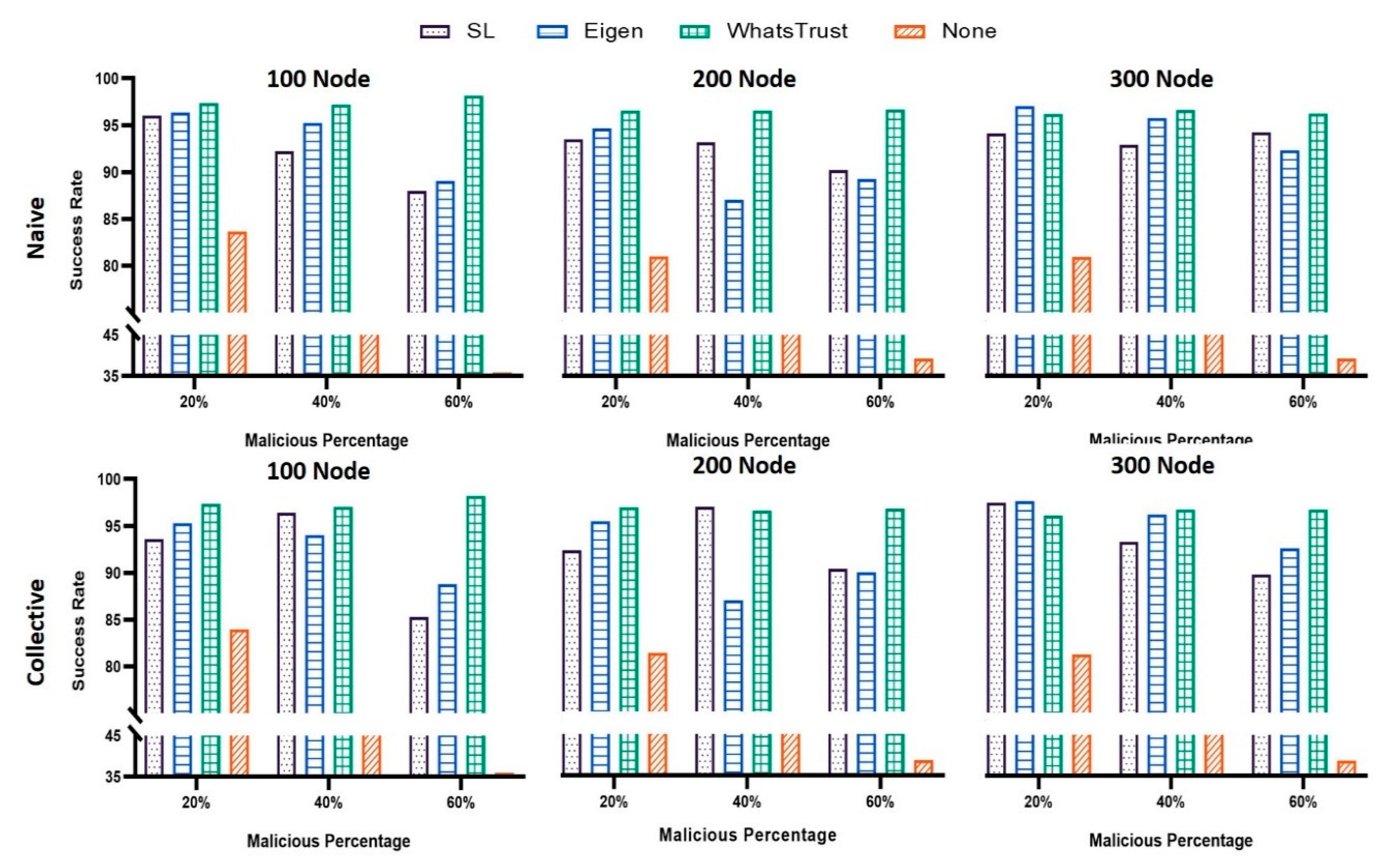
- Success rate: This metric is measured by dividing the total number of valid messages received from good nodes by that of transactions performed by good nodes, as shown in Equation (11).
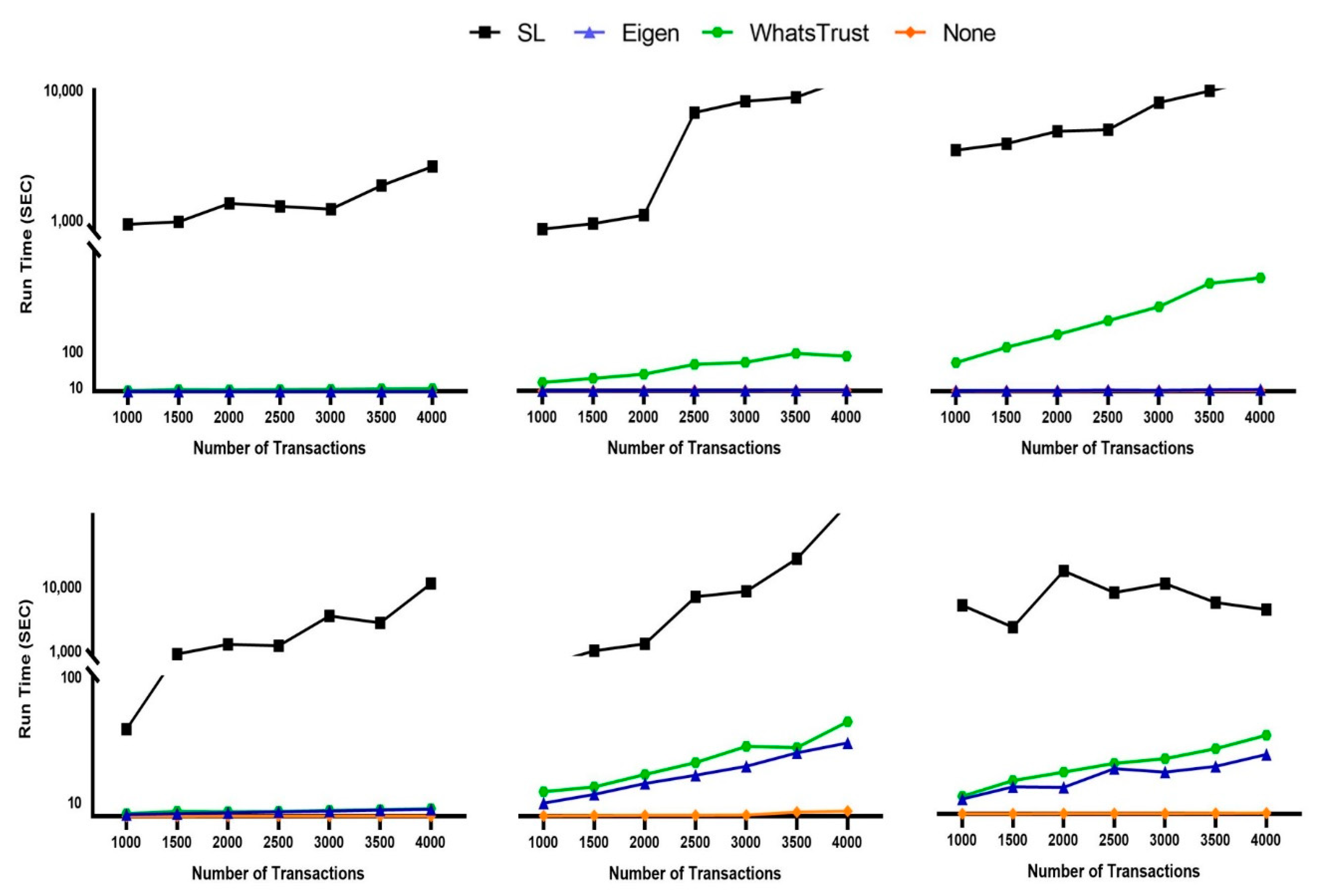
- Execution time: This metric measures the simulation running time of each algorithm: WhatsTrust, EigenTrust, TNA-SL and the none scenario. It is important to note that all algorithms were executed on the same computer cluster at the same load, so this measure can give a clear insight on the computing complexity and overheads of each algorithm.
5.2. Results and Discussion
5.2.1. Success Rate
5.2.2. Execution Time
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schneider, F.; Feldmann, A.; Krishnamurthy, B.; Willinger, W. Understanding online social network usage from a network perspective. In Proceedings of the 9th ACM SIGCOMM conference on Internet measurement, Chicago, IL, USA, 4–6 November 2009; pp. 35–48. [Google Scholar] [CrossRef]
- Statista. Available online: https://www.statista.com/statistics/272014/global-social-networks-ranked-by-number-of-users/ (accessed on 8 November 2020).
- WhatsApp. Available online: https://www.whatsapp.com/ (accessed on 8 November 2020).
- Nassif, L.N. Conspiracy communication reconstitution from distributed instant messages timeline. In Proceedings of the 2019 IEEE Wireless Communications and Networking Conference Workshop (WCNCW), Marrakech, Morocco, 15–18 April 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Hendrikx, F.; Bubendorfer, K.; Chard, R. Reputation systems: A survey and taxonomy. J. Parallel Distr. Comput. 2015, 75, 184–197. [Google Scholar] [CrossRef]
- West, A.G.; Kannan, S.; Lee, I.; Sokolsky, O. An evaluation framework for reputation management system. In Trust Modeling and Management in Digital Environments: From Social Concept to System Development; Zheng, Y., Ed.; IGI Global: Helsinki, Finland, 2009; pp. 282–308. [Google Scholar]
- Zhou, R.; Hwang, K. PowerTrust: A robust and scalable reputation system for trusted peer-to-peer computing. IEEE T. Parall. Distr. 2007, 18, 460–473. [Google Scholar] [CrossRef]
- QTM. 2020. Available online: https://rtg.cis.upenn.edu/qtm/ (accessed on 5 February 2020).
- Jøsang, A.; Hayward, R.; Pope, S. Trust network analysis with subjective logic. In Proceedings of the 29th Australasian Computer Science Conference, Hobart, Australia, 16–19 January 2006; pp. 85–94. [Google Scholar]
- Kurdi, H.A. HonestPeer: An enhanced EigenTrust algorithm for reputation management in P2P systems. J. King Saud Univ. 2015, 27, 315–322. [Google Scholar] [CrossRef]
- Fan, X.; Li, M.; Zhao, H.; Chen, X.; Guo, Z.; Jiao, D.; Sun, W. Peer cluster: A maximum flow-based trust mechanism in P2P file sharing networks. Secur. Commun. Netw. 2013, 6, 1126–1142. [Google Scholar] [CrossRef]
- Kurdi, H.; Alshayban, B.; Altoaimy, L.; Alsalamah, S. TrustyFeer: A subjective logic trust model for smart city peer-to-peer federated clouds. Wirel. Commun. Mob. Comput. 2018, 2018, 1–13. [Google Scholar] [CrossRef]
- Alhussain, A.; Kurdi, H.; Altoaimy, L. A Neural Network-Based Trust Management System for Edge Devices in Peer-to-Peer Networks. CMC-Comput. Mater. Contin. 2019, 59, 805–815. [Google Scholar] [CrossRef]
- Ma, X.; Wang, Z.; Liu, F.; Bian, J. A trust model based on the extended subjective logic for P2P networks. In Proceedings of the IEEE 2nd International Conference on e-Business and Information System Security, Wuhan, China, 31 May–1 June 2010; pp. 1–4. [Google Scholar]
- Dietzel, S.; van der Heijden, R.; Decke, H.; Kargl, F. A flexible, subjective logic-based framework for misbehavior detection in V2V networks. In Proceedings of the IEEE International Symposium on a World of Wireless, Mobile and Multimedia Networks, Sydney, Australia, 19 June 2014; pp. 1–6. [Google Scholar]
- Zhu, C.; Nicanfar, H.; Leung, V.C.; Yang, L.T. An authenticated trust and reputation calculation and management system for cloud and sensor networks integration. IEEE Trans. Inf. Forensics Secur. 2014, 10, 118–131. [Google Scholar]
- Kurdi, H.; Alnasser, S.; Alhelal, M. AuthenticPeer: A reputation management system for peer-to-peer wireless sensor networks. Int. J. Distrib. Sens. Netw. 2015, 11, 637831. [Google Scholar] [CrossRef][Green Version]
- Anwar, R.W.; Zainal, A.; Outay, F.; Yasar, A.; Iqbal, S. BTEM: Belief based trust evaluation mechanism for Wireless Sensor Networks. Future Gener. Comp. Syst. 2019, 96, 605–616. [Google Scholar] [CrossRef]
- Kurdi, H.; Alfaries, A.; Al-Anazi, A.; Alkharji, S.; Addegaither, M.; Altoaimy, L.; Ahmed, S.H. A lightweight trust management algorithm based on subjective logic for interconnected cloud computing environments. J. Supercomput. 2018, 75, 3534–3554. [Google Scholar] [CrossRef]
- Tang, M.; Dai, X.; Liu, J.; Chen, J. Towards a trust evaluation middleware for cloud service selection. Future Gener. Comp. Syst. 2017, 74, 302–312. [Google Scholar] [CrossRef]
- Liu, G.; Yang, Q.; Wang, H.; Lin, X.; Wittie, M.P. Assessment of multi-hop interpersonal trust in social networks by three-valued subjective logic. In Proceedings of the 2014 IEEE Conference on Computer Communications, Toronto, ON, Canada, 27 April–2 May 2014; pp. 1698–1706. [Google Scholar]
- Liu, G.; Chen, Q.; Yang, Q.; Zhu, B.; Wang, H.; Wang, W. Opinionwalk: An efficient solution to massive trust assessment in online social networks. In Proceedings of the 2017 IEEE Conference on Computer Communications, Atlanta, GA, USA, 1–4 May 2017; pp. 1–9. [Google Scholar]
- Ghavipour, M.; Meybodi, M.R. Trust propagation algorithm based on learning automata for inferring local trust in online social networks. Knowl.-Based Syst. 2018, 143, 307–316. [Google Scholar] [CrossRef]
- Yuji, W. The trust value calculating for social network based on machine learning. In Proceedings of the 9th International Conference on Intelligent Human-Machine Systems and Cybernetics, Hangzhou, China, 26–27 August 2017; pp. 133–136. [Google Scholar]
- Ghavipour, M.; Meybodi, M.R. A dynamic algorithm for stochastic trust propagation in online social networks: Learning automata approach. Comput. Commun. 2018, 123, 11–23. [Google Scholar] [CrossRef]
- AlRubaian, M.; Al-Qurishi, M.; Al-Rakhami, M.; Hassan, M.M.; Alamri, A. CredFinder: A real-time tweets credibility assessing system. In Proceedings of the 2016 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining (ASONAM), San Francisco, CA, USA, 18–21 August 2016; pp. 1406–1409. [Google Scholar]
- AlRubaian, M.; Al-Qurishi, M.; Al-Rakhami, M.; Hassan, M.M.; Alamri, A. Reputation-based credibility analysis of Twitter social network users. Concurr. Comp. Pract. E 2017, 29, e3873. [Google Scholar] [CrossRef]
- Jøsang, A. Subjective Logic; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Ruan, Y.; Durresi, A. A survey of trust management systems for online social communities–trust modeling, trust inference and attacks. Knowl.-Based Syst. 2016, 106, 150–163. [Google Scholar] [CrossRef]
- Kamvar, S.D.; Schlosser, M.T.; Garcia-Molina, H. The Eigentrust algorithm for reputation management in p2p networks. In Proceedings of the 12th international conference on World Wide Web, Budapest, Hungary, 20–24 May 2003; pp. 640–651. [Google Scholar] [CrossRef]
- Jøsang, A.; Bhuiyan, T. Optimal trust network analysis with subjective logic. In Proceedings of the 2nd International Conference on Emerging Security Information, Systems and Technologies, Cap Esterel, France, 25–31 August 2008; pp. 179–184. [Google Scholar]
- Bhuiyan, T.; Josang, A.; Xu, Y. Trust and reputation management in web-based social network. In Web Intelligence and Intelligent Agents; InTech: Rijeka, Croatia, 2010; pp. 207–232. [Google Scholar]
- Jiang, W.; Wang, G.; Wu, J. Generating trusted graphs for trust evaluation in online social networks. Future Gener. Comp. Syst. 2014, 31, 48–58. [Google Scholar] [CrossRef]
- Barbian, G. Assessing trust by disclosure in online social networks. In Proceedings of the IEEE International Conference on Advances in Social Networks Analysis and Mining, Kaohsiung, Taiwan, 25–27 July 2011; pp. 163–170. [Google Scholar]
- Li, M.; Bonti, A. T-OSN: A trust evaluation model in online social networks. In Proceedings of the IEEE IFIP 9th International Conference on Embedded and Ubiquitous Computing, Melbourne, Australia, 24–26 October 2011; pp. 469–473. [Google Scholar]
- Ureña, R.; Chiclana, F.; Herrera-Viedma, E. DeciTrustNET: A graph based trust and reputation framework for social networks. Inform. Fusion. 2020, 61, 101–112. [Google Scholar] [CrossRef]
- Li, P.; Zhao, W.; Yang, J.; Sheng, Q.Z.; Wu, J. Let’s CoRank: Trust of users and tweets on social networks. World Wide Web 2020, 23, 2877–2901. [Google Scholar] [CrossRef]
- Imran, M.; Khattak, H.A.; Millard, D.; Tiropanis, T.; Bashir, T.; Ahmed, G. Calculating Trust Using Multiple Heterogeneous Social Networks. Wirel. Commun. Mob. Comput. 2020, 2020, 1–14. [Google Scholar] [CrossRef]
- Chen, X.; Yuan, Y.; Lu, L.; Yang, J. A multidimensional trust evaluation framework for online social networks based on machine learning. IEEE ACCESS 2019, 7, 175499–175513. [Google Scholar] [CrossRef]
- Saeidi, S. A new model for calculating the maximum trust in Online Social Networks and solving by Artificial Bee Colony algorithm. Comput. Soc. Netw. 2020, 7, 1–21. [Google Scholar] [CrossRef]
- Zhou, R.; Hwang, K. Trust overlay networks for global reputation aggregation in P2P grid computing. In Proceedings of the 20th IEEE International Parallel & Distributed Processing Symposium, Rhodes, Greece, 25–29 April 2006; p. 29. [Google Scholar] [CrossRef]
- Rohr, D.; Kalcher, S.; Bach, M.; Alaqeeli, A.; Alzaid, H.; Eschweiler, D.; Lindenstruth, V.; Sakhar, A.; Alharthi, A.; Almubarak, A.; et al. An energy-efficient multi-GPU supercomputer. In Proceedings of the 16th IEEE International Conference on High Performance Computing and Communications, Paris, France, 20–22 August 2014; pp. 42–45. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almuzaini, F.; Alromaih, S.; Althnian, A.; Kurdi, H. WhatsTrust: A Trust Management System for WhatsApp. Electronics 2020, 9, 2190. https://doi.org/10.3390/electronics9122190
Almuzaini F, Alromaih S, Althnian A, Kurdi H. WhatsTrust: A Trust Management System for WhatsApp. Electronics. 2020; 9(12):2190. https://doi.org/10.3390/electronics9122190
Chicago/Turabian StyleAlmuzaini, Fatimah, Sarah Alromaih, Alhanoof Althnian, and Heba Kurdi. 2020. "WhatsTrust: A Trust Management System for WhatsApp" Electronics 9, no. 12: 2190. https://doi.org/10.3390/electronics9122190
APA StyleAlmuzaini, F., Alromaih, S., Althnian, A., & Kurdi, H. (2020). WhatsTrust: A Trust Management System for WhatsApp. Electronics, 9(12), 2190. https://doi.org/10.3390/electronics9122190




