A Comparative Study of Stochastic Model Predictive Controllers
Abstract
1. Introduction
- A detailed description of the theoretical background of each strategy is presented. Emphasis is made on the formulation of the optimal control problem and how uncertainties are addressed. In addition, the SCMPC formulation for worst case OCP is analyzed.
- The ways in which OCPs are stated in each strategy are compared with respect to the cost function and constraints on the states according to the statistical information. The structural similarity between the SMPC approach and classic MPC is shown by transforming probabilistic constraints into deterministic ones.
- The viability of these two control strategies is analyzed through two numerical examples: a two-mass spring SISO system with parametric and additive uncertainties and a nonlinear quadruple-tank system with additive uncertainties. The controllers comparison is made by using performance indices such as number of successful runs, number of times the constraints are violated, mean value of the integral absolute error and the computational cost.
- As complementary material, the specialized software Stochastic Model Predictive Control Toolbox, developed by the authors, is available in MATLAB Central [31]. This tool allows readers to reproduce part of the results here presented or to tune and simulate SMPCs or SCMPCs for controlling multivariable systems with additive disturbances which present Gaussian probability distributions.
2. Model Predictive Control Strategy
3. Stochastic MPC
3.1. SMPC Strategy
3.2. SCMPC Strategy
4. Numerical Examples, Results and Discussion
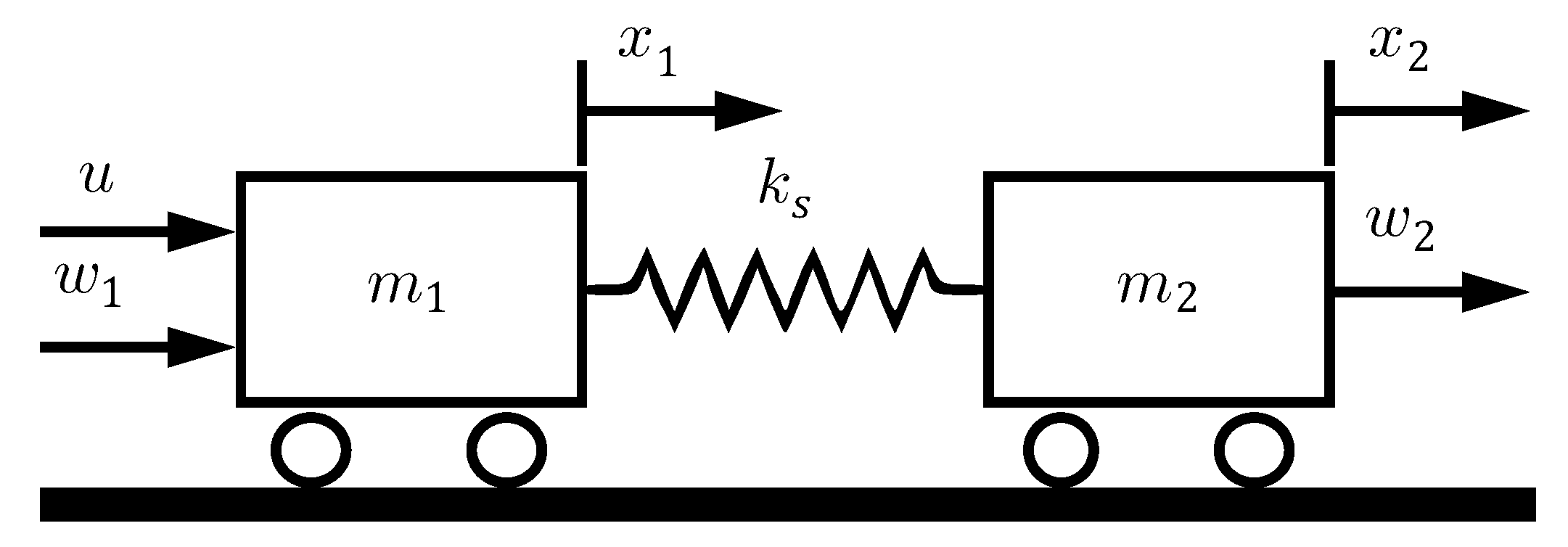
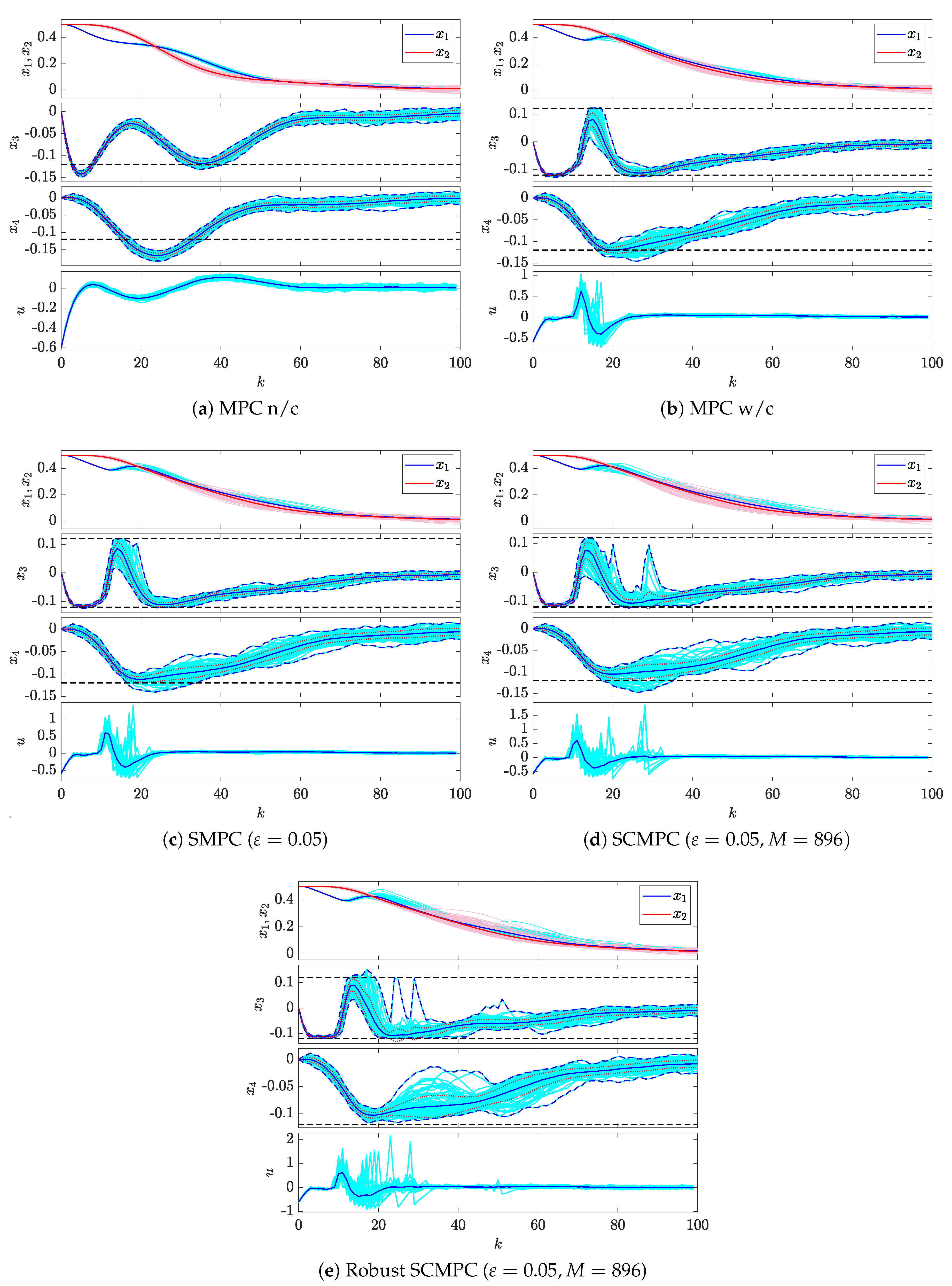
4.1. Example 1
- Case 1: is known, constant and it is set to its nominal value .
- Case 2: is unknown and varies according to its probability distribution at every control period.
- Case 3: is unknown and remains constant for all instants along each simulation. The value varies according to its probability distribution in each simulation.
4.2. Example 2
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Richalet, J.; Rault, A.; Testud, J.; Papon, J. Model predictive heuristic control: Applications to industrial processes. Automatica 1978, 14, 413–428. [Google Scholar] [CrossRef]
- Forbes, M.G.; Patwardhan, R.S.; Hamadah, H.; Gopaluni, R.B. Model Predictive Control in Industry: Challenges and Opportunities. IFAC Pap. 2015, 48, 531–538. [Google Scholar] [CrossRef]
- Jurado, I.; Millán, P.; Quevedo, D.; Rubio, F. Stochastic MPC with Applications to Process Control. Int. J. Control 2014, 88, 792–800. [Google Scholar] [CrossRef]
- Richalet, J.; Abu El Ata-Doss, S.; Arber, C.; Kuntze, H.; Jacubasch, A.; Schill, W. Predictive Functional Control-Application to Fast and Accurate Robots. IFAC Proc. Vol. 1987, 20, 251–258. [Google Scholar] [CrossRef]
- Tan, Y.; Cai, G.; Li, B.; Teo, K.L.; Wang, S. Stochastic Model Predictive Control for the Set Point Tracking of Unmanned Surface Vehicles. IEEE Access 2020, 8, 579–588. [Google Scholar] [CrossRef]
- Mueller, M.W.; D’Andrea, R. A model predictive controller for quadrocopter state interception. In Proceedings of the 2013 European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013; pp. 1383–1389. [Google Scholar] [CrossRef]
- Lamoudi, M.Y.; Alamir, M.; Béguery, P. Model predictive control for energy management in buildings Part 2: Distributed Model Predictive Control. IFAC Proc. Vol. 2012, 45, 226–231. [Google Scholar] [CrossRef]
- Salsbury, T.; Mhaskar, P.; Qin, S.J. Predictive control methods to improve energy efficiency and reduce demand in buildings. Comput. Chem. Eng. 2013, 51, 77–85. [Google Scholar] [CrossRef]
- Sultana, W.R.; Sahoo, S.K.; Sukchai, S.; Yamuna, S.; Venkatesh, D. A review on state-of-the-art development of model predictive control for renewable energy applications. Renew. Sustain. Energy Rev. 2017, 76, 391–406. [Google Scholar] [CrossRef]
- Luchini, E.; Schirrer, A.; Kozek, M. A hierarchical MPC for multi-objective mixed-integer optimisation applied to redundant refrigeration circuits. IFAC Pap. 2017, 50, 9058–9064. [Google Scholar] [CrossRef]
- Mercorelli, P.; Kubasiak, N.; Liu, S. Model predictive control of an electromagnetic actuator fed by multilevel PWM inverter. In Proceedings of the 2004 IEEE International Symposium on Industrial Electronics, Ajaccio, France, 4–7 May 2004; pp. 531–535. [Google Scholar] [CrossRef]
- Mayne, D.; Rawlings, J.; Rao, C.; Scokaert, P. Constrained Model Predictive Control: Stability and Optimality. Automatica 2000, 36, 789–814. [Google Scholar] [CrossRef]
- Maciejowski, J. Predictive Control: With Constraints, 1st ed.; Prentice Hall: London, UK, 2002. [Google Scholar]
- Kouvaritakis, B.; Cannon, M. Model Predictive Control. Classical, Robust and Stochastic, 1st ed.; Springer International Publishing: London, UK, 2016. [Google Scholar] [CrossRef]
- Mayne, D.Q. Model Predictive Control: Recent Developments and Future Promise. Automatica 2014, 50, 2967–2986. [Google Scholar] [CrossRef]
- Kothare, M.V.; Balakrishnan, V.; Morari, M. Robust Constrained Model Predictive Control Using Linear Matrix Inequalities. Automatica 1996, 32, 1361–1379. [Google Scholar] [CrossRef]
- Bemporad, A.; Morari, M. Robust Model Predictive Control: A Survey. In Robustness in Identification and Control; Springer: London, UK, 1999; pp. 207–226. [Google Scholar] [CrossRef]
- Mesbah, A. Stochastic Model Predictive Control: An Overview and Perspectives for Future Research. IEEE Control Syst. Mag. 2016, 36, 30–44. [Google Scholar] [CrossRef]
- Mayne, D. Robust and Stochastic MPC: Are We Going in the Right Direction? IFAC Pap. 2015, 48, 1–8. [Google Scholar] [CrossRef]
- Kouvaritakis, B.; Cannon, M. Stochastic Model Predictive Control. In Encyclopedia of Systems and Control, 1st ed.; Springer: London, UK, 2015; pp. 1350–1357. [Google Scholar] [CrossRef]
- Farina, M.; Giulioni, L.; Scattolini, R. Stochastic Linear Model Predictive Control with Chance Constraints—A Review. J. Process. Control 2016, 44, 53–67. [Google Scholar] [CrossRef]
- Hewing, L.; Zeilinger, M.N. Scenario-Based Probabilistic Reachable Sets for Recursively Feasible Stochastic Model Predictive Control. IEEE Control Syst. Lett. 2020, 4, 450–455. [Google Scholar] [CrossRef]
- Cannon, M.; Kouvaritakis, B.; Raković, S.V.; Cheng, Q. Stochastic Tubes in Model Predictive Control With Probabilistic Constraints. IEEE Trans. Autom. Control 2011, 56, 194–200. [Google Scholar] [CrossRef]
- Lorenzen, M.; Dabbene, F.; Tempo, R.; Allgöwer, F. Constraint-Tightening and Stability in Stochastic Model Predictive Control. IEEE Trans. Autom. Control 2017, 62, 3165–3177. [Google Scholar] [CrossRef]
- Heirung, T.A.N.; Paulson, J.A.; O’Leary, J.; Mesbah, A. Stochastic Model Mredictive Control-How Does It Work? Comput. Chem. Eng. 2018, 114, 158–170. [Google Scholar] [CrossRef]
- Paulson, J.A.; Buehler, E.A.; Braatz, R.D.; Mesbah, A. Stochastic Model Predictive Control with Joint Chance Constraints. Int. J. Control 2017, 93, 126–139. [Google Scholar] [CrossRef]
- Mayne, D.Q.; Falugi, P. Stabilizing Conditions for Model Predictive Control. Int. J. Robust Nonlinear Control 2018, 29, 894–903. [Google Scholar] [CrossRef]
- Calafiore, G.C.; Fagiano, L. Robust Model Predictive Control Via Scenario Optimization. IEEE Trans. Autom. Control 2013, 58, 219–224. [Google Scholar] [CrossRef]
- Schildbach, G.; Fagiano, L.; Frei, C.; Morari, M. The Scenario Approach for Stochastic Model Predictive Control with Bounds on Closed-Loop Constraint Violations. Automatica 2014, 50, 3009–3018. [Google Scholar] [CrossRef]
- Calafiore, G.; Campi, M.C. The Scenario Approach to Robust Control Design. IEEE Trans. Autom. Control 2006, 51, 742–753. [Google Scholar] [CrossRef]
- González Querubín, E.A. Stochastic Model Predictive Control Toolbox. Version 1.0.4. Available online: https://www.mathworks.com/matlabcentral/fileexchange/75803 (accessed on 5 December 2020).
- Boyd, S.; El Ghaoui, L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1994. [Google Scholar] [CrossRef]
- Cuzzola, F.A.; Geromel, J.C.; Morari, M. An Improved Approach for Constrained Robust Model Predictive Control. Automatica 2002, 38, 1183–1189. [Google Scholar] [CrossRef]
- Maeder, U.; Borrelli, F.; Morari, M. Linear Offset-Free Model Predictive Control. Automatica 2009, 45, 2214–2222. [Google Scholar] [CrossRef]
- Blanchini, F.; Miani, S. Set-Theoretic Methods in Control, 1st ed.; Birkhäuser Boston: Boston, MA, USA, 2008. [Google Scholar] [CrossRef]
- Khlebnikov, M.V.; Polyak, B.T.; Kuntsevich, V.M. Optimization of Linear Systems Subject to Bounded Exogenous Disturbances: The Invariant Ellipsoid Technique. Autom. Remote. Control 2011, 72, 2227–2275. [Google Scholar] [CrossRef]
- Zhang, X.; Grammatico, S.; Schildbach, G.; Goulart, P.; Lygeros, J. On the Sample Size of Randomized MPC for Chance-Constrained Systems with Application to Building Climate Control. In Proceedings of the 2014 European Control Conference (ECC), Strasbourg, France, 24–27 June 2014; pp. 478–483. [Google Scholar] [CrossRef]
- Parisio, A.; Varagnolo, D.; Molinari, M.; Pattarello, G.; Fabietti, L.; Johansson, K.H. Implementation of a Scenario-based MPC for HVAC Systems: An Experimental Case Study. IFAC Proc. Vol. 2014, 47, 599–605. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Y.; Xu, L.; Liu, J.; Sun, H. A Chance-Constrained Stochastic Model Predictive Control for Building Integrated with Renewable Resources. Electr. Power Syst. Res. 2020, 184, 106348. [Google Scholar] [CrossRef]
- Raimondi Cominesi, S.; Farina, M.; Giulioni, L.; Picasso, B.; Scattolini, R. A Two-Layer Stochastic Model Predictive Control Scheme for Microgrids. IEEE Trans. Control Syst. Technol. 2018, 26, 1–13. [Google Scholar] [CrossRef]
- Ramandi, M.Y.; Bigdeli, N.; Afshar, K. Stochastic Economic Model Predictive Control for Real-Time Scheduling of Balance Responsible Parties. Int. J. Electr. Power Energy Syst. 2020, 118, 105800. [Google Scholar] [CrossRef]
- Velarde, P.; Tian, X.; Sadowska, A.D.; Maestre, J.M. Scenario-Based Hierarchical and Distributed MPC for Water Resources Management with Dynamical Uncertainty. Water Resour. Manag. 2018, 33, 677–696. [Google Scholar] [CrossRef]
- Velasco, J.; Liniger, A.; Zhang, X.; Lygeros, J. Efficient Implementation of Randomized MPC for Miniature Race Cars. In Proceedings of the 2016 European Control Conference (ECC), Aalborg, Denmark, 29 June 2016; pp. 957–962. [Google Scholar] [CrossRef]
- Piovesan, J.L.; Tanner, H.G. Randomized Model Predictive Control for Robot Navigation. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 17 May 2009; pp. 94–99. [Google Scholar] [CrossRef]
- Goodwin, G.C.; Medioli, A.M. Scenario-Based, Closed-Loop Model Predictive Control With Application to Emergency Vehicle Scheduling. Int. J. Control 2013, 86, 1338–1348. [Google Scholar] [CrossRef]
- Mesbah, A. Stochastic Model Predictive Control with Active Uncertainty Learning: A Survey on Dual Control. Annu. Rev. Control 2018, 45, 107–117. [Google Scholar] [CrossRef]
- Cannon, M.; Kouvaritakis, B.; Ng, D. Probabilistic Tubes in Linear Stochastic Model Predictive Control. Syst. Control Lett. 2009, 58, 747–753. [Google Scholar] [CrossRef]
- Calafiore, G.C. Random Convex Programs. SIAM J. Optim. 2010, 20, 3427–3464. [Google Scholar] [CrossRef]
- Wie, B.; Bernstein, D.S. Benchmark Problems for Robust Control Design. J. Guid. Control Dyn. 1992, 15, 1057–1059. [Google Scholar] [CrossRef]
- Johansson, K.H.; Polyak, B.T.; Kuntsevich, V.M. The Quadruple-Tank Process: A Multivariable Laboratory Process With an Adjustable Zero. IEEE Trans. Control Syst. Technol. 2000, 8, 456–465. [Google Scholar] [CrossRef]
- Numsomran, A.; Tipsuwanporn, V.; Tirasesth, K. Modeling of the Modified Quadruple-Tank Process. In Proceedings of the 2008 SICE Annual Conference, Tokyo, Japan, 20–22 August 2008; pp. 818–823. [Google Scholar] [CrossRef]




| Index | Description |
|---|---|
| Number of simulations from where no constraints were violated. | |
| Probability of success of a simulation, . | |
| Number of constraints violated in all simulations. | |
| IAEavg | Mean value of the integral absolute error of the states, based on the closed-loop system responses of the simulations. |
| Mean value of the integral of the absolute value of the applied inputs of all . | |
| Average time taken for the algorithm to obtain a solution. | |
| Maximum standard deviation of the states with constraints. | |
| Average percentage overshoot of constraints in the violated states. |
| MPC | ||||||||
|---|---|---|---|---|---|---|---|---|
| MPC n/c | 0 | 2416 | ms | |||||
| MPC w/c | 3 | 702 | ms | |||||
| SMPC | 64 | 135 | ms | |||||
| SCMPC | 84 | 168 | ms | |||||
| SCMPC (robust) | 74 | 30 | ms |
| MPC | ||||||||
|---|---|---|---|---|---|---|---|---|
| MPC n/c | 0 | 611 | ms | |||||
| MPC w/c | 4 | 362 | ms | |||||
| SMPC | 65 | 77 | ms | |||||
| SCMPC | 94 | 7 | ms | |||||
| SCMPC (robust) | 86 | 21 | ms |
| MPC | ||||||||
|---|---|---|---|---|---|---|---|---|
| MPC n/c | 0 | 754 | ms | |||||
| MPC w/c | 1 | 462 | ms | |||||
| SMPC | 57 | 107 | ms | |||||
| SCMPC | 85 | 28 | ms | |||||
| SCMPC (robust) | 79 | 27 | ms |
| MPC | ||||||||
|---|---|---|---|---|---|---|---|---|
| MPC w/c | 2 | 263 | ms | |||||
| SCMPC | 87 | 15 | ms | |||||
| SCMPC | 88 | 14 | ms | |||||
| SCMPC | 91 | 10 | ms | |||||
| SCMPC | 93 | 7 | ms | |||||
| SCMPC | 94 | 6 | ms |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
González, E.; Sanchis, J.; García-Nieto, S.; Salcedo, J. A Comparative Study of Stochastic Model Predictive Controllers. Electronics 2020, 9, 2078. https://doi.org/10.3390/electronics9122078
González E, Sanchis J, García-Nieto S, Salcedo J. A Comparative Study of Stochastic Model Predictive Controllers. Electronics. 2020; 9(12):2078. https://doi.org/10.3390/electronics9122078
Chicago/Turabian StyleGonzález, Edwin, Javier Sanchis, Sergio García-Nieto, and José Salcedo. 2020. "A Comparative Study of Stochastic Model Predictive Controllers" Electronics 9, no. 12: 2078. https://doi.org/10.3390/electronics9122078
APA StyleGonzález, E., Sanchis, J., García-Nieto, S., & Salcedo, J. (2020). A Comparative Study of Stochastic Model Predictive Controllers. Electronics, 9(12), 2078. https://doi.org/10.3390/electronics9122078








