Optimized Distributed Subgraph Matching Algorithm Based on Partition Replication
Abstract
1. Introduction
2. Related Work
3. Problem Definition
- (1)
- , , ;
- (2)
- , ;
- (3)
- , .
- (1)
- , ;
- (2)
- , , .
4. Proposed PR-Match Algorithm
4.1. Graph Data Partition
- (1)
- is a partition of V, , and , is called as core vertex of ;
- (2)
- , where , is called as core edge of ;
- (3)
- is a set of crossing edges between and other partitions, is called as extended edge of ;
- (4)
- , where and , is called as extended vertex of .
| Algorithm 1: Graph Data Partition Algorithm |
 |
4.2. Query Decomposition
- (1)
- when , is called as the center point of graph G;
- (2)
- , where is the center point of the graph G.
| Algorithm 2: Query Graph Decomposition Algorithm |
 |
4.3. Subquery Matching
- (1)
- ;
- (2)
- .
| Algorithm 3: Subquery Matching |
 |
4.4. Intermediate Result Merge
- (1)
- The prediction merge cost of the matching result and the matching result is:
- (2)
- The prediction merge cost of merging operation and matching result is:
- (3)
- The prediction merge cost of merge plan Ω is:
| Algorithm 4: Subquery Matching Result Merge | ||
| input: | optimal merge plan , the matching results of all subqueries | |
| on all partitions | ||
| output: | all the matching subgraph of original query graph on graph database D | |
| 1 | ; | |
| 2 | Call recusiveJoin (curDepth, maxDepth, M, ); | |
| 3 | return ; | |
| Algorithm 5: Merge Subroutine recursiveJoin |
 |
5. Experiments
- (1)
- The subgraph matching on the small graph set uses the AIDS real data and the synthesized dataset generated by GraphGen;
- (2)
5.1. Subgraph Matching on Small Graphs
5.2. Subgraph Matching on a Single Large Graph
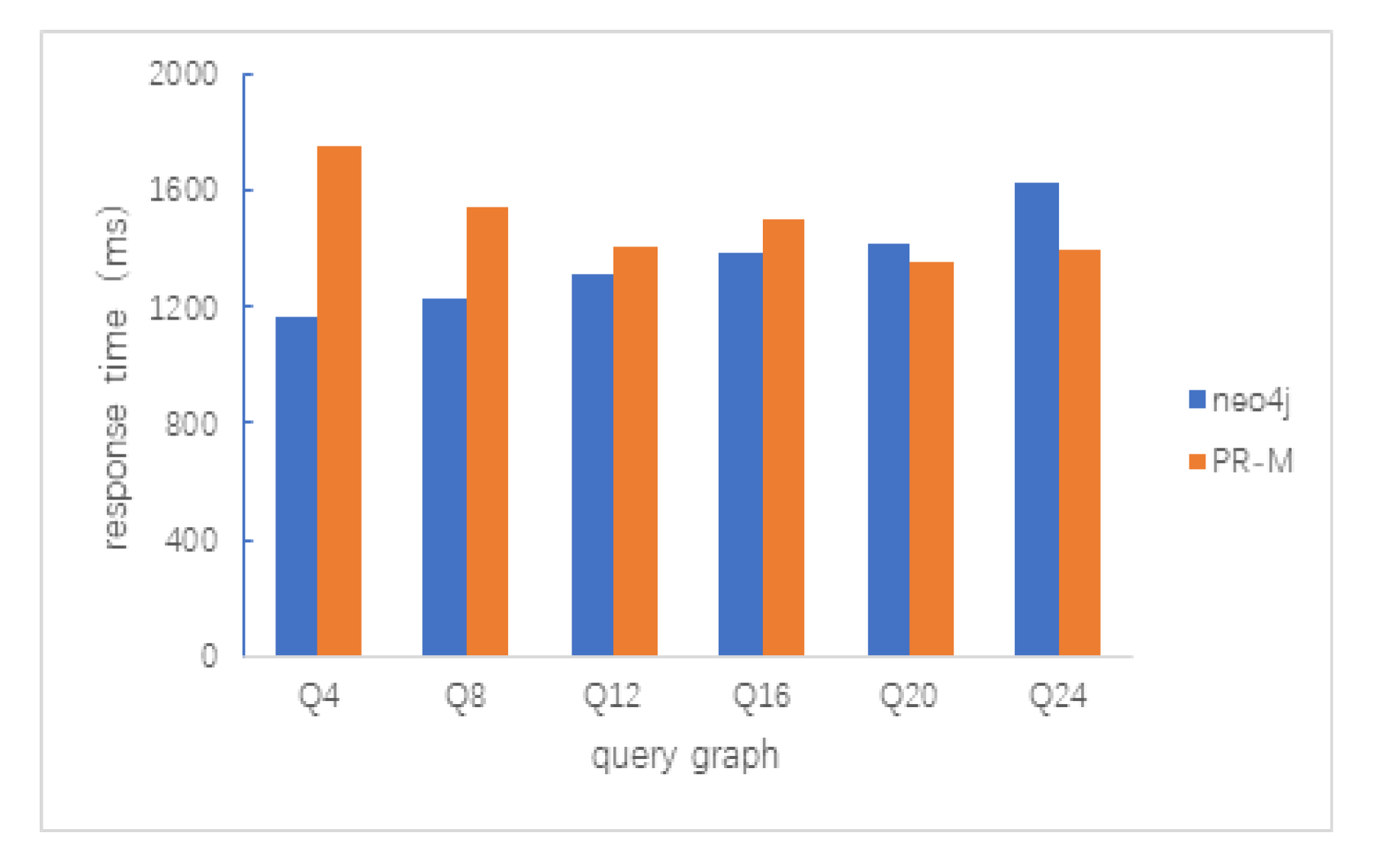
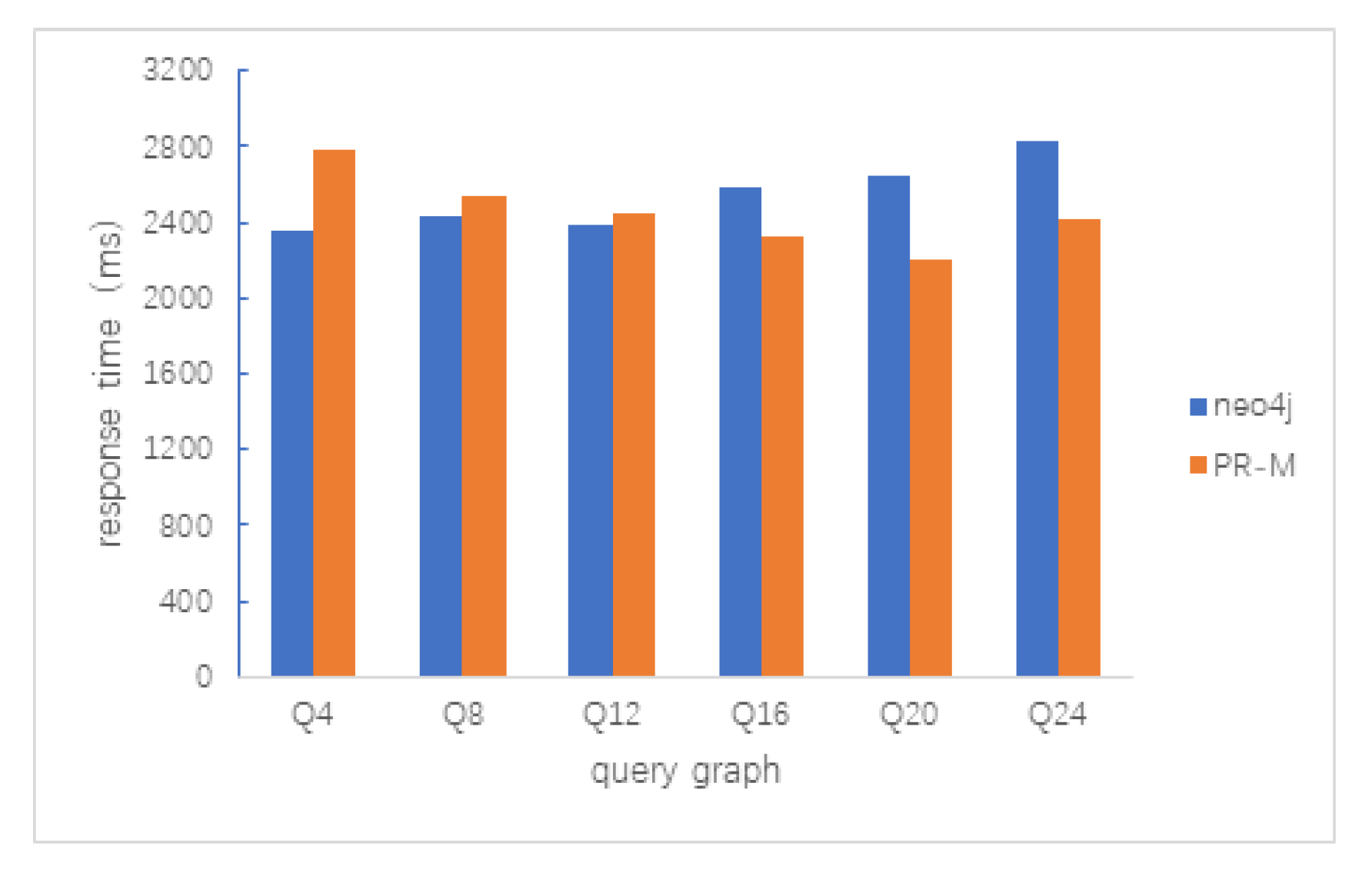
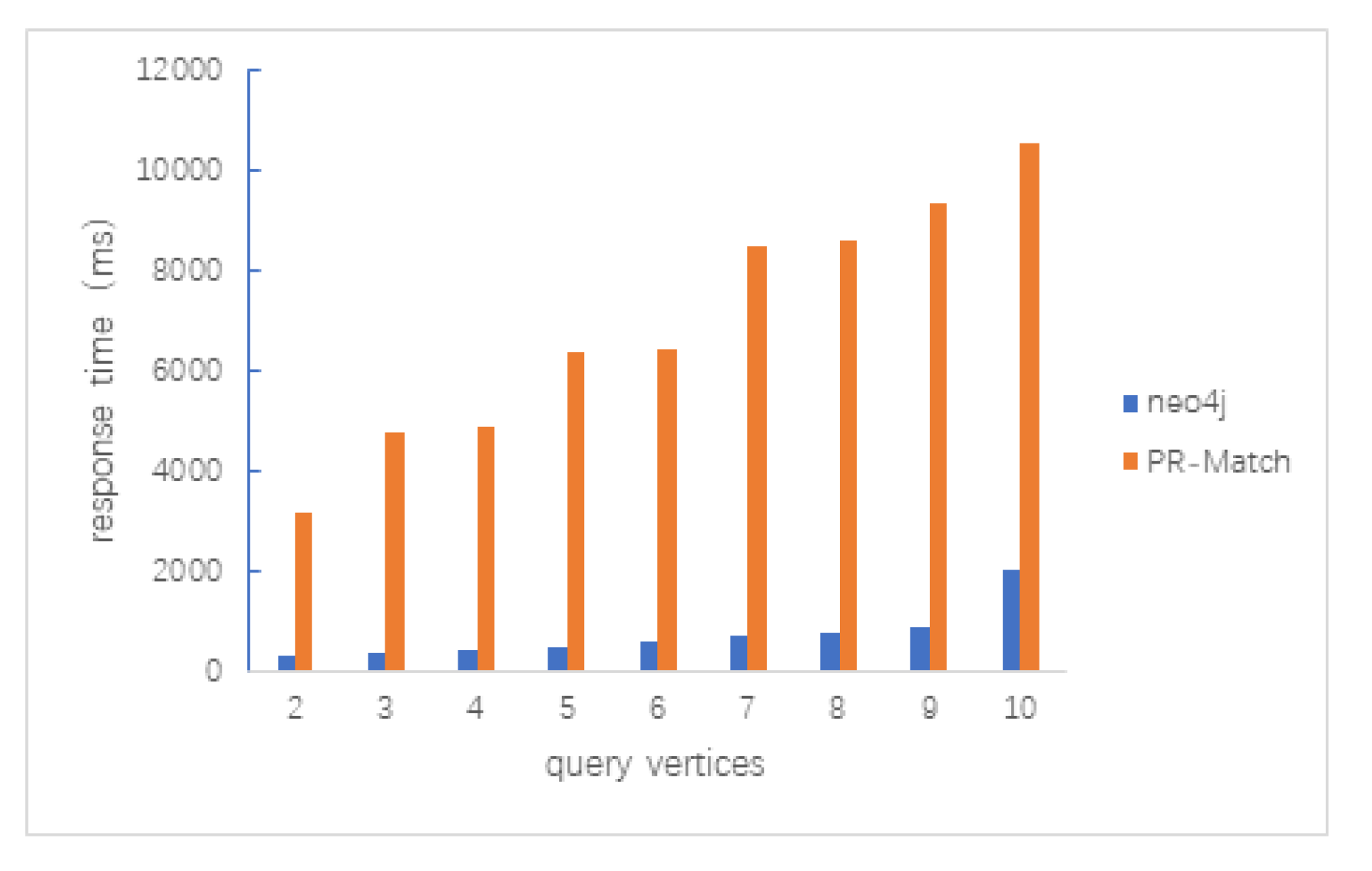
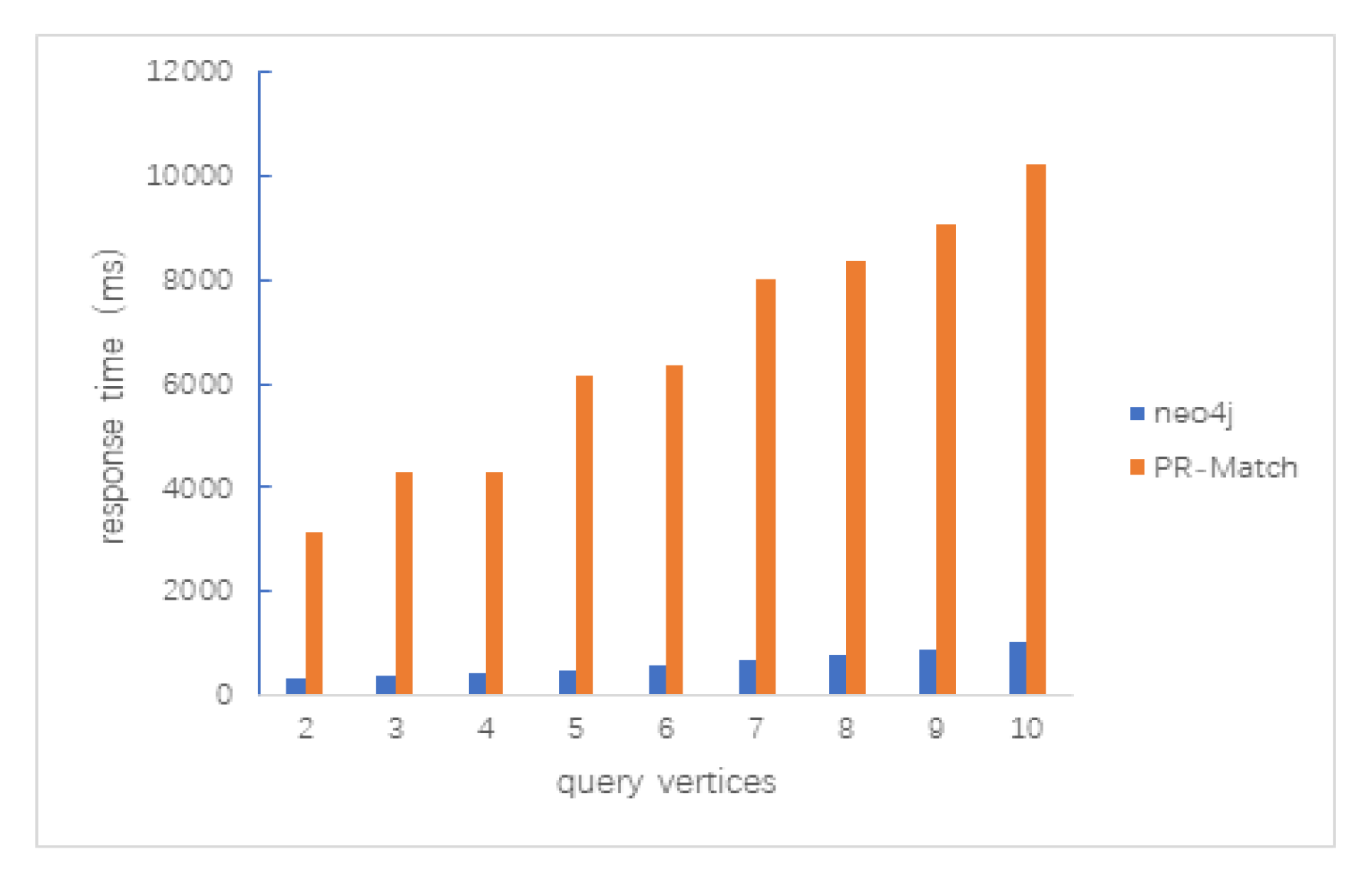
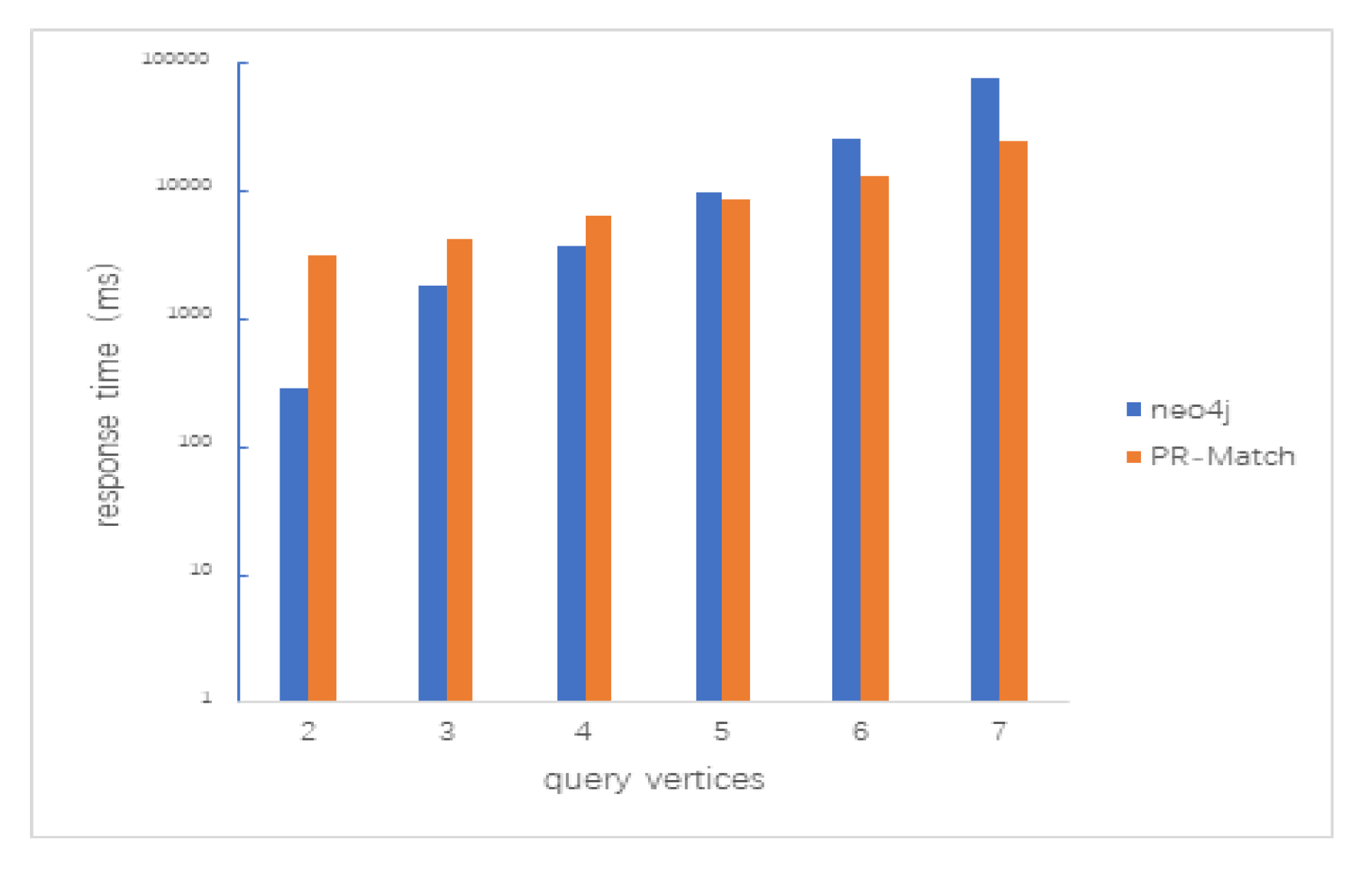
5.2.1. Path Query
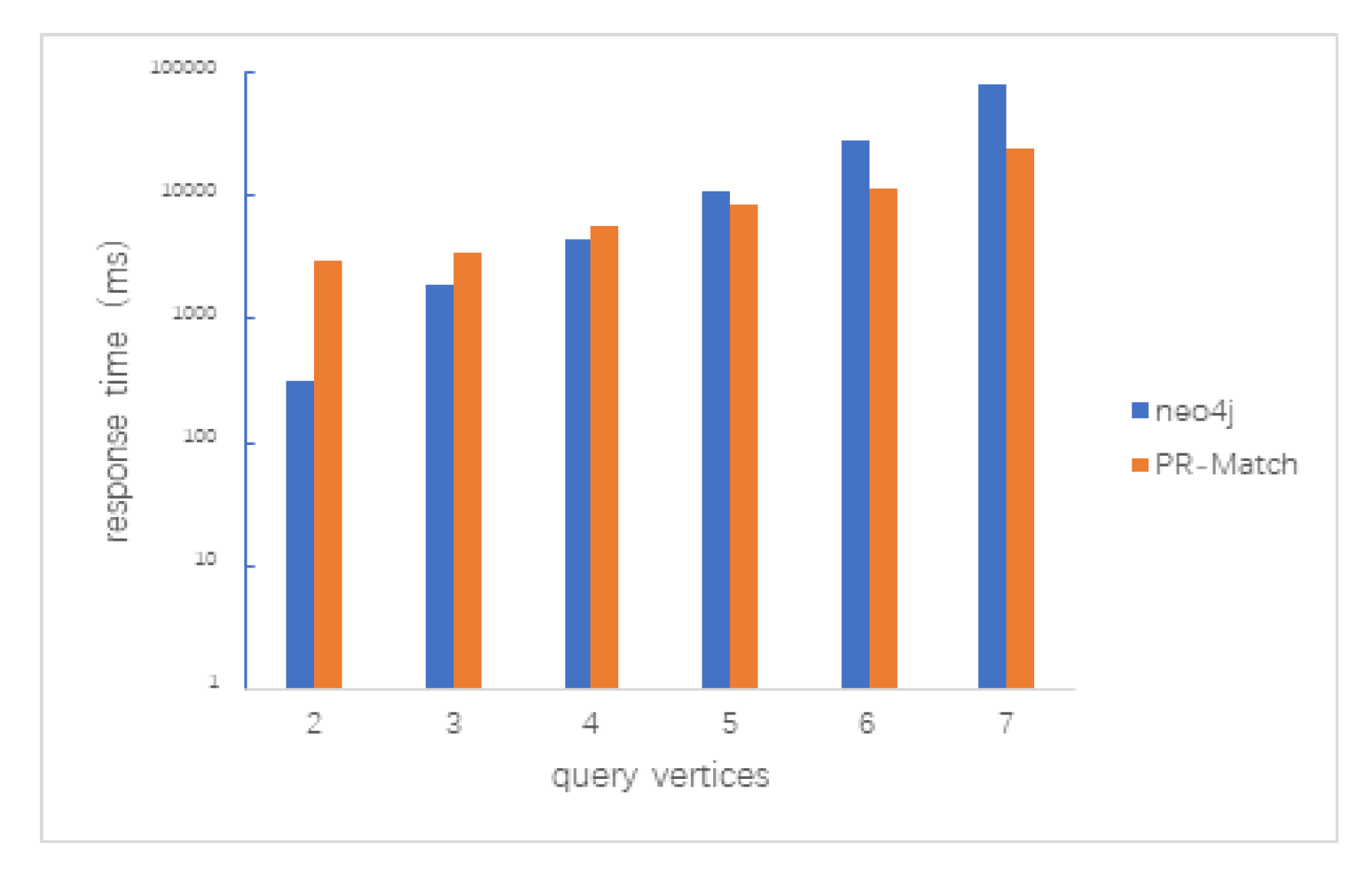
5.2.2. Clique Query
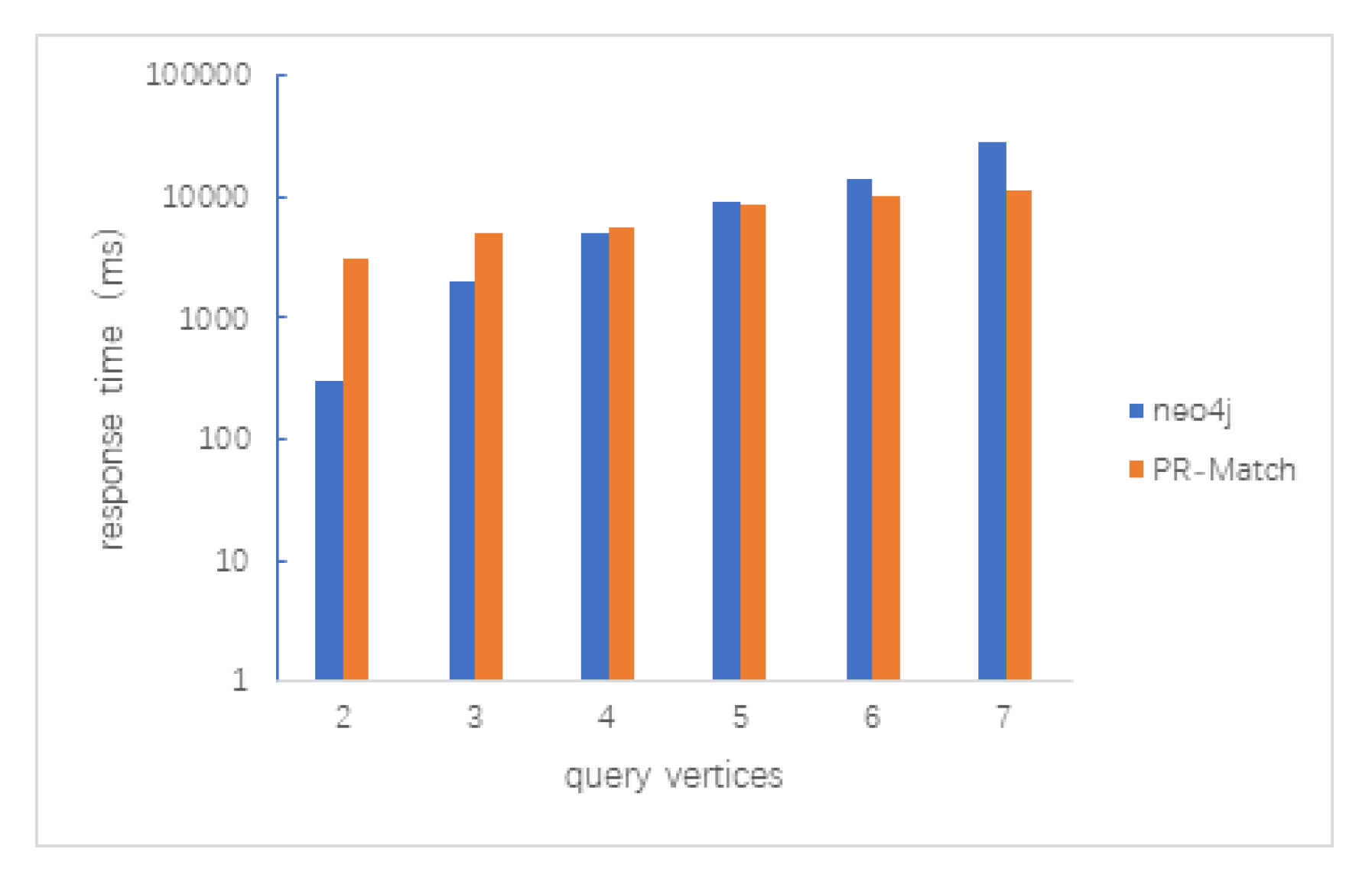
5.2.3. Random Query
5.3. Scalability Test of PR-Match Algorithm
5.3.1. Data Size
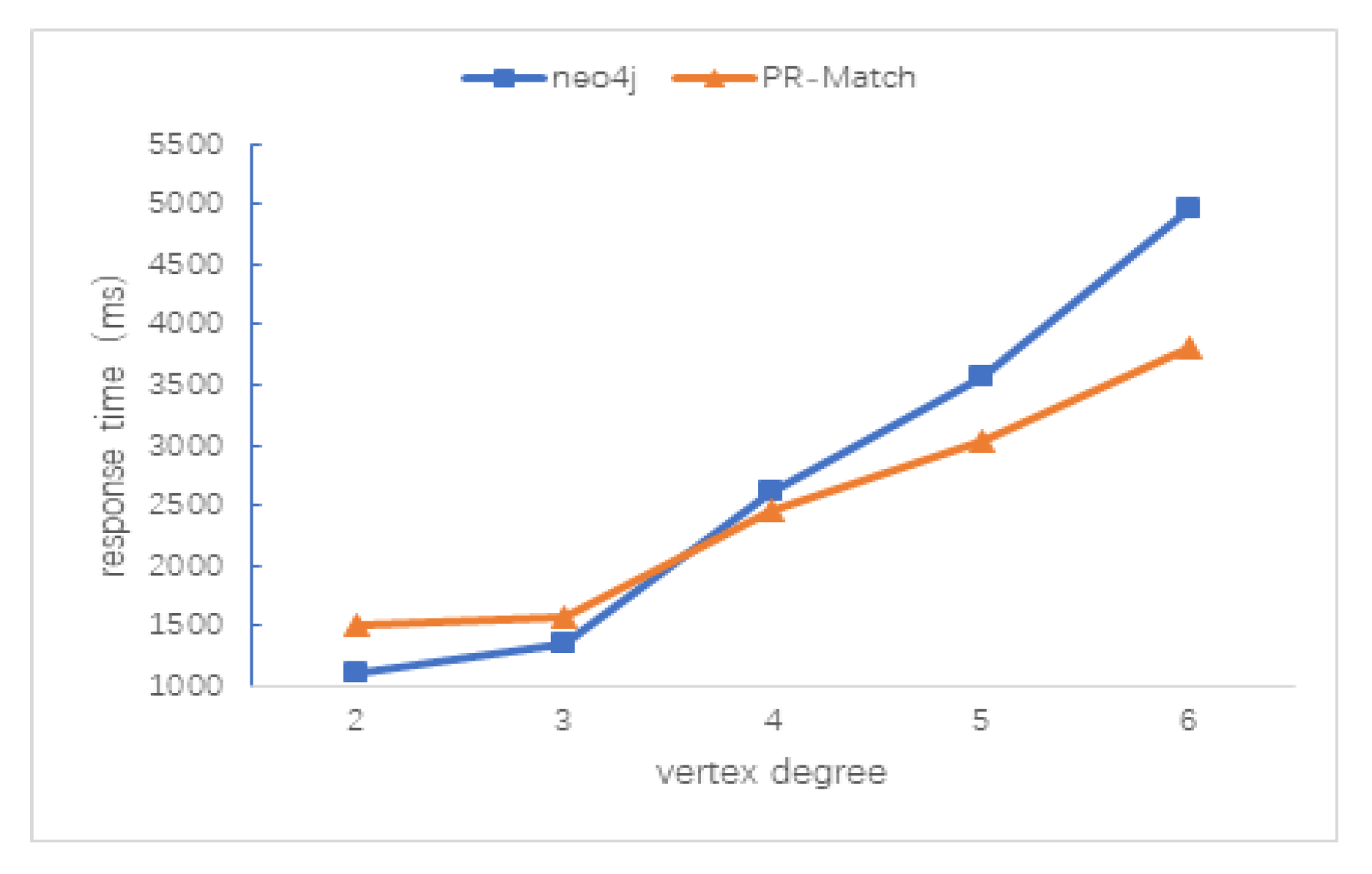
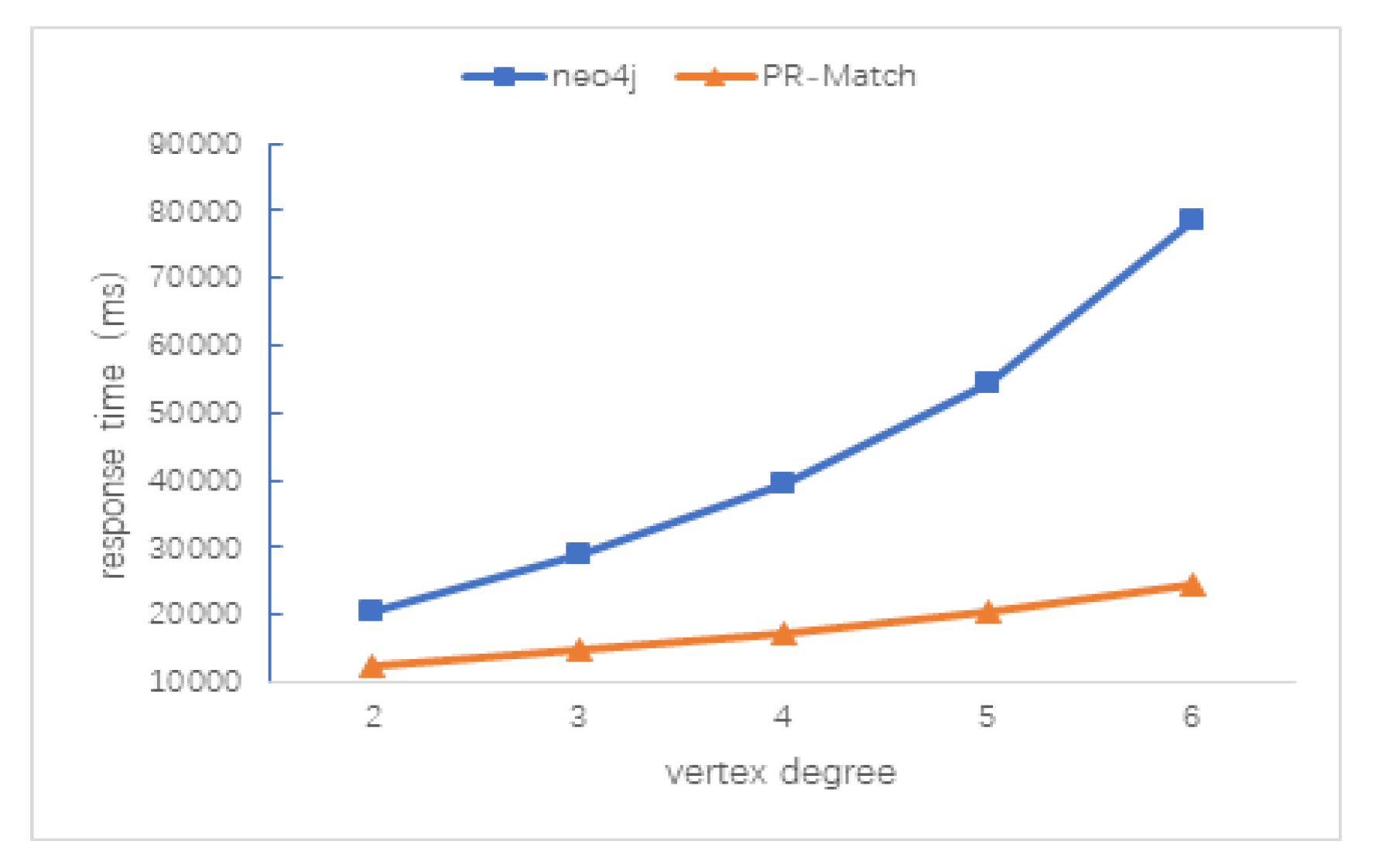
5.3.2. Average Vertex Degree
5.4. Experiment Summary
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Guo, W.; Shi, Y.; Wang, S.; Xiong, N. An unsupervised embedding learning feature representation scheme for network big data analysis. IEEE Trans. Netw. Sci. Eng. 2019, 1. [Google Scholar] [CrossRef]
- Cheng, H.; Xie, Z.; Shi, Y.; Xiong, N. Multi-step data prediction in wireless sensor networks based on one-dimensional CNN and bidirectional LSTM. IEEE Access 2019, 7, 117883–117896. [Google Scholar] [CrossRef]
- Cheng, H.; Su, Z.; Xiong, N.; Xiao, Y. Energy-efficient node scheduling algorithms for wireless sensor networks using Markov Random Field model. Inf. Sci. 2016, 329, 461–477. [Google Scholar] [CrossRef]
- Zheng, H.; Guo, W.; Xiong, N. A kernel-based compressive sensing approach for mobile data gathering in wireless sensor network systems. IEEE Trans. Syst. Man Cybern. Syst. 2017, 1–13. [Google Scholar] [CrossRef]
- Ullmann, J.R. An algorithm for subgraph isomorphism. J. ACM 1976, 23, 31–42. [Google Scholar] [CrossRef]
- Cheng, H.; Feng, D.; Shi, X.; Chen, C. Data quality analysis and cleaning strategy for wireless sensor networks. Eurasip J. Wirel. Commun. Netw. 2018, 61. [Google Scholar] [CrossRef]
- Sang, Y.; Shen, H.; Tan, Y.; Xiong, N. Efficient protocols for privacy preserving matching against distributed datasets. In Proceedings of the International Conference on Information and Communications Security, Raleigh, NC, USA, 4–7 December 2006; pp. 210–227. [Google Scholar] [CrossRef]
- Han, W.S.; Lee, J.; Pham, M.D.; Yu, J.X. iGraph: A framework for comparisons of disk-based graph indexing techniques. Proc. Vldb Endow. 2010, 3, 449–459. [Google Scholar] [CrossRef]
- Shang, H.; Zhang, Y.; Lin, X.; Yu, J.X. Taming verification hardness: an efficient algorithm for testing subgraph isomorphism. Proc. Vldb Endow. 2008, 1, 364–375. [Google Scholar] [CrossRef]
- Zhang, S.; Hu, M.; Yang, J. TreePi: A novel graph indexing method. In Proceedings of the IEEE International Conference on Data Engineering, Istanbul, Turkey, 15–20 April 2007; pp. 966–975. [Google Scholar]
- Jin, F.; Yang, Y.; Wang, S.; Xue, Y.; Yan, Z. TBSGM: A fast subgraph matching method on large-scale graphs. Int. J. Data Warehous. Min. (IJDWM) 2018, 14, 67–89. [Google Scholar] [CrossRef]
- Chen, W.; Li, M.; Chen, Z. Efficient index construction algorithm for isomorphism of subgraphs. J. Harbin Inst. Technol. 2019, 40, 548–554. [Google Scholar]
- Huang, Y.; Hong, J.; Jia, Z. Approximate subgraph matching based on double index. Comput. Appl. 2012, 32, 1994–1997. [Google Scholar]
- Han, W.S.; Lee, J.; Lee, J.H. Turbo iso: Towards ultrafast and robust subgraph isomorphism search in large graph databases. In Proceedings of the 2013 ACM SIGMOD International Conference on Management of Data, New York, NY, USA, 22–27 June 2013; pp. 337–348. [Google Scholar]
- Bi, F.; Chang, L.; Lin, X.; Qin, L.; Zhang, W. Efficient subgraph matching by postponing cartesian products. In Proceedings of the 2016 International Conference on Management of Data, Pune, India, 11–13 March 2016; pp. 1199–1214. [Google Scholar]
- Hong, L.; Zou, L.; Lian, X.; Yu, P.S. Subgraph matching with set similarity in a large graph database. IEEE Trans. Knowl. Data Eng. 2015, 27, 2507–2521. [Google Scholar] [CrossRef]
- Rivero, C.R.; Jamil, H.M. Efficient and Scalable Labeled Subgraph Matching Using SGMatch; Springer: New York, NY, USA, 2016; pp. 1–27. [Google Scholar]
- Wang, Z.; Li, T.; Xiong, N.; Pan, Y. A novel dynamic network data replication scheme based on historical access record and proactive deletion. J. Supercomput. 2012, 62, 227–250. [Google Scholar] [CrossRef]
- Xiong, N.; Vasilakos, A.V.; Yang, L.T.; Song, L.; Pan, Y.; Kannan, R.; Li, Y. Comparative analysis of quality of service and memory usage for adaptive failure detectors in healthcare systems. IEEE J. Sel. Areas Commun. 2009, 27, 495–509. [Google Scholar] [CrossRef]
- Xiong, N.; Jia, X.; Yang, L.T.; Vasilakos, A.V.; Li, Y.; Pan, Y. A distributed efficient flow control scheme for multi-rate multicast networks. IEEE Trans. Parallel Distrib. Syst. 2010, 21, 1254–1266. [Google Scholar] [CrossRef]
- Liu, Y.; Ota, K.; Zhang, K.; Ma, M.; Xiong, N.; Liu, A.; Long, J. QTSAC: An energy-efficient MAC protocol for delay minimization in wireless sensor networks. IEEE Access 2018, 6, 8273–8291. [Google Scholar] [CrossRef]
- Peng, P.; Zou, L.; Chen, L.; Zhao, D. Processing SPARQL queries over distributed RDF graphs. Vldb J. Int. J. Very Large Data Bases 2016, 25, 243–268. [Google Scholar] [CrossRef]
- Husain, M.; Mcglothlin, J.; Masud, M.M.; Khan, L.; Thuraisingham, B.M. Heuristics-Based query processing for large RDF graphs using cloud computing. IEEE Trans. Knowl. Data Eng. 2011, 23, 1312–1327. [Google Scholar] [CrossRef]
- Papailiou, N.; Tsoumakos, D.; Konstantinou, I.; Karras, P.; Koziris, N. H2 RDF+: An efficient data management system for big RDF graphs. In Proceedings of the 2014 ACM SIGMOD International Conference on Management of Data, Snowbird, UT, USA, 22 June 2014. [Google Scholar]
- Gao, J.; Lei, C.; Tian, L.; Ling, Y.; Chen, Z.; Song, B. Distributed Top-k subgraph matching in a big graph. In Proceedings of the 2018 IEEE International Conference on Big Data, Seattle, WA, USA, 10–13 December 2018; pp. 5325–5327. [Google Scholar]
- Hose, K.; Schenkel, R. WARP: Workload-aware replication and partitioning for RDF. In Proceedings of the IEEE International Conference on Data Engineering Workshops, Brisbane, QLD, Australia, 8–12 April 2013; pp. 1–6. [Google Scholar]
- Gurajada, S.; Seufert, S.; Miliaraki, I.; Theobald, M. TriAD: A Distributed Shared-Nothing RDF Engine Based on Asynchronous Message Passing. In Proceedings of the ACM SIGMOD International Conference on Management of Data, Snowbird, UT, USA, 22 June 2014; pp. 289–300. [Google Scholar]
- Lee, K.; Liu, L. Scaling queries over big RDF graphs with semantic hash partitioning. Proc. Vldb Endow. 2013, 6, 1894–1905. [Google Scholar] [CrossRef]
- Schwarte, A.; Haase, P.; Hose, K.; Schenkel, R.; Schmidt, M. FedX: Optimization techniques for federated query processing on linked data. In Proceedings of the International Conference on the Semantic Web, Bonn, Germany, 23–27 October 2011; pp. 601–616. [Google Scholar]
- Lin, B.; Guo, W.; Xiong, N.; Chen, G.; Vasilakos, A.V.; Zhang, H. A pretreatment workflow scheduling approach for big data applications in multi-cloud environments. IEEE Trans. Netw. Serv. Manag. 2016, 13, 1. [Google Scholar] [CrossRef]
- Xiong, N.; Vasilakos, A.V.; Yang, L.T.; Wang, C.; Kannan, R.; Chang, C.; Pan, Y. A novel self-tuning feedback controller for active queue management supporting TCP flows. Inf. Sci. 2010, 180, 2249–2263. [Google Scholar] [CrossRef]
- Nguyen, K. Inverse Location Theory with Ordered Median Function and Other Extensions; Epubli: Berlin, Germany, 2014. [Google Scholar]
- He, H.; Singh, A.K. Query language and access methods for graph databases. In Proceedings of the ACM SIGMOD International Conference on Management of Data, SIGMOD 2008, Vancouver, BC, Canada, 10–12 June 2008; pp. 405–418. [Google Scholar]
- Lee, J.; Han, W.S.; Kasperovics, R.; Lee, J.H. An in-depth comparison of subgraph isomorphism algorithms in graph databases. Proc. Vldb Endow. 2013, 6, 133–144. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, H.; Wang, H.; Shao, B.; Li, J. Efficient subgraph matching on billion node graphs. Proc. Vldb Endow. 2012, 5, 788–799. [Google Scholar] [CrossRef]
- Huang, J.; Abadi, D. Leopard: lightweight edge-oriented partitioning and replication for dynamic graphs. Proc. Vldb Endow. 2016, 9, 540–551. [Google Scholar] [CrossRef]
- Hall, B.H.; Jaffe, A.B.; Trajtenberg, M. The NBER Patent Citation Data File: Lessons, Insights and Methodological Tools; The MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Chakrabarti, D.; Zhan, Y.; Faloutsos, C. R-MAT: A recursive model for graph mining. In Proceedings of the Siam International Conference on Data Mining, Lake Buena Vista, FL, USA, 22–24 April 2004. [Google Scholar]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, L.; Bin, J.; Pan, P. Optimized Distributed Subgraph Matching Algorithm Based on Partition Replication. Electronics 2020, 9, 184. https://doi.org/10.3390/electronics9010184
Yuan L, Bin J, Pan P. Optimized Distributed Subgraph Matching Algorithm Based on Partition Replication. Electronics. 2020; 9(1):184. https://doi.org/10.3390/electronics9010184
Chicago/Turabian StyleYuan, Ling, Jiali Bin, and Peng Pan. 2020. "Optimized Distributed Subgraph Matching Algorithm Based on Partition Replication" Electronics 9, no. 1: 184. https://doi.org/10.3390/electronics9010184
APA StyleYuan, L., Bin, J., & Pan, P. (2020). Optimized Distributed Subgraph Matching Algorithm Based on Partition Replication. Electronics, 9(1), 184. https://doi.org/10.3390/electronics9010184



