An Investigation of Spectral Band Selection for Hyperspectral LiDAR Technique
Abstract
:1. Introduction
2. Instrument and Dataset Description
2.1. AOTF-HSL
2.2. Dataset Description
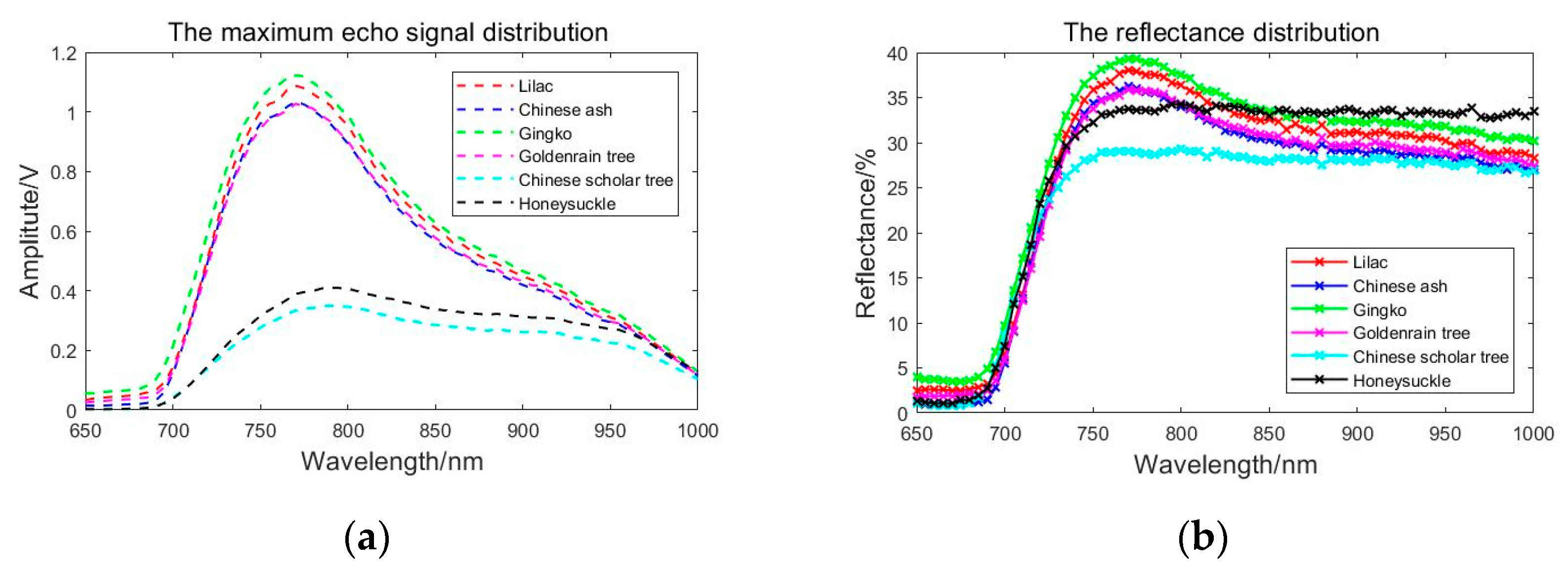
2.3. Feature Description
3. The Proposed Method
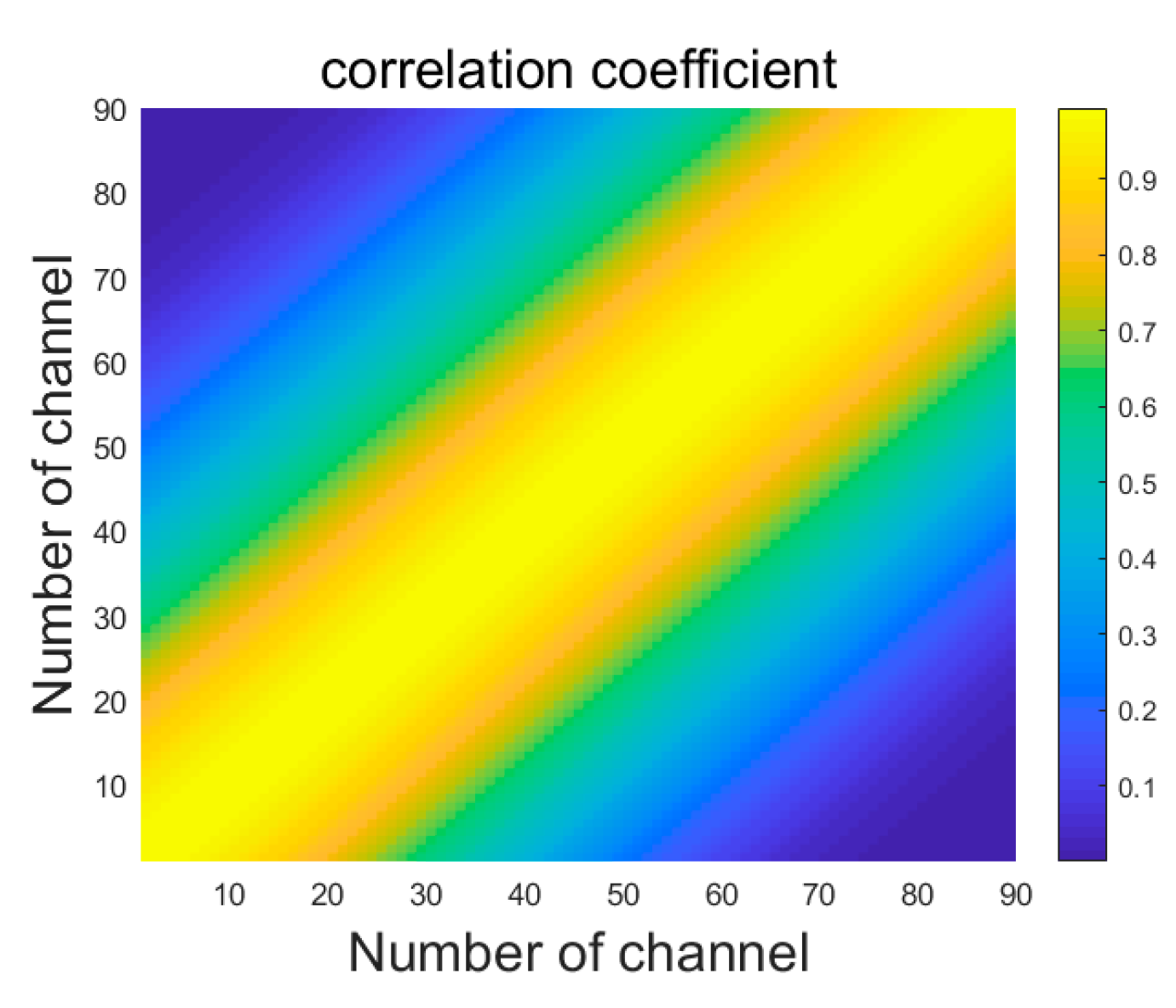
3.1. Redundancy Information
3.2. Method Based on Inter-Class Variance
| Method 1. Pseudo Code of the Proposed Method |
| Input: Set the indicating variable m=M (which is 91 or 71 in this study), initialize alternative index set as the full channels, i.e. alternative index set idx = {1, 2, 3, …., m}, and initialize the selected channels index set index = {ø}. |
| % Main loop |
| while the stop condition is not met |
| Step 1: Calculate Vinter(idx) among the classes of all the channels, using Equation (2). |
| Step 2: Find maximum and second highest values of Vinter (nj) in Vinter(idx), send the index of the channel to initial index set initial = {ni, nj}, and index = {ni, nj}. The alternative set of channel index idx = {1, 2, 3, …, ni−1, ni+1, nj−1, nj+1, …, …, m}. |
| Step 3: Find maximum of Vinter (nd) in Vinter(idx), send nd to the selected index set, index = {nd, index}. |
| Step 4: Remove nd form the alternative set, the new alternative set idx = {idx}−{nd}. |
| Step 5: Calculate the result of multiple classification with features corresponding to initial channels. |
| if the result reaches 100%, |
| Output the selected set {ni, nj} |
| else |
| go to Step 6 |
| end while |
| Step 6: Calculate the result of multiple classification with features corresponding to index channels. |
| if the result reach 100%, |
| Output the selected set {nd, ni, nj} |
| else |
| go to Step 3 |
| end while |
| Output the optimal channels corresponding to the selected set by maximum, sequenced as index = {n1, n2, nj, …, nq}. |
| Step 7: Sort values of Vinter (index), send the channel index to the optimal set in turn, index2 = {nm1, nm2, …., nmq}. |
| Output: The optimal channels corresponding to the optimal set, sequenced as index2 = {nm1, nm2, …., nmq}. |
4. Results and Analysis
4.1. Classification Performance
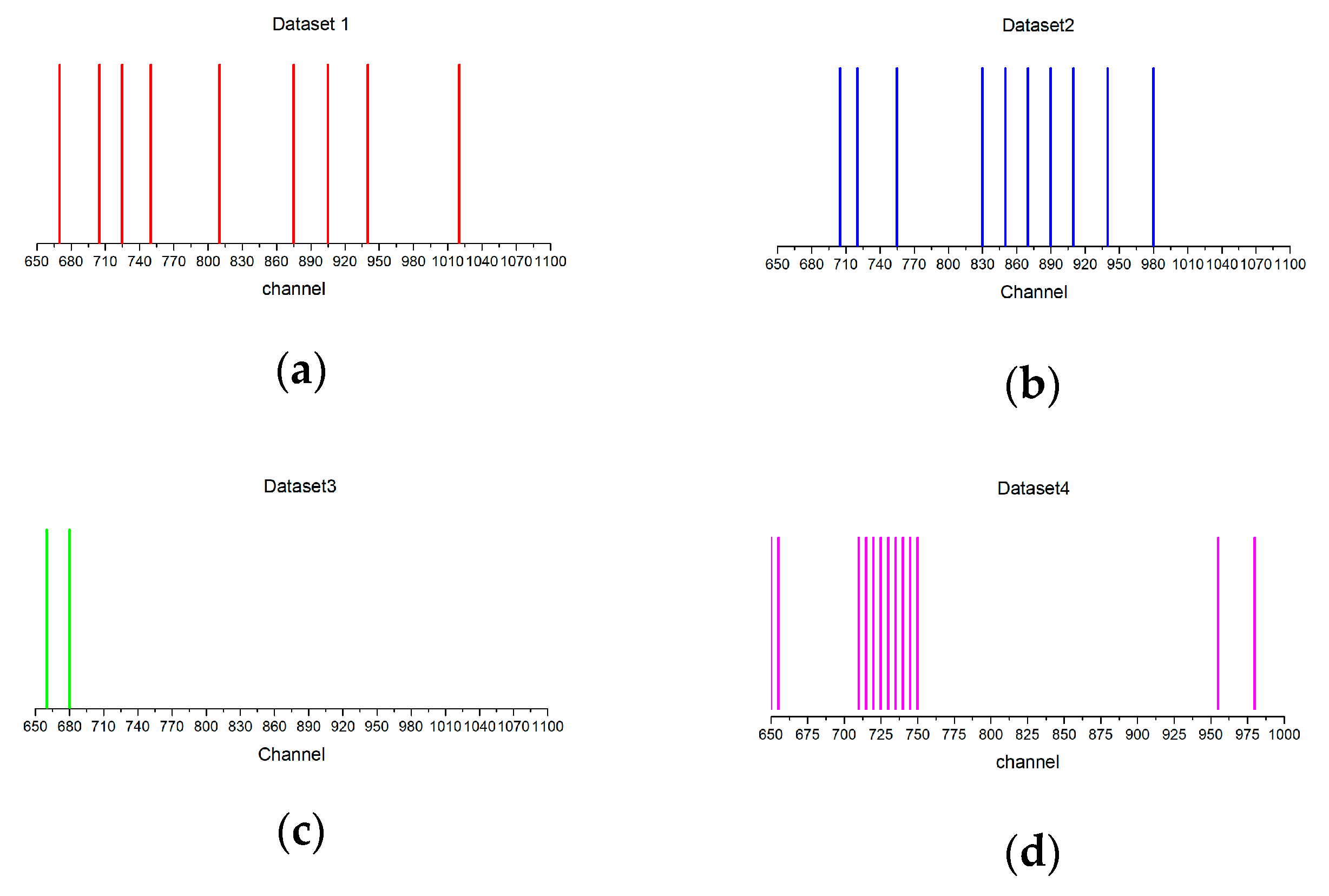
4.2. The Selected Channels
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Nakamura, R.Y.; Fonseca, L.M.G.; Dos Santos, J.A.; Torres, R.D.S.; Yang, X.S.; Papa, J.P. Nature-inspired framework for hyperspectral band selection. IEEE Geosci. Remote Sens. Lett. 2013, 52, 2126–2137. [Google Scholar] [CrossRef]
- Bajcsy, P.; Groves, P. Methodology for hyperspectral band selection. PE&RS 2004, 70, 793–802. [Google Scholar]
- Chan, J.C.; Paelinckx, D. Evaluation of Random Forest and Adaboost tree-based ensemble classification and spectral band selection for ecotope mapping using airborne hyperspectral imagery. Remote Sens. Environ. 2008, 112, 2999–3011. [Google Scholar] [CrossRef]
- MartÍnez-UsÓ, A.; Pla, F.; Sotoca, J.M.; García-Sevilla, P. Clustering-based hyperspectral band selection using information measures. IEEE Geosci. Remote Sens. Lett. 2007, 45, 4158–4171. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep learning-based classification of hyperspectral data. IEEE J.-STARS 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Wang, Q.; Lin, J.; Yuan, Y. Salient band selection for hyperspectral image classification via manifold ranking. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1279–1289. [Google Scholar] [CrossRef]
- Li, W.; Jiang, C.H.; Chen, Y.W.; Hyyppä, J.; Tang, L.L.; Li, C.R.; Wang, S.W. A Liquid Crystal Tunable Filter-Based Hyperspectral LiDAR System and Its Application on Vegetation Red Edge Detection. IEEE Geosci. Remote Sens. Lett. 2018, 16, 291–295. [Google Scholar] [CrossRef]
- Sun, J.; Shi, S.; Gong, W.; Yang, J.; Du, L.; Song, S.; Chen, B.; Zhang, Z. Evaluation of hyperspectral LiDAR for monitoring rice leaf nitrogen by comparison with multispectral LiDAR and passive spectrometer. Sci. Rep. 2017, 7, 40362. [Google Scholar] [CrossRef]
- Lim, E.H.; Suter, D. 3D terrestrial LIDAR classifications with super-voxels and multi-scale Conditional Random Fields. Comput.-Aided Des. 2009, 41, 701–710. [Google Scholar] [CrossRef]
- Ferraz, A.; Mallet, C.; Chehata, N. Large-scale road detection in forested mountainous areas using airborne topographic lidar data. ISPRS J. Photogramm. 2016, 112, 23–36. [Google Scholar] [CrossRef]
- Burton, D.; Dunlap, D.B.; Wood, L.J.; Flaig, P.P. Lidar intensity as a remote sensor of rock properties. J. Sediment. Res. 2011, 81, 339–347. [Google Scholar] [CrossRef] [Green Version]
- Kaasalainen, S.; Lindroos, T.; Hyyppa, J. Toward hyperspectral lidar: Measurement of spectral backscatter intensity with a supercontinuum laser source. IEEE Geosci. Remote Sens. Lett. 2007, 4, 211–215. [Google Scholar] [CrossRef]
- Du, L.; Gong, W.; Shi, S.; Yang, J.; Sun, J.; Zhu, B.; Song, S. Estimation of rice leaf nitrogen contents based on hyperspectral LIDAR. Int. J. Appl. Earth Obs. 2016, 44, 136–143. [Google Scholar] [CrossRef]
- Li, W.; Sun, G.; Niu, Z.; Gao, S.; Qiao, H. Estimation of leaf biochemical content using a novel hyperspectral full-waveform LiDAR system. Remote Sens. Lett. 2014, 5, 693–702. [Google Scholar] [CrossRef]
- Gong, W.; Song, S.L.; Zhu, B.; Shi, S.; Li, F.Q.; Cheng, X.W. Multi-wavelength canopy LiDAR for remote sensing of vegetation: Design and system performance. ISPRS J. Photogramm. 2012, 69, 1–9. [Google Scholar]
- Eitel, J.U.H.; Magney, T.S.; Vierling, L.A.; Dittmar, G. Assessment of crop foliar nitrogen using a novel dual-wavelength laser system and implications for conducting laser-based plant physiology. ISPRS J. Photogramm. 2014, 97, 229–240. [Google Scholar] [CrossRef]
- Dudley, M.J.; Genty, G.; Coen, S. Supercontinuum generation in photonic crystal fiber. Rev. Mod. Phys. 2006, 78, 1135–1184. [Google Scholar] [CrossRef]
- Chen, Y.W.; Räikkönen, E.; Kaasalainen, S.; Suomalainen, J.; Hakala, T.; Hyyppä, J.; Chen, R.Z. Two-channel hyperspectral LiDAR with a supercontinuum laser source. Sensors 2010, 10, 7057–7066. [Google Scholar] [CrossRef] [Green Version]
- Hakala, T.; Suomalainen, J.; Kaasalainen, S.; Chen, Y.W. Full waveform hyperspectral LiDAR for terrestrial laser scanning. Opt. Express 2012, 20, 7119–7127. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, Y.W.; Li, C.R.; Tian, M.; Zhou, M.; He, W.J.; Zhou, H.A.; Wu, H.H.; Zhang, H.J.; Tang, L.L.; et al. Hyperspectral LiDAR with Eight Channels Covering from VIS to SWIR. In Proceedings of the IGARSS 2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 4293–4296. [Google Scholar]
- Chen, Y.W.; Jiang, C.H.; Hyyppä, J.; Qiu, S.; Wang, Z.; Tian, M.; Li, W.; Puttonen, E.; Zhou, H.; Feng, Z.Y.; et al. Feasibility Study of Ore Classification Using Active Hyperspectral LiDAR. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1785–1789. [Google Scholar] [CrossRef]
- Chen, Y.W.; Li, W.; Hyyppä, J.; Wang, N.; Jiang, C.H.; Meng, F.R.; Tang, L.L.; Puttonen, E.; Li, C.R. A 10-nm Spectral Resolution Hyperspectral LiDAR System Based on an Acousto-Optic Tunable Filter. Sensors 2019, 19, 1620. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, C.H.; Chen, Y.W.; Wu, H.H.; Li, W.; Zhou, H.; Bo, Y.M.; Shao, H.; Song, S.J.; Puttonen, E.; Hyyppä, J. Study of a High Spectral Resolution Hyperspectral LiDAR in Vegetation Red Edge Parameters Extraction. Remote Sens. 2019, 11, 2007. [Google Scholar] [CrossRef] [Green Version]
- Shao, H.; Chen, Y.W.; Yang, Z.R.; Jiang, C.H.; Li, W.; Wu, H.H.; Wen, Z.J.; Wang, S.W.; Puttnon, E.; Hyyppä, J. A 91-Channel Hyperspectral LiDAR for Coal/Rock Classification. IEEE Geosci. Remote Sensing Lett. 2019, in press. [Google Scholar] [CrossRef] [Green Version]
- Du, Q.; Yang, H. Similarity-Based Unsupervised Band Selection for Hyperspectral Image Analysis. IEEE Geosci. Remote Sens. Lett. 2008, 5, 564–568. [Google Scholar] [CrossRef]
- Yang, H.; Du, Q.; Su, H.J.; Sheng, Y.H. An efficient method for supervised hyperspectral band selection. IEEE Geosci. Remote Sens. Lett. 2010, 8, 138–142. [Google Scholar] [CrossRef]
- Shao, H.; Chen, Y.; Yang, Z.; Jiang, C.; Li, W.; Wu, H.; Wang, S.; Yang, F.; Chen, J.; Puttonen, E.; et al. Feasibility Study on Hyperspectral LiDAR for Ancient Huizhou-Style Architecture Preservation. Remote Sens. 2020, 12, 88. [Google Scholar] [CrossRef] [Green Version]
- Datasheet of YLS AOTF. Available online: http://www.yslphotonics.com/ (accessed on 1 April 2017).
- Sanna, K.; Eero, A.; Juha, H.; Juha, S. Study of Surface Brightness From Backscattered Laser Intensity: Calibration of Laser Data. IEEE Geosci. Remote Sens. Lett. 2005, 2, 255–259. [Google Scholar]
- Sun, K.; Geng, X.R.; Ji, L.Y. An efficient unsupervised band selection method based on an autocorrelation matrix for a hyperspectral image. Int. J. Remote Sens. 2014, 35, 7458–7476. [Google Scholar] [CrossRef]
- Fergus, R.; Perona, P.; Zisserman, A. Object Class Recognition by Unsupervised Scale-Invariant Learning. In Proceedings of the 2003 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Madison, WI, USA, 18–20 June 2003. [Google Scholar]
- Zhang, M.L.; Peña, J.M.; Robles, V. Feature selection for multi-label naive Bayes classification. Inform. Sci. 2009, 179, 3218–3229. [Google Scholar] [CrossRef]
- Friedrichs, F.; Igel, C. Evolutionary tuning of multiple SVM parameters. Neurocomputing 2005, 64, 107–117. [Google Scholar] [CrossRef]
- Chang, C.I.; Du, Q.; Sun, T.L.; Althouse, M.L.G. A joint band prioritization and band-decorrelation approach to band selection for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2631–2641. [Google Scholar] [CrossRef] [Green Version]
- Douglas, E.S.; Martel, J.; Li, Z.; Howe, G.A.; Hewawasam, K.; Marshall, R.A.; Chakrabarti, S. Finding leaves in the forest: The Dual-Wavelength Echidna Lidar. IEEE Geosci. Remote Sens. Lett. 2015, 12, 776–780. [Google Scholar] [CrossRef]

| Characteristics | Value | ||
|---|---|---|---|
| AOTF Crystal | VIS | NIR | SWIR |
| Wavelength Range (nm) | 400–650 | 650–1100 | 1100–2400 |
| Spectral resolution (nm) | 2–7 | 2–6 | 4–16 |
| Response time (μs) | 10 | ||
| AOTF Diffraction Efficiency | >90% | ||
| Output Efficiency | >40% | ||
| Polarization | Linearly Polarized | ||
| Dataset | Categories | Number of Samples | Number of Channels | Spectrum Coverage (nm) |
|---|---|---|---|---|
| Dataset 1 | coal/rock | 4 | 91 | 650–1100 |
| Dataset 2 | timber | 7 | 91 | 650–1100 |
| Dataset 3 | ore | 6 | 91 | 650–1100 |
| Dataset 4 | plant leaf | 10 | 71 | 650–1000 |
| Dataset | NB | SVM | ||
|---|---|---|---|---|
| Normal Method | The Proposed Method | Normal Method | The Proposed Method | |
| Dataset 1 | 47 | 9 | 12 | 4 |
| Dataset 2 | 37 | 10 | 6 | 3 |
| Dataset 3 | 55 | 2 | 16 | 3 |
| Dataset 4 | 33 | 13 | 24 | 5 |
| average | 43 | 8.5 | 14.5 | 3.75 |
| Dataset | NB | SVM | ||
|---|---|---|---|---|
| Normal Method | The Proposed Method | Normal Method | The Proposed Method | |
| Dataset 1 | 30 | 6 | 7 | 3 |
| Dataset 2 | 7 | 3 | 5 | 2 |
| Dataset 3 | 24 | 2 | 7 | 2 |
| Dataset 4 | 19 | 7 | 22 | 3 |
| Average | 20 | 4.5 | 10.25 | 2.5 |
| Dataset | Echo Maximum | Reflectance |
|---|---|---|
| Dataset 1 | {5, 12, 16, 21, 33, 46, 52, 59, 75} | {21, 5, 12, 16, 33} |
| Dataset 2 | {12, 15, 22, 38, 41, 45, 49, 53, 59, 67} | {7, 11, 6} |
| Dataset 3 | {3, 7} | {2, 1} |
| Dataset 4 | {17, 16, 18, 19, 15, 20, 2, 14, 13, 21, 62, 67, 1} | {2, 17, 16, 3, 1, 4, 5} |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, H.; Chen, Y.; Li, W.; Jiang, C.; Wu, H.; Chen, J.; Pan, B.; Hyyppä, J. An Investigation of Spectral Band Selection for Hyperspectral LiDAR Technique. Electronics 2020, 9, 148. https://doi.org/10.3390/electronics9010148
Shao H, Chen Y, Li W, Jiang C, Wu H, Chen J, Pan B, Hyyppä J. An Investigation of Spectral Band Selection for Hyperspectral LiDAR Technique. Electronics. 2020; 9(1):148. https://doi.org/10.3390/electronics9010148
Chicago/Turabian StyleShao, Hui, Yuwei Chen, Wei Li, Changhui Jiang, Haohao Wu, Jie Chen, Banglong Pan, and Juha Hyyppä. 2020. "An Investigation of Spectral Band Selection for Hyperspectral LiDAR Technique" Electronics 9, no. 1: 148. https://doi.org/10.3390/electronics9010148
APA StyleShao, H., Chen, Y., Li, W., Jiang, C., Wu, H., Chen, J., Pan, B., & Hyyppä, J. (2020). An Investigation of Spectral Band Selection for Hyperspectral LiDAR Technique. Electronics, 9(1), 148. https://doi.org/10.3390/electronics9010148








