Abstract
This paper proposes a design methodology for an active power filter (APF) system to suppress the second harmonic subgroup injected by an AC electric arc furnace (EAF) to the utility grid. The APF system is composed of identical parallel units connected to the utility grid via a specially-designed coupling transformer. Each APF converter is a three-phase three-wire two-level voltage source converter (VSC). The number of parallel APF units, coupling transformer MVA rating, and turns ratio are optimized in the view of the ratings of commercially-available high voltage (HV) IGBTs. In this research work, line current waveforms sampled at 25.6-kS/s on the medium voltage (MV) side of a 65-MVA EAF transformer are then used to extract the second harmonic subgroup, 95-, 100-, and 105-Hz current components, by multiple synchronous reference frame (MSRF) analysis, which was previously proposed to decompose EAF current interharmonics and harmonics in real-time. By summing up this digital data of the second harmonic subgroup, the reference current signal for the APF system is produced in real-time. A detailed model of the APF system is then run on EMTDC/PSCAD to follow the produced reference current signal according to hysteresis band control philosophy. The simulation results show that the proposed APF system can successfully suppress the second harmonic subgroup of an AC EAF.
1. Introduction
Alternating current electric arc furnaces (AC EAF), which are widely used in steel melting and shaping industry, are nonlinear loads with rapidly changing operating characteristics. For this reason, AC EAFs cause serious power quality problems on the utility grid such as voltage flicker, large and highly-fluctuating reactive power, harmonics, and interharmonics [1,2,3,4,5,6,7,8]. Salor et al. and Hsu et al. [1,4] describe the AC EAF as an important voltage flicker source causing severe problems for the power system. Interharmonic and harmonic content of the AC EAF line current has been analyzed in [5,6,7]. In addition to low-order characteristic and uncharacteristic harmonics (second, third, 4th, 5th, etc.), dominant interharmonics have been found out to be around the fundamental frequency up to the second harmonics [6,7]. Some suggestions to suppress those harmonic and interharmonic current components have already been made in the literature [8,9]. White et al. [8] proposes the use of second and third passive harmonic filters (HF) in order to suppress the harmonic content of the AC EAF. Additionally, a C-type second HF has been suggested in [9] in order to eliminate the amplification of interharmonics due to passive harmonic filter resonances. However, since the operation characteristics of the AC EAF is rapidly changing during the steel melting process, a fast-responding resonant-free filter can be much more effective for the suppression of the harmonics and interharmonics of AC EAF. The use of active filters has been suggested and a method extracting each harmonic and interharmonic current reference with 5 Hz resolution has been proposed in [6,7] by using multiple synchronous reference frame (MSRF) technique.
Active power filters (APF) have been a hot research topic for nearly three decades due to their superiorities to passive harmonic filters [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28]. There are various APF types, summarized in [10], and they are classified with respect to their circuit topology and application area. While [11,12] utilize series APFs, shunt APF systems are proposed in [13,14,15,16,17,18,19,20] in order to mitigate unwanted voltage and current harmonics, respectively. APF can also be used together with passive filters as hybrid active power filters (HAPF) [24,25,26]. APFs can be used to improve the power quality in various applications such as metal industry [24,25], distribution systems [26], micro grids [27], motor drives [28], and other industrial loads.
In this research work, a design methodology for an APF system to suppress second harmonic subgroup injected by an AC EAF to the utility grid is proposed. The number of parallel APF units, coupling transformer MVA rating and turns ratio are optimized in the view of the high voltage (HV) IGBT power semiconductors available in the market. APF harmonic and interharmonic current references are obtained in real-time using MSRF analysis employing parallel processing on a graphics processing unit (GPU) framework, which provides fast and accurate current reference estimations for the highly time-varying EAF currents.
2. Problem Definition
Static VAr compensation (SVC) systems are widely used in steel industry in order to (i) provide reactive power compensation, (ii) suppress low-order characteristics and uncharacteristic integer harmonics, and (iii) minimize light flicker. An SVC is generally composed of a 6- or 12-pulse thyristor-controlled reactor bank and passive shunt harmonic filter banks. The field measurements have shown that a well-designed conventional SVC can successfully bring the input power factor of an AC EAF installation to unity, minimize light flicker, and suppress low order integer harmonics except the second current harmonic component [1]. If the SVC system is equipped with a second harmonic passive shunt filter with a very sharp operating characteristic, this second HF topology leads to some operational problems and cannot suppress second harmonic subgroup [29] as reported in [9]. This is because interharmonic content of the line currents around the fundamental and the second harmonic components is rich and especially those around the second harmonic interact with the passive second HF resulting in the amplification of the second harmonic subgroup and group components.
In order to clarify the filtering performances of various commercially available passive filter topologies, filter characteristics have been obtained based on the block diagram given in Figure 1 using field data collected from a transmission system substation supplying an EAF plant.
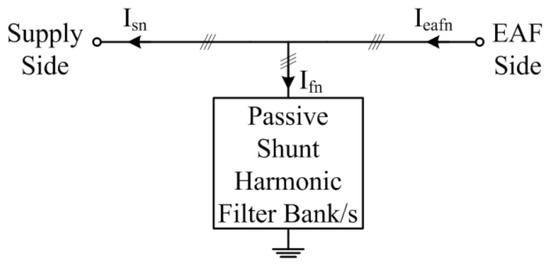
Figure 1.
Block diagram illustrating all harmonics and interharmonics of an EAF power system. (Ieafn, Isn, and Ifn denote the harmonics and interharmonics injected by the EAF, all harmonic and interharmonic components in the supply lines, and harmonic and interharmonic components sunk by the passive shunt harmonic filter bank/s, respectively).
Current data used in this analysis is especially selected from the boring phase of the EAF, which is the most severe operation phase in terms of the time varying interharmonic current content. Typical second and third harmonic passive filter topologies shown in Figure 2 are then used in this analysis. Field performances of six different combinations or versions of the topologies in Figure 2 are calculated and given in Table 1 in comparison with no-filter case for the second harmonic subgroup frequencies according to [29].
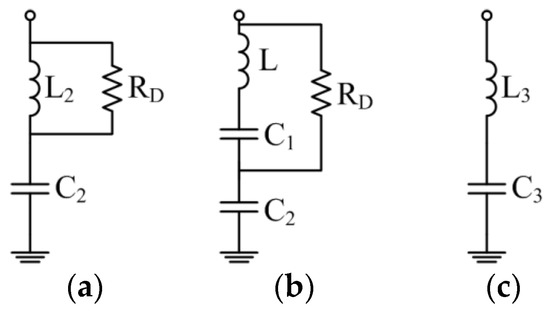
Figure 2.
Typical second and third harmonic passive filter topologies (a) single-tuned damped second HF; (b) C-type third HF; and (c) single-tuned undamped third HF.

Table 1.
EAF and supply-side current components of second harmonic subgroup for the block diagram in Figure 1 for various filter topologies.
Second harmonic subgroups for each case are computed as the geometrical sum of the 95-, 100, and 105 Hz components given in Table 1 according to the subgroup computation method in [29] and then given in Table 2. Second harmonic subgroups in Table 2 on the source side for all cases are expressed not only as percentages of the fundamental component, but also as percentages of the furnace second harmonic subgroup in order to quantify the effectiveness of the filter topologies in Table 1.

Table 2.
Second harmonic subgroup content of the supply line current waveform for different passive shunt harmonic filter bank/s as defined in Table 1 (Case-0 is the no filter case, therefore, Isn = Ieafn).
Results given in Table 2 show that second harmonic subgroups from cases (a) to (d) are seriously amplified. However, for cases (e) and (f), the second harmonic subgroup is suppressed, but not more than 50%. In fact, the results given in Table 1 and Table 2 are not enough to draw a conclusion on the field performances of filter topologies defined as cases (a) to (f). The effects of resulting filter characteristics on all harmonics and interharmonics with 5 Hz resolution as recommended in [29] should also be considered. These are also obtained and presented in Figure 3.
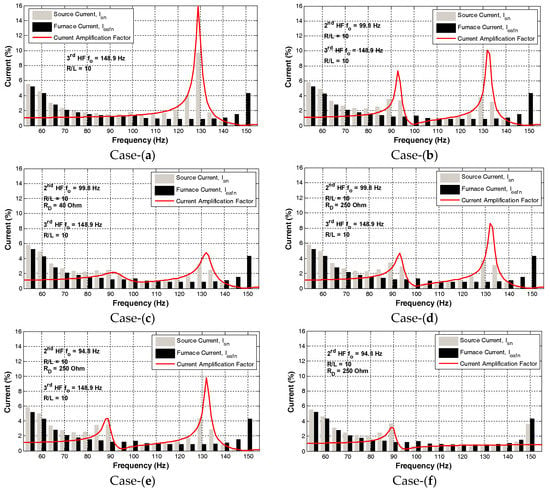
Figure 3.
Filtering performances of different passive shunt harmonic filter topologies against harmonics and interharmonics with 5 Hz resolution injected by the EAF. Case-(a): single-tuned third HF with fo = 148.9 Hz, no second HF; Case-(b): single-tuned second HF with fo = 99.8 Hz and single-tuned third HF with fo = 148.9 Hz; Case-(c): heavily-damped C-type second HF with RD = 40 Ω and fo = 99.8 Hz and single-tuned third HF with fo = 148.9 Hz; Case-(d): lightly-damped C-type second HF with RD = 250 Ω and fo = 99.8 Hz and single-tuned third HF with fo = 148.9 Hz; Case-(e): lightly-damped C-type second HF with RD = 250 Ω and fo = 94.8 Hz and single-tuned third HF with fo = 148.9 Hz; and Case-(f): lightly-damped C-type second HF with RD = 250 Ω and fo = 94.8 Hz, no third HF (ESR/L is assumed to be 10 for all HF reactors; ESR is the equivalent series resistance of all HF reactors).
As observed in Figure 3, although the second harmonic subgroup is suppressed by approximately 50% for cases (e) and (f), interharmonic amplification problem still exists, especially for the frequencies below 90 Hz. It is known that EAF currents are rich in interharmonics between the fundamental and the second harmonic for all operating phases of the EAF [30], hence, the current amplification problem for the interharmonics needs to be solved for passive shunt harmonic filter banks. Therefore in this paper, the use of a shunt active power filter (APF) together with an SVC is recommended to suppress the second harmonic subgroup satisfactorily.
3. Proposed Hybrid Solution Including APF
The single-line diagram of an AC EAF installation containing an APF in addition to an SVC system which does not include a second harmonic HF is shown in Figure 4a. Suppression of the second harmonic subgroup is assumed to be achieved by APF in this hybrid solution. For this purpose, more than one shunt-connected voltage sourced converter (VSC)-based APF unit can be operated in parallel and connected to the medium voltage bus (34.5 kV one-to-one) via a specially-designed coupling transformer as illustrated in Figure 4c. A satisfactory current sharing between APF units is to be obtained by using equalizing inductors, Leq. More than one APF unit is considered to be used in order to eliminate the need for series operation of power semiconductor switches. The three-phase three-wire bridge converter topology for each APF unit is chosen, as illustrated in Figure 4b.
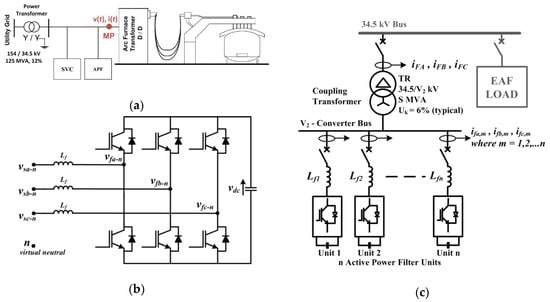
Figure 4.
Proposed EAF system (a) block diagram including an APF and an SVC; (b) m APF units operating in parallel and connected to the grid via a coupling transformer; and (c) the three-phase three-wire two-level VSC converter for each APF unit.
4. Proposed APF Design Methodology
Preliminary design of active power filter, which minimizes second harmonic subgroup injected into the supply by the AC EAF, can be carried out in four steps: (i) Determination of maximum RMS value of the second harmonic subgroup, (ii) Estimation of coupling transformer MVA rating, (iii) Estimation of coupling transformer secondary voltage, and (iv) performance evaluation of the preliminary design by EMTDC/PSCAD and MATLAB. Preliminary design steps (i) to (iii) are described in this section, and step (iv) will be presented in Section IV.
4.1. Determination of the Maximum RMS Value of the Second Harmonic Subgroup
The AC EAF installation is a balanced (IA(t) + IB(t) + IC(t) = 0), but asymmetrical, load on the power system for the vast majority of time as reported in [6]. Sample line current waveforms of an AC EAF installation recorded in the field and the corresponding 95-, 100-, and 105-Hz components obtained by the real-time interharmonic and harmonic detection method recommended in [7] are given in Figure 5a–d, respectively. As observed from Figure 5, AC EAF currents contain significant amounts of second harmonic subgroup components (95-, 100-, 105-Hz) and they are highly time-varying. The maximum RMS value of the second harmonic subgroup is determined during the boring phase of the EAF operation in which the currents are more rapidly fluctuating in comparison with those of the consecutive melting and refining periods. Instantaneous current variations in Figure 6a–c are obtained by MSRF analysis in boring phase for 40 s of measurement period. Their sample-by-sample summation is as given in Figure 6d. Their maximum peak values are also marked on Figure 6a–d. The true RMS value of the resultant reference signal by using the maximum RMS values (obtained by dividing the max peak values by √2) is calculated from Equation (1) and is found to be 166.3 A.
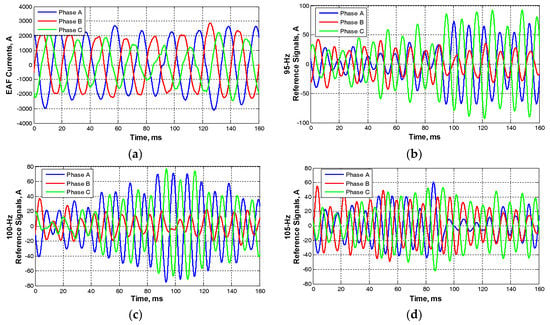
Figure 5.
EAF line currents on MV side (a) a sample line current waveforms collected in the field at a sampling rate of 25.6 kS/s and (b) 95-Hz components (c) 100-Hz components, and (d) 105-Hz components obtained from field data by MSRF analysis in real-time.
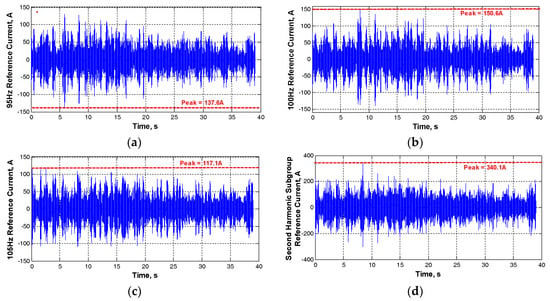
Figure 6.
A sample set of EAF current waveforms obtained by MSRF analysis in real-time (a) 95-Hz, (b) 100-Hz, (c) 105-Hz components, and (d) the reference current signal produced from (a–c).
The true RMS value of the second harmonic subgroup current components could also be calculated from the time maximum value of the waveform in Figure 6d, which is 240.5 A, by assuming the frequency of it is nearly 100-Hz. However, the maximum true RMS value of the second harmonic subgroup is assumed to be 166.3 A from Equation (1) owing to the following reasons:
- (i)
- for the vast majority of the operating time, the true RMS value is lower than 166.3 A;
- (ii)
- the peak values of the subgroup current harmonic components rarely coincide in time;
- (iii)
- the optimum solution to the preliminary design study is chosen to be the minimization of the second harmonic subgroup currents instead of the elimination of them entirely; and
- (iv)
- the fundamental current component flowing through the coupling transformer compensates only for APF switching and conduction losses and to magnetize the transformer core. Since it is much lower than the true RMS value of the second harmonic subgroup, it is neglected in the preliminary design procedure.
4.2. Estimation of Coupling Transformer MVA Rating
MVA rating of the coupling transformer can be calculated from Equation (2) [31,32,33]:
where Vl-to-l is the line-to-line value of the fundamental component of the primary voltage (33.5 kV is the most probable value), and Iline is the true RMS value of the second harmonic subgroup (166.3 A).
This calculation yields, 9.65 MVA as the power rating of the coupling transformer. Unfortunately, this transformer cannot be designed as a 50-Hz distribution transformer. Operating voltage determines the time maximum value of the flux density, Bm, created in the core, however, minor hysteresis loops arising from 95-, 100-, and 105-Hz components will be superimposed on the major hysteresis loop obtained at 50-Hz. Furthermore, these minor loops will move on the major loop depending upon the frequency and phase differences. Therefore, the variations in Bm should be taken into account in hysteresis loss, Ph, and eddy current loss, Pe, calculations. Their expressions are given in Equations (3) and (4), respectively:
where Kh, Ke, and Kf are constants depending on the core material, and f is the corresponding frequency.
On the other hand, in the design of 50-Hz distribution transformers made up of high-quality electrical sheet steels, Bm is usually taken to be 1.8 T. As can be understood from Equations (3) and (4), the increase in Ph and Pe owing to the second harmonic subgroup current components can only be compensated by keeping the design value of Bm much lower than 1.8 T. Our experience shows that Bm should be chosen in the range from 1 T to 1.2 T in order to compensate for the extra core loss components [34]. Total leakage reactance of 6% is implementable for this size of a transformer. These considerations result in an oversized coupling transformer.
4.3. Estimation of Transformer Secondary Voltage
In the preliminary design stage, an optimum value for the transformers turns ratio, n, should be chosen. n dictates the number of paralleled voltage sourced APF converters in order to minimize the second current harmonic subgroup on the supply side. In choosing the optimum value of n, the objective is to eliminate the need for series power semiconductor operation and to minimize the number of paralleled APF units. The commercially-available HV IGBTs which are suitable for such high power applications are given in Figure 7.
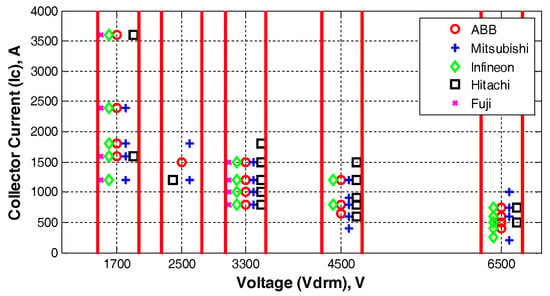
Figure 7.
Commercially-available HV IGBT ratings.
In the design of the three-phase three-wire two-level VSC converter, the over-modulation phenomenon should be avoided by keeping the DC link voltage, Vdc, at a value greater than, or equal to, the peak value of the AC voltage appearing at the coupling transformer secondary terminals. For this purpose, peak values of individual harmonic and interharmonic voltages should be superimposed on peak value of the fundamental component of the transformer secondary voltage. Here, it is assumed that all peak voltages should be added algebraically. Single phase equivalent circuit of the overall system on the MV side is as shown in Figure 8a. In this figure, Ls is the equivalent source inductance, Ltr the transformer leakage inductance, Lapf the current sharing inductors, and m the number of parallel APF units. Figure 8a shows the equivalent circuit for the fundamental component. A very small current at the fundamental frequency flows through the APF system, therefore the fundamental voltage component of each APF unit should be nearly equal to the supply voltage Vs. Figure 8b shows the harmonic and interharmonic equivalent circuits of the APF system, in which the supply side provides a short-circuit return path to the harmonic and interharmonic current components changing at 95-, 100-, and 105-Hz. Therefore, in this equivalent circuit, only these particular harmonic and interharmonic components are considered to be injected by the AC EAF, Ieaf,h. Vapf for 95-, 100-, and 105-Hz components, can then be calculated as the potential drop on Lapf/m and Ltr, owing to the amount of harmonic and interharmonic components to be suppressed by the APF system.
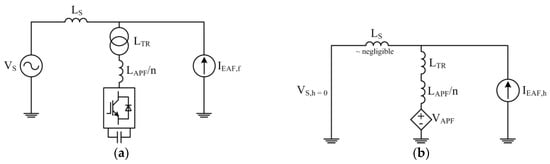
Figure 8.
Single-phase equivalent circuit of the proposed system at (a) the fundamental frequency (50 Hz) and (b) any harmonic or interharmonic frequency.
The relationship between the transformer secondary voltage and the minimum required DC link voltage is given by Equation (5) [25,35]:
where is the peak value of the transformer’s line to neutral primary voltage, n the transformer turns ratio, reference current peak for interharmonic and harmonic frequencies, and Xtr,k the transformer impedance calculated at the kth interharmonic and harmonic frequency and referred to as the MV side.
The required minimum DC link voltage is calculated from Equation (5) and plotted as a function of n in Figure 9. The relationship between maximum permissible value of DC link voltage and minimum semiconductor voltage rating for the three-phase three-wire two-level VSC topology in Figure 4b is as given in (6) as recommended by [36]:
where γ is a constant whose recommended value is 60 [36], VDRM the maximum repetitive peak blocking voltage, and VDC the DC link voltage.
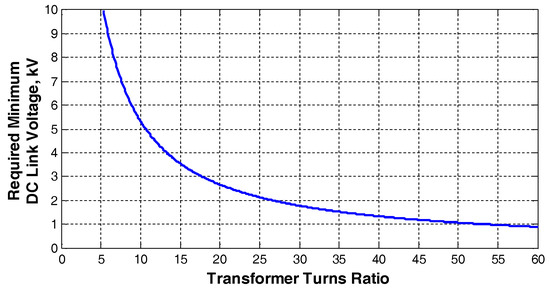
Figure 9.
Minimum DC link voltages required for various transformer turns ratios.
Maximum permissible DC link voltages, VDC, are then calculated from Equation (6) for typical blocking voltage ratings of HV IGBTs as given in Table 3.

Table 3.
Maximum permissible DC link voltage against blocking voltage capability of commercially available HV IGBTs.
There remains only the determination of number of paralleled APF units. For this purpose, for each blocking voltage rating from 6500 to 1700 V, the HV IGBTs having the highest collector current, IC, rating should be considered for the sake of minimum number of parallel APF units. Required transformer line currents in peak amps on the secondary side are than calculated from the peak current in Figure 6d by multiplying it by the required n. These results are given in Table 4 as a function of HV IGBT ratings.

Table 4.
Optimized design parameters for the coupling transformer and shunt APF units.
Among these optimum designs, the use of HV IGBTs having VDRM = 4500 V, IC = 1500 A is the preferred one because it minimizes the number of parallel APF units with the lowest possible semiconductor voltage rating and, hence, the cost.
4.4. Proposed Control Strategy
The basic operating strategy of the proposed APF system is to inject 95-, 100-, and 105-Hz current components in anti-phase with those of the AC EAF to the common connection point. Since the APF converters are of the VSC type, their output voltages at the desired harmonic and interharmonic frequencies are obtained by the pulse width modulation (PWM) technique. Although the APF units are of VSC type converters, their output currents are to be controlled in order to be able to follow the reference current signal that should be injected to the connection point. The reference current signal for each line is formed by summing up the instantaneous values of 95-, 100-, and 105-Hz current components injected by the AC EAF and estimated by the MSRF method described in [7]. As shown in Figure 5a, EAF line currents are highly time-varying such that magnitudes and phases are different at almost every cycle of the fundamental component. The rates of changes for the individual harmonic and interharmonic components are even more severe as shown in Figure 5b–d. Hence, real time detection of the frequency components of the EAF currents is unavoidable if successful APF operation is the main focus. In [7], the MSRF method is applied on a parallel framework employing a GPU to detect all interharmonics and harmonics individually in real-time. Since the sampling rate of the EAF line currents is 25.6 kS/s, there are 512 samples of digital reference current signal in one complete cycle of the fundamental voltage (20 ms). Unfortunately, the chosen high-voltage high-current power semiconductor cannot be switched on and off at such high frequencies. Practical experience has shown that the switching frequency should be kept at a value less than, or equal to, 1.5-kHz on average [37].
The most basic and effective waveform modulation technique for generating a current reference with a voltage source converter is to use hysteresis band modulation philosophy [38,39,40,41,42,43,44]. The hysteresis band modulation technique has been widely used in the literature for APF systems [25,43,44] due to its advantages, like easy implementation, dynamic stability, controllability on current, and perfect tracking of the reference signal [25,44]. However, it has also some drawbacks like high and varying switching frequency, thus high switching losses [25,44]. The use of the hysteresis band modulation technique is suggested for this particular application due to its superiority for current reference tracking with a voltage source converter topology.
Traditional implementation of hysteresis band modulation technique is as given below:
If Ifx > Ifx* + HB then SX = 1,
If Ifx < Ifx* − HB then SX = 0,
Else the previous switching state is sustained
where Ifx is the actual current flowing through phase x, Ifx* is the reference current which should be tracked for phase x, and SX is the switching state of the converter leg corresponding to phase x.
The switching state SX = 1 corresponds to the case where upper semiconductor in converter leg of phase x is turned on while lower one is turned off. Likely, state SX = 0 corresponds to the case where lower semiconductor in converter leg of phase x is turned on while the upper one is turned off. The digital implementation of the hysteresis band modulation technique is as illustrated in Figure 10.
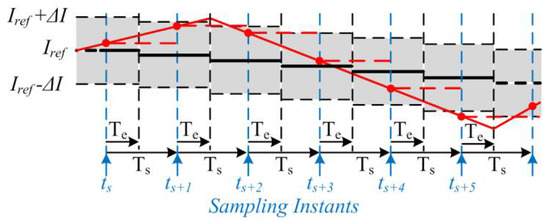
Figure 10.
Illustration of digital implementation of hysteresis band current control philosophy (— current generated by HAPF unit; Te = execution time typical values 20–30 µs; Ts = sampling time typical value is nearly 40 µs).
In this research work, a fixed hysteresis band control technique is exercised. The current control system tends to keep the actual current injected by each APF unit between Iref − ΔI and Iref + ΔI, as illustrated in Figure 10, and according to the fixed hysteresis band current control strategy.
5. Performance of Proposed APF System by EMTDC/PSCAD Simulations
The preliminary design of the proposed APF system to suppress second harmonic subgroup injected into the grid via 65 MVA EAF transformer has been tested by EMTDC/PSCAD simulations including a detailed model of the APF and AC EAF. Line current waveforms of the EAF system at the measurement point (MP) in Figure 4a are sampled in the field at a sampling rate of 25.6 kS/s, and then used in the preliminary design work and PSCAD simulations. 95-, 100-, and 105-Hz harmonic and interharmonic components are extracted in real-time from the line current waveforms by using the MSRF analysis recommended in [7]. Digitized instantaneous values of these interharmonic and harmonic components (95-, 100-, and 105-Hz) are then summed up and inversed (multiplied by −1) in real-time in order to produce the reference current signal for the APF system. A sample reference current signal waveform for a period of 80 ms is given in Figure 11. The APF model is then controlled according to fixed hysteresis band control in order to follow the reference current signal. The corresponding current waveform generated by the APF system is also shown in Figure 11.
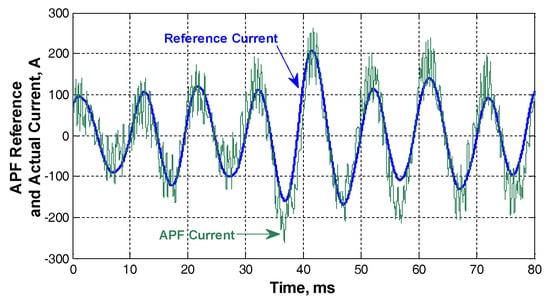
Figure 11.
A sample reference current signal including 95-, 100-, and 105-Hz (deduced from field data) and corresponding current waveform injected by the APF system (simulation results).
In order to illustrate the performance of the APF system in suppressing second harmonic subgroup injected by the EAF, 10-cycle FFT expansion of line phase-A currents on the EAF side, Ieafn, and supply side, Isn, are simultaneously given in Figure 12. As can be understood from Figure 12:
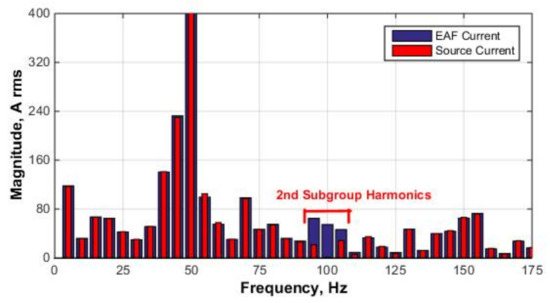
Figure 12.
Harmonic spectrum of the load (field data) and source current in phase-A (simulation results), referring to the MV side.
- (a)
- 100-Hz component is eliminated;
- (b)
- 95- and 105-Hz components are significantly suppressed;
- (c)
- The non-idealities in the performance are attributed to the facts that extraction of interharmonic and harmonic components using MSRF analysis in real-time may lead to small magnitude and phase errors, hence, the APF system cannot suppress the second harmonic subgroup perfectly.
- (d)
- The proposed APF system does not affect interharmonic and harmonic current components other than the second harmonic subgroup; and
- (e)
- Second harmonic subgroup reduction is computed for the harmonic spectrum given in Figure 12 and it is found to be 36.9% without affecting the neighboring interharmonic components by using the proposed APF topology. This is much better than the best cases for passive shunt harmonic filters given in Table 2, which are case-e and -f. Although 56.4 and 48.0% of the second harmonic subgroup of the EAF current are reflected to the supply-side for case-e and –f in Table 2, these topologies still amplify other interharmonic components, as shown in Figure 3.
In order to make a comparison between the second harmonic subgroup current components of EAF and APF, the associated waveforms are expanded into DFT for a 10-cycle window. They are given in Figure 13a,b, respectively. Although these components are very close to each other in magnitude, this does not mean that the APF system can entirely suppress the above EAF current components owing to the possible phase errors arising from MSRF analysis. The mismatch between the side-bands of the second harmonic subgroups of the EAF current and the APF current in Figure 13a,b, respectively, is due to the fact that MSRF analysis runs sample by sample; however, DFT expansion is the average of the 200 ms window for both current waveforms. Hence, there is the rounding effect of the DFT window.
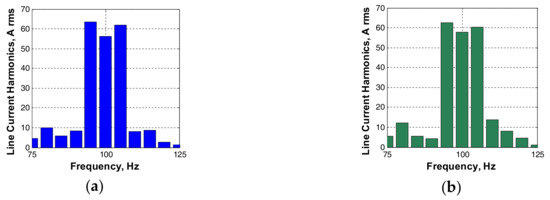
Figure 13.
Ten-cycle DFT expansion of (a) EAF current (deduced from field data) and (b) APF current (deduced from simulation results) on the MV side.
The average switching frequency of the power semiconductors are found to be less than 2-kHz. In order to investigate the effects of switching frequency on the harmonic spectrum of supply side line current waveforms, these waveforms are expanded in DFT with 5-Hz resolution. As can be understood from a sample expansion given in Figure 14, the switching frequency of power semiconductors operating in hysteresis band control has a negligible effect on the harmonic spectrum of the supply side line current waveforms.
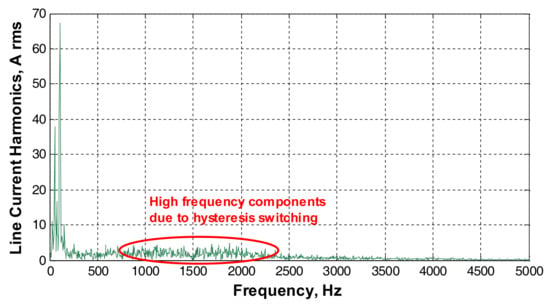
Figure 14.
Harmonic spectrum of the APF line current showing the effect of hysteresis switching (simulation results).
Finally, a hybrid filtering topology for the suppression of second and third harmonic subgroups is exercised as shown in Figure 15. The recommended solution involves an APF which is designed to suppress the second harmonic subgroup and a damped third harmonic passive filter for the suppression of third harmonic subgroup. The damped third harmonic passive filter suppresses considerably the third harmonic subgroup, without having an effect on the remaining second harmonic subgroup after filtered out by APF. As can be understood from Figure 15b, the use of APF only has no filtering effect on the third harmonic subgroup. Furthermore, the use of third HF only has no effect on the second harmonic subgroup. Therefore, their combined utilization as illustrated in Figure 15 gives the best suppression of second and third harmonic subgroups at the expense of amplification of 130, 135, and 140 Hz interharmonic components. However, these interharmonic frequencies are less severe from the viewpoint of the light flicker problem [9].
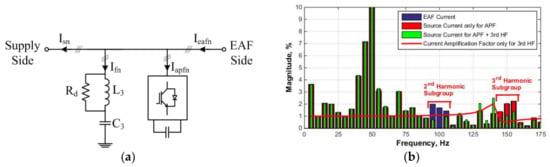
Figure 15.
Proposed hybrid filter topology for the suppression of second and third harmonic subgroups, (a) block diagram including APF and third HF and (b) filtering performance of the proposed topology in comparison with APF only and third HF only solutions (EAF current collected in the field and single phase currents are expanded in DFT with 5 Hz resolution).
6. Conclusions
The work in this paper and the field experience of the authors have shown that it is not possible to satisfactorily suppress the second harmonic subgroup of EAF currents using passive HF topologies. Hence, an APF has been recommended to solve this problem and design considerations for an optimized APF are presented, in this paper. Instead of suppressing only the second harmonic subgroup, a much larger APF can be recommended to suppress all interharmonics in the range from 55 to 125 Hz. However, this would be an extremely expensive solution. On the other hand, hybrid combination of a smaller size APF to suppress the second harmonic subgroup and a damped third harmonic passive filter have been shown to suppress the second and third harmonic subgroups successfully without amplifying the interharmonics around the fundamental frequency.
For an APF to exhibit a superior filtering performance, time-varying interharmonics and harmonics to be suppressed should be detected in a considerably short time interval, i.e., almost real-time. This can be achieved by employing the detection algorithm based on MSRF analysis and Kalman filtering running on a GPU framework in real time. It has been shown in this paper that the usage of fixed-band hysteresis band control as the control strategy provides satisfactory performance to suppress the second harmonic subgroup.
Author Contributions
M. Ermiş and Ö. Salor conceived of the presented idea. M. Ermis and E. Durna developed the theory and performed the computations. E. Durna and C. Ö. Gerçek carried out the simulations. All authors discussed the results and contributed to the final manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Salor, O.; Gultekin, B.; Buhan, S.; Boyrazoglu, B.; Inan, T.; Atal, T.; Acik, A.; Terciyanli, A.; Unsar, O.; Altintas, E.; et al. Electrical Power Quality of Iron and Steel Industry in Turkey. IEEE Trans. Ind. Appl. 2010, 46, 60–80. [Google Scholar] [CrossRef]
- Srdic, S.; Nedeljkovic, M.; Vukosavic, S.N.; Radakovic, Z. Fast and Robust Predictive Current Controller for Flicker Reduction in DC Arc Furnaces. IEEE Trans. Ind. Electron. 2016, 63, 4628–4640. [Google Scholar] [CrossRef]
- Esfahani, M.T.; Vahidi, B. A New Stochastic Model of Electric Arc Furnace Based on Hidden Markov Model: A Study of Its Effects on the Power System. IEEE Trans. Power Del. 2012, 27, 1893–1901. [Google Scholar] [CrossRef]
- Hsu, Y.-J.; Chen, K.-H.; Huang, P.-Y.; Lu, C.N. Electric Arc Furnace Voltage Flicker Analysis and Prediction. IEEE Trans. Instrum. Meas. 2011, 69, 3360–3368. [Google Scholar] [CrossRef]
- Beites, L.F.; Mayordomo, J.G.; Hernandez, A.; Asensi, R. Harmonics, Interharmonics and Unbalances of Arc Furnaces: A New Frequency Domain Approach. IEEE Trans. Power Del. 2001, 16, 661–668. [Google Scholar] [CrossRef]
- Uz-Logoglu, E.; Salor, O.; Ermis, M. Online Characterization of Interharmonics and Harmonics of AC Electric Arc Furnaces by Multiple Synchronous Reference Frame Analysis. IEEE Trans. Ind. Appl. 2016, 52, 2673–2683. [Google Scholar] [CrossRef]
- Uz-Logoglu, E.; Salor, O.; Ermis, M. Real-time Detection of Interharmonics and Harmonics of AC Electric Arc Furnaces on GPU Framework. In Proceedings of the IEEE Industry Applications Society Annual Meeting, Cincinnati, OH, USA, 1–5 October 2017; pp. 1–8. [Google Scholar]
- White, R.S.; Dionise, T.J.; Baron, J.A. Design, Analysis, and Operation of the Electrical Distribution System for a Modern Electric Arc Furnace and Ladle Melt Furnace. IEEE Trans. Ind. Appl. 2010, 46, 2267–2275. [Google Scholar] [CrossRef]
- Gercek, C.O.; Ermis, M.; Ertas, A.; Kose, K.N.; Unsar, O. Design, Implementation, and Operation of a New C-Type 2nd Harmonic Filter for Electric Arc and Ladle Furnaces. IEEE Trans. Ind. Appl. 2011, 47, 1545–1557. [Google Scholar] [CrossRef]
- Akagi, H. Active Harmonic Filters. IEEE Proc. 2005, 93, 2128–2141. [Google Scholar] [CrossRef]
- De Almeida Carlos, G.A.; Jacobina, C.B. Series Compensator Based on Cascaded Transformers Coupled With Three-Phase Bridge Converters. IEEE Trans. Ind. Appl. 2017, 53, 1271–1279. [Google Scholar] [CrossRef]
- Teixeira, N.F.; Pinto, J.G.O.; Freitas, M.J.S.; Afonso, J.L. New Control Algorithm for Single-Phase Series Active Power Filter. Electr. Power Compon. Syst. 2015, 43, 1752–1760. [Google Scholar] [CrossRef]
- Tang, Y.; Loh, P.C.; Wang, P.; Choo, F.H.; Gao, F.; Blaabjerg, F. Generalized Design of High Performance Shunt Active Power Filter with Output LCL Filter. IEEE Trans. Ind. Electron. 2012, 59, 1443–1452. [Google Scholar] [CrossRef]
- Panigrahi, R.; Subudhi, B. Performance Enhancement of Shunt Active Power Filter Using a Kalman Filter-based H. Control Strategy. IEEE Trans. Power Electron. 2017, 32, 2622–2630. [Google Scholar] [CrossRef]
- Panigrahi, R.; Panda, P.C.; Subudhi, B. A Robust Extended Complex Kalman Filter and Sliding-mode Control Based Shunt Active Power Filter. Electr. Power Compon. Syst. 2014, 42, 520–532. [Google Scholar] [CrossRef]
- Narongrit, T.; Areerak, K.; Areerak, K. Adaptive Fuzzy Control for Shunt Active Power Filters. Electr. Power Compon. Syst. 2016, 44, 647–657. [Google Scholar] [CrossRef]
- Anjana, P.; Gupta, V.; Tiwari, H.; Gupta, N.; Bansal, R. Hardware Implementation of Shunt APF Using Modified Fuzzy Control Algorithm with STM32F407VGT Microcontroller. Electr. Power Compon. Syst. 2016, 44, 1530–1542. [Google Scholar] [CrossRef]
- Fereidouni, A.; Masoum, M.A.S. Shunt Active Power Filter Enhancement by Means of Frequency-locking Complex Adaptive Linear Combiner. Electr. Power Compon. Syst. 2016, 44, 2256–2270. [Google Scholar] [CrossRef]
- Ghamri, A.; Benchouia, M.T.; Golea, A. Sliding-mode Control Based Three-phase Shunt Active Power Filter: Simulation and Experimentation. Electr. Power Compon. Syst. 2012, 40, 383–398. [Google Scholar] [CrossRef]
- Suresh, D.; Singh, S.P. Type-2 Fuzzy Logic Controlled Three-level Shunt Active Power Filter for Power Quality Improvement. Electr. Power Compon. Syst. 2016, 44, 873–882. [Google Scholar] [CrossRef]
- Ngo, T.; Biricik, S.; Basu, M. A Self-tuning Grid Synchronization Method for Active Power Filter. Electr. Power Compon. Syst. 2016, 44, 1947–1957. [Google Scholar] [CrossRef]
- Wiebe, E.; Duran, J.L.; Acosta, P.R. Integral Sliding-mode Active Filter Control for Harmonic Distortion Compensation. Electr. Power Compon. Syst. 2011, 39, 833–849. [Google Scholar] [CrossRef]
- Boukezata, B.; Chaoui, A.; Gaubert, J.-P.; Hachemi, M. Power Quality Improvement by an Active Power Filter in Grid-connected Photovoltaic Systems with Optimized Direct Power Control Strategy. Electr. Power Compon. Syst. 2016, 44, 2036–2047. [Google Scholar] [CrossRef]
- Yilmaz, I.; Durna, E.; Ermis, M. Design and Implementation of a Hybrid System for the Mitigation of PQ Problems of Medium-Frequency Induction Steel-Melting Furnaces. IEEE Trans. Ind. Appl. 2016, 52, 2700–2713. [Google Scholar] [CrossRef]
- Durna, E.; Yilmaz, I.; Ermis, M. Suppression of Time-Varying Interharmonics Produced by Medium-Frequency Induction Melting Furnaces by a HAPF System. IEEE Trans. Power Electron. 2017, 32, 1030–1043. [Google Scholar] [CrossRef]
- Corasaniti, V.F.; Barbieri, M.B.; Arnera, P.L.; Valla, M.I. Hybrid Power Filter to Enhance Power Quality in a Medium-Voltage Distribution Network. IEEE Trans. Ind. Electron. 2009, 56, 2885–2893. [Google Scholar] [CrossRef]
- Xie, C.; Zhao, X.; Savaghebi, M.; Meng, L.; Guerrero, J.M.; Vasquez, J.C. Multi rate Fractional-Order Repetitive Control of Shunt Active Power Filter Suitable for Microgrid Applications. IEEE J. Sel. Top. Power Electron. 2017, 5, 809–819. [Google Scholar] [CrossRef]
- Akagi, H.; Kondo, R. A Transformerless Hybrid Active Filter Using a Three-Level Pulse width Modulation (PWM) Converter for a Medium-Voltage Motor Drive. IEEE Trans. Power Electron. 2010, 25, 1365–1374. [Google Scholar] [CrossRef]
- Testing and Measurement Techniques-General Guide on Harmonics and Interharmonics Measurements and Instrumentation for Power Supply Systems and Equipment Connected Thereto. IEC Std. 61000-4-7, 2002, 2.0 ed. Available online: https://webstore.iec.ch/preview/info_iec61000-4-7%7Bed2.0%7Den_d.pdf (accessed on 19 April 2018).
- Bollen, M.H.; Gu, I. Signal Processing of Power Quality Disturbances; Wiley-IEEE Press: Hoboken, NJ, USA, 2006; ISBN 978-0-471-73168-9. [Google Scholar]
- Gunther, E.W.; Mc Granaghan, M.F. Power measurements in distorted and unbalanced conditions-an overview of IEEE Trial-Use Standard 1459–2000. In Proceedings of the IEEE Power Engineering Society Summer Meeting, Chicago, IL, USA, 21–25 July 2002; pp. 930–934. [Google Scholar]
- Filipski, P.S. Polyphase apparent power and power factor under distorted waveform conditions. IEEE Trans. Power Del. 1991, 6, 1161–1165. [Google Scholar] [CrossRef]
- IEEE Standard Definitions for the Measurement of Electric Power Quantities Under Sinusoidal, Nonsinusoidal, Balanced, or Unbalanced Conditions. IEEE Std 1459-2010 2010. [CrossRef]
- Gerçek, C.O.; Ermis, M. Elimination of Coupling Transformer Core Saturation in Cascaded Multilevel Converter-Based T-STATCOM Systems. IEEE Trans. Power Electron. 2014, 29, 6796–6809. [Google Scholar] [CrossRef]
- Lam, C.-S.; Cui, X.-X.; Choi, W.-H.; Wong, M.C.; Han, Y.D. Minimum inverter capacity design for LC-hybrid active power filters in three-phase four-wire distribution systems. IET Power Electron. 2012, 5, 956–968. [Google Scholar] [CrossRef]
- Voltage Ratings of High Power Semiconductors. ABB Switzerland Ltd. Semiconductors: Lenzburg, Switzerland, 2013. Available online: https://library.e.abb.com/public/6f03cdd0f2264ff48f2992e62497dd5a/Voltage%20ratings%20of%20high%20power%20_%205SYA%202051NLay.pdf (accessed on 19 April 2018).
- Cetin, A.; Ermis, M. VSC-Based D-STATCOM with Selective Harmonic Elimination. IEEE Trans. Ind. Appl. 2009, 45, 1000–1015. [Google Scholar] [CrossRef]
- Ingram, D.M.; Round, S.D. A Fully Digital Hysteresis Current Controller for an Active Power Filter. Int. J. Electron. 1999, 86, 1217–1232. [Google Scholar] [CrossRef]
- Chen, C.; Cramer, A.M.; Liu, X. Average-value Modeling of Hysteresis Current Controlled Three-phase Inverters. Electr. Power Compon. Syst. 2016, 44, 693–700. [Google Scholar] [CrossRef]
- Tian, B.; Mao, C.; Lu, J.; Wang, D.; He, Y.; Zhou, B.; Zhang, J.; Chen, X. Seamless Transfer Control Strategy for Grid-Interactive Inverters. Electr. Power Compon. Syst. 2014, 42, 1587–1597. [Google Scholar] [CrossRef]
- Wu, F.; Feng, F.; Luo, L.; Duan, J.; Sun, L. Sampling Period Online Adjusting-Based Hysteresis Current Control Without Band with Constant Switching Frequency. IEEE Trans. Ind. Electron. 2015, 62, 270–277. [Google Scholar] [CrossRef]
- Davoodnezhad, R.; Holmes, D.G.; McGrath, B.P. A Novel Three-Level Hysteresis Current Regulation Strategy for Three-Phase Three-Level Inverters. IEEE Trans. Power Electron. 2014, 29, 6100–6109. [Google Scholar] [CrossRef]
- Malesani, L.; Mattavelli, P.; Tomasin, P. High-performance hysteresis modulation technique for active filters. IEEE Trans. Power Electron. 1997, 12, 876–884. [Google Scholar] [CrossRef]
- Lam, C.-S.; Wong, M.-C.; Han, Y.-D. Hysteresis current control of hybrid active power filters. IET Power Electron. 2012, 5, 1175–1187. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).