Abstract
This research work deals with a hybrid control system based integrated Cuk converter fed brushless DC motor (BLDCM) for power factor correction. In this work, moth-flame optimization (MFO) and a fuzzy logic controller (FLC) have been combined and a moth-flame fuzzy logic controller (MFOFLC) has been proposed. Firstly, the BLDC motor modeling is composed with the power factor correction (PFC) based integrated Cuk converter and BLDC speed is regulated using variable DC-Link inverter voltage which results in a low switching operation with fewer switched losses. Here, with the use of a switched inductor, the task and execution of the proposed converter is redesigned. The DBR (diode bridge rectifier) trailed by a proposed PFC based integrated Cuk converter operates in discontinuous inductor conduction mode (DICM) for achievement of better power factor. MFO is exhibited for gathering of a dataset from the input voltage signal. At that point, separated datasets are sent to the FLC to improve the updating function and minimization of torque ripple. However, our main objective is to assess adequacy of the proposed method, but the power factor broke down. The execution of the proposed control methodology is executed in the MATLAB/Simulink working platform and the display is assessed with the existing techniques.
1. Introduction
Nowadays there is a trend to use a Brushless DC motor rather than a brushed DC motor in an expanding number of uses [1]. Compared to brush DC motors and induction motors, a BLDC motor has a couple of favorable circumstances [2]. It works as a synchronous motor in which the stator and rotor magnetic fields generate comparative frequencies. BLDC engines don’t encounter the “slip” that is consistently found in induction motors [3]. Ordinarily, the BLDCM is made out of three stator coils with a permanent magnetic rotor in which the magnetic field is turned by two coils and a floating coil is responsible for back electro-motive force (EMF) [4]. Speed regulation is a fundamental viewpoint as far as BLDC speed and position controlling is concerned [5,6,7]. As an average speed controller framework, it employed a double-loop structure which can be used in multiple applications such as in the household; in electronics based self-propelled, précised apparatus; and in automated systems used in offices, and so on [8].
Because of torque ripple commutation, the BLDC motor has a torque ripple problem. Subsequently, concealment of torque ripple commutation is responsible for reduction of torque ripple in a BLDC motor [9]. The torque for the most part incorporates cogging, mutual, and reluctance torque cogging; torque has been activated using the stator connected rotor’s magnetic field which is independent from the stator’s current excitation [10,11]. Because of power electronic commutation, torque ripples are generated which is responsible for high switched frequency and stator’s blemish [12]. The trapezoidal back-EMF is responsible for reduction of torque ripples in a BLDC motor which can be achieved by utilizing condensed winding and use of one pitch slot with skewed stator slot skewing. Therefore, a productive controller is required for minimization of supply voltage and line current harmonics present in a motor system [13].
Practically speaking, the design of the BLDC motor drive includes a mind boggling procedure. Traditionally, various BLDC motor speed controllers have been discussed in literature [14]. The phase change method, the hysteresis current method, and the pulse width modulation (PWM) controller have already been discussed to smoothen torque ripple in BLDC motor but are unable to handle over or under compensation problems [15]. Sensors are employed for rotor speed and position estimations [16]. A proportional Integral (PI) based speed controller has been used for this purpose, with the major issues of having more rise/settled time with high speed oscillations [17]. Routinely, least-squares approximation strategy, genetic algorithm (GA), particle swarm optimization (PSO) algorithm, NN (neural network), and enhanced gradient descent algorithm have been discussed to improve speed and positions estimation of BLDC motor [18,19]. Ghanaatian et al. [20] has discussed using a predictive controller for controlling a flywheel energy storing system. DC-link utilization with flywheel velocity has been effectively controlled in this research work. However, practical investigation is missing in this paper. Nag et al. [21] described fuzzy logic based core and copper minimization methods using harmonic removal based pulse width modulation for BLDC motor drives. It reduces the harmonic contents present in the phase current of the BLDC motor and provides optimization of switched losses of the converter. However, design of a rule based fuzzy system with hardware implementation is difficult under changing operating conditions. Ziaeinejad et al. [22] have analyzed the torque ripple commutation method of BLDC motor. This paper deals with the simpler method of minimization of torque ripple commutation which works on voltage reduction phase of commutation period.
Nowadays, regulation of speed and torque with torque ripple minimization is of great concern for the BLDX motor. PWM controllers are the best suited technology for controlling a BLDC motor in which a two-phase feeding scheme has been employed. However, it has vulnerability issues because of load as well as in-set speed variations. Additionally, tuning of the PID controller prompts vulnerability in the control system parameters. To overcome these challenges, an optimal torque control technique utilizing advanced technology is required. Here, an enhanced controller has been employed which solves the above issues. MFO technique, numerous parameters will be considered which will identify with the PFC and torque ripple minimization, for example, the speed, torque, back EMF, torque ripple and so forth individually. Using these parameters, the objective function will be characterized that will be comprehended by the MFO strategy. Simulation results reveal employed controller exhibit and predicts best control signals to the converter. The accompanying section portrays the configuration of the proposed converter.
The rest of this paper is organized as follows: The design and modeling of proposed converter and BLDC motor is indicated in Section 2. The proposed control algorithm is portrayed in Section 3. The itemized examination and re-enactment after-effect of the proposed method is displayed in Section 4. At long last, Section 5 finishes up the paper.
2. PFC of BLDC Motor Utilizing Proposed Technique
The schematic of proposed BLDC motor correcting power factor scheme with controlling strategy is appeared in Figure 1. Here, the BLDC motor comprises of two phases: modeling and controlling phases. This framework constitutes an AC voltage as input source, voltage source inverter, integrated Cuk converter, and MFFLC based controller as main components. In the modeling phase, the BLDC motor is associated with three phases of voltage source inverter (VSI). After that with respect to the neutral point () the phase voltage is estimated. IGBT are employed for inverter lower frequency execution. In the controlling phase, a MFFLC strategy is applied for efficiency enhancement of DC motor through switched inductor operation. Also, BLDC electronic commutation and speed regulation is carried out with PWM pulses to the inverter. Generally, the VSI comprises of six solid-state switches which encounter more switched losses because of higher PWM pulses used in motor speed control. The following sections elaborate proposed system design, BLDC motor modeling, and control methodologies.
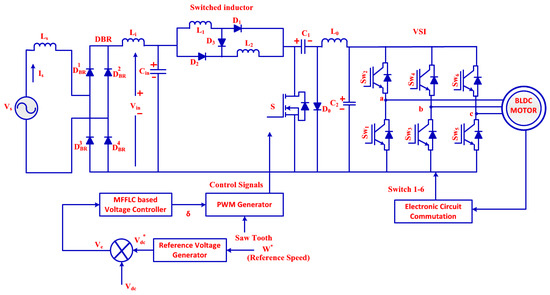
Figure 1.
Schematic structure of integrated Cuk converter based controlling strategy for brushless DC motor (BLDCM).
2.1. Modelling Phase
The design of the Cuk converter and modeling of the BLDC motor is described in this section. Initially, the three phase (AC) supply is given as input source to DBR which is defined in Equation (1).
where, ; is line frequency and represents peak input voltage.
The voltage appearing after DBR is
The DBR is utilized for converting the input AC voltage to DC voltage and the direct current supply is given to the switched inductor. Voltage/current stress occurs while giving DC supply in boost segment and power factor corrected based power switch is expanded in DICM (discontinuous inductor current mode). Consequently, the Cuk converter works as an inverter in [23] which consists of a switch, diode, switched inductors, and capacitors. The inductor gets parallel charged in the case of a switch condition and discharged in series during a condition with same energy level. Here, the switched inductors have been mainly utilized for transferring supply and output voltages to the current source [24,25]. The following section includes the design and performance of proposed converter with different modes.
Design of Integrated Converter with Various Modes
The integrated Cuk converter operates in various modes of Continuous Conduction Mode and discontinuous conduction mode. DICM (Discontinuous Inductor Current Mode) and Discontinuous Capacitor Voltage Mode (DCVM) are treated as two modes of discontinuous conduction mode operation. The Cuk converter execution [26] in CCM is described as following intervals. In the first interval, when switch S is turned , the switched L1 and L2 store energy while C1 discharges energy, which is shown in Figure 2a. In the second interval, the S is turned , the switched inductor is responsible for energy storing, and C1 gets discharged using switch (S) which relocates DC link capacitor (C2) depicted with Figure 2b.
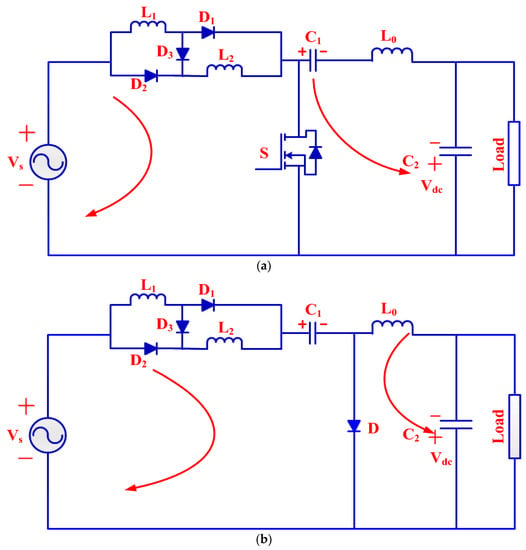
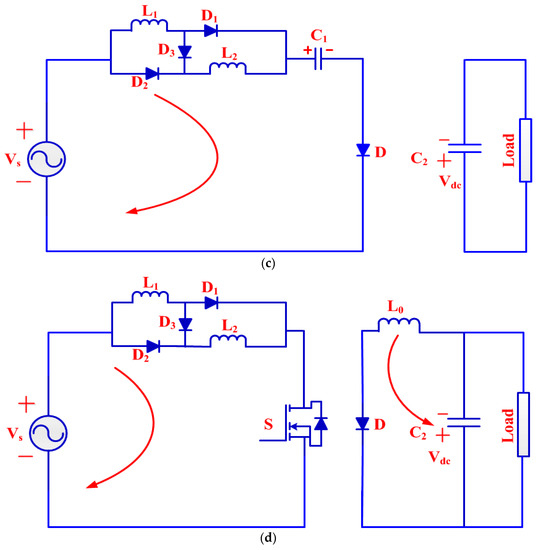
Figure 2.
Design of integrated Cuk converter with different intervals of switching period: (a,b) continuous conduction mode (CCM), (c) discontinuous inductor conduction mode(DICM) and (d) Discontinuous Capacitor Voltage Mode (DCVM) modes.
The operation of integrated Cuk converter in DICM and DCVM [27] operation with different intervals of switching period is illustrated using Figure 2c,d. In the first interval, S works in conduction state, the inductor stores energy and is discharged in the capacitor through switch and energy transferring to C2. While S is in the second state but C1 (intermediate capacitor) completely discharged energy and performs the DCM operation; hence no energy is left in switched inductor input and voltage remains zero during this operation. In the third interval, the intermediate capacitor starts charging continuously by input inductor L1 during turn off condition.
The output summed energy is then given to VSI, so that the voltage level is increased. Then, the VSI is connected to the BLDC motor [28] for controlling speed and torque. Figure 3 illustrates the equivalent circuit of motor phase.
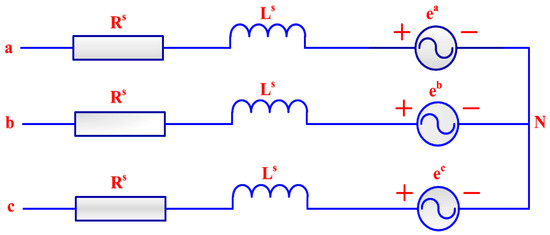
Figure 3.
BLDCM Equivalent model.
The voltage condition of the BLDCM is composed of Equation (3).
where represents stator resistance, stator voltage is , is stator current, and denotes flux linkage. Stator’s resistance matrix can be calculated in the following condition (4):
The electromagnetic torque is created by considering back-EMF is characterized as
Here
θr = ωrt = angular displacement of rotor in degrees,
ωr = angular speed in RPS,
x = pi = 180 degrees,
N = number of iterations,
K = constant value taken according to the parameters of the motor,
pF = No. of poles.
Evaluation of phase back-EMF voltages at the stator terminals is carried out by rotating the machine with the prime mover and the open circuit terminal. The mechanical condition of motor speed is expressed as
Here, is the rotor angular speed with respect to , p represents magnetic poles number, and specifies mechanical torque. In the proposed method the normal and speed reference is estimated from the speed estimator, and the torque ripple of the BLDC motor is minimized from the control strategy specified in the below section.
2.2. Controlling Phase
The Speed/Torque of the BLDCM has been controlled using the proposed method based PI (proportional integral) controller that was developed. From Figure 1, the output signals from VSI generated the optimal pulses for controlling the motor.
(a) Voltage Controller
The PI is the feedback control loop mechanism used in the control system. Here, the BLDC motor speed is estimated by utilizing the speed estimator. From actual and reference values the speed error is calculated and passed through the voltage controller for speed controlling and error correcting. The output of PI controller depends on and parameters and is specified as
In general, the proportional gain () is providing the entire controlling performance. It can be expressed as proportional to signal error with associated gain and the transfer function is given as follows.
where,.
In the proposed controller, by utilizing the FLC method, MFO strategy is executed and updated. Hence, the gain parameters value () is stored from the output of the proposed controller algorithm. Thus, the optimal value of power is controlled and the controlled signal is given to PWM generator for controlling inverter switching operation and BLDC motor performance. The torque ripples are minimized from the following Equation (9).
where
tmax = Maximum time at which peak torque occurs
tmin = Minimum time at which minimum torque occurs
For generating the optimal control pulses of motor the torque is applied as input for the proposed method by multiplying with 100 and evaluated the torque ripple percentage. The developed mathematical equation for optimal control signals is formulated as
Here, is the threshold value, is on and off period of the switches and the duty cycle is represented as . With the Figure 1 the modeling of BLDC motor is composed. The following section explained the detailed working procedures of proposed MFFLC control approach for getting optimal pulses.
3. Proposed MFFLC Algorithm
Using the traditional fuzzy logic controller, the generation of control signals to the converter is a difficult task because of complications of designing an inference rule base system with proper membership functions. The MFO method is basically based on transverse direction of moths in universe which works on navigation methodology [29,30,31]. The MFFLC method will be the joined execution of both MFO and FLC for controlling the motor speed and torque of BLDC motor. The MFO can have the capacity to enhance the underlying irregular arrangements and joining to a superior point in the pursuit space. Here, the MFO method can be employed to differentiate proper and accessible required orientation with the selection of suitable activation function. In light of a fulfilled dataset, the FLC performs and predicts the most ideal control signals of the converter. With this control strategy, the BLDC motor speed and PFC will be regulated; likewise the harmonics and torque ripples will be minimized. The MFO algorithm consists of following steps.
3.1. Steps for Proposed MFO Algorithm
Step 1: Setting of Parameters
Voltage, current, and speed variables are the deciding parameters. Number of dim variables,, moths and flames numbers, and lower bound () and upper bound () of variables is defined as and are considered as MFO main parameters.
Step 2: Initialization
In MFO algorithm the moths arrangement is initialized in a form of matrix, since it is a population based algorithm.
where, the matrix location of moths is , is the parameter (variables) value of the moth (), , and . By using the random distribution can be given as in Equation (12).
Here, denotes uniform randomly created values lies in [0, 1]. The set of flames are expressed as
where, the matrix location of flames is , represents the parameter value of flame, , and . FLC values are randomly initiated with iterations .
Step 3: Determination of Fitness Function
The voltage/current parameters corresponding to BLDC motor are appeared in the moth evaluation. To store the fitness values of moth and flames and matrix are employed.
The main objective of the activation function of the proposed algorithm is to minimize error generated from reference and measured signal. Also, The can be expressed mathematically as where is the error signal.
Step 4: Position Updating
Each moth position is updated based on the best fitness value and is expressed in Equation (16). Here, is the random number, is distance, and is spiral function.
where .
During spatial orientation, no moths should cross upper limit and when moth becomes closer to flame, preceding parameters should be updated with respect to current parameters. The random number is in interval [r, 1] and iteration process decreases with linear relation from −1 to −2.
Step 5: Final Process
The adaptive mechanism employed in number of flames over the iterations as follows:
where and represents the maximal flames number and iteration. Positions of moths have been updated by considering best flame from end iterations which provides adjustments of gradually minimization of investigated and searched position. These fulfilled datasets are given to the fuzzy logic controller to perform and predicts the most ideal control signals of the converter. The flowchart of proposed MFO algorithm with FLC is delineated in the Figure 4.
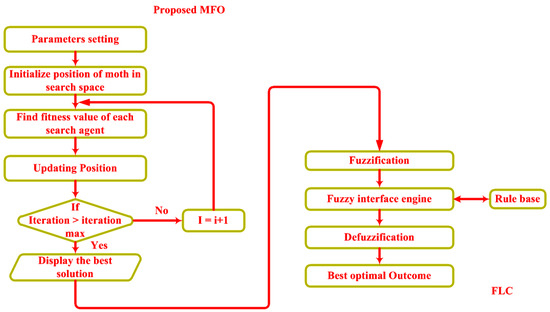
Figure 4.
Flow chart of proposed MFFLC method.
3.2. Prediction of Control Signals Using FLC
The FLC algorithm is utilized to perform and predicts the most ideal control signals of the converter. The procedure of FLC is indicated underneath. FLC controller makes results encourage decisively by improved interest and MFFLC strategy is utilized for power factor correction with parameters gain.
- (i)
- Fuzzification Process: With the help of membership function selection, it converts crisp to linguistic parameters [32,33]. The error and the change of error are considered as supply parameters of FLC, which is given as follows:where, the reference voltage is , the present output voltage is , and subscripts denotes the initial considered parameters.
- (ii)
- Fuzzy Inference Engine: With the application of If-Then fuzzy rules, decisions are taken as follows:where,, and are subsets and singleton parameters, respectively.
- (iii)
- De-Fuzzification Process: In this method, fuzzy variables are defuzzified and converted to numerical output. It decides membership ability of output parameters. The outcome of the framework database iswhere, is represents the solution of target after fuzzification.
This segment deals MFFLC strategy performance with VSI controlled BLDCM which are implemented using MATLAB/Simulink platform. At first, the parameters like speed, torque, stator current, back EMF, and torque ripple minimization of BLDC motor are examined. For creating the closed loop of BLDC motor the Cuk converter is utilized and optimal torque reference signal is generated based on speed controller. Meanwhile, to control BLDC motor the control signals are given to DC-DC converter by PWM generator from voltage based controller. In view of above procedure, the simulation is performed for various speed and torque conditions under three different test cases.
4. Simulated Results and Discussions
4.1. Test Case 1: Analysis of Constant Speed and Torque
In the sub section, the steady state performance of BLDCM has been discussed. For this steady state analysis of BLDC motor the speed (1500 rpm) and torque (5 Nm) is fixed as constant. Here, by using the proposed methodologies, the optimized speed and torque in BLDC motor is controlled. Additionally, enhancements of existing techniques are MFO and PI controller, which are equated versus the proposed method. The proposed tuning process has been tested under constant speed and torque, which is illustrated in the Figure 5 respectively. Here, the proposed method to reach the settling time is 0.25 s respectively. The existing methods are achieving the settling process at 0.27 s and 0.32 s respectively. The optimization methodology optimizes the current, speed, EMF, and torque of the proposed technique based on the minimization of error produced from measured performance and reference output performance. The optimized tuning parameters from the proposed methodology assure the best fit output system behavior. Speed at constant speeds (1500 rpm) to reach the settling time at 0.38 s is achieved using a PI controller.
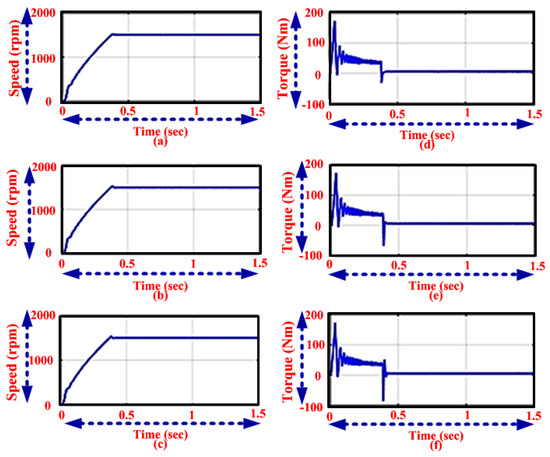
Figure 5.
Analysis of Speed using the (a) proposed (b) moth-flame optimization (MFO) method and (c) proportional integral (PI) controller and Torque using the (d) proposed (e) MFO method and (f) PI controller.
Figure 6 shows the analysis of capacitor and inductor, current, and voltage using the proposed method. Figure 6a–c shows the behavior of proposed drives used inductor and capacitor components for correction of the power factor which resulted in improvement of power quality and can be achieved by the complete range of speed control. Figure 6d,e shows the different operations of the switch with optimal voltage/current. By increasing time, DC-link voltage is increases and reached maximum of 387 V, thereby corrected the power it can be seen in Figure 6f.
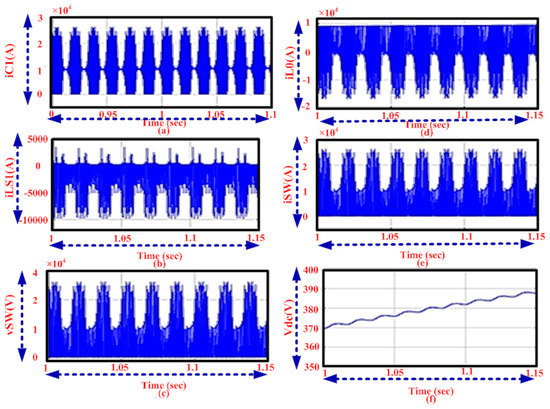
Figure 6.
Analysis of current using the (a) C1, (b) L1, (d) L0, (e) switch and voltage using (c) switch, (f) DC link.
The output performance analysis of EMF and PWM with proposed and existing methodologies is described in Figure 7. In the figure, the output performance of the BLDC motor, the proposed method has rise time at 0 speeds (rpm) and takes 1.02 s to achieve the stable condition. Figure 7b shows that MFO methodology gets the speed at constant speeds (rpm) rise time and settling process at 0.4 s. The PI controller speed process requires 0.41 s for the settling process. Similarly, the dynamic states are analyzed in the following section. In Figure 7d, when the switch is ON, the pulse is generated at the time interval of 1 to 1.00007 s and in the existing method the pulses are generated in between the time interval of 1.00007 s to 1.00011 s as illustrated in Figure 7e,f.
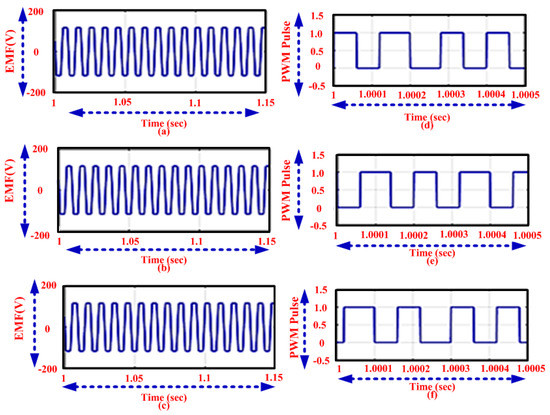
Figure 7.
Analysis of EMF using the (a) proposed (b) MFO method and (c) PI controller and pulse width modulation (PWM) using the (d) proposed (e) MFO method and (f) PI controller.
4.2. Test Case 2: Analysis of Constant Torque with Speed Variation
In this segment, the torque is constant and speed is varied and the proposed method based BLDC motor effectiveness is simulated with the different methods such as the MFO method, and the PI controller. Based on the motor regulated speed and torque, the torque ripple is minimized. The motor speed is controlled in view of input parameters of BLDC motor like current and back electromotive force. Comparison between speed and time of the proposed, MFO, and PI controller simulation is illustrated in Figure 8. As Figure 8a shows, the motor initially starts at a speed of 0 rpm and gradually increases to 1500 rpm by stepped periods of 0.38 s and 0.4 to 1 s of the settling period. After that the speed of motor decreased to 900 rpm. Figure 8b shows that the motor initially starts at a speed of 0 rpm and gradually increases in speed by stepped periods of 0.37 s settling period is 0.37 to 1 s. After that the speed of motor decreased to 900 rpm in the MFO technique. Figure 8c shows that the motor initially starts at a speed of 0 rpm and gradually increases inspeed by stepped periods of 0.35 sand 0.35 to 1 s of settling period in PI controller. After that the speed of motor decreased to 900 rpm. The comparison between Torque and time of the proposed, MFO, and PI controller simulation is illustrated in Figure 8. Figure 8d shows the motor torque is kept at constant. But the time will be varied from0 to 0.42 s in the proposed method. Figure 8e shows that the time variation in the motor in the MFO method is 0 to 0.38 s due to the constant torque condition. Figure 8f shows that the time variation in the motor in PI controller is 0 to 0.37 s due to the constant torque condition.
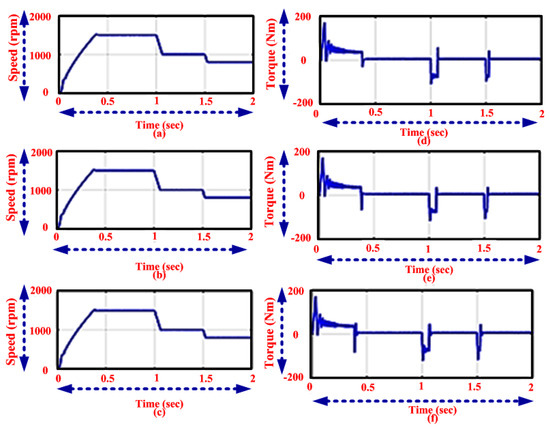
Figure 8.
Analysis of Speed using the (a) proposed, (b) MFO method, and (c) PI controller and Torque using the (d) proposed, (e) MFO method, and (f) PI controller.
Figure 9 shows the analysis of capacitor and inductor, current and voltage using the proposed method. Figure 9a–c shows the performance of proposed drive system operates using supply/output inductor/capacitor for power factor correction. The power quality improvement has been realized by the entire range of speed control. Figure 9d,e illustrates the different modes of switch working with optimal voltage/current stress. By increment in time period, DC-link voltage is increased and reached a maximum of 383 V with a time interval of 0.9 to 1.1 s.
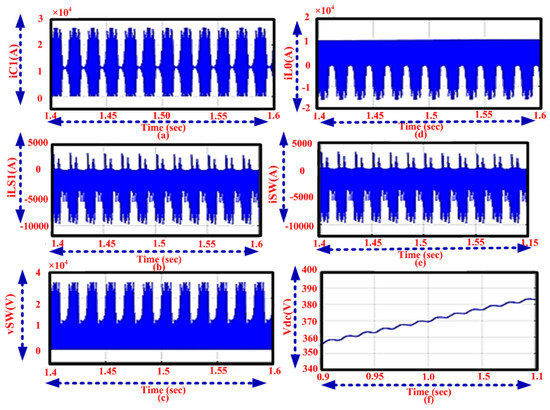
Figure 9.
Analysis of current using the (a) C1, (b) L1, (d) L0, (e) switch and voltage using (c) switch, (f) DC-link.
The comparison between EMF and time of the proposed, MFO and PI controller simulation has been described using Figure 10. It explains the EMF of the proposed technique start run at normally. The value of the EMF value ranges from 1.2 to 1.6 s. Figure 10b shows the EMF of the MFO technique start run at normally. The value of the EMF ranges from 1.1 to 1.6 s. Figure 10c shows the EMF of the PI controller starts the run normally. The value of the EMF value ranges from 0.9 to 1.6 s. The comparison between PWM signals and time of the proposed, MFO, and PI controller simulation is illustrated in Figure 10. Comparing the proposed technique with existing technique, the proposed technique PWM generates full pulse. However in the existing technique, the PWM generates half the pulse in the proposed technique.
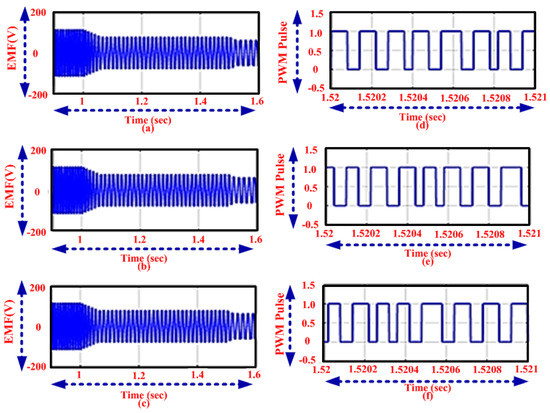
Figure 10.
Analysis of EMF using the (a) proposed (b) MFO method and (c) PI controller and PWM using the (d) proposed (e) MFO method and (f) PI controller.
4.3. Test Case 3: Analysis of Torque Variation with Constant Speed
This section describes about the performance analysis of proposed method based on the minimization of BLDCM torque distortion. The employed strategy is utilized to achieve the power factor control of BLDC motor. The output performance by using the proposed methodologies and other methods are described in Figure 11. While comparing the proposed methods, take the constant rise time with speed ranges from 0 to 0.4 s in 1500 rpm, that is, the speed is constant. The MFO method based speed process takes from 0 to 0.42 s and it needed constant seconds to stabilize the system in Figure 11b, and in the PI controller the speed process is not constant as shown in Figure 11c. However the proposed method describes the nature of braking torque which increases as none zero current for any step. Figure 11 shows that, the analysis of torque is varied in every 0.45 s with employed and classical methodologies have been illustrated. The behavior of speed output of employed controller contains constant rise and settling time of 1500 (rpm) seconds.
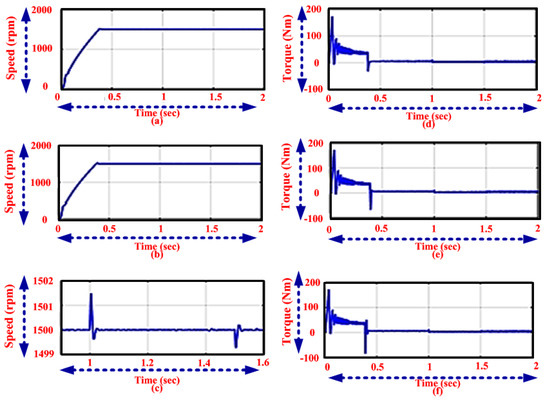
Figure 11.
Analysis of Speed using the (a) proposed (b) MFO method and (c) PI controller and Torque using the (d) proposed (e) MFO method and (f) PI controller.
Figure 12 shows the analysis of capacitor and inductor, current and voltage using the proposed method. Figure 12a–c shows the steady state behavior of proposed drive system which operates using supply inductor and capacitor with output inductor and capacitor for power factor correction. The enhanced quality of power can be obtained by entire speed adjustment range. Different modes of operation of the switch with optimal voltage/current stress has been explained using Figure 12d,e. By increments of time period, DC-link voltage increased and reached maximum of 381 V with a time interval of 0.9 to 1.1 s.
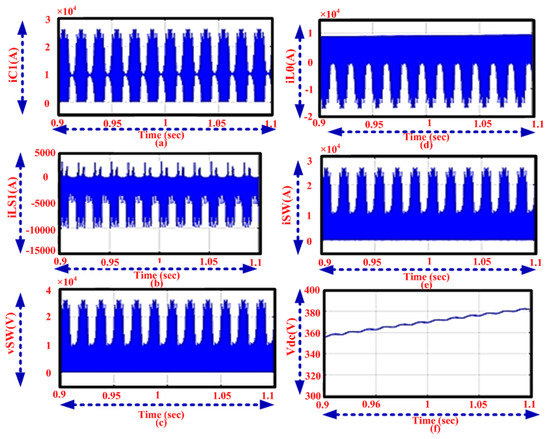
Figure 12.
Analysis of current using the (a) C1, (b) L1, (d) L0, (e) switch and voltage using (c) switch, (f) DC link.
Figure 13 shows the BLDC motor is optimized as the EMF analysis for the proposed method, MFO, PI controller operation. In Figure 13, the EMF of the proposed method and other techniques time are varied for settling process. Here, the proposed method takes the less time settling process with compare to the existing methods like as MFO and PI controller. The analysis of EMF and PWM output performance of the proposed and existing methods has been illustrated in Figure 13.
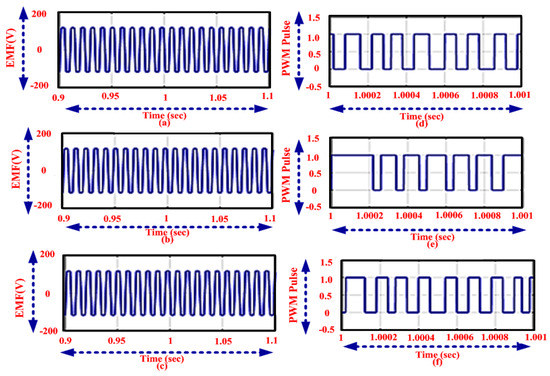
Figure 13.
Analysis of EMF using the (a) proposed (b) MFO method and (c) PI controller and PWM using the (d) proposed (e) MFO method and (f) PI controller.
In the proposed method, the pulse is generated within the seconds when the switch is in the condition and in existing the pulse is generated (rising) from zero and falls at t = 1.00021 s. Figure 14 and Table 1 shows the power factor correction of BLDC motor with three different test cases. While comparing with existing method, the proposed MFFLC method has a power factor of 0.777 in the test case 1, 0.767 in test case 2, and 0.742 in test case 3. Hence, by utilizing the proposed strategy the PFC is identified and there is a decrement in ripple torque by half the amount in the BLDC motor by different speed and torque variations. On the other hand, the existing methods have been analyzed to reduce the torque ripples and provide superiority over the existing methods having more complex computational analysis. Thus, proposed control system enhances the stability and accurateness of the drive scheme and reduces complex computation performance by correcting and adding supplementary components associated with conventional approaches.
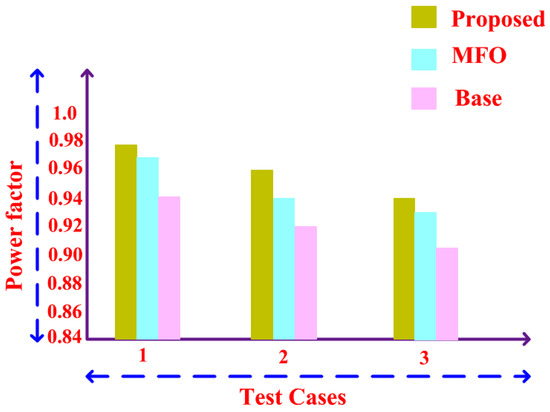
Figure 14.
Performance comparison of power factor with different test cases.

Table 1.
Power factor of BLDC motor with proposed technique.
5. Conclusions
In this paper, the MFFLC strategy was utilized for analyzing the dynamic behavior of the BLDC motor. The proposed strategy based BLDC motor was actualized in MATLAB/Simulink stage. Here, the modeling and controlling process are both done by using the proposed technique. In the modeling part, the BLDC motor was fed through the DBR, DC filter, enhanced PFC based Cuk converter and VSI devices. In the controlling part, the voltage and current is controlled utilizing the proposed control strategy. Thus, an enhanced PI controller is presented for PFC at ac supply, and reducing torque ripple of BLDCM. It was tested with three different test cases of speed and torque conditions. In these conditions, the actual speed, rated speed, torque, current, back EMF, PFC, and the minimization of ripple in torque of BLDC motor is dissected. The proposed controller has been executed by taking account of present controllers such as the MFO method and PI controller. Additionally, the generation of PWM signals minimizes the torque ripples. The viability of employed methods have been discussed with suitable rise/settling periods. From the performance analysis, the suggested method shows better execution over that of the current strategies.
Author Contributions
All authors are involved developing the concept, simulation and experimental validation and to make the article error free technical outcome for the set investigation work.
Acknowledgments
We authors acknowledge the Center for Bioenergy and Green Engineering, Department of Energy Technology, Aalborg University, Esbjerg, Denmark for supporting this research activities for insight technical guidance received.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Priyadarshi, N.; Padmanaban, S.; Mihet-Popa, L.; Blaabjerg, F.; Azam, F. Maximum Power Point Tracking for Brushless DC Motor-Driven Photovoltaic Pumping Systems Using a Hybrid ANFIS-FLOWER Pollination Optimization Algorithm. Energies 2018, 11, 1–16. [Google Scholar] [CrossRef]
- Ibrahim, H.E.A.; Hassan, F.N.; Shomer, A.O. Optimal PID control of a brushless DC motor using PSO and BF techniques. Ain Shams Eng. J. 2014, 5, 371–398. [Google Scholar] [CrossRef]
- Niapour, S.A.KH.M.; Tabarraie, M.; Feyzi, M.R. A new robust speed-sensor less control strategy for high-performance brushless DC motor drives with reduced torque ripple. Control Eng. Pract. 2014, 24, 42–54. [Google Scholar] [CrossRef]
- Masmoudi, M.; Badsi, B.E.; Masmoudi, A. Direct Torque Control of Brushless DC Motor Drives with Improved Reliability. IEEE Trans. Ind. Appl. 2014, 50, 3744–3753. [Google Scholar] [CrossRef]
- Sheng, T.; Wang, X.; Zhang, J.; Deng, Z. Torque Ripple Mitigation for Brushless DC Machine Drive Systems Using One-Cycle Average Torque Control. IEEE Trans. Ind. Electr. 2015, 62, 2114–2122. [Google Scholar] [CrossRef]
- Lu, H.; Zhang, L.; Qu, W. A New Torque Control Method for Torque Ripple Minimization of BLDC Motors with Un-Ideal Back EMF. IEEE Trans. Power Electr. 2008, 23, 750–758. [Google Scholar] [CrossRef]
- Shi, T.; Guo, Y.; Song, P.; Xia, C. A new approach of minimizing commutation torque ripple for brushless DC motor based on DC–DC converter. IEEE Trans. Ind. Electr. 2010, 57, 3483–3490. [Google Scholar] [CrossRef]
- Fang, J.; Zhou, X.; Liu, G. Precise Accelerated Torque Control for Small Inductance Brushless DC Motor. IEEE Trans. Power Electr. 2013, 28, 1400–1412. [Google Scholar] [CrossRef]
- Potnuru, D.; Chandra, K.P.B.; Arasaratnam, I.; Gu, D.W.; Mary, K.A.; Ch, S.B. Derivative-free square-root cubature Kalman filter for non-linear brushless DC motors. IET Electr. Power Appl. 2016, 10, 417–427. [Google Scholar] [CrossRef]
- Fang, J.; Zhou, X.; Liu, G. Instantaneous Torque Control of Small Inductance Brushless DC Motor. IEEE Trans. Power Electr. 2012, 27, 4952–4964. [Google Scholar] [CrossRef]
- Devendra, P.; Kalyan, P.; Mary, K.A.; Ch, S.B. Simulation Approach for Torque Ripple Minimization of BLDC Motor Using Direct Torque Control. Int. J. Adv. Res. Electr. Electron. Instrum. Eng. 2013, 7, 3703–3710. [Google Scholar]
- Shanmugasundram, R.; Zakariah, K.M.; Yadaiah, N. Implementation and Performance Analysis of Digital Controllers for Brushless DC Motor Drives. IEEE/ASME Trans. Mechatron. 2014, 19, 213–224. [Google Scholar] [CrossRef]
- Sathyan, A.; Milivojevic, N.; Lee, Y.J.; Krishnamurthy, M.; Emadi, A. An FPGA-Based Novel Digital PWM Control Scheme for BLDC Motor Drives. IEEE Trans. Ind. Electr. 2007, 56, 3040–3047. [Google Scholar] [CrossRef]
- Lee, B.K.; Kim, T.H.; Ehsani, M. On the feasibility of four-switch three-phase BLDC motor drives for low cost commercial applications: Topology and control. IEEE Trans. Power Electr. 2003, 18, 164–172. [Google Scholar]
- Park, S.J.; Park, H.W.; Lee, M.H.; Harashima, F. A new approach for minimum-torque-ripple maximum-efficiency control of BLDC motor. IEEE Trans. Ind. Electr. 2000, 47, 107–114. [Google Scholar]
- Liu, Y.; Zhu, Z.Q.; Howe, H. Direct Torque Control of Brushless DC Drives with Reduced Torque Ripple. IEEE Trans. Ind. Appl. 2005, 41, 577–608. [Google Scholar] [CrossRef]
- Wang, Y.; Chau, K.T.; Chan, C.C.; Jiang, J.Z. Transient Analysis of a New Outer-Rotor Permanent-Magnet Brushless DC Drive Using Circuit-Field-Torque Coupled Time-Stepping Finite-Element Method. IEEE Trans. Magn. 2002, 38, 1277–1300. [Google Scholar] [CrossRef]
- Chau, K.T.; Chan, C.C.; Liu, C. Overview of Permanent-Magnet Brushless Drives for Electric and Hybrid Electric Vehicles. IEEE Trans. Ind. Electr. 2008, 55, 2246–2257. [Google Scholar] [CrossRef]
- Priyadarshi, N.; Padmanaban, S.; Maroti, P.K.; Sharma, A. An Extensive Practical Investigation of FPSO-Based MPPT for Grid Integrated PV System Under Variable Operating Conditions with Anti-Islanding Protection. IEEE Syst. J. 2018, 1–11. [Google Scholar] [CrossRef]
- Ghanaatian, M.; Lotfifard, S. Control of Flywheel Energy Storage Systems in Presence of Uncertainties. IEEE Trans. Sustain. Energy 2018, 1–9. [Google Scholar] [CrossRef]
- Nag, T.; Santra, S.B.; Chatterjee, A.; Chatterjee, D.; Ganguli, A. Fuzzy logic-based loss minimisation scheme for brushless DC motor drive system. IET Power Electron. 2016, 9, 1581–1589. [Google Scholar] [CrossRef]
- Ziaeinejad, S.; Sangsefidi, Y.; Shoulaie, A. Analysis of Commutation Torque Ripple of BLDC Motors and a Simple Method for Its Reduction. In Proceedings of the 2011 International Conference on Electrical Engineering and Informatics, Bandung, Indonesia, 17–19 July 2011. [Google Scholar]
- Pandey, R.; Singh, B. Improved power quality SEPIC converter fed series resonant inverter for induction heater. In Proceedings of the 1st International Conference on Power Electronics, Intelligent Control and Energy System (ICPEICES), Delhi, India, 4–6 July 2016; pp. 1–6. [Google Scholar]
- Foroozeshfar, R.; Farzanehfard, H.; Adib, E. New single-stage, single-switch, soft-switching three-phase SEPIC and Cuk-type power factor correction converters. IET Power Electr. 2014, 7, 1878–1885. [Google Scholar] [CrossRef]
- Poorali, B.; Adib, E.; Farzanehfard, H. Soft-switching DC–DC Cuk converter operating in discontinuous-capacitor-voltage mode. IET Power Electr. 2017, 10, 1677–1686. [Google Scholar] [CrossRef]
- Buso, S.; Spiazzi, G.; Tagliavia, D. Simplified control technique for high-power-factor flyback Cuk and Sepic rectifiers operating in CCM. IEEE Trans. Ind. Appl. 2000, 36, 1413–1418. [Google Scholar] [CrossRef]
- Jiang, G.; Xia, C.; Chen, W.; Tingna, S.; Li, X.; Cao, Y. Commutation Torque Ripple Suppression Strategy for Brushless DC Motors with a Novel Non-inductive Boost Front End. IEEE Trans. Power Electr. 2017, 33, 4274–4284. [Google Scholar] [CrossRef]
- Nasirian, V.; Karimi, Y.; Davoudi, A.; Zolghadri, M.; Ahmadian, M.; Moayedi, S. Dynamic Model Development and Variable Switching-Frequency Control for DCVM Cúk Converters in PFC Applications. IEEE Trans. Ind. Appl. 2013, 47, 2636–2650. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl. Based Syst. 2015, 87, 228–249. [Google Scholar] [CrossRef]
- Gaston, K.; Bennie, J.; Davies, T.; Hopkins, J. The ecological impacts of nighttime light pollution: A mechanistic appraisal. Biol. Rev. 2013, 88, 712–727. [Google Scholar] [CrossRef] [PubMed]
- Langevelde, F.V.; Ettema, J.; Donners, M.; WallisDeVries, M.F.; Groenendijk, D. Effect of spectral composition of artificial light on the attraction of moths. Biol. Conserv. 2011, 144, 2274–2281. [Google Scholar] [CrossRef]
- Ali, J.A.; Hannan, M.A.; Mohamed, A.; Abdolrasol, M.G. Fuzzy logic speed controller optimization approach for induction motor drive using backtracking search algorithm. Measurement 2016, 78, 49–62. [Google Scholar] [CrossRef]
- Priyadarshi, N.; Padmanaban, S.; Bhaskar, M.S.; Blaabjerg, F.; Sharma, A. A Fuzzy SVPWM Based Inverter Control Realization of Grid Integrated PV-Wind System with FPSO MPPT Algorithm for a Grid-Connected PV/Wind Power Generation System: Hardware Implementation. IET Electr. Power Appl. 2018, 12, 962–971. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).