Fractional Calculus Based FDTD Modeling of Layered Biological Media Exposure to Wideband Electromagnetic Pulses
Abstract
:1. Introduction
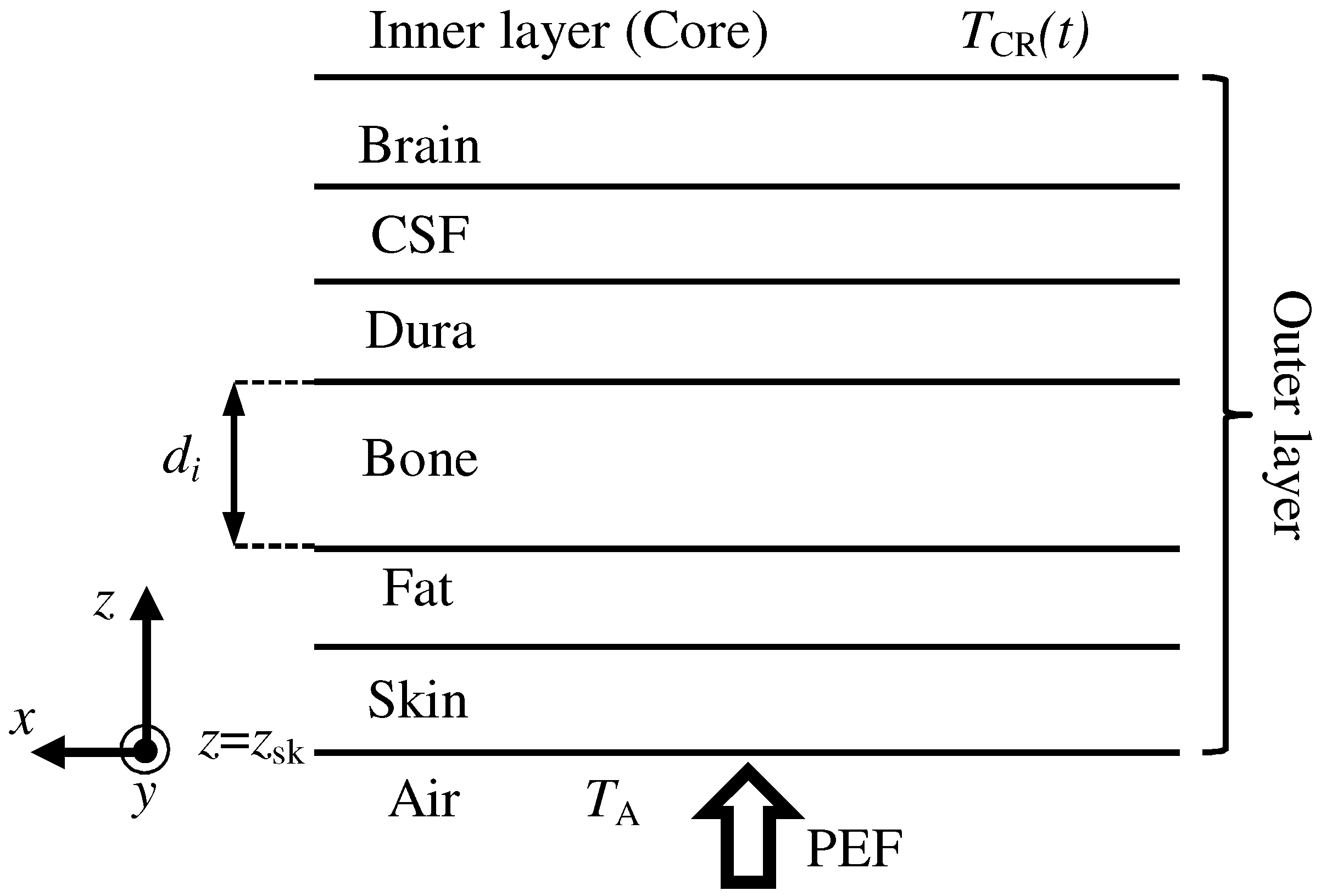
2. Mathematical Formulation
2.1. Complex Permittivity
2.2. Electromagnetic Analysis
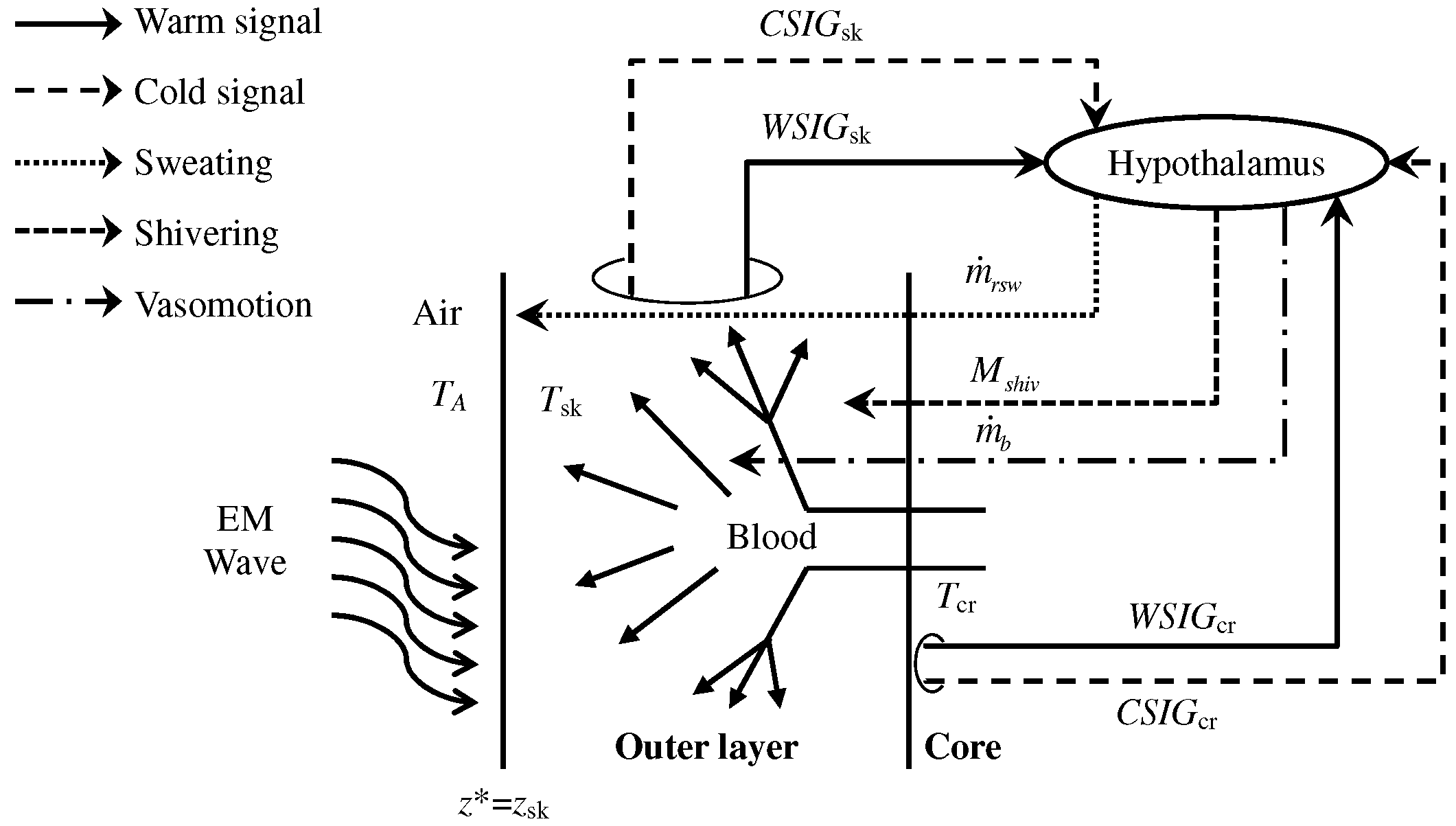
2.3. Bioheat Equation with Thermoregulation
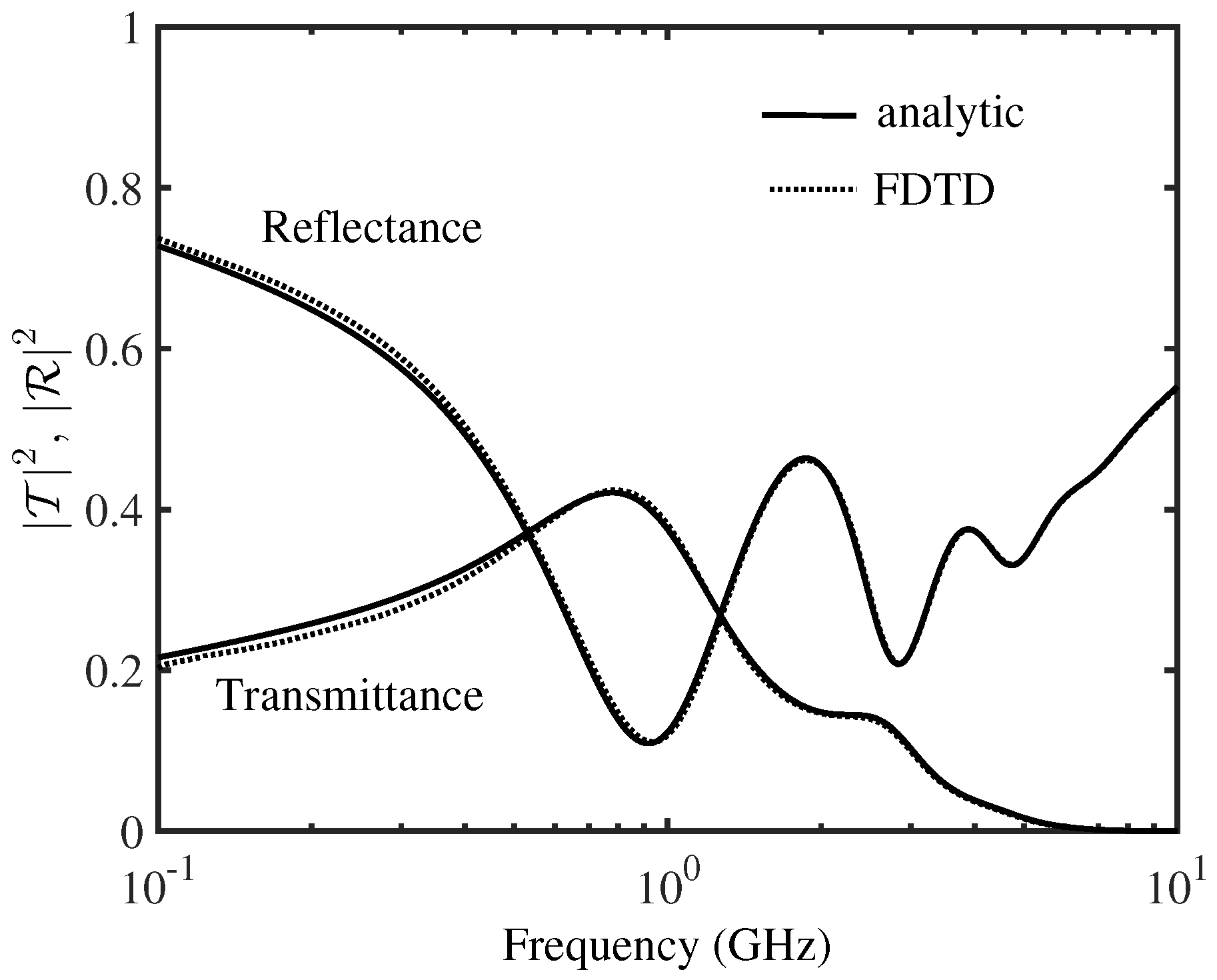
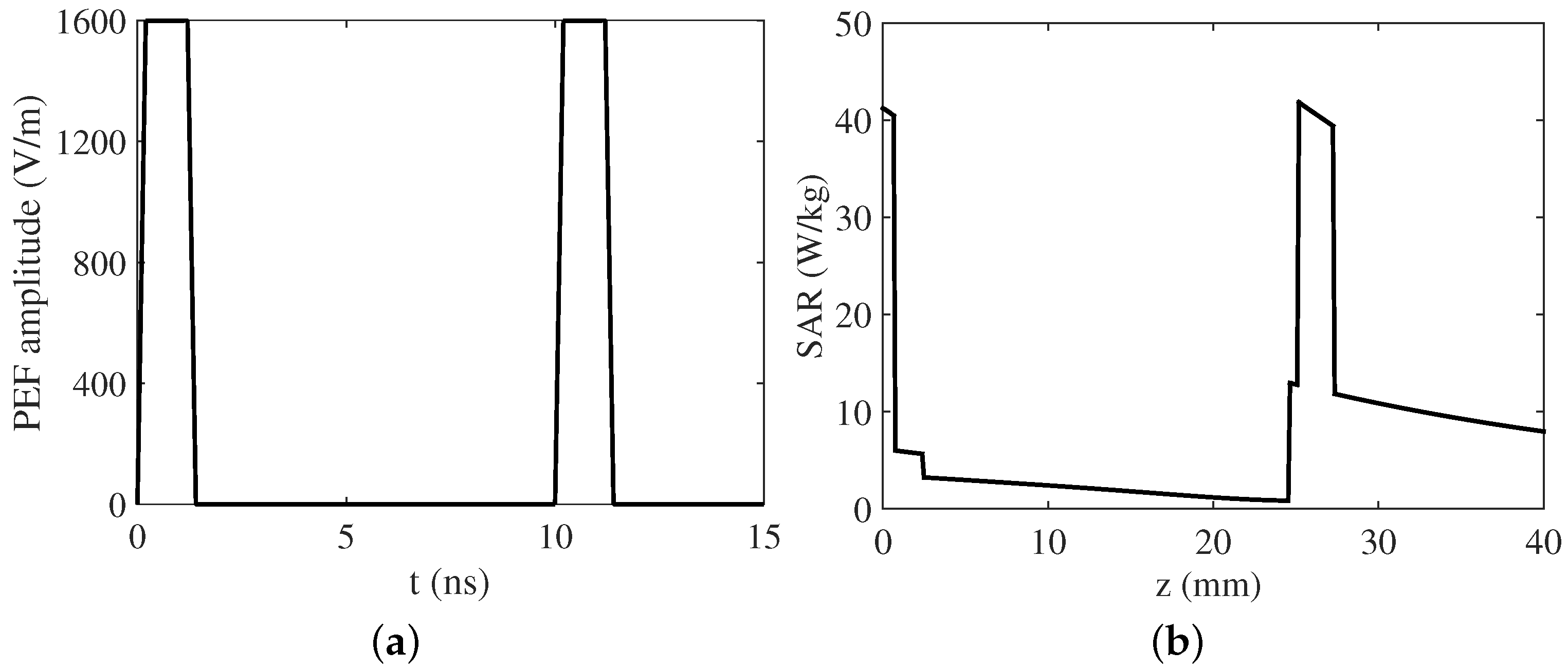
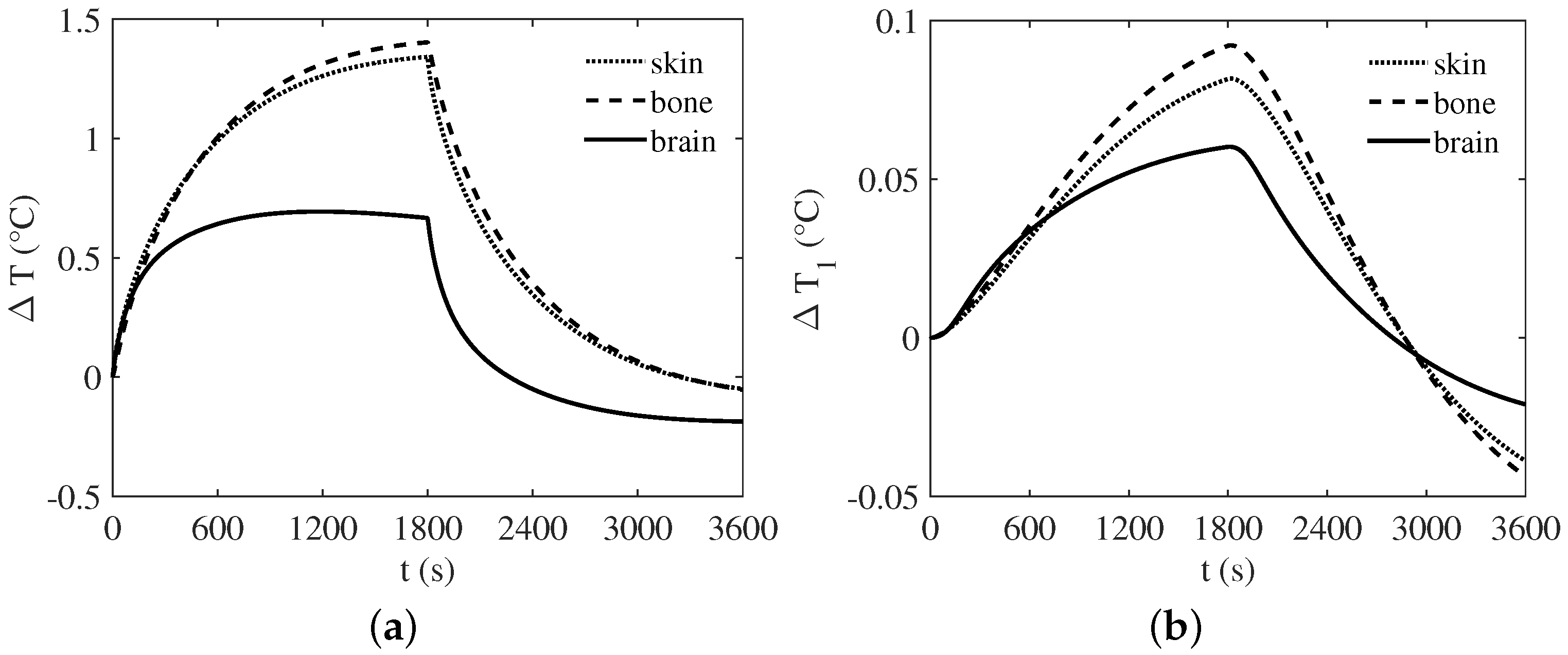
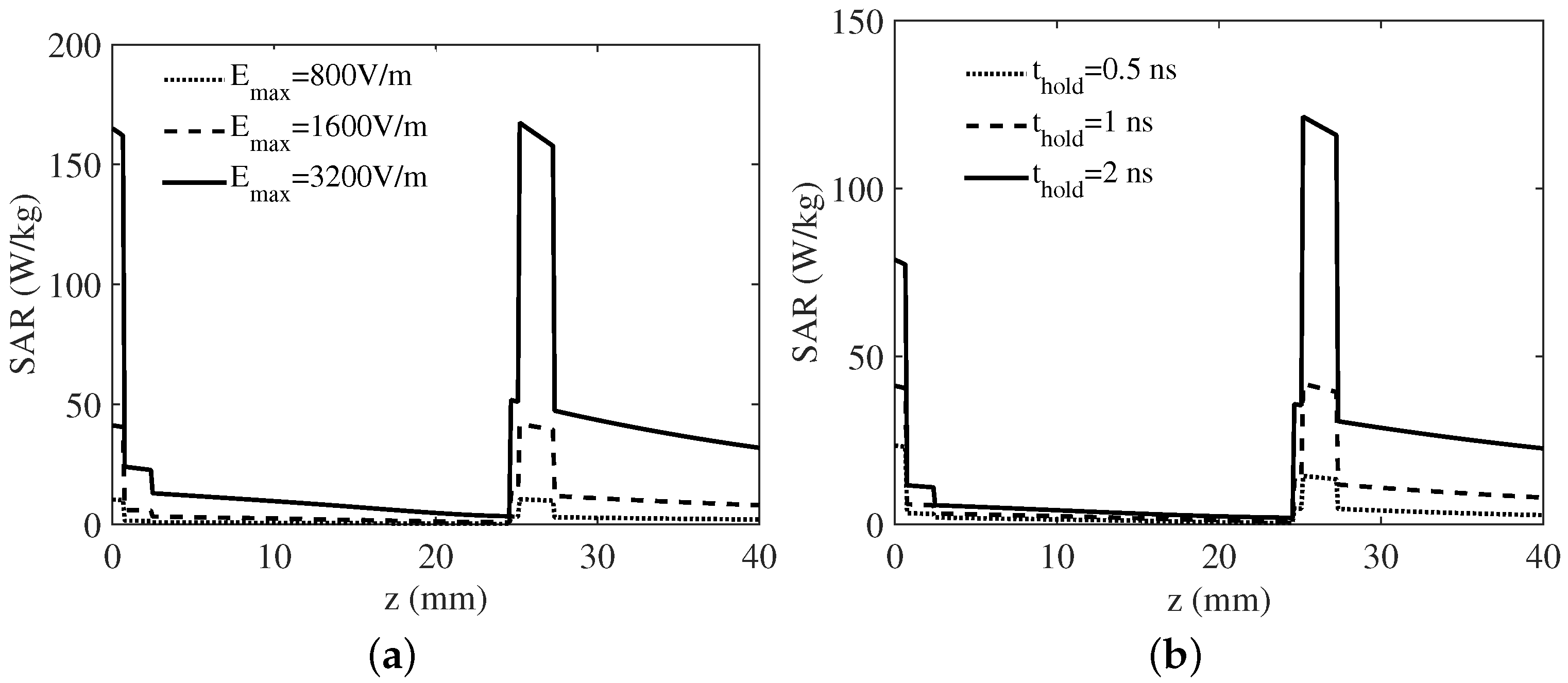
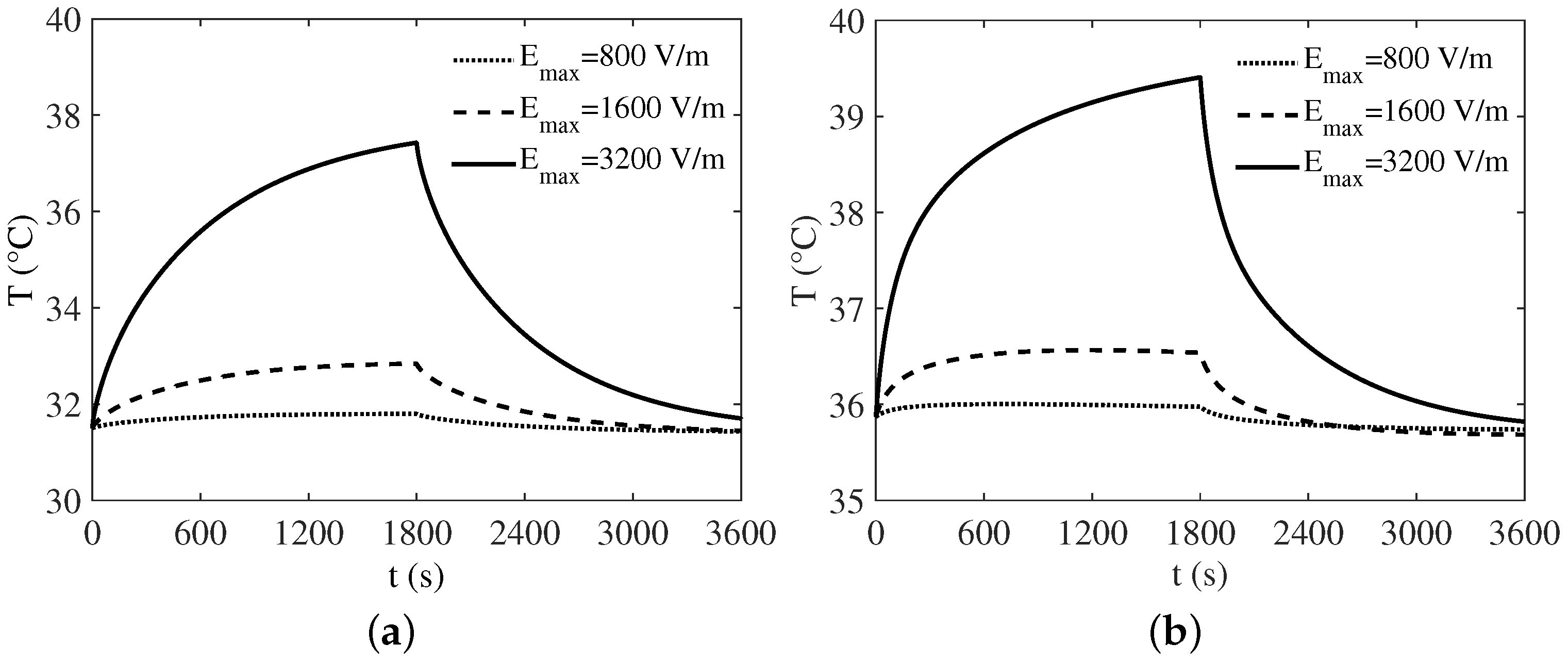
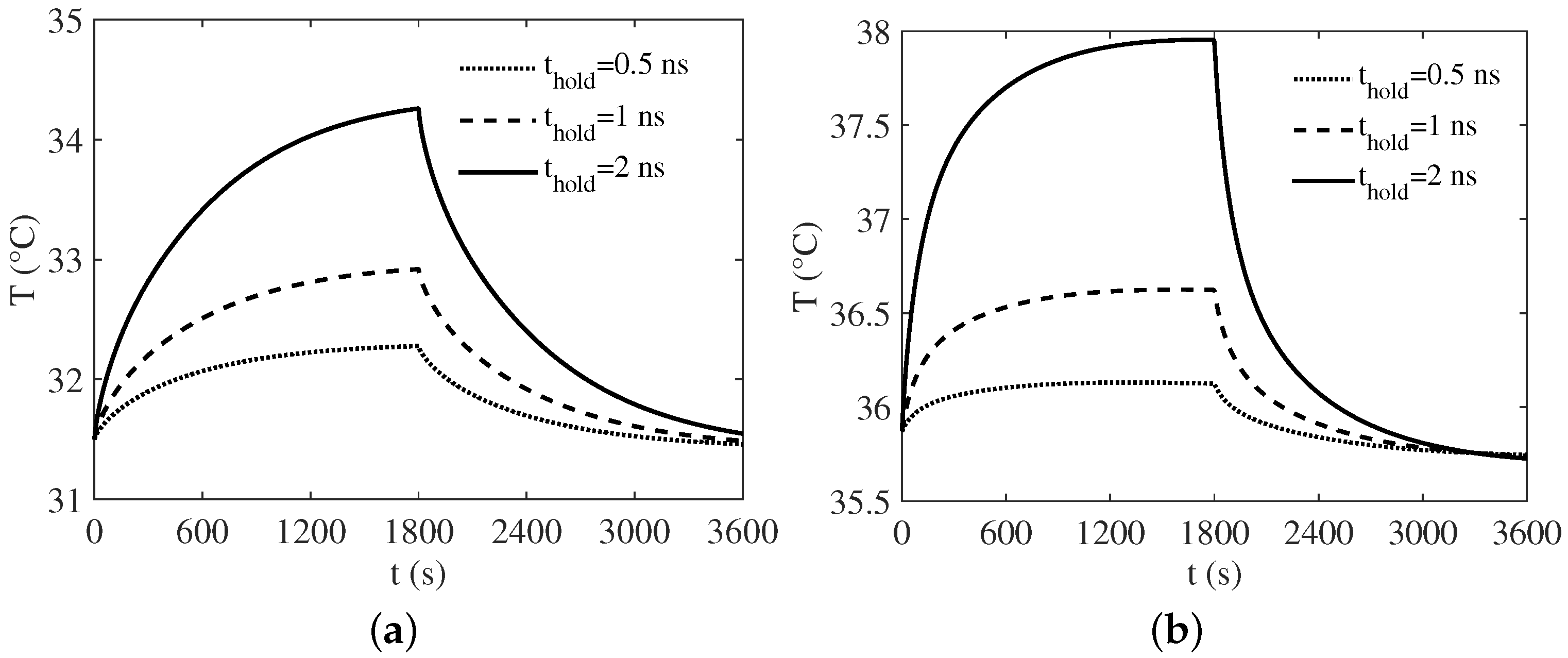
3. Numerical Results
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| FDTD | Finite difference time domain |
| PEF | Pulsed electric field |
| EM | Electromagnetic |
| CSF | Cerebro-spinal fluid |
| SAR | Specific absorption rate |
| HN | Havriliak-Negami |
| UPML | Uniaxial perfectly-matched layer |
| RF | Radio frequency |
| EWQPSO | Enhanced weighted quantum particle swarm optimization |
References
- Chen, W.J.; Shao, W.; Wang, B.Z. ADE-Laguerre-FDTD method for wave propagation in general dispersive materials. IEEE Microw. Wirel. Compon. Lett. 2013, 23, 228–230. [Google Scholar] [CrossRef]
- Maradei, F.; Ke, H.; Hubing, T.H. Full-wave model of frequency-dispersive media with Debye dispersion relation by circuit-oriented FEM. IEEE Trans. Electromagn. Compat. 2009, 51, 312–319. [Google Scholar] [CrossRef]
- Lin, Z.; Fang, Y.; Hu, J.; Zhang, C. On the FDTD formulations for modeling wideband lorentzian media. IEEE Trans. Antennas Propag. 2011, 59, 1338–1356. [Google Scholar] [CrossRef]
- Ramadan, O. General ADI-FDTD formulations for multi-term dispersive electromagnetic applications. IEEE Microw. Wireless Compon. Lett. 2011, 21, 513–515. [Google Scholar] [CrossRef]
- Ha, S.G.; Cho, J.; Choi, J.; Kim, H.; Jung, K.Y. FDTD dispersive modeling of human tissues based on quadratic complex rational function. IEEE Trans. Antennas Propag. 2013, 61, 996–999. [Google Scholar] [CrossRef]
- Ha, M.; Swaminathan, M. A Laguerre-FDTD formulation for frequency-dependent dispersive materials. IEEE Microw. Wirel. Compon. Lett. 2011, 21, 225–227. [Google Scholar]
- Feliziani, M.; Cruciani, S.; Santis, V.D.; Maradei, F. FD2TD analysis of electromagnetic field propagation in multipole Debye media with and without convolution. Prog. Electromagn. Res. B 2012, 42, 181–205. [Google Scholar] [CrossRef]
- Exposure to high frequency electromagnetic fields, biological effects and health consequences (100 Hz–300 GHz). Available online: http://www.icnirp.org/en/publications/article/hf-review-2009.html (accessed on 28 November 2017).
- Baker-Jarvis, J.; Kim, S. The interaction of radio-frequency fields with dielectric materials at macroscopic to mesoscopic scales. J. Res. NIST 2012, 117, 1–60. [Google Scholar] [CrossRef] [PubMed]
- A Rationale for Biologically-Based Exposure Standards for Low-Intensity Electromagnetic Radiation. Available online: http://www.bioinitiative.org/ (accessed on 28 November 2017).
- Weaver, J.C. Electroporation of cells and tissues. IEEE Trans. Plasma Sci. 2000, 88, 28–33. [Google Scholar] [CrossRef]
- Teissi, J.; Escoffre, J.M.; Rols, M.P.; Golzio, M. Time dependence of electric field effects on cell membranes. A review for a critical selection of pulse duration for therapeutical applications. Radiol. Oncol. 2008, 42, 196–206. [Google Scholar] [CrossRef]
- Guo, F.; Yao, C.; Li, C.; Mi, Y.; Wen, Y.; Tang, J. Dependence on pulse duration and number of tumor cell apoptosis by nanosecond pulsed electric fields. IEEE Trans. Dielectr. Electr. Insul. 2013, 20, 1195–1200. [Google Scholar]
- Esser, A.T.; Smith, K.C.; Gowrishankar, T.R.; Weaver, J.C. Towards solid tumor treatment by nanosecond pulsed electric fields. Technol. Cancer Res. Treat. 2009, 8, 289–306. [Google Scholar] [CrossRef] [PubMed]
- Breton, M.; Mir, L.M. Microsecond and nanosecond electric pulses in cancer treatments. Bioelectromagnetics 2012, 33, 106–123. [Google Scholar] [CrossRef] [PubMed]
- Lamberti, P.; Tucci, V.; Romeo, S.; Sannino, A.; Scarfì, M.R.; Zeni, O. nsPEF-induced effects on cell membranes: Use of electrophysical model to optimize experimental design. IEEE Trans. Dielectr. Electr. Insul. 2013, 20, 1231–1238. [Google Scholar] [CrossRef]
- Fernand, F.; Rubinsky, L.; Golberg, A.; Rubinsky, B. Variable electric fields for high throughput electroporation protocol design in curvilinear coordinates. Biotechnol. Bioeng. 2012, 109, 2168–2171. [Google Scholar] [CrossRef] [PubMed]
- Mescia, L.; Chiapperino, M.A.; Bia, P.; Gielis, J.; Caratelli, D. Modeling of Electroporation Induced by Pulsed Electric Fields in Irregularly Shaped Cells. IEEE Trans. Biomed. Eng. in press. [CrossRef]
- Foster, K.; Schwan, H. Dielectric properties of tissues. In Biological Effects of Electromagnetic Fields; Polk, C., Postow, E., Eds.; CRC Press: New York, NY, USA, 1996. [Google Scholar]
- Taflove, A.; Hagness, S. Computational Electrodynamics: The Finite-Difference Time-Domain Method; Artech House: Norwood, MA, USA, 2005. [Google Scholar]
- Caratelli, D.; Massaro, A.; Cingolani, R.; Yarovoy, A. Accurate time domain modeling of reconfigurable antenna sensors foe non-invasive melanoma skin cancer detection. J. Sens. 2012, 12, 635–643. [Google Scholar] [CrossRef]
- Mescia, L.; Bia, P.; Caratelli, D. Fractional Derivative Based FDTD Modeling of Transient Wave Propagation in Havriliak–Negami Media. IEEE Trans. Microw. Theory Tech. 2014, 62, 1920–1929. [Google Scholar] [CrossRef]
- Bia, P.; Caratelli, D.; Mescia, L.; Cicchetti, R.; Maione, G.; Prudenzano, F. A novel FDTD formulation based on fractional derivatives for dispersive Havriliak–Negami media. Signal Process. 2015, 107, 312–318. [Google Scholar] [CrossRef]
- Mescia, L.; Bia, P.; Caratelli, D. Authors’ reply. IEEE Trans. Microw. Theory Tech. 2015, 63, 4191–4193. [Google Scholar] [CrossRef]
- Bia, P.; Mescia, L.; Caratelli, D. Fractional Calculus–based Modelling of Electromagnetic Field Propagation in Arbitrary Biological Tissue. Math. Probl. Eng. 2016, 2016. [Google Scholar] [CrossRef]
- Caratelli, D.; Mescia, L.; Bia, P.; Stukach, O. Fractional-Calculus-Based FDTD Algorithm for Ultrawideband Electromagnetic Characterization of Arbitrary Dispersive Dielectric Materials. IEEE Trans. Antennas Propag. 2016, 64, 3533–3544. [Google Scholar] [CrossRef]
- Zolfaghari, A.; Maerefat, M. A new simplified thermoregulatory bioheat model for evaluating thermal response of the human body to transient environments. Build. Environ. 2010, 45, 2068–2076. [Google Scholar] [CrossRef]
- Drossos, A.; Santomaa, V.; Kuster, N. The Dependence of Electromagnetic Energy Absorption Upon Human Head Tissue Composition in the Frequency Range of 300–3000 MHz. IEEE Trans. Microw. Theory Tech. 2000, 48, 1988–1995. [Google Scholar]
- Havriliak, S.; Negami, S. A complex plane representation of dielectric and mechanical relaxation processes in some polymers. Polymer 1967, 8, 161–210. [Google Scholar] [CrossRef]
- Wolf, M.; Gulich, R.; Lunkenheimer, P.; Loidl, A. Broadband dielectric spectroscopy on human blood. Biochim. Biophys. Acta 2011, 1818, 727–740. [Google Scholar] [CrossRef] [PubMed]
- Sabbah, A.; Dib, N.; Al-Nimr, M. Evaluation of specific absorption rate and temperature elevation in a multi-layered human head model exposed to radio frequency radiation using the finite-difference time domain method. IET Microw. Antennas Propag. 2011, 5, 1073–1080. [Google Scholar] [CrossRef]
- Miklavcic, D.; Pavcelj, N.; Hart, F.X. Electric Properties of Tissues. In Encyclopedia of Biomedical Engineering; Wiley-InterScience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Gabriel, S.; Lau, R.; Gabriel, C. The dielectric properties of biological tissues: II measurements in the frequency range 10 Hz to 20 GHz. Phys. Med. Biol. 1996, 41, 2231–2249. [Google Scholar] [CrossRef] [PubMed]
- Bia, P.; Caratelli, D.; Mescia, L.; Gielis, J. Analysis and synthesis of supershaped dielectric lens antennas. IET Microw. Antennas Propag. 2015, 9, 1497–1504. [Google Scholar] [CrossRef]
- Sanchez-Hernandez, D.A. High Frequency Electromagnetic Dosimetry; Artech House: Norwood, MA, USA, 2009. [Google Scholar]
- Parson, K. Human Thermal Environments; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Du Bois, D.; Du Bois, E.F. A formula to estimate approximate surface area, if height and weight are known. Arch. Intern. Med. 1916, 17, 863–871. [Google Scholar] [CrossRef]
- Developments in Heat Transfer. Available online: https://www.intechopen.com/books/developments-in-heat-transfer (accessed on 28 November 2017).
- Wang, L.K.; Yang, C.T.; Wang, M.S. Advances in Water Resources Management; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Kaynakli, O.; Kilic, M. Investigation of indoor thermal comfort under transient conditions. Build. Environ. 2005, 40, 165–174. [Google Scholar] [CrossRef]
- Yeh, P. Optical Waves in Layered Media; Wiley: New York, NY, USA, 1988. [Google Scholar]
- Wang, J.; Fujiwara, O. FDTD Computation of Temperature Rise in the Human Head for Portable Telephones. IEEE Trans. Microw. Theory Tech. 1999, 47, 1528–1534. [Google Scholar] [CrossRef]
| Parameter | Skin | Fat | Bone | Dura | CSF | Brain |
|---|---|---|---|---|---|---|
| 0.93 | 0.92 | 0.91 | 0.88 | 0.92 | 0.93 | |
| 0.92 | 0.91 | 0.70 | 0.81 | 0.99 | 0.99 | |
| 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | |
| 0.87 | 0.85 | 0.99 | 0.97 | 0.85 | 0.79 | |
| 8.02 | 8.34 | 13.79 | 8.02 | 8.03 | 8.01 | |
| 67.68 | 23.98 | 63.96 | 105.85 | 24.71 | 117.25 | |
| 36.94 | 2.35 | 8.18 | 37.89 | 63.23 | 42.93 | |
| 1789.8 | 79.20 | 130 | 1087.4 | 315.09 | 2823.9 | |
| 0 | 0.01 | 0.006 | 0.5 | 2 | 0.02 | |
| 4 | 2.5 | 2.5 | 4 | 4 | 4 | |
| 0.7 | 1.6 | 20.5 | 0.5 | 2 | ∞ |
| Medium | ||||
|---|---|---|---|---|
| Skin | 1100 | 3600 | 0.42 | 0.0025 |
| Fat | 920 | 3000 | 0.25 | 0.0005 |
| Bone | 1850 | 3100 | 0.39 | 0.0005 |
| Dura | 1050 | 3600 | 0.5 | 0.0003 |
| CSF | 1060 | 4000 | 0.62 | 0 |
| Brain | 1030 | 3650 | 0.535 | 0.011 |
| Blood | 937 | 3889 | - | - |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mescia, L.; Bia, P.; Chiapperino, M.A.; Caratelli, D. Fractional Calculus Based FDTD Modeling of Layered Biological Media Exposure to Wideband Electromagnetic Pulses. Electronics 2017, 6, 106. https://doi.org/10.3390/electronics6040106
Mescia L, Bia P, Chiapperino MA, Caratelli D. Fractional Calculus Based FDTD Modeling of Layered Biological Media Exposure to Wideband Electromagnetic Pulses. Electronics. 2017; 6(4):106. https://doi.org/10.3390/electronics6040106
Chicago/Turabian StyleMescia, Luciano, Pietro Bia, Michele Alessandro Chiapperino, and Diego Caratelli. 2017. "Fractional Calculus Based FDTD Modeling of Layered Biological Media Exposure to Wideband Electromagnetic Pulses" Electronics 6, no. 4: 106. https://doi.org/10.3390/electronics6040106
APA StyleMescia, L., Bia, P., Chiapperino, M. A., & Caratelli, D. (2017). Fractional Calculus Based FDTD Modeling of Layered Biological Media Exposure to Wideband Electromagnetic Pulses. Electronics, 6(4), 106. https://doi.org/10.3390/electronics6040106







