1. Introduction
With the development of modern mobile devices and increase in user demand for a wide range of applications such as education, communication, navigation and entertainment; the need for cellular data has grown exponentially, which results in a significant spectrum shortage of current cellular networks. It is estimated that by the year of 2020, 130 exabits (
of cellular data will be required, [
1,
2,
3]. Conventional cellular spectrum below 3 GHz is experiencing severe shortage, and cannot keep up with this exponential traffic growth. Therefore, the need for new technology to provide extensive bandwidth, and thus significantly increase the throughput of cellular networks has brought millimeter wave (mmWave) communications into the context as one of the contenders for the fifth generation (5G) wireless networks. With orders of magnitude more available spectrum in the mmWave band than current cellular allocations, [
4], mmWave communications technology has the potential to achieve multiple gigabit-per-second data rates to support a wide range of services such as ultra-high definition video (UHDV) and virtual reality [
5,
6,
7]. However, there are a number of technical challenges for mmWave communications; such as high propagation loss even in free space according to Friis’ law [
8]. Reflection and penetration characteristics of common building materials as well as diffraction effects are also factors that greatly impact the propagation of mmWave signals [
9]. It was shown in [
10] that the penetration loss of 9.6, 28.8 and 57.6 GHz waves increased by 25 dB to 50 dB when the glass surface was metal coated. The research in [
10,
11] also shows that no signal was detected through brick pillars throughout the mmWave signals, yet signals through a hollow plasterboard wall resulted in a penetration loss ranging between 5.4 dB and 8.1 dB. To overcome these loss mechanisms, higher gain, i.e., directional antennas, are necessary. Since the wavelengths at the mmWave frequencies can be orders of magnitude smaller than the frequency band of the current state of art, and thanks to the advances in materials and low-power CMOS RF circuitry, it is possible to pack a large number of antenna elements in compact transceiver systems [
12,
13,
14,
15,
16,
17,
18]. Therefore, it is feasible to integrate highly directional antennas in base station (BS) and user equipment (UE) systems to enhance the quality of mmWave communications.
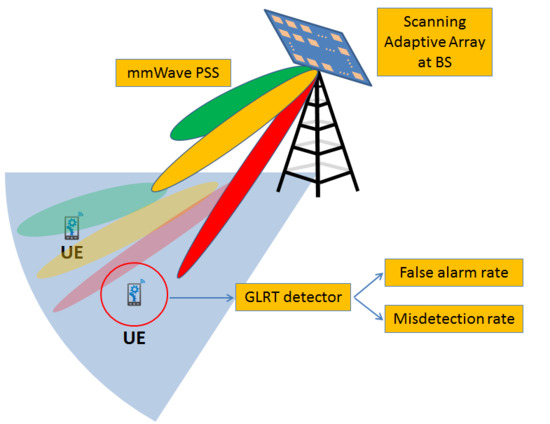
While the use of highly directional antennas in mmWave cellular networks addresses the loss issues, another challenge emerges due to the complication of the initial cell search procedure [
19,
20], i.e., a mobile device needs to discover an available base station and establish initial communications. Although current cellular networks such as 3GPP LTE/4G have been using beamforming techniques to enhance the quality of communication links, they are still based on using omnidirectional transmissions or transmissions with fixed antenna patterns for the initial cell search process [
20,
21]. This is not the case in mmWave cellular networks because it is essential to use high gain antennas for propagation loss compensation. Although the use of omnidirectional antennas simplifies the cell search problem, they may default to establishing connection only with the closest UEs even though communications may be feasible with other UEs that may reside further away using a high-gain directional antenna. Such UEs cannot be detected by the omni-directional antenna.
The initial cell search problem was recently investigated in [
21], where the authors established a Generalized Likelihood Ratio Test (GLRT) at the mmWave receiver to assess the performance of signal detection. Although the idea of using GLRT for signal detection is not new for traditional cellular networks, it is novel in [
21] that the authors applied the concept of GLRT in a mmWave network where directional array at BS was used to scan for the coverage region at random directions in time. The authors in [
21] showed that omnidirectional transmissions from the BS generally have better performance than random directional scanning over a given scan time. In [
22,
23,
24], the authors proposed and analyzed the performance of the initial access problem using an exhaustive method (the BS performs a brute-force sequential beam searching) and an iterative method (minimize the region of interest in the first stage and focus only on this region in the second stage). It was shown in these works that each method has its own advantages and drawbacks. While iterative techniques require a shorter search time, they may present higher misdetection rates. When a multipath channel is considered in a dense, urban environment, the exhaustive approach is more preferable since it offers lower misdetection rates.
This paper further investigates the initial cell search problem based on the iterative search method proposed in [
21] to see whether we can exploit directional transmissions with a carefully designed scanning pattern, instead of random scanning, to enhance the cell search process. We show that for a given coverage area, it is possible to design a scanning procedure for the BS using a set of directional antenna patterns so that the misdetection rate is significantly reduced compared to omnidirectional transmissions or random scanning. It should be noted that the previous work in [
22,
23,
24] is implemented only in angular spaces, which simplified the beamforming procedure. In this paper, we consider the 3D transmission scheme where beamforming of BS and UE are created based on both azimuth and elevation angles. Furthermore, to maximize the performance of the search process, we propose the use of an adaptive array antenna to reduce the total scanning time while keeping the coverage capability the same and misdetection rate low. We believe that our transmission scheme is comprehensive; therefore, it can be applied to practical problems. The mobile terminals are assumed to detect the signals from the base station based on a GLRT detector, which will be discussed in detail in
Section 3. Furthermore, we consider the 28 GHz band, which is also referred to as the Local Multipoint Distribution Service (LMDS) band in the USA, and operates under FCC Part 101 rules for Fixed Microwave Services [
25]. Compared with other bands, the signals at 28 GHz band suffer from lower rain attenuation (0.18–0.9 dB/200 m) and oxygen absorption (0.04 dB/200 m) [
26].
The remainder of the paper is organized as follows.
Section 2 introduces the fundamentals of the initial cell search problem in traditional cellular networks, and our proposed framework.
Section 3 presents the formulations for GLRT detection.
Section 4 applies the GLRT detector to analyze the performance of the cell search procedure with omnidirectional antenna at BS.
Section 5 describes the proposed scanning scheme, and evaluates its performance under line-of-sight (LOS) channels assumption.
Section 6 discusses the applicability of the proposed algorithm to non-line-of-sight (NLOS) channels assumption.
Section 7 presents conclusions of the paper.
4. Scanning Algorithm Using Omnidirectional Antenna at BS
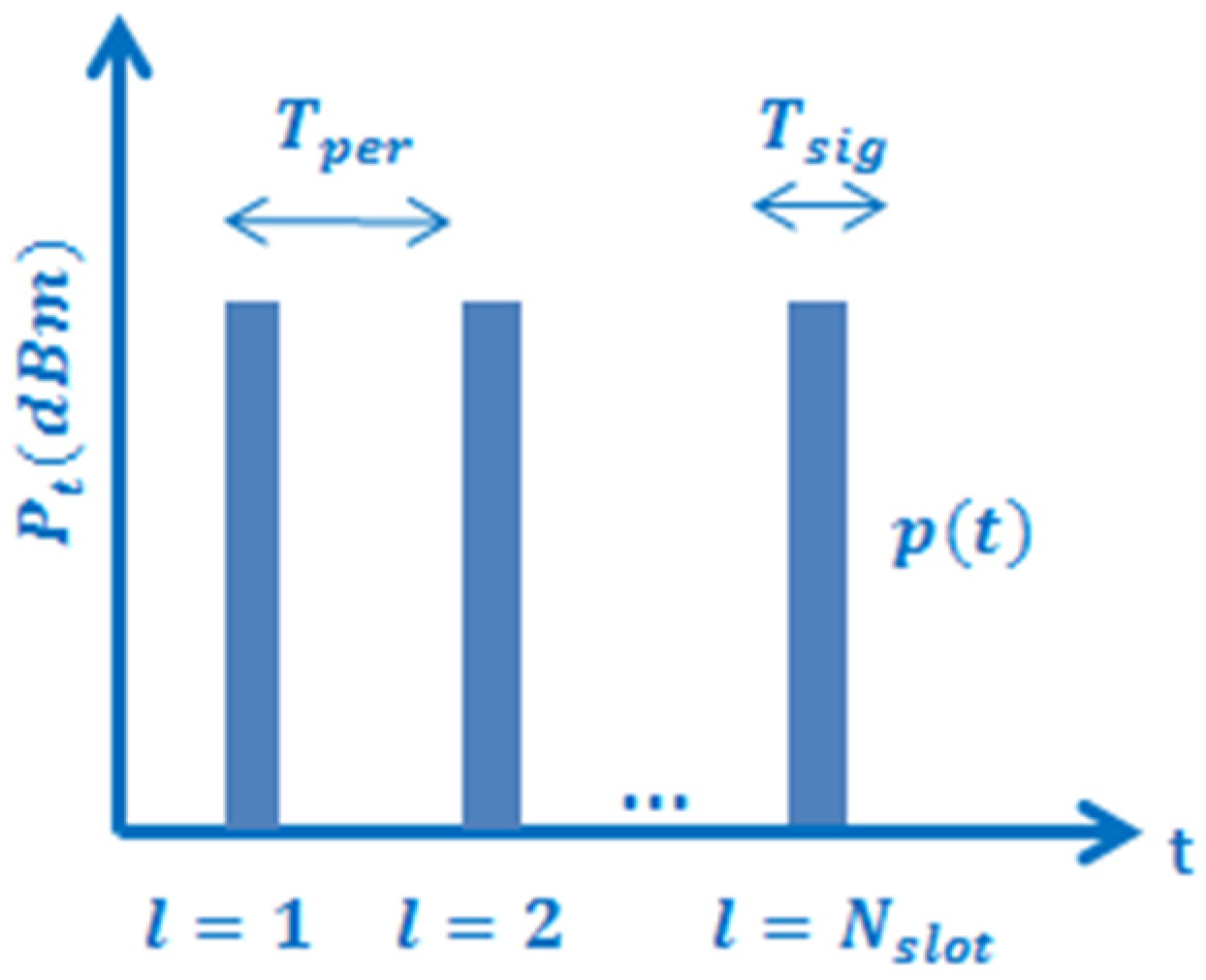
We first assess the performance of the GLRT detector for the case when an omnidirectional antenna is used at the BS. The parameters used for the PSS signal transmission are specified in
Table 1. The value of
is chosen similar to that of current cellular networks while
is chosen to keep a low total PSS overhead
which is slightly higher than the overhead values of current systems (1.5%). The values of false alarm probability used to estimate the threshold level of the GLRT detector are
, which are similar to that used in [
21]. As will be shown in the next section, the choice of
is necessary so that the BS antenna can cover the region of interest without any gaps. If
, the BS will likely not be able to cover the region, resulting in instability of the probability of misdetection. On the other hand,
is not necessary and leads to a waste of transmitted power and resources.
The SNR of the PSS signal is defined as
where
is the received power at the receiver,
is the duration of the signal, and
is the noise power. It should be noted that the transmitted power for all BS antenna configurations (omni, 4 × 4, 8 × 8, etc.) are kept at the same level; i.e.,
.
We will initially focus on LOS channels to present different scanning algorithms. For LOS channels, the omnidirectional path loss coefficient is calculated based on the Friis’ transmission principles as in Equation (13). Later on in
Section 6, we will investigate the impacts of more realistic scenarios for NLOS channels.
where
is the distance between TX and RX, for LOS channels
, and the lognormal shadowing
with
.
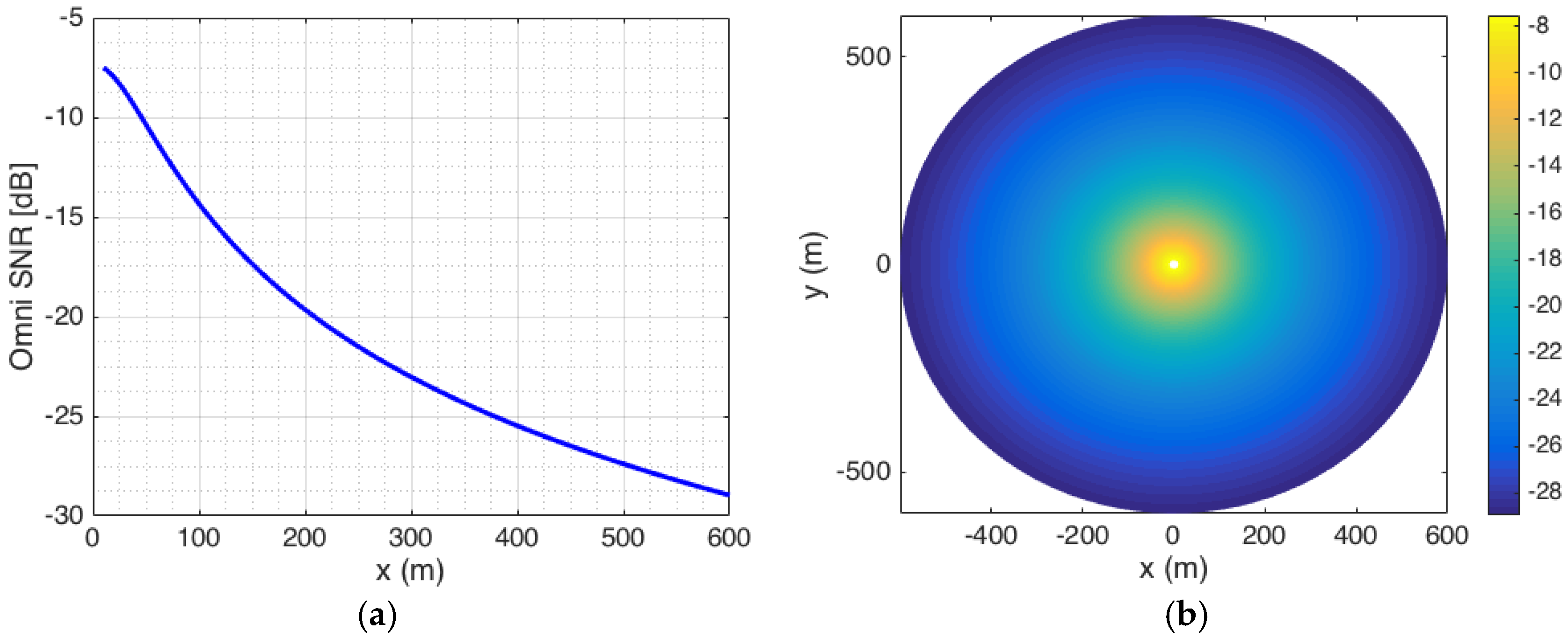
Figure 3 shows the SNR levels for an omnidirectional transmitter as a function of distance between the BS and the UE in a LOS setting. As shown, for omnidirectional TX and 4 × 4 directional RX antennas with a noise power as specified in
Table 1, the value of SNR levels at RX is −8 dB when RX is located on radial contours 10 m away from TX, while the value drops to −28 dB as RX is located on radial contours 600 m away from the TX.
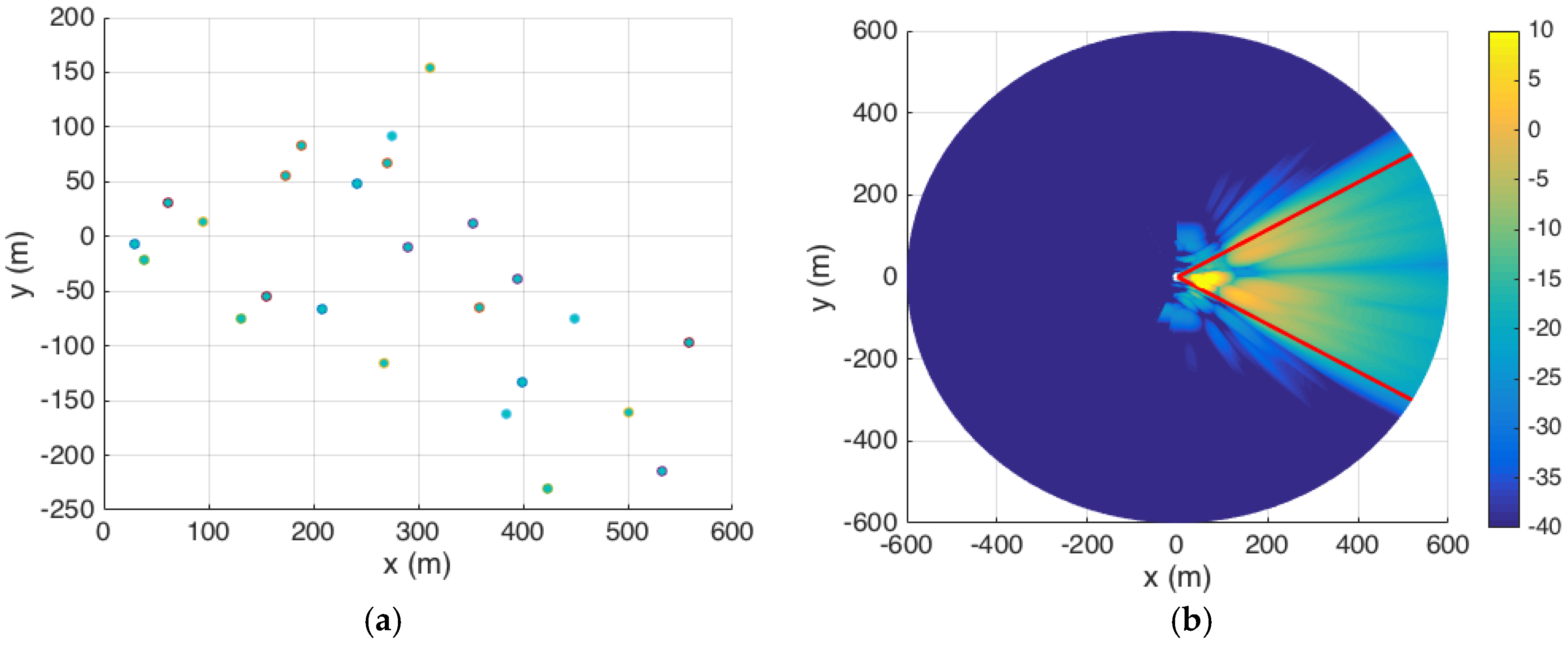
To demonstrate the concept, we focus on one facet of the hexagonal BS antenna structure in
Figure 1, corresponding to a 60°-segment of cell. The performance for the other cell segments is similar assuming that: (i) the same antenna arrays will be employed in all cell segments, and (ii) channel characteristics are uniform across the coverage area. To assess the GLRT detector at different SNR levels, 46 different 4 × 4 directional UEs are distributed randomly over different radial contours corresponding to different PSS SNR contours. Applying Equations (5)–(11), the misdetection probability of the cell search procedure at each of the 46 distributed UEs with an omnidirectional antenna at BS is calculated as shown in
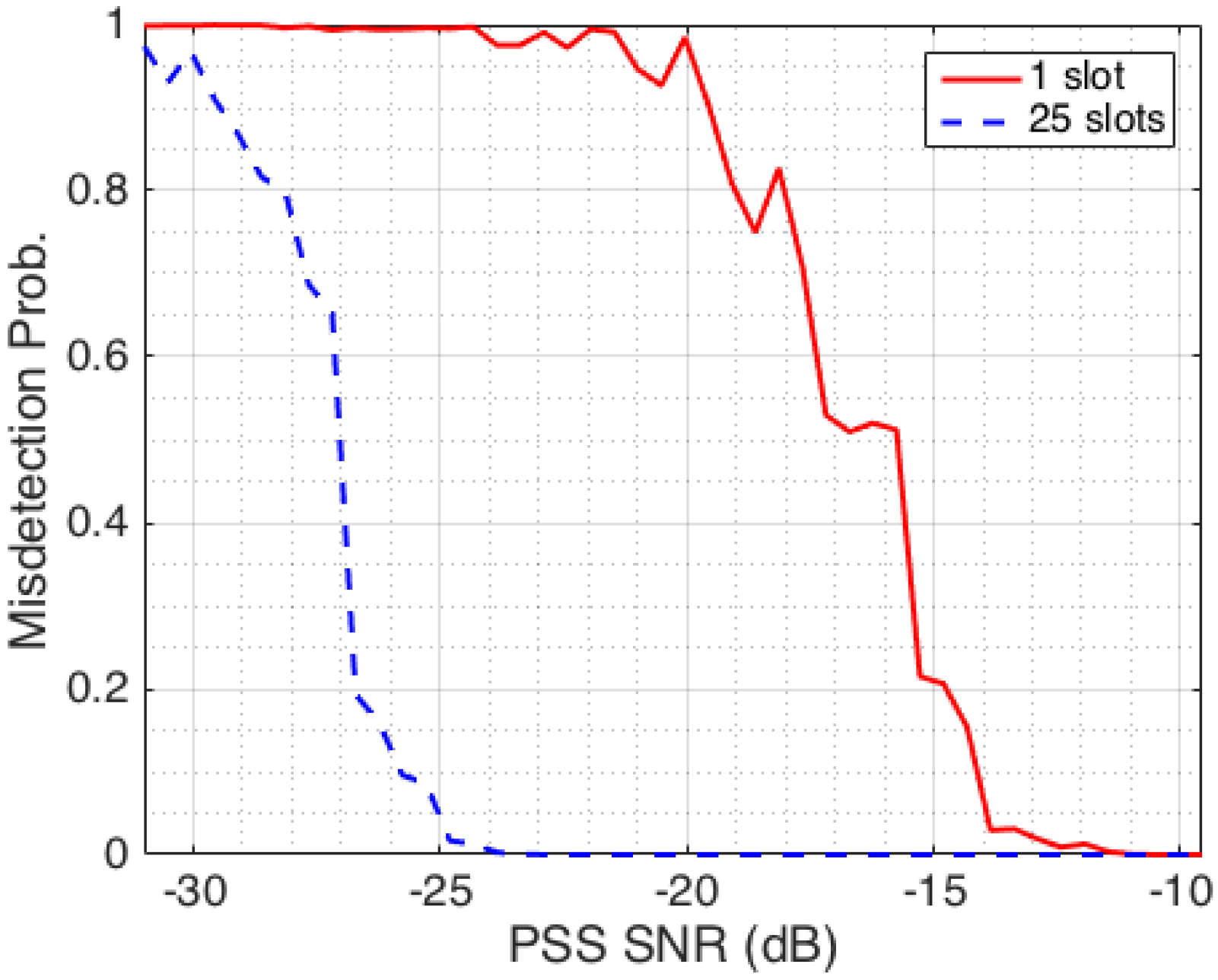
Figure 4.
The solid red line in
Figure 4 shows that with the use of an omnidirectional antenna at BS, the detection of PSS signals at UEs does not perform well at low SNR conditions, and the performance depends on the search time, that is, the duration that an UE receives the signal. With the use of only one time slot within 5 ms of search time, only the UEs within the −13 dB SNR contour can detect the PSS signal with a high probability. In the SNR range of −25 to −13 dB, the UEs can still detect the PSS signals, but the misdetection rate sharply increases as a function of SNR levels. For UEs located where the SNR is lower than −25 dB, it becomes almost impossible to detect the PSS signal. Thus, if a UE wants to detect the PSS signal with a low misdetection probability within one timeslot, the SNR at the UEs should be greater than −13 dB. In the case where 25 time slots are used within 125 ms of search time, the misdetection rate improves as observed by the dashed blue line in
Figure 4. The detection is achieved with high probability for UEs beyond the SNR level of −25 dB. As SNR levels decrease from −25 to −32 dB, the misdetection rate increases to almost 1. For UEs at locations with SNR levels lower than −32 dB, the PSS detection becomes impossible.
5. Scanning the Coverage Area with Directional BS Antennas (LOS Channels)
Based on the misdetection probability rates for the omnidirectional antenna in
Figure 4, we realize that to keep the misdetection rate
low for each slot of search time, the SNR level received at the UEs should be at least −13 dB. Directional antennas can be used to compensate for the path loss, and improve the cell search procedure.
Figure 5 demonstrates the concept of using a directional antenna at BS to focus the main beam to a specific location on the ground. We will consider two scanning schemes in this paper: random and deterministic.
Both random scanning and deterministic scanning schemes have been proposed in the past work shown in [
21,
22,
23,
24]. Authors used an 8 × 8 array antenna at BS to scan randomly in [
21]. Exhaustive and iterative searching methods were employed in [
22,
23,
24] to address the cell searching problem deterministically. We employ an adaptive array antenna in our analysis. Depending on our scanning scheme, we choose between three possible configurations: 4 × 4, 8 × 8 and 12 × 12 element arrays.
Table 2 shows the different adaptive array configurations we employ, and their relevant antenna properties.
We will investigate two scenarios as indicated in
Table 3. For the random scanning algorithm, we employ an 8 × 8 element array similar to [
21]. Our deterministic approach utilizes all three configurations as indicated in
Table 2. The specific beam positions for the array configurations are calculated so as to minimize any gaps; i.e., SNR less than −13 dB in the coverage area, for the deterministic algorithm. We will explain in detail the methodology we use in identifying these beam positions in the following subsection. For both random and deterministic algorithms, we first consider a LOS channel. Later on, we demonstrate how the same concepts can be applied to NLOS channels, and the key factors to be considered in adapting these ideas to more realistic NLOS scenarios.
5.1. Random Scanning Algorithm
In the random scan process, an arbitrary location
(both
and
are chosen randomly based on Gaussian distribution) inside the coverage region. The 8 × 8 BS antenna will re-focus its main beam to these random locations for each time slot. The results of the random beam positions and the resulting coverage (assuming a LOS channel) area within the 60° segment of the circle after 25 slots are shown in
Figure 6a,b, respectively. We observe that random scanning does not guarantee a complete coverage, and there are regions with SNR levels less than −13 dB.
5.2. Deterministic Scanning Algorithm
For the deterministic approach, the exhaustive method was shown to be effective in [
22,
23,
24]. While this method presents a low misdetection probability at UEs, it is considered too cumbersome in practice since the BS antenna needs to scan both in angular and radial spaces. In this paper, we propose an optimized deterministic scanning pattern employing directional antennas at the BS. This step will be considered as stage 2 of the iterative method in [
22,
23,
24]. The objective is to use adaptive directional antennas to cover the regions where the omnidirectional transmission suffers from high misdetection rate due to propagation loss. This way, the misdetection rate can be reduced for UEs residing far away from the BS by improving the SNR levels. Furthermore, to maximize the performance of the search process, we propose the use of an adaptive array antenna to reduce the total scanning time while keeping the coverage capability the same and misdetection rate low.
Based on the misdetection probability rates for the omnidirectional antenna in
Figure 4, we realize that to keep the misdetection rate
low for each slot of search time, the SNR level received at the UEs should be at least −13 dB. With the required SNR values, we can calculate the required power
at each receiver based on (12). Therefore, the specific antenna configuration at each time slot is based on the required SNR level at a target area to acquire a low value of
. Furthermore, we assume the BS antenna can only scan in one direction at a time. The BS will then need to scan multiple slots to guarantee good SNR levels anywhere within the segment. The array can be scanned to different directions by applying the necessary phase excitations to the array elements as described in (2) while the transmitted power is fixed.
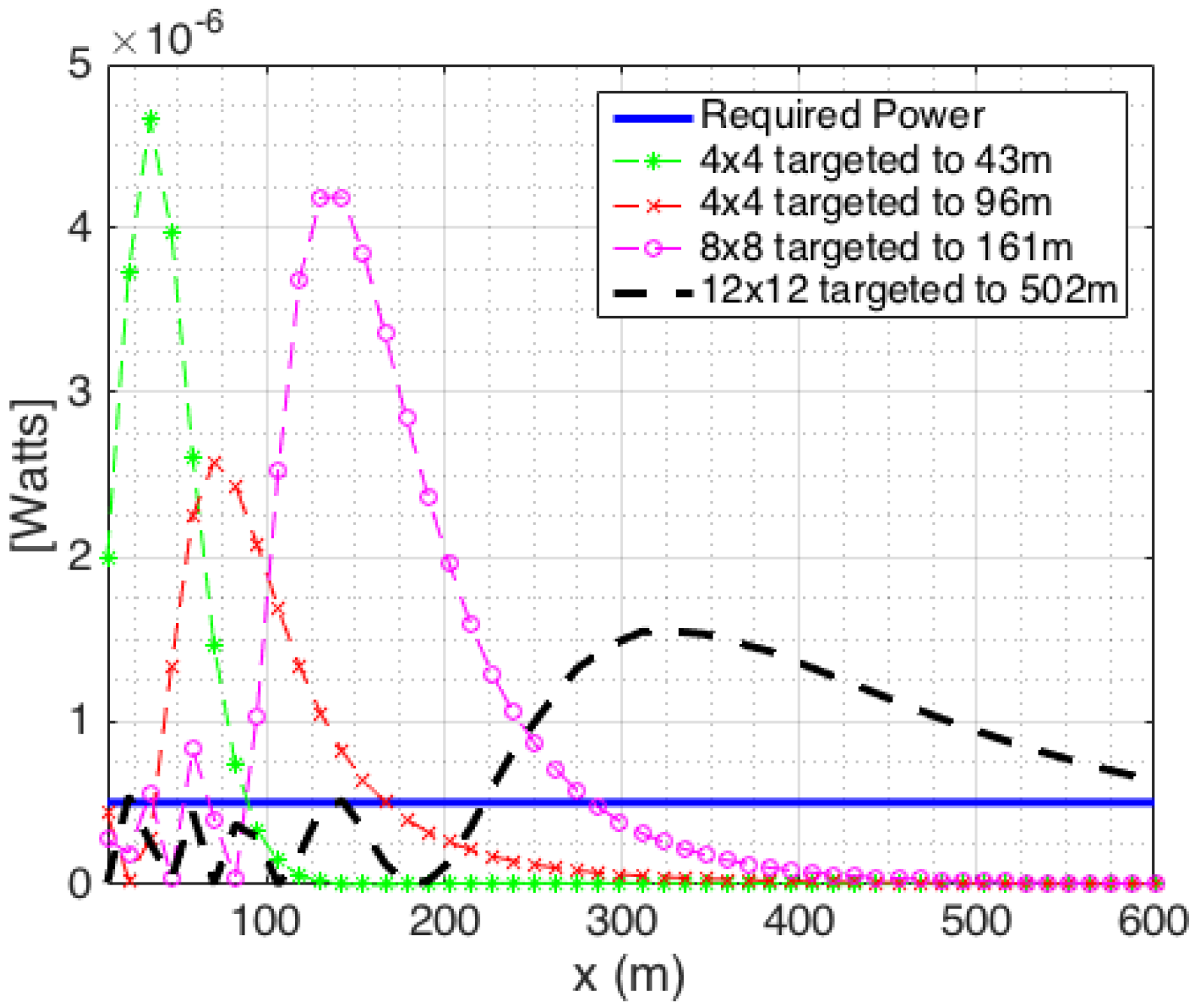
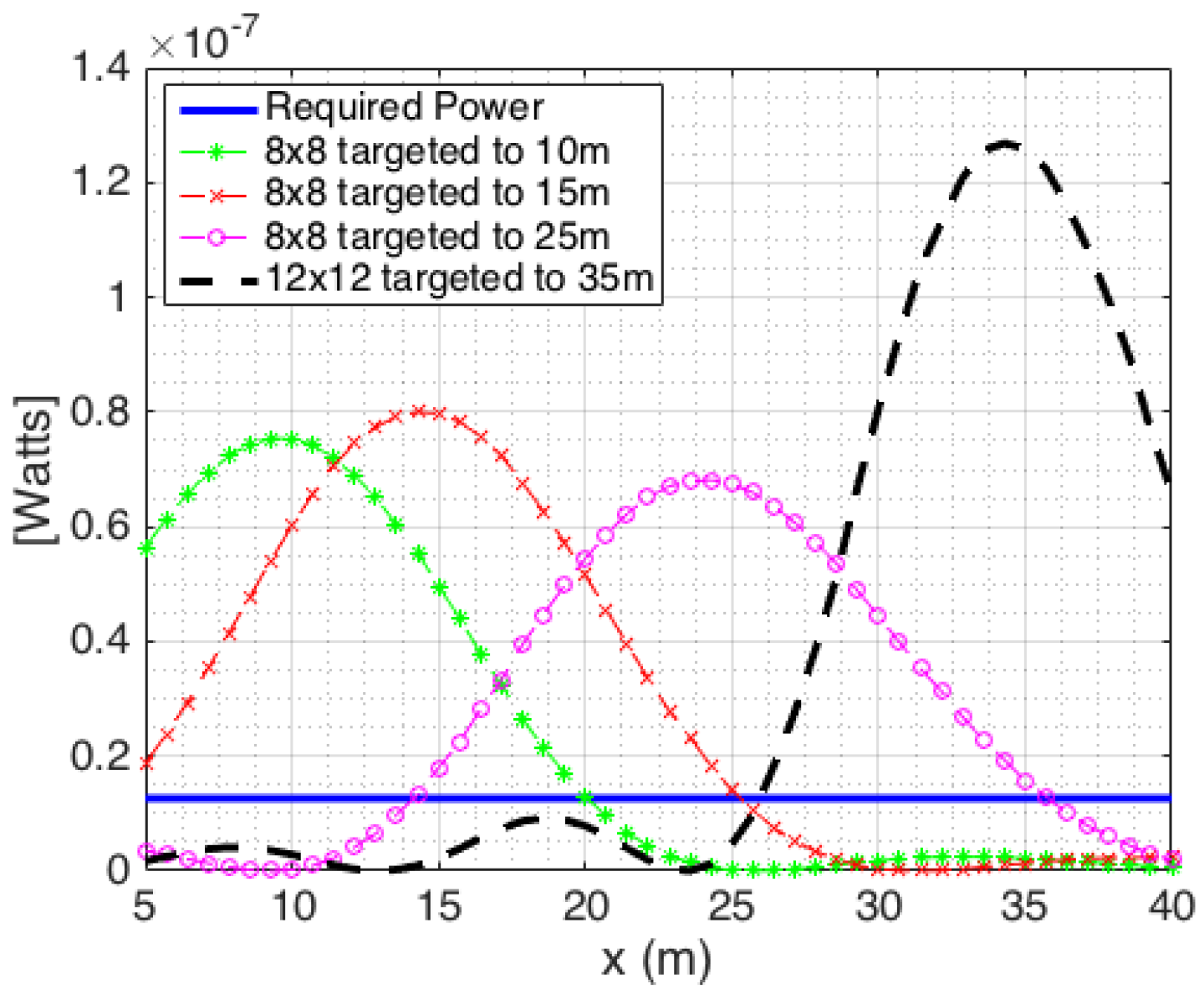
Figure 7 shows the received power at UEs distributed along the
x-axis. It is observed that with the appropriate array configurations directed towards points on the
x-axis at 43 m, 96 m, 161 m and 502 m, all UEs acquire the required power levels for high probability of detection. From the choices in
Figure 7, the BS antenna is then scanned azimuthally to fully cover the area of interest. This is where the total of
is equal to 25.
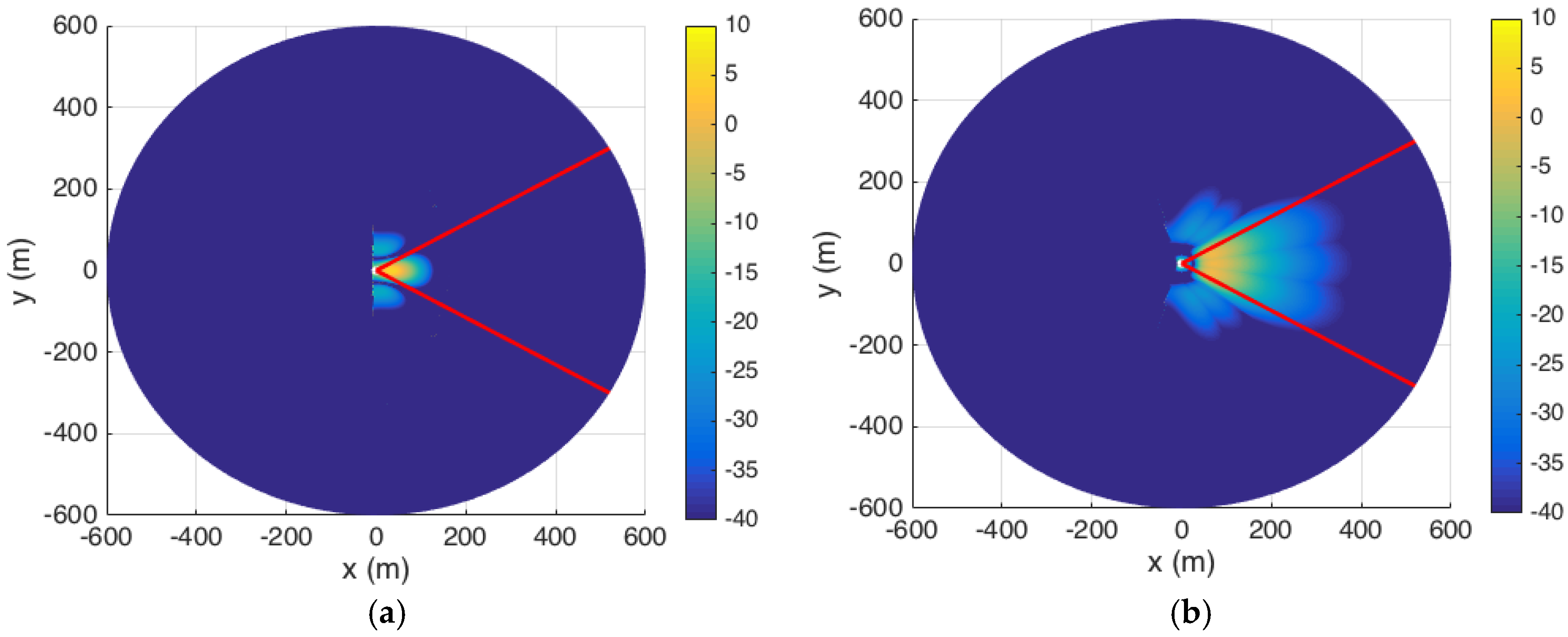
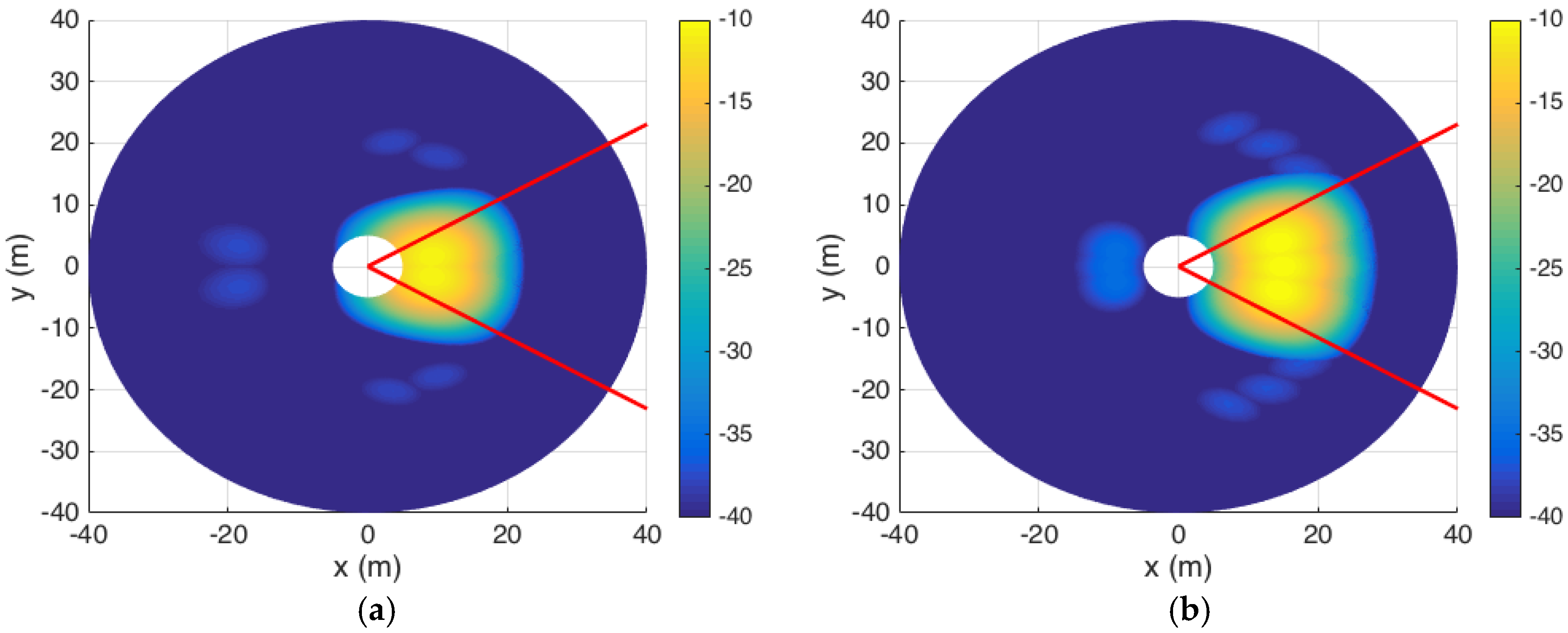
Figure 8a shows the color mapping of SNR levels after scanning for one slot within 43 m. For all of the UEs located within 43 m of BS, they will acquire a low misdetection rate since the powers received at these UEs are higher than the required power.
Figure 8b shows the color mapping of the next three slots as the BS scans to the 96 m contour using a 4 × 4 array antenna. As observed, three beams with an azimuthal scan step of
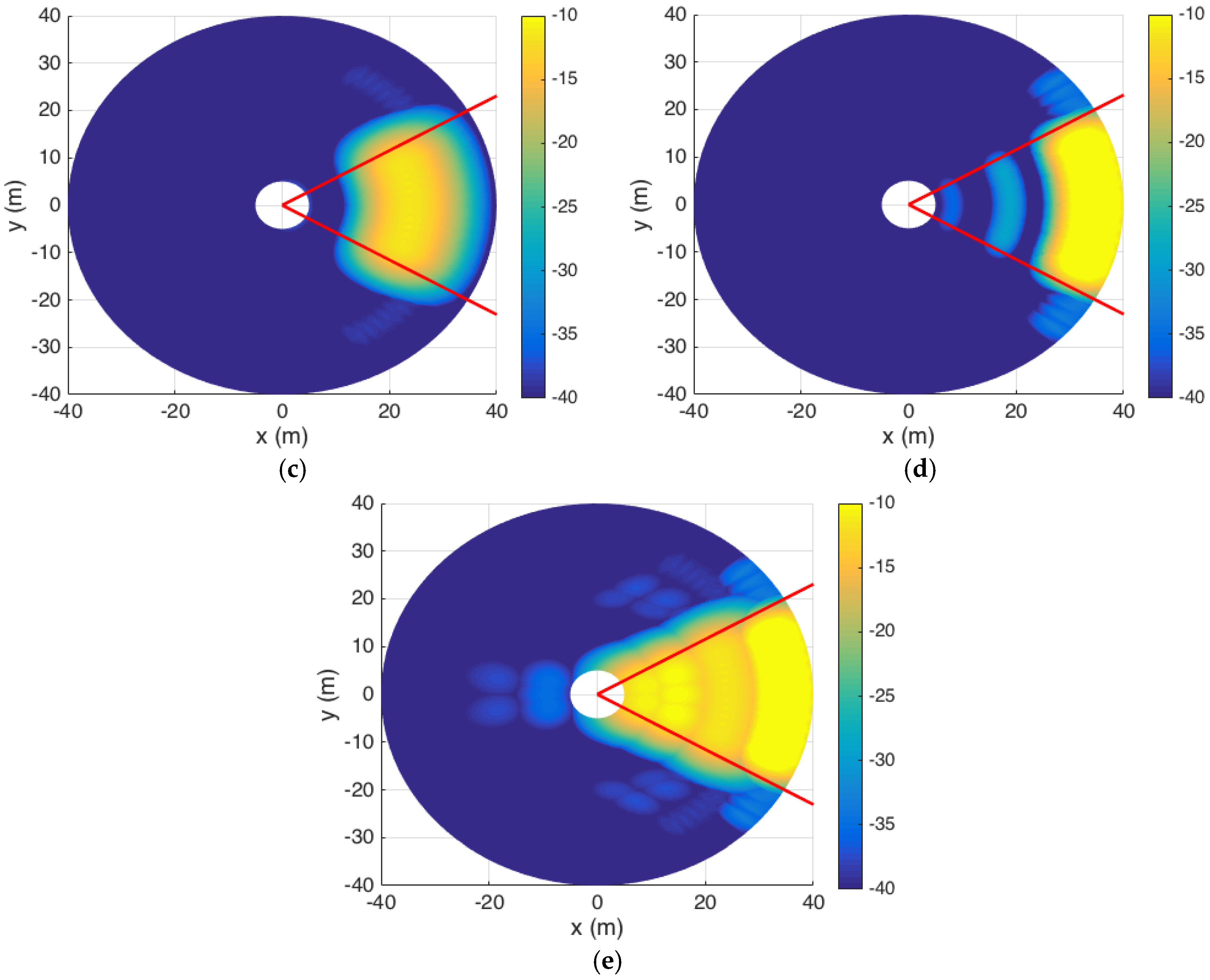
, cover the radial range between 43 and 200 m with the required received power. Similarly,
Figure 8c shows six slots targeting the 161 m contour using an 8 × 8 element array with an azimuth scan step of
, and
Figure 8d shows 15 slots targeting the 502 m contour using a 12 × 12 element array with an azimuth scan step of
. As the dimension of the antenna increases, its beamwidth decreases and more scan points are required to make sure the BS antenna covers the region of interest contiguously.
Figure 8e shows the combined SNR levels corresponding to all scan positions as listed in
Table 3 for the deterministic case. We observe that the SNR levels within the entire area of interest are maintained at the required values; i.e., higher than −13 dB, which allows us to keep a low value of
at the output of the GLRT detectors. It should be noted that the antenna configuration proposed above is not necessarily a unique solution for a given microcell. Different antenna configurations may be exploited in the scanning procedure to obtain a similar SNR performance to that shown in
Figure 8.
5.3. Performance Comparison between Deterministic and Random Scanning Algorithms (LOS Channels)
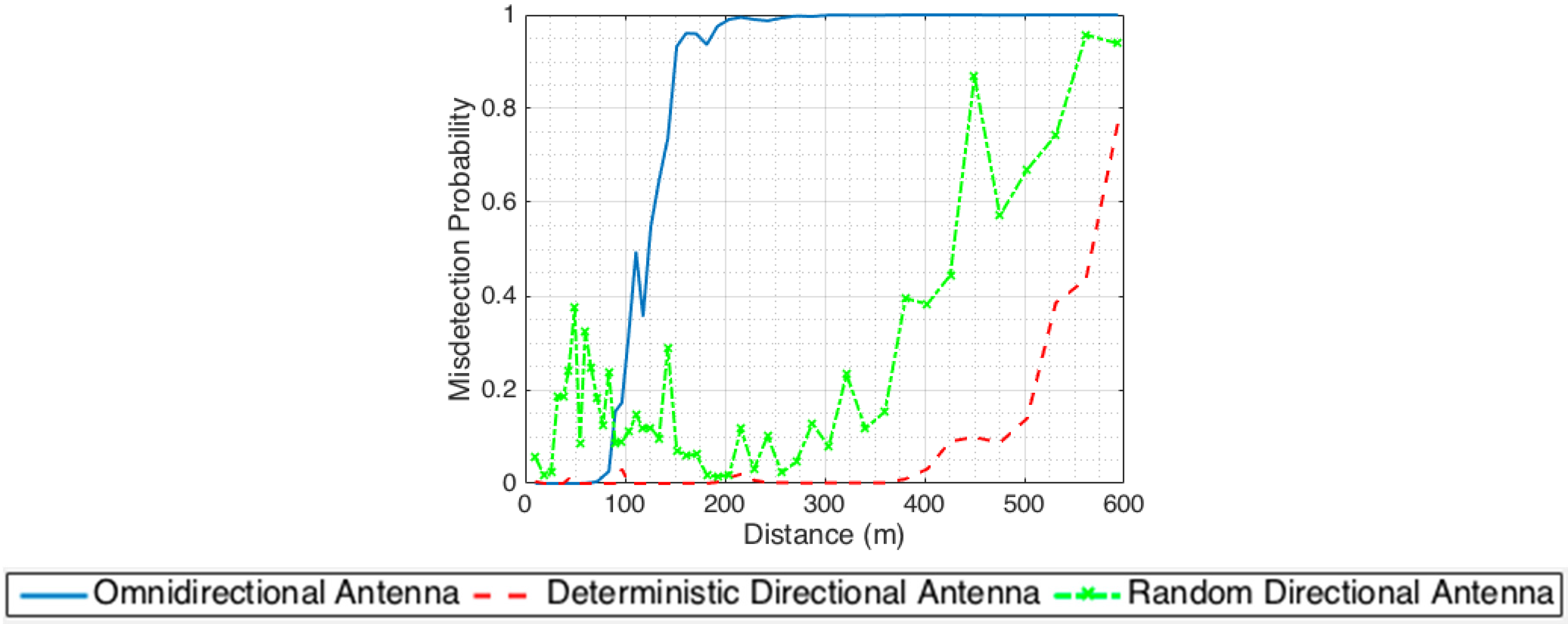
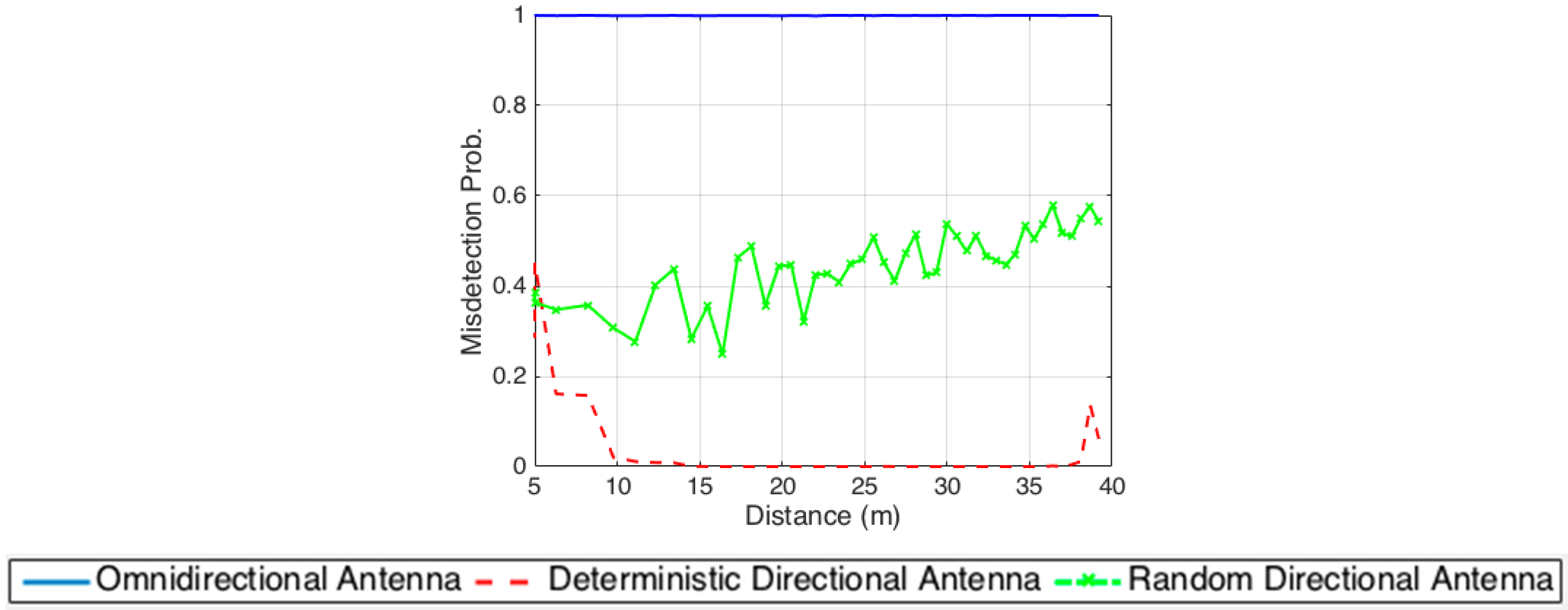
To compare the performance of different scanning strategies,
Figure 9 shows the misdetection probability versus the distance of a UE from the BS for three scenarios: (i) omnidirectional BS, (ii) random scanning with an 8 × 8 BS antenna array, and (iii) scanning with the proposed pattern of an adaptive array as described in
Table 3.
We observe that the misdetection rate is significantly improved when an adaptive antenna is exploited under the proposed scanning scheme. With an omnidirectional antenna at BS (blue line), the detection of PSS signals does not perform well at UEs located at distances greater than 100 m away from the BS. Within the 100 m to 200 m range, the UEs can still detect the PSS signals, but the misdetection rate sharply increases as a function of distance. For UEs located at distances greater than 200 m, it becomes impossible to detect the PSS signal. This is consistent with the results in
Figure 4. For the random scanning case using an 8 × 8 array antenna at BS, the misdetection rate (green-dashed-x line) fluctuates over the region. Although the random scan method is simple and can be applied to different coverage areas, it is not necessarily efficient to achieve a short search time. The mean misdetection probability of the UEs is very high within a required search time of 125 ms (25 time slots). This is due to the fact that the antenna beam width versus the area of coverage is not considered, which results in the rise of the misdetection rate on these regions. The proposed deterministic scanning scheme using an adaptive array achieves low misdetection rates (red dashed line) even for UEs located at ~400 m away from the BS. For UEs located beyond 400 m, although the misdetection probability starts increasing, it is still better compared to the case of omnidirectional transmission or random scanning with a directional antenna.
6. Scanning the Coverage Area with Directional BS Antennas (NLOS Channels)
While the same procedure described above can be applied for NLOS channels, the excess path loss encountered results in reduced coverage area. As mentioned earlier, we employ the empirical model given in [
4,
28] to model NLOS channel behavior. The path loss is described by the empirical relationship given in Equation (14) as:
where for NLOS channels
,
, and the lognormal shadowing
with
. The NLOS path loss as a function of distance (solid blue line) is compared in
Figure 10 to the LOS loss (dashed red line). We observe that as high as 30 dB excess loss can be experienced.
Therefore, with the available antenna configuration specified in
Table 2, it is necessary to reduce the cell size so that the detection of UEs inside the coverage region is guaranteed. If larger cell sizes need to be supported, larger antennas with finer scan steps; i.e., higher number of time slots, would need to be deployed. Since we want to keep the total number of slots
and with the maximum antenna dimensions of 12 × 12, the radius of the cell size under NLOS channels is chosen as R = 40 m to pose an equivalent problem to the LOS case discussed before. The procedure of choosing the appropriate scanning solutions is similar to the LOS case. Based on the required SNR (−13 dB) as shown in
Section 5.2, we can calculate the required power
at each receiver based on (12). As a result, the antenna dimensions as well as scanning directions at each time slots are designed to satisfy the required power received at each receiver in the region.
Table 4 shows such a choice of antenna configuration and scanning position for the NLOS case.
Figure 11 shows the received power at UEs distributed along the
x-axis. Similarly, as in the LOS case, it is observed that with the appropriate array configurations directed towards points on the
x-axis at 10, 15, 25 and 35 m, all UEs acquire the required power levels for high probability of detection. From these choices, the BS antenna is then scanned azimuthally to fully cover the area of interest.
Figure 12 shows the color mapping of SNR levels after scanning for 25 slots. As similar to
Section 5.2, we observe that the SNR levels within the entire area of interest are maintained at the required values; i.e., higher than −13 dB, which allows us to keep a low value of
at the output of the GLRT detectors.
Similar with the LOS case,
Figure 13 shows the misdetection probability versus the distance of a UE from the BS for three scenarios: (i) omnidirectional BS, (ii) random scanning with an 8 × 8 BS antenna array, and (iii) scanning with the proposed pattern of an adaptive array as described in
Table 4.
As observed, under NLOS assumption, the proposed deterministic scanning scheme using an adaptive array achieves low misdetection rates (red dashed line) even for UEs located at ~40 m away from the BS. With an omnidirectional antenna at BS (blue line), the detection of PSS signals does not perform well since the misdetection probability at all UEs is 1 meaning that they are incapable of detecting the signals. This shows the drawback of omnidirectional antenna under NLOS channels. For the random scanning case using an 8 × 8 array antenna at BS, the misdetection rate (green-dashed-x line) fluctuates over the region. Although the performance of the random scanning concept is better than using omnidirectional antenna, the performance is still much less efficient than the use of the deterministic scanning scheme.