Energy-Aware Real-Time Task Scheduling in Multiprocessor Systems Using a Hybrid Genetic Algorithm
Abstract
:1. Introduction
2. Literature Review
3. System Model and Problem Formulation
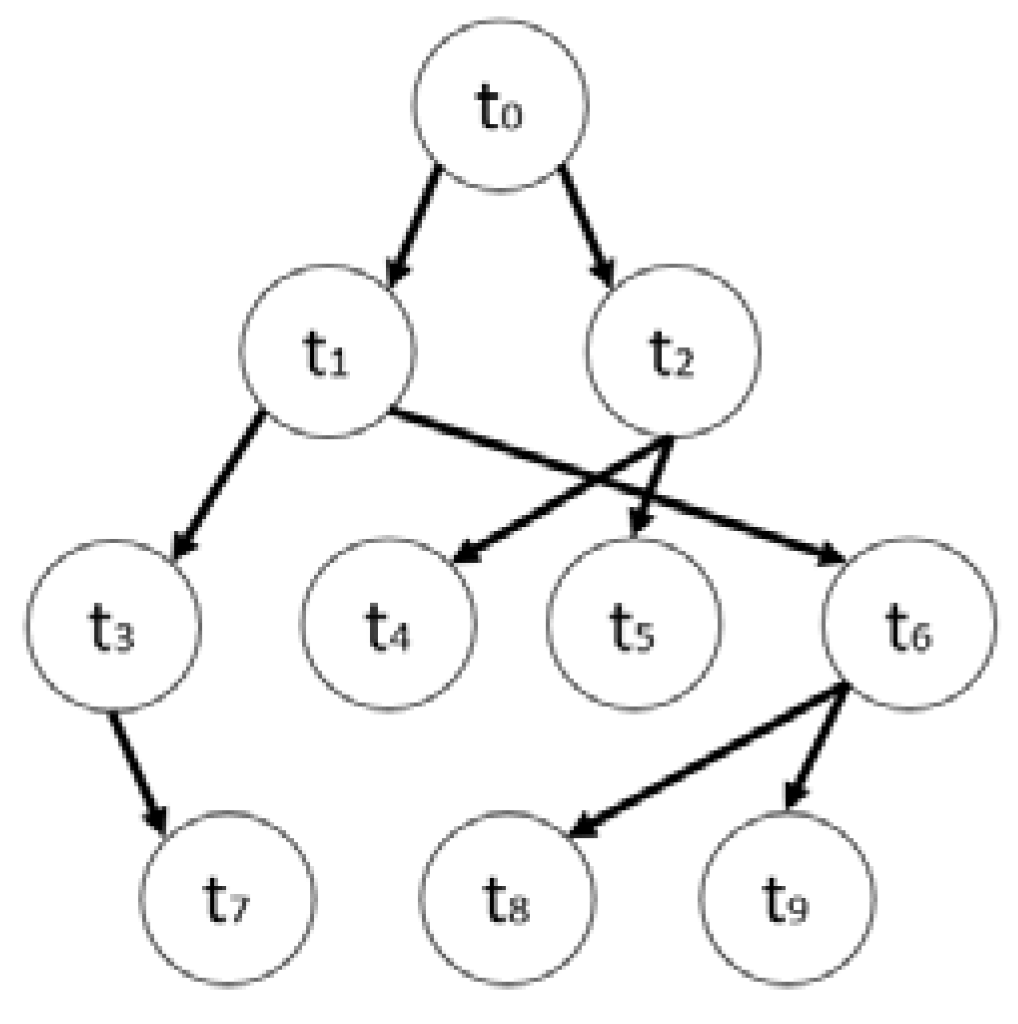
3.1. Task Model
- Succ (t4) = and Succ(t6) = {t8, t9}.
- Pre(t2) = {t0} and Pre(t5) = {t2}.
- aPre(t5) = {t0, t2} and aPre(t7) = {t0, t1, t3}.
3.2. Energy Model
3.3. Objective Function and Constraints
4. Task Scheduling Using Hybrid Genetic Algorithm
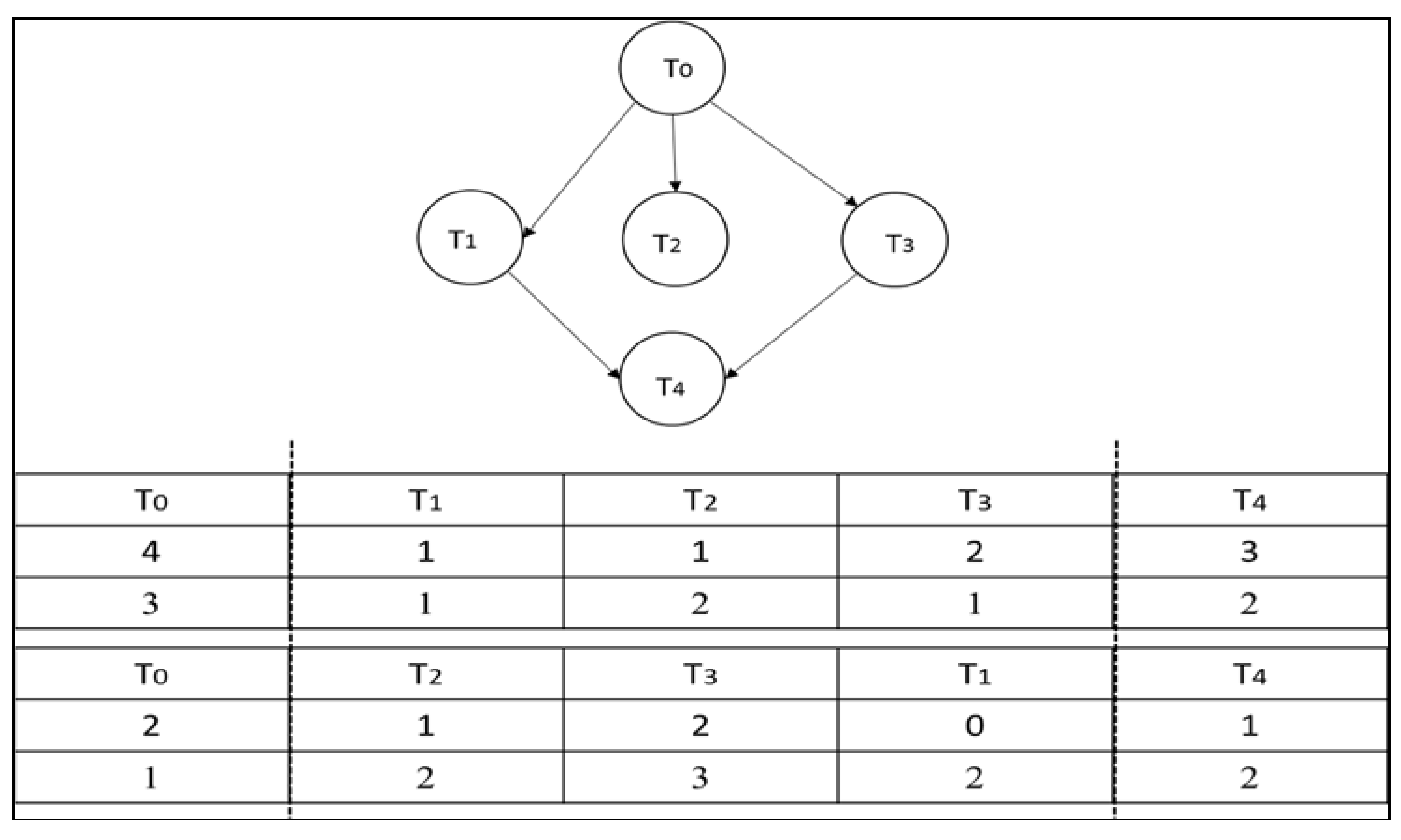
4.1. Solution Encoding and Generation of the Initial Population
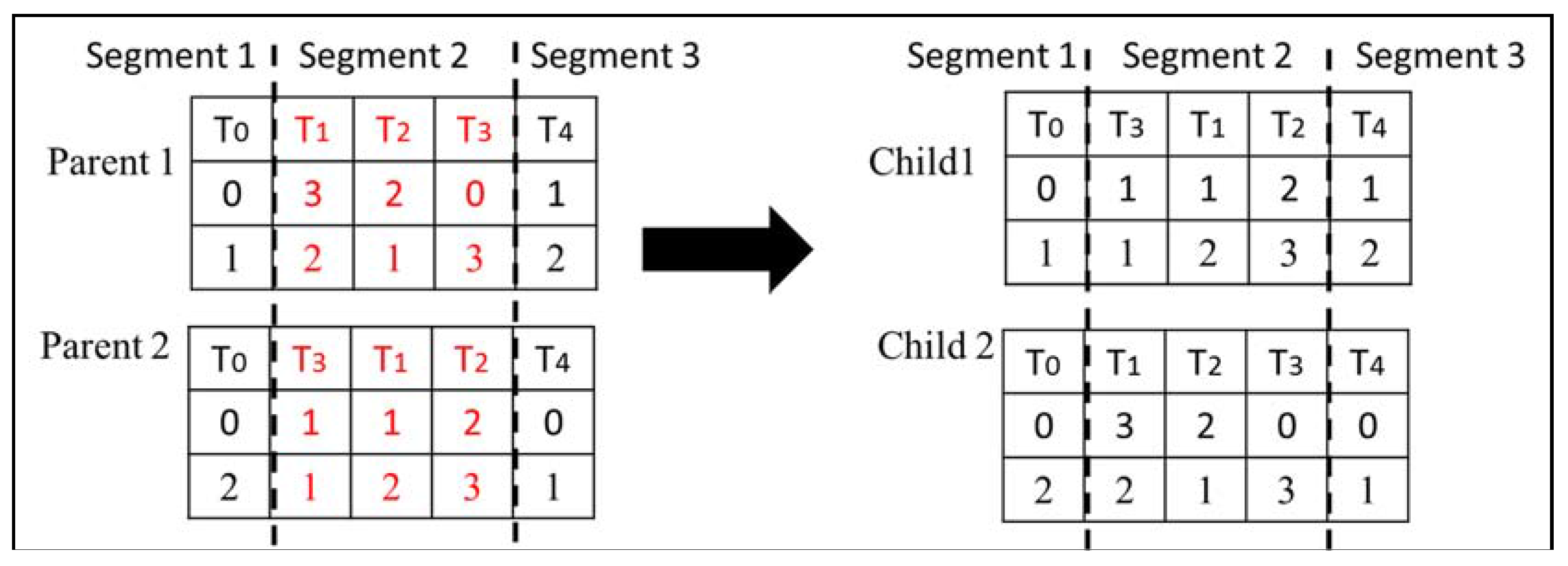
4.2. Crossover Operator
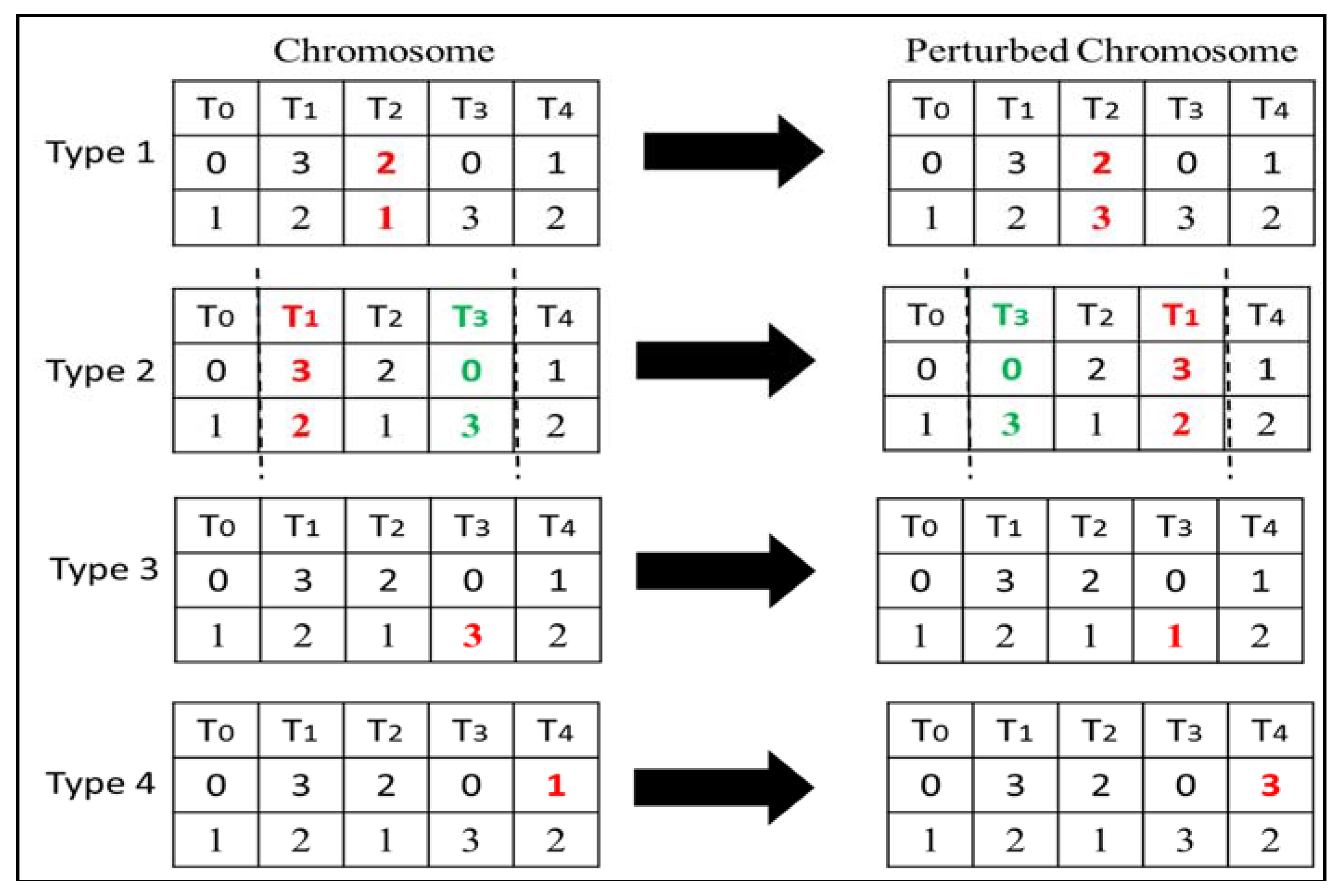
4.3. Perturbation Operator
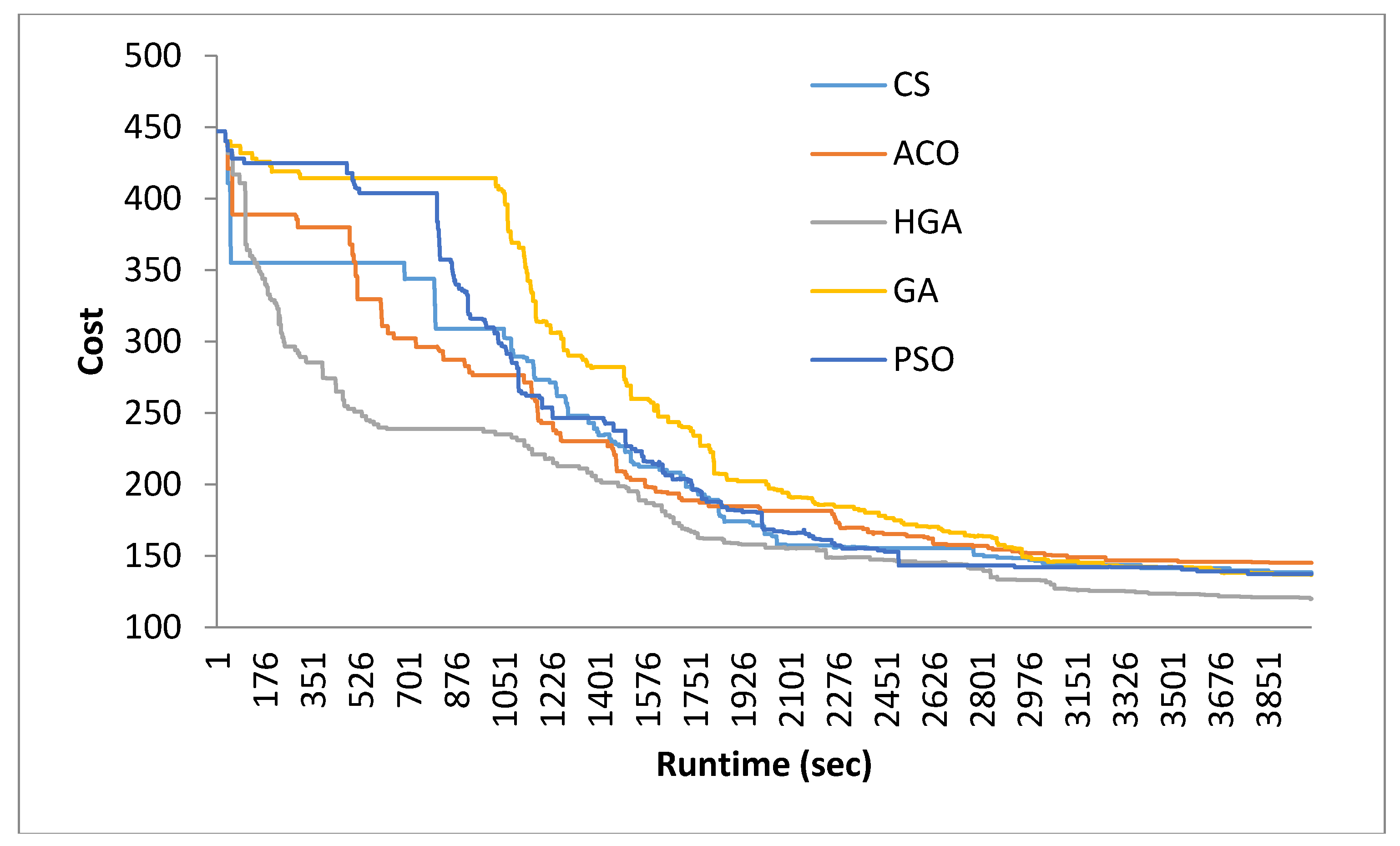
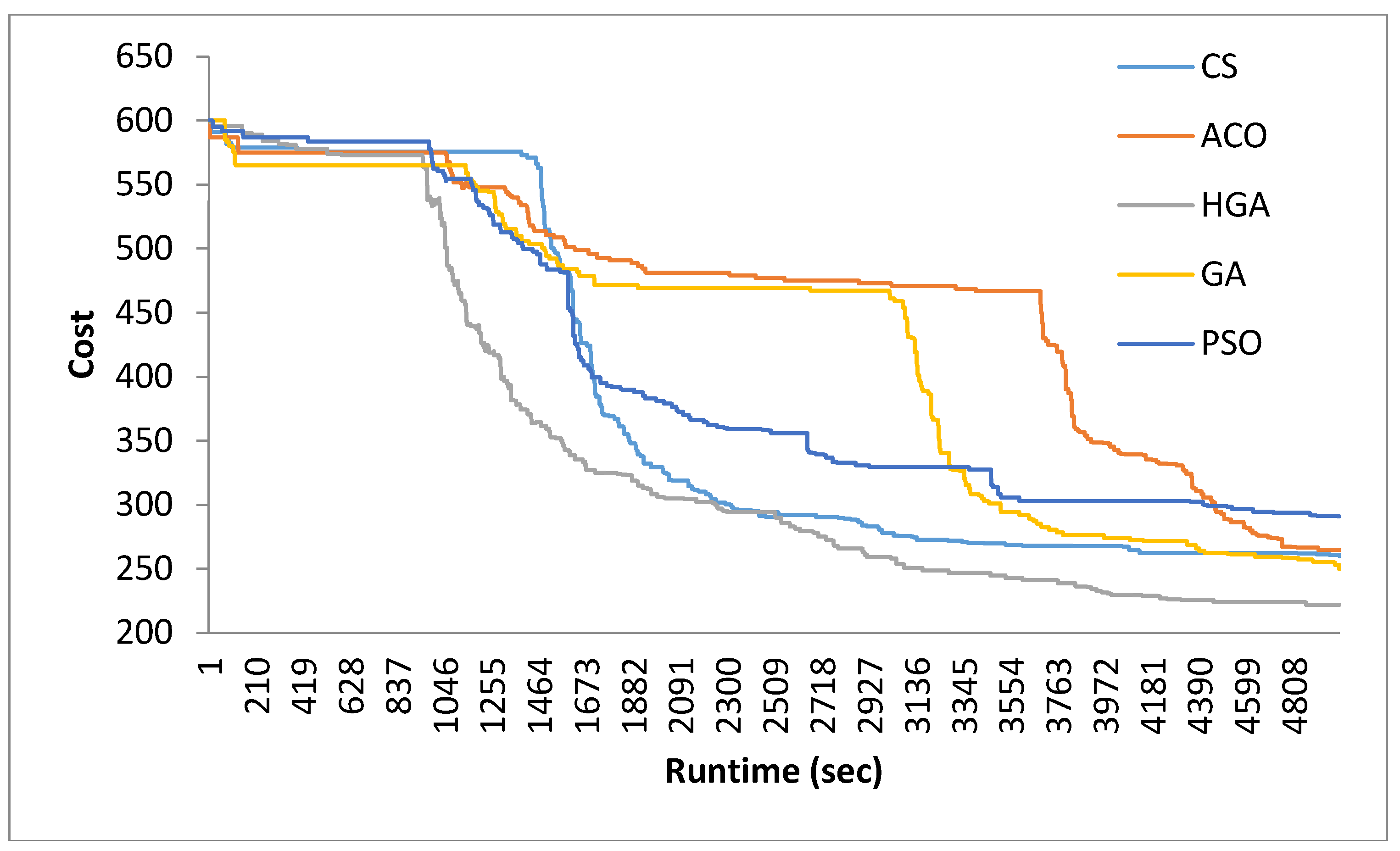
5. Results and Discussion
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Zhuo, J.; Chakrabarti, C. Energy-efficient dynamic task scheduling algorithms for DVS systems. ACM Trans. Embed. Comput. Syst. 2008, 7, 1–22. [Google Scholar] [CrossRef]
- Jejurikar, R.; Gupta, R. Energy-aware task scheduling with task synchronization for embedded real-time systems. IEEE Trans. Comput. Aided Des. 2006, 25, 1024–1037. [Google Scholar] [CrossRef]
- Shin, D.; Kim, J. Power-aware scheduling of conditional task graphs in real-time multiprocessor systems. In Proceedings of the 2003 International Symposium on Low Power Electronics and Design, Seoul, Korea, 25–27 August 2003; pp. 408–413. [Google Scholar]
- Tchamgoue, G.M.; Kim, K.H.; Jun, Y.K. Power-aware scheduling of compositional real-time frameworks. J. Syst. Softw. 2015, 102, 58–71. [Google Scholar] [CrossRef]
- Wei, Y.H.; Yang, C.Y.; Kuo, T.W.; Hung, S.H.; Chu, Y.H. Energy-efficient real-time scheduling of multimedia tasks on multi-core processors. In Proceedings of the 2010 ACM Symposium on Applied Computing, Sierre, Switzerland, 22–26 March 2010; pp. 258–262. [Google Scholar]
- Pering, T.; Burd, T.; Brodersen, R. Dynamic voltage scaling and the design of a low-power microprocessor system. In Proceedings of the Power Driven Microarchitecture Workshop ISCA98, Barcelona, Spain, 28 June 1998; pp. 96–101. [Google Scholar]
- Irani, S.; Pruhs, K.R. Algorithmic problems in power management. ACM Sigact News 2005, 36, 63–76. [Google Scholar] [CrossRef]
- Chen, J.J.; Kuo, T.W. Energy-efficient scheduling of periodic real-time tasks over homogeneous multiprocessors. In Proceedings of the PARC, September 2005; pp. 30–35. Available online: http://www.cs.utsa.edu/~dzhu/conference/parc05/papers/05-parc05-105.pdf (accessed on 4 April 2017).
- Tavares, E.; Maciel, P.; Silva, B.; Oliveira, M.N. Hard real-time tasks’ scheduling considering voltage scaling, precedence and exclusion relations. Inf. Process. Lett. 2008, 108, 50–59. [Google Scholar] [CrossRef]
- Hua, S.; Qu, G.; Bhattacharyya, S.S. Energy reduction techniques for multimedia applications with tolerance to deadline misses. In Proceedings of the 40th Annual Design Automation Conference, Anaheim, CA, USA, 2–6 June 2003; pp. 131–136. [Google Scholar]
- Zhu, Y.; Mueller, F. Feedback EDF scheduling exploiting dynamic voltage scaling. In Proceedings of the 10th IEEE Real-Time and Embedded Technology and Applications Symposium, Toronto, ON, Canada, 26–28 May 2004; pp. 84–93. [Google Scholar]
- Xian, C.; Lu, Y.H.; Li, Z. Dynamic voltage scaling for multitasking real-time systems with uncertain execution time. IEEE Trans. Comput. Aided Des. 2008, 27, 1467–1478. [Google Scholar] [CrossRef]
- Wang, W.; Mishra, P. PreDVS: Preemptive dynamic voltage scaling for real-time systems using approximation scheme. In Proceedings of the ACM 47th Design Automation Conference, Anaheim, CA, USA, 13–18 June 2010; pp. 705–710. [Google Scholar]
- Zhu, D.; Melhem, R.; Childers, B.R. Scheduling with dynamic voltage/speed adjustment using slack reclamation in multiprocessor real-time systems. IEEE Trans. Parallel Distrib. 2003, 14, 686–700. [Google Scholar]
- Kang, J.; Ranka, S. Dynamic slack allocation algorithms for energy minimization on parallel machines. J. Parallel Distrib. Comput. 2010, 70, 417–430. [Google Scholar] [CrossRef]
- Kim, W.; Kim, J.; Min, S.L. Dynamic voltage scaling algorithm for fixed-priority real-time systems using work-demand analysis. In Proceedings of the 2003 International Symposium on Low Power Electronics and Design, Seoul, Korea, 25–27 August 2003; pp. 396–401. [Google Scholar]
- Abbas, A.; Loudini, M.; Grolleau, E.; Mehdi, D.; Hidouci, W.K. A real-time feedback scheduler for environmental energy with discrete voltage/frequency modes. Comput. Stand. Interface 2016, 44, 264–273. [Google Scholar] [CrossRef]
- Zhou, J.; Wei, T. Stochastic thermal-aware real-time task scheduling with considerations of soft errors. J. Syst. Softw. 2015, 102, 123–133. [Google Scholar] [CrossRef]
- Rehaiem, G.; Gharsellaoui, H.; Ahmed, S.B. Real-Time scheduling approach of reconfigurable embedded systems based on neural networks with minimization of power consumption. IFAC-PapersOnLine 2016, 49, 1827–1831. [Google Scholar] [CrossRef]
- Hua, S.; Qu, G.; Bhattacharyya, S.S. Energy-efficient embedded software implementation on multiprocessor system-on-chip with multiple voltages. ACM Trans. Embed. Comput. Syst. 2006, 5, 321–341. [Google Scholar] [CrossRef]
- Liu, J.; Guo, J. Energy efficient scheduling of real-time tasks on multi-core processors with voltage islands. Future Gener. Comput. Syst. 2016, 56, 202–210. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, X.S.; Chen, D.Z. Task scheduling and voltage selection for energy minimization. In Proceedings of the 39th Annual Design Automation Conference, New Orleans, LA, USA, 10–12 June 2002; pp. 183–188. [Google Scholar]
- Nelis, V.; Goossens, J. Mora: An energy-aware slack reclamation scheme for scheduling sporadic real-time tasks upon multiprocessor platforms. In Proceedings of the 2009 15th IEEE International Conference on Embedded and Real-Time Computing Systems and Applications, Beijing, China, 24–26 August 2009; pp. 210–215. [Google Scholar]
- Alahmad, B.N.; Gopalakrishnan, S. Energy efficient task partitioning and real-time scheduling on heterogeneous multiprocessor platforms with QoS requirements. Sustain. Comput. Inf. Syst. 2011, 1, 314–328. [Google Scholar] [CrossRef]
- Liu, C. Efficient Design, Analysis, and Implementation of Complex Multiprocessor Real-Time Systems. Doctoral Dissertation, University of North Carolina at Chapel Hill, Chapel Hill, NC, USA, 2013. [Google Scholar]
- Lin, M.; Ng, S.M. A genetic algorithm for energy aware task scheduling in heterogeneous systems. Parallel Process. Lett. 2005, 15, 439–449. [Google Scholar] [CrossRef]
- Malakooti, B.; Sheikh, S.; Al-Najjar, C.; Kim, H. Multi-objective energy aware multiprocessor scheduling using bat intelligence. J. Intell. Manuf. 2013, 24, 805–819. [Google Scholar] [CrossRef]
- Burmyakov, A.; Bini, E.; Tovar, E. Compositional multiprocessor scheduling: The GMPR interface. Real Time Syst. 2014, 50, 342–376. [Google Scholar] [CrossRef]
- Chen, G.; Huang, K.; Knoll, A. Energy optimization for real-time multiprocessor system-on-chip with optimal DVFS and DPM combination. ACM Trans. Embed. Comput. Syst. 2014, 13, 111. [Google Scholar] [CrossRef]
- Shieh, W.Y.; Pong, C.C. Energy and transition-aware runtime task scheduling for multicore processors. J. Parallel Distrib. Comput. 2013, 73, 1225–1238. [Google Scholar] [CrossRef]
- Lipari, G.; Bini, E. A framework for hierarchical scheduling on multiprocessors: From application requirements to run-time allocation. In Proceedings of the IEEE 21st Real-Time Systems Symposium, San Diego, CA, USA, 30 November 2010; pp. 249–258. [Google Scholar]
- Singh, A.K.; Das, A.; Kumar, A. Energy optimization by exploiting execution slacks in streaming applications on multiprocessor systems. In Proceedings of the 50th Annual Design Automation Conference, Austin, TX, USA, 29 May–7 June 2013; p. 115. [Google Scholar]
- Hyung, K.; Sungho, K. Communication-aware task scheduling and voltage selection for total energy minimization in a multiprocessor system using Ant Colony Optimization. Inf. Sci. 2011, 181, 3995–4008. [Google Scholar]
- Zhang, W.; Xie, H.; Cao, B.; Cheng, A. Energy-Aware Real-Time Task Scheduling for Heterogeneous Multiprocessors with Particle Swarm Optimization Algorithm. Math. Probl. Eng. 2014, 2014, 287475. [Google Scholar] [CrossRef]
- Burd, T.D.; Pering, T.A.; Stratakos, A.J.; Brodersen, R.W. A dynamic voltage scaled microprocessor system. IEEE J. Solid-State Circuits. 2000, 35, 1571–1580. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Sait, S.; Youssef, H. Iterative Computer Algorithms with Applications in Engineering; IEEE Computer Society Press: Washington, DC, USA, 1999. [Google Scholar]
- Zhang, A.; Sun, G.; Wang, Z.; Yao, Y. A hybrid genetic algorithm and gravitational search algorithm for global optimization. Neural Netw. World 2015, 25, 53–73. [Google Scholar] [CrossRef]
- Kao, Y.T.; Zahara, E. A hybrid genetic algorithm and particle swarm optimization for multimodal functions. Appl. Soft Comput. 2008, 8, 849–857. [Google Scholar] [CrossRef]
- Ciornei, I.; Kyriakides, E. Hybrid ant colony-genetic algorithm (GAAPI) for global continuous optimization. IEEE Trans. Syst. Man Cybern. B 2012, 42, 234–245. [Google Scholar] [CrossRef] [PubMed]
- Zeb, A.; Khan, M.; Khan, N.; Tariq, A.; Ali, L.; Azam, F.; Jaffery, S.H. Hybridization of simulated annealing with genetic algorithm for cell formation problem. Int. J. Adv. Manuf. Technol. 2016, 86, 2243–2254. [Google Scholar] [CrossRef]
- Hadded, M.; Jarray, F.; Tlig, G.; Hasni, H. Hybridisation of genetic algorithms and tabu search approach for reconstructing convex binary images from discrete orthogonal projections. Int. J. Metaheuristics 2014, 3, 291–319. [Google Scholar] [CrossRef]
- Kanagaraj, G.; Ponnambalam, S.G.; Jawahar, N. A hybrid cuckoo search and genetic algorithm for reliability–redundancy allocation problems. Comput. Ind. Eng. 2013, 66, 1115–1124. [Google Scholar] [CrossRef]
- Siddiqi, U.F.; Shiraishi, Y.; Dahb, M.; Sait, S.M. A memory efficient stochastic evolution based algorithm for the multi-objective shortest path problem. Appl. Soft Comput. 2014, 14, 653–662. [Google Scholar] [CrossRef]
- Saab, Y.G.; Rao, V.B. Combinatorial Optimization by Stochastic Evolution. IEEE Trans. Comput. Aided Des. 1991, 10, 525–535. [Google Scholar] [CrossRef]
- Oh, J.; Wu, C. Genetic-algorithm-based real-time task scheduling with multiple goals. J. Syst. Softw. 2014, 71, 245–258. [Google Scholar] [CrossRef]
- Dick, R.P.; Rhodes, D.L.; Wolf, W. TGFF: Task graphs for free. In Proceedings of the 6th International Workshop on Hardware/Software Codesign, Seattle, WA, USA, 15–18 March 1998; pp. 97–101. [Google Scholar]
- Balbastre, P.; Ripoll, I.; Crespo, A. Minimum deadline calculation for periodic real-time tasks in dynamic priority systems. IEEE Trans. Comput. 2008, 57, 96–109. [Google Scholar] [CrossRef]
- Zeng, G.; Yokohama, T.; Tomiyama, H.; Takada, H. Practical Energy aware scheduling for real-time multiprocessor systems. In Proceedings of the 15th IEEE International Conference on Embedded and Real-time Computing Systems and Applications, Beijing, China, 24–26 August 2009; pp. 383–392. [Google Scholar]
- Zhang, W.; Bai, E.; Cheng, A. Solving Energy-Aware Real-Time Tasks Scheduling Problem with Shuffled Frog Leaping Algorithm on Heterogeneous Platforms. Sensors 2015, 15, 13778–13804. [Google Scholar] [CrossRef] [PubMed]
- Embedded System Synthesis Benchmark Suite (E3S). Available online: http://ziyang.eecs.umich.edu/~dickrp/e3s (accessed on 16 April 2017).

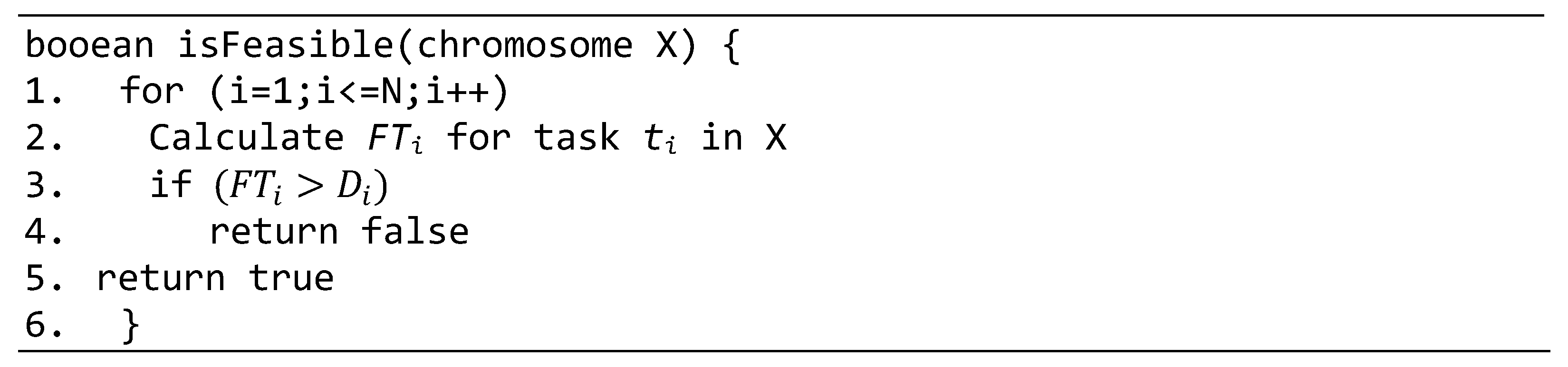


| Notation | Description |
|---|---|
| M | Number of processors |
| N | Number of tasks |
| vi | Supply voltage provided to execute task ti. |
| vt | Threshold voltage |
| ei | Energy consumed for processing task ti |
| ceff | Effective switching capacitance |
| lk | Number of discrete voltage levels on which processor pj can operate on |
| fi | Clock frequency at run time (operational frequency) |
| T | Task set |
| ti | A task in the task set, ti∊T |
| P | Set of Processors |
| pk | A processor, pk∊P |
| τi | Execution time of task ti |
| ci | Number of clock cycles required to process task ti. |
| powi | Power consumption of executing task ti |
| eikl | Energy consumed by task ti on processor pke at voltage vl |
| E | Total energy consumed by all the tasks |
| X | An N × M matrix corresponding to a task allocation |
| An element of X | |
| ESTi | Earliest start time for task ti |
| LSTi | Latest start time of task ti |
| FTi | Finish time of task ti |
| Pre(ti) | Set of predecessors of task ti (precedence tasks) |
| Succ(ti) | Set of immediate successors of task ti |
| STi | Actual start time of task i |
| di | Deadline of task ti |
| vk | Set of voltage levels at which a processor pj can operate. Voltage levels at which processor k can operate |
| C1 and C2 | Acceleration coefficients in PSO algorithm |
| W | Constriction factor in PSO algorithm |
| Vmax | Maximum velocity in PSO algorithm |
| A | Weight parameter for pheromone trail in ACO algorithm |
| B | Weight parameter for heuristic value in ACO algorithm |
| P | Evaporation ratio in ACO algorithm |
| Λ | Step size in cuckoo search algorithm |
| ph | Selection probability of chromosome for perturbation |
| Algorithm | Parameter Setting |
|---|---|
| GA | pop size: 40 |
| crossover rate: 0.8 | |
| mutation rate: 0.1 | |
| HGA | pop size: 20, 40, 60 |
| crossover rate: 0.6 and 0.8 | |
| perturbation rate: 0.05 and 0.1 | |
| ph: 0.1, 0.2, 0.3 | |
| rewarded iterations ρ: 3 and 5 | |
| PSO | C1 = C2 =1.49 |
| w = 0.72 | |
| Vmax = 5 | |
| ACO | α = 2 |
| β = 2 | |
| P = 0.2 | |
| CS | λ = 0.25 |
| Data Type | No. of Tasks | HGA | GA | Cuckoo Search | ACO | PSO |
|---|---|---|---|---|---|---|
| synthetic data | 10 | 42 ± 0.00 | 42 ± 0.00 | 42 ± 0.00 | 42 ± 0.00 | 43 ± 0.80 |
| 15 | 67 ± 1.49 | 74 ± 4.80 | 69 ± 3.30 | 75 ± 2.36 | 75 ± 5.68 | |
| 30 | 85 ± 2.68 | 94 ± 3.07 | 99 ± 4.81 | 89 ± 6.50 | 95 ± 3.37 | |
| 50 | 125 ± 5.09 | 141 ± 6.01 | 145 ± 5.87 | 152 ± 7.22 | 143 ± 5.99 | |
| 75 | 180 ± 3.77 | 205 ± 5.39 | 201 ± 7.67 | 223 ± 7.29 | 230 ± 8.15 | |
| 100 | 227 ± 4.96 | 258 ± 8.22 | 269 ± 8.79 | 271 ± 6.07 | 300 ± 9.49 | |
| 200 | 293 ± 3.99 | 329 ± 7.32 | 341 ± 6.93 | 352 ± 7.23 | 384 ± 8.02 | |
| 400 | 409 ± 5.03 | 447 ± 7.56 | 436 ± 6.76 | 430 ± 7.41 | 447 ± 6.29 | |
| 500 | 483 ± 5.70 | 535 ± 6.21 | 552 ± 5.19 | 516 ± 8.35 | 530 ± 9.01 | |
| real data [49,50,51] | 45 | 92 ± 2.33 | 99 ± 3.76 | 104 ± 2.58 | 101 ± 2.09 | 107 ± 3.66 |
| 100 | 170 ± 1.67 | 192 ± 2.32 | 189 ± 1.98 | 201 ± 3.11 | 199 ± 1.59 | |
| 400 | 319 ± 3.84 | 351 ± 3.09 | 364 ± 4.30 | 382 ± 2.97 | 346 ± 3.89 |
| Data Type | Tasks | HGA vs. GA | HGA vs. CS | HGA vs. ACO | HGA vs. PSO |
|---|---|---|---|---|---|
| synthetic data | 10 | 0.00 | 0.00 | 0.00 | 2.38 |
| 15 | 10.45 | 2.99 | 11.94 | 11.94 | |
| 30 | 10.59 | 16.47 | 4.71 | 11.76 | |
| 50 | 12.80 | 16.00 | 21.60 | 14.40 | |
| 75 | 13.89 | 11.67 | 23.89 | 27.78 | |
| 100 | 13.66 | 18.50 | 19.38 | 32.16 | |
| 200 | 12.29 | 16.38 | 20.14 | 31.06 | |
| 400 | 9.29 | 6.60 | 5.13 | 9.29 | |
| 500 | 10.77 | 14.29 | 6.83 | 9.73 | |
| real data | 45 | 7.61 | 13.04 | 9.78 | 16.30 |
| 100 | 12.94 | 11.18 | 18.24 | 17.06 | |
| 400 | 10.03 | 14.11 | 19.75 | 8.46 |
| Synthetic Data | Real Benchmark Data | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| # of tasks | 10 | 15 | 30 | 50 | 75 | 100 | 200 | 400 | 500 | 45 | 100 | 400 |
| % of invalid solutions | 4% | 3% | 6% | 7% | 13% | 11% | 8% | 10% | 14% | 8.5% | 13% | 14% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahmood, A.; Khan, S.A.; Albalooshi, F.; Awwad, N. Energy-Aware Real-Time Task Scheduling in Multiprocessor Systems Using a Hybrid Genetic Algorithm. Electronics 2017, 6, 40. https://doi.org/10.3390/electronics6020040
Mahmood A, Khan SA, Albalooshi F, Awwad N. Energy-Aware Real-Time Task Scheduling in Multiprocessor Systems Using a Hybrid Genetic Algorithm. Electronics. 2017; 6(2):40. https://doi.org/10.3390/electronics6020040
Chicago/Turabian StyleMahmood, Amjad, Salman A. Khan, Fawzi Albalooshi, and Noor Awwad. 2017. "Energy-Aware Real-Time Task Scheduling in Multiprocessor Systems Using a Hybrid Genetic Algorithm" Electronics 6, no. 2: 40. https://doi.org/10.3390/electronics6020040
APA StyleMahmood, A., Khan, S. A., Albalooshi, F., & Awwad, N. (2017). Energy-Aware Real-Time Task Scheduling in Multiprocessor Systems Using a Hybrid Genetic Algorithm. Electronics, 6(2), 40. https://doi.org/10.3390/electronics6020040





