Fully Quaternion-Valued Adaptive Beamforming Based on Crossed-Dipole Arrays
Abstract
:1. Introduction
2. Quaternion Model for Crossed-Dipole Array
2.1. Basics of Quaternion
2.1.1. Quaternion Vector and Matrix
2.1.2. The Gradient for a Quaternion Function
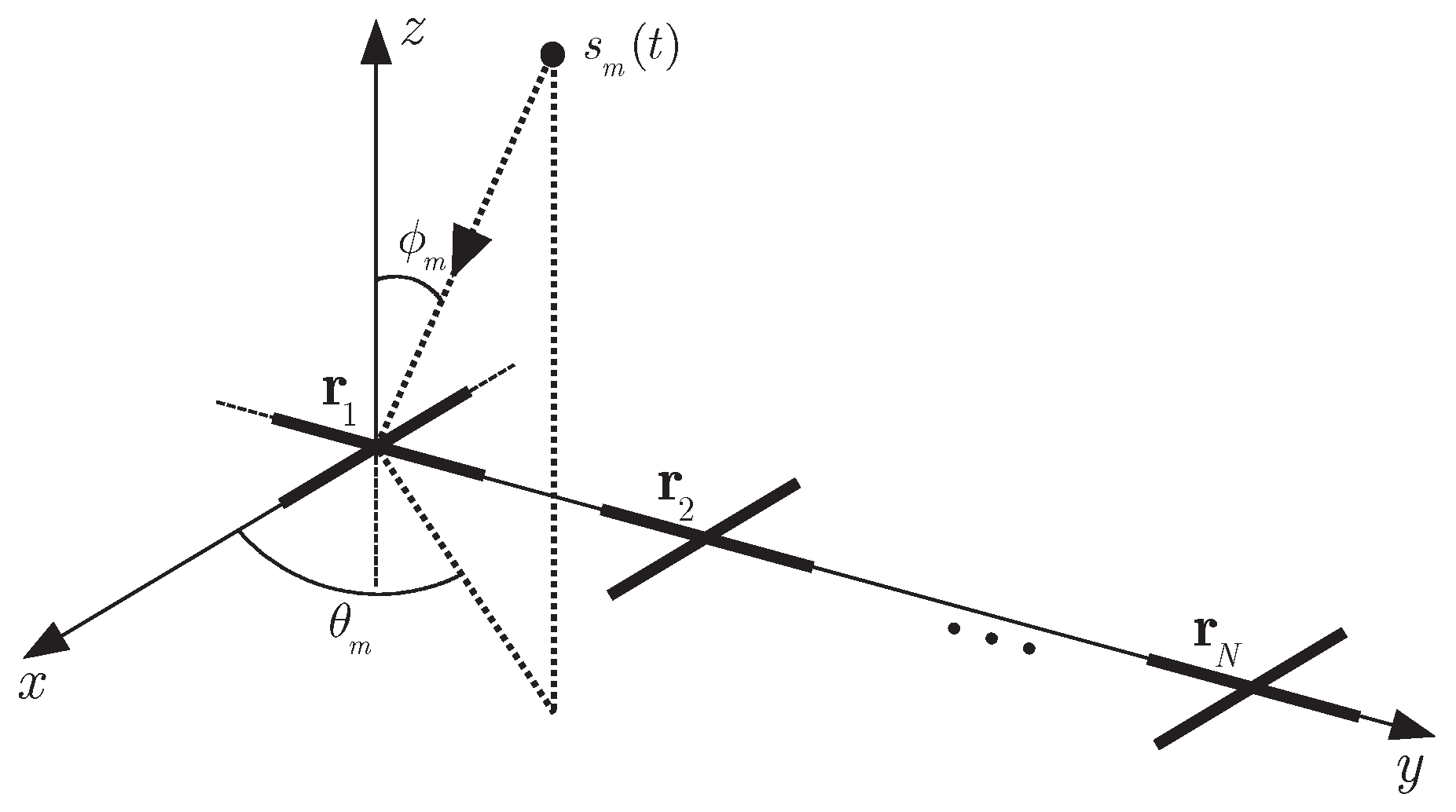
2.2. Model for Crossed-Dipole Array
3. The Full Quaternion-Valued Capon Beamformer
4. Worst-Case-Based Robust Adaptive Beamforming
4.1. Worst-Case Constrained Algorithm
4.2. SOC Implementation of FQWCCB
4.3. Complexity Analysis
5. Simulations Results
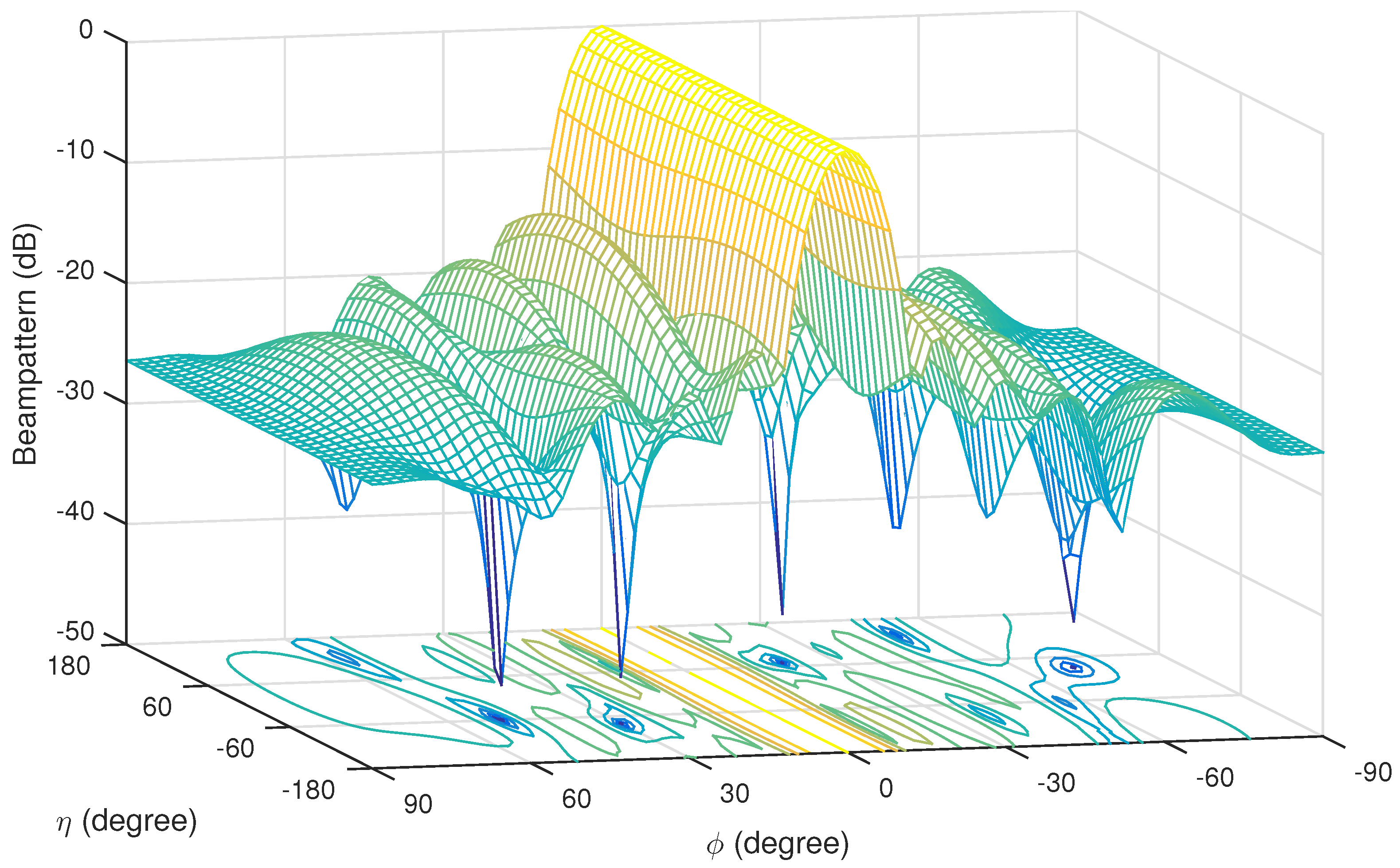
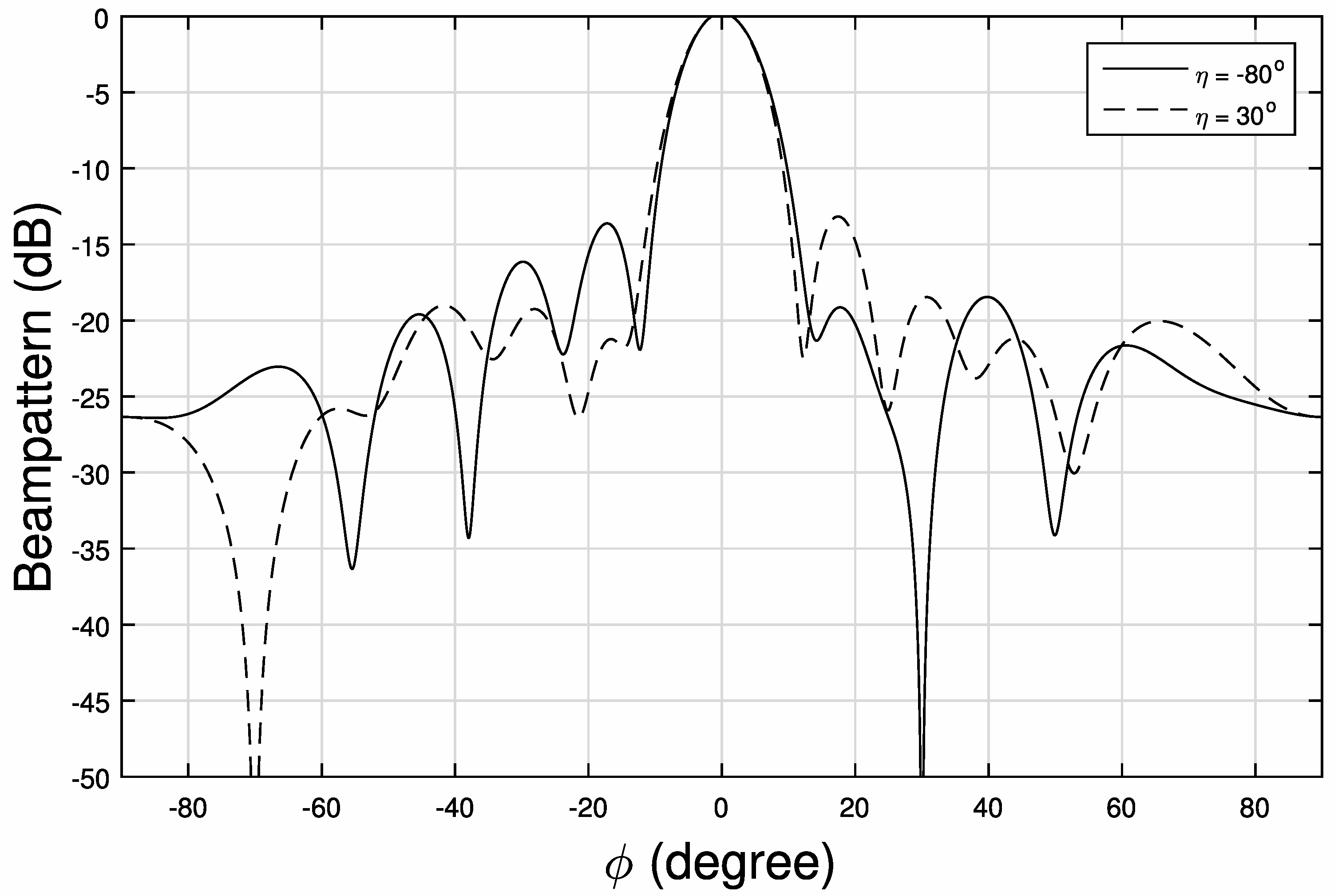
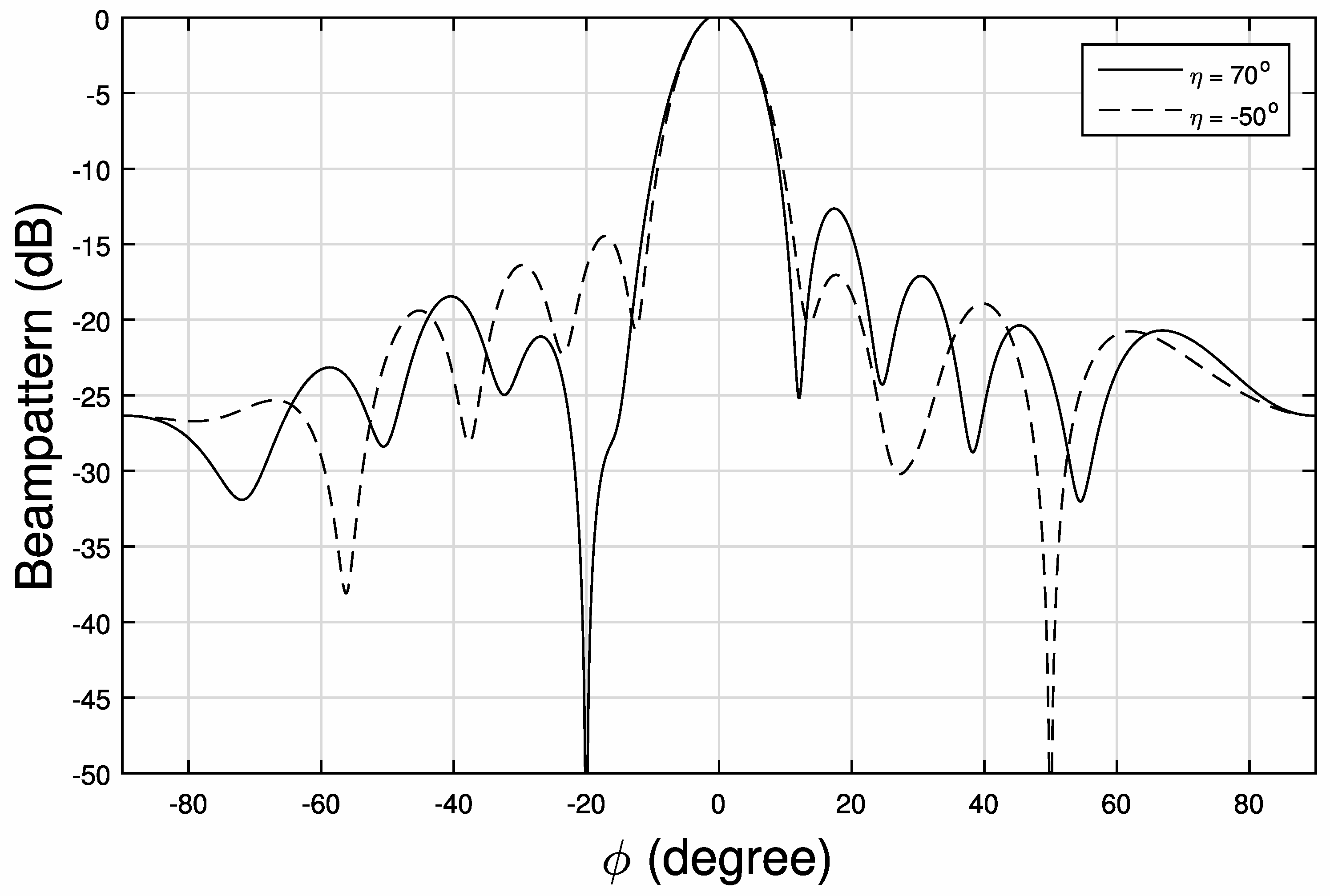
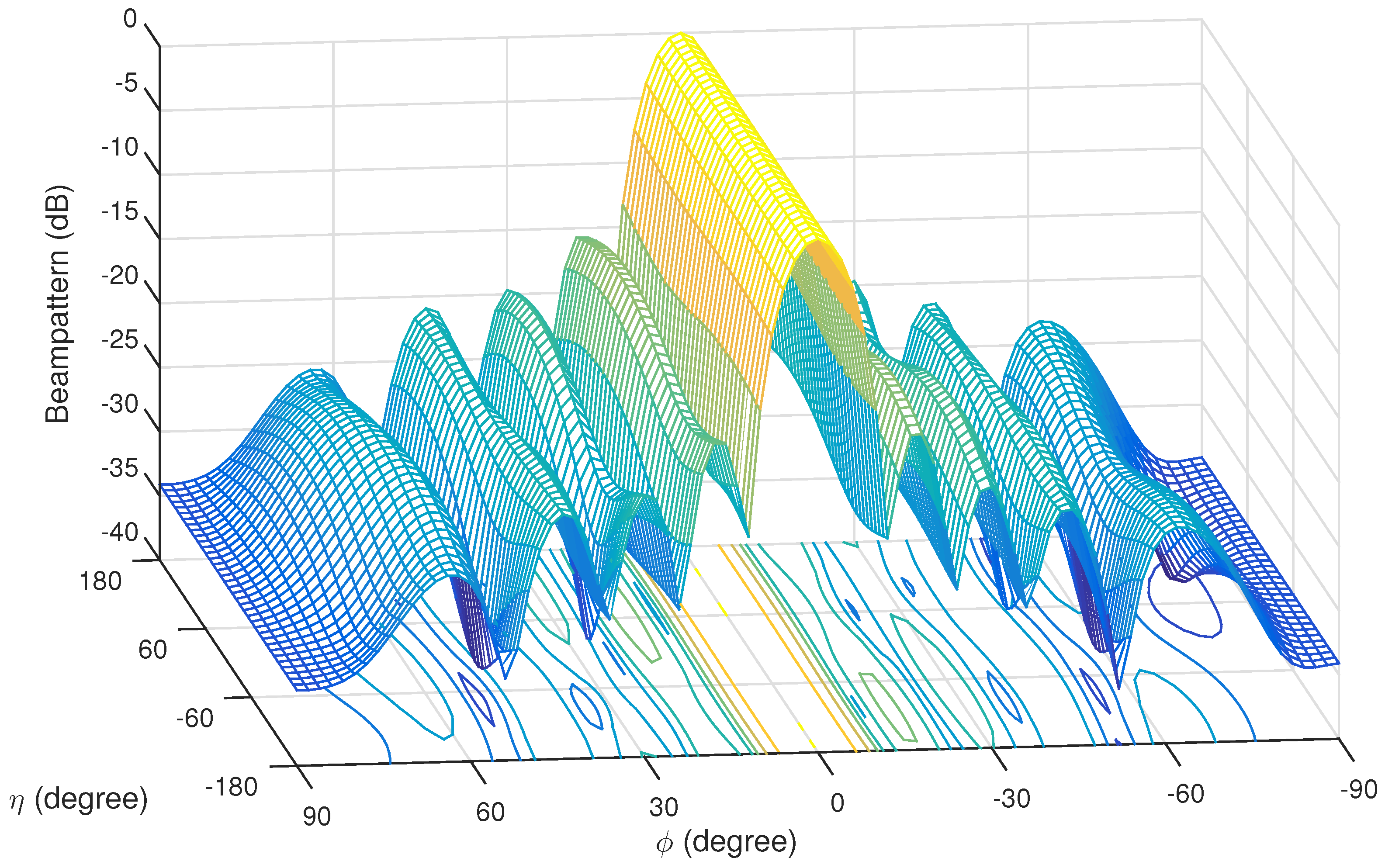
5.1. Beam Pattern
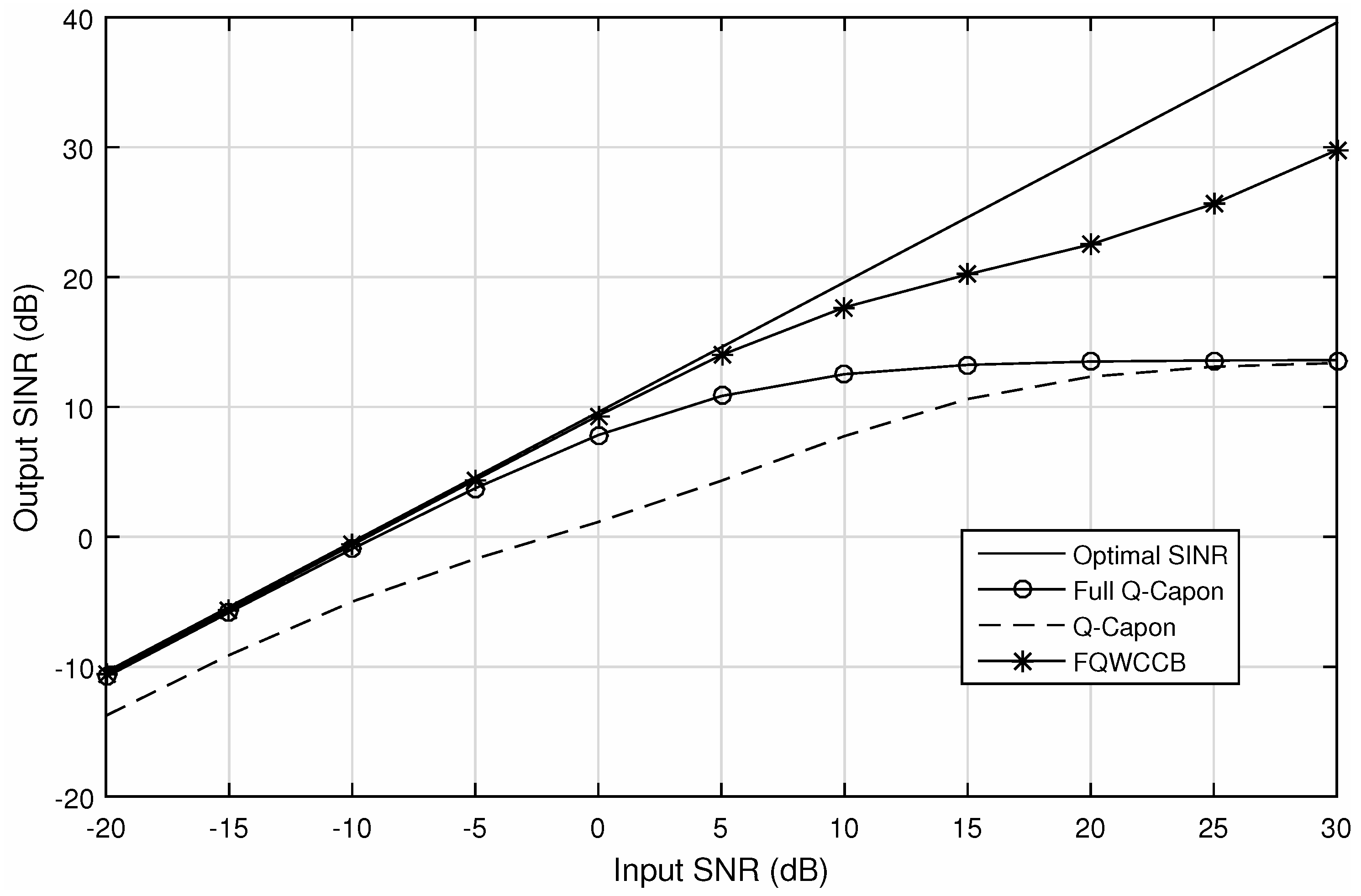
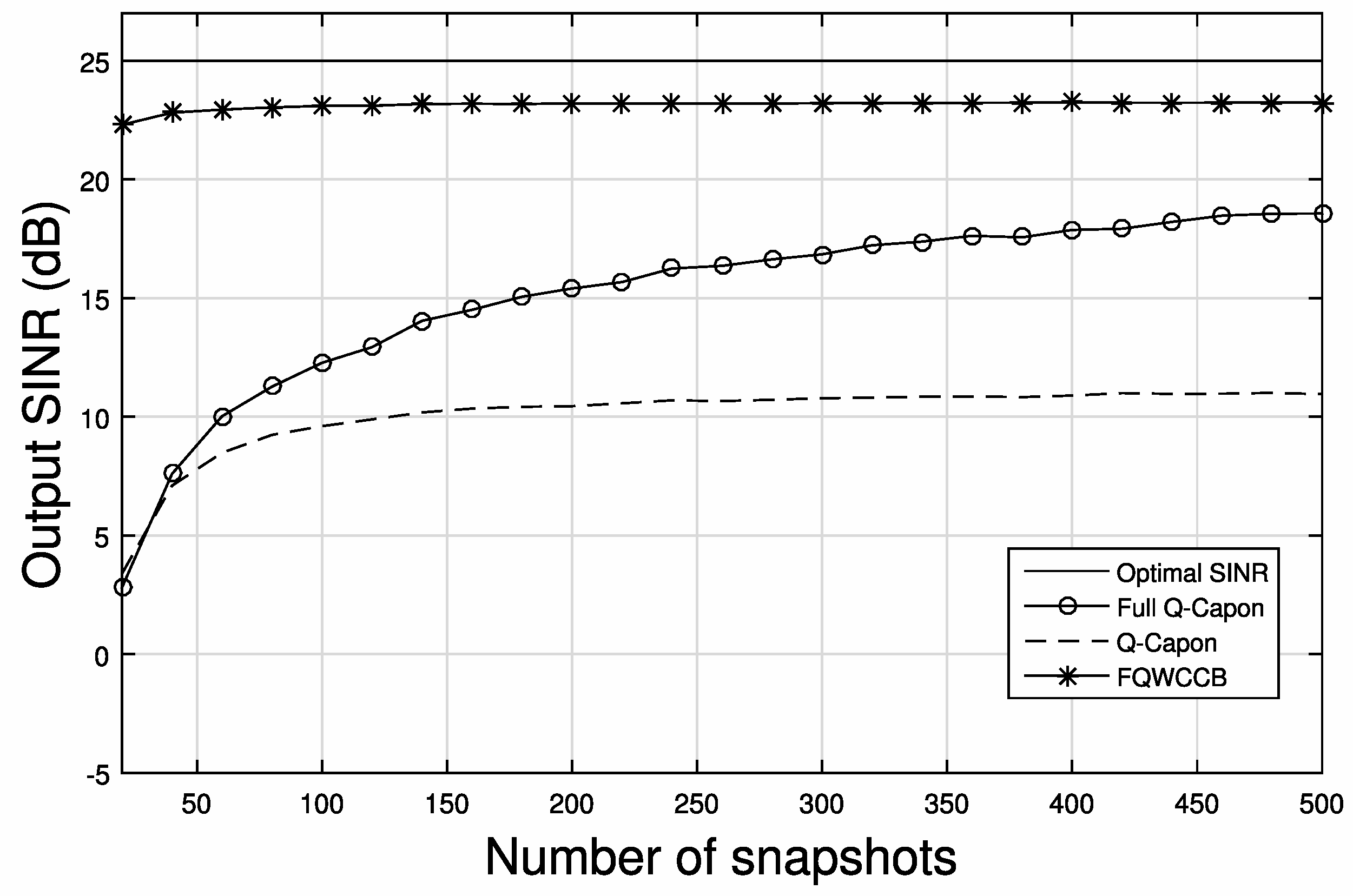
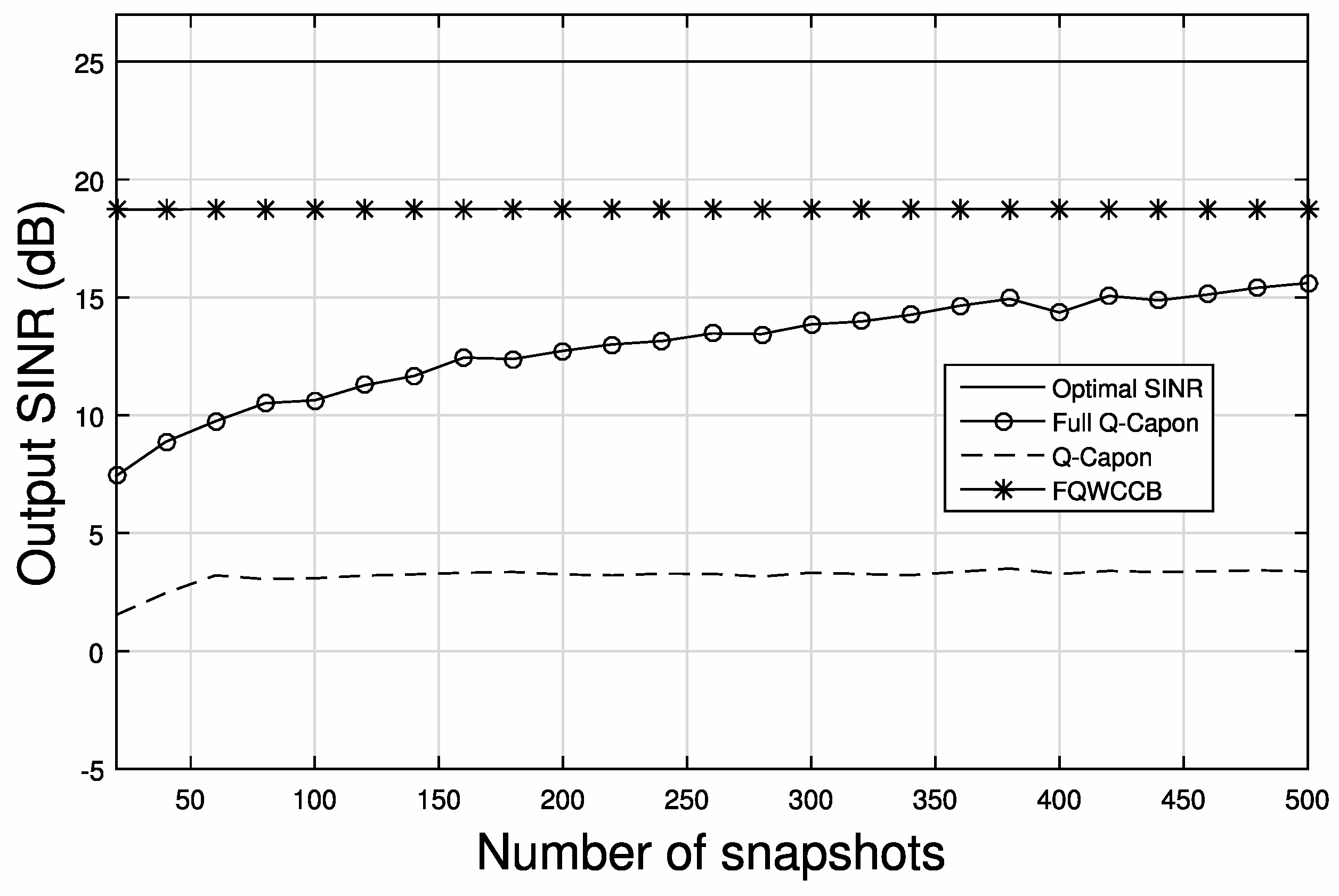
5.2. Output SINR Performance
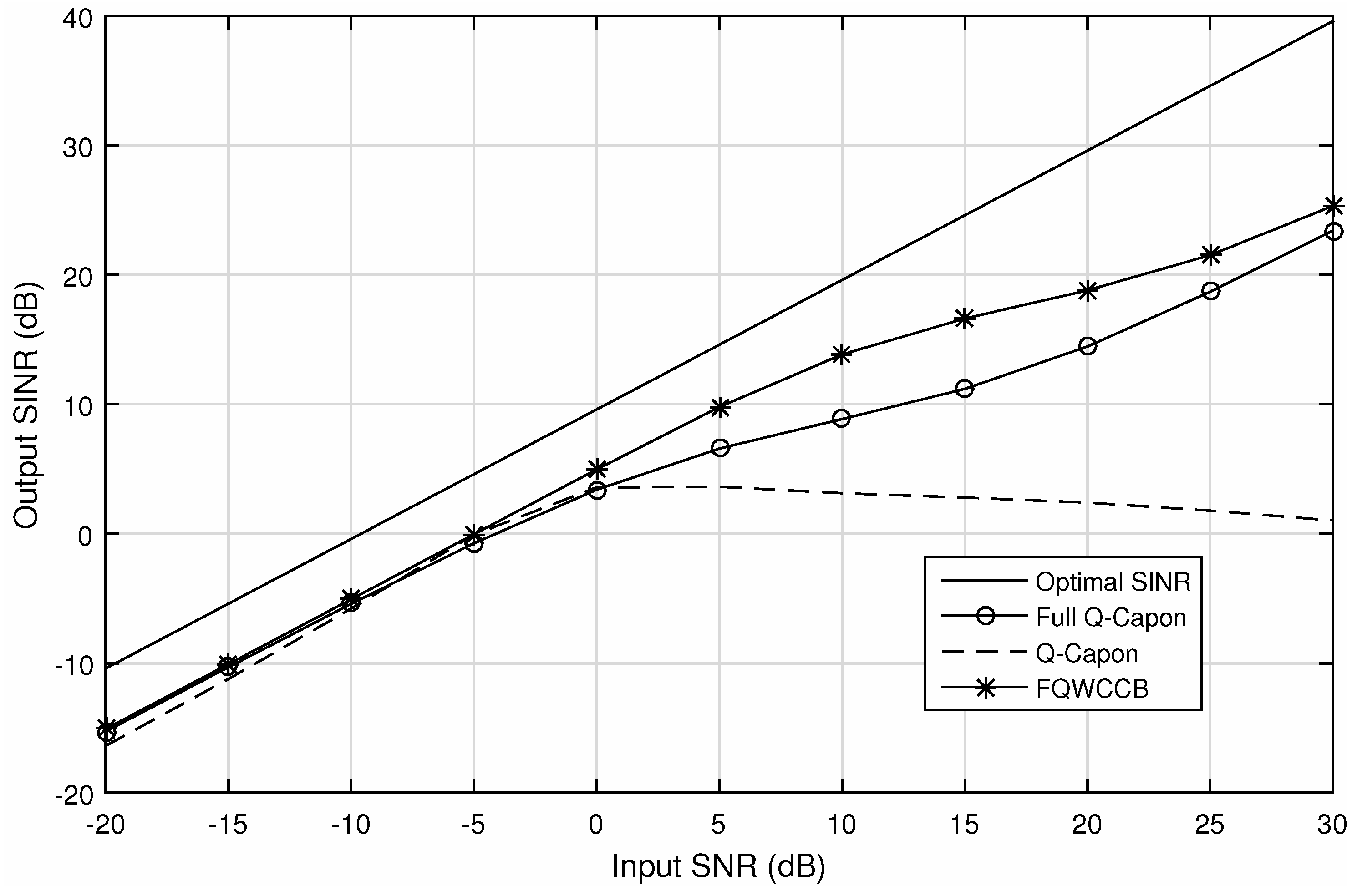
5.3. Performance with DOA and Polarization Mismatch
6. Conclusions
Appendix A
References
- Compton, R., Jr. On the performance of a polarization sensitive adaptive array. IEEE Trans. Antennas Propag. 1981, 29, 718–725. [Google Scholar] [CrossRef]
- Nehorai, A.; Ho, K.C.; Tan, B.T.G. Minimum-noise-variance beamformer with an electromagnetic vector sensor. IEEE Trans. Signal Process. 1999, 47, 601–618. [Google Scholar] [CrossRef]
- Godara, L.C. Application of antenna arrays to mobile communications. II. Beam-forming and direction-of-arrival considerations. Proc. IEEE 1997, 85, 1195–1245. [Google Scholar] [CrossRef]
- Xu, Y.G.; Liu, T.; Liu, Z.W. Output SINR of MV beamformer with one EM vector sensor of and magnetic noise power. In Proceedings of the International Conference on Signal Processing, Montreal, QC, Canada, 17–21 May 2004; pp. 419–422. [Google Scholar]
- Le Bihan, N.; Mars, J. Singular value decomposition of quaternion matrices: A new tool for vector-sensor signal processing. Signal Process. 2004, 84, 1177–1199. [Google Scholar] [CrossRef]
- Miron, S.; Le Bihan, N.; Mars, J.I. High resolution vector-sensor array processing using quaternions. In Proceedings of the IEEE Workshop on Statistical Signal Processing, Bordeaux, France, 17–20 July 2005; pp. 918–923. [Google Scholar]
- Miron, S.; Le Bihan, N.; Mars, J.I. Quaternion-MUSIC for vector-sensor array processing. IEEE Trans. Signal Process. 2006, 54, 1218–1229. [Google Scholar] [CrossRef]
- Gong, X.; Xu, Y.; Liu, Z. Quaternion ESPRIT for direction finding with a polarization sentive array. In Proceedings of the International Conference on Signal Processing, Beijing, China, 26–29 October 2008; pp. 378–381. [Google Scholar]
- Tao, J.W.; Chang, W.X. A novel combined beamformer based on hypercomplex processes. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 1276–1289. [Google Scholar] [CrossRef]
- Tao, J.W. Performance analysis for interference and noise canceller based on hypercomplex and spatio-temporal-polarisation processes. IET Radar Sonar Navig. 2013, 7, 277–286. [Google Scholar] [CrossRef]
- Zhang, X.R.; Liu, W.; Xu, Y.G.; Liu, Z.W. Quaternion-valued Robust Adaptive Beamformer for Electromagnetic Vector-sensor Arrays with Worst-case Constraint. Signal Process. 2014, 104, 274–283. [Google Scholar]
- Jiang, M.D.; Liu, W.; Li, Y. Adaptive Beamforming for Vector-Sensor Arrays Based on Reweighted Zero-Attracting Quaternion-Valued LMS Algorithm. IEEE Trans. Circuits Syst. II Express Br. 2016, 63, 274–278. [Google Scholar] [CrossRef]
- Gou, X.; Xu, Y.; Liu, Z.; Gong, X. Quaternion-capon beamformer using crossed-dipole arrays. In Proceedings of the IEEE International Symposium on Microwave, Antenna, Propagation, and EMC Technologies for Wireless Communications (MAPE), Beijing, China, 1–3 November 2011; pp. 34–37. [Google Scholar]
- Isaeva, O.M.; Sarytchev, V.A. Quaternion presentations polarization state. In Proceedings of the 2nd IEEE Topical Symposium of Combined Optical-Microwave Earth and Atmosphere Sensing, Atlanta, GA, USA, 3–6 April 1995; pp. 195–196. [Google Scholar]
- Wysocki, B.J.; Wysocki, T.A. On an Orthogonal Space-Time-Polarization Block Code. J. Commun. 2009, 4, 20–25. [Google Scholar]
- Liu, W. Channel equalization and beamforming for quaternion-valued wireless communication systems. J. Frankl. Inst. 2016. [Google Scholar] [CrossRef]
- Li, J.; Stoica, P. (Eds.) Robust Adaptive Beamforming; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Liu, W.; Weiss, S. Wideband Beamforming: Concepts and Techniques; John Wiley & Sons: Chichester, UK, 2010. [Google Scholar]
- Vorobyov, S.A.; Gershman, A.B.; Luo, Z.Q. Robust adaptive beamforming using worst-case performance optimization: A solution to the signal mismatch problem. IEEE Trans. Signal Process. 2003, 51, 313–324. [Google Scholar] [CrossRef]
- Yu, L.; Liu, W.; Langley, R.J. Novel robust beamformers for coherent interference suppression with DOA estimation errors. IET Microw. Antennas Propag. 2010, 4, 1310–1319. [Google Scholar] [CrossRef]
- Hamilton, W.R., II. On quaternions; or on a new system of imaginaries in algebra. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1844, 25, 10–13. [Google Scholar]
- Huang, L.; So, W. On left eigenvalues of a quaternionic matrix. Linear Algebra Appl. 2001, 323, 105–116. [Google Scholar] [CrossRef]
- Zhang, F. Quaternions and matrices of quaternions. Linear Algebra Appl. 1997, 251, 21–57. [Google Scholar] [CrossRef]
- Jiang, M.D.; Li, Y.; Liu, W. Properties of a General Quaternion-Valued Gradient Operator and Its Application to Signal Processing. Front. Inf. Technol. Electron. Eng. 2016, 17, 83–95. [Google Scholar]
- Capon, J. High-resolution Frequency-wavenumber Spectrum Analysis. Proc. IEEE 1969, 57, 1408–1418. [Google Scholar] [CrossRef]
- Frost, O.L., III. An algorithm for linearly constrained adaptive array processing. Proc. IEEE 1972, 60, 926–935. [Google Scholar] [CrossRef]
- Wang, M.; Ma, W. A structure-preserving algorithm for the quaternion Cholesky decomposition. Appl. Math. Comput. 2013, 223, 354–361. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lan, X.; Liu, W. Fully Quaternion-Valued Adaptive Beamforming Based on Crossed-Dipole Arrays. Electronics 2017, 6, 34. https://doi.org/10.3390/electronics6020034
Lan X, Liu W. Fully Quaternion-Valued Adaptive Beamforming Based on Crossed-Dipole Arrays. Electronics. 2017; 6(2):34. https://doi.org/10.3390/electronics6020034
Chicago/Turabian StyleLan, Xiang, and Wei Liu. 2017. "Fully Quaternion-Valued Adaptive Beamforming Based on Crossed-Dipole Arrays" Electronics 6, no. 2: 34. https://doi.org/10.3390/electronics6020034
APA StyleLan, X., & Liu, W. (2017). Fully Quaternion-Valued Adaptive Beamforming Based on Crossed-Dipole Arrays. Electronics, 6(2), 34. https://doi.org/10.3390/electronics6020034






