1. Introduction
Robotic systems have been playing an important role in the modern world. They are applied in several areas: in manufacturing, entertainment, the toy industry, the medical field, exploration, military and multimedia applications [
1,
2,
3]. Most commercial robots need manual programming or teleoperation for the executing of movements. This important task requires human intervention that results in long set-up times, and the expertise of operators to control robots. Autonomous navigation is an alternative for solving this issue. Flexibility and energy efficiency are also important achievements of modern robotics [
4,
5].
Navigation includes algorithms for perception and motion estimation, and also for path planning and optimization in order to connect the start point with the goal point. Several techniques, such as proximity sensors, have been used for perception. However, 3D point cloud processing is one of the most important areas of computer vision because it obtains a better description of the world. Different range imaging cameras are used to capture depth maps, such as stereo cameras, structured light scanners, time-of-flight cameras and others.
In this system, we use a low-cost 3D sensor to generate the 3D binary occupancy grid map and to describe the workspace. Our approach consists of a path planning system that obtains the environment description from a Kinect V2 point cloud, recognizes the start and goal point by computer vision techniques and solves the path planning issue using a variant of the RRT algorithm. The system includes calibration between the Kinect coordinate frame and the workspace coordinate frame using a registration technique.
Path planning determines a collision-free path between start and goal positions in a workspace clustered with obstacles [
6]. Different path planning algorithms are used to find an optimal solution trajectory. Sample-based methods are widely used because of their effectiveness and low computational cost on high dimensional spaces. These methods use a representative configuration space and build a collision-free roadmap connecting points sampled from the obstacle free space.
The Probabilistic Roadmaps (PRM) and the RRT are sample-based methods. The RRT algorithm has been commonly used for a fast trajectory search because of its incremental nature. There are several versions of the RRT developed to improve the cost of the solution path. In our work, we compared the RRT with the RRT* algorithm and two other variations using the path cost as evaluation metrics.
This paper is organized as follows: The next section is focused on a brief description of related works. In
Section 3,
Section 4 and
Section 5 we introduce the methods proposed to solve each part of the system in order to achieve the goal: registration, RGB segmentation and RRT path planning methods. Finally, experimental results and conclusions are presented in the last two sections.
2. Related Work
Research groups on robotics and computer vision have developed different techniques for robot navigation such as 3D perception and mapping based on RGB-D cameras [
7], laser range scanners [
8] and stereo cameras [
9]. The Kinect was released in November 2010 as an RGB-D commercial camera, and after that, several applications on robotics appeared [
10,
11].
Segmentation and object recognition are fundamental algorithms for vision applications. Recently, the growing interest in 3D environments for robot navigation has increased the research on 3D segmentation. In [
12], a color and depth segmentation is proposed to detect objects of an indoor environment by finding boundaries between regions based on the norm of the pixel intensity. A novel technique for depth segmentation uses the divergence of a 2D vector field to extract 3D object boundaries [
13].
There are also several works on the literature for path planning to connect start and goal locations. The Ant Colony Algorithm, based on the behavior of ants searching for food, is used in many research projects due to its global optimization performance in multi goal applications [
14]. Others use neural networks to give an effective path planning and obstacle avoidance solution that leads the robot to the target neuron that corresponds to the target position [
15,
16]. Some other strategies use behavior-based navigation and fuzzy logic approaches. In this solution, the image provides the data for the fuzzy logic rules that guide the robot to the safest and most traversable terrain region [
17].
In this paper, we use a probabilistic path planning algorithm. Several optimizations have been developed in this area such as the RRT-Connect approach [
18] that uses a simple greedy heuristic. Other variants have been presented in [
19,
20]. Our contribution is focused on the overall system of an optimal robot path planner, comparing the resulting paths of two different variants of the RRT* algorithm.
3. Workspace Data
A path planning algorithm requires a workspace, the initial and goal positions, and a robot. Our proposed system has three stages: environment perception, detection of target points and path planning.
In 2013, the Kinect V2 was introduced with a different technology with respect to the previous Kinect V1. The Kinect V2 is based on the measurement principle of time of flight: the distance to be measured is proportional to the time needed by the active illumination source for traveling from the emitter to the target [
21]. Therefore, a matrix of time of flight cameras allows us to estimate the distance to an object, for each pixel. The Kinect V2 also has an RGB-D camera and an infrared camera.
In
Table 1, Kinect V2 characteristics and technical specifications are presented.
Depending on the distance between the object point and sensor, the pixel size has an estimated value between 1.4 mm at 0.5 m of depth and 12 mm at 4.5 m of depth, as shown in
Table 1, giving the approximate resolution of our point cloud.
We have used the open-source software developed by Hatledal, L.I. [
23] to obtain the colored point cloud in millimeters from the delivered depth and RGB data. This point cloud will be processed with the proposed algorithm. We align the point cloud relative to the Kinect, to the point cloud relative to the workspace coordinate frame (real physical set of points), previous to image segmentation. A technique to solve this issue is point cloud registration. The objective of registration is the matching of two point sets by the estimation of the transformation matrix that maps one point set to the other [
24,
25]. A widely used registration method is the Iterative Closest Point (ICP) due to its simplicity and low computational complexity. ICP assigns correspondence based on the nearest distance criteria and the least-squares rigid transformation giving the best alignment of the two point sets [
26].
Assuming that the point set
and
are matched and related by:
where
is a
rotation matrix,
is a 3D translation vector and
is a noise vector [
27].
The goal is to obtain the optimal transformation for mapping the set
onto
minimizing the least-square error:
The least-squares solution is not optimal if there are many outliers or incorrect correspondences on the dataset, and therefore other techniques should be added. Several algorithms are able to compute the closed-form solution for
and
. In this work, we use the ICP algorithm to register two point clouds, as presented in
Figure 1.
This algorithm uses an outlier filter before the transformation matrix calculation, in order to solve the incorrect correspondence issue.
We find the rigid transformation matrix (
) that aligns point set
to point set
so:
where
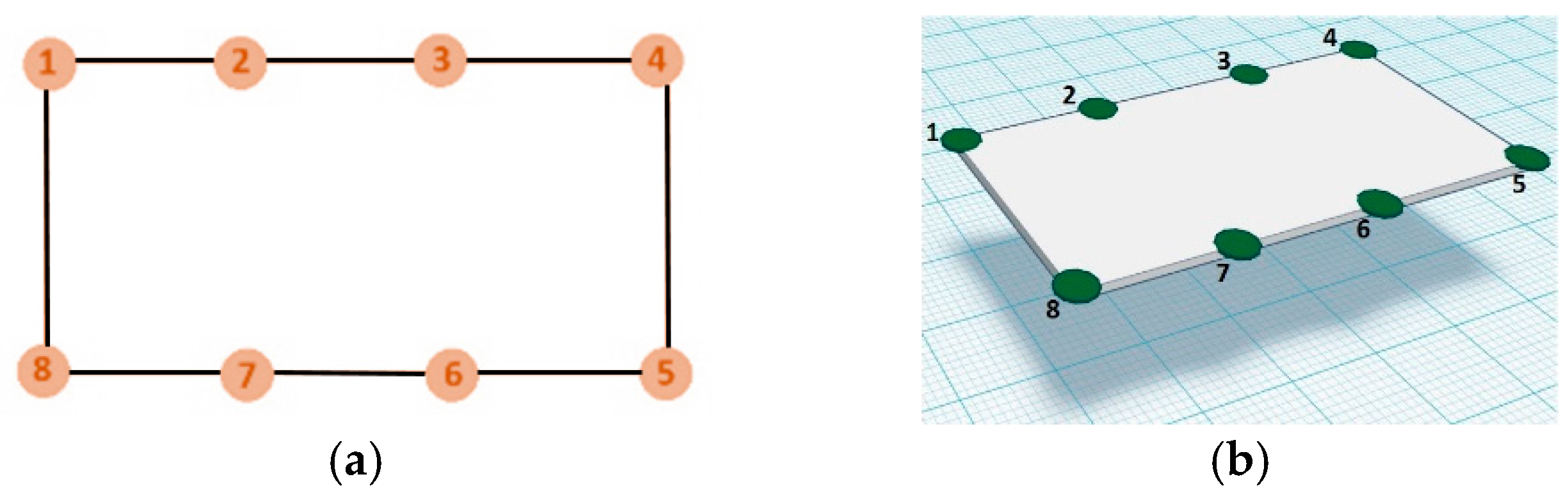
is a vector with the centroid coordinates of the boundary circles extracted from the point cloud in the work plane, and
are the corresponding data points from the workspace coordinate frame, as shown in
Figure 2.
With this technique, we get the point cloud on the robot coordinate frame suitable for feature extraction and path planning algorithms.
4. Target Points
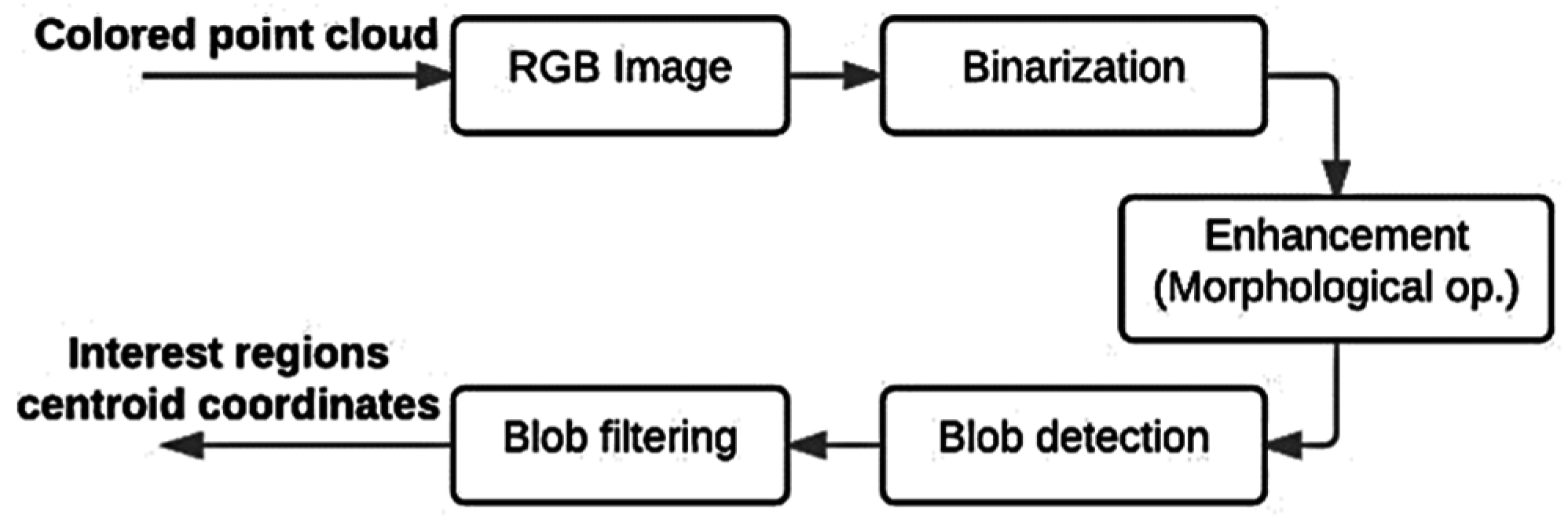
Image segmentation is the process of separating an image into regions. Each region is defined as a homogenous group of connected pixels with respect to a selected interest property, such as color intensity or texture [
29]. For this purpose, one of the most effective approaches is segmentation using color threshold [
30]. This method is used in object recognition, assuming that pixels with a color value, inside of a defined range in the color channels, belong to the same class or object. A threshold image can be defined by:
where
is a set of pixels from the input image,
is the output binary image (binarization) and
is the threshold value [
31] (a threshold value is needed for each color channel).
In our work, the input image is generated from the point cloud, so each pixel has a corresponding
xyz coordinate. The thresholds are obtained locally by selecting a target region pixel to obtain its color component and a sensibility value chosen experimentally. The threshold of our image was defined by:
where
are the manually-selected pixel color components and
is the sensibility.
After the binary mask is obtained, we use morphological operations to remove noise and unwanted holes. Some of the main morphological operations that can be used are dilatation, erosion, opening and close.
Dilation is applied to each element of the mask image
using a structuring element
, resulting in a new mask image with a different size. The dilation
removes holes and indentations smaller or equal to the structuring element [
32].
Erosion removes noise smaller than the structuring element.
The opening eliminates edges and removes some of the foreground bright pixels.
The closing operation keeps the background regions with a similar size of the structuring element, and removes all other pixels of the background.
We use the opening and close operations to enhance our binary image and obtain a better approximation of the interest regions.
The next step is representation where adjacent pixels of the same class are connected to form spatial sets
. For the representation of our binary image, we use the blob detection method of Corke P. [
33]. Blob is a spatial contiguous region of pixels. Properties or features such as area, perimeter, circularity, moments or centroid coordinates are widely used to identify these regions.
We identify our interest regions by filtering the blobs based on their position and area in order to simplify the problem. Knowing the boundaries of the workspace and the minimum and maximum size of the target circles, we obtained the interest blobs and their centroid coordinates.
In
Figure 3, we can see the segmentation process implemented in our system.
5. Path Planning
5.1. Travelling Salesman Problem
This path planning problem, known as the travelling salesman problem (TSP), is focused on the organization of points and the search of an optimal path through all of them. We have a set
of cities and a Euclidean distance
for each pair
of cities. The goal of the algorithm is to order the cities so as to minimize the total length of the tour [
34].
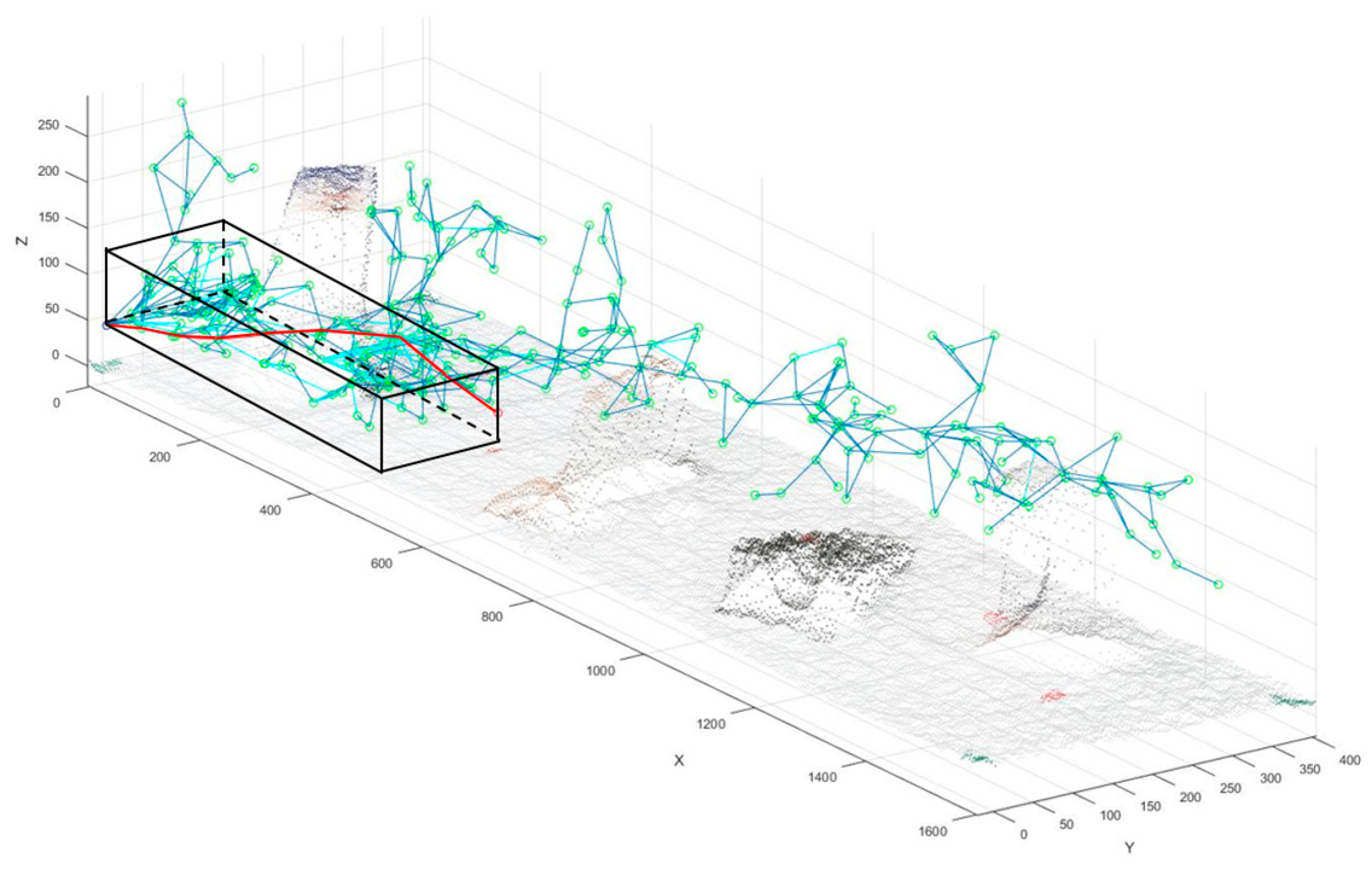
Our solution for the TSP is based on the Nearest Neighbor (NN) algorithm shown on Algorithm 1. The performance of this approach is not the best in the literature, but NN gives suitable solutions with respect to our workspace and the possible locations of the target points. An example of the workspace and target points is presented in
Figure 4.
The algorithm is approached as follows:
| Algorithm 1: The nearest neighbor algorithm |
| 1: |
| 2: starting point |
| 3: from unvisited points |
| 4: mark as visited |
| 5: if all are visited, end |
| 6: return to step 3 |
Once the points are ordered, we develop the path planner based on the RRT algorithm, as mentioned above.
5.2. RRT
Using the notation from [
35], the path planning problem can be denoted as:
is a bounded connected open subset of where .
is a graph composed by a set of vertexes and edges .
and , subsets of , are the obstacle region and the goal region respectively.
The obstacle free space is denoted as and the initial state is an element of .
A path in should be a collision-free path.
In path planning algorithms, there are two variations: the feasibility problem that refers to the searching of a feasible path and the failure report otherwise; and the optimization problem that focuses on a feasible path with minimal cost. The cost is assigned to a non-negative cost of each collision-free path. A feasible path is a collision free-path that starts in and ends in .
In this part, we introduce the standard RRT algorithm and the RRT* variations tested in our system. These algorithms rely on the following functions:
Function Sample: returns , an independent identically distributed sample from .
Function Nearest Neighbor: returns the closest vertex to the point , in terms of the Euclidean distance function.
Function Steer returns a point at a distance , from in direction to .
Function Obstacle Free: Given two points , the function returns true if the line segment between and lies in and returns false otherwise.
Function Near Vertices: returns a set of vertices that are close to the point within the closed ball of radius centered at .
Function Parent: returns the parent vertex of .
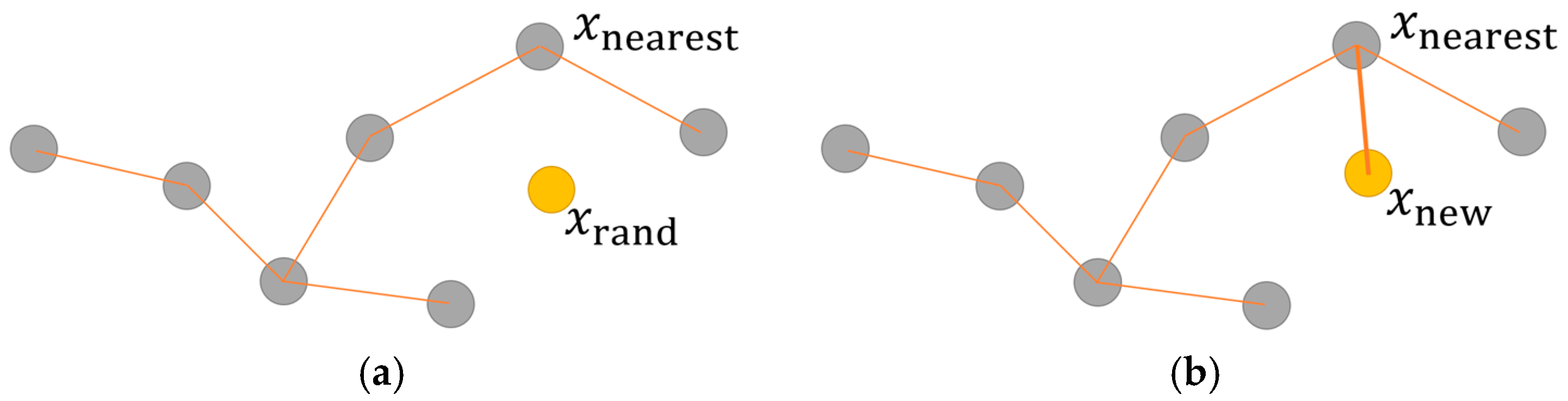
As shown in
Figure 5, the RRT algorithm starts in the initial state. For each iteration, the graph incrementally grows by sampling a random state
from
, and connecting
returned by function
Steer with the nearest vertex in the tree
, when the connection is obstacle-free.
is added to the vertex set and
to the edge set. This algorithm is detailed in Algorithms 2 and 3.
The connections between two edges, considered in this paper as straight-line connections, are made by increasing the distance from the start position using the local planner.
| Algorithm 2: RRT main algorithm |
| 1: |
| 2: |
| 3: |
| 4: |
| 5: ; |
| 6: |
| Algorithm 3: Extend function of the RRT algorithm |
| 1: |
| 2: |
| 3: |
| 4: |
| 5: |
| 6: |
| 7: return |
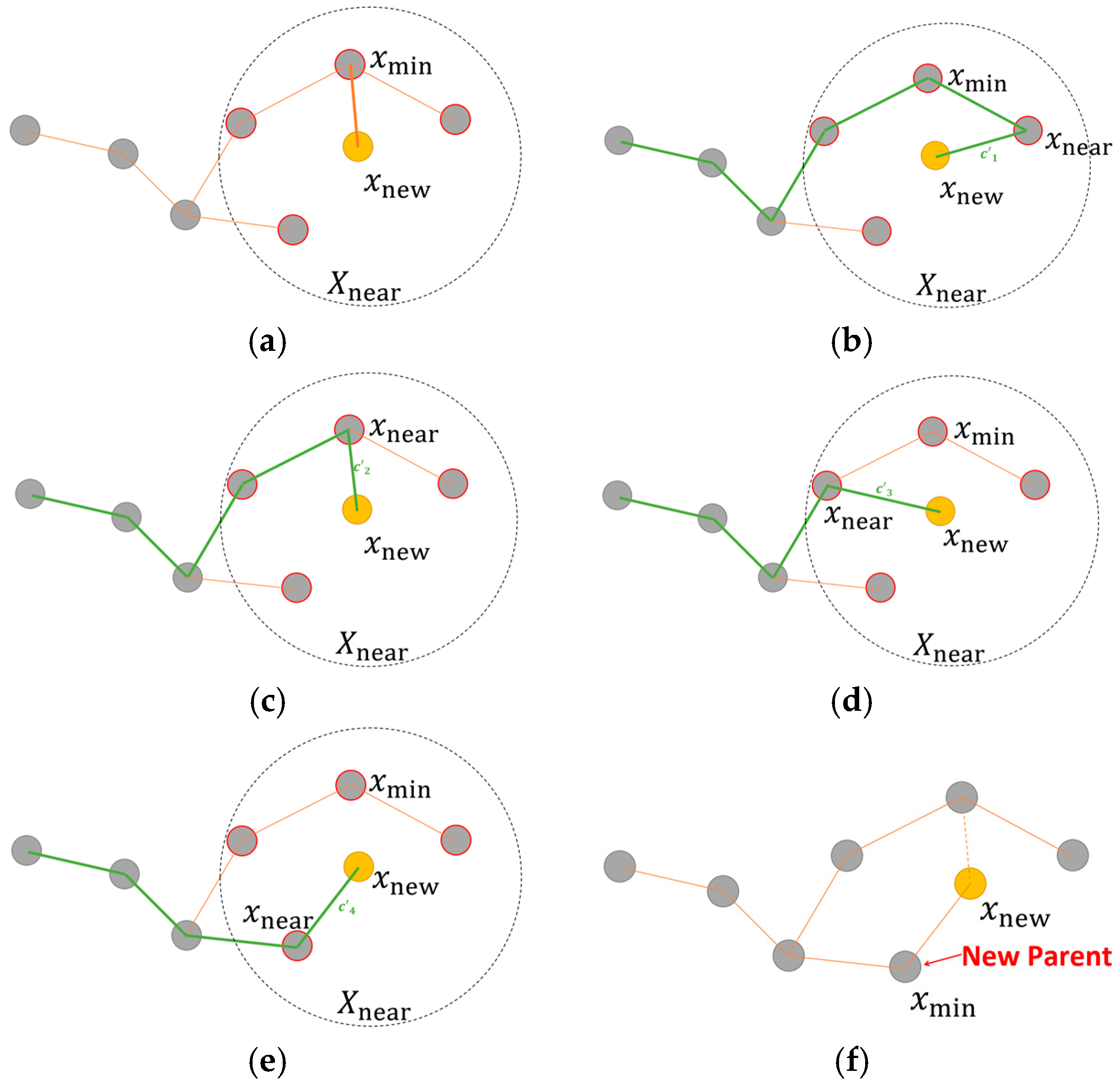
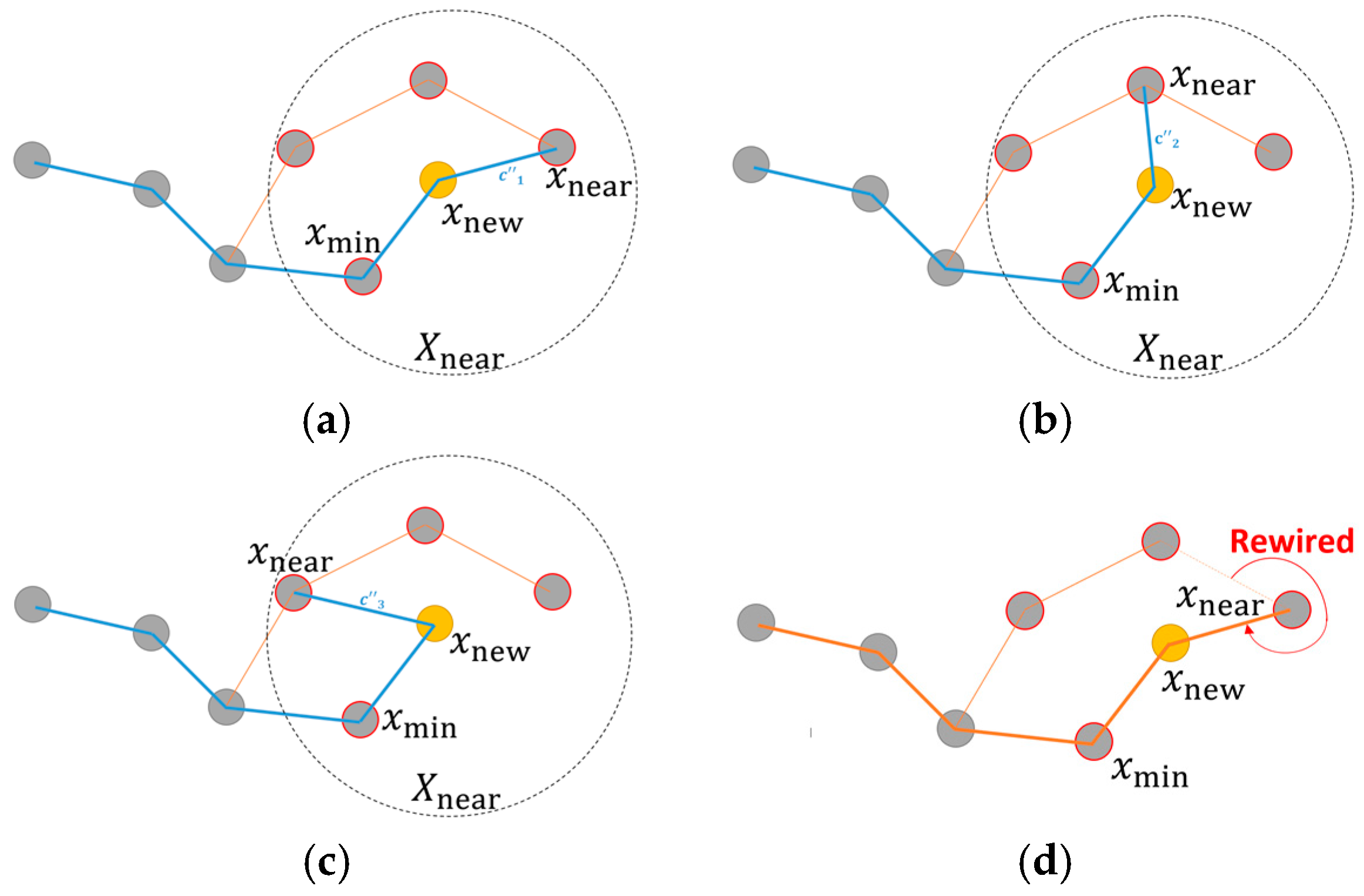
5.2.1. RRT* Algorithm
The RRT* algorithm adds vertices in the same way as the RRT (Algorithm 2), but has two optimization procedures in the extend function shown in Algorithm 4. These optimizations connect vertices to obtain a path with minimum cost. The first one, done after
, is added to the vertex set of the tree. The function Near Vertices returns the set of vertices
. If the obstacle-free connection between
and one of the vertices of
has a lower cost than the path through
then
is added to the edge set, and the other connections are ignored. An example of this optimization is shown in
Figure 6.
| Algorithm 4: Extended function of the RRT* algorithm |
| 1: |
| 2: |
| 3: |
| 4: |
| 5: |
| 6: |
| 7: |
| 8: |
| 9: |
| 10: |
| 11: |
| 12: |
| 13: |
| 14: |
| 15: |
| 16: |
| 17: |
| 18: |
| 19: |
| 20: |
| 21: return |
The second optimization procedure checks if the cost of one of the remaining vertices of
is lower when it is connected through the new vertex
. If it is lower, then the edge
is deleted and the edge
is added to the edge set
, as shown in
Figure 7.
The result is an optimal path where each vertex has the lowest cost. The result of the example is presented in
Figure 8.
In order to decrease the time of finding a feasible solution, and to accelerate the rate of convergence and optimization, we proved two variations of the RRT*. The modifications were made on the Sample function by changing the probability of the generated random node. We have called these versions RRT* Goal, RRT* Limits and the combination of both RRT* Goal Limit (RRT* GL).
5.2.2. RRT* Goal Algorithm
In Algorithm 5, we present the sample function algorithm. In this function we guide the exploration of the tree in the direction of the goal region. We give a probability of 50% for sampling the goal region. The other 50% returns an identically distributed sample from .
| Algorithm 5: function of the RRT* Goal algorithm |
| 1: |
| 2: |
| 3: |
| 4: |
| 5: |
5.2.3. RRT* Limits Algorithm
Once the feasible path is found, we increase the probability of the random sample in a specific space. This accelerates the rate of convergence to an optimal, low-cost path.
As shown in
Figure 9, we obtain the uniform distributed random sample by delimiting the range to the minimum and maximum coordinates (
x,
y,
z) of the path found. This increases the density of random samples at the path surroundings, avoiding unnecessary optimizations in other sections of the tree. This is shown on Algorithm 6.
| Algorithm 6: function of the RRT* Limits algorithm |
| 1: |
| 2. |
| 3. |
| 4. |
| 5. |
| 6. |
| 7. |
6. Experiment
The system was implemented on a laptop with the following characteristics: Processor Intel Core i7-4500 @1.90 GHz and 8.00 GB RAM. The graphics card used was a GeForce GT 735 (NVIDIA, Santa Clara, CA, USA).
A real 3D image captured by a Kinect V2 was processed off-line for three different scenes on the workspace. Each scenario had one, two and three obstacles, respectively, between the start and goal point.
The experiment was divided into three parts: (a) the alignment of the workspace point cloud of the Kinect to the workspace coordinate frame; (b) the target point recognition; and (c) the path planning algorithm with the variations. During the testing, we used a Cartesian robot to reach the target points and measure the obtained coordinates that do not depend on the robot dynamics [
36,
37,
38].
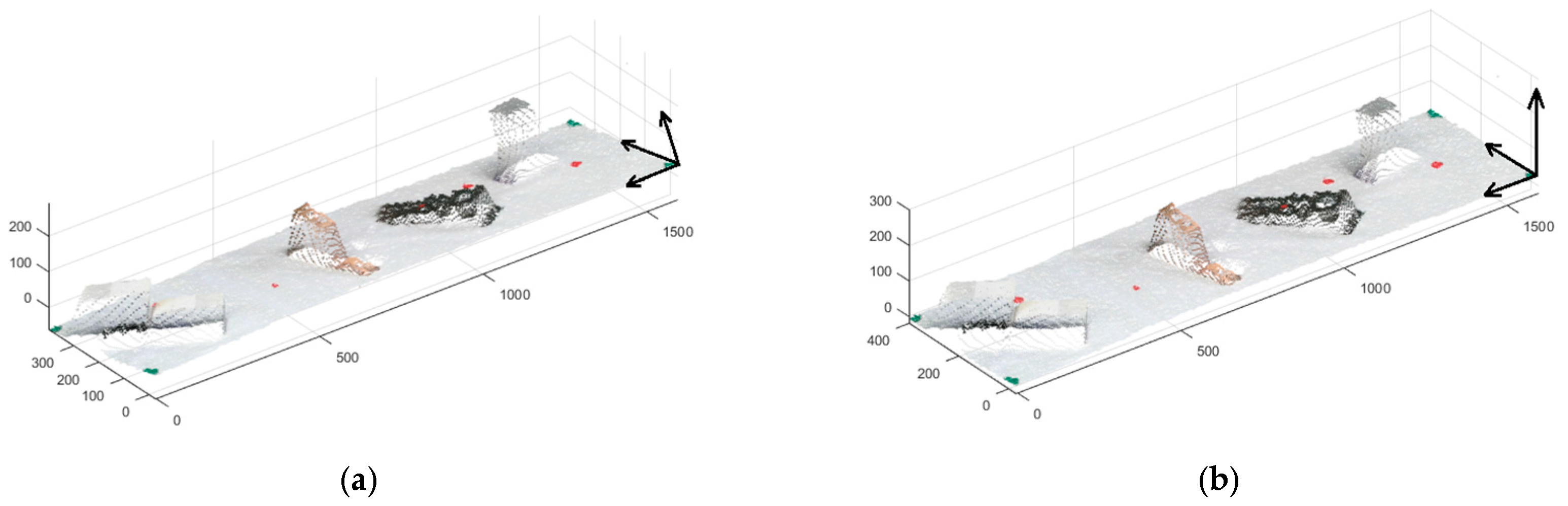
6.1. Point Cloud Alignment
As mentioned above, the method used for point cloud alignment was the registration of two data sets. We rotated the Kinect for testing the transformation matrix effect on the original point cloud, as shown in
Figure 10.
In
Table 2, we present information on eight workspace boundary circles (landmarks), their centroid coordinates estimated from the Kinect coordinate frame, the real coordinates on the workspace, the calibrated coordinates after registration and the error percentage of each circle centroid coordinate.
Because all of the circles are located on the same plane, we can calculate the average error percentage as the error of the workspace plane on the robot coordinate frame related to the Kinect pose by:
where
is the difference between the maximum and minimum value of the workspace seen by the Kinect on the
x coordinate.
We can see in
Table 2 that our system obtains an aligned point cloud with high accuracy.
6.2. Target Points Recognition
In this section, in
Table 3 we present the location on millimeters of five circle centroids recognized with the algorithm on the
xy plane and the corresponding error percentage.
The error was also calculated with respect to the robot workspace seen by the Kinect. The points locations were obtained very accurately.
6.3. Path Planning
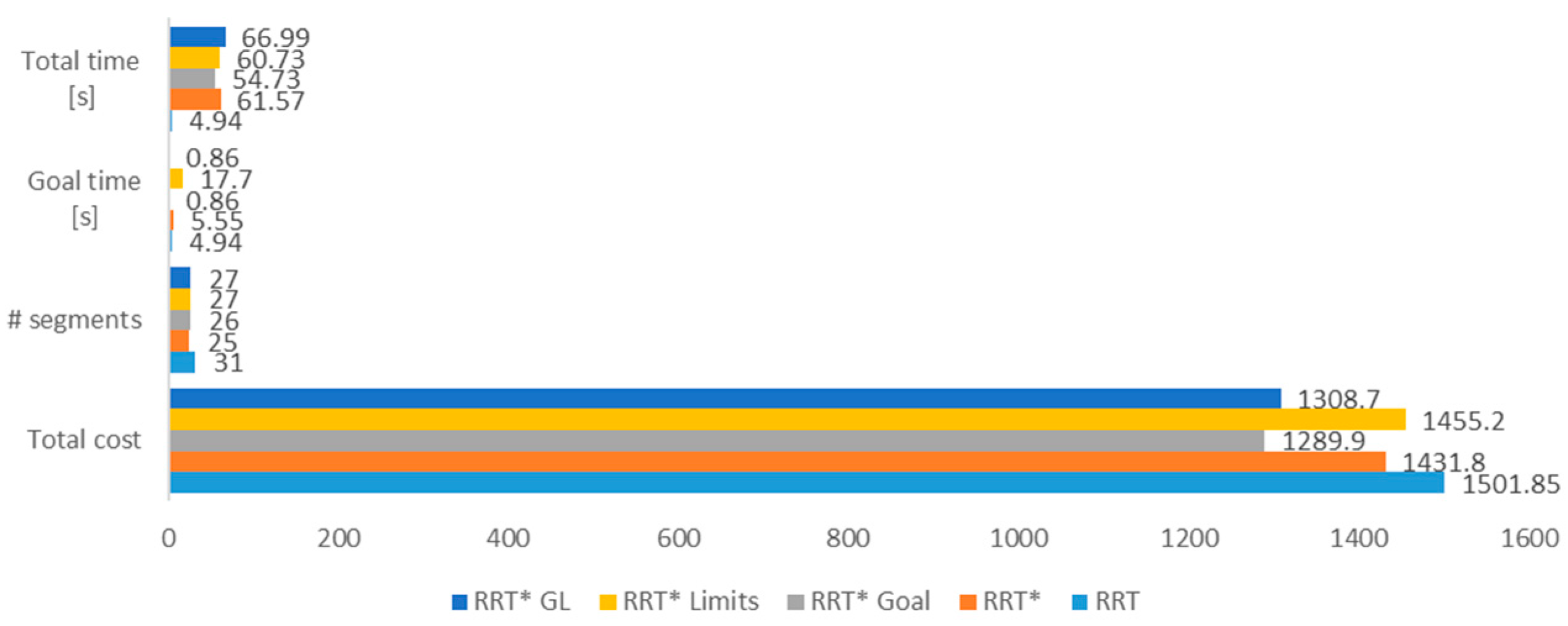
Each algorithm was tested ten times to obtain the mean cost, number of segments in the resulting path, the time for locating the target point and the execution time of the algorithm through all of the iterations.
We tested each algorithm with 300, 600 and 1000 iterations in order to compare their results with respect to path optimization.
Figure 11,
Figure 12 and
Figure 13 show a bar chart of the three experiments with 600 iterations, respectively, to visually compare the resulting values of the tested algorithms.
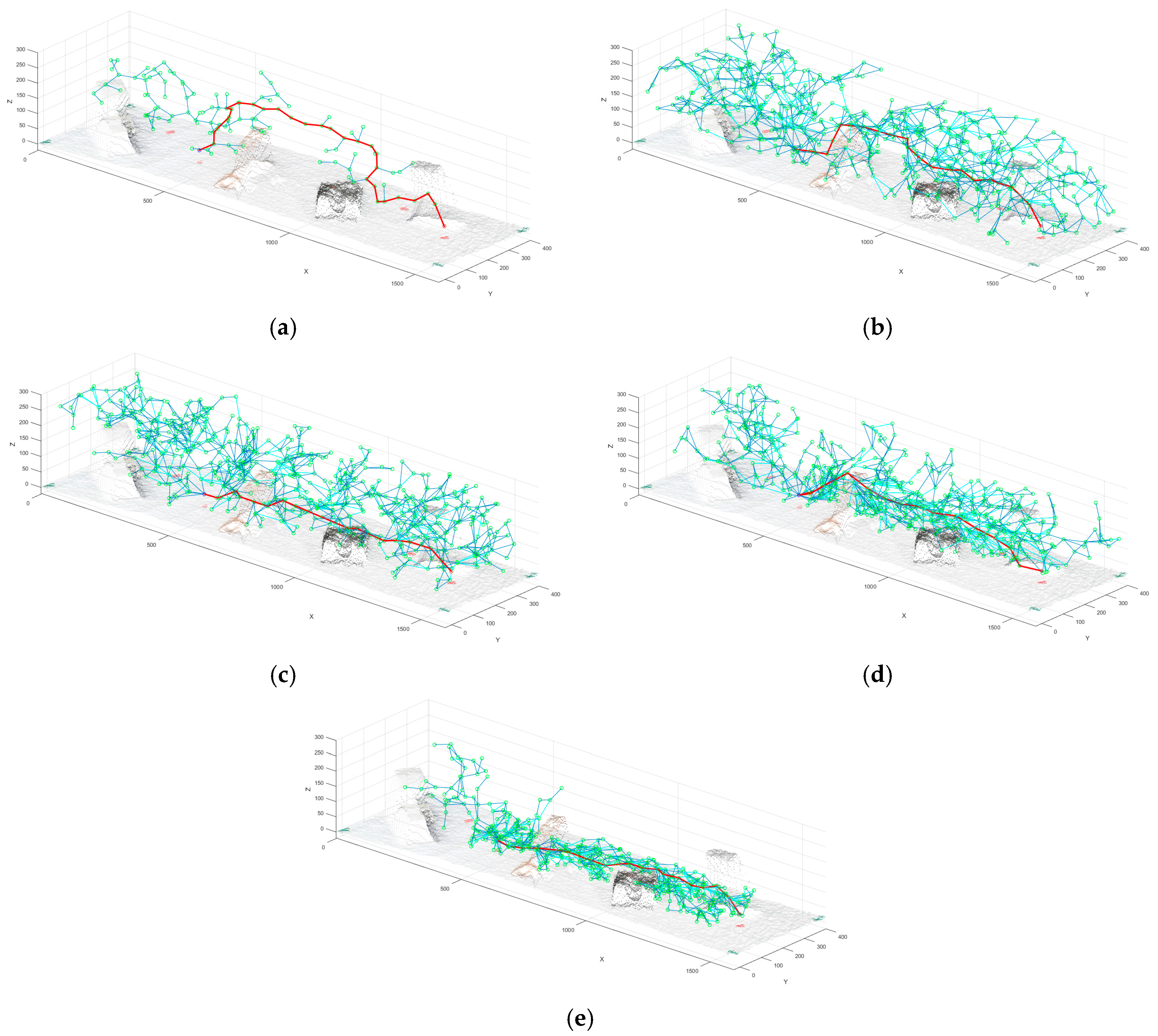
As we can see in the results tables, the RRT* Goal algorithm significantly decreases the time of finding a feasible solution (Goal time), providing more time and computational resources to the path optimization. The RRT* Limits algorithm increases the density of the tree branches around the path, as seen in
Figure 14d, which results in lower path costs with respect to the standard RRT*. The combination of both methods shows a significant improvement in the performance of the path planning algorithm, producing a more optimal path without increasing the number of iterations. However, this method requires more time and therefore more computational resources to run. This disadvantage can be balanced by decreasing the number of iterations to obtain similar path costs in less time.
The number of segments of the path in the RRT* is the lowest in most of the cases, which means that in order to achieve a more optimal path, the algorithms need more segments to reduce the path cost.
Video results are provided in [
39].
7. Conclusions
In this paper, we experimentally tested the optimal and robust performance of our system including point clouds alignment, target point detection and path planning algorithms.
Flexibility and energy efficiency are important features for the autonomous navigation of robots in a workspace. In our approach, flexibility is given by the automatic alignment of the Kinect V2 point cloud to the robot coordinate frame, using the ICP algorithm. Target point detection also provided flexibility to the system. The color based threshold technique was sufficient for obtaining the goal region centroid of each target point. This approach showed a high performance with the RGB source of the Kinect.
Several variations of the RRT algorithm were successfully tested in order to compare their results with respect to the autonomy and energy efficiency of robots’ navigation. We have selected RRT* GL, which achieves a fast and optimal path between the start and goal point. The RRT* Goal algorithm reduces the time required for finding a feasible solution. The RRT* Limits algorithm improves the optimization by increasing the density of the tree branches in the path region.