On Goodput and Energy Measurements of Network Coding Schemes in the Raspberry Pi
Abstract
:1. Introduction
2. Coding Schemes
2.1. Random Linear Network Coding
2.1.1. Encoding
2.1.2. Decoding
2.1.3. Recoding
2.2. Sparse Random Linear Network Coding
2.2.1. Method 1: Fixing the Coding Density
2.2.2. Method 2: Sampling the Amount of Packets to Combine
| Algorithm 1: Computation of the set of indexes for packet combination in SRLNC. |
| Data: k: Size of . g: Generation Size |
| Result: : The set of non-repeated indexes |
| = { }; |
| while do |
 |
| end |
2.3. Tunable Sparse Network Coding
2.4. Network Coding Implementation for the Raspberry Pi Multicore Architecture
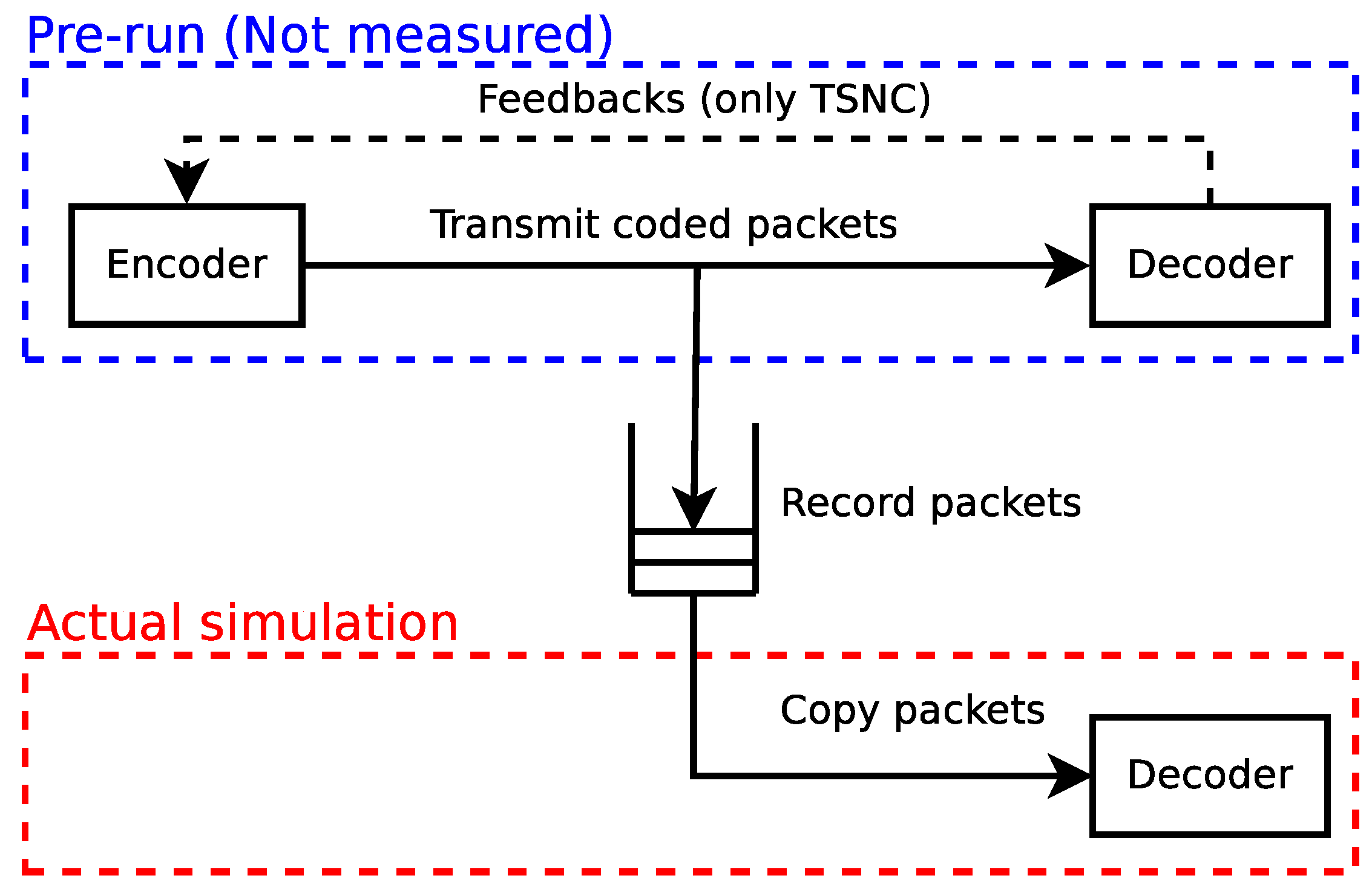
3. Metrics and Measurement Methodology
3.1. Goodput
3.1.1. Encoding Benchmark
3.1.2. Decoding Benchmark
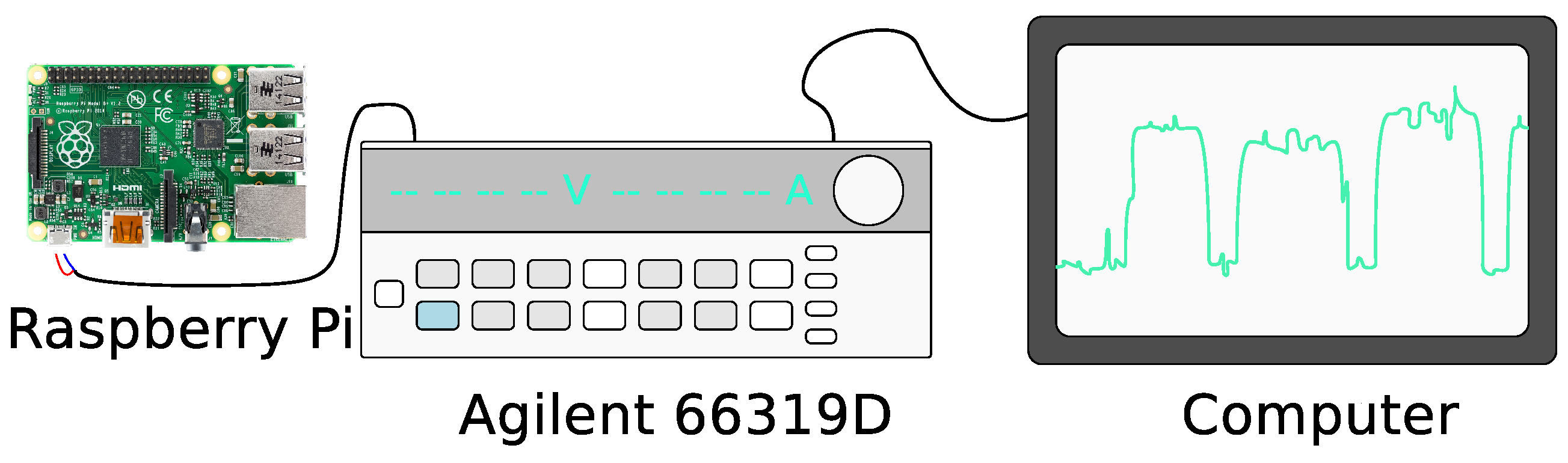
3.2. Energetic Expenditure
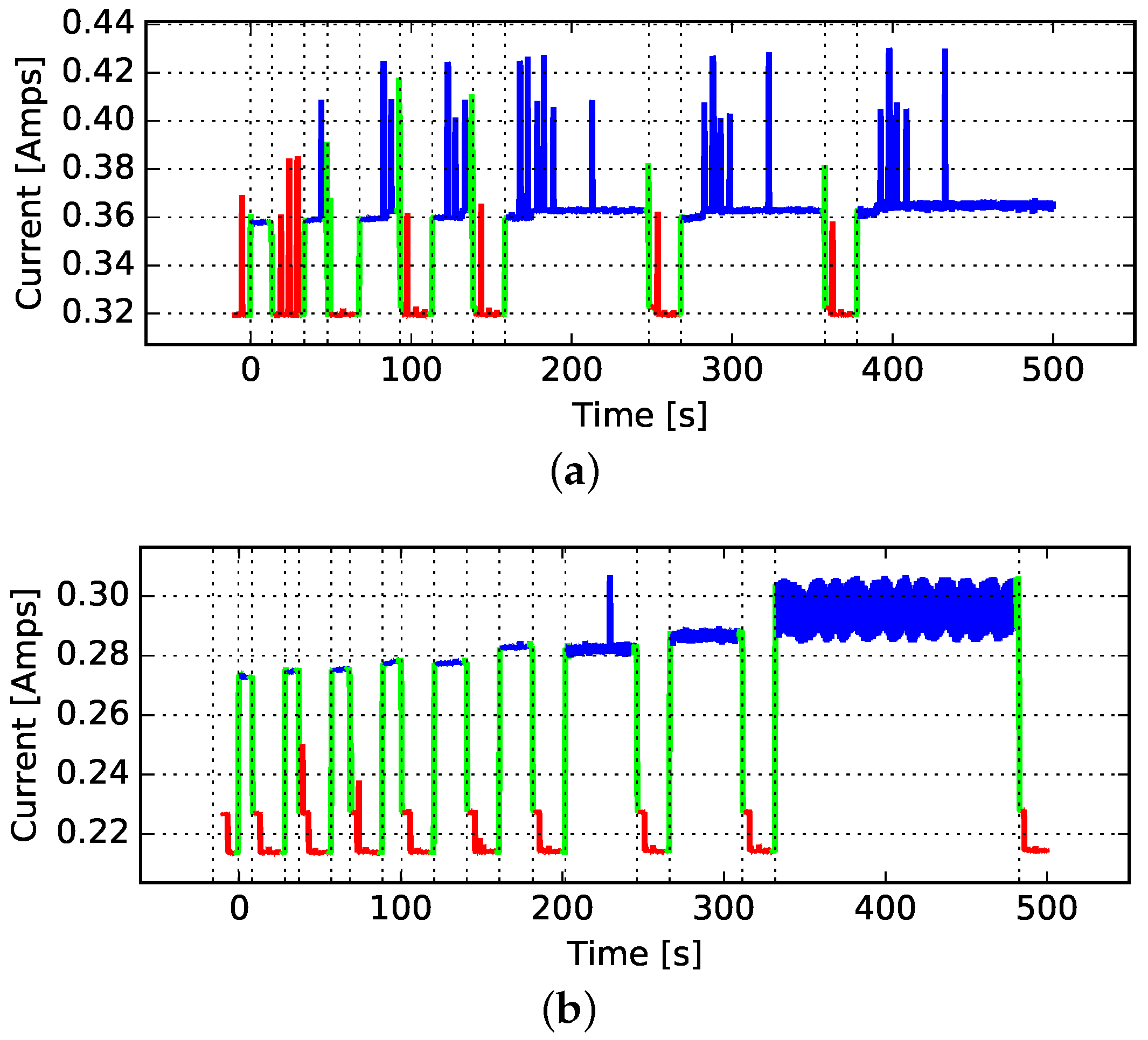
3.2.1. Average Power Expenditure
3.2.2. Energy per Bit Consumption
4. Measurements and Discussion
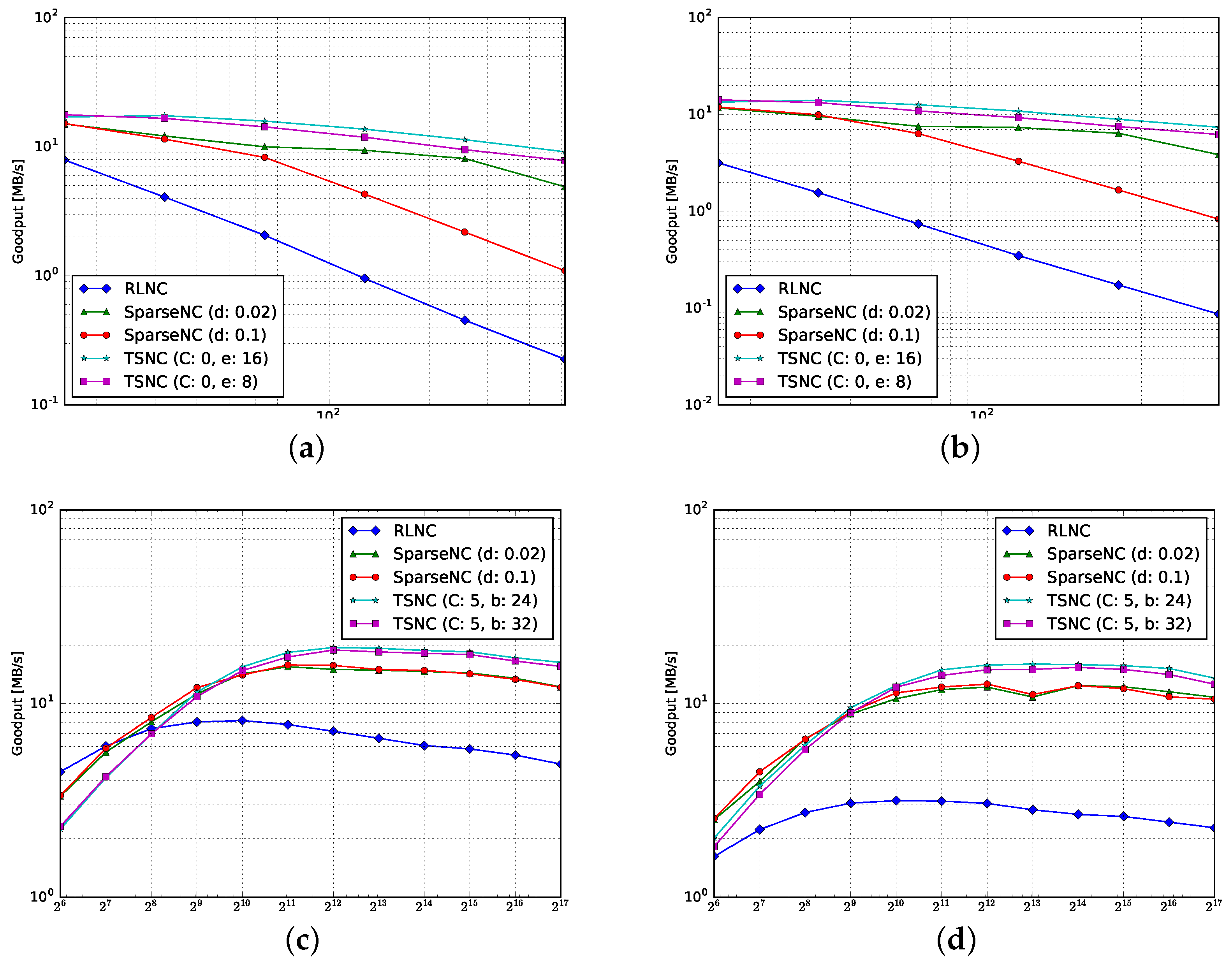
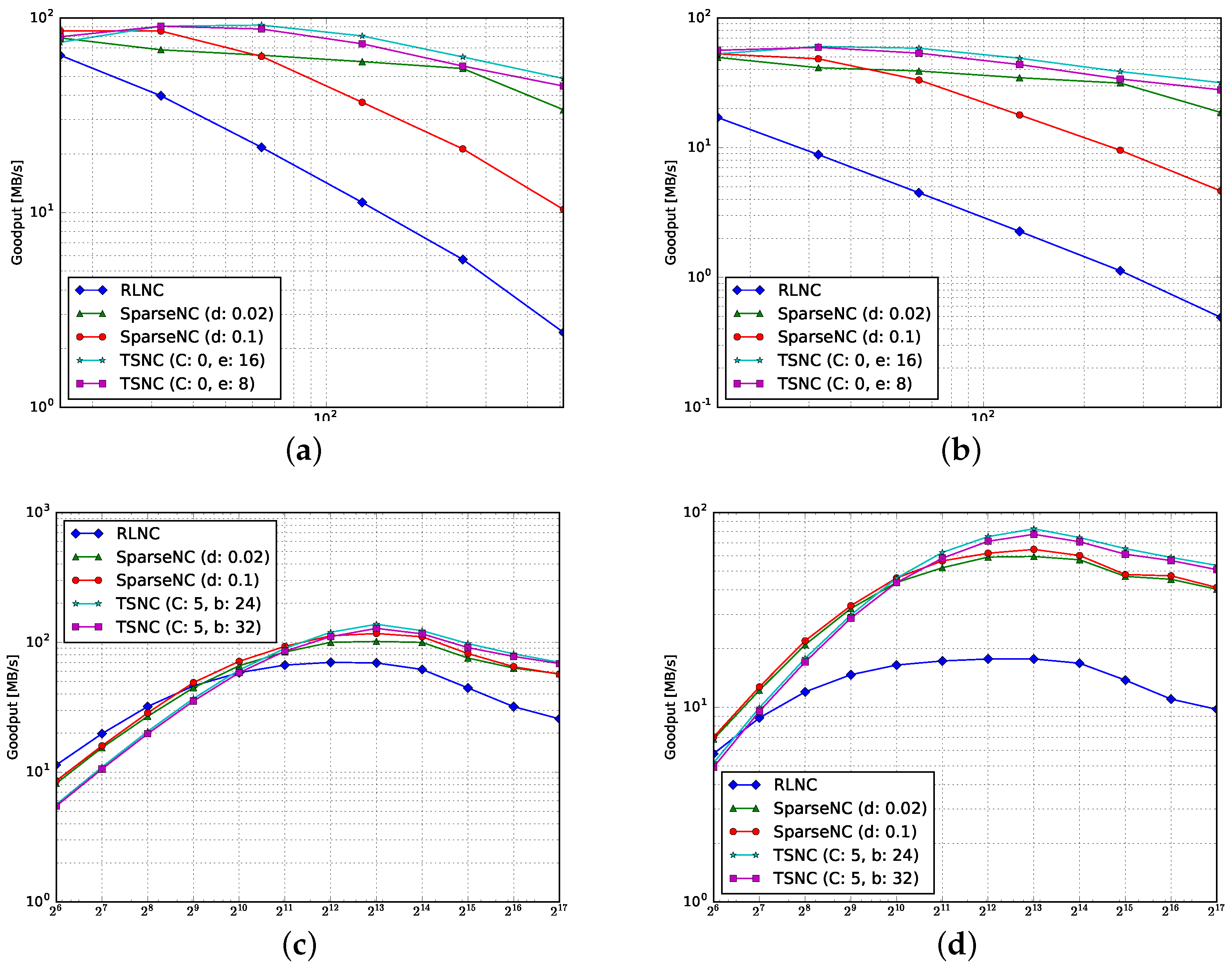
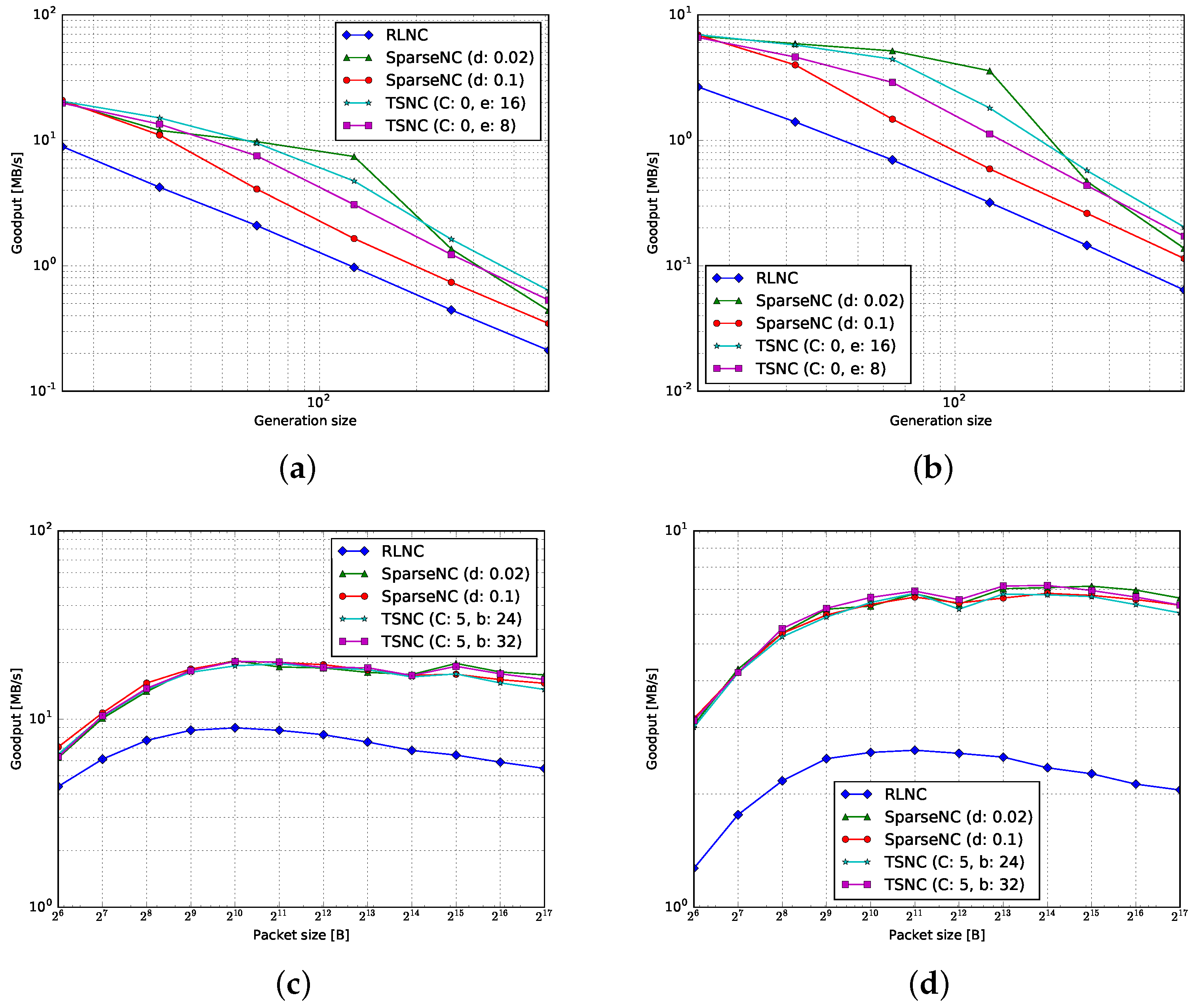
4.1. Goodput
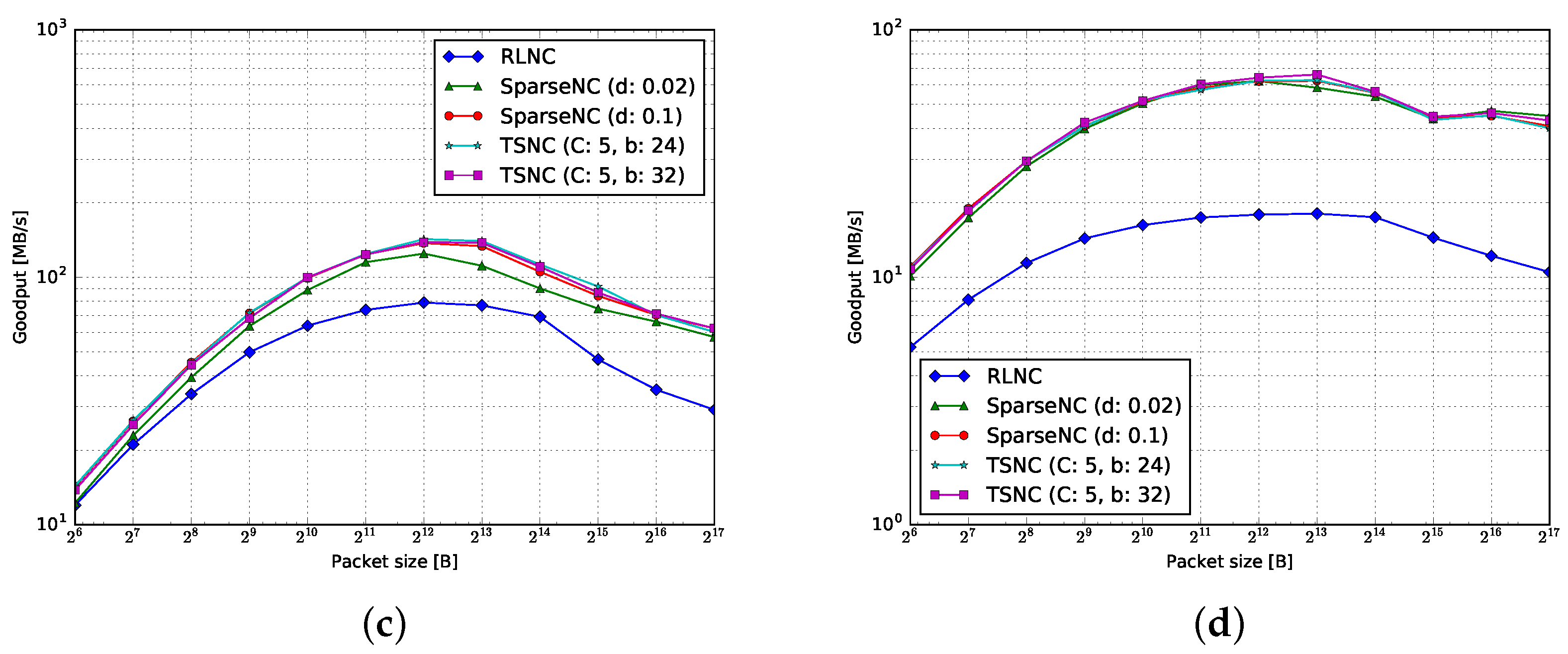
4.1.1. Encoding
4.1.2. Decoding
4.2. Average Power
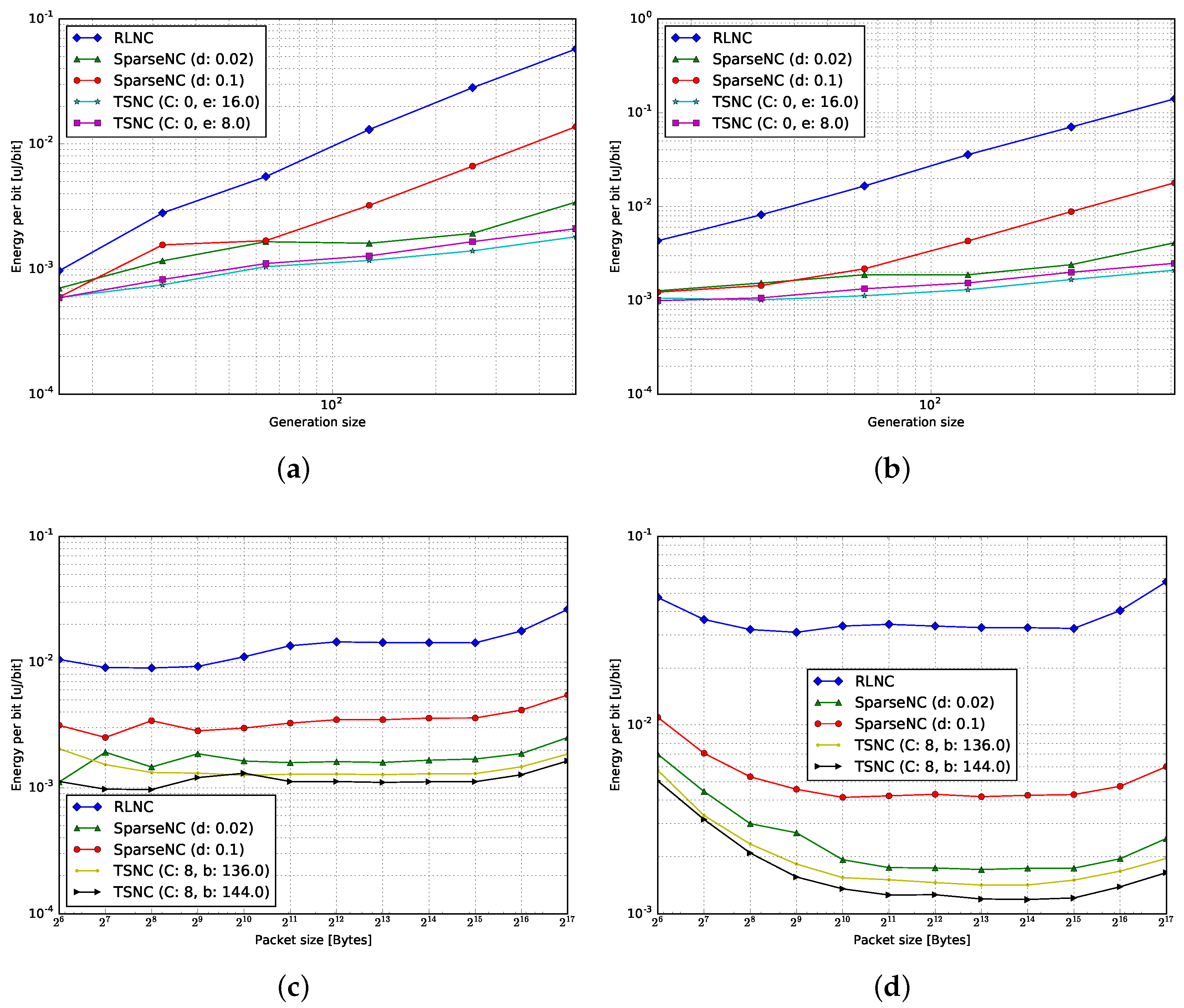
4.3. Energy per Bit
4.3.1. Encoding
4.3.2. Decoding
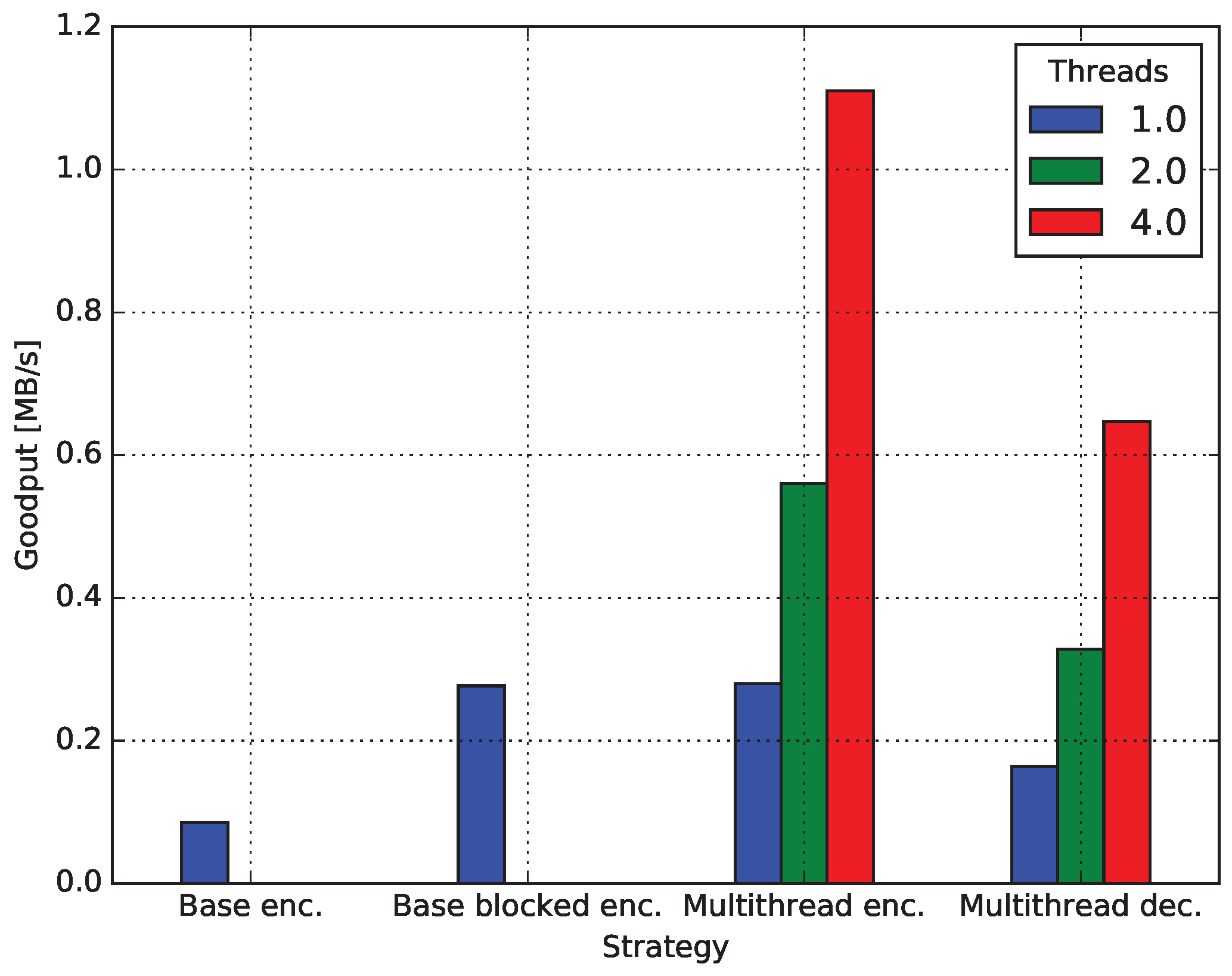
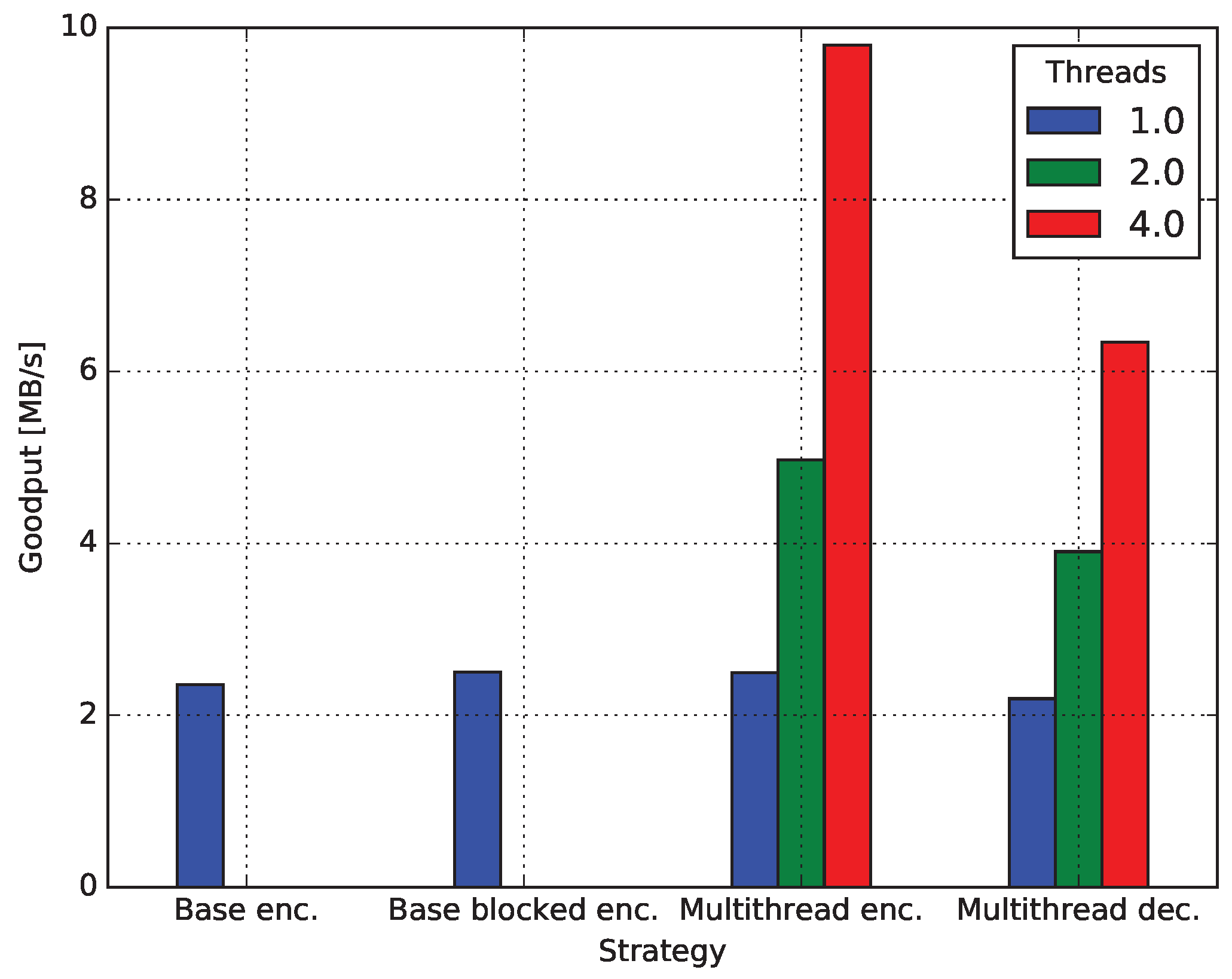
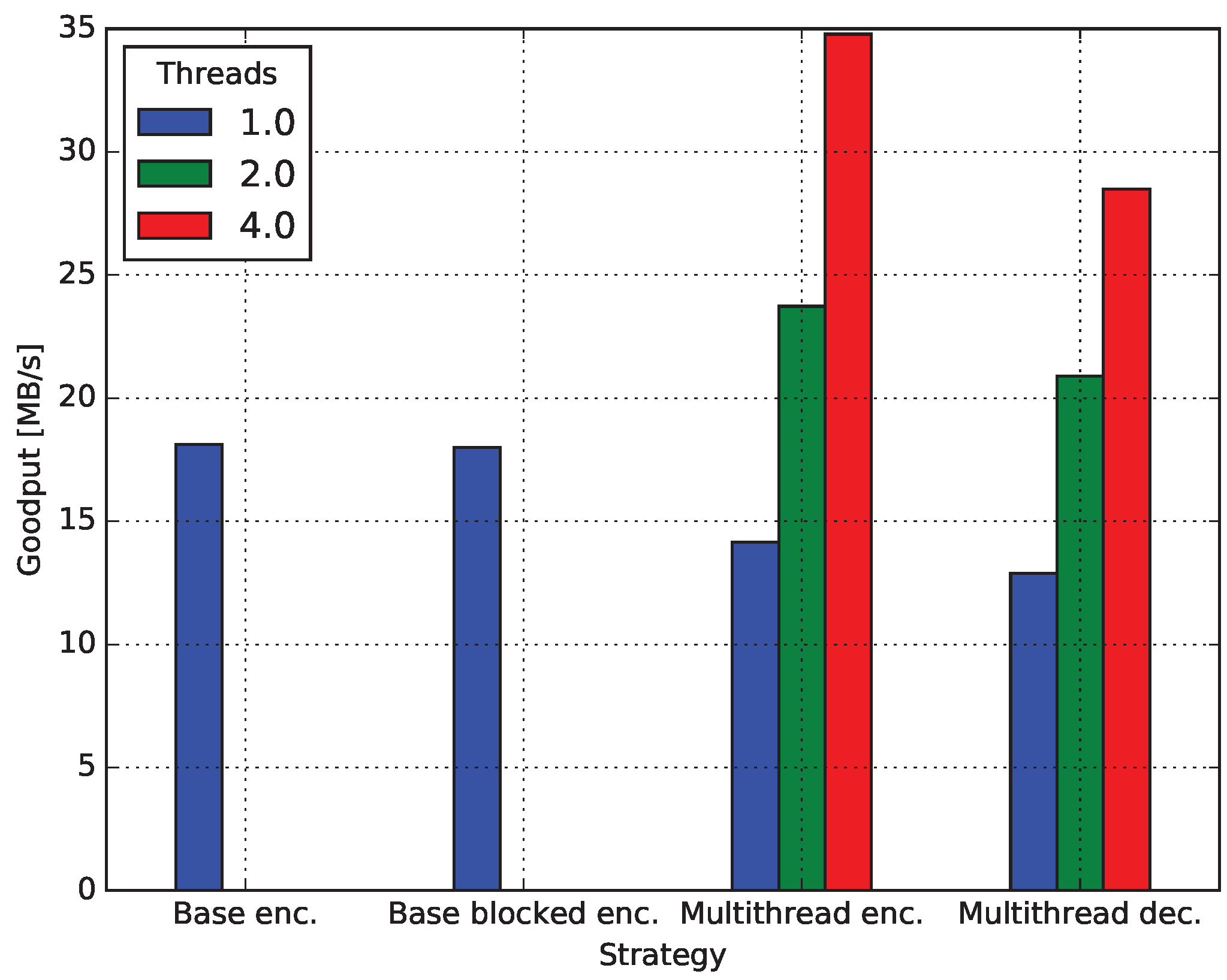
4.4. Multicore Network Coding
4.4.1. Baseline Encoding
4.4.2. Encoding Blocked
4.4.3. Decoding Blocked
4.4.4. Comparison of the Load of Matrix Multiplications and Inversions
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| 6LoWPAN | IPv6 over low power Wireless Personal Area Networks |
| ARM | advanced RISC machine |
| BLAS | basic linear algebra subprograms |
| CPU | central processing unit |
| D2D | device to device |
| DAG | direct acyclic graph |
| DC | direct current |
| dof | degrees of freedom |
| GB | Gigabyte |
| GF | Galois field |
| GPU | graphic processing unit |
| IoT | Internet of Things |
| IP | Internet Protocol |
| LAN | local area network |
| LDPC | low density parity check |
| MAC | medium access control |
| NC | network coding |
| NFS | network file system |
| OS | operating system |
| PC | personal computer |
| QoE | quality of experience |
| RAM | random access memory |
| Raspi | Raspberry Pi |
| RLNC | random linear network coding |
| SCP | secure copy |
| SIMD | single instruction multiple data |
| SMP | symmetric multiprocessor |
| SOC | system on chip |
| SRLNC | sparse random linear network coding |
| SSH | secure shell |
| Telnet | Telnet |
| TSNC | tunable sparse network coding |
| USB | Universal Serial Bus |
References
- Evans, D. The Internet of Things: How the Next Evolution of the Internet Is Changing Everything; CISCO White Papers; CISCO: San Jose, CA, USA, 2011; Volume 1, pp. 1–11. [Google Scholar]
- Al-Fuqaha, A.; Guizani, M.; Mohammadi, M.; Aledhari, M.; Ayyash, M. Internet of things: A survey on enabling technologies, protocols, and applications. IEEE Commun. Surv. Tutor. 2015, 17, 2347–2376. [Google Scholar] [CrossRef]
- Vujović, V.; Maksimović, M. Raspberry Pi as a Wireless Sensor node: Performances and constraints. In Proceedings of the 2014 37th International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 26–30 May 2014; pp. 1013–1018.
- Kruger, C.P.; Abu-Mahfouz, A.M.; Hancke, G.P. Rapid prototyping of a wireless sensor network gateway for the internet of things using off-the-shelf components. In Proceedings of the 2015 IEEE International Conference on Industrial Technology (ICIT), Seville, Spain, 17–19 March 2015; pp. 1926–1931.
- Mahmoud, Q.H.; Qendri, D. The Sensorian IoT platform. In Proceedings of the 2016 13th IEEE Annual Consumer Communications Networking Conference (CCNC), Las Vegas, NV, USA, 9–12 January 2016; pp. 286–287.
- Wirtz, H.; Rüth, J.; Serror, M.; Zimmermann, T.; Wehrle, K. Enabling ubiquitous interaction with smart things. In Proceedings of the 2015 12th Annual IEEE International Conference on Sensing, Communication, and Networking (SECON), Seattle, WA, USA, 22–25 June 2015; pp. 256–264.
- Alletto, S.; Cucchiara, R.; Fiore, G.D.; Mainetti, L.; Mighali, V.; Patrono, L.; Serra, G. An indoor location-aware system for an IoT-based smart museum. IEEE Internet Things J. 2016, 3, 244–253. [Google Scholar] [CrossRef]
- Jalali, F.; Hinton, K.; Ayre, R.; Alpcan, T.; Tucker, R.S. Fog computing may help to save energy in cloud computing. IEEE J. Sel. Areas Commun. 2016, 34, 1728–1739. [Google Scholar] [CrossRef]
- Ueyama, J.; Freitas, H.; Faical, B.S.; Filho, G.P.R.; Fini, P.; Pessin, G.; Gomes, P.H.; Villas, L.A. Exploiting the use of unmanned aerial vehicles to provide resilience in wireless sensor networks. IEEE Commun. Mag. 2014, 52, 81–87. [Google Scholar] [CrossRef]
- Ahlswede, R.; Cai, N.; Li, S.Y.; Yeung, R.W. Network information flow. IEEE Trans. Inf. Theory 2000, 46, 1204–1216. [Google Scholar] [CrossRef]
- Koetter, R.; Médard, M. An algebraic approach to network coding. IEEE/ACM Trans. Netw. 2003, 11, 782–795. [Google Scholar] [CrossRef]
- Gallager, R.G. Low-density parity-check codes. IRE Trans. Inf. Theory 1962, 8, 21–28. [Google Scholar] [CrossRef]
- Reed, I.S.; Solomon, G. Polynomial codes over certain finite fields. J. Soc. Ind. Appl. Math. 1960, 8, 300–304. [Google Scholar] [CrossRef]
- Ho, T.; Médard, M.; Koetter, R.; Karger, D.R.; Effros, M.; Shi, J.; Leong, B. A random linear network coding approach to multicast. IEEE Trans. Inf. Theory 2006, 52, 4413–4430. [Google Scholar] [CrossRef]
- Chachulski, S.; Jennings, M.; Katti, S.; Katabi, D. Trading structure for randomness in wireless opportunistic routing. SIGCOMM Comput. Commun. Rev. 2007, 37, 169–180. [Google Scholar] [CrossRef]
- Katti, S.; Rahul, H.; Hu, W.; Katabi, D.; Médard, M.; Crowcroft, J. XORs in the air: Practical wireless network coding. IEEE/ACM Trans. Netw. 2008, 16, 497–510. [Google Scholar] [CrossRef]
- Pedersen, M.V.; Fitzek, F.H. Implementation and performance evaluation of network coding for cooperative mobile devices. In Proceedings of the 2008 IEEE International Conference on Communications Workshops (ICC Workshops’ 08), Beijing, China, 19–23 May 2008; pp. 91–96.
- Pedersen, M.; Heide, J.; Fitzek, F. Kodo: An open and research oriented network coding library. In Networking 2011 Workshops; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6827, pp. 145–152. [Google Scholar]
- Hundebøll, M.; Ledet-Pedersen, J.; Heide, J.; Pedersen, M.V.; Rein, S.A.; Fitzek, F.H. Catwoman: Implementation and performance evaluation of IEEE 802.11 based multi-hop networks using network coding. In Proceedings of the 2012 76th IEEE Vehicular Technology Conference (VTC Fall), Québec City, QC, Canada, 3–6 September 2012; pp. 1–5.
- Johnson, D.; Ntlatlapa, N.; Aichele, C. Simple pragmatic approach to mesh routing using BATMAN. In Proceedings of the 2nd IFIP International Symposium on Wireless Communications and Information Technology in Developing Countries, CSIR, Pretoria, South Africa, 6–7 October 2008.
- Pahlevani, P.; Lucani, D.E.; Pedersen, M.V.; Fitzek, F.H. Playncool: Opportunistic network coding for local optimization of routing in wireless mesh networks. In Proceedings of the 2013 IEEE Globecom Workshops (GC Wkshps), Atlanta, GA, USA, 9–13 December 2013; pp. 812–817.
- Krigslund, J.; Hansen, J.; Hundebøll, M.; Lucani, D.; Fitzek, F. CORE: COPE with MORE in Wireless Meshed Networks. In Proceedings of the 2013 77th IEEE Vehicular Technology Conference (VTC Spring), Dresden, Germany, 2–5 June 2013; pp. 1–6.
- Paramanathan, A.; Pedersen, M.; Lucani, D.; Fitzek, F.; Katz, M. Lean and mean: Network coding for commercial devices. IEEE Wirel. Commun. Mag. 2013, 20, 54–61. [Google Scholar] [CrossRef]
- Seferoglu, H.; Markopoulou, A.; Ramakrishnan, K.K. I2NC: Intra- and inter-session network coding for unicast flows in wireless networks. In Proceedings of the 30th IEEE International Conference on Computer Communications ( INFOCOM), Shanghai, China, 10–15 April 2011; pp. 1035–1043.
- Paramanathan, A.; Pahlevani, P.; Thorsteinsson, S.; Hundebøll, M.; Lucani, D.; Fitzek, F. Sharing the Pi: Testbed Description and Performance Evaluation of Network Coding on the Raspberry Pi. In Proceedings of the 2014 IEEE 79th Vehicular Technology Conference, Seoul, Korea, 18–21 May 2014.
- Chou, P.A.; Wu, Y.; Jain, K. Practical network coding. In Proceedings of the 41st Annual Allerton Conference on Communication, Control, and Computing, Monticello, IL, USA, 1–3 October 2003.
- Fragouli, C.; Le Boudec, J.Y.; Widmer, J. Network coding: An instant primer. ACM SIGCOMM Comput. Commun. Rev. 2006, 36, 63–68. [Google Scholar] [CrossRef]
- Pedersen, M.V.; Lucani, D.E.; Fitzek, F.H.P.; Soerensen, C.W.; Badr, A.S. Network coding designs suited for the real world: What works, what doesn’t, what’s promising. In Proceedings of the 2013 IEEE Information Theory Workshop (ITW), Seville, Spain, 9–13 September 2013; pp. 1–5.
- Sorensen, C.W.; Badr, A.S.; Cabrera, J.A.; Lucani, D.E.; Heide, J.; Fitzek, F.H.P. A Practical View on Tunable Sparse Network Coding. In Proceedings of the 21th European Wireless Conference European Wireless, Budapest, Hungary, 20–22 May 2015; pp. 1–6.
- Feizi, S.; Lucani, D.E.; Médard, M. Tunable sparse network coding. In Proceedings of the 2012 International Zurich Seminar on Communications (IZS), Zurich, Switzerland, 29 February–2 March 2012; pp. 107–110.
- Feizi, S.; Lucani, D.E.; Sorensen, C.W.; Makhdoumi, A.; Medard, M. Tunable sparse network coding for multicast networks. In Proceedings of the 2014 International Symposium on Network Coding (NetCod), Aalborg Oest, Denmark, 27–28 June 2014; pp. 1–6.
- Shojania, H.; Li, B.; Wang, X. Nuclei: GPU-Accelerated Many-Core Network Coding. In Proceedings of the IEEE 28th Conference on Computer Communications (INFOCOM 2009), Rio de Janeiro, Brazil, 20–25 April 2009; pp. 459–467.
- Shojania, H.; Li, B. Parallelized progressive network coding with hardware acceleration. In Proceedings of the 2007 Fifteenth IEEE International Workshop on Quality of Service, Evanston, IL, USA, 21–22 June 2007; pp. 47–55.
- Wunderlich, S.; Cabrera, J.; Fitzek, F.H.; Pedersen, M.V. Network coding parallelization based on matrix operations for multicore architectures. In Proceedings of the 2015 IEEE International Conference on Ubiquitous Wireless Broadband (ICUWB), Montreal, QC, Canada, 4–7 October 2015; pp. 1–5.
- Lawson, C.L.; Hanson, R.J.; Kincaid, D.R.; Krogh, F.T. Basic linear algebra subprograms for Fortran usage. ACM Trans. Math. Softw. (TOMS) 1979, 5, 308–323. [Google Scholar] [CrossRef]
- Dumas, J.G.; Giorgi, P.; Pernet, C. Dense linear algebra over word-size prime fields: The FFLAS and FFPACK packages. ACM Trans. Math. Softw. (TOMS) 2008, 35, 19. [Google Scholar] [CrossRef]
- Dumas, J.G.; Gautier, T.; Giesbrecht, M.; Giorgi, P.; Hovinen, B.; Kaltofen, E.; Saunders, B.D.; Turner, W.J.; Villard, G. LinBox: A generic library for exact linear algebra. In Proceedings of the 2002 International Congress of Mathematical Software, Beijing, China, 17–19 August 2002; pp. 40–50.
- Golub, G.H.; Van Loan, C.F. Matrix Computations; JHU Press: Baltimore, MD, USA, 2012; Volume 3. [Google Scholar]
- Dongarra, J.; Faverge, M.; Ltaief, H.; Luszczek, P. High performance matrix inversion based on LU factorization for multicore architectures. In Proceedings of the 2011 ACM International Workshop on Many Task Computing on Grids and Supercomputers (MTAGS ’11), Seattle, WA, USA, 14 November 2011; ACM: New York, NY, USA, 2011; pp. 33–42. [Google Scholar]
- Sparse Network Codes Implementation Based in the Kodo Library. Available online: https://github.com/chres/kodo/tree/sparse-feedback2 (accessed on 2 September 2016).
- Trullols-Cruces, O.; Barcelo-Ordinas, J.M.; Fiore, M. Exact decoding probability under random linear network coding. IEEE Commun. Lett. 2011, 15, 67–69. [Google Scholar] [CrossRef]
- Zhao, X. Notes on “Exact decoding probability under random linear network coding”. IEEE Commun. Lett. 2012, 16, 720–721. [Google Scholar] [CrossRef]
- Sample Availability: The testbed and measurements in this publication are both available from the authors.


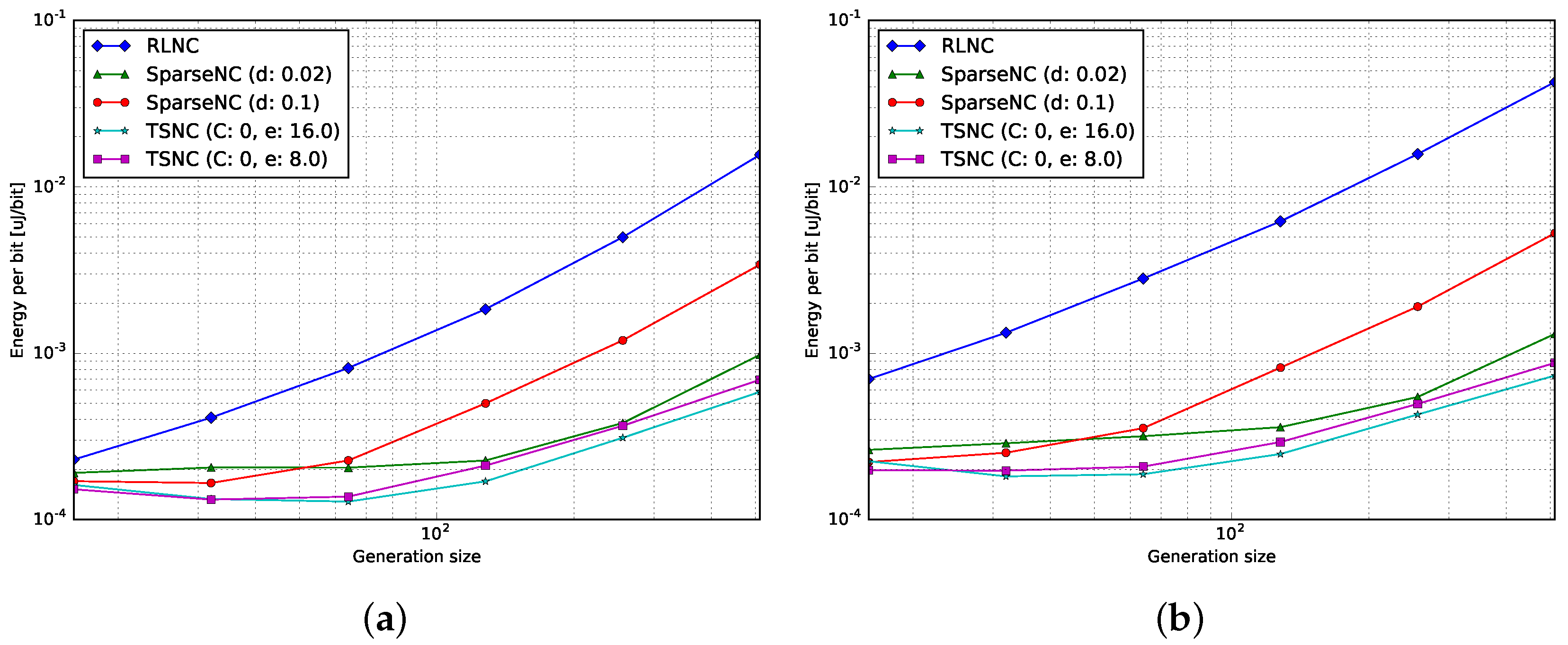
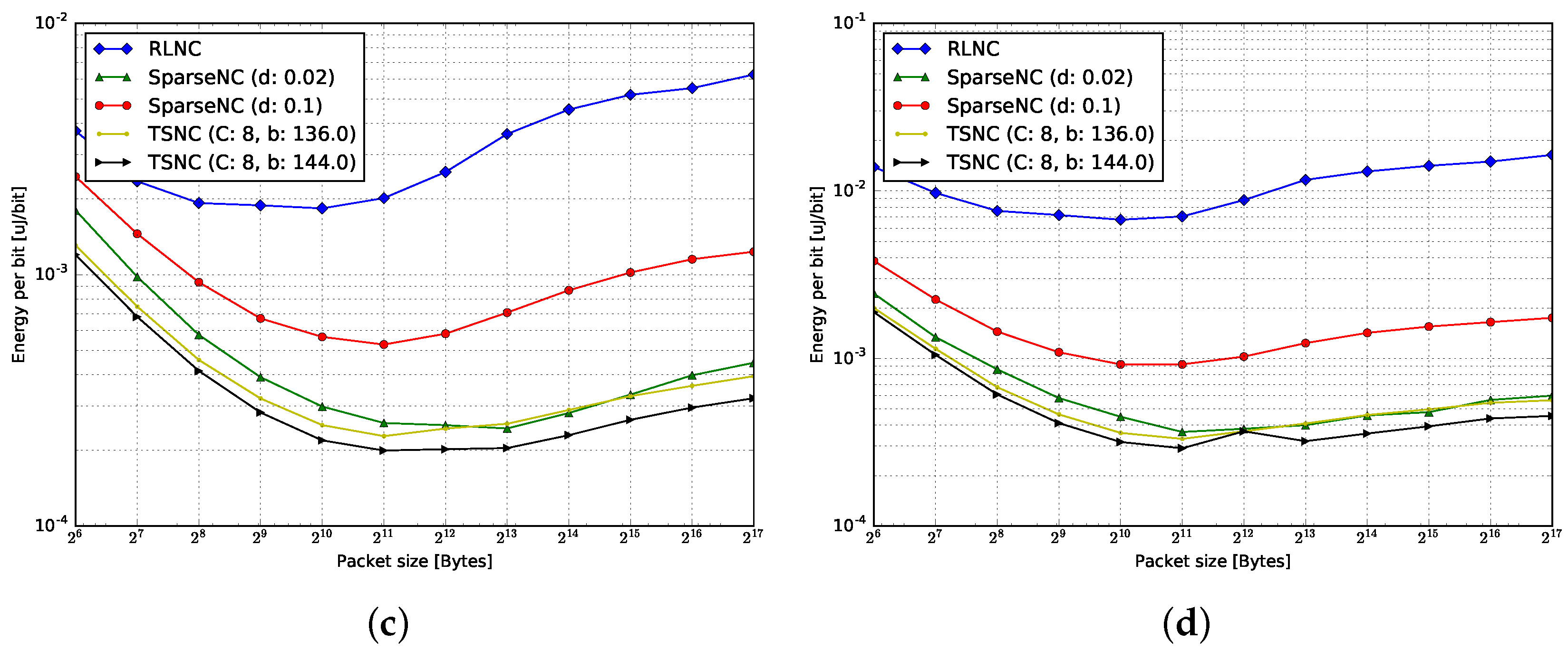
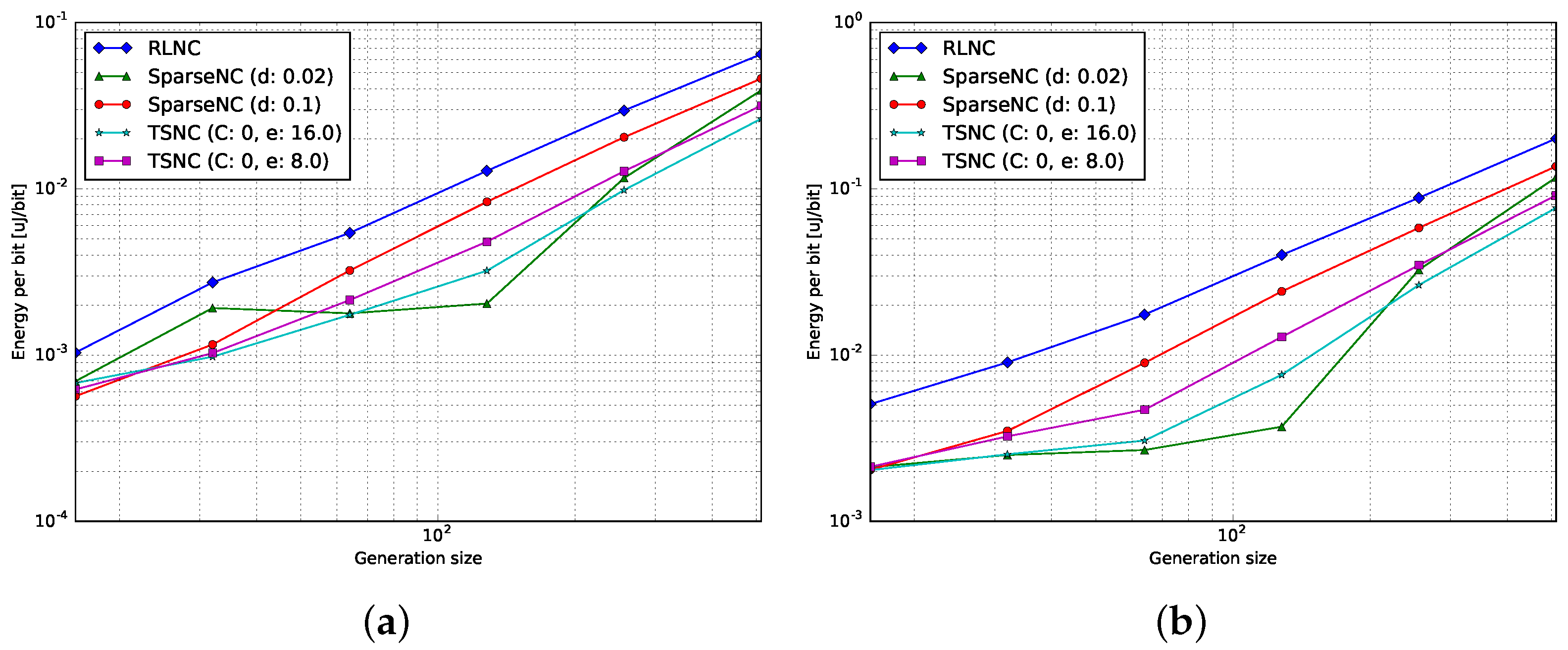

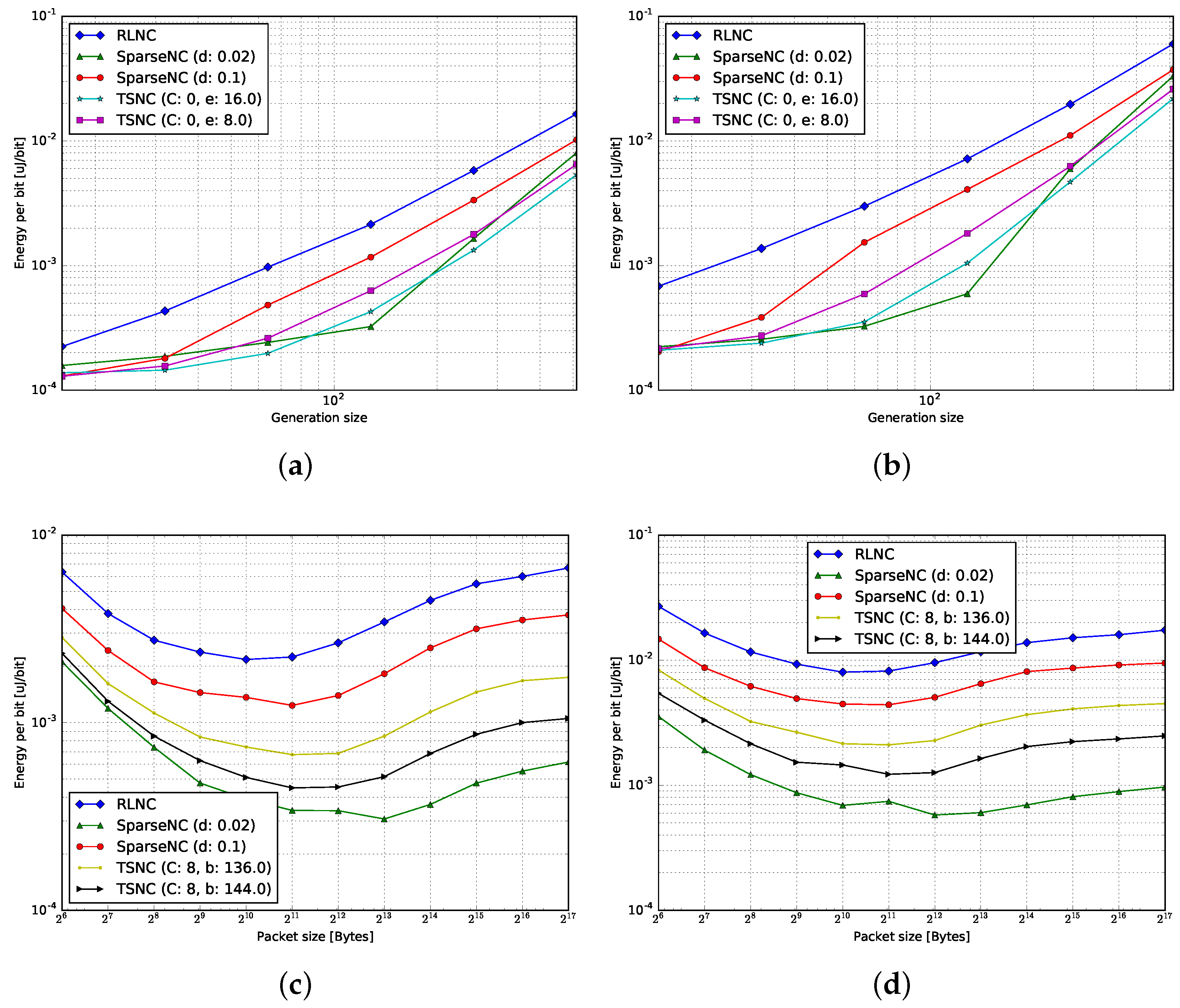
| Raspi Model | (A) | (A) | (W) |
|---|---|---|---|
| Raspi 1 | 0.320 | 0.360 | 0.200 |
| Raspi 2 | 0.216 | 0.285 | 0.345 |
| g | (ms) | (ms) | r |
|---|---|---|---|
| 16 | 1.495 | 0.169 | 8.8 |
| 32 | 5.365 | 0.514 | 10.4 |
| 64 | 20.573 | 2.024 | 10.1 |
| 128 | 81.357 | 11.755 | 6.9 |
| 256 | 326.587 | 75.451 | 4.3 |
| 512 | 1354.012 | 540.469 | 2.5 |
| 1024 | 5965.284 | 4373.329 | 1.3 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hernández Marcano, N.J.; Sørensen, C.W.; Cabrera G., J.A.; Wunderlich, S.; Lucani, D.E.; Fitzek, F.H.P. On Goodput and Energy Measurements of Network Coding Schemes in the Raspberry Pi. Electronics 2016, 5, 66. https://doi.org/10.3390/electronics5040066
Hernández Marcano NJ, Sørensen CW, Cabrera G. JA, Wunderlich S, Lucani DE, Fitzek FHP. On Goodput and Energy Measurements of Network Coding Schemes in the Raspberry Pi. Electronics. 2016; 5(4):66. https://doi.org/10.3390/electronics5040066
Chicago/Turabian StyleHernández Marcano, Néstor J., Chres W. Sørensen, Juan A. Cabrera G., Simon Wunderlich, Daniel E. Lucani, and Frank H. P. Fitzek. 2016. "On Goodput and Energy Measurements of Network Coding Schemes in the Raspberry Pi" Electronics 5, no. 4: 66. https://doi.org/10.3390/electronics5040066
APA StyleHernández Marcano, N. J., Sørensen, C. W., Cabrera G., J. A., Wunderlich, S., Lucani, D. E., & Fitzek, F. H. P. (2016). On Goodput and Energy Measurements of Network Coding Schemes in the Raspberry Pi. Electronics, 5(4), 66. https://doi.org/10.3390/electronics5040066







