A Multi-Modal Sensing Glove for Human Manual-Interaction Studies
Abstract
:1. Introduction
2. Materials and Methods
2.1. Kinaesthetic Sensing
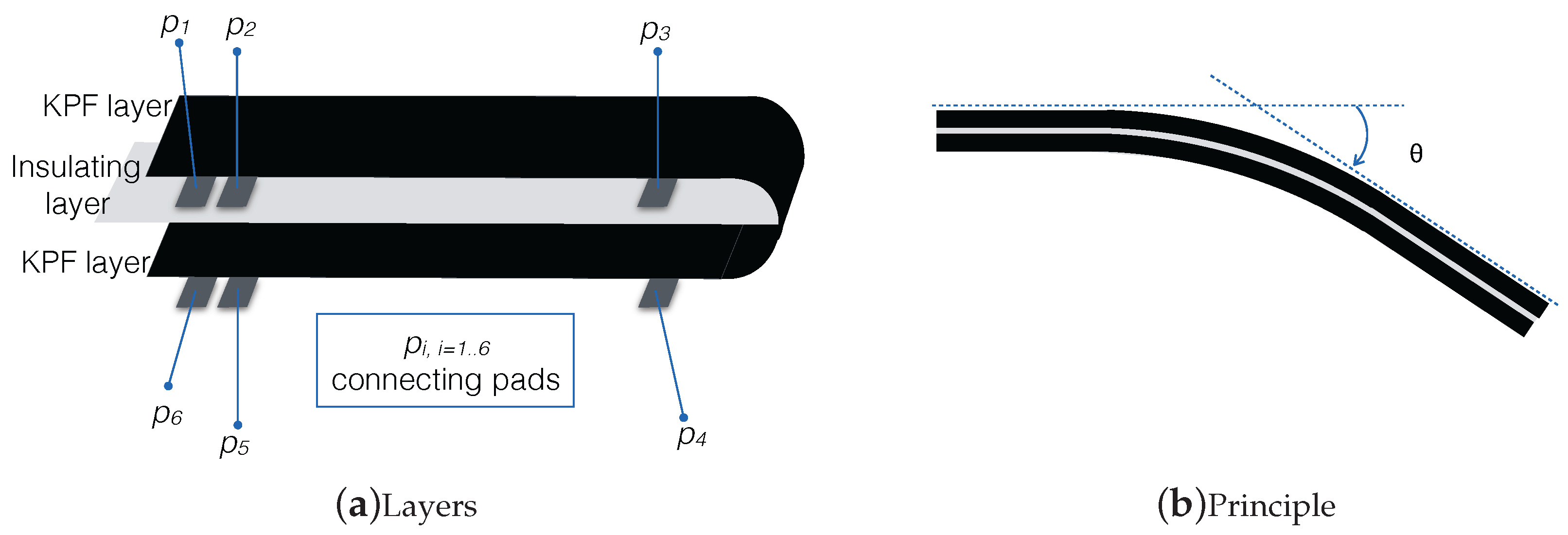
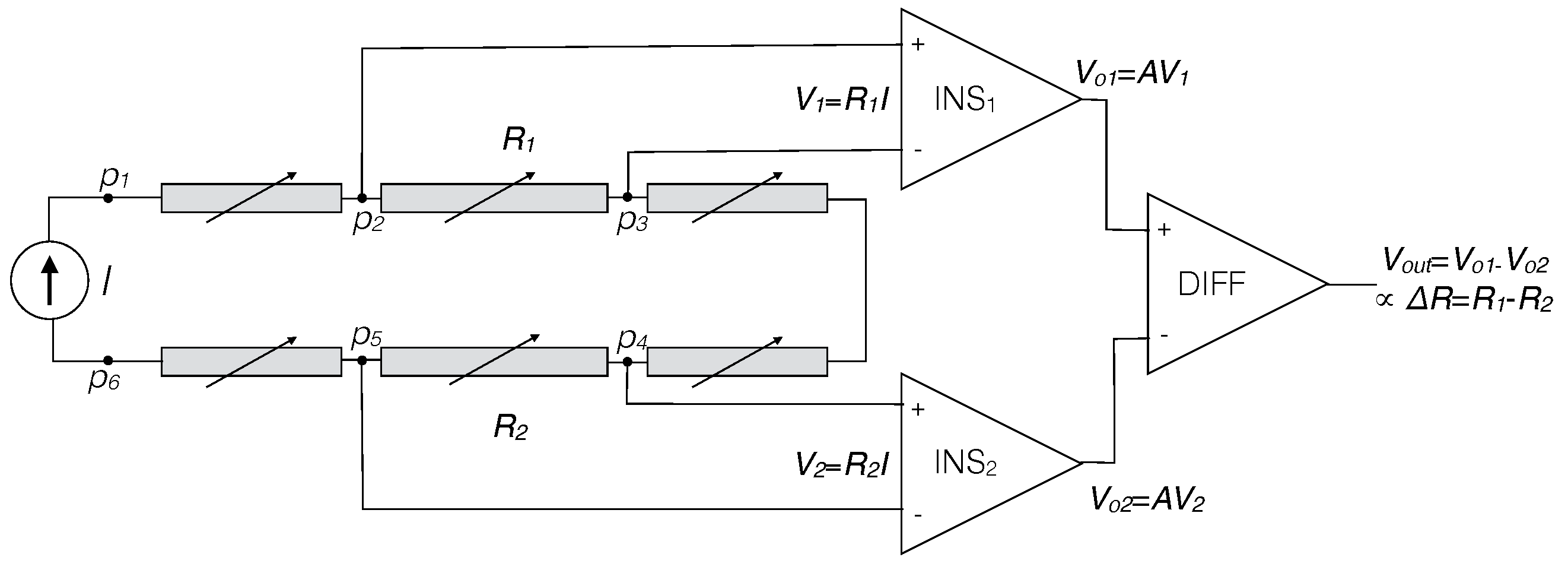
2.1.1. Textile-Based Goniometers
2.1.2. Glove Design
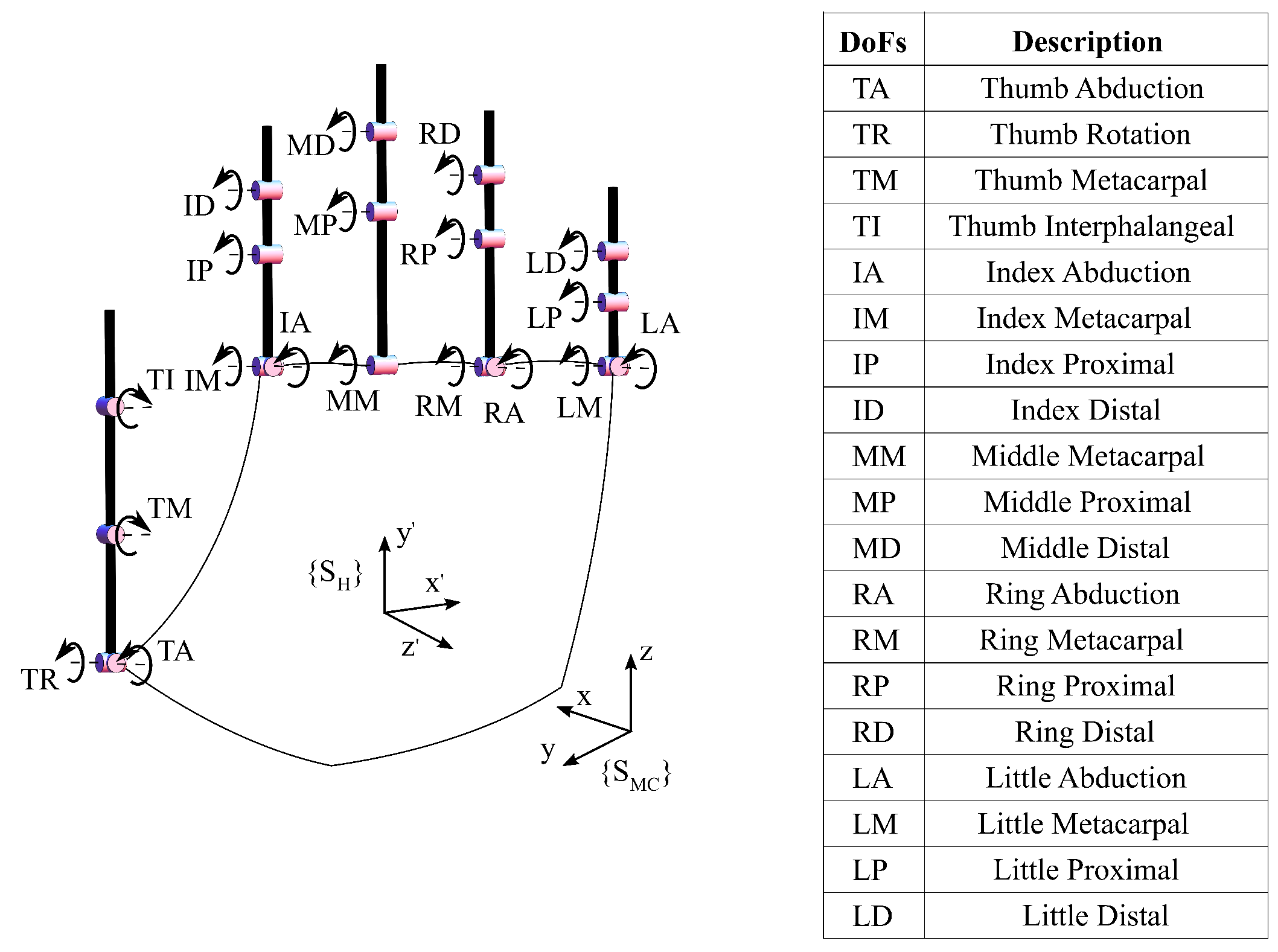
2.1.3. Synergy-Based Hand Pose Reconstruction
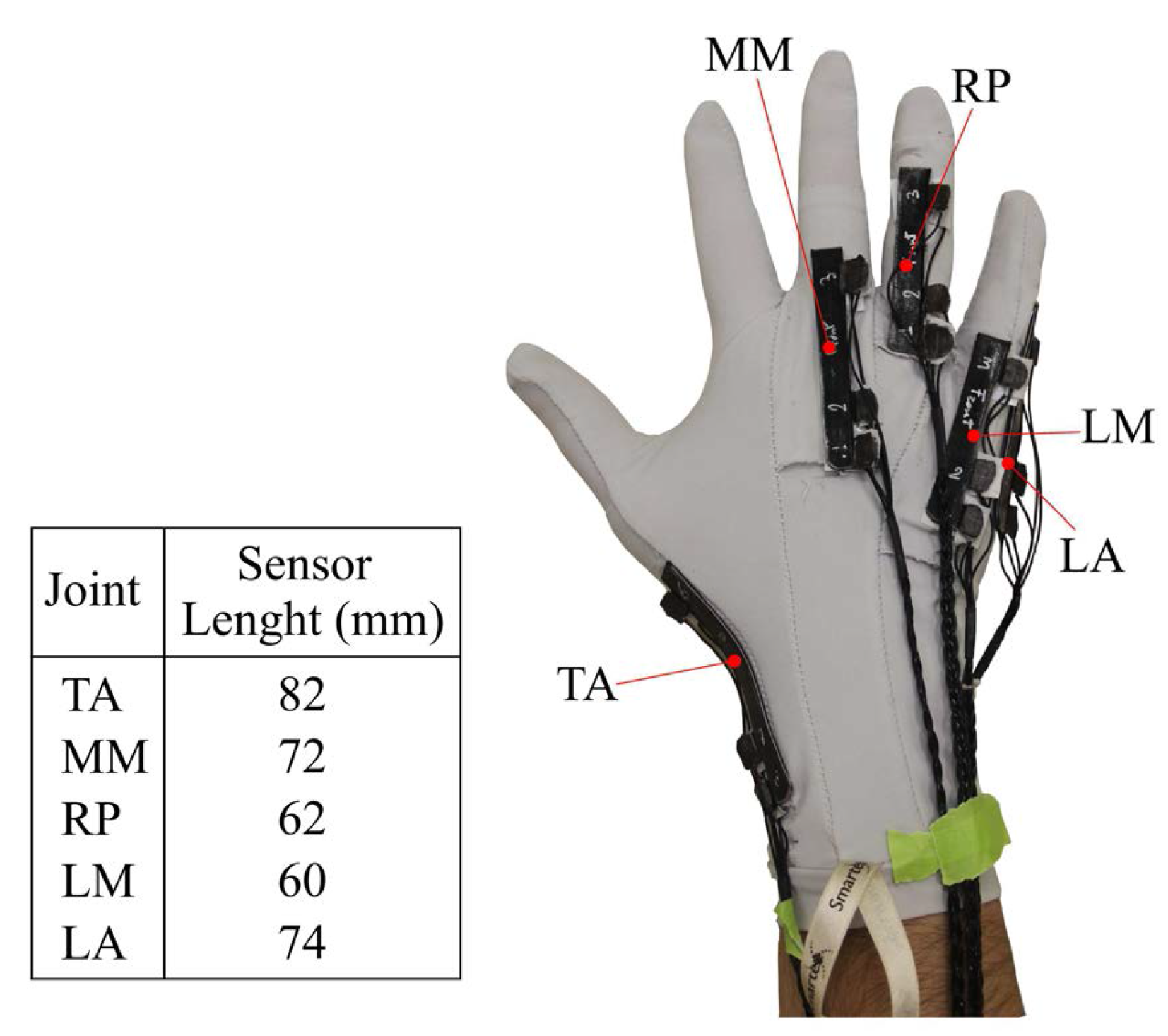
2.1.4. Sensor Layout
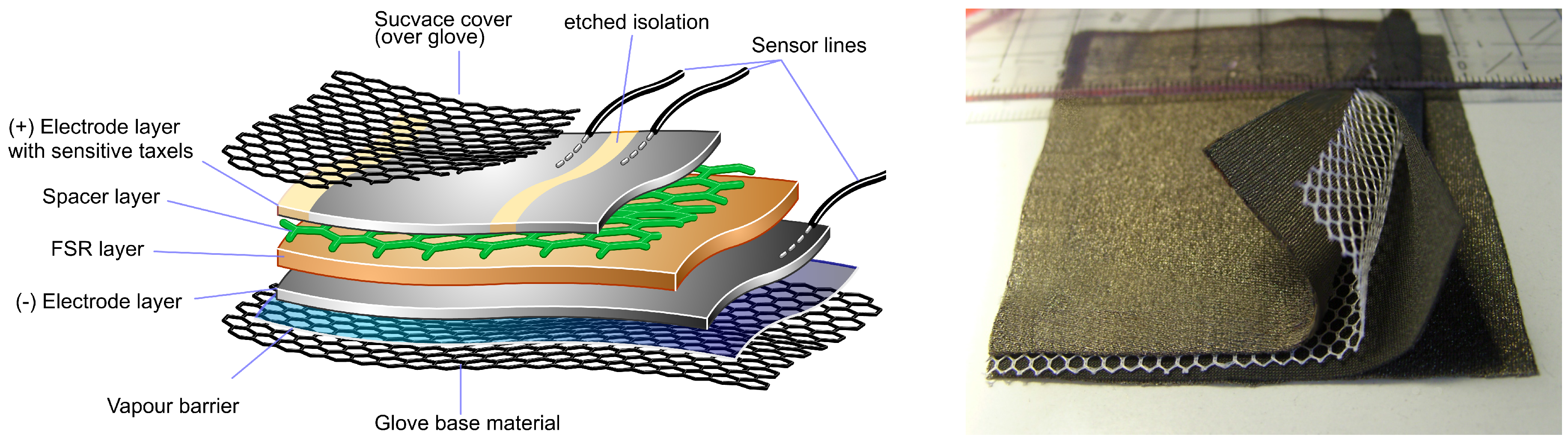
2.2. Tactile Sensing
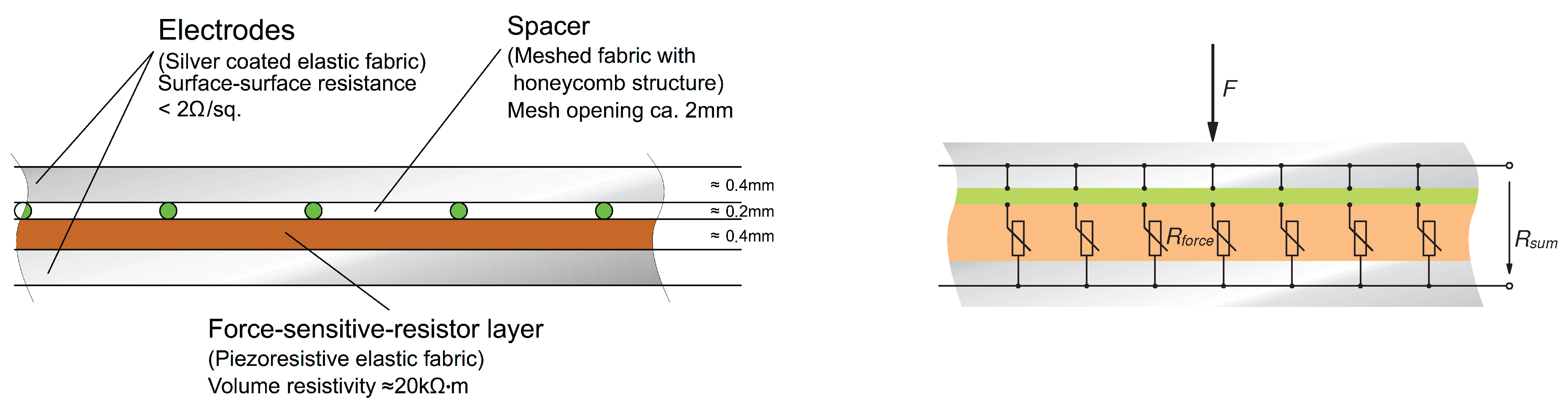
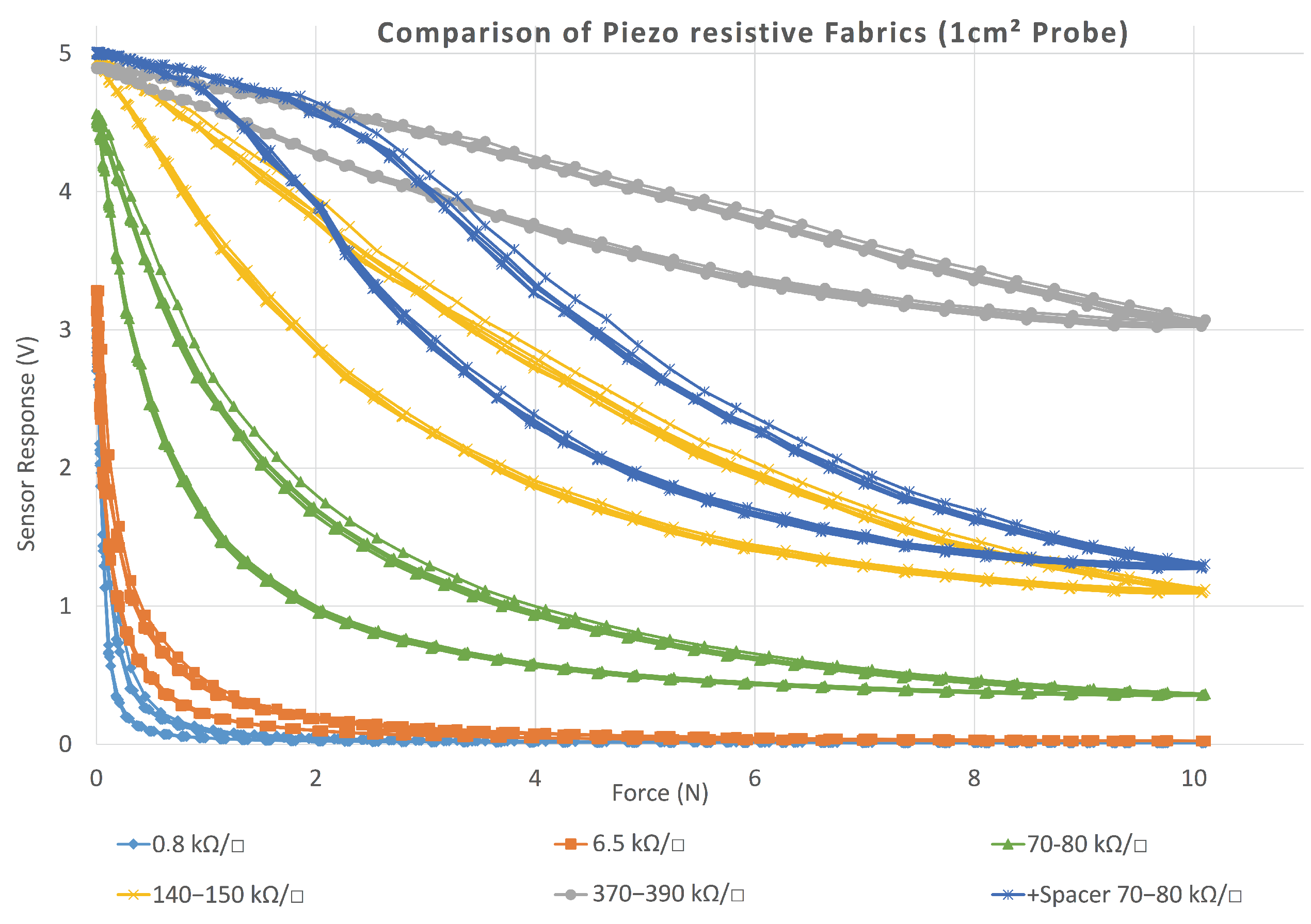
2.2.1. Tactile Sensor Characteristics
2.2.2. Taxel Layout and Glove Design
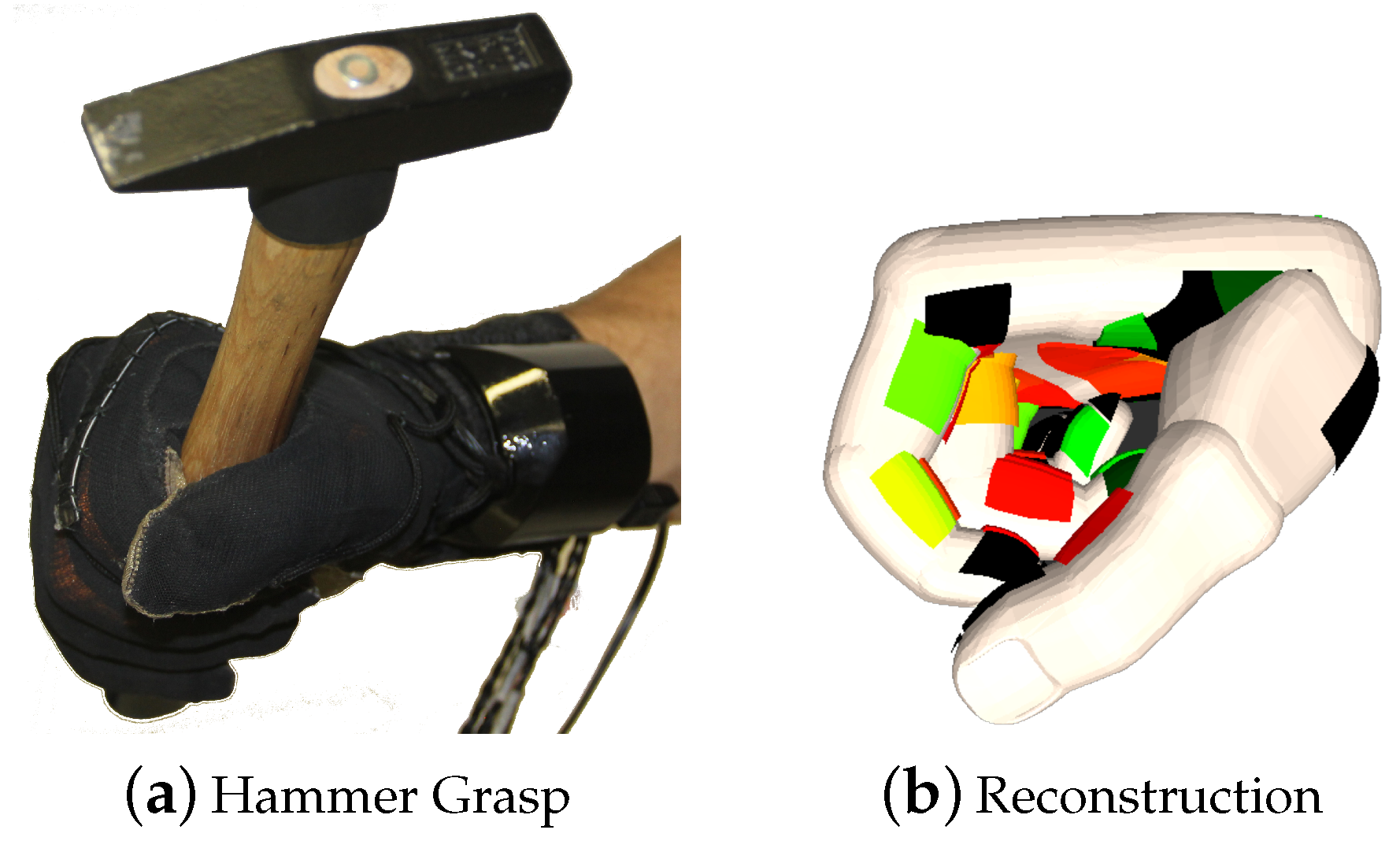
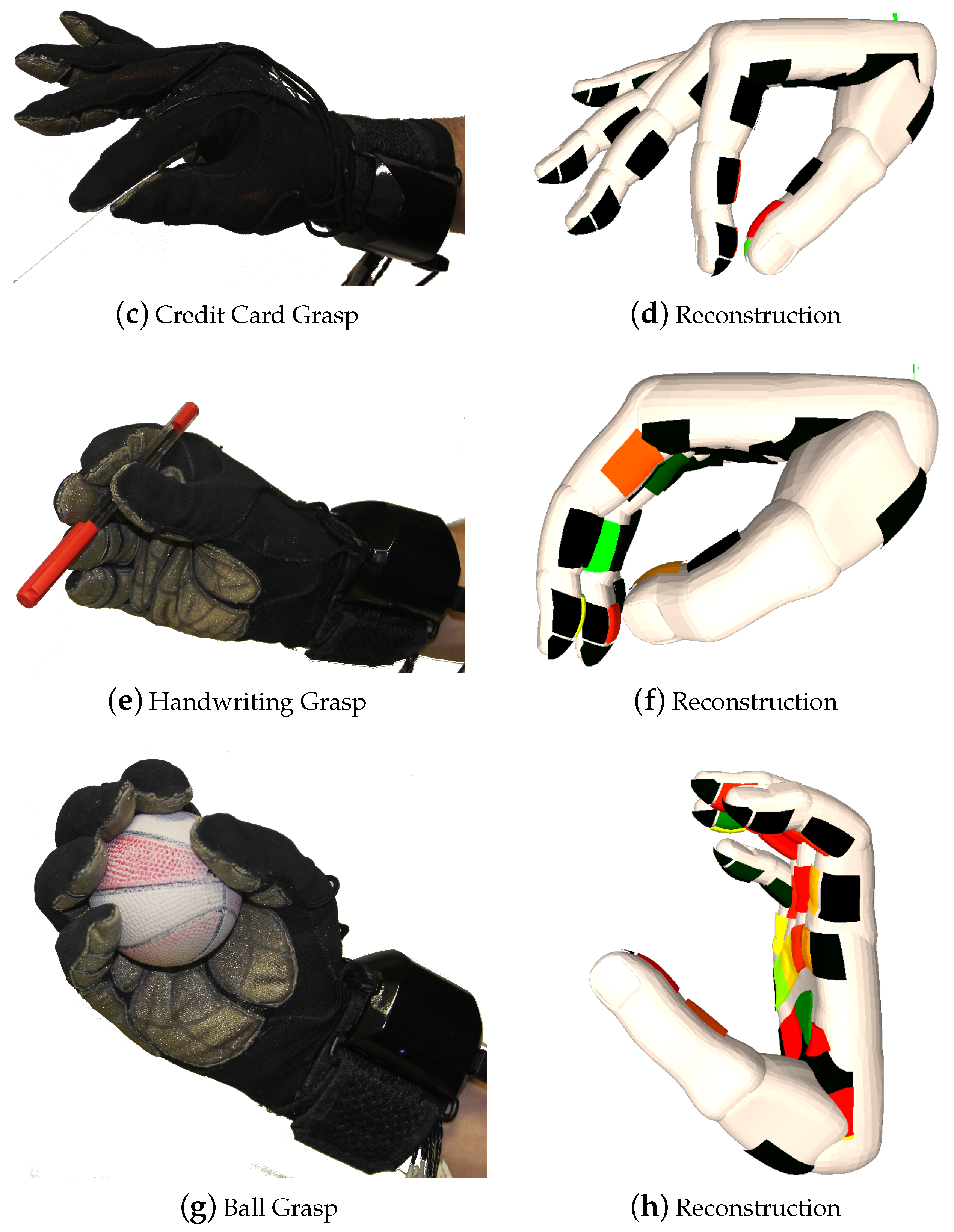
2.3. Experiment Approach
3. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| DOF | degree of freedom |
| HPR | hand pose reconstruction |
| KPF | knitted piezoresistive fabric |
| PCA | principal component analysis |
References
- Lu, G.; Shark, L.K.; Hall, G.; Zeshan, U. Immersive manipulation of virtual objects through glove-based hand gesture interaction. Virtual Real. 2012, 16, 243–252. [Google Scholar] [CrossRef]
- Hürst, W.; Van Wezel, C. Gesture-based interaction via finger tracking for mobile augmented reality. Multimed. Tools Appl. 2013, 62, 233–258. [Google Scholar] [CrossRef]
- Borghetti, M.; Sardini, E.; Serpelloni, M. Sensorized glove for measuring hand finger flexion for rehabilitation purposes. IEEE Trans. Instrum. Meas. 2013, 62, 3308–3314. [Google Scholar] [CrossRef]
- Kortier, H.G.; Sluiter, V.I.; Roetenberg, D.; Veltink, P.H. Assessment of hand kinematics using inertial and magnetic sensors. J. Neuroeng. Rehabil. 2014, 11. [Google Scholar] [CrossRef] [PubMed]
- Liarokapis, M.V.; Artemiadis, P.K.; Kyriakopoulos, K.J. Telemanipulation with the DLR/HIT II robot hand using a dataglove and a low cost force feedback device. In Proceedings of the 2013 21st Mediterranean Conference on Control Automation (MED), Platanias-Chania, Greece, 25–28 June 2013; pp. 431–436.
- Kim, Y.; Leonard, S.; Shademan, A.; Krieger, A.; Kim, P.C. Kinect technology for hand tracking control of surgical robots: Technical and surgical skill comparison to current robotic masters. Surg. Endosc. 2014, 28, 1993–2000. [Google Scholar] [CrossRef] [PubMed]
- Erol, A.; Bebis, G.; Nicolescu, M.; Boyle, R.D.; Twombly, X. Vision-based hand pose estimation: A review. Comput. Vis. Image Underst. 2007, 108, 52–73. [Google Scholar] [CrossRef]
- Suarez, J.; Murphy, R.R. Hand gesture recognition with depth images: A review. In Proceedings of the 21st IEEE International Symposium on Robot and Human Interactive Communication, Paris, France, 9–13 September 2012; pp. 411–417.
- Dipietro, L.; Sabatini, A.; Dario, P. A Survey of Glove-Based Systems and Their Applications. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2008, 38, 461–482. [Google Scholar] [CrossRef]
- Cyberglove. Available online: https://www.cyberglovesystems.com (accessed on 23 May 2016).
- O’Brien, B.; Gisby, T.; Anderson, I.A. Stretch sensors for human body motion. In Proceedings of SPIE, Electroactive Polymer Actuators and Devices (EAPAD), San Diego, CA, USA, 9 March 2014; Volume 905618.
- Sareh, S.; Noh, Y.; Li, M.; Ranzani, T.; Liu, H.; Althoefer, K. Macrobend optical sensing for pose measurement in soft robot arms. Smart Mater. Struct. 2015, 24, 125024. [Google Scholar] [CrossRef]
- Westling, G.; Johansson, R.S. Factors influencing the force control during precision grip. Exp. Brain Res. 1984, 53, 277–284. [Google Scholar] [CrossRef] [PubMed]
- Cannata, G.; Maggiali, M.; Metta, G.; Sandini, G. An embedded artificial skin for humanoid robots. In Proceedings of the 2008 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems (MFI 2008), Seoul, Korea, 20–22 August 2008; pp. 434–438.
- Fishel, J.A. Design and Use of a Biomimetic Tactile Microvibration Sensor with Human-Like Sensitivity and Its Application in Texture Discrimination Using Bayesian Exploration. Ph.D. Thesis, University of Southern California, Los Angeles, CA, USA, August 2012. [Google Scholar]
- Kõiva, R.; Zenker, M.; Schürmann, C.; Haschke, R.; Ritter, H. A highly sensitive 3D-shaped tactile sensor. In Proceedings of the 2013 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Wollongong, NSW, Australia, 9–12 July 2013; pp. 1084–1089.
- Kappassov, Z.; Corrales, J.A.; Perdereau, V. Tactile Sensing in Dexterous Robot Hands—Review. Robot. Auton. Syst. 2015, 74, 195–220. [Google Scholar] [CrossRef]
- Li, Q.; Haschke, R.; Ritter, H. A Visuo-Tactile Control Framework for Manipulation and Exploration of Unknown Objects. In Proceedings of the 2015 IEEE-RAS 15th International Conference on Humanoid Robots (Humanoids), Seoul, Korea, 3–5 November 2015.
- Dang, H.; Weisz, J.; Allen, P. Blind grasping: Stable robotic grasping using tactile feedback and hand kinematics. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011; pp. 5917–5922.
- Ward-Cherrier, B.; Cramphorn, L.; Lepora, N.F. Tactile Manipulation With a TacThumb Integrated on the Open-Hand M2 Gripper. IEEE Robot. Autom. Lett. 2016, 1, 169–175. [Google Scholar] [CrossRef]
- Maycock, J.; Dornbusch, D.; Elbrechter, C.; Haschke, R.; Schack, T.; Ritter, H. Approaching Manual Intelligence. KI Künstliche Intell. 2010, 24, 287–294. [Google Scholar] [CrossRef]
- Kerpa, O.; Weiss, K.; Wörn, H. Development of a flexible tactile sensor system for a humanoid robot. In Proceedings of the 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003), Karlsruhe, Germany, 27–31 October 2003.
- Lowe, M.; King, A.; Lovett, E.; Papakostas, T. Flexible tactile sensor technology: Bringing haptics to life. Sens. Rev. 2004, 24, 33–36. [Google Scholar] [CrossRef]
- Kim, K.; Lee, K.R.; Kim, W.H.; Park, K.B.; Kim, T.H.; Kim, J.S.; Pak, J.J. Polymer-based flexible tactile sensor up to 32×32 arrays integrated with interconnection terminals. Sens. Actuators A Phys. 2009, 156, 284–291. [Google Scholar] [CrossRef]
- Ohmura, Y.; Kuniyoshi, Y.; Nagakubo, A. Conformable and scalable tactile sensor skin for curved surfaces. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–19 May 2006.
- Shimojo, M.; Namiki, A.; Ishikawa, M.; Makino, R.; Mabuchi, K. A tactile sensor sheet using pressure conductive rubber with electrical-wires stitched method. IEEE Sens. J. 2004, 4, 589–596. [Google Scholar] [CrossRef]
- Alirezaei, H.; Nagakubo, A.; Kuniyoshi, Y. A highly stretchable tactile distribution sensor for smooth surfaced humanoids. In Proceedings of the 7th IEEE-RAS International Conference on Humanoid Robots, Pittsburgh, PA, USA, 29 November–1 December 2007; pp. 167–173.
- OptoForce Ltd. Optical Force Sensors. Available online: http://optoforce.com (accessed on 19 July 2016).
- Sareh, S.; Jiang, A.; Faragasso, A.; Noh, Y.; Nanayakkara, T.; Dasgupta, P.; Seneviratne, L.D.; Wurdemann, H.A.; Althoefer, K. Bio-inspired tactile sensor sleeve for surgical soft manipulators. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA 2014), Hong Kong, China, 31 May–7 June 2014; pp. 1454–1459.
- Sagisaka, T.; Ohmura, Y.; Kuniyoshi, Y.; Nagakubo, A.; Ozaki, K. High-density conformable tactile sensing glove. In Proceedings of the 2011 11th IEEE-RAS International Conference on Humanoid Robots (Humanoids), Bled, Slovenia, 26–28 October 2011; pp. 537–542.
- Tognetti, A.; Lorussi, F.; Dalle Mura, G.; Carbonaro, N.; Pacelli, M.; Paradiso, R.; De Rossi, D. New generation of wearable goniometers for motion capture systems. J. Neuroeng. Rehabil. 2014, 11. [Google Scholar] [CrossRef] [PubMed]
- Dalle Mura, G.; Lorussi, F.; Tognetti, A.; Anania, G.; Carbonaro, N.; Pacelli, M.; Paradiso, R.; De Rossi, D. Piezoresistive goniometer network for sensing gloves. In Proceedings of the XIII Mediterranean Conference on Medical and Biological Engineering and Computing 2013, Seville, Spain, 25–28 September 2013; Volume 41, pp. 1547–1550.
- Carbonaro, N.; Dalle Mura, G.; Lorussi, F.; Paradiso, R.; De Rossi, D.; Tognetti, A. Exploiting wearable goniometer technology for motion sensing gloves. IEEE J. Biomed. Health Inf. 2014, 18, 1788–1795. [Google Scholar] [CrossRef] [PubMed]
- Cianchetti, M.; Renda, F.; Licofonte, A.; Laschi, C. Sensorization of continuum soft robots for reconstructing their spatial configuration. In Proceedings of the 2012 4th IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics (BioRob), Rome, Italy, 24–27 June 2012; pp. 634–639.
- Bianchi, M.; Salaris, P.; Bicchi, A. Synergy-based Hand Pose Sensing: Reconstruction Enhancement. Int. J. Robot. Res. 2013, 32, 396–406. [Google Scholar] [CrossRef]
- Bianchi, M.; Salaris, P.; Bicchi, A. Synergy-based hand pose sensing: Optimal glove design. Int. J. Robot. Res. 2013, 32, 407–424. [Google Scholar] [CrossRef]
- Büscher, G.; Kõiva, R.; Schürmann, C.; Haschke, R.; Ritter, H. Tactile dataglove with fabric-based sensors. In Proceedings of the 12th IEEE-RAS International Conference on Humanoid Robots (Humanoids 2012), Osaka, Japan, 29 November–1 December 2012; pp. 204–209.
- Büscher, G.; Kõiva, R.; Schürmann, C.; Haschke, R.; Ritter, H. Flexible and stretchable fabric-based tactile sensor. Robot. Auton. Syst. 2015, 63, 244–252. [Google Scholar] [CrossRef]
- Kõiva, R.; Hilsenbeck, B.; Castellini, C. FFLS: An accurate linear device for measuring synergistic finger contractions. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC 2012), San Diego, CA, USA, 28 August–1 September 2012.
- Santello, M.; Flanders, M.; Soechting, J.F. Postural hand synergies for tool use. J. Neurosci. 1998, 18, 10105–10115. [Google Scholar] [PubMed]
- Lin, J.; Wu, Y.; Huang, T.S. Modeling the constraints of human hand motion. In Proceedings of the 2000 Workshop on Human Motion, Los Alamitos, CA, USA, 7–8 December 2000; pp. 121–126.
- Bianchi, M.; Salaris, P.; Turco, A.; Carbonaro, N.; Bicchi, A. On the use of postural synergies to improve human hand pose reconstruction. In Proceedings of the 2012 IEEE Haptics Symposium (HAPTICS), Vancouver, BC, Canada, 4–7 March 2012; pp. 91–98.
- Bianchi, M.; Carbonaro, N.; Battaglia, E.; Lorussi, F.; Bicchi, A.; De Rossi, D.; Tognetti, A. Exploiting hand kinematic synergies and wearable under-sensing for hand functional grasp recognition. In Proceedings of the 2014 EAI 4th International Conference on Wireless Mobile Communication and Healthcare (Mobihealth), Athens, Greece, 3–5 November 2014; pp. 168–171.
- Bianchi, M.; Salaris, P.; Bicchi, A. Synergy-based optimal design of hand pose sensing. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura, Portugal, 7–12 October 2012; pp. 3929–3935.
- Santello, M.; Flanders, M.; Soechting, J.F. Patterns of hand motion during grasping and the influence of sensory guidance. J. Neurosci. 2002, 22, 1426–1435. [Google Scholar] [PubMed]
- Weiß, K.; Wörn, H. The working principle of resistive tactile sensor cells. In Proceedings of the IEEE International Conference Mechatronics and Automation (ICMA), Karlsruhe, Germany, 29 July–1 August 2005; Volume 1, pp. 471–476.
- Stevens, S.S. On the psychophysical law. Psychol. Rev. 1957, 64, 153–181. [Google Scholar] [CrossRef] [PubMed]
- Vallbo, Å.B.; Johansson, R.S. Properties of cutaneous mechanoreceptors in the human hand related to touch sensation. Hum. Neurobiol. 1984, 3, 3–14. [Google Scholar] [PubMed]
- Software to handle tactile sensors in ROS. Available online: http://github.com/ubi-agni/tactiletoolbox (accessed on 19 July 2016).
- Ciotti, S.; Battaglia, E.; Carbonaro, N.; Bicchi, A.; Tognetti, A.; Bianchi, M. A Synergy-Based Optimally Designed Sensing Glove for Functional Grasp Recognition. Sensors 2016, 16, 811. [Google Scholar] [CrossRef] [PubMed]
- Naceri, A.; Santello, M.; Moscatelli, A.; Ernst, M.O. Digit Position and Force Synergies During Unconstrained Grasping. In Human and Robot Hands: Sensorimotor Synergies to Bridge the Gap Between Neuroscience and Robotics; Bianchi, M., Moscatelli, A., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 29–40. [Google Scholar]
- Fu, Q.; Zhang, W.; Santello, M. Anticipatory planning and control of grasp positions and forces for dexterous two-digit manipulation. J. Neurosci. 2010, 30, 9117–9126. [Google Scholar] [CrossRef] [PubMed]
- Battaglia, E.; Bianchi, M.; Altobelli, A.; Grioli, G.; Catalano, M.G.; Serio, A.; Santello, M.; Bicchi, A. ThimbleSense: A Fingertip-Wearable Tactile Sensor for Grasp Analysis. IEEE Trans. Haptics 2016, 9, 121–133. [Google Scholar] [CrossRef] [PubMed]
- Casini, S.; Morvidoni, M.; Bianchi, M.; Catalano, M.; Grioli, G.; Bicchi, A. Design and realization of the CUFF-clenching upper-limb force feedback wearable device for distributed mechano-tactile stimulation of normal and tangential skin forces. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 1186–1193.
- Bianchi, M.; Battaglia, E.; Poggiani, M.; Ciotti, S.; Bicchi, A. A Wearable Fabric-based display for haptic multi-cue delivery. In Proceedings of the 2016 IEEE Haptics Symposium (HAPTICS), Philadelphia, PA, USA, 8–11 April 2016; pp. 277–283.

© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bianchi, M.; Haschke, R.; Büscher, G.; Ciotti, S.; Carbonaro, N.; Tognetti, A. A Multi-Modal Sensing Glove for Human Manual-Interaction Studies. Electronics 2016, 5, 42. https://doi.org/10.3390/electronics5030042
Bianchi M, Haschke R, Büscher G, Ciotti S, Carbonaro N, Tognetti A. A Multi-Modal Sensing Glove for Human Manual-Interaction Studies. Electronics. 2016; 5(3):42. https://doi.org/10.3390/electronics5030042
Chicago/Turabian StyleBianchi, Matteo, Robert Haschke, Gereon Büscher, Simone Ciotti, Nicola Carbonaro, and Alessandro Tognetti. 2016. "A Multi-Modal Sensing Glove for Human Manual-Interaction Studies" Electronics 5, no. 3: 42. https://doi.org/10.3390/electronics5030042
APA StyleBianchi, M., Haschke, R., Büscher, G., Ciotti, S., Carbonaro, N., & Tognetti, A. (2016). A Multi-Modal Sensing Glove for Human Manual-Interaction Studies. Electronics, 5(3), 42. https://doi.org/10.3390/electronics5030042






