4. Module Reliability of VSC Multilevel Converter
The development of power electronics and controllable device in power system is rapidly expanding the field of applications for voltage source converter (VSC)-based HVDC technologies. VSC HVDC system is based on insulated-gate bipolar transistor (IGBT) and the topology is multilevel topologies. The recent trends on multilevel converters for HVDC systems use modular multilevel converter (MMC) topology which connects two-level converter modules in cascade to achieve the desired AC voltage.
The HVDC model presented in this paper considers 600MW VSC-HVDC link with two MMCs, including about 400 SMs per phase.
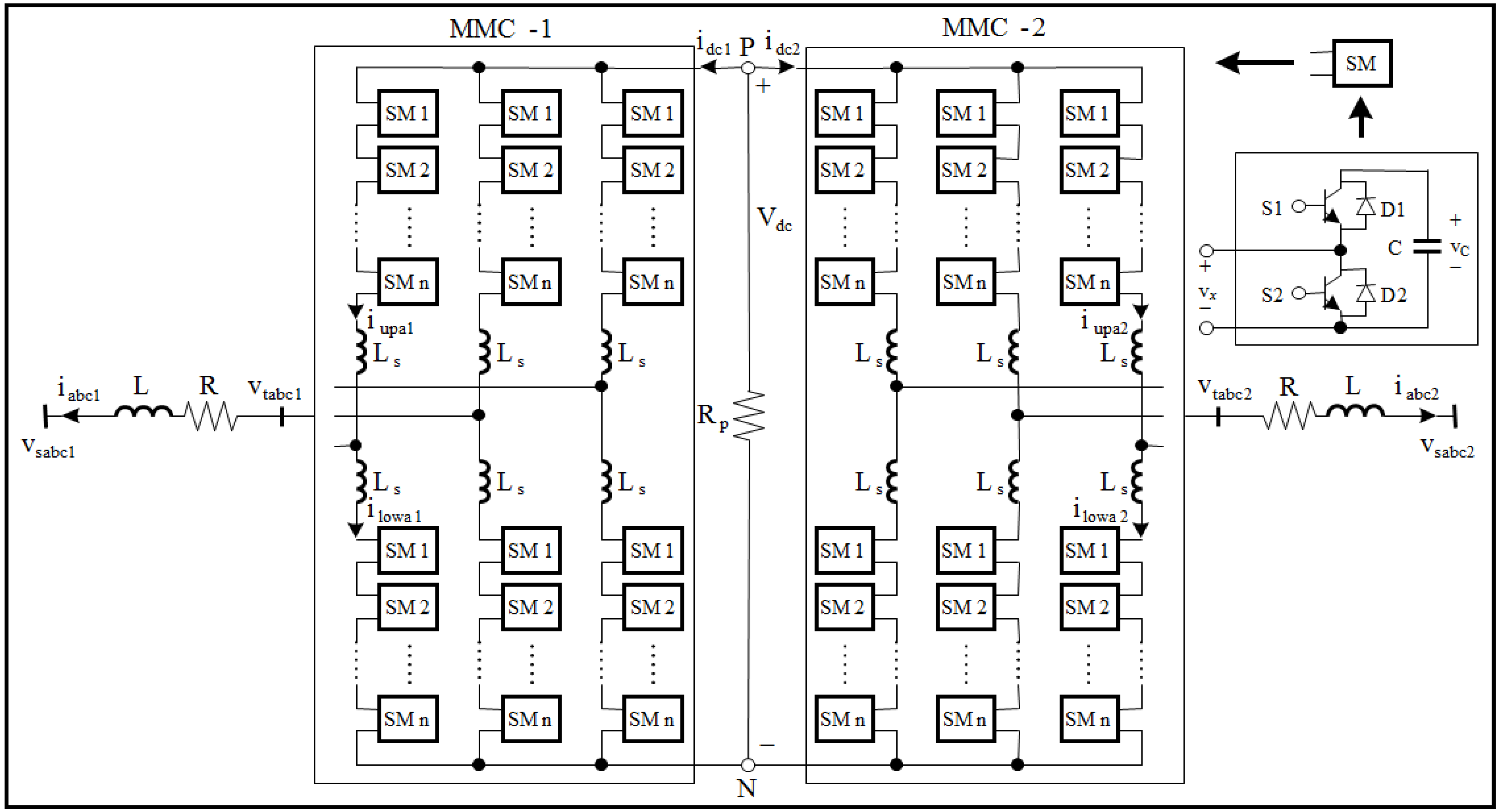
Figure 2 shows the MMC topology where each SM (submodule) contains a capacitor and two insulated-gate bipolar transistor (IGBT) switches (S1 and S2). At any instant during normal operation, only one of the two switches (S1 or S2) is ON. As a result, when the switch S1 is ON (S2 is OFF), the voltage of the SM is and when the switch S2 is ON (S1 is OFF), the SM voltage is zero. The numbers of submodule of MMC depend on the selected IGBT devices, in this paper, 3 kinds of IGBT, as 1.6 kV, 1.8 kV and 2 kV were considered. The numbers of submodules required in the target system are
Table 1.
Table 1.
Numbers of Submodules.
Table 1.
Numbers of Submodules.
| Module Voltage | Number of Submodule |
|---|
| 1.6 kV | 375 |
| 1.8 kV | 334 |
| 2.0 kV | 300 |
Figure 2.
Modular Multilevel Converter Topology.
Figure 2.
Modular Multilevel Converter Topology.
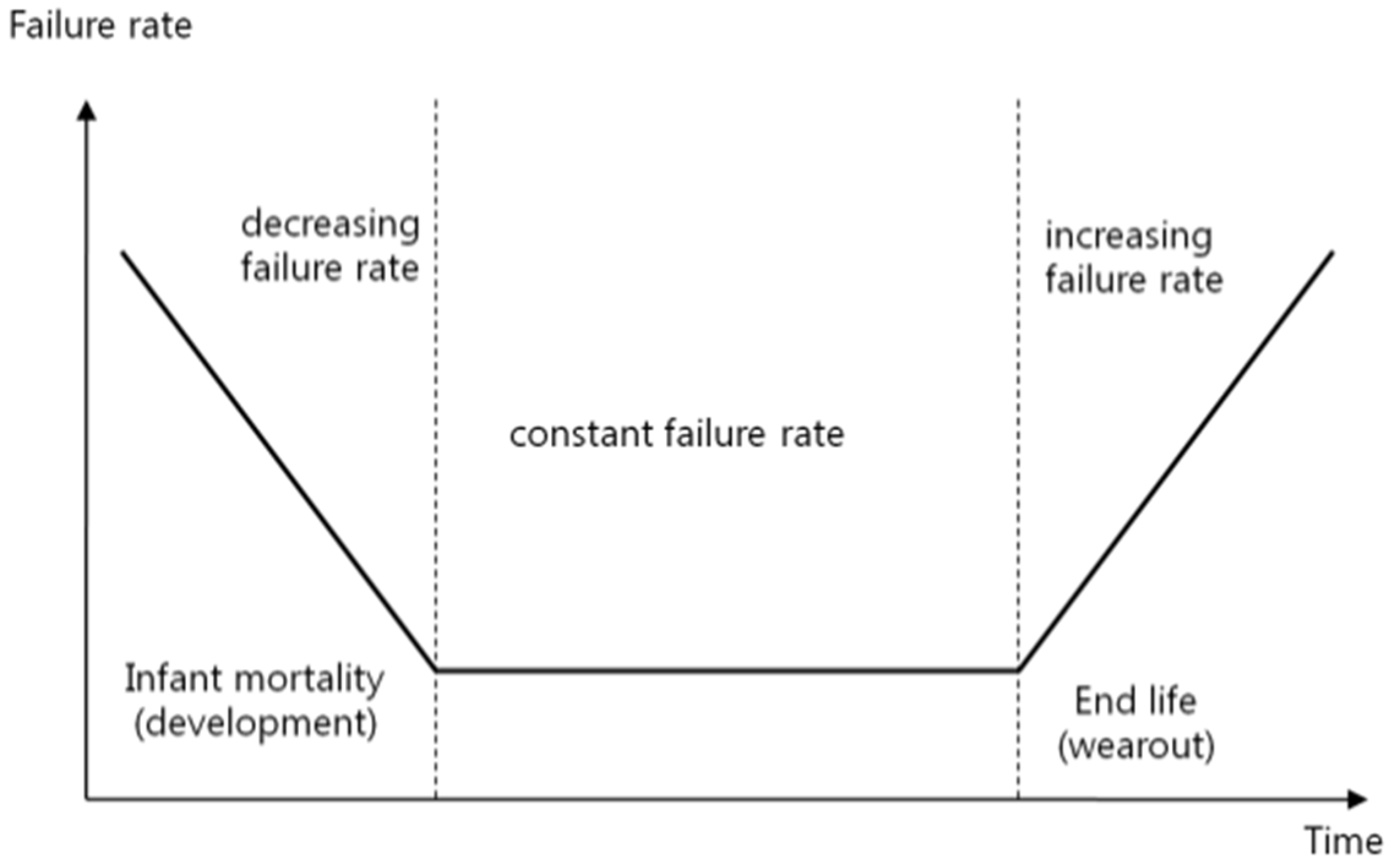
In order to estimate the number of additional modules required in each converter arm an estimate of the system reliability is made. This will then need to be refined by substituting the values with values obtained after more calculation and revising the circuit to reduce areas that are vulnerable.
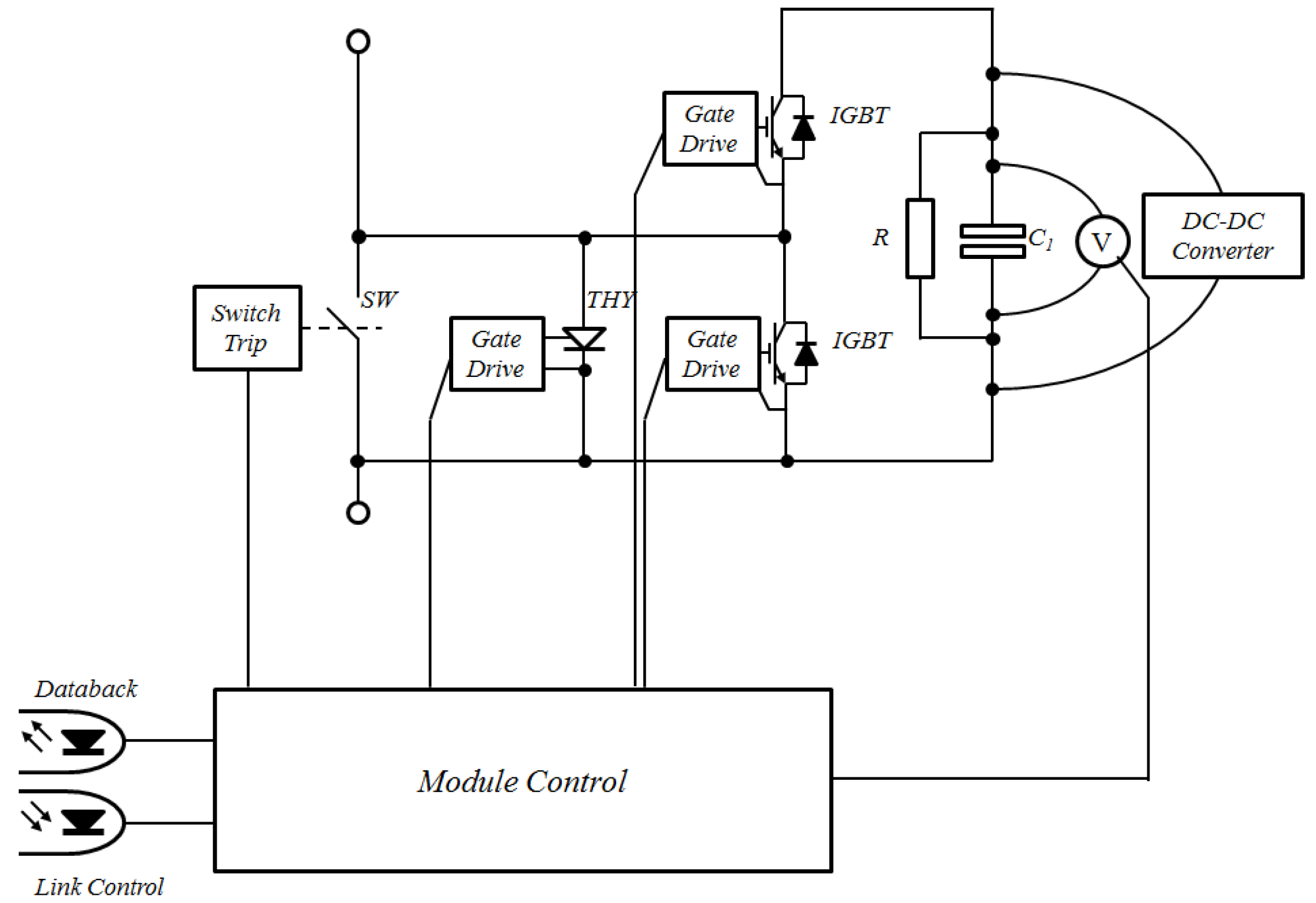
The components such as the thyristor and the shorting switch shown by
Figure 3 are only operated under exceptional circumstances and so will not be included in the main calculation at this time. The main source for component reliability is the maker’s catalogues and the failure rate data of SM of the MMC is presented in
Table 2 [
6]. The values are presented in units of “Failures In Time”, which are defined as failures per billion hours (1e
−9 failures/hour).
Figure 3.
Submodule of modular multilevel converter (MMC) Voltage Source Converter.
Figure 3.
Submodule of modular multilevel converter (MMC) Voltage Source Converter.
Table 2.
Failure Rate Data.
Table 2.
Failure Rate Data.
| Component | No. | Failure Rate (FIT) | Total Failure Rate | Comments |
|---|
| - IGBT and gate drive | 2 | 40 | 80 | Power Circuit |
| - Thyristor and gate drive | 1 | 47 | 47 |
| - Bypass Switch | 1 | 1000 | 1000 |
| - Power Capacitor | 1 | 10 | 10 |
| - Power Resistor | 1 | 265 | 265 |
| - Custom IC | 1 | 150 | 150 | Control |
| - Optical Rx/Tx | 2 | 100 | 200 |
| - IC Circuit | 1 | 13 | 13 |
| - Ferrite Core | 2 | 22 | 44 | Power Supply |
| - Switching Power Supply | 1 | 1000 | 1000 |
As stated above only the values shown rows 3, 6, 7, 9–11, 13 and 14 in
Table 2 are combined to give the failure rate of the module. If 𝛾
0 to 𝛾
11 represent the values from the “Total Failure Rate” column as elements in a vector the expression becomes:
The mean time to failure [MTTF] then becomes:
Since this reflects a random event it is more meaningful to convert it to an value representing the availability of the module over a given time span, and by this obtain an estimate of the availability of the complete converter system over its life. This is commonly done by expression values in terms of “Unavailability”, Q:
where “
t” is the “time at risk”. Thus, assuming full time operation, over the three-year maintenance period the proportion of the all modules in the target MMC HVDC arm to fail will be 4.5%, while over the 30-year life of the equipment, 37 % of the modules will have failed.
This equation can be adapted further to relate a service life and the maintenance period:
where “
t” is the overall time at risk, in this case the equipment life, and “
μ” is the maintenance rate, that is, 1/(3years). As would be expected the result is very similar to that above for the 3-year maintenance period, thus, 4.4% of the modules will fail.
To determine the availability of a complete inverter limb of “n” modules in which “m” modules can be allowed to fail before the limb fails the Binomial Failure Model needs to be used:
When
N is large, then the binomial distribution is well approximated by the normal distribution [
7].
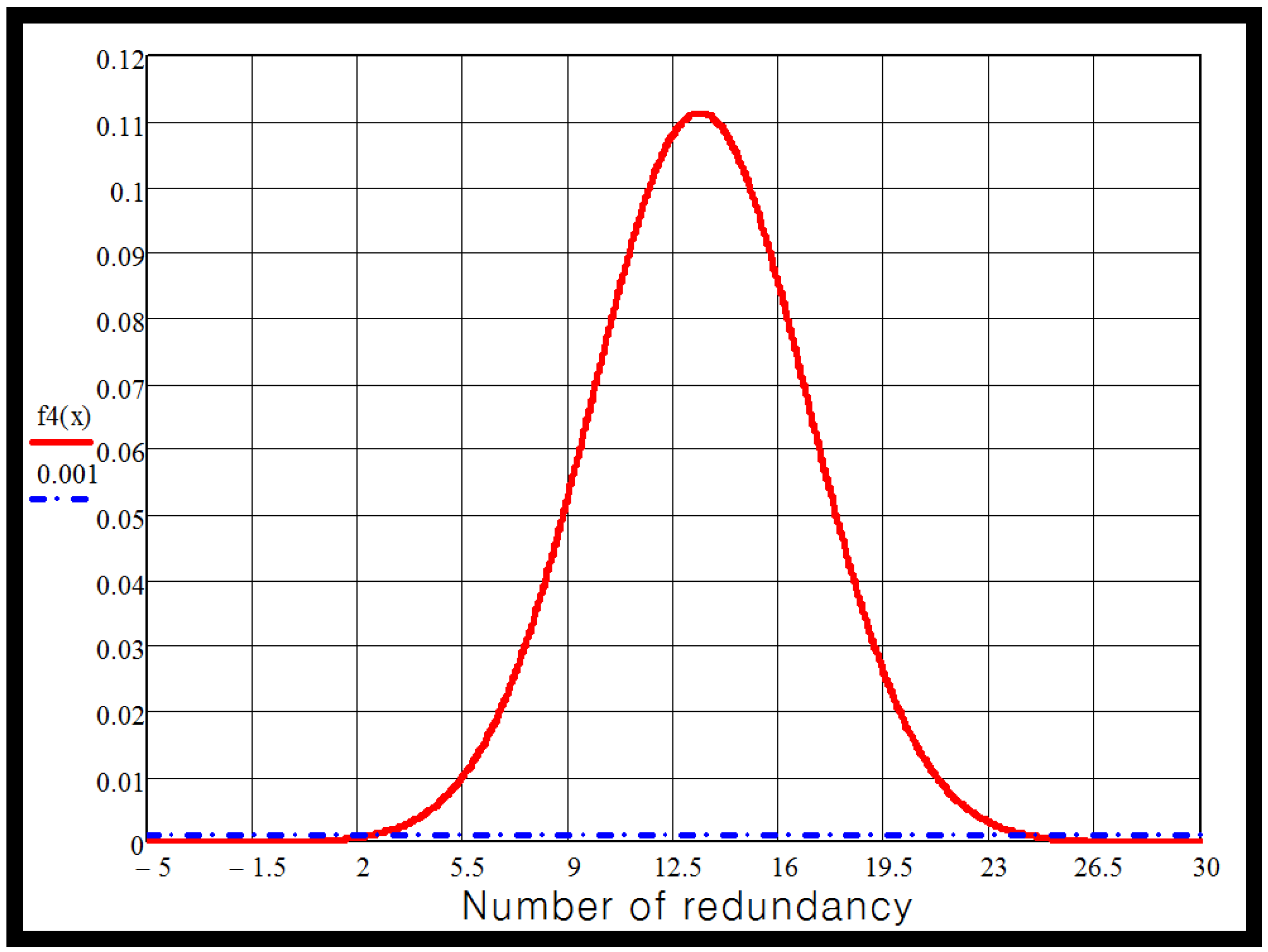
The unavailability for a single inverter arm for the target system has been designed to operate with a minimum of 334 modules, the unavailability of the system according to redundant modules increment is shown in
Figure 4.
Figure 4.
Unavailability function for the target system with 334 modules according to redundant modules increment.
Figure 4.
Unavailability function for the target system with 334 modules according to redundant modules increment.
In order to determinate the number of the redundant modules for MMC, several scenarios are considered following as:
Maintenance periods are 1 year, 2 years and 3 years
IGBT devices used are 1.6 kV, 1.8 kV and 2 kV
FIT of DC/DC converter changed 1000 to 500
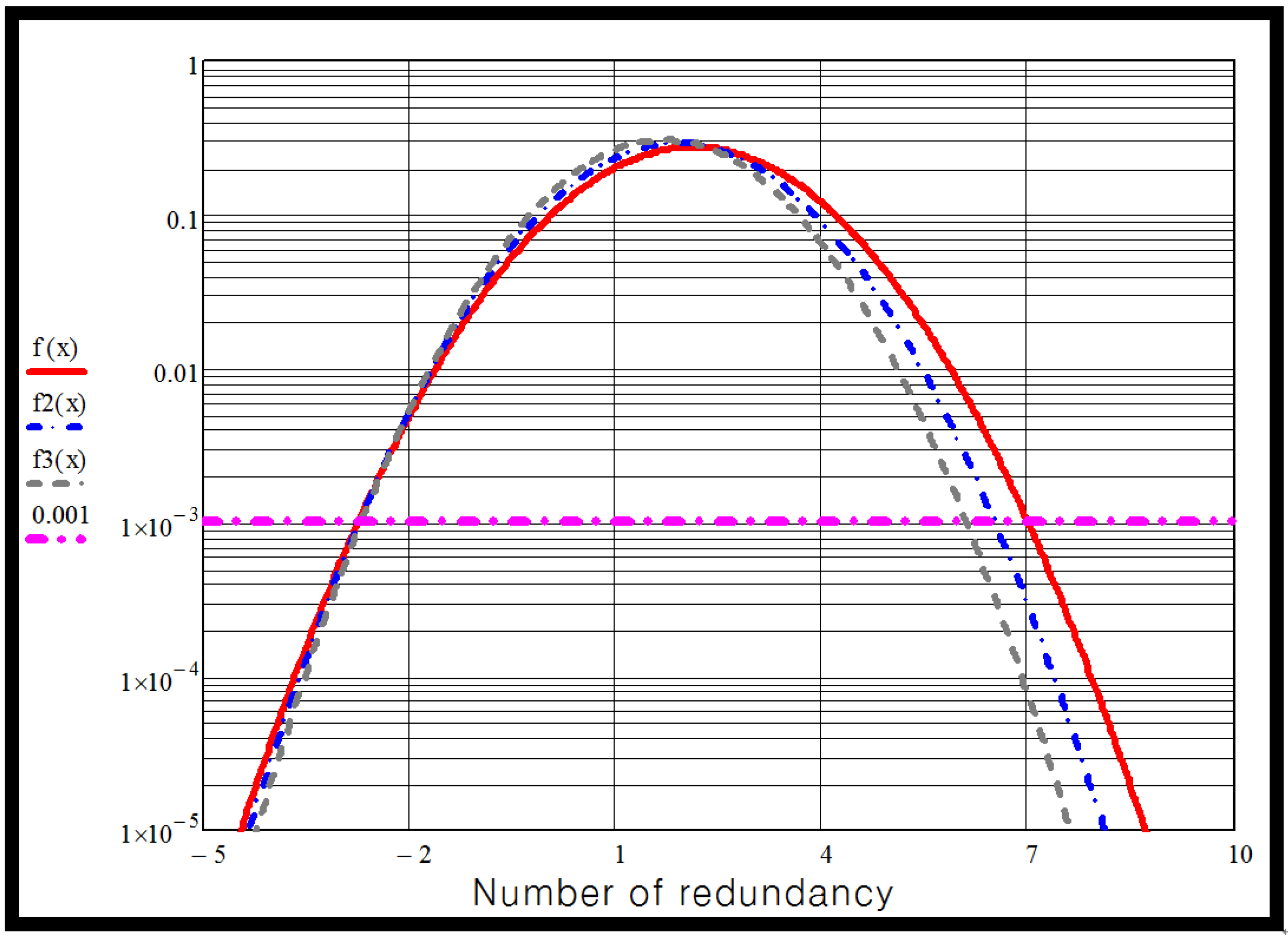
Figure 5 shows the graph of MMC valve unavailability for several IGBT valves against numbers of modules in case of 1-year maintenance. In this case, the unavailability is 0.00568. To achieve better than 99.9% availability requires:
- •
seven modules for a 1.6 kV IGBT device,
- •
six modules for a 1.8 kV IGBT device,
- •
five modules for a 2 kV IGBT device
Figure 5.
Unavailability function for MMC valve in case of 1-year maintenance.
Figure 5.
Unavailability function for MMC valve in case of 1-year maintenance.
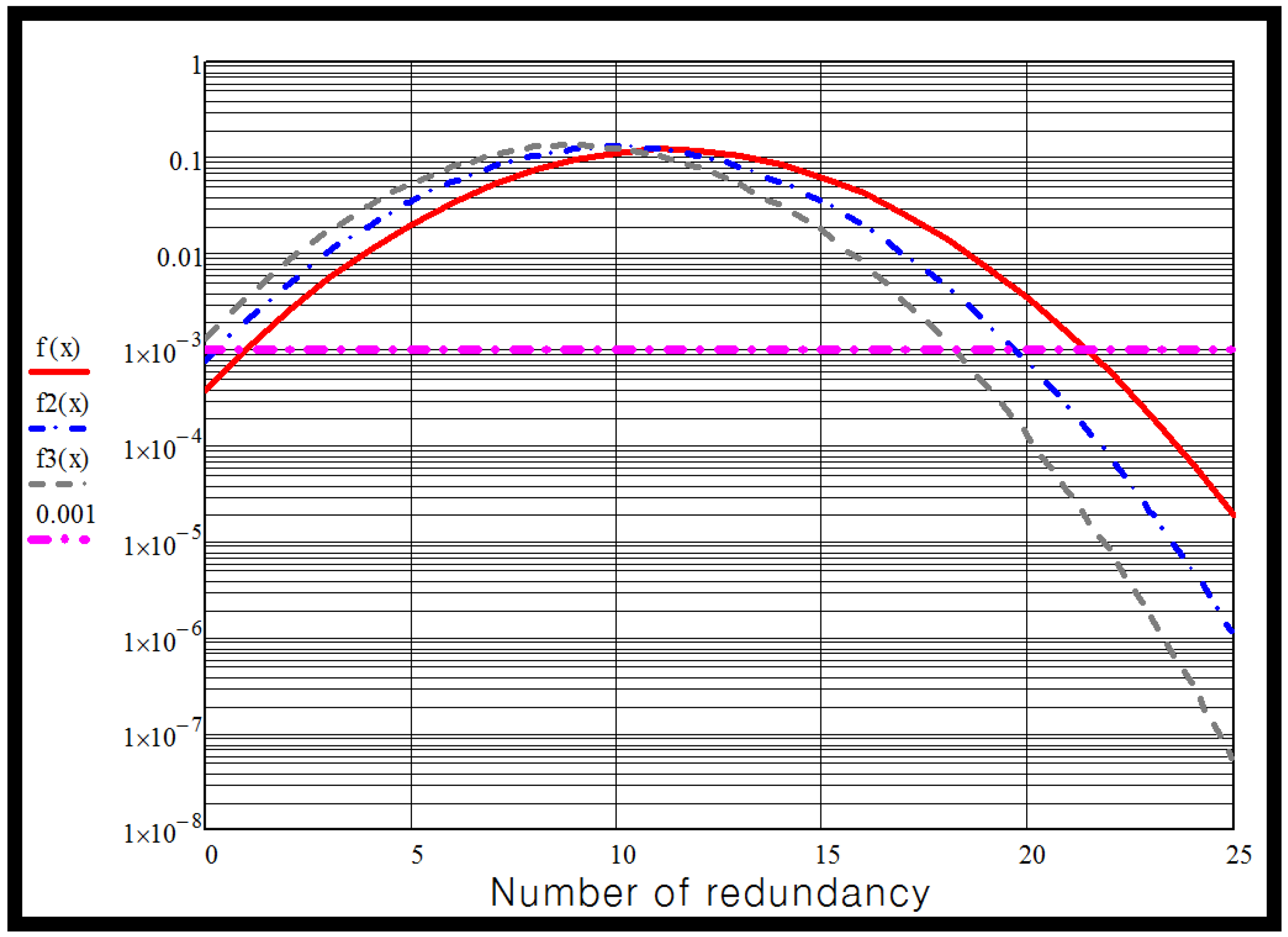
Figure 6 shows the graph of MMC valve unavailability for several IGBT valves against numbers of modules in case of 2-year maintenance. In this case, the unavailability is 0.0299. To achieve better than 99.9% availability requires:
- •
22 modules for a 1.6 kV IGBT device,
- •
20 modules for a 1.8 kV IGBT device5,
- •
17 modules for a 2 kV IGBT device
Figure 6.
Unavailability function for MMC valve in case of 2-year maintenance.
Figure 6.
Unavailability function for MMC valve in case of 2-year maintenance.
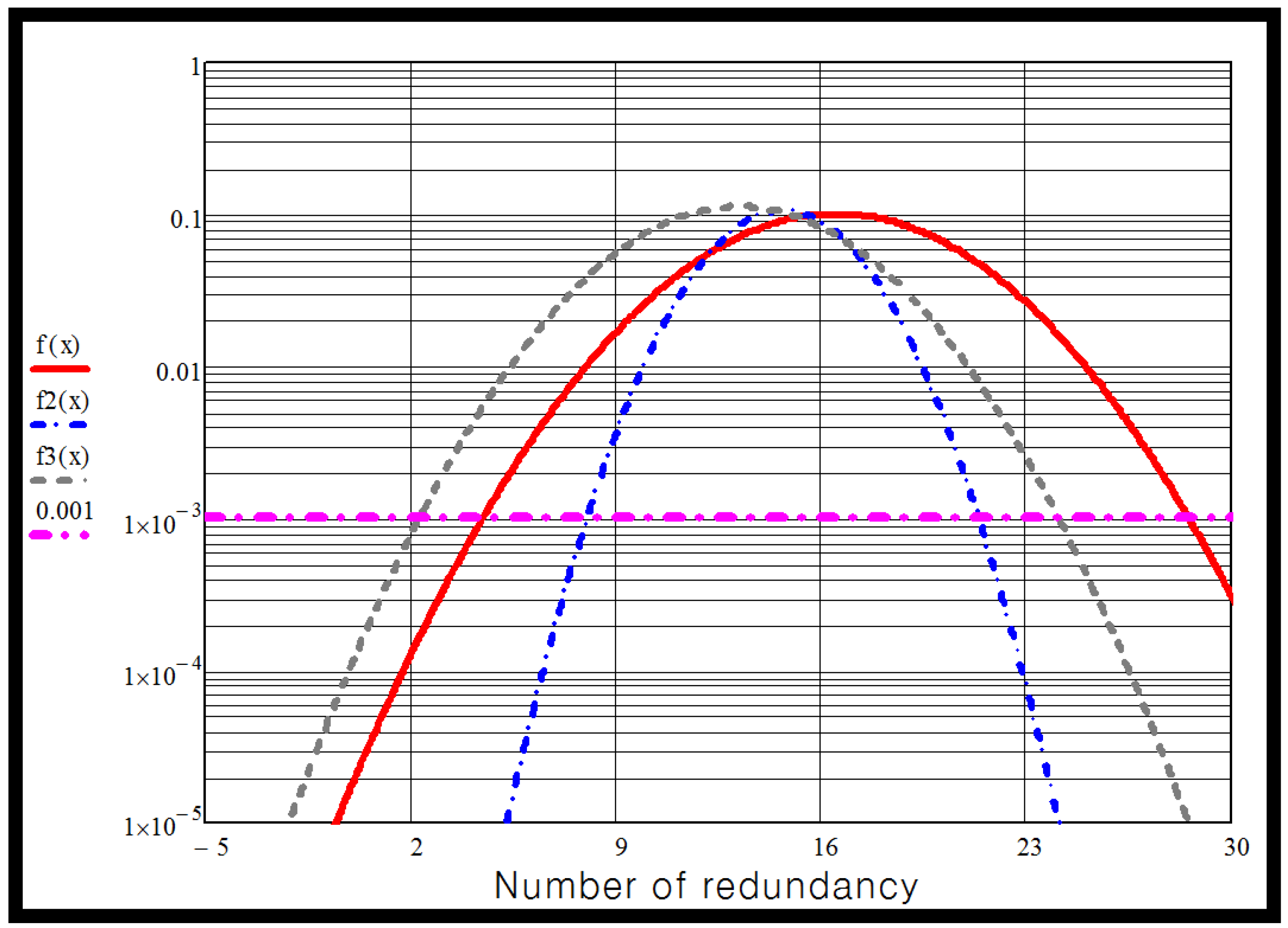
Figure 7 shows the graph of MMC valve unavailability for several IGBT valves against numbers of modules in case of 3-year maintenance. In this case, the unavailability is 0.044. To achieve better than 99.9% availability requires:
- •
28 modules for a 1.6 kV IGBT device,
- •
25 modules for a 1.8 kV IGBT device5,
- •
20 modules for a 2 kV IGBT device
Figure 7.
Unavailability function for MMC valve in case of 3-year maintenance.
Figure 7.
Unavailability function for MMC valve in case of 3-year maintenance.
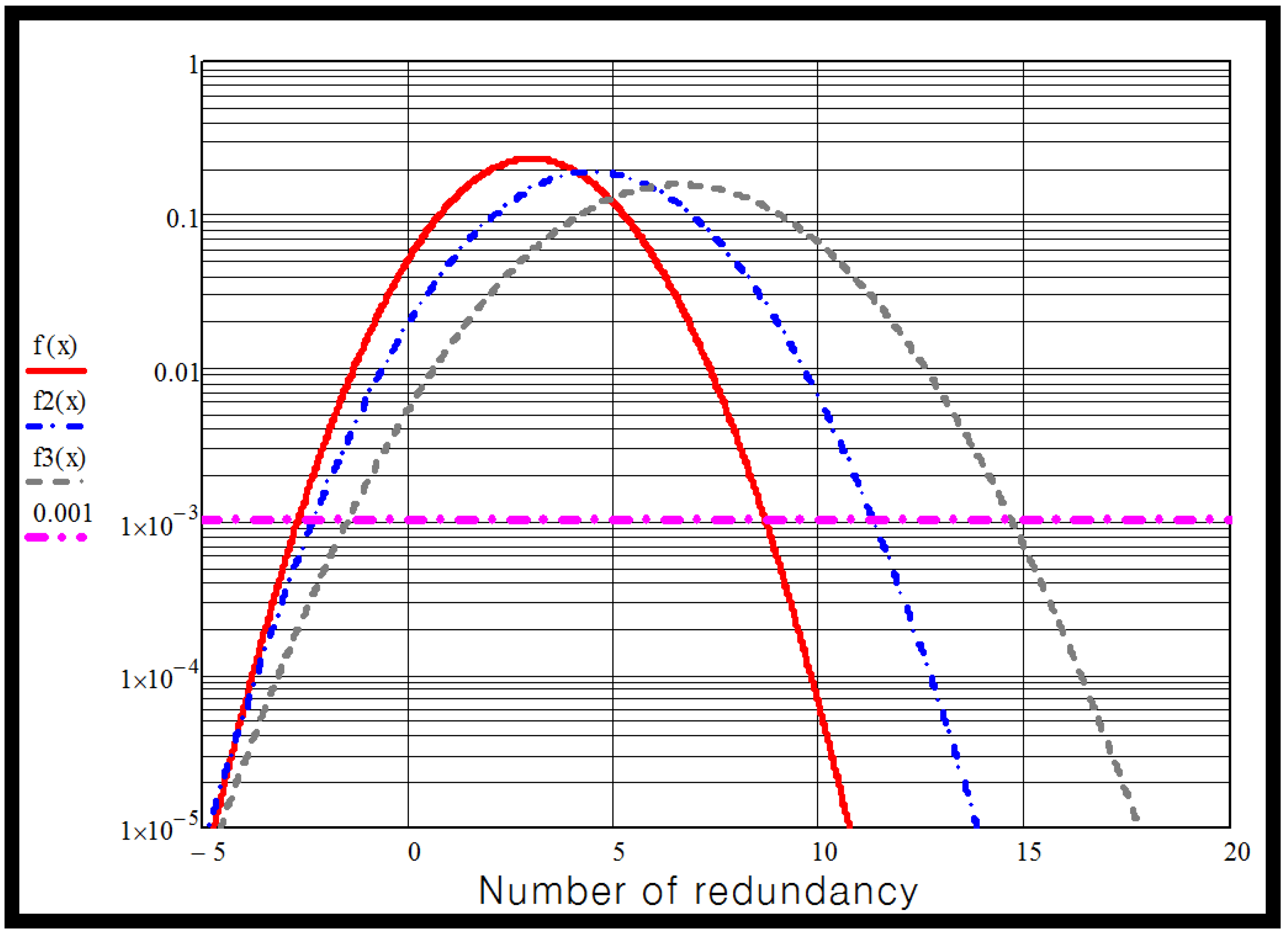
The graph of MMC valve unavailability but with the DC/DC converter failure rate reduced to 500FIT is shown in
Figure 8. In this case, the rate of IGBT is 2 [kV] with 300 modules. This shows the equivalent module requirement to be:
- •
7 modules for a 1-year maintenance interval,
- •
12 modules for a 2-year maintenance interval,
- •
15 modules for a 3-year maintenance interval.
Figure 8.
Unavailability function for MMC valve with failure rate of DC/DC converter = 500.
Figure 8.
Unavailability function for MMC valve with failure rate of DC/DC converter = 500.
Consequently, the number of MMC module for the maintenance and the range of mean capacitor voltage is given in
Table 3.
Table 3.
Additional modules against maintenance period and module voltage.
Table 3.
Additional modules against maintenance period and module voltage.
| Module Voltage | No. of Module | Additional Cells Against Maintenance Period |
|---|
| 1 Year | 2 Years | 3 Years |
|---|
| 1.6 kV | 375 | 7 | 22 | 28 |
| 1.8 kV | 334 | 6 | 20 | 25 |
| 2.0 kV | 300 | 5 | 17 | 20 |