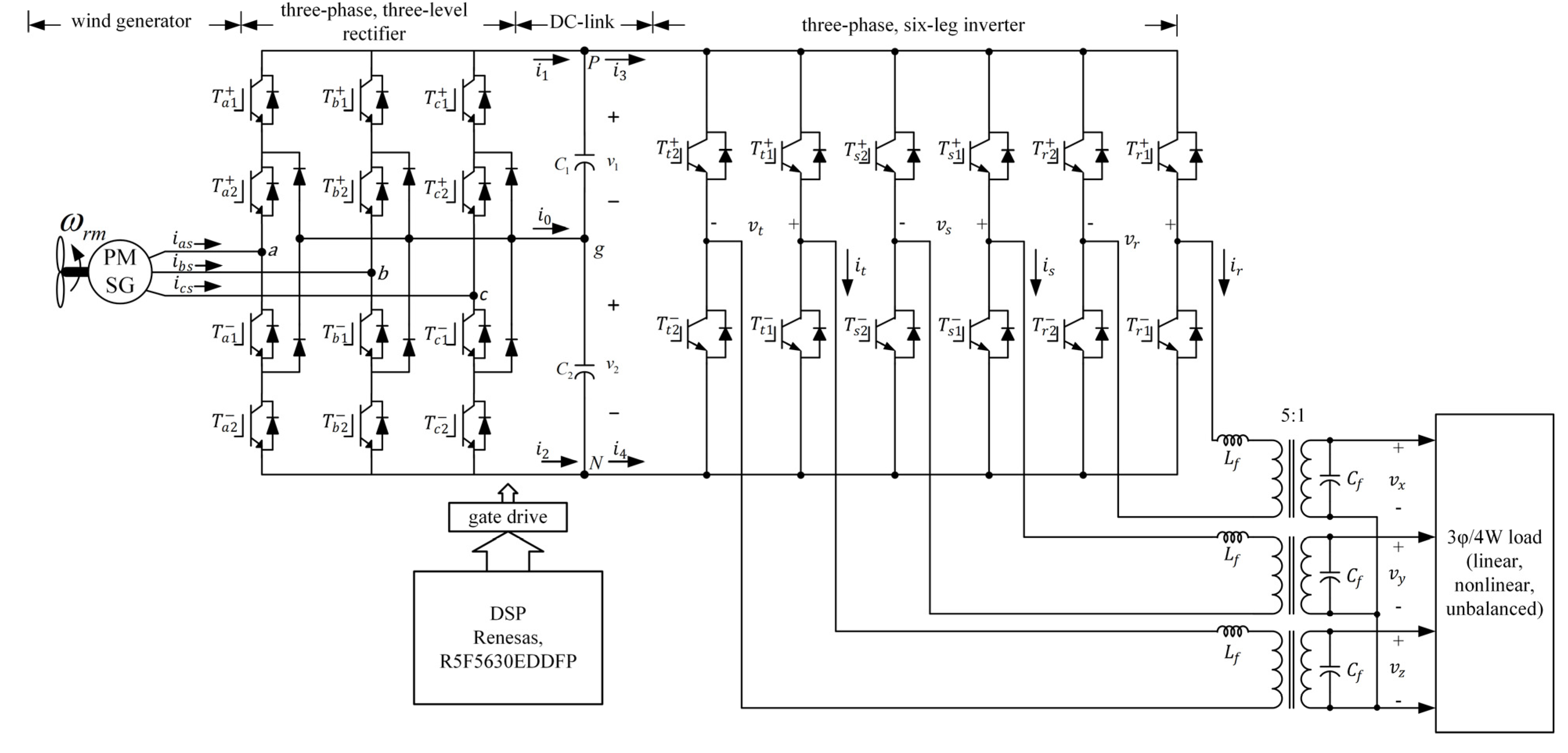
2.1. Mathematical Model of PMSG
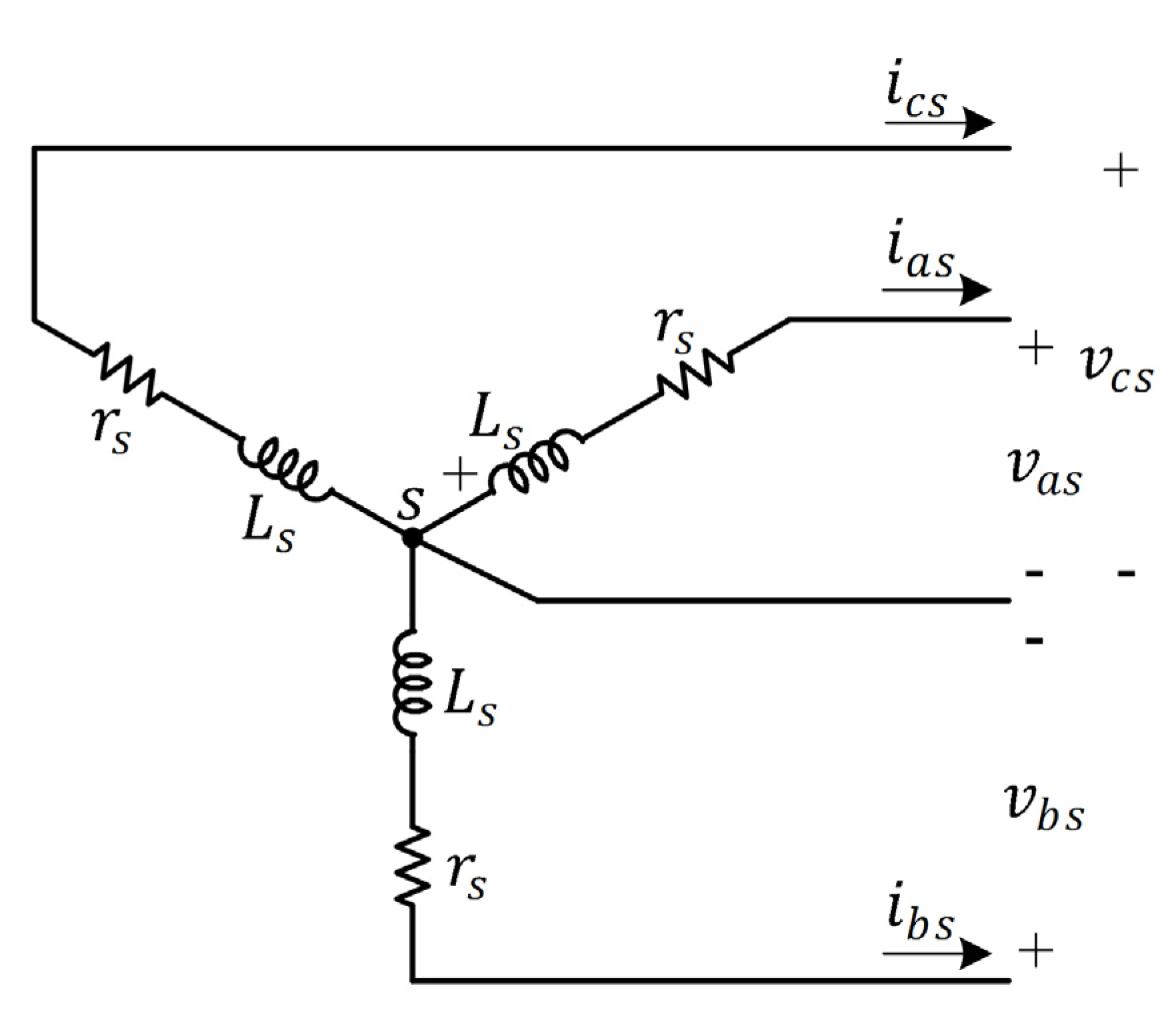
The equivalent circuit of a PMSG is shown in
Figure 2. The voltage equation can be written as [
6,
8]
where
Here,
,
, and
denote the phase voltages of the generator, and
,
, and
denote the line currents of the generator; furthermore,
represents the equivalent resistance of the stator, and
,
,
are the flux linkages of the stator. Assume that the flux harmonics of the rotor and stator are negligible. Consequently, the fluxes of the rotor and stator are sinusoidally distributed. Therefore, the flux linkage can be expressed as
where
Here,
and
;
is the rotor flux angle,
is the rotor speed,
is the equivalent number of turns in the stator winding,
is the leakage inductance of the stator winding,
is the equivalent reluctance of the stator, and
is the equivalent flux linkage of the rotor relative to the stator. According to Equations (1)–(8), the phase voltage of the generator can be obtained as
where
denotes the internal voltage of the generator and is proportional to
. In other words,
The equation for the output power of the generator is
According to Equations (10) and (11), the output power equation can be rewritten as
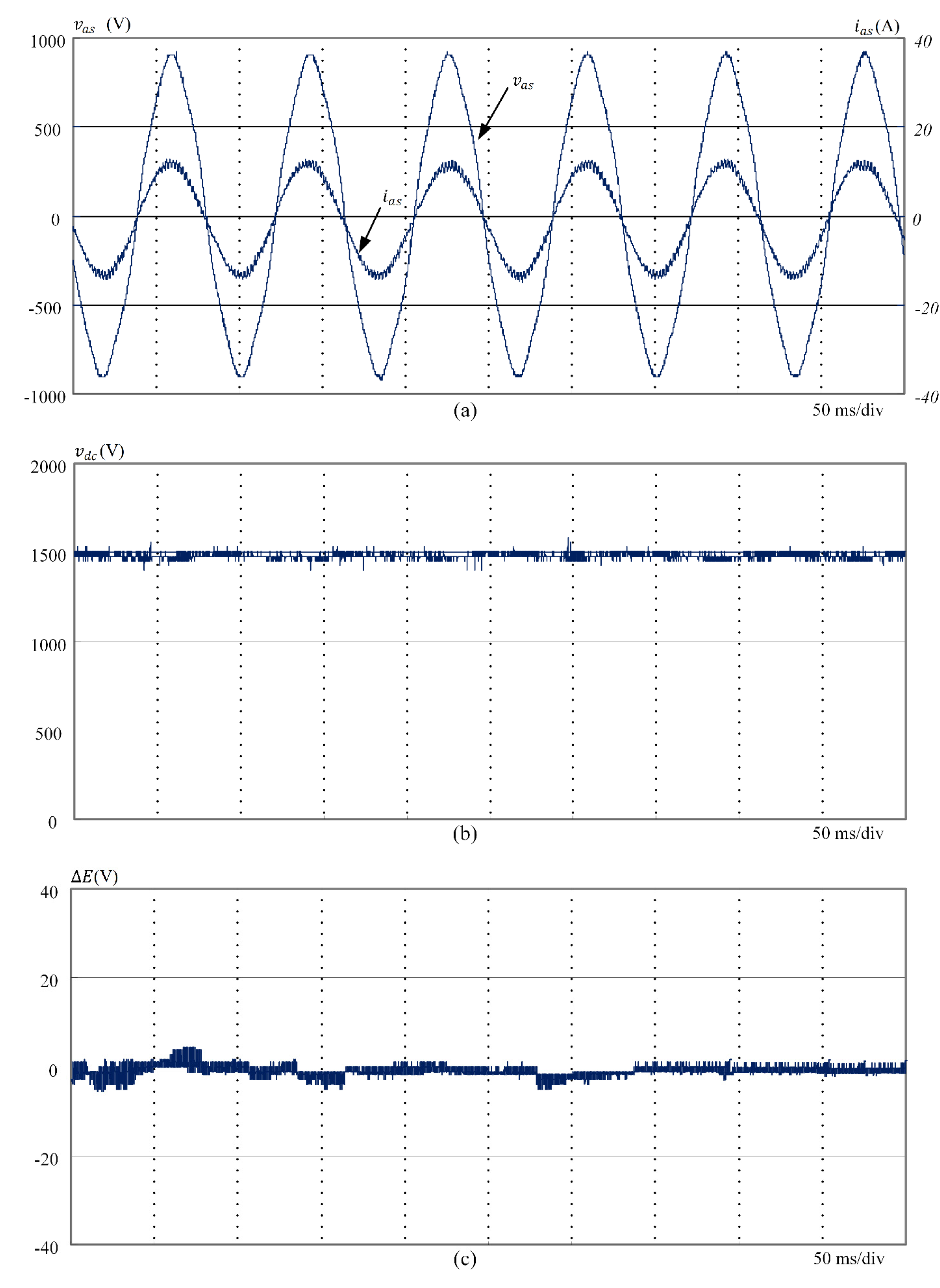
This equation shows that the output power of the generator is proportional to the rotor speed and the peak value of the three-phase currents, implying that the output power of the generator can be controlled by varying the peak value of the currents. This principle was used in this study to implement a current controller for the three-phase, three-level rectifier.
Figure 2.
Equivalent circuit of a Y-connection PMSG.
Figure 2.
Equivalent circuit of a Y-connection PMSG.
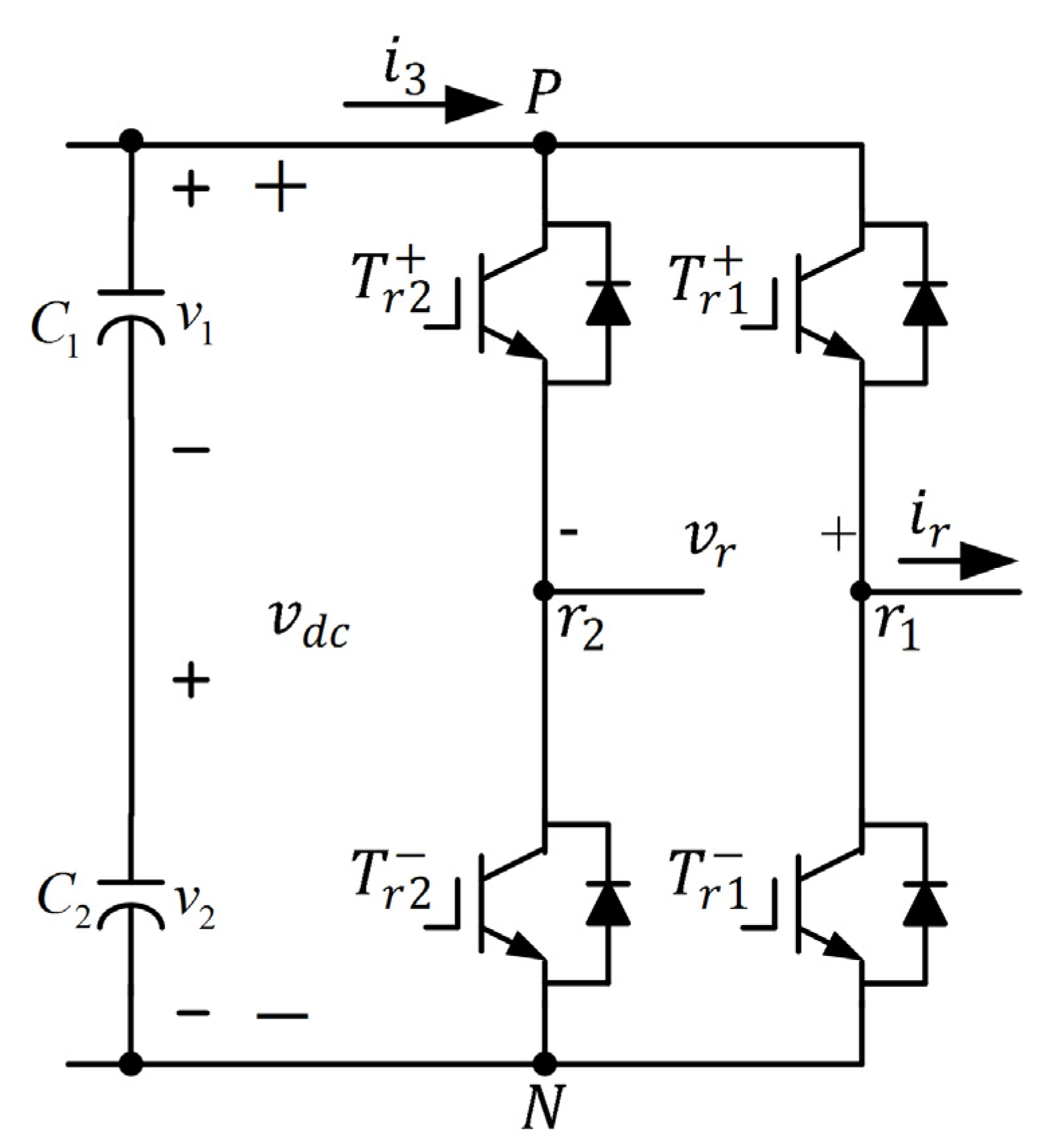
2.2. Three-Phase, Three-Level Rectifier
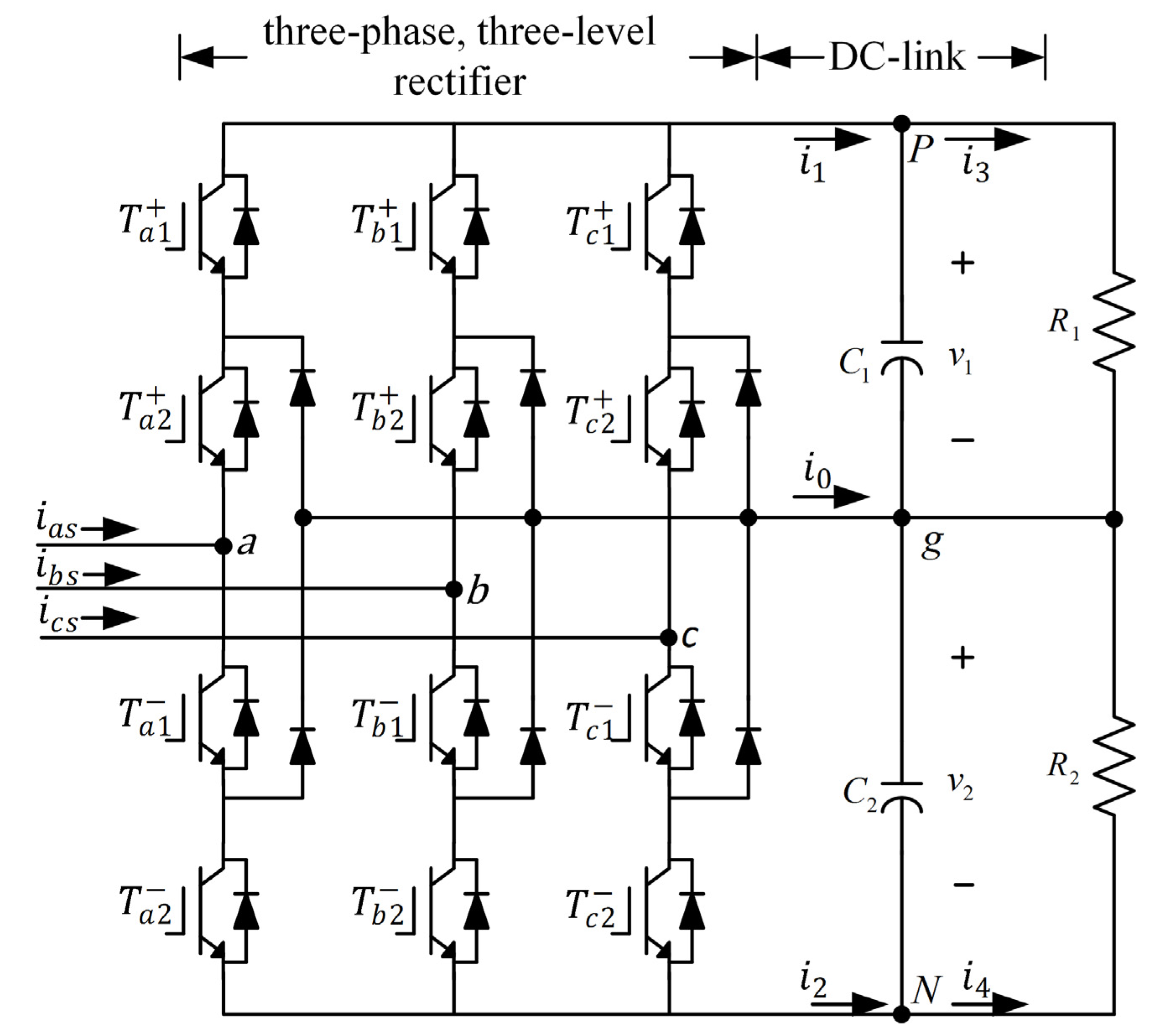
A schematic of the three-phase, three-level rectifier is shown in
Figure 3. It was constructed by adding six clamping diodes with the six power switches to the conventional bridge structure. These six switches can be appropriately controlled for obtaining three levels of the DC supply voltage across the DC-link capacitors [
11]. In
Figure 3, the voltages of
and
are
and
, respectively. The three voltage levels of the three-phase, three-level rectifier defined by two mutually exclusive switching states—(
,
) and (
,
)—are listed in
Table 1, where x denotes a, b, or c. The sinusoidal PWM is used to generate gating signals for the power switches [
12].
Figure 3.
Schematic of a three-phase, three-level rectifier.
Figure 3.
Schematic of a three-phase, three-level rectifier.
Table 1.
Phase voltages of the three-phase, three-level rectifier.
Table 1.
Phase voltages of the three-phase, three-level rectifier.
| Output | Switching State |
|---|
| | | |
|---|
| 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 1 |
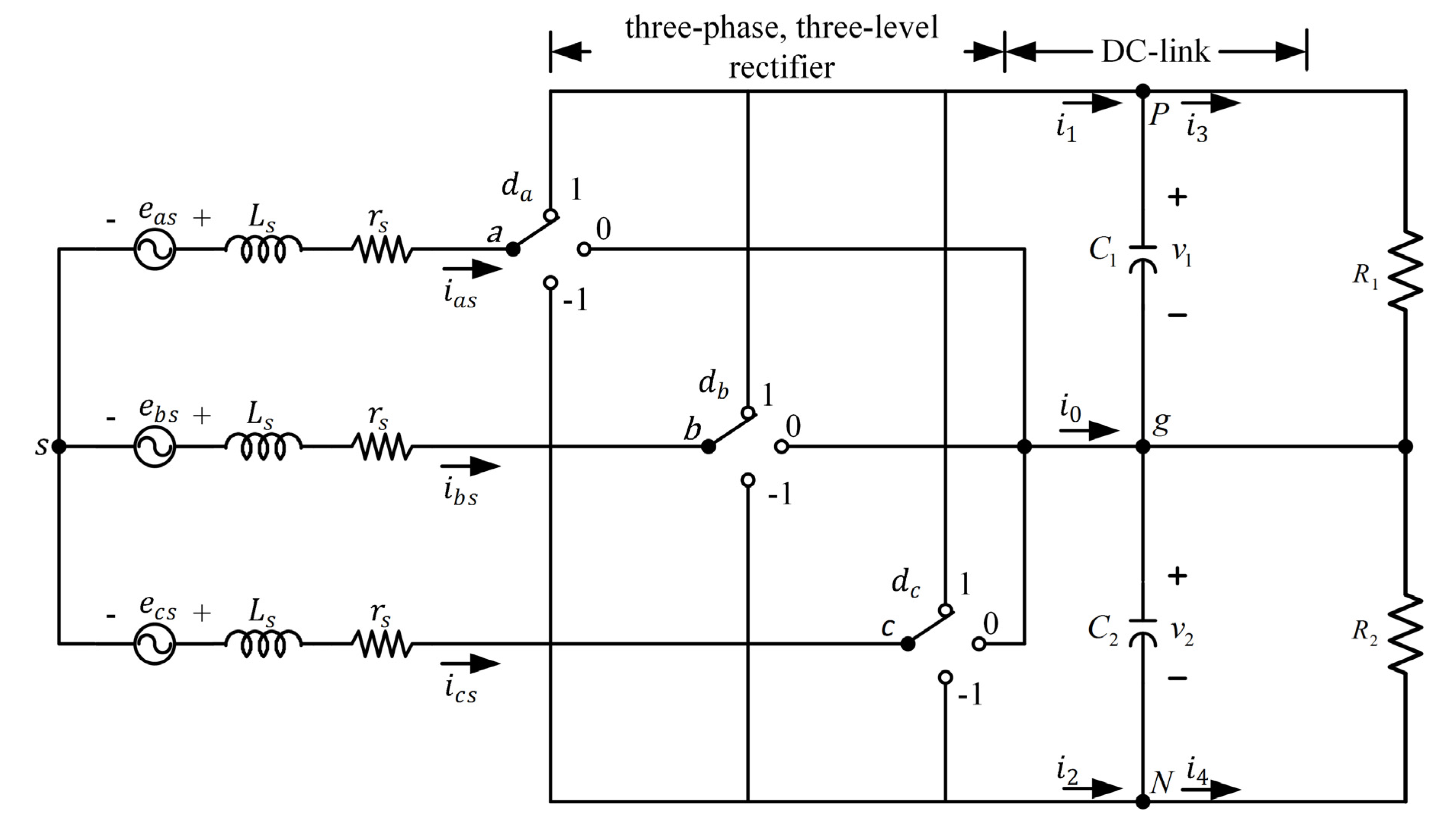
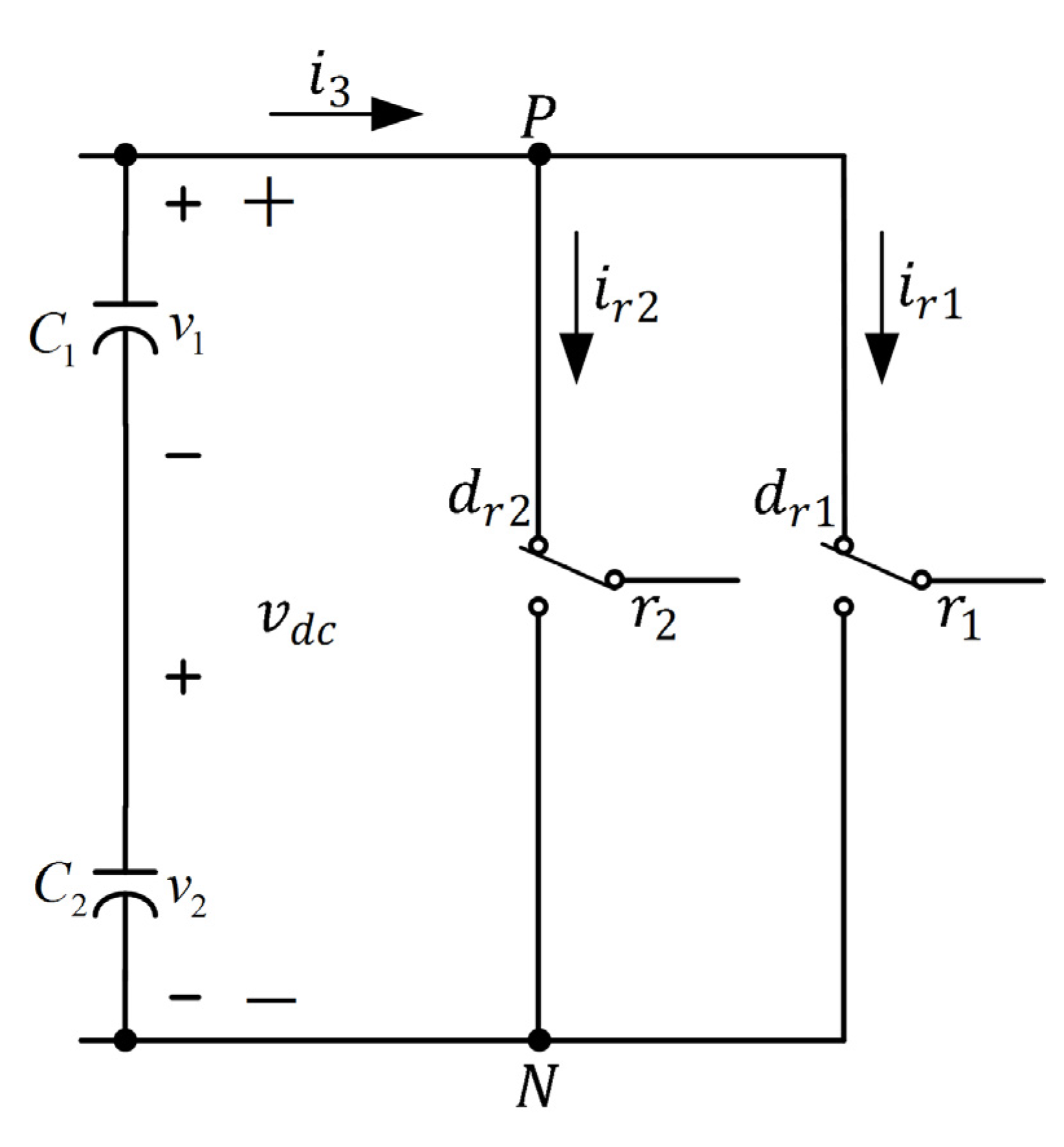
Assume that the power switches are ideal. The equivalent circuit of
Figure 3 is shown in
Figure 4. The following situations are illustrated:
where
. The switching of the phase voltage
can be expressed as
Because the three-phase voltages from the wind generator are balanced, the following expression holds:
where
,
, and
are the phase voltages relative to the neutral point of the wind generator. In
Figure 4, currents
and
are given by
Furthermore, the current
at point
is
where
,
, and
are determined as
Here, and .
In
Figure 4, the differential equations of the voltages of the upper and lower capacitors are
and the voltage error between the upper and the lower capacitors is
where
and
are upper and lower DC-link capacitors, respectively. Equation (22) indicates that the voltage error of the upper and lower capacitors can be controlled by varying duty cycles of
, and this principle was used in this study to implement a voltage controller for the three-phase, three-level rectifier [
13].
Figure 4.
Equivalent circuit of the three-phase, three-level rectifier.
Figure 4.
Equivalent circuit of the three-phase, three-level rectifier.
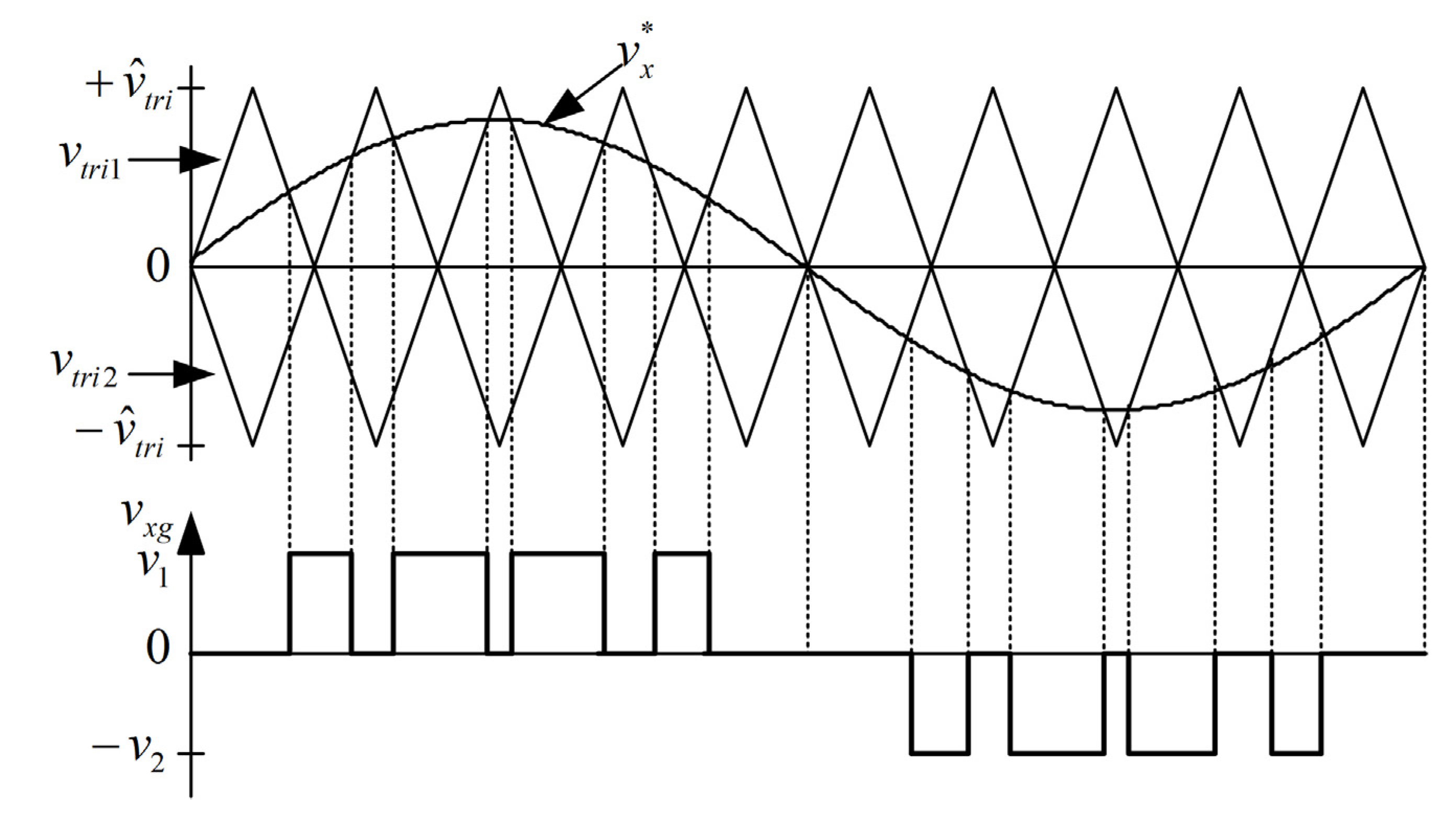
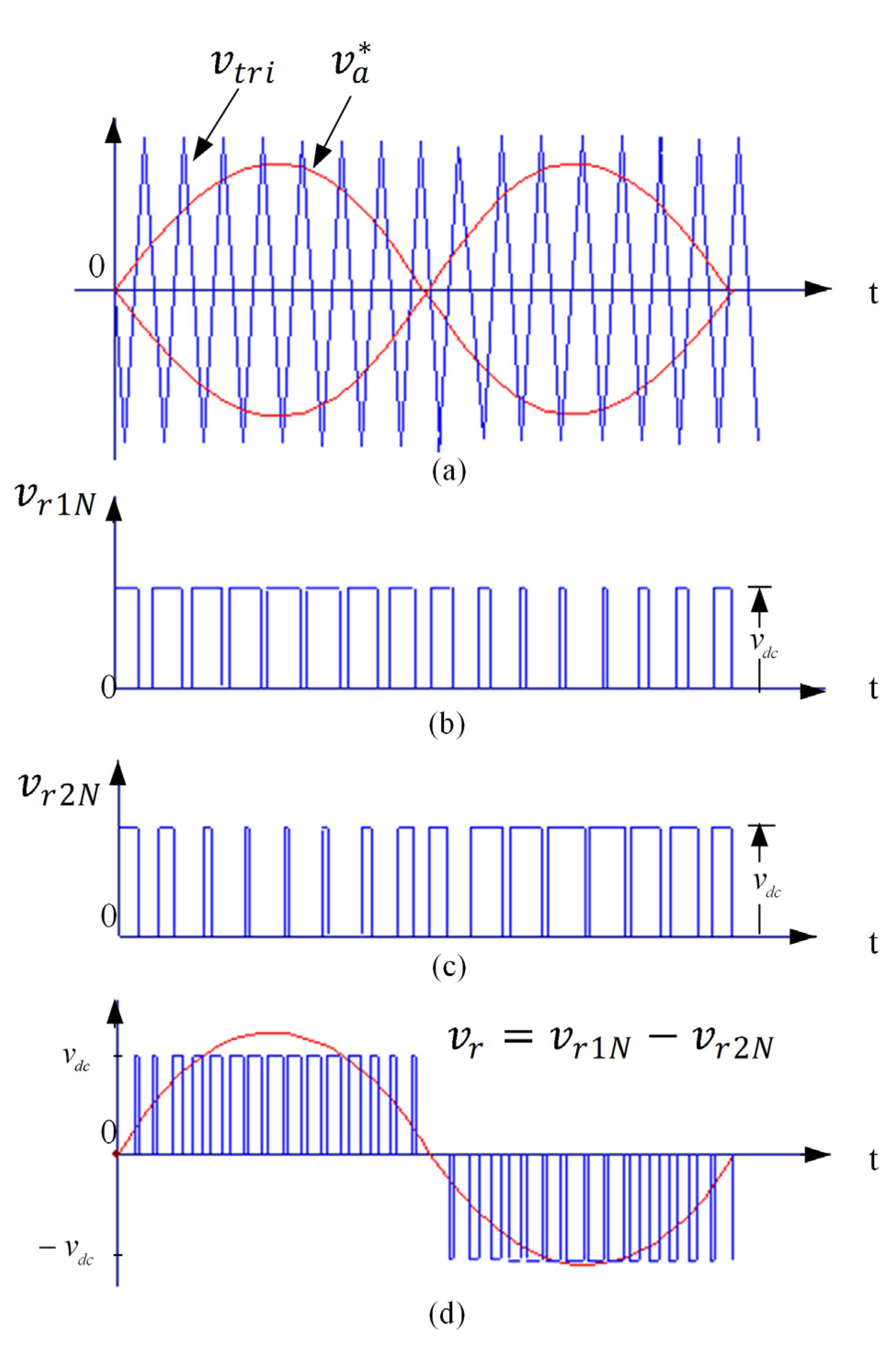
To control the three-phase, three-level rectifier, a sinusoidal PWM technique involving two carrier waves was used [
14]. Gating signals for the power transistors were generated by comparing the commanding signal magnitude of
with the magnitude of two inverse carrier waves having the same peak-to-peak amplitude, frequency, and phase, as shown in
Figure 5. The rectifier is illustrated by the following three modes of operation:
- (1)
when and ,
- (2)
when ,
- (3)
when and ,
where
.
Figure 5.
Sinusoidal PWM with two carrier waves.
Figure 5.
Sinusoidal PWM with two carrier waves.
Figure 5 shows that the peak values of
and
are
and −
, respectively. Therefore, there are three switching modes according to the level of the commanding signal. If the commanding signal can be produced using only half of the DC-link voltage, for example,
, the magnitude of the carrier waves is compared with the commanding signal magnitude, thereby yielding the first mode of operation. If the commanding signal magnitude lies between the signal magnitudes of two carrier waves, the second mode of operation, in which the switching pattern is produced by comparing the carrier waves with the commanding signal magnitude, is conducted. Gating signals for power transistors in the third mode of operation can be obtained by comparing the magnitude of the carrier waves with the magnitude of
. Finally,
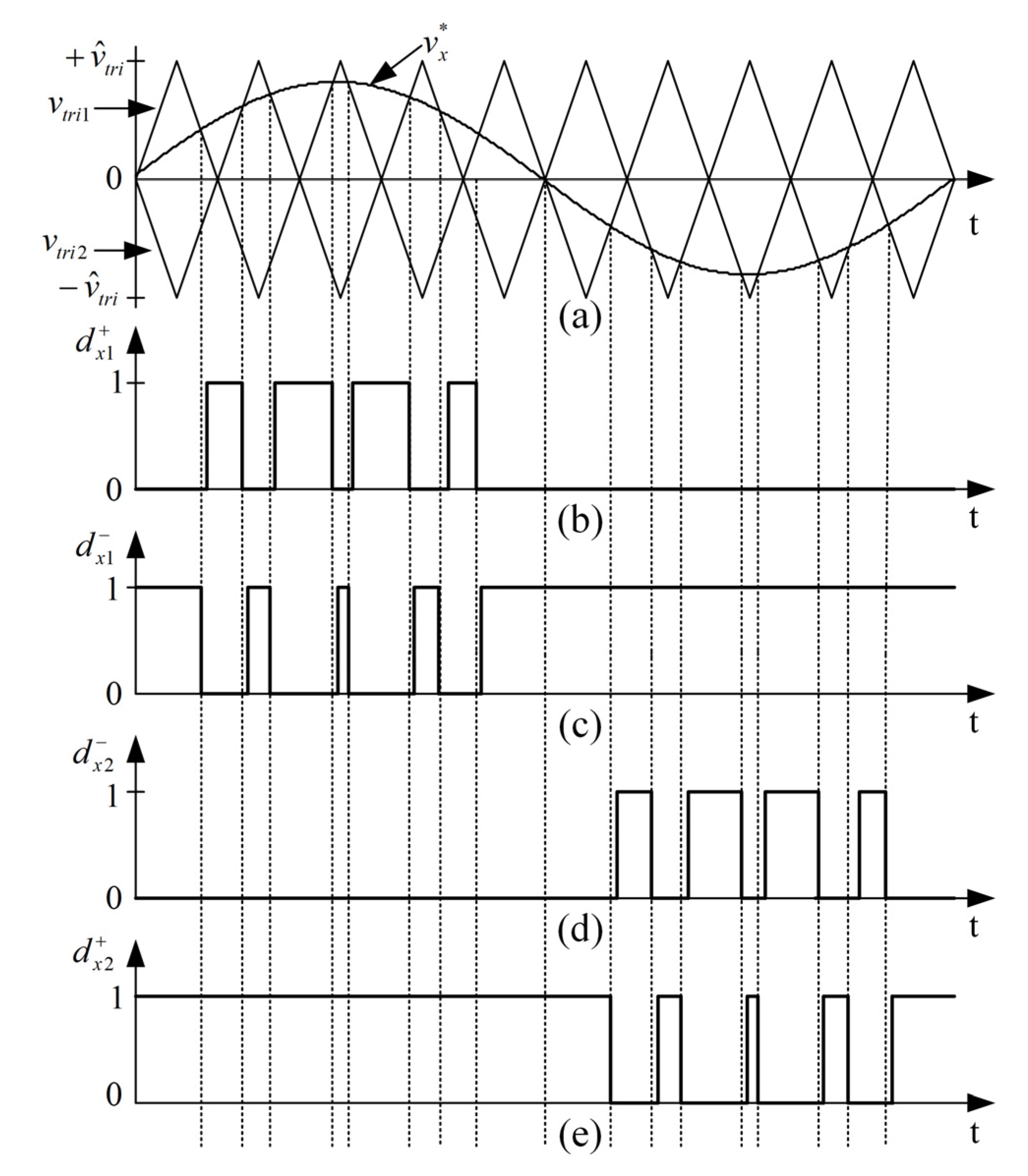
Figure 6 shows the gating signals for the three modes of operation, illustrating that the switching pattern of the three-phase, three-level rectifier is generated by the aforementioned three modes of operation. The switching loss can be reduced by reducing the switching frequency or by reducing the instantaneous current or voltage during the switching period.
Figure 6.
Switching pattern of the three-phase, three-level rectifier.
Figure 6.
Switching pattern of the three-phase, three-level rectifier.
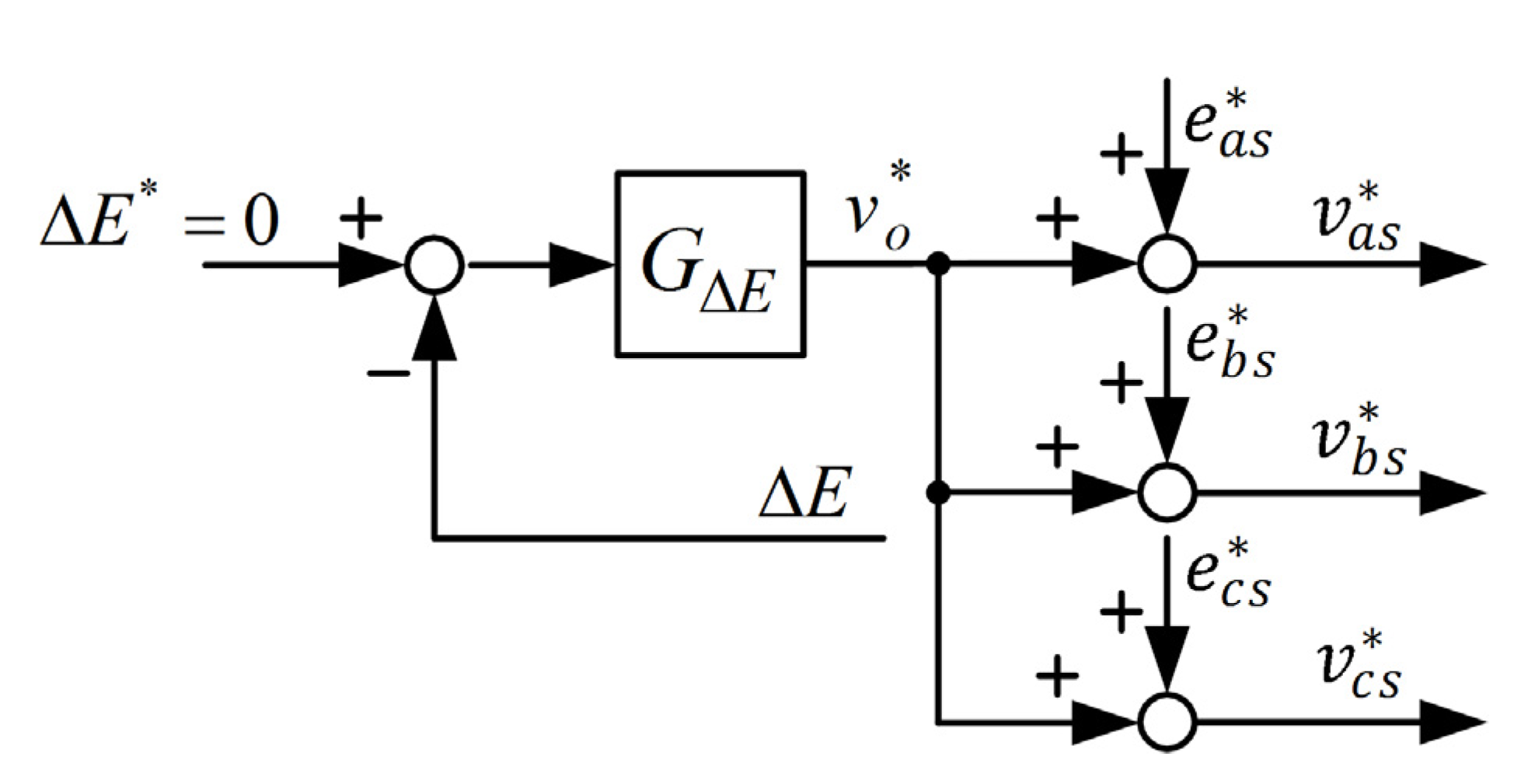
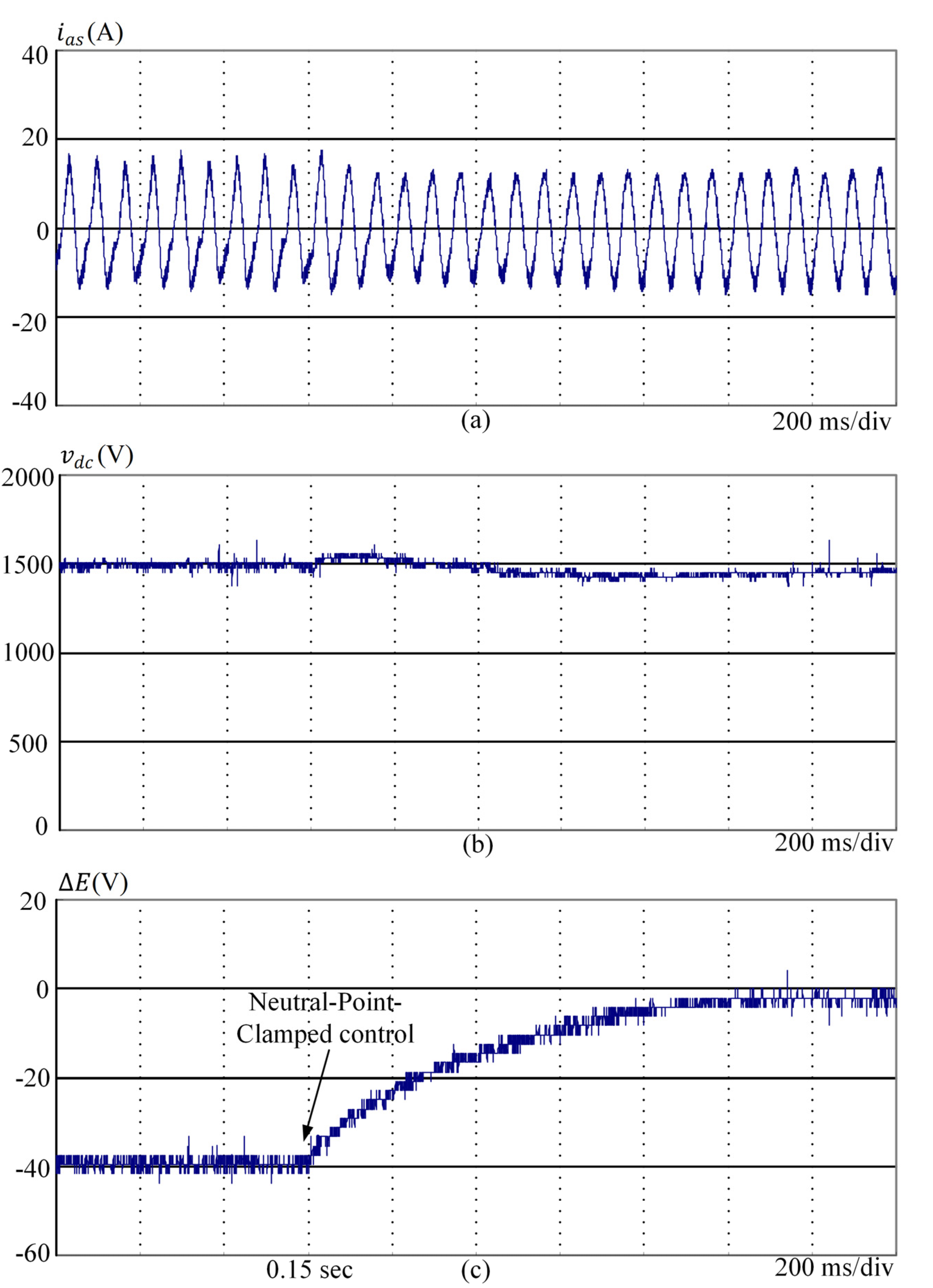
2.3. Neutral-Point-Clamped Controller
The three-phase, three-level rectifier is implemented using switch-mode devices, and three-phase voltages are obtained from the wind generator. The statuses of the upper and lower switches are mutually exclusive, and the DC-link voltage is not shorted in normal operation. Assume that the power transistors are ideal and that the currents
,
, and
are continuous. When the load varies, the voltage of the upper capacitor is lower than that of the lower capacitor; in other words, the current passing through the upper capacitor is lower than that passing through the lower capacitor. Therefore, the command voltage for the DC-link can be regulated by varying the voltage error between the upper and the lower capacitors [
14]. According to Equations (16) and (19),
can be increased by regulating the turn-on time for
so that
increases, and vice versa. The voltage error command is
where
and
are the voltage commands of the upper and lower capacitors and their values are half that of the DC-link voltage; in other words,
. If
is zero, the voltages across the DC-link capacitors are symmetrical. According to Equation (23), the compensation voltage for the DC link is
where
is the gain of the proportional-integral voltage controller, and
is the voltage command of the DC-link capacitor voltage; the symbol “
” denotes proportional-integral operation. Specifically, Equation (24) shows that
can be obtained by achieving proportional-integral control of the DC-link voltage error. A control block diagram of the neutral-point-clamped controller is shown in
Figure 7.
Figure 7.
Control block diagram of the three-phase, three-level rectifier.
Figure 7.
Control block diagram of the three-phase, three-level rectifier.
2.4. Three-Phase, Six-Leg Inverter
A schematic diagram of the three-phase, six-leg inverter with phase-r consideration is shown in
Figure 8. The inverter has the conventional single-phase, full-bridge structure. Assume that
where
denotes
,
,
,
,
, or
. Therefore, the equivalent circuit of phase-r shown in
Figure 9 can be obtained. A similar result can be obtained for phase-s and phase-t. The switching functions of the three-phase voltages
,
, and
and the DC-link current
can be written as
where
,
,
,
,
, and
;
is the DC-link voltage. According to Equation (29), the DC-link current
can be obtained as
Equations (26)–(28) indicate that the instantaneous voltages of each phase are
, 0, and
, where the voltage of phase-r can be written as
Therefore, the output voltage of phase-r can be determined by the states and and the DC-link voltage. If the DC-link voltage is constant, and can be varied to adjust the output voltage of phase-r. The output voltages for phase-s and phase-t can be similarly obtained. Equations (26)–(28) were used in this study to implement a three-phase, six-leg inverter.
Figure 8.
Power circuit of the three-phase, six-leg inverter (phase-r).
Figure 8.
Power circuit of the three-phase, six-leg inverter (phase-r).
Figure 9.
Equivalent circuit of the three-phase, six-leg inverter (phase-r).
Figure 9.
Equivalent circuit of the three-phase, six-leg inverter (phase-r).
The inverter power circuit with appropriate control can provide three different voltage levels to the load. This is illustrated by the following four modes of operation:
- (1)
When , is ON and is OFF, leading to
- (2)
When , is OFF and is ON, resulting in
- (3)
When , is ON and is OFF, resulting in
- (4)
When , is OFF and is ON, leading to
The voltage ratings of switches are identical and equal to . The antiparallel diodes across the switches enable continuous current to flow and thus facilitate maintaining a sinusoidal output current.
To control the three-phase inverter, a multicarrier disposition PWM technique is used. Gating signals for the power transistors are generated by comparing the commanding signal magnitudes of
and
with a contiguous carrier wave.
Figure 10 shows that there are four switching modes corresponding to the level of the commanding signal, as shown in
Figure 10b–d. In the first mode of operation, the magnitude of the carrier wave is compared with the commanding signal magnitudes. If the commanding signal magnitude is lower than the carrier wave magnitude, the second mode of operation, in which the switching pattern produced by comparing the carrier wave magnitude with the commanding signal magnitude, is performed. Similarly, gating signals for the power transistors in the third and fourth modes of operation can be obtained by comparing the carrier wave magnitude with the magnitudes of
and
, respectively.
Figure 10d shows that the switching pattern of the three-phase, six-leg inverter is generated by the aforementioned four modes of operation and that the average output voltage
is sinusoidal. The switching loss of the inverter can be reduced by reducing the switching frequency or by reducing the instantaneous value of the current or voltage in the switching period. Conventional bipolar modulation results in high commutation losses because the four switches are modulated at a high frequency in all modulation cycles. However, in unipolar modulation, only
and 0 are presented in the positive half-cycle. Therefore, unipolar modulation is more efficient for practical applications.
Figure 10.
Switching pattern of the three-phase, six-leg inverter (phase-r).
Figure 10.
Switching pattern of the three-phase, six-leg inverter (phase-r).
2.5. Design of Voltage Regulator
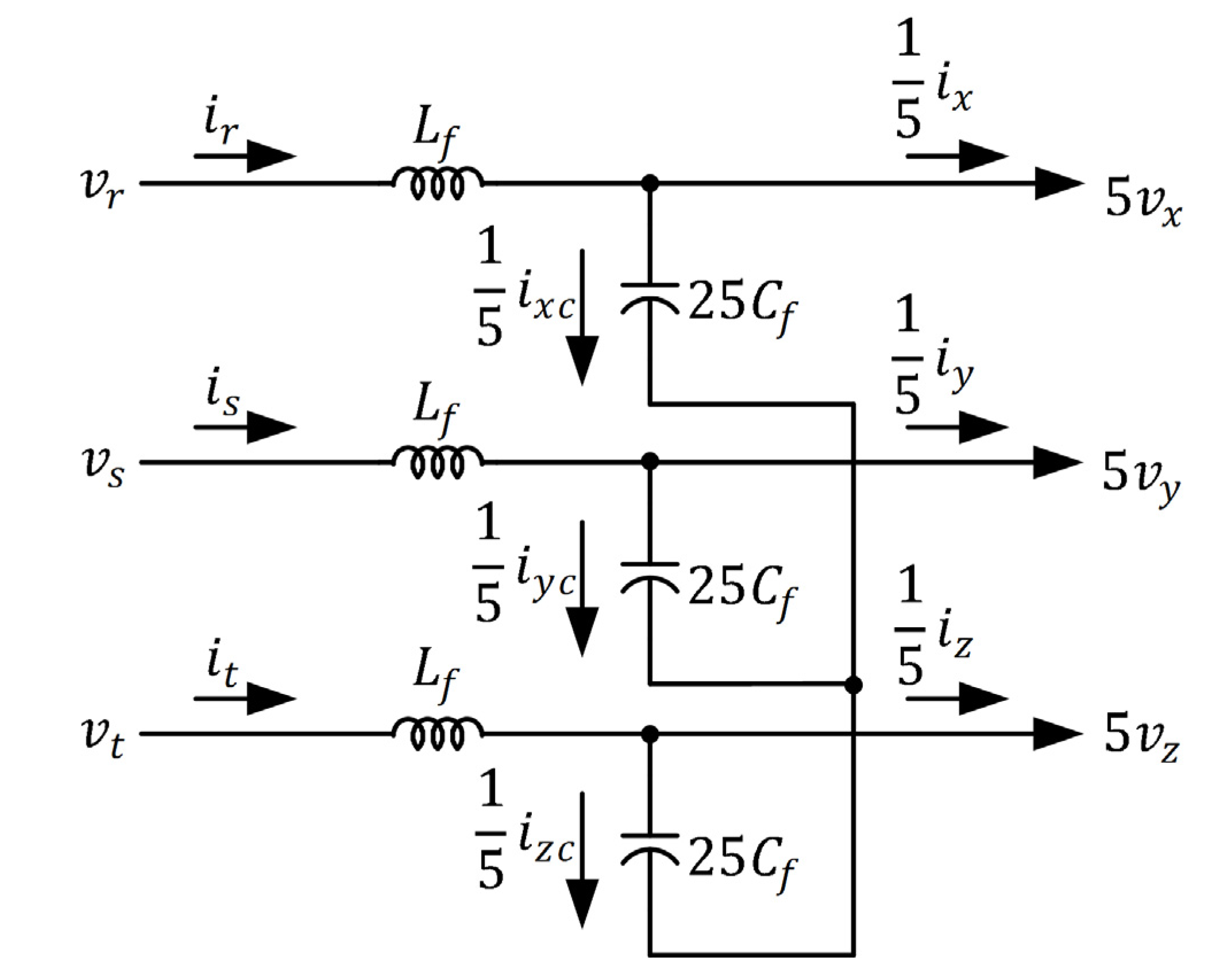
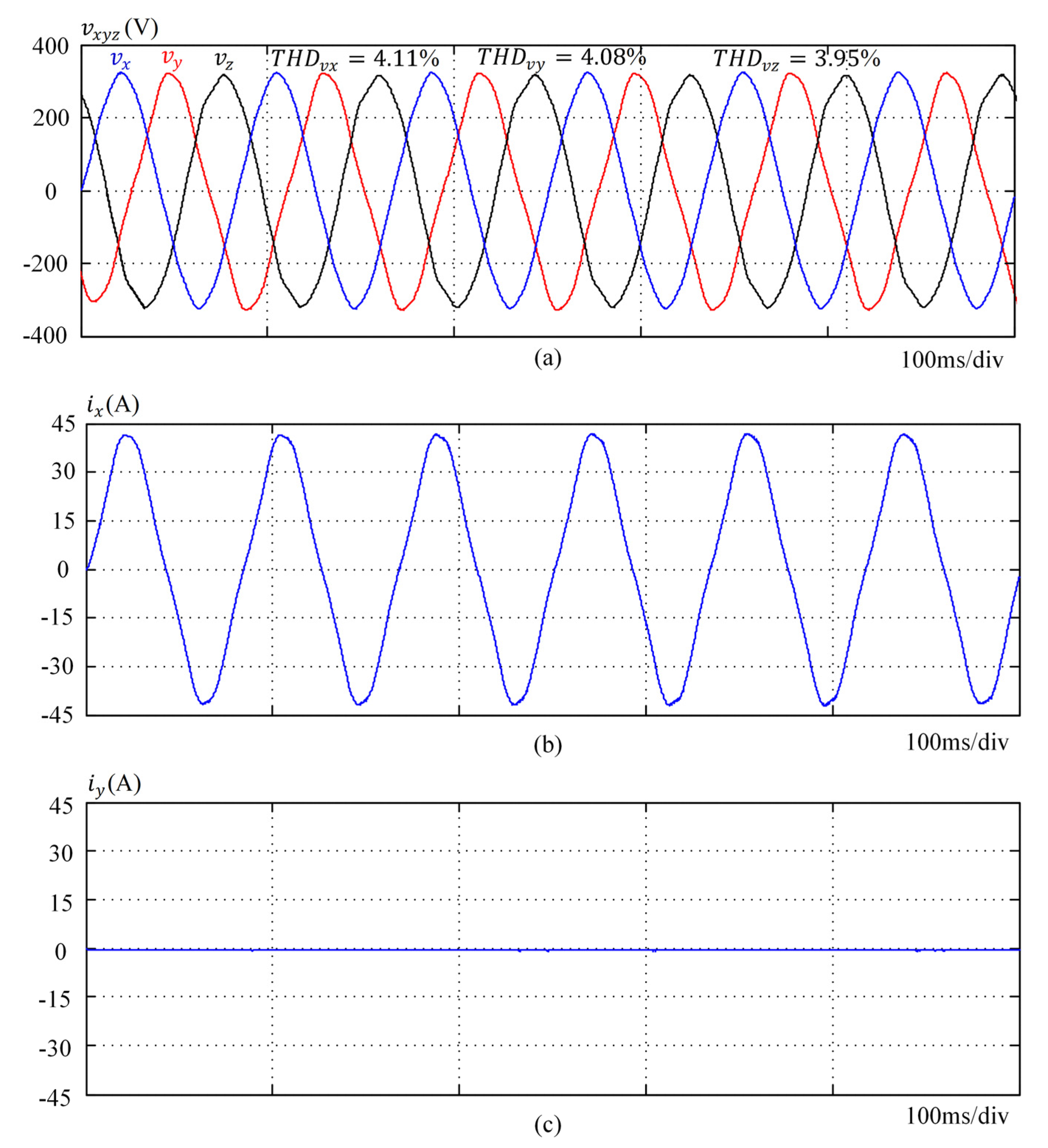
The low-pass filter for the three-phase, six-leg inverter shown in
Figure 1 was implemented using three inductors, capacitors, and transformers. The inductors and capacitors are connected in series and in parallel on the primary and the secondary sides of each transformer, respectively. Assume the turn ratios of the transformers to be 5. To simplify the analysis of the transformer, the equivalent copper, iron losses, leakage, and excitation inductors are neglected, as shown in
Figure 11. Therefore, the three-phase voltage and current equations can be written as
where
: phase voltages on the secondary sides of transformers;
: phase voltages on the primary sides of transformers;
: phase currents on the secondary sides of transformers;
: phase currents on the primary sides of transformers;
: currents to capacitors;
;
;
: equivalent resistors of the line and inductor;
: inductor in the low-pass filter;
: capacitor in the low-pass filter.
For model analysis and controller design, the three-phase voltages, currents, and switching functions can be transformed to a q-d-0 rotating frame. This yields
where
is the transformation angle of the rotating frame and
denotes voltages, currents, or switching functions.
Figure 11.
Equivalent circuit of the low-pass filter.
Figure 11.
Equivalent circuit of the low-pass filter.
According to Equations (32) and (35), the voltage equations can be derived as
where
,
, and
are the q-d-0 axis voltage outputs of the power inverter;
,
, and
are the q-d-0 axis voltage outputs of the transformers; and
,
, and
are the q-d-0 axis current outputs of the power inverter. Similarly, the current equations can be derived from Equations (33) and (35) as
where
,
, and
are the q-d-0 axis currents on the load side. Equations (37)–(42) were used in this study to design the voltage regulator.
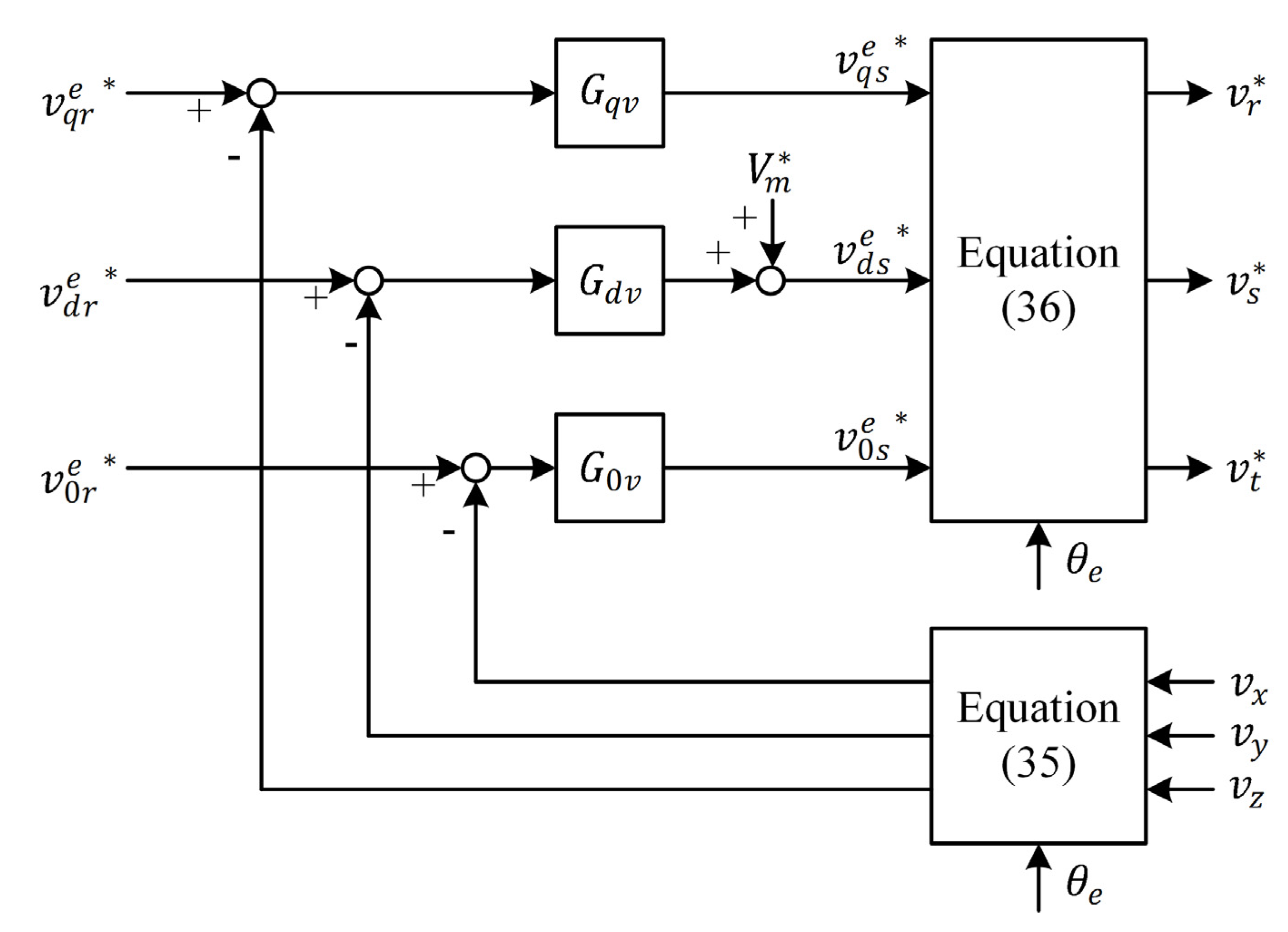
The three-phase source commands can be written as
Therefore, the three-phase source commands in the rotating frame with
can be expressed as
where
is the peak voltage. Equations (37)–(42) show that the voltage and current equations in the rotating frame are time invariant. Equations (46)–(48) were used to derive the block diagram of the voltage regulator and calculate the voltage comments of the power inverter shown in
Figure 12. The proportional-integral controls for voltage regulators of a power inverter are given by
where
denotes q, d, or 0;
and
are the proportional-integral gains of the q- and d-axis voltage regulators. In the following section, an experimental evaluation of the proposed system is described.
Figure 12.
Control block diagram of the voltage regulator.
Figure 12.
Control block diagram of the voltage regulator.