Abstract
The complexity of large-scale group decision-making (LSGDM) in the digital society is becoming increasingly prominent. How to achieve efficient consensus through social networks (SNs) has become a core challenge in improving the decision quality. First, conventional clustering methods often rely on a single-distance metric, neglecting both numerical assessments and preference rankings. Second, ensuring the decision authenticity requires considering diverse behaviors, such as trust propagations, risk preferences, and minority opinion expressions, for scientific decision-making in SNs. To address these challenges, a consensus-reaching process (CRP) method based on an enhanced K-means++ clustering is proposed. The above method not only focuses on minority opinion handling (MOH), but also incorporates decision indicator sets (DISs) to analyze the degree of opinion divergences within groups. First, the Hamacher aggregation operator with a decay factor completes trust matrices, improving the trust representation. Second, a personalized distance metric that combines cardinal distances with ordinal distances is incorporated into the enhanced K-means++ clustering, enabling more precise clustering. Third, weights for decision-makers (DMs) and subgroups are determined based on trust levels and degree centrality indices. Fourth, minority opinions are appropriately handled via considering the diverse backgrounds and expertise of DMs, leveraging a difference-oriented DIS to detect and adjust these opinions via weight modifications until a consensus is reached. Fifth, the alternative ranking is objectively generated via DIS scores derived from multigranulation rough approximations. Finally, the feasibility of the proposed method is validated via a case study on unmanned aerial vehicle (UAV) selection using online reviews, supported by a sensitivity analysis and comparative experiments demonstrating superior performances over existing methods. The result shows that the proposed model can enhance clustering accuracies with hybrid distances, objectively measure the consensus via DISs, handle minority opinions effectively, and improve LSGDM’s overall efficiencies.
1. Introduction
The rapid development of digital economies has led to the emergence of increasingly complex decision-making problems, reshaping the processes and methods of decision management, particularly in the domain of group decision-making [1,2]. Even in individual decision-making scenarios, DMs often seek advice or opinions from others. Consequently, decision-making is inherently social, involving multiple group members. While group decision-making offers broad application potential as an effective solution, it also faces limitations, such as difficulties in managing diverse individual preferences and the high complexity of decision processes [3]. To address these challenges, large-scale group decision-making (LSGDM) has been developed. LSGDM serves as a collaborative process involving no fewer than 13 or 20 decision-makers (DMs) [4,5], encompassing challenges such as trust levels within groups, different types of decision-making methods, benefits obtained from varying perspectives, conflict resolution, and their impacts on the decision quality [6,7]. Under the typical LSGDM theoretical framework, the decision outcome is derived by rationally and reliably integrating individual and group preferences via clustering and the consensus-reaching process (CRP). This approach has been widely applied in real-world scenarios. In practice, LSGDM has been successfully applied in diverse domains such as healthcare resource allocation [8], supply chain management [9], and urban planning [10]. Additionally, LSGDM has proven valuable in consumer electronics procurement, assisting in determining optimal selections for smartphones, tablets, and wearable devices [11].
The growing influence of the Internet and social media platforms such as Weibo, Instagram, LinkedIn, and Facebook have greatly enhanced information dissemination and interpersonal interactions, significantly impacting group decision-making [12,13]. Social network analysis (SNA), a method for studying the structure of relationships and interactions between individuals (nodes), reveals key insights into trust propagation, influence patterns, and opinion dynamics [14,15].
Integrating SNA into LSGDM enhances potential communications among group members, accelerates CRP, and improves decision quality. This integration is commonly referred to as SN-LSGDM. However, existing approaches in SN-LSGDM face three critical limitations: (1) the reliance on single-dimensional similarity metrics for clustering, which fails to capture the duality of numerical assessments and preference rankings; (2) the incomplete handling of behavioral diversity, particularly in modeling trust decay over propagation paths and integrating minority opinions; and (3) subjective consensus thresholds that may suppress innovative dissent. To systematically address these challenges, this paper is structured as follows: Section 1.1 discusses the limitations of existing trust propagation methods and proposes the use of Hamacher aggregation operators combined with a decay factor to complete the trust matrix. Section 1.2 focuses on improvements to the K-means++ clustering algorithm, highlighting the importance of integrating hybrid distance metrics. Section 1.3 addresses issues in the CRP, particularly the measuring of consensus and the handling of minority opinions. Section 1.4 establishes an empirical scenario for unmanned aerial vehicle (UAV) selection, revealing core challenges of dynamic trust networks and multi-attribute decision conflicts via multi-source online review data. Finally, Section 1.5 summarizes the innovative aspects and contributions of the proposed method.
1.1. Trust Propagations in SN-LSGDM
For LSGDM, existing methods often assume that DMs can provide complete evaluation information. However, in SN-LSGDM, DMs may be influenced by their social neighbors or exhibit hesitation during the initial evaluation phase. In other words, understanding DMs’ behavioral patterns in SNs—especially their reliance on others during the decision process—is crucial, yet it has been insufficiently addressed in existing research [16]. To tackle this issue, various trust propagation methods have been developed to estimate unknown trust values.
For instance, Wu et al. [17] proposed a trust propagation operator based on the strength of relationships, considering the intensity of connections between DMs. Liu et al. [18] designed a trust propagation operator based on multi-path relationship strength, accounting for all propagation paths. Liu et al. [19] introduced a method from the perspective of trust utility and path reliability, further exploring the integrity of social trust networks. However, most existing methods for handling missing values rely on simple statistical estimates, such as the weighted averaging [20] or consistency strategies [21,22]. While these approaches are widely used in practical applications, they may introduce biases that compromise decision accuracy. Moreover, in the actual process of information dissemination within SNs, the influence of information tends to gradually diminish as the propagation distance increases and the number of propagation stages multiplies, potentially leading to overestimated trust-values.
To address these limitations, this paper adopts a propagation operator based on the Hamacher aggregation operator and introduces a decay factor to refine the trust matrix. The Hamacher aggregation operator is chosen due to its ability to flexibly model the interaction between trust relationships by balancing conjunctive and disjunctive properties, thus effectively capturing partial trust dependencies among DMs. Liu [23] validated the effectiveness of the Hamacher aggregation operator with an attenuation factor () in air quality assessment. The results showed that while different values affected the score function, the ranking remained consistent, indicating the robustness and adaptability of the Hamacher operator under varying parameters. The decay factor accounts for the attenuation of trust influence over long propagation paths, mitigating the risk of trust inflation and ensuring a more realistic representation of trust relationships. This dual enhancement not only improves the robustness of trust estimations, but also supports more reliable decision-making in SN-LSGDM.
1.2. Enhancements in K-means++ Clustering Methods
In clustering analysis, LSGDM often involves massive datasets. Clustering methods effectively reduce dimensionality in high-dimensional spaces, uncovering hidden patterns and structures within the data. As an unsupervised learning technique, the primary goal of clustering is to partition a dataset into several disjoint subsets (i.e., “clusters”), ensuring that samples within the same cluster exhibit high similarity, while those in different clusters demonstrate lower similarities [24,25,26].
Clustering methods can be broadly classified into three categories: prototype-based methods (e.g., K-means, K-means++), density-based methods (e.g., density-based spatial clustering of applications with noise), and hierarchical methods (e.g., agglomerative nesting). Kapoor and Singhal [27] compared partition-based clustering techniques such as K-means, K-means++, and fuzzy C-means, analyzing their clustering performance. Mahsa et al. [28] explored the density-based clustering algorithm and its applications in geochemical data analysis of stream deposits.
K-means++ enhances traditional K-means by optimizing the selection of initial cluster centers. It employs a distance-based probabilistic method to choose initial centroids, ensuring a more uniform distribution. This approach mitigates instability and poor convergence issues caused by random initialization in conventional K-means. Cheng et al. [29] implemented and tested K-means, K-means++, and Canopy+ K-means on the Spark platform, analyzing their performance under Euclidean and Manhattan distance metrics. Guo et al. [30] introduced a fuzzy C-means clustering algorithm incorporating ranking-based distance metrics, reducing decision complexity and enhancing intra-cluster decision similarities.
However, traditional clustering methods primarily rely on single-dimensional similarity metrics, making it challenging to capture the multi-dimensional behavioral characteristics of DMs. To address this limitation, this study proposes an enhanced K-means++ algorithm that integrates both cardinal and ordinal distance metrics. Cardinal distance focuses on the numerical evaluation differences among DMs, using Euclidean and Manhattan distances to quantify the direct discrepancies in evaluation matrices. In contrast, ordinal distance captures the discreteness of preference rankings, measuring the divergence in ranking vectors among DMs via Hamming distances. This dual representation allows the model to better distinguish between different DM behaviors, as it preserves both the numerical characteristics of the evaluation data and the subjective preference logic of the DMs. It enables more accurate identification of subgroups with similar preferences and a more precise division of group structures, thereby improving the overall efficiency of the CRP.
1.3. CRP in LSGDM
CRP constitutes the core mechanism in LSGDM for reconciling divergent opinions, resolving conflicts, and ensuring scientifically rigorous and socially acceptable decision outcomes [31,32]. From a methodological perspective, CRP can be categorized into three principal types based on interaction mechanisms: (1) feedback-driven CRP: this requires DMs to iteratively adjust preferences via guidance from a moderator or automated feedback system [33]; (2) autonomous adjustment CRP: this implements automatic opinion convergence via mathematical optimization models under predefined rules [34]; (3) negotiation-based CRP: this facilitates consensus via multi-round discussions and interest bargaining among subgroup representatives [35]. These approaches differ in intervention intensity and computational complexity, with feedback-driven methods excelling in solution interpretability, autonomous adjustment in computational efficiency, and negotiation-based methods in stakeholder satisfaction.
Behaviorally, CRP involves three critical operational phases [32]: (1) conflict detection: this identifies opinion divergence via distance metrics or information entropy measures; (2) direction guidance: this determines adjustment directions using minimum-cost or maximum-consensus principles; (3) dynamic weighting: this adjusts DM/subgroup influence via adaptive weight-allocation mechanisms. The selection of conflict-resolution strategies typically follows prospect–regret theory principles, where DMs weigh potential gains from consensus against regret risks from opinion adjustments.
Traditional methods typically calculate the consensus level using distance formulas and rely on predefined consensus thresholds. If the computed value exceeds the threshold, consensus is considered achieved; otherwise, adjustments are made to reach consensus. For instance, Zhang et al. [33] introduced a consensus index to measure each expert’s consensus level with the group. If an expert’s consensus index falls below a threshold, supportive measures are implemented to improve their consensus level. However, these thresholds are often subjectively determined.
To address this issue, this paper introduces decision indicator sets (DISs) from rough set theory [36], optimizing CRP via three key points. First, it replaces manual threshold settings with multidimensional analysis to objectively quantify consensus and conflict levels. Second, it employs attribute-level diagnostics to precisely identify evaluation criteria causing divergence. Lastly, it establishes a “gradient consensus” mechanism that balances decision efficiency with the preservation of minority opinions’ innovative potential. This design addresses limitations in traditional methods, offering a more flexible solution for complex decision scenarios.
In real-world decision contexts, consensus-driven approaches may inadvertently suppress dissenting voices, as evidenced by historical cases where breakthrough innovations predominantly originated from nonconforming perspectives (e.g., the Copernican revolution). Minority opinions in LSGDM frequently play a crucial role, particularly in guiding the group toward innovative thinking and exploration [37]. The risks associated with safeguarding minority opinions mainly manifest in SNs and group dynamics. Complex mechanisms are required in LSGDM to identify and evaluate minority opinions. Ren et al. [38] suggested using an 18% threshold to define minority groups in microgrid planning. Xu et al. [39] proposed a subgroup-quantification mechanism that systematically evaluates both the cardinality and influence of the weight of minority-advocating subgroups within CRPs, particularly addressing the challenge of preserving valuable dissent while maintaining decision efficiency. They adjusted subgroup weights based on the value of minority opinions, achieving more reasonable solutions. While these studies provide valuable insights, they have yet to address the subjectivity involved in identifying minority opinions.
This study proposes a dynamic optimization framework for minority opinions based on group trust. By employing social influence analysis and logical verification to precisely identify high-value dissenting opinions, and utilizing prospect–regret theory to intelligently balance opinion refinement with innovation preservation, the framework enhances decision-making contributions while ensuring consensus efficiencies, thereby overcoming the limitations of traditional approaches.
1.4. Case Study Context in UAVs
UAVs, as a rapidly evolving technology, have been widely adopted across diverse domains such as logistics, surveillance, and environmental monitoring. The selection of UAVs involves intricate decision-making processes due to the multiplicity of attributes (e.g., flight endurance, payload capacity, and cost), the heterogeneity of stakeholders (e.g., manufacturers, operators, and regulators), and the introduction of massive opinions and dynamic trust relationships via online reviews and social media platforms [4]. Addressing these challenges necessitates robust LSGDM frameworks capable of integrating multi-source data, reconciling conflicting preferences, and ensuring consensus.
To operationalize sentiment-aware decision modeling, textual reviews from platforms like Amazon and specialized UAV forums are collected and preprocessed. Sentiment scores are computed using a lexicon-based approach combined with bidirectional encoder representations from transformers fine-tuned for product reviews. This study employs UAV online reviews as a real-world case study to validate the proposed model, demonstrating its applicability in practical decision scenarios and bridging the gap between theoretical LSGDM research and real-world implementation.
1.5. Summary of Our Method
Building upon the limitations highlighted in previous LSGDM approaches, this paper aims to address several key objectives:
- (1)
- In SN-LSGDM, DMs may be influenced by their social neighbors or experience hesitation during the evaluation process. Therefore, examining their behavioral patterns within SNs is crucial. While various trust propagation operators have been proposed to enhance the decision process, existing methods for handling missing values often rely on simple statistical estimations, which introduce bias and lack interpretability. Hence, developing a propagation algorithm that not only improves the decision accuracy, but also enhances the interpretability is essential for completing trust matrices.
- (2)
- Most existing clustering methods [27] primarily focus on a single influencing factor, which often leads to suboptimal or even contradictory clustering results. To overcome this limitation, it is necessary to design a more robust clustering method that integrates two key influencing factors, ensuring greater accuracy and consistency in clustering outcomes.
- (3)
- The consensus measurement plays a pivotal role in CRP. Current methods typically determine consensus levels by setting predefined thresholds, which are often subjective. Therefore, developing a more objective and formula-driven measurement approach is essential for improving fairness and reliability in consensus assessment.
- (4)
- Existing methods for managing minority opinions generally rely on analyzing subjective discussions to assess their significance. However, given the inherent uncertainty and risk in real-world decision-making, a trust-based detection and weight-management approach can provide a more effective solution for evaluating and integrating minority opinions in the decision process.
As shown in Figure 1, our proposed framework outlines the systematic process as follows. The entire process begins with data intuitionistic fuzzification, where data are transformed into IF matrices, which are the evaluation matrices of DMs. Secondly, an enhanced K-means++ clustering method is adopted. The formula for hybrid distances is defined, and then K-means++ clustering is carried out to form subgroups. For each subgroup, subgroup-evaluation matrices will be created. The process also involves SNA. The adjacency matrices are processed through the Hamacher aggregation operator with a decay factor to derive trust matrices. The degree centrality index is calculated, providing a basis for weight calculation and trust propagation. Then, by using the IF lower approximation and upper approximation, decision index sets , , and are formed. A consensus measure based on DISs is calculated. The decision-making step checks for minority opinions. If a large-scale conflict is detected, an identification mechanism is triggered. Depending on the result, either or is applied. If there is no large-scale conflict, a small-scale conflict is checked. For each alternative, scores are obtained from , and the final ranking is determined through the selection process. This systematic flowchart integrates multiple techniques and can effectively handle LSGDM problems.
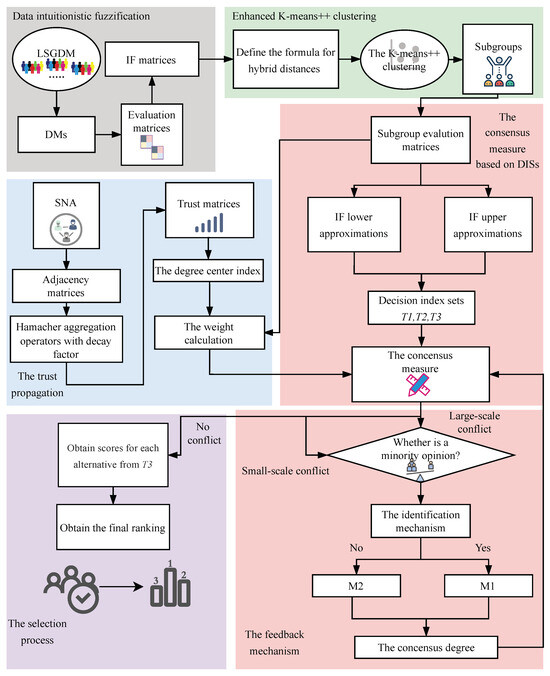
Figure 1.
LSGDM flowchat.
The key contributions and innovations of this paper are summarized as follows:
- (1)
- The completion of incomplete trust matrices: combining the Hamacher aggregation operator with a decay factor to handle missing values in incomplete trust matrices.
- (2)
- Enhanced K-means++ clustering: integrating both cardinal and ordinal distance metrics to develop a personalized distance formula for the classical K-means++ algorithm. An advanced weighting method is proposed, considering the number of DMs and trust levels within the community.
- (3)
- The objective consensus measurement: introducing a DIS for conflict detection, offering a high level of objectivity and fairness in determining whether consensus has been reached.
- (4)
- The management of minority opinions: developing an improved method for identifying and adjusting minority opinions, leveraging group trusts to assess their importance and adjusting their weights accordingly.
The remainder of this paper is structured as follows: Section 2 introduces key concepts and methods discussed in this research. Section 3 describes the data-processing workflow and the construction of SNs. Section 4 details the clustering and weighting methods. Section 5 focuses on the consensus-reaching method based on rough decision indicators and minority opinions. In Section 6, a case study of UAV online reviews for selection is used to validate the model’s feasibility, with sensitivity analysis and comparison experiments. Finally, the paper concludes with a summary and outlook for future research.
2. Preliminaries
This section first introduces the framework of the LSGDM model presented in this study. It then reviews intuitionistic fuzzy numbers (IFNs), the trust relationships under SNA, and their propagation operators. Finally, it provides a detailed introduction to minority opinion handling (MOH) and prospect–regret theory. These foundational concepts will aid in understanding the proposed method.
2.1. A Dynamic Consensus-Driven Framework for LSGDM
As application scenarios evolve, the decision-making process integrates various evaluation methods to better address increasing complexity and uncertainty. This section focuses on some of the basic concepts and main processes associated with LSGDM to gain a deeper understanding of LSGDM. More detailed and relevant symbols are introduced as shown in Table 1.

Table 1.
Notations and related descriptions.
The methodological framework for LSGDM problem-solving is structured as follows:
Step 1: Data processing. In real-world decision contexts, the ontological fuzziness (inherent unobservability of essence) and epistemological uncertainty (cognitive limitations in subjective judgment) jointly constitute dual cognitive barriers. Intuitionistic fuzzy set (IFS) theory addresses such bimodal uncertainties via constructing a triple-measure space satisfying . For sentiment scores derived from textual analysis, the bijective mapping rule is formalized as:
- (1)
- The meaning of sentiment scores: let the raw sentiment score , where indicates extreme the positivity and indicates extreme the negativity.
- (2)
- The decomposition of bipolar affective measures: positive certainty: ; negative skepticism: .
- (3)
- The quantification of cognitive uncertainty: certainty index (confidence in affective judgment): .
- (4)
- The synthesis of IFNs: the final IFN triplet is constructed via certainty-modulated fusion: ; .
Step 2: Trust propagation. Within the context of socio-structural evolution driving enhanced interpersonal connectivity, the trust diffusion mechanism employs Hamacher aggregation operators to model trust relationships, thereby effectively establishing trust links between initially disconnected nodes.
Step 3: The clustering process. To minimize redundant calculations and reduce the complexity of LSGDM problems, DMs with similar viewpoints are grouped into distinct subgroups. Consider an large-scale group partitioned into b disjoint subgroups, denoted as . The subgroup decision matrices are subsequently derived via the weighted average (WA) operator [40]. Specifically, the decision matrix for the subgroup , represented as , is obtained via the WA calculation.
Step 4: The CRP. The consensus-reaching mechanism within group-based structures should be grounded in intra-group collaboration, subsequently achieving hierarchical integration via inter-group negotiation and adjustment mechanisms, thereby ensuring broad acceptance of decision outcomes at the macro-group level.
Step 5: Obtaining final ranking. Once the group reaches the predefined consensus level, the final group decision matrix is obtained. To rank all alternatives, the score value for each alternative is calculated based on the method outlined in the following Equation (1):
2.2. IFNs
This section primarily introduces the basic definition, operational rules, and comparison rules of IFNs.
2.2.1. The Basic Concept of IFNs
IFNs serve as an important extension for classic fuzzy numbers, designed to more accurately represent uncertainty and fuzziness. The key feature of IFNs lies in the introduction of three fundamental concepts: membership degrees, non-membership degrees, and hesitation degrees. These elements collectively provide a more comprehensive representation of the degree of fuzziness and uncertainty in fuzzy sets.
Definition 1.
For convenience, is directly referred to as an IFN, satisfying the condition .
2.2.2. IF Operations
2.2.3. IF Comparison Rules
Definition 3.
Rule 1.
2.3. SNA
This subsection primarily introduces three different representations of trust networks and the Hamacher aggregation operator.
2.3.1. The Basic Concept of SNs
SNA constitutes a computational paradigm for modeling relational structures among social actors. This methodology constructs group relational networks to uncover three-tier structural characteristics [42]: (1) macroscopic social topology, (2) mesoscopic node centrality metrics, and (3) microscopic individual behavioral dynamics. The standardized SNA framework comprises three fundamental elements: first, node sets representing heterogeneous social agents (e.g., individuals, organizations, nation-states); second, edge sets defining multiplex relational ties (including affective bonds, trust relationships, collaborative linkages); third, attribute vectors characterizing multidimensional nodal features (e.g., demographic variables, social capital indices, preference parameters). These elements can be systematically represented via a multilayer network framework as demonstrated in Table 2.

Table 2.
SN representational taxonomies.
- (1)
- The graph representation: A graph is used to model the trust network among members, where nodes represent individuals, and directed edges denote trust relationships. Specifically, an edge indicates a direct trust relationship from to .
- (2)
- The algebraic representation: This method differentiates various types of relationships and demonstrates how these relationships can be combined for analysis.
- (3)
- The sociometric representation: Trust relationships between members are expressed in a matrix , where each element indicates the presence or absence of a direct trust relationship. Specifically, if , it represents a direct trust relationship from to . Conversely, if , it signifies the lack of such a relationship.
The aforementioned representations are limited to explicit trust relationships, which imply either full trust or complete distrust. However, in real-world scenarios, trust relationships among DMs are often ambiguous and cannot be described with absolute certainty. To address this, Zhang et al. [43] devised a granular computing-based social trust-quantification paradigm, enabling DMs to explicitly quantify interpersonal trust degrees via unit interval [0,1]-valued mappings. In this framework, the trust relationships within a social trust network are described using the fuzzy sociometric representation.
Definition 4.
Let the fuzzy social trust matrix be over an expert set E with . Its membership function is denoted by , where , and indicates the trust level assigned by to [42].
Example 1.
The trust levels among five DMs, are represented by an incomplete fuzzy sociometric matrix :
In social trust networks, the direct observation of trust values between specific DMs often encounters data incompleteness, resulting in a partially defined fuzzy adjacency matrix. As illustrated in Figure 2 depicting a triadic network structure comprising three DMs, the direct trust relationship between and is unobserved. This structural gap necessitates applying trust transitivity principles, where the mediated path facilitates the probabilistic inference of indirect trust propagations.

Figure 2.
The DIS consensus-measurement process.
2.3.2. Hamacher Aggregation Operator
Before explaining our trust propagation method, it is important to introduce key concepts related to triangular norms. define the generalized intersection and union of fuzzy sets. A more flexible approach was introduced by generalizing t-norm operations, leading to the development of Hamacher operations, specifically the Hamacher product ⨂, which are broader formulations of t-norms [44,45]. Thus, these operations are referred to as Hamacher t-norms. The mathematical definition of this operation is as Equation (12):
where is the weighted product and adjustment factor, which controls the interaction between the two values and plays a key role in adjusting their impact on the final aggregated value.
In order to incorporate n independent variables, the equation is extended via the use of Equation (13):
Remark 1.
Pilot experiments with UAV reveal that strikes an optimal balance between retaining the reasonable influence of historical information and adapting to current changes. It gradually reduces the impact of historical information on the current iteration’s results, ensuring the stability and convergence of the trust propagation process. Specifically, when compared with other potential values (e.g., α = 0.5 or α = 0.9), minimizes the convergence error in trust-value calculations.
Remark 2.
To ensure that all missing values in the final trust matrix are effectively filled, any positions that remain labeled as “none” after trust propagation are assigned a default value of 0.5. This choice reflects a neutral, compromise-level trust score, which-absent more precise information-provides a reasonably fair estimate for subsequent analyses. As a result, the trust matrix becomes fully populated and is ready for further in-depth analysis and presentation.
Remark 3.
During the propagation process, for each missing trust value (i.e., none), the algorithm propagates trust from neighboring nodes (other evaluators) based on the weight values in the weight matrix, in order to estimate the missing values and gradually refine the trust distribution.
2.4. Theoretical Synthesis of Prospect and Regret Mechanisms
The prospect–regret dual decision framework establishes a robust analytical framework for modeling cognitive biases in behavioral decision-making. This innovative paradigm synthesizes two cornerstone theories: prospect theory that accounts for reference-dependent preferences under risk, and regret theory that formalizes anticipated emotional responses to counterfactual outcomes. Through this theoretical integration, the framework particularly elucidates two pervasive behavioral anomalies in financial decision contexts: (1) herd mentality driven by social reference dependence, and (2) systematic distortion of probability weighting in risk-appraisal processes [46,47].
Definition 5.
The axiomatic foundation of this framework is formalized via a value function with distinct mathematical representations for gain and loss domains [48], as shown in Equation (14):
Definition 6.
The regret–rejoice function. is mathematically characterized by [49], as shown in Equation (15):
where represents the utility differential between alternatives X and Y. The function exhibits:
- Monotonicity: .
- Diminishing sensitivity: .
- Sign-dependent interpretation: signifies rejoicing, otherwise regret.
Definition 7.
The perceived utility synthesizes intrinsic value and counterfactual emotion, as shown in Equation (16):
where maps alternatives to cardinal utilities, and modulates emotional responses.
Table 3 presents the preset values of each constant and their corresponding behavioral interpretations.

Table 3.
Key parameters.
3. Clustering and Calculating Weights
This section focuses on the detailed implementation process of the enhanced K-means++ clustering algorithm and provides a thorough explanation of how the weights for each evaluator and group are calculated based on trust values.
3.1. Enhanced K-means++ Clustering
The enhanced K-means++ clustering proposed in this paper is an improvement upon the traditional K-means++ method, which utilizes the elbow method to determine the optimal number of clusters, k. Specifically, the optimal k is selected by plotting the relationship between the sum of squared errors (SSE) and the number of clusters, choosing the “elbow” point where the rate of decrease in SSE begins to slow down. Additionally, the algorithm optimizes the selection of initial centroids and distance calculations. In the distance computation, it considers not only the DMs’ evaluation of the alternatives but also takes into account their preferences for ranking these alternatives, while incorporating SNs. By further clustering the DMs in multiple dimensions, the algorithm enhances the accuracy and effectiveness of the decision process.
3.1.1. A Hybrid Distance Metric Integrating Cardinal and Ordinal Distances
Conventional LSGDM divergence metrics predominantly operate on the value space. This section develops a novel multidimensional divergence metric that simultaneously accounts for both numerical evaluation discrepancies and preferential ranking interdependencies among DMs. Operationally, we integrate two complementary measurement paradigms: continuous-space metrics (Euclidean/Manhattan norms) to quantify value-based discrepancies in evaluative judgments, coupled with discrete metric analysis (Hamming distances) to assess ordinal mismatches in alternative preference orderings.
Definition 8.
Let and be evaluation matrices of DMs , where . Using the Euclidean distance, the distance between them is calculated as Equation (17) [30]:
Definition 9.
Let and be evaluation matrices of DMs , where . Using the Manhattan distance, the distance between them is calculated as in Equation (18) [27]:
Prior to computing the Hamming distance, a necessary precondition is to algorithmically construct a total order of alternatives for each DM via systematic processing of the evaluation matrix, with explicit tie-breaking rules for handling equivalent preference scores.
Definition 10.
Let be an evaluation matrix of any DM and a weight of the j-th attribute, then the DM’s evaluation value for each option is as in Equation (19) [30]:
in this context, represents the ranking assessment values given by the k-th DM for each option. By ordering the values in from highest to lowest, we can derive the ranking of alternatives for the k-th DM, denoted by .
Upon establishing the complete ordinal preference structures for all DMs via total ordering transformation, an enhanced Hamming distance metric can be applied to quantify inter-DM ordinal space dispersion. This measure operationalizes cognitive divergence by identifying the number of discrepancy loci between two ranking vectors, formally defined as follows.
Definition 11.
Let and denote two alternatives ranking vectors from distinct DMs , , The Hamming distance between these ordinal rankings is defined as Equation (20) [30]:
where:
- indexes the ordinal position in the ranking;
- The indicator function is defined as:
The distance formulas discussed above focus on capturing the connection between DMs’ evaluation values and their resulting rankings of alternatives. Building on this foundation, the subsequent analysis integrates both dimensions—numerical assessments and final rankings—into a unified framework. This approach ensures a comprehensive view of how DMs’ evaluations translate into preference orders.
Definition 12.
Let and denote evaluation matrices DMs and , respectively, with corresponding alternative ranking vectors and . The composite distance metric integrating both evaluation and ranking similarities is formulated as Equation (21):
where are weighting parameters (default: ).
The parameters and in the hybrid distance metric were set to default values of 0.5 based on the principle of balanced contribution between ranking and evaluation similarities.
Specifically: ensures equal emphasis on ranking divergence (via normalized Hamming distance) and numerical evaluation divergence (via Euclidean/Manhattan distances). This design acknowledges that both ordinal preferences and cardinal evaluations are critical in capturing DMs’ behavioral duality. assigns equal weight to Euclidean and Manhattan distances, as both metrics are widely recognized for their complementary strengths in quantifying numerical discrepancies (Euclidean for geometric dissimilarity, Manhattan for grid-like deviations).
Remark 4.
The distance formula proposed in Definition 12 combines the Euclidean distance with the Manhattan distance to jointly measure the similarity of the evaluation information between DMs, while also integrating the Hamming distance to evaluate the similarity between alternative ranking outcomes. To effectively balance the contributions of these three distances, the Hamming distance is normalized to ensure it is on the same scale as the Euclidean and Manhattan distances, creating a unified metric system.
Remark 5.
Additionally, two parameters are introduced to further adjust the relative impact of these three distances in the final result. These parameters not only allow for flexible weight adjustment of each distance but also optimize the distance calculation based on specific circumstances, improving the model’s applicability and accuracy.
3.1.2. K-means++ Clustering
The original K-means algorithm randomly selects k data points from the dataset as initial cluster centers. However, the selection of these initial centroids significantly impacts both the final clustering results and computational efficiency. A purely random initialization may lead to slow convergence. The K-means++ algorithm addresses this limitation by optimizing the initialization process for selecting initial centroids.
The core principle of K-means++ lies in maximizing the distances between initial cluster centers to mitigate suboptimal convergence. Its initialization procedure operates as follows: (1) first cluster center: randomly select one data point from the dataset; (2) subsequent cluster centers: for each remaining data point, calculate its shortest distance to any existing cluster center. New centers are then selected based on a distance-dependent probability distribution, where the greater the distance of a data point from existing centers, the higher its probability of being chosen as the next cluster center. This process repeats until k initial centroids are determined. Finally, the standard K-means algorithm iteratively refines these initial centers to obtain the final clustering solution.
Definition 13.
Let be the i-th cluster, q be the sample point in , and be the particle of (the mean of all samples in ), which represents the quality of the clustering effect, as shown in Equation (22).
Additionally, the selection of k value adopts the elbow method. In the process of clustering, with the increase of the number of clusters, the sample division will become more refined, the degree of aggregation of each category is higher, then the SSE will gradually become smaller, the sum of squares of error is the sum of squares of the distance between the center of gravity of this class and the position of its internal members. SSE is the core index of the elbow method. When k is less than the real cluster number, SSE will decrease greatly because the increase of k will increase the degree of aggregation of each cluster. When k reaches the real number of clusters, the return on the degree of aggregation obtained by increasing k will quickly become smaller, thus the decline of SSE will sharply decrease, and then it will flatten out with the continuous increase of k value. That is to say, the relationship between SSE and k is the shape of an elbow, and the corresponding k value of this elbow is the real cluster number of data.
The complete implementation workflow of the proposed enhanced K-means++ clustering algorithm is formally presented in Algorithm 1.
| Algorithm 1 Enhanced K-means++ clustering with hybrid features |
| Input: The DM evaluation matrix set , the attribute weight W. |
| Output: The subgroup partition result . |
| Step 1: Data preprocessing |
| Compute the alternative sorting vector for all DMs using Equation (19); |
| Construct the mixed feature space: ; |
| Step 2: Determine the number of clusters |
| Initialize , the SSE list; |
| for to do |
| Perform standard K-means++ clustering; |
| Compute within-cluster squared error using Equation (22); |
| end for |
| Determine the optimal k value using the elbow method; |
| Step 3: Mixed distance clustering |
| Initialize cluster centers (density peak selection); |
| while not converged do |
| for each DM do |
| Compute the mixed distance to each cluster center using Equation (21); |
| Assign to the nearest cluster; |
| end for |
| Update cluster centers (weighted IF averaging); |
| end while |
3.2. Weight Determination Framework
The traditional majority principle typically calculates weights based on the number of DMs within a subgroup, and this method has been widely applied. However, it overlooks other important characteristics within the subgroup, such as the diversity of opinions, the experience of DMs, and their influence on the decision process. Therefore, relying solely on the number of individuals to determine the weights has its limitations. As a result, there is an urgent need to develop a more comprehensive weight determination method that considers these additional factors to improve the accuracy and fairness of the weight assignment process [30].
Definition 14.
Let the sociomatrix of a trust network be . where quantifies the directed trust intensity from to . The normalized degree centrality measure for the DM is calculated as in Equation (23) [44]:
Within SNA, the degree centrality metric serves as a quantifiable proxy for evaluating nodal influence, wherein elevated centrality values correlate with enhanced structural prominence of decision agents. This property establishes degree centrality as a principal determinant in nodal weighting schemes, given its capacity to systematically prioritize stakeholders exhibiting maximal social capital accumulation via trust linkage density.
Then, the weight of the DM can be defined as Equation (24):
Definition 15.
The credibility of the subgroup is computed as the following Equation (25) [42]:
where is the number of DMs within , represents the trust degree assigned by to .
Definition 16.
By calculating that can be applied to measure the credibility of , and the DMs in that can also be applied to reflect the significance of the subgroup, we define the weights of the subgroup by integrating these two indicators as in Equation (26):
Consequently, the weighting scheme for subgroup can be established as in Equation (27):
This framework addresses the limitations of conventional approaches by systematically incorporating SN metrics and trust dynamics while maintaining computational tractability. The parametric structure allows decision facilitators to balance between subgroup size importance and quality of social connections, particularly crucial when managing minority opinions [37].
4. A CRP Method Based on MOH and DISs
In this section, multigranulation rough set (MGRS) theory is first used to perform consensus measurement, from which the opinion divergence degree within the group is derived. This step accurately assesses the consistency and differences in opinions by considering the evaluations at different granularity levels. Next, for groups with high opinion divergence, minority opinion detection and handling are carried out to ensure that minority opinions are effectively identified and appropriately integrated into the decision-making process. Finally, prospect regret theory is applied for weight adjustment, taking into account psychological factors such as regret and risk preferences of DMs. This ensures that the weight of group members are adjusted in a rational manner, ultimately leading to consensus.
4.1. Consensus Measurement
This section provides a detailed explanation of how to use the MGRS theory in consensus measurement. By incorporating the concept of the multi-granularity concept, we are able to analyze data at different levels and scales [50], thereby obtaining more precise and comprehensive consensus results. This method not only considers the information differences at various granularities but also effectively integrates the information from each granularity level, providing a more flexible and detailed analytical framework for consensus decision-making.
To address this issue, this paper proposes an MGRS approach, specifically applying rough set theory to fuzzy decision-making. Rough set theory is designed to extract both deterministic and possible rules from an inconsistent complete system, effectively handling the widespread inconsistencies found in information systems. In rough set decision-making, any indiscernible set Y is described using two precisely definable sets: the upper approximation and the lower approximation . These approximations help characterize uncertain information, improving decision-making accuracy and robustness.
Specifically, the DIS leverages MGRS theory to objectively measure consensus by analyzing decision choices at multiple granular levels. This approach replaces subjective threshold settings with a formula-driven framework, which includes three key indicators (, , ) derived from the optimistic and pessimistic approximations of the target set X. This structured process, combined with the flowchart in Figure 2, aims to illustrate how DIS systematically quantifies conflicts and guides feedback adjustments, avoiding ambiguities in the research. Below is a structured explanation of the involved terms.
Definition 17.
Given an arbitrary, non-definable set X, this paper introduces the concepts of lower and upper approximations to describe its boundaries. The lower approximation of X, denoted as , represents the smallest definable subset entirely contained within X. Conversely, the upper approximation, denoted as , refers to the largest definable set that encompasses X in its entirety. These approximations provide a structured approach to handling uncertainty, enabling a more precise characterization of sets within rough set theory.
MG analysis involves approaching a problem from multiple perspectives and levels, utilizing various granular structures to approximate a target concept. Building upon this MG framework, we explore the concept of MGRSs, which can be categorized into two primary models:
- 1.
- Optimistic MGRS—based on the ”seeking common ground while preserving differences” strategy, this model defines rough set approximations in a more inclusive manner, allowing for flexibility in classification.
- 2.
- Pessimistic MGRS—rooted in the ”seeking common ground while rejecting differences” approach, this model applies stricter constraints to ensure a higher level of consistency across granular structures.
Definition 18.
Definition 19.
Definition 20.
Rule 2.
- (1)
- If holds, then consensus has been reached.
- (2)
- If and both hold, then consensus partially reach consensus.
- (3)
- If and both hold, then consensus has not been reached.
4.2. MOH (M1)
This section addresses the treatment of minority opinions via two key stages: detection and management. The process begins with identifying divergent opinions within the group, followed by implementing strategies to adjust or integrate these viewpoints. By effectively handling minority opinions, the goal is to enhance group consensus while maintaining decision diversity and fairness.
4.2.1. Detection Mechanism
To objectively and efficiently identify minority opinions within subgroups exhibiting low consensus levels, it is assumed that a subgroup represents the minority opinion. The subgroup should meet the following three characteristics:
- (1)
- The consensus level of and its alignment with the group opinion are the lowest.
- (2)
- consists of a limited number of DMs. the minority opinion should satisfy the threshold , (where [.] is a floor function).
- (3)
- should hold a relatively high level of authority and gain recognition and trust from the majority of DMs within the group.
Therefore, to classify the subgroup as a minority opinion subgroup, it must simultaneously satisfy both of the following conditions, as shown in Equation (35):
4.2.2. Management Mechanism
Based on the aforementioned criteria, the subgroup is classified as reliable and trustworthy if its opinions are deemed valuable. In such cases, a weight-adjustment mechanism is activated. Conversely, if minority opinions lack credibility or fail to gain support from other DMs, they may impede consensus formation. For such scenarios, Section 4.3 outlines principles to recalibrate the minority subgroup’s initial opinions. When ’s opinions are validated as reasonable and credible, their influence is amplified via a trust-driven weight-adjustment process.
Definition 21.
Let denote the subgroup weight vector at iteration t. For subgroup holding minority opinions in round t, its adjusted weight for the subgroup , is computed as in Equation (36):
where denotes the maximum weight of any subgroup in the t-th round. Once the adjusted weights for the minority opinion subgroup have been calculated, it is necessary to normalize all subgroup weights to ensure that the sum of the normalized weights equals 1, i.e., , This normalization step ensures consistency in the weight distribution and maintains the integrity of the decision process.
This design addresses a common issue in classical methods, where weight adjustments can escalate drastically, sometimes expanding by tens of times. In these cases, the changes may go unrecognized by other subgroups, leading to unreasonable outcomes. By constraining weight adjustments in this way, the proposed method ensures a more balanced and rational decision process.
4.3. Opinion Divergence-Driven Dynamic Weight Adjustment (M2)
For subgroups that consistently show the lowest consensus levels under the M1 method and remain unaddressed, these clusters are often considered impediments to effective decision-making. In this section, we introduce targeted modifications designed to enhance the CRP by directly addressing these problematic subgroups.
Traditional consensus feedback mechanisms tend to presuppose that DMs’ opinions are broadly acceptable. In practice, however, psychological factors play a significant role in how individuals update their views, often leading to overly rationalized decisions that lean heavily on subjective experience. As a result, final outcomes may not adequately capture the objective realities of the situation.
To overcome this limitation, we propose a novel framework within the context of SNs. This framework integrates prospect–regret theory with an analysis of interpersonal influences, thereby mitigating the bias introduced by psychological factors. By contrasting the original evaluations with an ideal group assessment, our approach not only reduces subjectivity but also anchors feedback in a more objective baseline. Moreover, by incorporating the dynamics of social relationships-recognizing that DMs frequently consult peers-the modified feedback mechanism better mirrors real-world decision processes.
The subsequent sections provide a detailed exposition of these modification rules, outlining how they contribute to more robust and realistic decision outcomes.
Step 1. The endogenous reference point generation
- (1)
- The subgroup reference point definition using Equation (37):
- Note: Dynamically generated from subgroup historical evaluations.
- (2)
- The prospect-deviation calculation using Equation (38):
- Function: Quantifies deviation from reference standards.
Step 2. The prospect–regret joint valuation
- (1)
- The nonlinear value function using Equation (14):
- (2)
- The social comparison regret value using Equation (15):
- (3)
- The integrated prospect value using Equation (41):
Step 3. Subgroup weight iteration
- (1)
- The dynamic weight update using Equation (42):
- Parameter: (recommended initial value: 0.2).
- (2)
- The weight normalization using Equation (43):
The parameter was selected to balance convergence speed and stability. A smaller (e.g., ) risks overly sluggish adjustments, while a larger (e.g., ) may cause oscillations or premature convergence. Therefore, set the initial value to 0.2.
The pseudocode meticulously outlining the full operational procedure of the CRP is vividly showcased in Algorithm 2.
| Algorithm 2 A CRP method based on DISs and MOH |
| Input: The subgroup partition , the initial weights , the initial target matrix B. |
| Output: The final ranking . |
| Step 1: The consensus measurement |
| repeat |
| Compute MGRS indicators: , , using Equations (32)–(34); |
| until convergence condition met; |
| Step 2: Minority opinion handling |
| if then |
| Identify the candidate minority subgroups using Equation (35); |
| for each do |
| if credibility verification passes then |
| Adjust subgroup weights using Equation (36); |
| else |
| Start Step 3; |
| end if |
| end for |
| end if |
| Step 3: Dynamic weight update |
| Compute the subgroup foreground-regret value using Equation (41); |
| Update the weight using Equation (42); |
| Normalize weights using Equation (43); |
| Step 4: Target matrix evolution |
| Update the consensus matrix B using Equations (44) and (45); |
| Step 5: Generate results |
| Acquire the comprehensive score from ; |
| return ranking the result . |
5. Empirical Validation and Analysis
Case study experiments are presented in this section to assess and analyze the performance of the proposed LSGDM modeling framework. We first provide a comprehensive explanation of how the proposed method can be applied to real-world decision-making problems. Furthermore, we conduct both comparative and sensitivity analyses to evaluate how variations in model parameters influence its stability, thereby validating its feasibility and effectiveness. Finally, we discuss the practical implications of the proposed model in managing minority group opinions, highlighting its potential to enhance decision-making processes.
5.1. Empirical Validation
In this section, we collect online reviews of drone products from 13 verified stores on the JD.com platform (https://www.jd.com/ (16 January 2025)), a leading Chinese e-commerce platform renowned for its comprehensive and authentic product evaluations. Spanning from January 2023 to December 2024, the dataset encompasses two years of consumer feedback, strategically curated to capture temporal trends in UAV preferences and ensure representativeness. A total of 1280 reviews were systematically curated, corresponding to five UAV models evaluated across five key attributes: operability, functionality, appearance, durability, and quality. These attributes were selected to assist users in making informed purchasing decisions. The following will illustrate the application of the model via the experimental process.
Step 1: Data fuzzy processing
For textual evaluations from 13 suppliers on five critical UAV attributes (e.g., operation, functionality), sentiment scores are computed, then transformed into IFNs . The complete DM opinion matrix is provided in Appendix A.
Step 2: Completing the trust propagation matrix
The trust matrix among different merchants is completed via propagation using Equation (13), resulting in a fully completed trust matrix. Detailed information about this trust matrix can be found in Appendix B. Figure 3 shows the heatmaps of the incomplete trust matrix and the completed trust matrix.
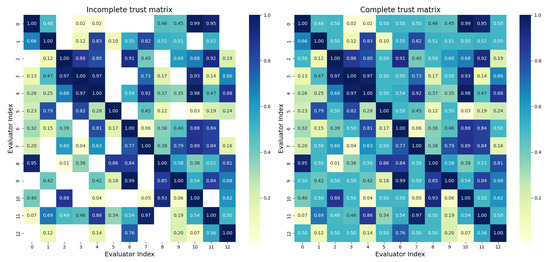
Figure 3.
Comparison of heatmaps: incomplete vs completed trust matrices.
Step 3: Clustering and aggregation processes
The elbow criterion was employed to determine the optimal cluster number k via curvature analysis of the SSE trajectory. For our cohort of thirteen DMs, the concavity variation rate reached statistical significance at k = 4, indicating an optimal trade-off between model complexity and information loss (Figure 4). Next, the DMs are grouped using the enhanced K-means++ clustering method, as shown in Table 4. Afterward, aggregation is performed within each subgroup of DMs to obtain the evaluation matrix for the subgroups, with the detailed information provided in Appendix C.
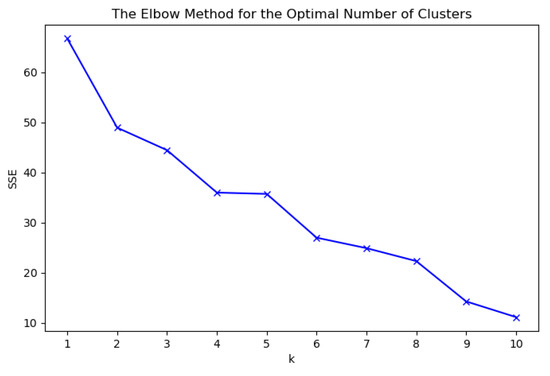
Figure 4.
Elbow method: SSE vs. number of clusters (k).

Table 4.
Result of enhanced K-means++ clustering analysis.
Step 4: Calculating the DMs and group weights of different DMs
The weights of each subgroup are determined based on two key factors: the closeness of trust relationships among members within the group and the size of the group’s membership. Specifically, subgroups with stronger internal trust connections and larger membership sizes are assigned proportionally greater weights.
Additionally, trust correlations between different subgroups are calculated using trust relationships identified within each subgroup. The final computational results are presented in Table 5 and Table 6, where all data are retained to three decimal places for precision.

Table 5.
Weights of DMs.

Table 6.
Groups’ weights.
Step 5: The consensus measurement
A multi-criteria decision matrix is utilized to quantify inter-subgroup consensus levels, with an initial target preference matrix
Three-phase consensus indicators (–) are computed to validate group convergence using Equations (29) and (31)–(34) (see Table 7 for experimental results).

Table 7.
DIS outcomes.
With the subgroup number and its corresponding score value, and taking the subgroup corresponding to the largest score value, we obtain , but , so there is a partial contradiction.
Step 6: CRP
- (1)
- Round 1After testing, it is concluded using Equation (35) that there are minorities in subgroup 1 and subgroup 2. The management mechanism is implemented for the groups with minorities, the weights are adjusted by Equation (36), and the final weights of the subgroups are obtained as shown in Table 8. The target matrix B is updated by using the weights. After obtaining the new target matrix B, the degree of consensus is re-measured.
 Table 8. Adjusted group weight.
Table 8. Adjusted group weight.
After re-measuring for consensus, the values of , , and are presented in Table 9. Since there is an intersection among these values, a consensus is reached, terminating the current loop.

Table 9.
Adjusted DIS outcomes.
Step 7: Reaching the final result
The final score of each alternative plan is determined using the weighted average of different attribute scores. A line graph is used to visually represent these scores (when the score values are equal, the group is ranked in order). The result for the case is presented in Table 10.

Table 10.
Ranking results.
5.2. Sensitivity Analysis
Within the framework of prospect–regret theory, this section presents sensitivity tests on parameters , , and to deeply analyze the specific effects of their fluctuations on the ranking of solutions.
Figure 5 presents radar charts of rankings corresponding to different values, with fixed at 0.92 and at 2.25. Visually, despite variations in , the relative positions of the solutions () on the radar chart almost overlap, with no significant differences noticeable. This strongly suggests that under the given conditions, changes in have negligible impact on the ranking of solutions, with the results exhibiting high stability.
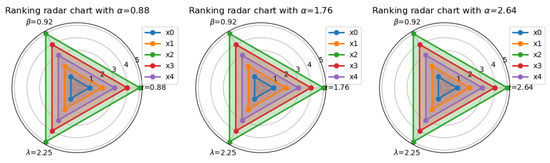
Figure 5.
Ranking changes with .
A similar trend is observed when comparing Figure 6 and Figure 7. In Figure 6, with and fixed, changes in do not lead to any noticeable dispersions or reordering of the solutions on the radar chart. The relative positions of the solutions remain stable, suggesting that the parameter has minimal disturbance on the ranking. In Figure 7, after fixing and , variations in also do not significantly affect the ranking, and the overall shape of the radar chart and the relative positions of the solutions remain consistent.
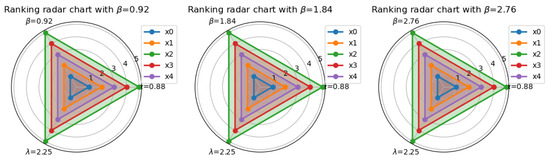
Figure 6.
Ranking changes with .

Figure 7.
Ranking changes with .
Considering the sensitivity test results for these three parameters, we can conclude that under the experimental conditions set in this study, changes in , , and do not have a significant or substantial effect on the solution ranking. This suggests that the theoretical model exhibits high stability and robustness within the current parameter range.
5.3. Simulation Analysis
In this section, we present a series of simulation tests designed to evaluate the feasibility of the proposed method on a moderate scale. All simulations were carried out using PyCharm Community Edition 2024.3.3 on a personal computer equipped with an Intel Core i5-12500H processor running at 2.50 GHz. These tests aim to examine how variations in the number of DMs and the scale of the decision problem affect the overall CRP time.
Figure 8 is a visualization of the time distribution for the LSGDM process under various decision scales (, and 1000) and different problem sizes (n and m ranging from 3 to 7). The horizontal axis represents the trial number (from 0 to 100), while the vertical axis shows the time required (in seconds) for each trial. Each colored line and marker corresponds to a specific (n, m) combination.

Figure 8.
Performance analysis of execution time across various parameter settings.
From Figure 8, it is evident that as d (the number of DMs) increases, the overall running time tends to rise. In particular, when d reaches the hundreds or thousands, certain (n, m) combinations exhibit significant spikes in time consumption. For instance, at d = 800 or d = 1000, some curves show notably higher peak values compared to smaller-scale scenarios. This indicates that when both the decision scale and problem dimension grow, the computational complexity of the LSGDM process increases, resulting in more pronounced time overhead.
Furthermore, for a fixed d value, different (n, m) combinations lead to varying time distributions. Some combinations (e.g., (n = 3, m = 3) or (n = 4, m = 4)) generally require less time, with relatively minor fluctuations across most trials. By contrast, when both n and m are larger (e.g., (n = 7, m = 7)), there are higher time-consumption peaks during multiple trials, indicating that higher-dimensional problems demand greater computational effort and exhibit less predictable run times.
Overall, these plots illustrate that as both the decision scale d and the problem dimensions (n, m) increase, the running time for the LSGDM method shows a greater variability and a clear upward trend. These findings offer insights for future research focused on algorithmic optimization, parallelization, or improved data structures.
5.4. Comparison Analysis
To further substantiate the superiority and practicality of the method put forward in this paper, this section meticulously conducts comparative experiments against a set of well-established existing methods. These experiments are designed to systematically evaluate how the proposed method performs relative to others in terms of crucial aspects such as execution efficiency, consensus-reaching effectiveness, and the rationality of sorting results, thereby offering a comprehensive and reliable validation of its advantages.
5.4.1. Component Necessity Analysis via Ablation Study
To comprehensively evaluate the functional necessity of each algorithm component, we mainly conducted systematic ablation experiments across three dimensions: computational efficiency, consensus formation quality, and ranking effectiveness. By applying a control variable approach, we systematically removed each sub-method and observed its impact on specific process indicators.
Table 11 summarizes the deformation methods implemented in our proposed framework.

Table 11.
A summary of the required comparison methods.
A benchmarking framework employing Monte Carlo iterations () was implemented to quantitatively assess performance differentials between baseline method and enhanced method , with a particular focus on algorithmic refinements in cluster optimization. Statistical aggregates of these metrics, calculated over 100 independent trials, are systematically tabulated in Table 12 (values truncated at 3 decimal places for precision consistency).

Table 12.
An in-depth analysis of sub-methods in clustering.
Based on the comparative analysis of methods and , it can be concluded that method exhibits certain advantages. In terms of the total execution time, although takes 0.0234 s which is longer than ’s 0.0091 s, when considering the clustering execution time alone, the difference between ’s 0.0188 s and ’s 0.0045 s is not extremely significant. More importantly, in terms of the initial consensus degree, both methods show partial contradiction, but method may have a more stable underlying consensus-reaching mechanism during the clustering process. Regarding the final sorting result, the ranking sequence provided by might be more in line with the expected decision-making logic or practical application requirements. Overall, considering multiple key metrics comprehensively, method is a relatively better choice in this clustering-related scenario.
In an endeavor to discern how the inclusion of MOH impacts the outcomes within the CRP, a meticulous comparative analysis is conducted. This analysis juxtaposes scenarios featuring MOH against those lacking it. Three pivotal metrics serve as the cornerstone of this comparison: The CRP time, the number of iterations, the final sorting result.
To ensure the reliability of the results, both conditions, with and without MOH, are executed a hundred times each. During these runs, corresponding data for each metric are carefully recorded. Subsequently, the average values for every indicator are calculated and presented. All these comprehensive findings are neatly summarized in Table 13, offering a clear-cut view of the necessity of MOH in CRP.

Table 13.
Analysis of the necessity of MOH in CRP.
Based on the comparative analysis of scenarios with and without MOH in the CRP, as presented in Table 13, in terms of CRP time, although is quicker with a time of 0.0012 s compared to ’s 0.0046 s, the difference is relatively small. Significantly, both methods have the same number of iterations, indicating that does not sacrifice efficiency in terms of the iterative process. More importantly, the final sorting result provided by might align better with the anticipated decision-making logic or practical application requirements. Considering these pivotal metrics comprehensively, proves to be a more suitable choice, highlighting the relative necessity and advantage of its approach in the CRP context.
An in-depth comparative analysis is conducted to explore the implications of substituting the DIS with a weighted sum during the decision-making process, as presented in Table 14. This analysis focuses on two critical metrics: the CRP time and the final sorting result. By juxtaposing method against , this analysis aims to gain a comprehensive understanding of the impact of this substitution.

Table 14.
Analysis of replacing DISs with weighted sum during decision-making.
The comparative analysis in Table 14 examines the effect of replacing DIS with a weighted sum in the decision-making context. Focusing on CRP time and the final sorting result, it contrasts method and . shows a CRP time of 0.0046 s, shorter than ’s 0.0054 s. Meanwhile, both methods result in the same final sorting order. Efficiency in decision-making is often crucial, and with a shorter CRP time while achieving an identical result, proves to be more advantageous. This comparison offers a clear view of the performance differences between the two methods, which can guide the selection of appropriate decision-making approaches in practical applications.
To evaluate the impact of integrating prospect–regret theory into the CRP, we conduct a comparative experiment between two scenarios: CRP with prospect–regret theory () and CRP without prospect–regret theory (). The former employs the prospect–regret theory-based weight-adjustment mechanism, while the latter uses a uniform weight update rule without considering risk preferences or regret aversion. Key metrics include CRP time, number of iterations, and the rationality of the final ranking result. Using the same initial trust matrix and clustering results. Each condition is executed 100 times to ensure statistical reliability, with average values reported in Table 15.

Table 15.
Comparison of CRP with and without prospect–regret theory.
takes slightly longer (0.0046 s) than m 4 (0.0032 s) primarily due to the added computational overhead of the nonlinear value function and regret calculation in prospect–regret theory. However, the time difference is minimal, suggesting that the inclusion of behavioral factors does not significantly impact efficiency. Notably, reaches consensus in just one iteration, whereas requires four iterations. This highlights the advantage of prospect–regret theory in accelerating convergence by directing weight adjustments toward a risk-sensitive consensus, thereby reducing the need for multiple iterations. Overall, the results demonstrate that incorporating behavioral factors enhances convergence speed with only a marginal computational cost.
5.4.2. Comparative Analysis of Trust Propagation Operators
To validate the superiority of our trust propagation mechanism, we compare the Hamacher-based operator (denoted as ) with two benchmark methods across three critical metrics: computational efficiency, error control (relative error), and the ability to model trust decay in SNs. Table 16 presents the representations and descriptions of the three methods.

Table 16.
Method descriptions.
For the three operators, we randomly generated initial trust matrices with some empty entries. After completing them through trust propagation, we conducted 100 experiments on indicators like relative error and took the averages, which are summarized in Table 17 to compare the operators’ performance.

Table 17.
A qualitative analysis comparing the trust propagation operators.
achieves the lowest relative error (0.9992), demonstrating superior accuracy in reconstructing incomplete trust matrices. This is attributed to the Hamacher operator’s ability to balance conjunctive and disjunctive trust interactions, unlike Methods A and B, which either oversimplify relationships () or ignore decay dynamics ().
Only explicitly incorporates a decay factor to mitigate trust inflation over long paths, a critical feature for realistic SN modeling. While is marginally faster, it lacks decay modeling; ’s moderate time overhead (0.001242 s/iteration) is justified by its superior behavioral fidelity and error control, essential for complex LSGDM scenarios.
This comparison highlights that our dual strategy of Hamacher aggregation and decay factor adjustment effectively balances mathematical rigor, behavioral realism, and computational practicality in SN-LSGDM, outperforming classical and heuristic alternatives in both accuracy and theoretical consistency.
5.4.3. Comparison Among Different Clustering Methods
In clustering analysis, the selection of distance metric is pivotal in dictating the clustering results. Classical single-distance clustering methods, such as those widely used and well-established approaches, construct their clustering models relying on distinct distance measures. This leads to significant disparities in their efficacy and applicability across various scenarios.
To offer a clear and comprehensive juxtaposition of these classical methods, we meticulously compiled Figure 9. This figure contrasts our single-distance clustering approach with the classical ones proposed by Huang et al. [41] and Chen et al. [29]. The comparison spans four crucial dimensions: the name of the method, the components of the distance metric, the clustering time and the average subgroup credibility.
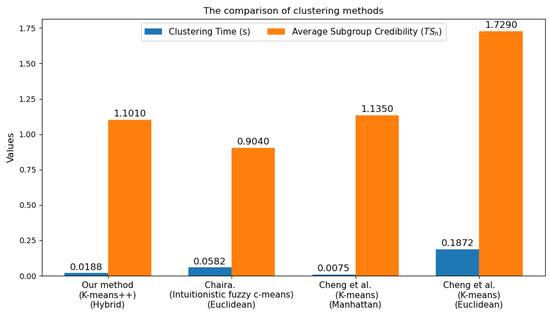
Figure 9.
Comparison of clustering methods [30,44].
Based on the comparative analysis of single-distance clustering methods in Table 14, in terms of clustering time, our method only takes 0.0188 s, which is more efficient than Huang et al. [41]’s 0.0582 s and the simple Euclidean distance-based method’s 0.1872 s. Although Cheng et al. [29]’s method has a shorter time of 0.0075 s, our method shows greater advantages in other aspects.
Regarding the average subgroup credibility, our method reaches 1.101, which is higher than Huang et al. [41]’s 0.904. This indicates that the subgroups formed by our method have higher credibility and better internal consistency. Additionally, our method combines Hamming distances based on ranking results, Euclidean distances, and Manhattan distances, enabling it to comprehensively consider different characteristics of data. This multi-distance-metric approach endows our method with stronger adaptability to various data distributions and structures, making it more suitable for complex clustering tasks.
5.4.4. Comparison Between the Proposed Method and Existing Consensus Models
To enable a systematic comparison, existing models are categorized into three groups: traditional LSGDM models (TL), enhanced LSGDM models integrated with SN (SNL), and behavior-management-oriented LSGDM models to handle misbehaviors (ML). This classification framework allows for a clearer presentation of the applicability scenarios and performance variations among different consensus models.
Yuan et al. [51] developed a fuzzy LSGDM method using trust relationships and opinion similarities, applying the improved Louvain algorithm for clustering and weight determination. A two-stage dual fine-tuning CRP reduced decision-making scale, and prospect–regret theory ranked the schemes.
Chen et al. [52] developed an emergency decision-making method for large groups based on uncertain linguistic cloud similarity, which transforms linguistic preferences into cloud models, clusters DMs, determines weights, and reaches consensus via trust updates and opinion interactions.
Meng et al. [53] addressed the shortcomings of consensus-adjustment mechanisms in LSGDM. They introduced cooperative game theory, proposed two-stage Shapley and core-Nash bargaining consensus-adjustment mechanisms.
Liang et al. [54] constructed a threshold-free model for LSGDM based on SNA. The model involves adjusting the trust degree, conducting comprehensive clustering, using the SNDG model to adjust preferences, terminating the feedback based on the consensus conversion rate.
Liu et al. [19] proposes a consensus model for LSGDM driven by an SN. It improves the network through a two-stage analysis, determines expert weights, and constructs a consensus optimization model to achieve minimum adjustments and promote CRP.
Liu et al. [55] developed a consensus model for managing non-cooperative behavior in LSGDM under a dynamic dual SNs. This model constructs a dynamic dual trust network and designs a minimal adjustment consensus model and non-cooperative behavior-management method based on it.
Xu et al. [39] presents an improved consensus model for multi-criteria large-group emergency decision-making, which clusters and analyzes group opinions, determines parameters such as the comprehensive adjustment coefficient, and addresses minority opinions and non-cooperative behaviors to reach a consensus.
Xu et al. [11] proposed the HOAL-MOH-DFT model. It optimizes Leiden clustering with the hippopotamus optimization algorithm, groups based on trust relationships and opinion similarities, and conducts two-stage adjustments to handle various situations in group decision-making. Table 16 compares the core features of the consensus model proposed in this study with above methods, emphasizing the innovative strengths of our approach.
The comparative analysis in Table 18 reveals significant limitations in the key mechanism designs of existing LSGDM models:

Table 18.
A comparative analysis of consensus methods from a qualitative approach.
TL, while simplifying processes via basic clustering, relies on single indicators (e.g., Chen et al. [52] and Meng et al. [53]) to capture the multidimensional correlations of DMs’ behaviors, resulting in incomplete behavioral characterization. Additionally, their lack of a quantitative framework for consensus level (DIS) and proactive intervention in MOH often leads to majority-dominated decision bias.
SNL models enhance opinion adjustment by integrating SN trust relationships, yet their static SNs struggle to adapt to dynamic scenarios. Furthermore, the decoupling of DIS from decision-generation fragments consensus management. ML models attempt to address minority opinions but fail to balance group diversity and decision efficiency due to reliance on single clustering indicators.
In contrast, the proposed method overcomes these bottlenecks via multidimensional collaborative design: The integration of dynamic trust propagation and hybrid distance clustering resolves group partitioning bias; the DIS establishes a closed-loop linkage between objective consensus measurement (e.g., entropy-weighted deviation) and decision generation, eliminating the “measurement-decision decoupling” flaw in traditional models; simultaneously, the dynamic weighting strategy for MOH and hierarchical behavior-management mechanism ensure iterative integration of minority opinions while precisely suppressing both explicit and implicit misbehaviors. This organic synergy among mechanisms significantly enhances the model’s complexity, inclusivity, and practicality, providing a more realistic solution for LSGDM.
The above approach offers a qualitative comparison between existing methods and the proposed LSGDM approach. To facilitate a more objective comparison and present more convincing results, Table 19 provides a quantitative analysis comparing the LSGDM method with other methods from machine learning.

Table 19.
A quantitative analysis comparing our method with other methods.
Based on the quantitative analysis results presented in Table 19, our method demonstrates significant advantages in multiple aspects, clearly outperforming other methods.
Firstly, in terms of total execution time, our method requires only 0.0234 s, which is slightly higher than the methods proposed by Liu et al. [55] and Xu et al. [39], but significantly lower than the method by Xu et al. [11] and Liang et al. [54]. This indicates that our method has a high level of computational efficiency, capable of completing tasks in a shorter time. Secondly, regarding the number of iterations, our method only requires 1 iteration to reach the final result, which is the least among all methods. This not only enhances computational efficiency but also reduces the consumption of computational resources, highlighting the advantages of our method in algorithm optimization.
Lastly, in terms of the final ranking result, our method yields the ranking , consistent with the result of Xu et al. [39]’s method and superior to those of Liu et al. [19] and Xu et al. [11]. This demonstrates the high reliability of our method in terms of decision-making accuracy. In summary, our method excels in execution time, number of iterations, and final ranking results, showcasing high computational efficiency and decision-making accuracy. It is a method worthy of promotion and application.
6. Conclusions
This study addresses critical challenges in LSGDM via an enhanced consensus-reaching framework that integrates SNA, refined clustering techniques, a DIS, and minority opinion management. Below are the key contributions and findings:
- (1)
- The proposed method leverages the Hamacher aggregation operator with a decay factor to effectively complete incomplete trust matrices while mitigating biases inherent in traditional statistical imputation. This approach enhances the interpretability and reliability of trust relationships in SNs.
- (2)
- By integrating hybrid distance metrics (Euclidean, Manhattan, and Hamming distances) into the K-means++ algorithm, we achieve fine-grained clustering of DMs. This multidimensional strategy accounts for both evaluation data and preference rankings, significantly improving subgroup homogeneity and reducing computational complexity.
- (3)
- A DIS grounded in MGRSs provides a robust, formula-driven mechanism for assessing consensus levels. By replacing subjective thresholds with granular approximations, this method ensures fairness and transparency in conflict detections.
- (4)
- A systematic mechanism for detecting and adjusting minority opinions is proposed, incorporating subgroup credibility and trust centrality. This balances minority influence without over-amplification, fostering innovation while preserving decision stability.
Empirical validation using UAV procurement datasets demonstrates the framework’s effectiveness. Sensitivity analyses confirm the stability of parameter choices, while comparative experiments highlight the superiority of the proposed method over existing approaches in terms of clustering accuracy, consensus efficiency, and ranking rationality.
Potential extensions include adapting the framework to dynamic real-time decision scenarios and optimizing trust propagation via deep learning architectures. Investigating cross-cultural variations in MOH can further enhance global applicability.
By harmonizing technical rigor with practical adaptability, this research advances LSGDM methodology, offering a scalable solution for complex, socially embedded decision challenges. The integration of theoretical innovation and empirical validation establishes a new benchmark in consensus-driven decision systems.
The proposed method offers DMs a more refined tool to reconcile opinion divergences and incorporate dissent constructively—key in high-stakes domains such as public policy, healthcare, or technology procurement. By operationalizing user-generated content through sentiment analysis and trust modeling, the system supports decisions that are both data-driven and socially grounded. The application to UAV selection illustrates how organizations can leverage multi-source evaluations to make informed, balanced choices.
While the proposed consensus-reaching framework demonstrates significant theoretical and empirical advantages, there are several aspects that could be further improved:
- (1)
- The current model is demonstrated in the context of UAV selection based on structured and semi-structured data. Future extensions may consider more heterogeneous decision scenarios, such as new energy vehicles [56].
- (2)
- Although we incorporated social trust propagation, the model does not yet address trust decay over time or dynamic trust formation, which are relevant in evolving SNs.
- (3)
- While our current work integrates sentiment analysis indirectly, future implementations could enhance this component with real-time emotion detection and contextual semantic embeddings.
For further research, one direction is to adapt the framework to dynamic real-time decision scenarios. This could involve developing algorithms that can update trust relationships, clustering results, and consensus levels in real-time as the decision-making environment changes. Another direction is to optimize trust propagation via deep-learning architectures. Deep learning can potentially capture more complex relationships in SNs and decision-making data, improving the accuracy of trust propagation. Additionally, investigating cross-cultural variations in MOH can enhance the global applicability of the model. Different cultures may have different attitudes towards minority opinions, and understanding these differences can help the model better adapt to various cultural backgrounds.
Author Contributions
Conceptualization, X.H. and C.Z.; Methodology, C.Z.; Validation, X.H. and T.X.; Data curation, X.H.; Writing—original draft, X.H.; Writing—review & editing, C.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Central Government Guides Local Science and Technology Innovation (YDZJSX2024D015), the Special Fund for the Training Program for Young Scientific Researchers of Higher Education Institutions in Shanxi, the Wenying Young Scholars of Shanxi University, the Science and Technology Innovation Teams of Shanxi (202204051001015), the 22nd Undergraduate Innovation and Entrepreneurship Training Program of Shanxi University (202410108008), and the Cultivate Scientific Research Excellence Programs of Higher Education Institutions in Shanxi (2019SK036).
Data Availability Statement
The original contributions presented in this study are included in the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this paper:
| LSGDM | Large-scale group decision-making |
| DMs | Decision-makers |
| SNs | Social networks |
| SNA | Social network analysis |
| CRP | Consensus-reaching process |
| MOH | Minority opinion handling |
| DISs | Decision indicator sets |
| IFNs | Intuitionistic fuzzy numbers |
| IFSs | Intuitionistic fuzzy sets |
| SSE | Sum of squared errors |
| UAVs | Unmanned aerial vehicles |
| MGRS | Multigranulation rough set |
| TL | Traditional LSGDM models |
| SNL | Enhanced LSGDM models integrated with SN |
| ML | Behavior-management-oriented LSGDM models to handle misbehaviors |
Appendix A
| DMs’ Evaluation Matrices | |
Appendix B
| Trust Degree Matrix Among DMs (Completed) |
Appendix C
| Sub-Group Evaluation Matrices | |
References
- Kiesler, S.; Sproull, L. Group decision making and communication technology. Organ. Behav. Hum. Decis. Process. 1992, 52, 96–123. [Google Scholar] [CrossRef]
- Wang, Y.; Song, H.; Dutta, B.; García-Zamora, D.; Martínez, L. Consensus reaching in LSGDM: Overlapping community detection and bounded confidence-driven feedback mechanism. Inf. Sci. 2024, 679, 121104. [Google Scholar] [CrossRef]
- Tang, M.; Liao, H. From conventional group decision making to large-scale group decision making: What are the challenges and how to meet them in big data era? A state-of-the-art survey. Omega 2021, 100, 102141. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, Y.; Sangaiah, A.; Alenazi, M.J.F.; Aborokbah, M. An incomplete three-way consensus algorithm for unmanned aerial vehicle purchase using optimization-driven sentiment analysis. Future Gener. Comput. Syst. 2025, 107761. [Google Scholar] [CrossRef]
- Garcia-Zamora, D.; Labella, A.; Ding, W.; Rodríguez, R.M.; Martínez, L. Large-scale group decision making: A systematic review and a critical analysis. IEEE/CAA J. Autom. Sin. 2022, 9, 949–966. [Google Scholar] [CrossRef]
- Li, X. Big data-driven fuzzy large-scale group decision making (LSGDM) in circular economy environment. Technol. Forecast. Soc. Change 2022, 175, 121285. [Google Scholar]
- Shen, Y.; Ma, X.; Xu, Z.; Herrera-Viedma, E.; Maresova, P.; Zhan, J. Opinion evolution and dynamic trust-driven consensus model in large-scale group decision-making under incomplete information. Inf. Sci. 2024, 657, 119925. [Google Scholar] [CrossRef]
- Mahmoudi, A.; Abbasi, M.; Yuan, J.; Li, L. Large-scale group decision-making (LSGDM) for performance measurement of healthcare construction projects: Ordinal Priority Approach. Appl. Intell. 2022, 52, 13781–13802. [Google Scholar] [CrossRef]
- Zhang, R.; Huang, J.; Xu, Y. Consensus models with aggregation operators for minimum quadratic cost in group decision making. Appl. Intell. 2023, 53, 1370–1390. [Google Scholar] [CrossRef]
- Wang, Y.; He, S.; Zamora, D.; Pan, X.; Martínez, L. A large scale group three-way decision-based consensus model for site selection of new energy vehicle charging stations. Expert Syst. Appl. 2023, 214, 119107. [Google Scholar] [CrossRef]
- Xu, T.; He, S.; Yuan, X.; Zhang, C. Enhancing group consensus in social networks: A two-stage dual-fine tuning consensus model based on adaptive Leiden algorithm and minority opinion management with non-cooperative behaviors. Electronics 2024, 13, 4930. [Google Scholar] [CrossRef]
- Hsieh, Y.; Lu, L.; Ku, Y. Review evaluation for hotel recommendation. Electronics 2023, 12, 4673. [Google Scholar] [CrossRef]
- Tian, X.; Ma, W.; Wu, L.; Xie, M.; Kou, G. Large-scale consensus with dynamic trust and optimal reference in social network under incomplete probabilistic linguistic circumstance. Inf. Sci. 2024, 661, 120123. [Google Scholar] [CrossRef]
- Harshavardhan, A.; Boyapati, P.; Neelakandan, S.; Abdul-Rasheed Akeji, A.A.; Singh Pundir, A.K.; Walia, R. LSGDM with Biogeography-Based Optimization (BBO) Model for Healthcare Applications. J. Healthc. Eng. 2022, 2022, 2170839. [Google Scholar] [CrossRef]
- Chunaev, P. Community detection in node-attributed social networks: A survey. Comput. Sci. Rev. 2020, 37, 100286. [Google Scholar] [CrossRef]
- Jin, F.; Cai, Y.; Zhou, L.; Ding, T. Regret–rejoice two-stage multiplicative DEA models-driven cross-efficiency evaluation with probabilistic linguistic information. Omega 2023, 117, 102839. [Google Scholar] [CrossRef]
- Wu, J.; Chiclana, F.; Fujita, H.; Herrera-Viedma, E. A visual interaction consensus model for social network group decision making with trust propagation. Knowl.-Based Syst. 2017, 122, 39–50. [Google Scholar] [CrossRef]
- Liu, B.; Zhou, Q.; Ding, R.X.; Palomares, I.; Herrera, F. Large-scale group decision making model based on social network analysis: Trust relationship-based conflict detection and elimination. Eur. J. Oper. Res. 2019, 275, 737–754. [Google Scholar] [CrossRef]
- Liu, P.; Li, Y.; Wang, P. Social trust-driven consensus reaching model for multiattribute group decision making: Exploring social trust network completeness. IEEE Trans. Fuzzy Syst. 2023, 31, 3040–3054. [Google Scholar] [CrossRef]
- Chu, J.; Wang, Y.; Liu, X.; Liu, Y. Social network community analysis based large-scale group decision making approach with incomplete fuzzy preference relations. Inf. Fusion 2020, 60, 98–120. [Google Scholar] [CrossRef]
- Xu, Y.; Li, C.; Wen, X. Missing values estimation and consensus building for incomplete hesitant fuzzy preference relations with multiplicative consistency. Int. J. Comput. Intell. Syst. 2018, 11, 101–119. [Google Scholar] [CrossRef]
- Song, Y.; Li, G. Handling group decision-making model with incomplete hesitant fuzzy preference relations and its application in medical decision. Soft Comput. 2019, 23, 6657–6666. [Google Scholar] [CrossRef]
- Liu, P. Some Hamacher aggregation operators based on the interval-valued intuitionistic fuzzy numbers and their application to group decision making. IEEE Trans. Fuzzy Syst. 2013, 22, 83–97. [Google Scholar] [CrossRef]
- Ren, Y.; Pu, J.; Yang, Z.; Xu, J.; Li, G.; Pu, X.; Yu, P.S.; He, L. Deep clustering: A comprehensive survey. IEEE Trans. Neural Netw. Learn. Syst. 2024, 36, 5858–5878. [Google Scholar] [CrossRef]
- Xu, D.; Tian, Y. A comprehensive survey of clustering algorithms. Ann. Data Sci. 2015, 2, 165–193. [Google Scholar] [CrossRef]
- Wang, Y.; Qian, J.; Hassan, M.; Zhang, X.; Zhang, T.; Yang, C.; Zhou, X.; Jia, F. Density peak clustering algorithms: A review on the decade 2014–2023. Expert Syst. Appl. 2024, 238, 121860. [Google Scholar] [CrossRef]
- Kapoor, A.; Singhal, A. A comparative study of K-Means, K-Means++ and Fuzzy C-Means clustering algorithms. In Proceedings of the 2017 3rd International Conference on Computational Intelligence & Communication Technology (CICT), Ghaziabad, India, 9–10 February 2017; pp. 1–6. [Google Scholar]
- Hajihosseinlou, M.; Maghsoudi, A.; Ghezelbash, R. Intelligent mapping of geochemical anomalies: Adaptation of DBSCAN and mean-shift clustering approaches. J. Geochem. Explor. 2024, 258, 107393. [Google Scholar] [CrossRef]
- Cheng, F. A comparative study of the performance of Spark-based k-means algorithm based on Euclidean distance and Manhattan distance. In Proceedings of the 2024 3rd International Conference on Big Data, Information and Computer Network (BDICN), Sanya, China, 12–14 January 2024; pp. 1–6. [Google Scholar]
- Guo, L.; Zhan, J.; Zhang, C.; Xu, Z. A large-scale group decision-making method fusing three-way clustering and regret theory under fuzzy preference relations. IEEE Trans. Fuzzy Syst. 2023, 32, 4846–4860. [Google Scholar] [CrossRef]
- Labella, A.; Liu, H.; Rodríguez, R.M.; Martínez, L. A cost consensus metric for consensus reaching processes based on a comprehensive minimum cost model. Eur. J. Oper. Res. 2020, 281, 316–331. [Google Scholar] [CrossRef]
- Zou, W.; Wan, S.; Dong, J.; Martínez, L. A new social network driven consensus reaching process for multi-criteria group decision making with probabilistic linguistic information. Inf. Sci. 2023, 632, 467–502. [Google Scholar] [CrossRef]
- Tang, M.; Liao, H.; Mi, X.; Lev, B.; Pedrycz, W. A hierarchical consensus reaching process for group decision making with noncooperative behaviors. Eur. J. Oper. Res. 2021, 293, 632–642. [Google Scholar] [CrossRef]
- Cheng, X.; Zhang, K.; Wu, T.; Xu, Z.; Gou, X. An opinions-updating model for large-scale group decision-making driven by autonomous learning. Inf. Sci. 2024, 662, 120238. [Google Scholar] [CrossRef]
- Gai, T.; Wu, J.; Cao, M.; Liu, Y.; Liang, C. Blockchain platform selection for supply chain finance: A bilateral-negotiation-based group multiattribute decision making method. IEEE Trans. Comput. Soc. Syst. 2024, 11, 6072–6086. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Q.; Zhang, C.; Zhan, J. New fuzzy rough set models based on implication operators. Comput. Appl. Math. 2025, 44, 125. [Google Scholar] [CrossRef]
- Laor, T. Breaking the silence: The role of social media in fostering community and challenging the spiral of silence. Online Inf. Rev. 2024, 48, 710–724. [Google Scholar] [CrossRef]
- Ren, R.; Tang, M.; Liao, H. Managing minority opinions in micro-grid planning by a social network analysis-based large scale group decision making method with hesitant fuzzy linguistic information. Knowl.-Based Syst. 2020, 189, 105060. [Google Scholar] [CrossRef]
- Xu, X.; Du, Z.; Chen, X. Consensus model for multi-criteria large-group emergency decision making considering non-cooperative behaviors and minority opinions. Decis. Support Syst. 2015, 79, 150–160. [Google Scholar] [CrossRef]
- Liu, P.; Li, Y.; Wang, P. Opinion dynamics and minimum adjustment-driven consensus model for multi-criteria large-scale group decision making under a novel social trust propagation mechanism. IEEE Trans. Fuzzy Syst. 2022, 31, 307–321. [Google Scholar] [CrossRef]
- Chaira, T. A novel intuitionistic fuzzy C means clustering algorithm and its application to medical images. Appl. Soft Comput. 2011, 11, 1711–1717. [Google Scholar] [CrossRef]
- Shen, Y.; Ma, X.; Zhang, H.; Zhan, J. Fusion social network and regret theory for a consensus model with minority opinions in large-scale group decision making. Inf. Fusion 2024, 112, 102548. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, Y.; Hao, W.; Yu, X. A signed network analysis-based consensus reaching process in group decision making. Appl. Soft Comput. 2021, 100, 106926. [Google Scholar] [CrossRef]
- Zhang, H.; Palomares, I.; Dong, Y.; Wang, W. Managing non-cooperative behaviors in consensus-based multiple attribute group decision making: An approach based on social network analysis. Knowl.-Based Syst. 2018, 162, 29–45. [Google Scholar] [CrossRef]
- Tan, C.; Yi, W.; Chen, X. Hesitant fuzzy Hamacher aggregation operators for multicriteria decision making. Appl. Soft Comput. 2015, 26, 325–349. [Google Scholar] [CrossRef]
- Liu, X.; Yang, Y.; Jiang, J. The behavioral TOPSIS based on prospect theory and regret theory. Int. J. Inf. Technol. Decis. Mak. 2023, 22, 1591–1615. [Google Scholar] [CrossRef]
- Bisht, G.; Pal, A.K. Prospect–regret theory based decision-making approach for incomplete probabilistic hesitant fuzzy environment: An application to medical field. Expert Syst. Appl. 2024, 250, 123906. [Google Scholar] [CrossRef]
- Kahneman, D.; Tversky, A. Prospect theory: An analysis of decision under risk. In Handbook of the Fundamentals of Financial Decision Making: Part I; World Scientific: Hackensack, NJ, USA, 2013; pp. 99–127. [Google Scholar]
- Zhang, S.; Zhu, J.; Liu, X.; Chen, Y. Regret theory-based group decision-making with multidimensional preference and incomplete weight information. Inf. Fusion 2016, 31, 1–13. [Google Scholar] [CrossRef]
- Li, R.; Zhang, C.; Li, D.; Li, W.; Zhan, J. Improved evidential three-way decisions in incomplete multi-scale information systems. Int. J. Approx. Reason. 2025, 181, 109417. [Google Scholar] [CrossRef]
- Yuan, X.; Xu, T.; He, S.; Zhang, C. An online review data-driven fuzzy large-scale group decision-making method based on dual fine-tuning. Electronics 2024, 13, 2702. [Google Scholar] [CrossRef]
- Chen, G.; Wei, L.; Fu, J.; Li, C.; Zhao, G. A large group emergency decision-making method based on uncertain linguistic cloud similarity method. Math. Comput. Appl. 2022, 27, 101. [Google Scholar] [CrossRef]
- Meng, F.; Tang, J.; An, Q. Cooperative game based two-stage consensus adjustment mechanism for large-scale group decision making. Omega 2023, 117, 102842. [Google Scholar] [CrossRef]
- Liang, X.; Guo, J.; Liu, P. A large-scale group decision-making model with no consensus threshold based on social network analysis. Inf. Sci. 2022, 612, 361–383. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, W.; Zhang, X.; Liu, P. A dynamic dual-trust network-based consensus model for individual non-cooperative behaviour management in group decision-making. Inf. Sci. 2024, 674, 120750. [Google Scholar] [CrossRef]
- Ding, J.; Zhang, C.; Li, D.; Li, W.; Zhan, J. A three-way large-scale group decision-making method integrating sentiment analysis and quantum interference-based prospect theory for the selection of new energy vehicles. Expert Syst. Appl. 2025, 275, 126940. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).