Calculations of Electrical Parameters of Cables in Wide Frequency Range
Abstract
1. Introduction
2. Structures and Arrangements of Cables
2.1. Structures of Cables
2.2. Bonding and Earthing Arrangements of Cables
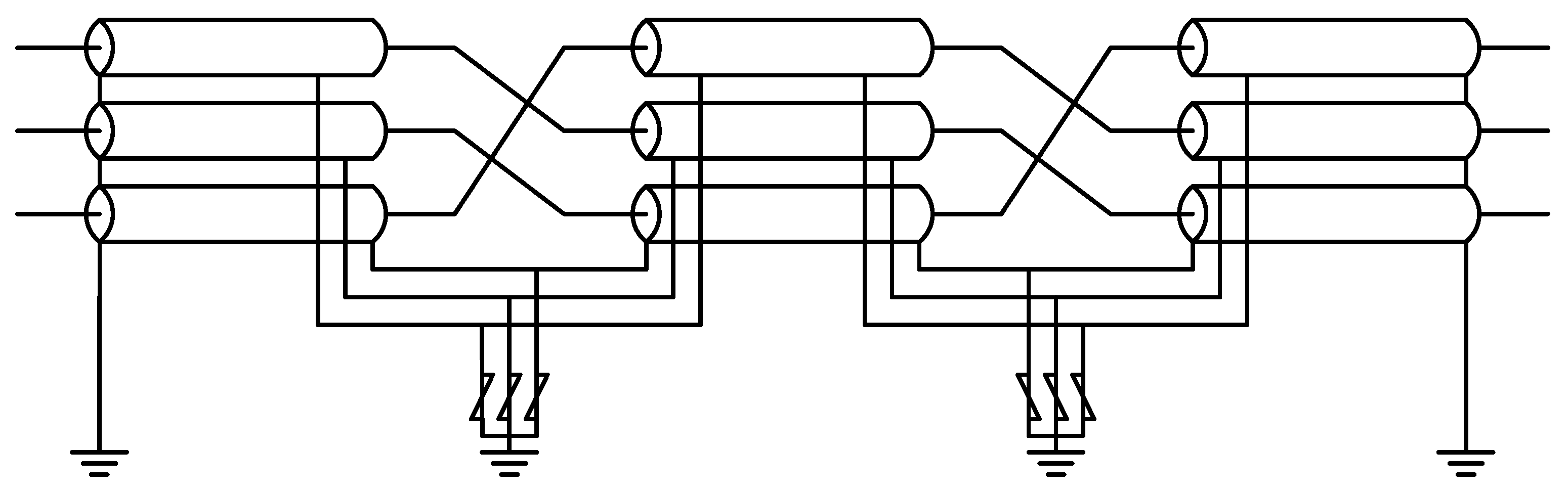
2.3. Layouts of Cables
3. Calculations of Electrical Parameters of Cables
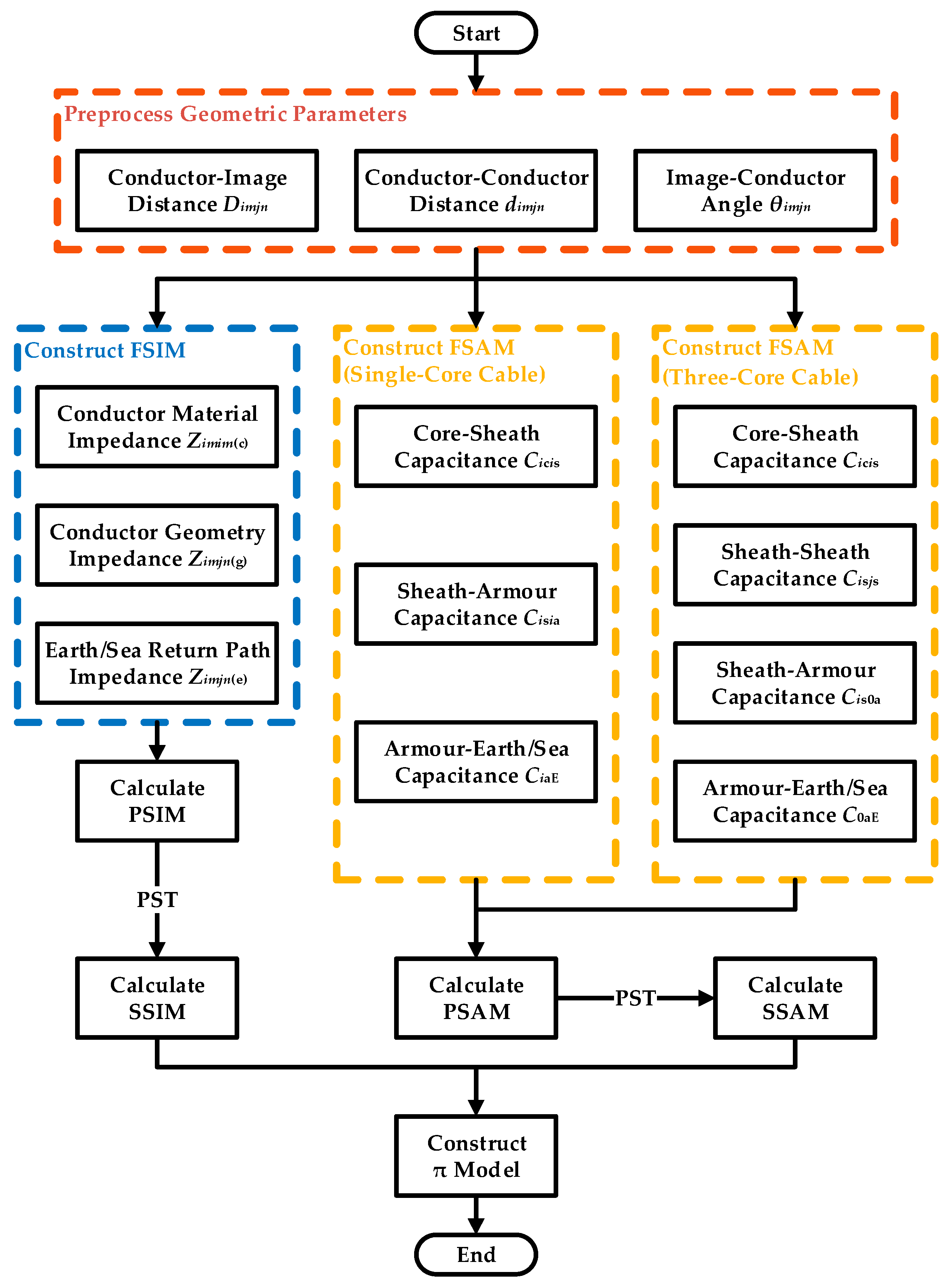
3.1. Process Overview
3.2. Geometric Parameters Preprocessing
3.3. Construction of FSIM
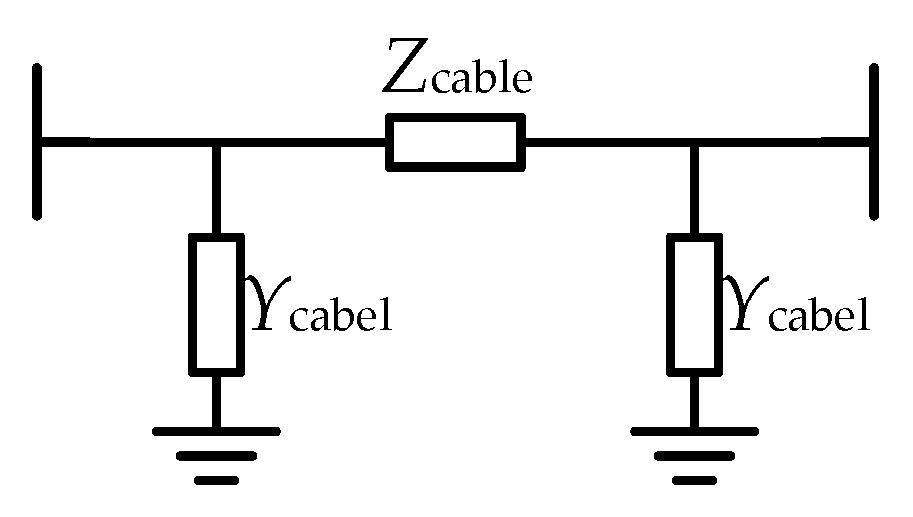
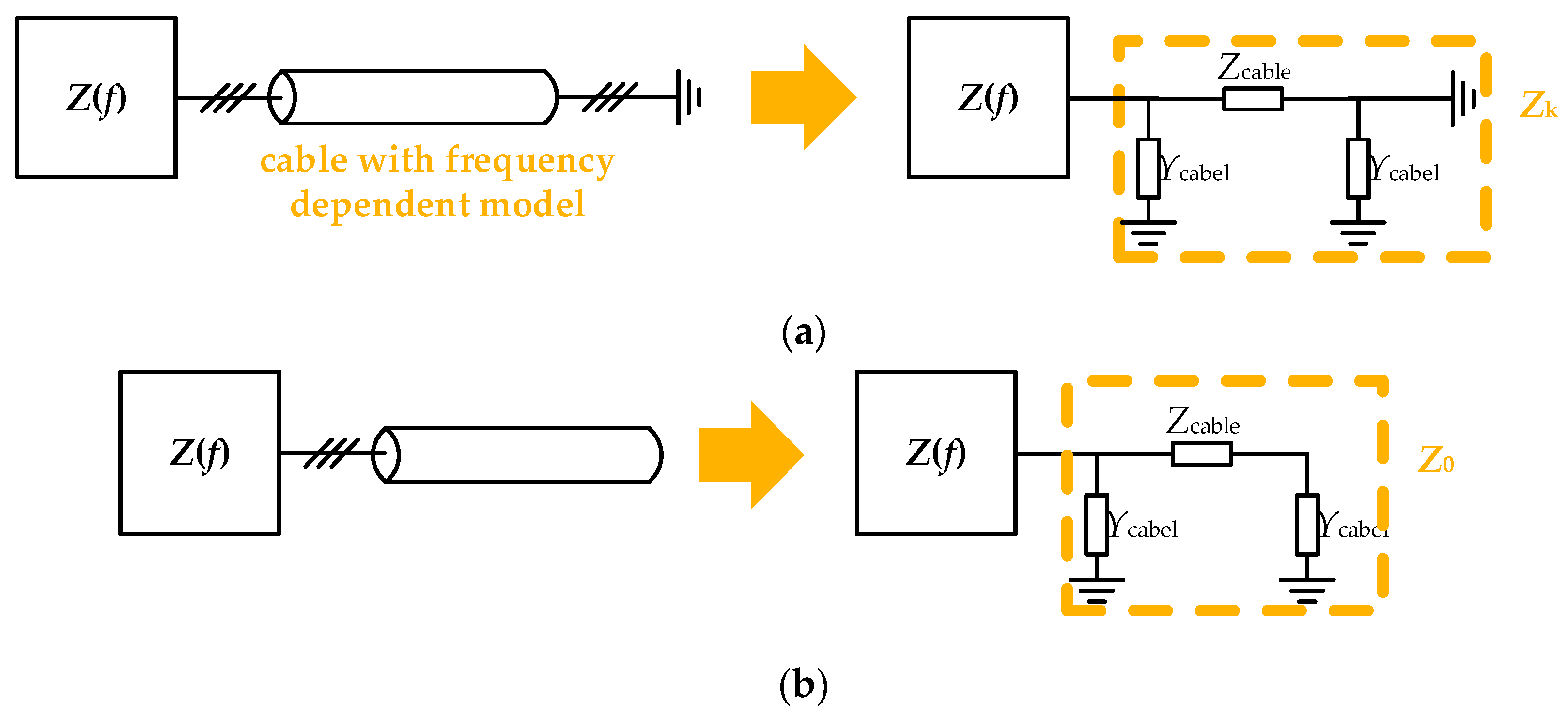
3.4. Transformation from FSIM to SSIM
3.5. Construction of FSAM
3.6. Transformation from FSAM to SSAM
4. Case Studies
4.1. Case Introduction
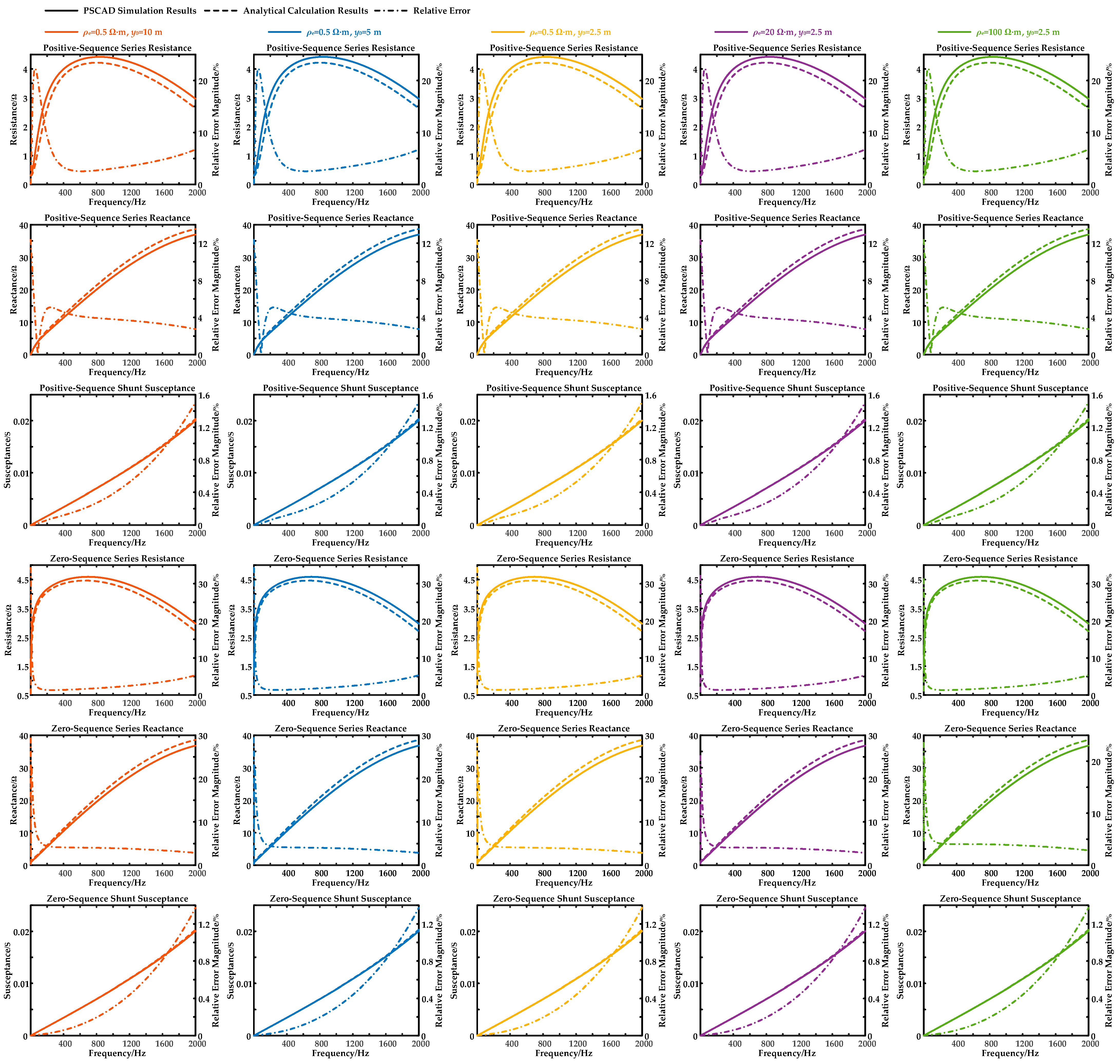
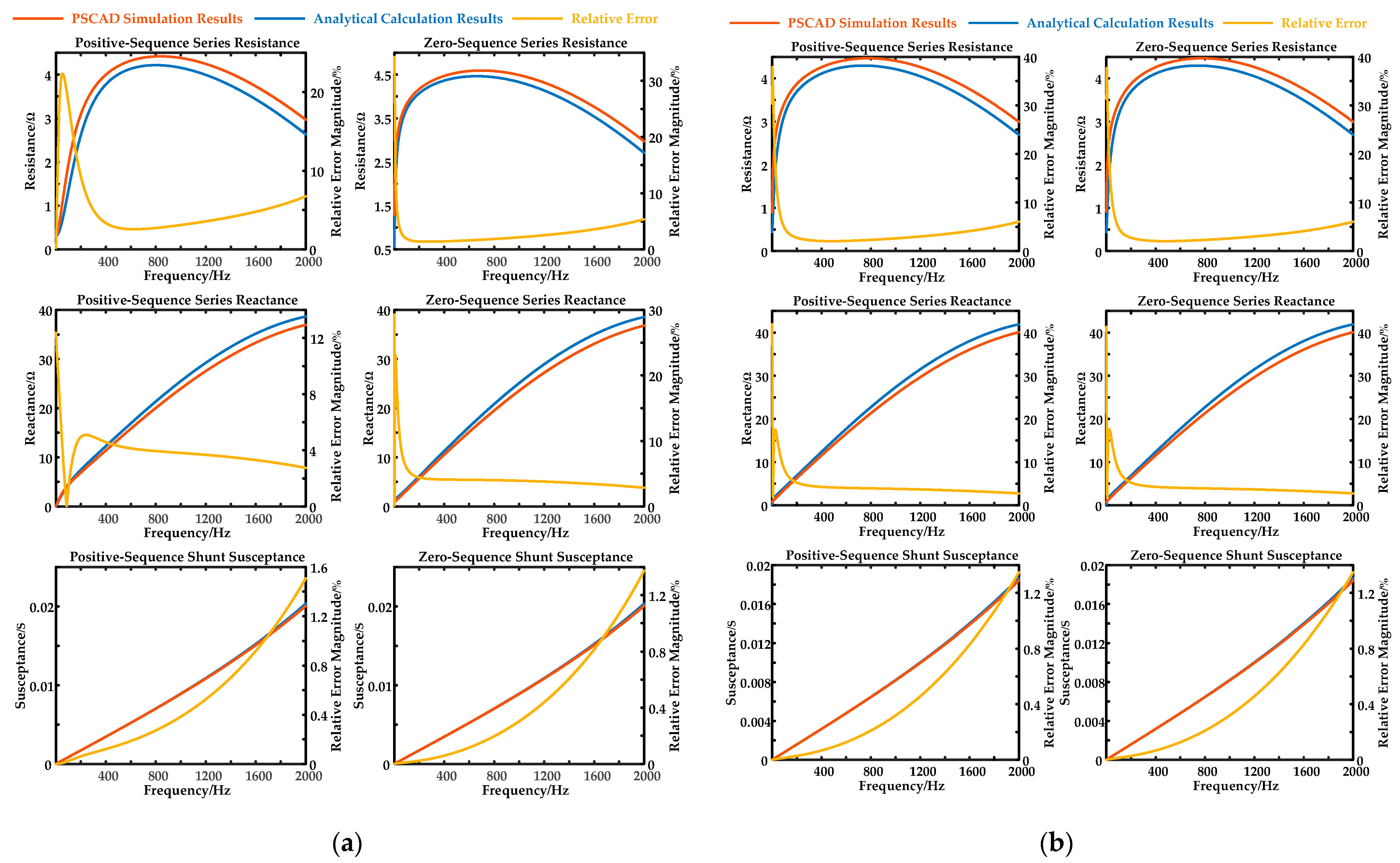
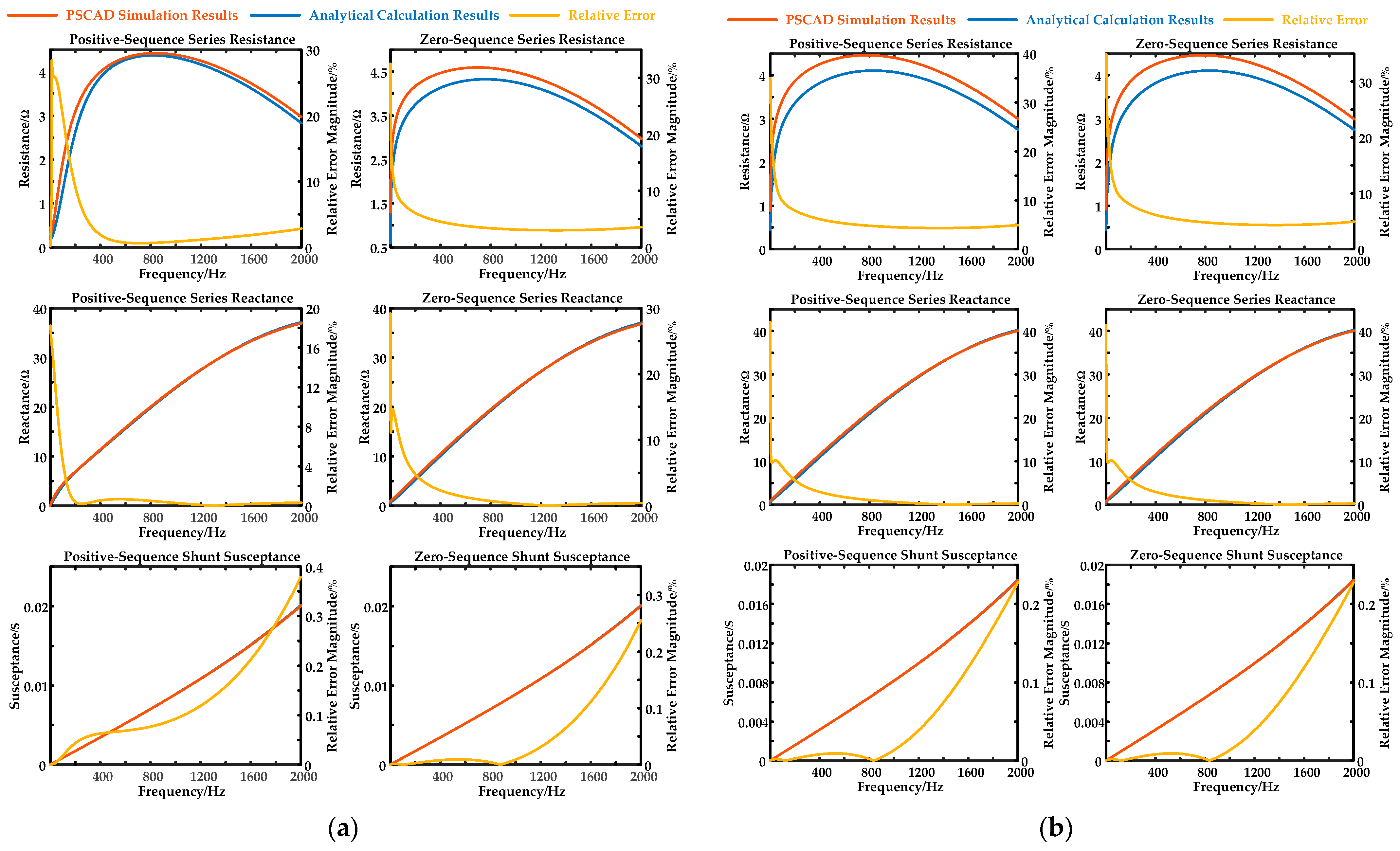
4.2. Simulation Verification
4.3. Analysis for Per-Unit-Length Parameters
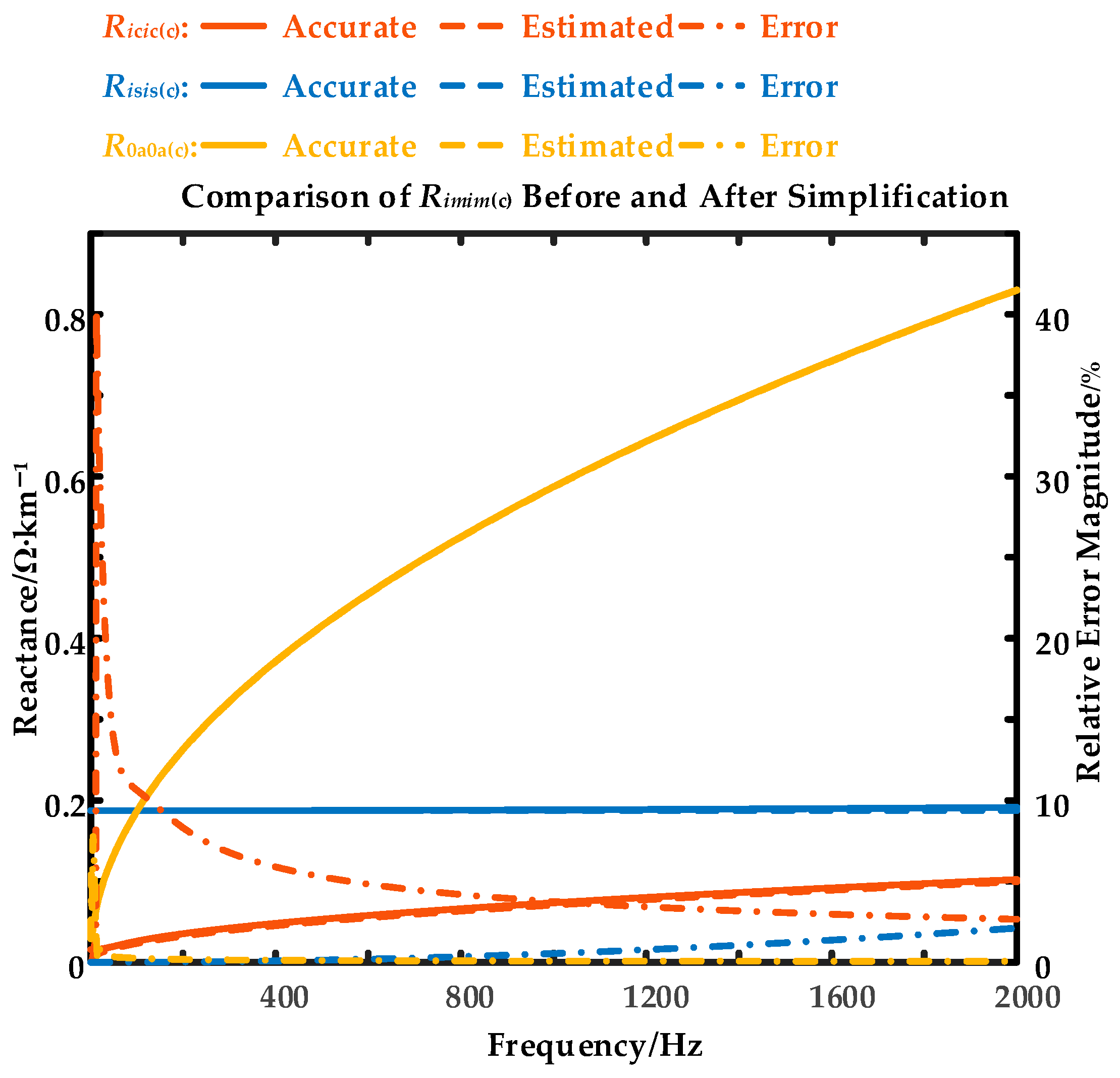
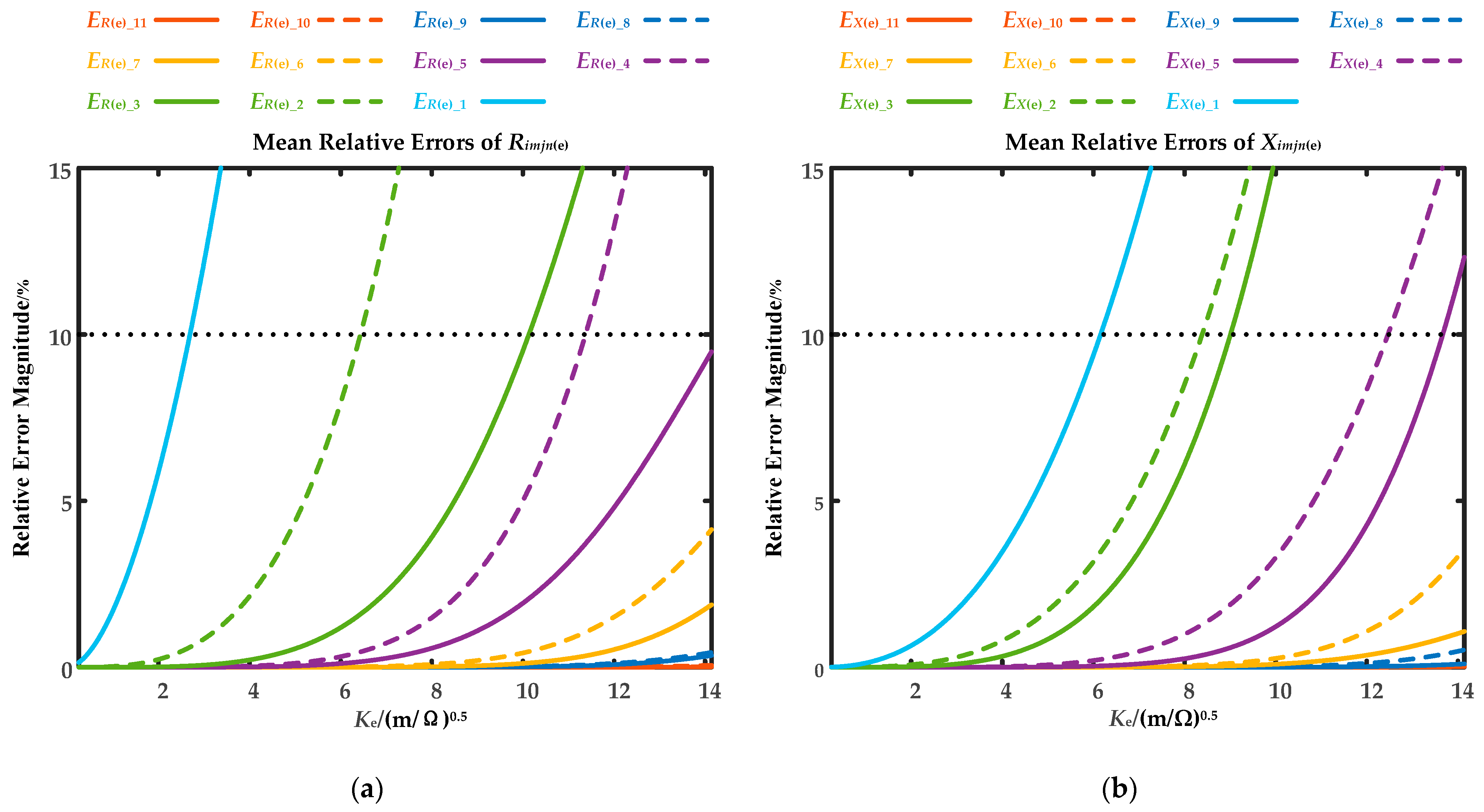
4.4. Exploration of Algorithm Simplification
5. Conclusions
- The concise analytical method for cable modeling involves geometric parameter preprocessing, construction of full electrical parameter matrices, and transformation to sequence electrical parameter matrices based on bonding and earthing arrangements. The case studies of three-core and single-core submarine cables are presented to demonstrate the effectiveness of the improved analytical method.
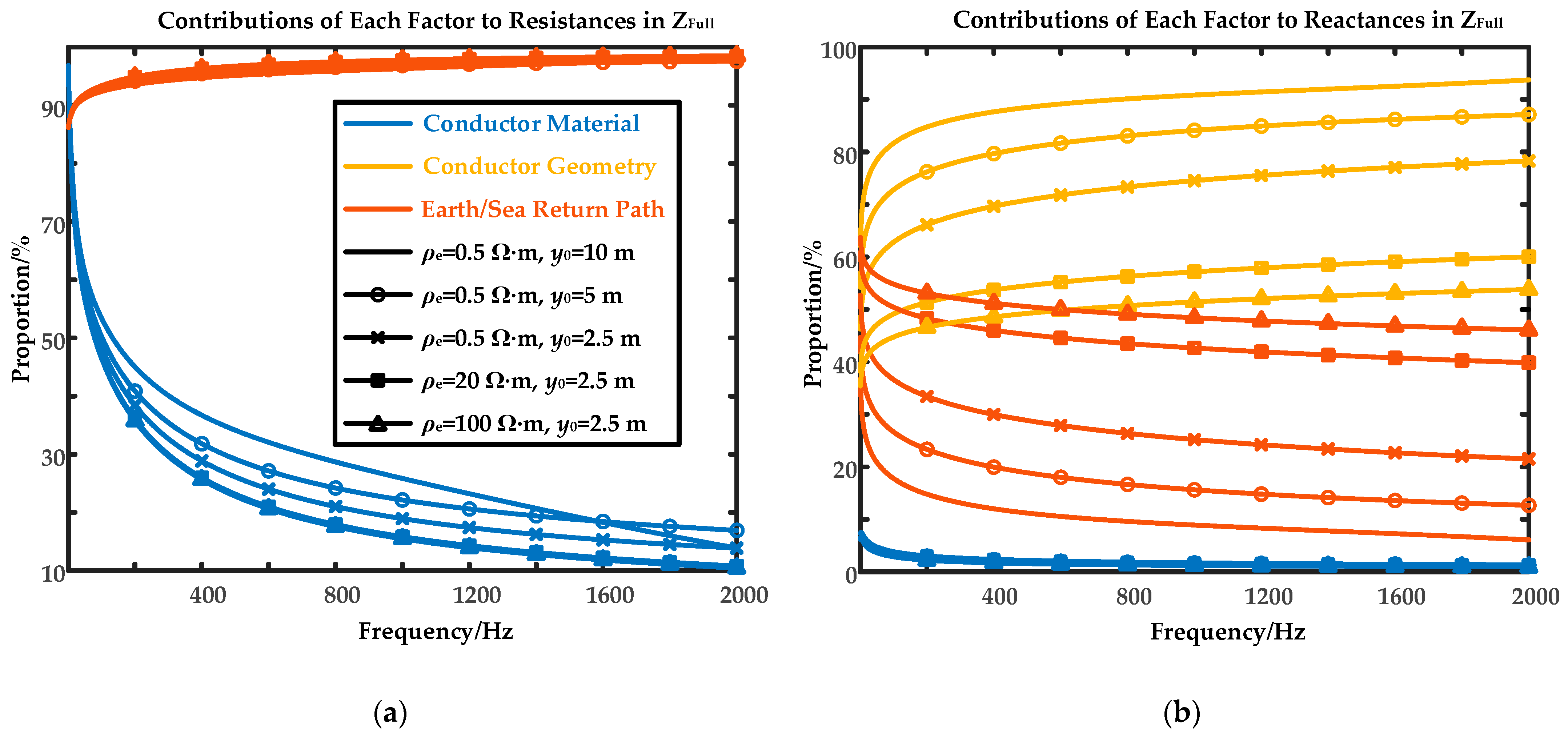
- Cable series impedance arises from conductor material, conductor geometry, and earth/sea return path. The earth/sea return path significantly affects series resistance, while the conductor material’s influence decreases with frequency. Furthermore, conductor geometry and the return path contribute largely to series reactance, which is strongly dependent on the cables’ environment, while conductor material has little effect on series reactance.
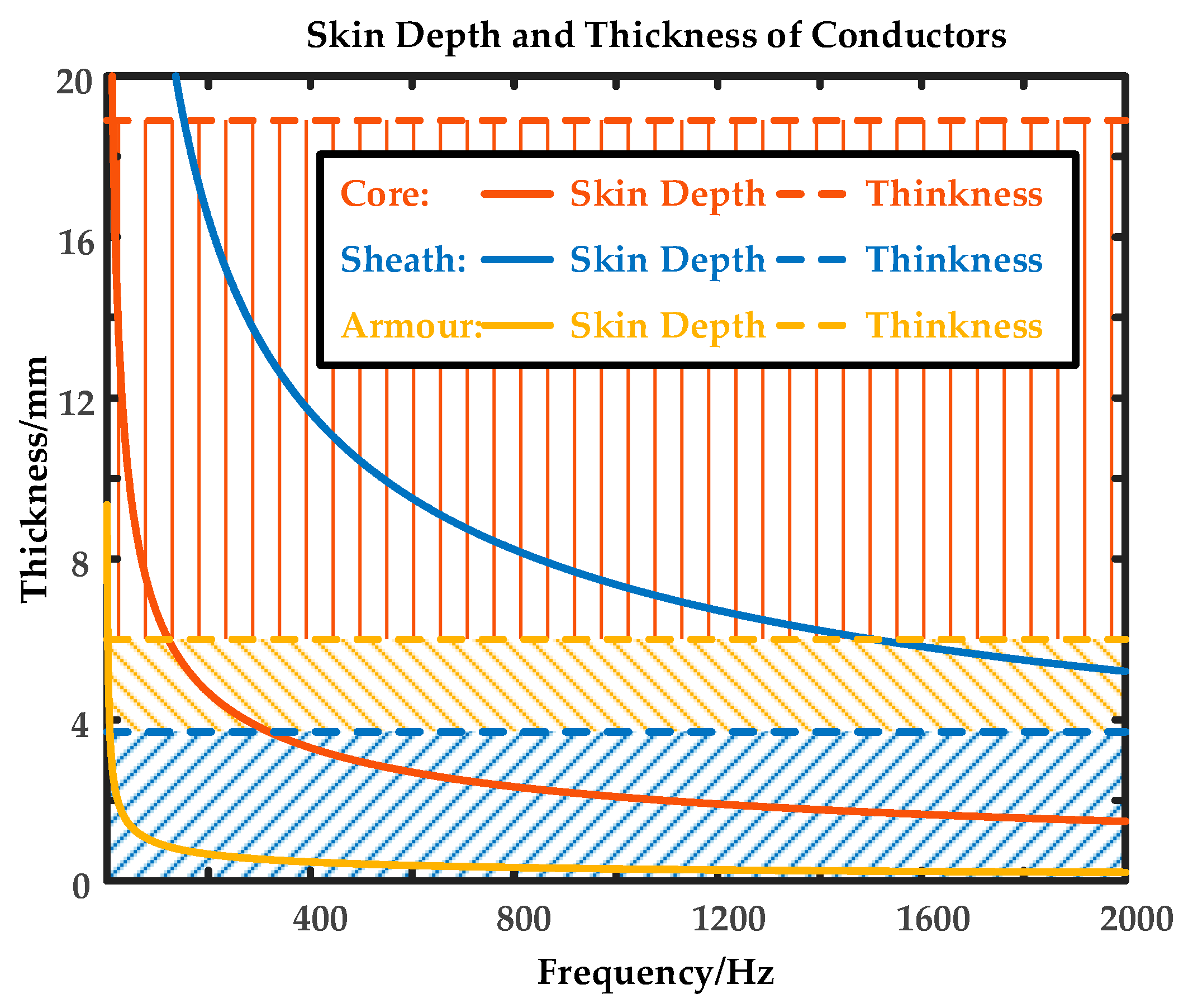
- Cable per-unit-length series impedance’ frequency variation corresponds to that of its component contributions. At low-to-mid frequencies, series resistance increases rapidly while series inductance decreases sharply, both due to the conductors’ skin effect. At high frequencies, the rate of increase in series resistance and decrease in series inductance slows down, with the contribution from the earth/sea return path to series resistance and from the conductor geometry to series inductance becoming dominant.
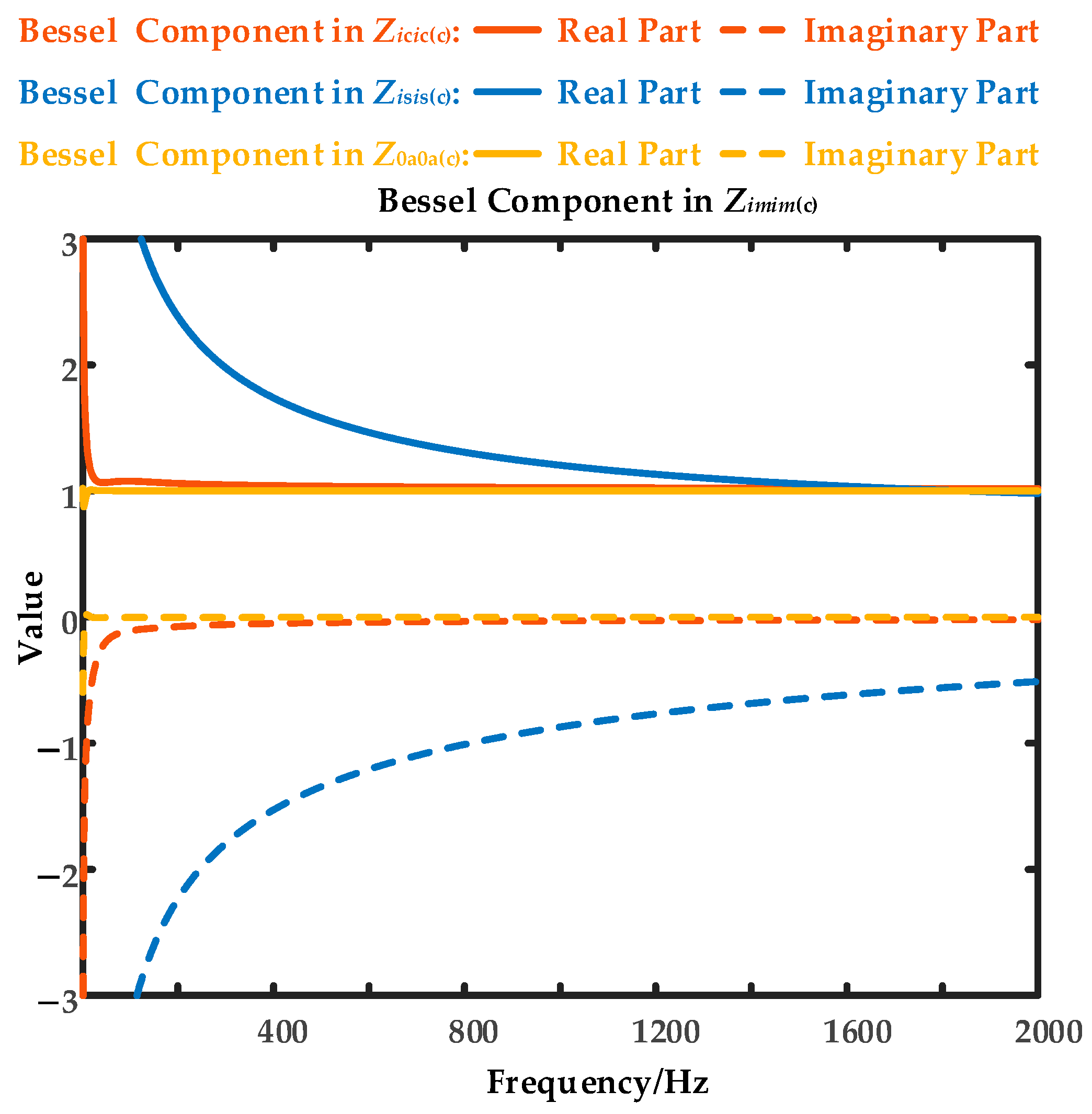
- By ignoring the reactance from the conductor material and considering only its resistance, roughly estimated through the skin depth definition, this simplified algorithm proves feasible while avoiding the Bessel functions. Furthermore, for three-core cables, the earth/sea return path position factor helps determine the simplest series, avoiding the infinite series in the earth/sea return path impedance.
- Single installation environment: The inhomogeneity of soil and seawater may lead to discrepancies between calculated and measured values. It is recommended to increase soil and seawater sampling points or use more accurate earth/sea return path impedance models. Additionally, variations in temperature and humidity can affect cable parameters (such as resistance and insulation performance), so it is advisable to make corrections for these factors in practical applications.
- Relatively “wide” frequency range: In power systems, resonance stability issues typically occur below 2 kHz, and harmonic analysis focuses on the 50–2500 Hz range. The proposed cable modeling provides good accuracy within these ranges, and the algorithm can be integrated into resonance stability analysis software for constructing the system’s node admittance matrix. However, for higher frequencies, such as those above 10 kHz, more precise modeling may be needed.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FSIM | Full Series Impedance Matrix |
| FSAM | Full Shunt Admittance Matrix |
| PSIM | Phase Series Impedance Matrix |
| PSAM | Phase Shunt Admittance Matrix |
| SSIM | Sequence series impedance matrix |
| SSAM | Sequence shunt admittance matrix |
| PST | Phase-sequence transformation |
Appendix A
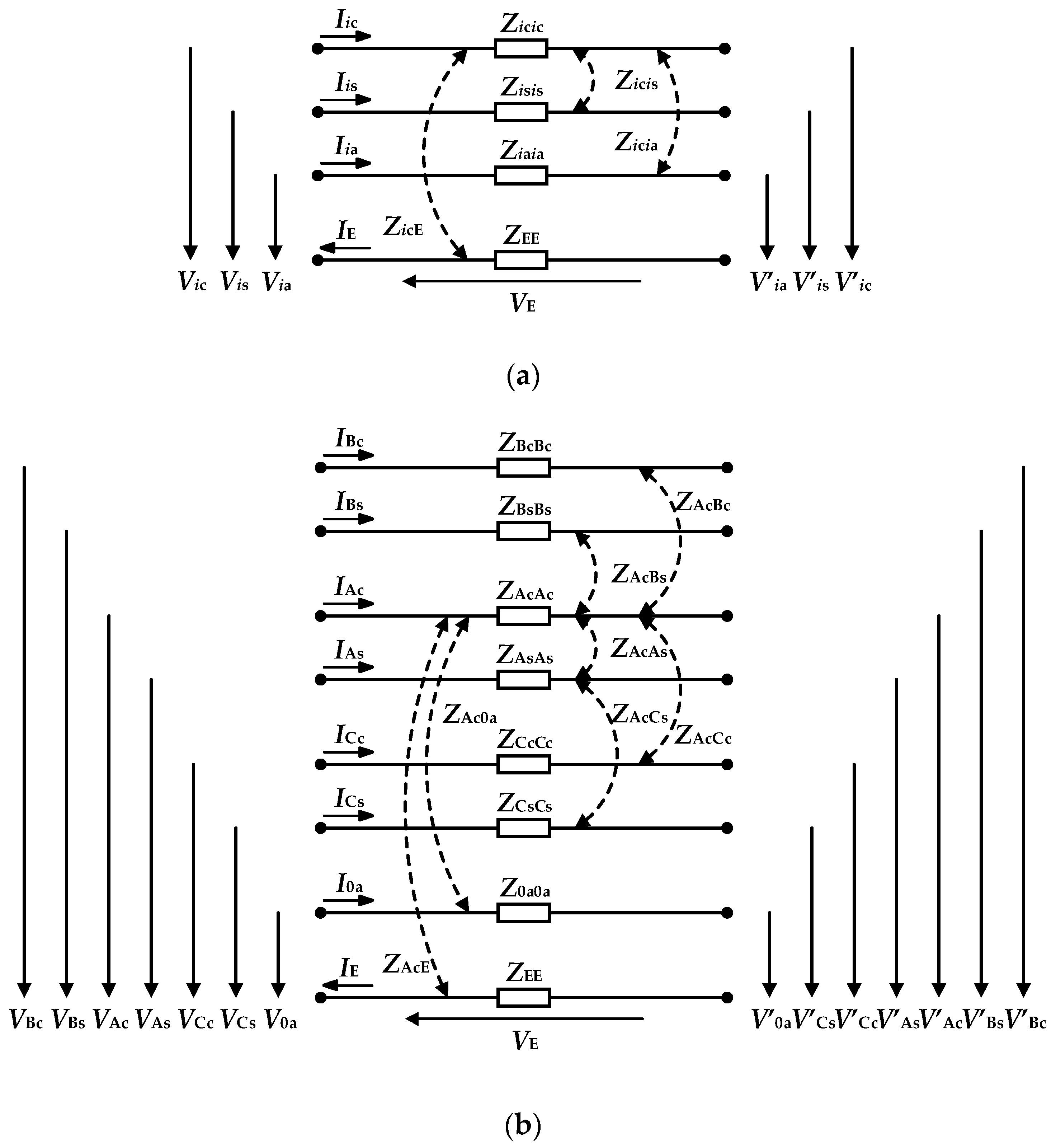
Appendix B
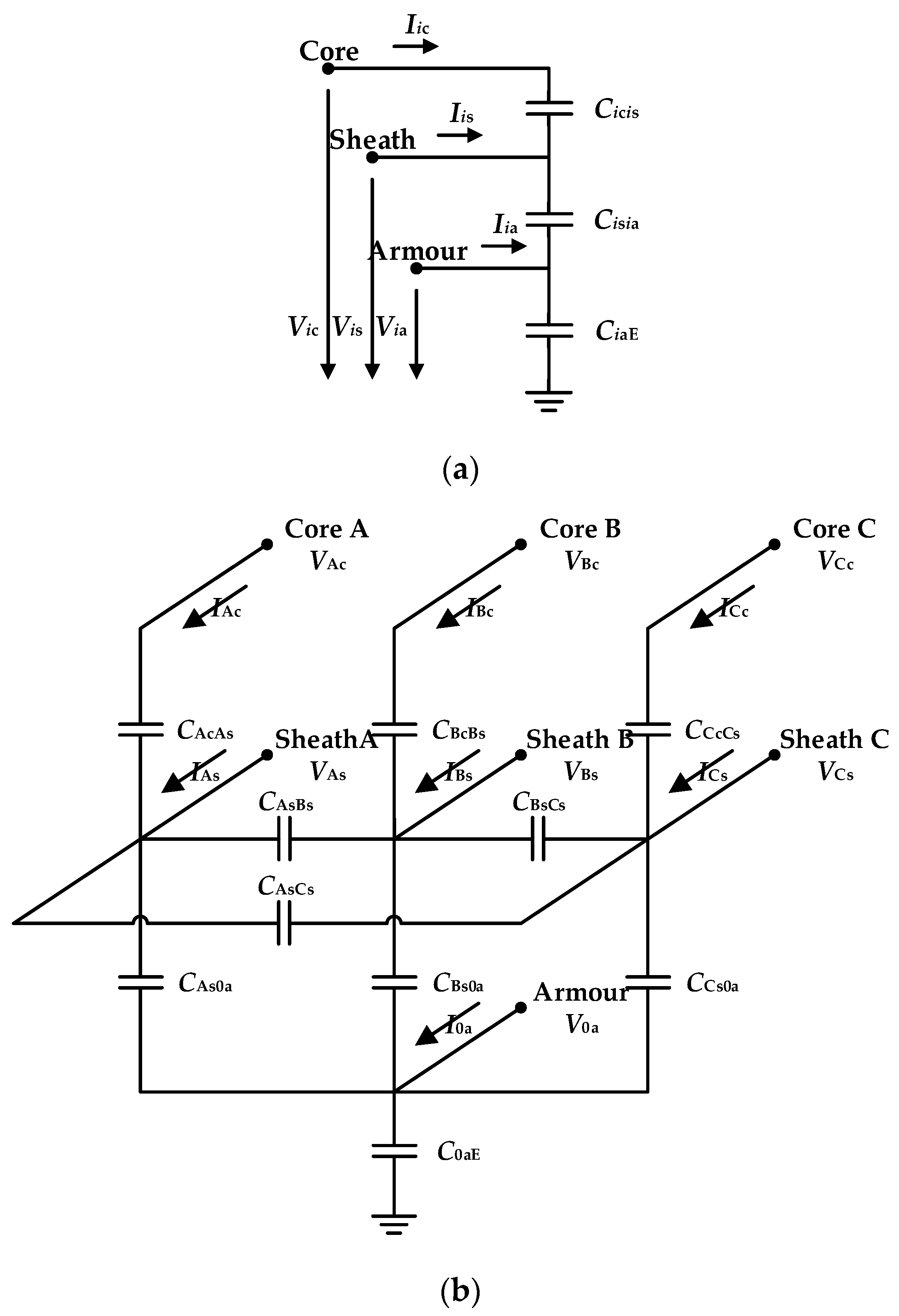
Appendix C
| Installation Environment | Ke/(m/Ω)0.5 | Number of Terms in the Simplest Rimjn(e) | Number of Terms in the Simplest Ximjn(e) |
|---|---|---|---|
| ρe = 0.5 Ω·m, y0 = 10 m | 14.14 | 5 | 6 |
| ρe = 0.5 Ω·m, y0 = 5 m | 7.07 | 3 | 2 |
| ρe = 0.5 Ω·m, y0 = 2.5 m | 3.54 | 2 | 1 |
| ρe = 20 Ω·m, y0 = 2.5 m | 0.56 | 1 | 1 |
| ρe = 100 Ω·m, y0 = 2.5 m | 0.25 | 1 | 1 |

References
- Benato, R.; Paolucci, A. EHV AC Undergrounding Electrical Power: Performance and Planning; Springer: New York, NY, USA, 2010; pp. 1–28. [Google Scholar]
- Apostolaki-Iosifidou, E.; Mccormack, R.; Kempton, W.; Mccoy, P.; Ozkan, D. Transmission design and analysis for large-scale offshore wind energy development. IEEE Power Energy Technol. Syst. J. 2019, 6, 22–31. [Google Scholar] [CrossRef]
- Taormina, B.; Bald, J.; Want, A.; Thouzeau, G.; Lejart, M.; Desroy, N.; Carlier, A. A review of potential impacts of submarine power cables on the marine environment: Knowledge gaps, recommendations and future directions. Renew. Sustain. Energy Rev. 2018, 96, 380–391. [Google Scholar] [CrossRef]
- Bollen, M.; Yang, K. Harmonic aspects of wind power integration. J. Mod. Power Syst. Clean Energy 2013, 1, 14–21. [Google Scholar] [CrossRef]
- Fillion, Y.; Deschanvres, S. Background harmonic amplifications within offshore wind farm connection projects. In Proceedings of the International Conference on Power Systems Transients (IPST 2015), Cavtat, Croatia, 15–18 June 2023; pp. 1–8. [Google Scholar]
- Zhan, Y.; Xie, X.; Liu, H.; Liu, H.; Li, Y. Frequency-domain modal analysis of the oscillatory stability of power systems with high-penetration renewables. IEEE Trans. Sustain. Energy 2019, 10, 1534–1543. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, S.; Xing, F.; Xiao, H. Study on the method for analyzing electric network resonance stability. Energies 2018, 11, 646. [Google Scholar] [CrossRef]
- Chen, Z.; Luo, A.; Kuang, H.; Zhou, L.; Chen, Y.; Huang, Y. Harmonic resonance characteristics of large-scale distributed powerplant in wideband frequency domain. Electr. Power Syst. Res. 2016, 10, 53–65. [Google Scholar]
- Zhang, S.; Jiang, S.; Lu, X.; Ge, B.; Peng, F.Z. Resonance issues and damping techniques for grid-connected inverters with long transmission cable. IEEE Trans. Power Electron. 2014, 29, 110–120. [Google Scholar] [CrossRef]
- Liu, Z.; Li, D.; Wang, W.; Wang, J.; Gong, D. A review of the research on the wide-band oscillation analysis and suppression of renewable energy grid-connected systems. Energies 2024, 17, 1809. [Google Scholar] [CrossRef]
- Carson, J.R. Wave propagation in overhead wires with ground return. Bell Syst. Tech. J. 1926, 5, 539–554. [Google Scholar] [CrossRef]
- Pollaczek, F. On the field produced by an infinity long wire carrying alternating current. Elektr. Nachrichtentechnik 1926, 3, 339–359. [Google Scholar]
- Shelkunoff, S.A. The electromagnetic theory of coaxial transmission lines and cylindrical shields. Bell Syst. Tech. J. 1934, 13, 532–579. [Google Scholar] [CrossRef]
- Wedepohl, L.M.; Wilcox, D.J. Transient analysis of underground power-transmission systems—System model and wave propagation characteristics. Proc. Inst. Electr. Eng. 1973, 120, 253–260. [Google Scholar] [CrossRef]
- Ametani, A. A general formulation of impedance and admittance of cables. IEEE Trans. Power Appar. Syst. 1980, 99, 902–910. [Google Scholar] [CrossRef]
- Tleis, N.D. Power Systems Modelling and Fault Analysis: Theory and Practice; Newnes: Oxford, UK, 2008; pp. 74–199. [Google Scholar]
- Ruiz, C.; Abad, G.; Zubiaga, M.; Madariaga, D.; Arza, J. Frequency-dependent pi model of a three-core submarine cable for time and frequency domain analysis. Energies 2018, 11, 2778. [Google Scholar] [CrossRef]
- Yin, Y.; Dommel, H.W. Calculation of frequency-dependent impedances of underground power cables with finite element method. IEEE Trans. Magn. 1989, 25, 3025–3027. [Google Scholar] [CrossRef]
- Cristina, S.; Feliziani, M. A finite element technique for multiconductor cable parameters calculation. IEEE Trans. Magn. 1989, 25, 2986–2988. [Google Scholar] [CrossRef]
- Darcherif, A.; Raizer, A.; Meunier, G.; Imfoff, J.; Sabonnadiere, J. New techniques in FEM field calculation applied to power cable characteristics computation. IEEE Trans. Magn. 1990, 26, 2388–2390. [Google Scholar] [CrossRef]
- Habib, S.; Kordi, B. Calculation of multiconductor underground cables high-frequency per-unit-length parameters using electromagnetic modal analysis. IEEE Trans. Power Deliv. 2013, 28, 276–284. [Google Scholar] [CrossRef]
- Arizon, P.D.; Dommel, H.W. Computation of cable impedances based on subdivision of conductors. IEEE Trans. Power Deliv. 1987, 2, 21–27. [Google Scholar] [CrossRef]
- Feng, J.; Cheng, W. Calculation of cable electrical parameters considering proximity effect. In Proceedings of the 8th Asia Conference on Power and Electrical Engineering (ACPEE 2023), Tianjin, China, 14–16 April 2023; pp. 2174–2179. [Google Scholar]
- Wakileh, G.J. Power Systems Harmonics/Fundamentals, Analysis and Filter Design; Springer: New York, USA, 2001; pp. 221–274. [Google Scholar]
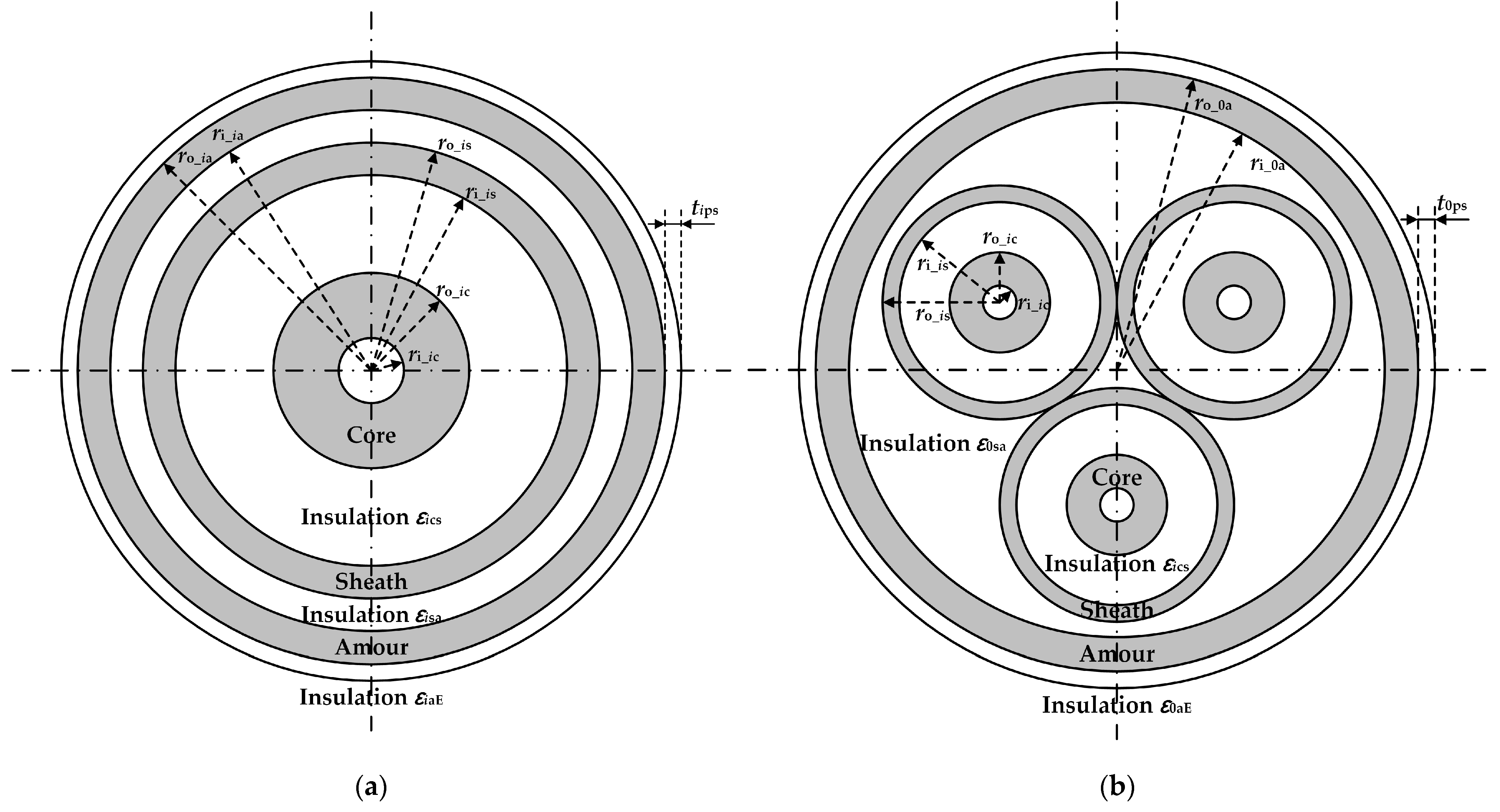





| Parameters of Conductors | |||
| Structure | Inner Radius/mm | Outer radius/mm | DC Resistivity/Ω·m |
| Core | 0.00 | 18.90 | 1.7241 × 10−8 |
| Sheath | 47.30 | 51.00 | 2.14 × 10−7 |
| Armor | 120.65 | 126.65 | 1.38 × 10−7 |
| Parameters of Insulations | |||
| Structure | Thickness/mm | Relative permittivity | Relative permeability |
| Core Insulation | 28.40 | 2.25 | 1 |
| Sheath Insulation | / | 2.25 | 1 |
| Armor Insulation | 4.00 | 2.25 | 1 |
| Positional Parameters | |||
| Average Burial Depth/m | 10.00 | ||
| Other Parameters | |||
| Cable Length/km | 20.00 | ||
| Sea DC Resistivity/Ω·m | 0.50 | ||
| Parameters of Conductors | |||
| Structure | Inner Radius/mm | Outer radius/mm | DC Resistivity/Ω·m |
| Core | 0.00 | 17.10 | 1.7241 × 10−8 |
| Sheath | 46.40 | 50.30 | 2.14 × 10−7 |
| Armor | 62.20 | 68.20 | 1.38 × 10−7 |
| Parameters of Insulations | |||
| Structure | Thickness/mm | Relative permittivity | Relative permeability |
| Core Insulation | 29.30 | 2.25 | 1 |
| Sheath Insulation | 11.90 | 2.25 | 1 |
| Armor Insulation | 4.00 | 2.25 | 1 |
| Positional Parameters | |||
| Average Burial Depth/m | 10.00 | ||
| Layout | Symmetrical Flat Layout | ||
| Adjacent Cable Axis Distance/m | 200 | ||
| Other Parameters | |||
| Cable Length/km | 20.00 | ||
| Sea DC Resistivity/Ω·m | 0.50 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, B.; Zhang, Z.; Ye, Q.; Xu, Z.; Huang, X.; Yang, L. Calculations of Electrical Parameters of Cables in Wide Frequency Range. Electronics 2025, 14, 1570. https://doi.org/10.3390/electronics14081570
He B, Zhang Z, Ye Q, Xu Z, Huang X, Yang L. Calculations of Electrical Parameters of Cables in Wide Frequency Range. Electronics. 2025; 14(8):1570. https://doi.org/10.3390/electronics14081570
Chicago/Turabian StyleHe, Bingxin, Zheren Zhang, Qixin Ye, Zheng Xu, Xiaoming Huang, and Liu Yang. 2025. "Calculations of Electrical Parameters of Cables in Wide Frequency Range" Electronics 14, no. 8: 1570. https://doi.org/10.3390/electronics14081570
APA StyleHe, B., Zhang, Z., Ye, Q., Xu, Z., Huang, X., & Yang, L. (2025). Calculations of Electrical Parameters of Cables in Wide Frequency Range. Electronics, 14(8), 1570. https://doi.org/10.3390/electronics14081570








