Assessment and Influencing Factor Analysis of Multi-Type Load Acceptance Capacity of Active Distribution Network
Abstract
1. Introduction
- (1)
- The development of a time-series load flow calculation model integrated with a probabilistic electric vehicle demand model employing the Monte Carlo method, which facilitates initial load generation and acceptance capacity computation in distribution networks.
- (2)
- The establishment of a load growth prediction framework combined with an improved repetitive power flow method specifically designed for multi-modal load acceptance capacity assessment, effectively addressing computational requirements for diverse load types.
- (3)
- A systematic investigation of DG-induced impacts on multi-modal load integration capabilities, including a quantitative analysis of load–network compatibility characteristics under predefined distribution network constraints, which provides operational guidance for supply expansion scheme optimization.
2. Active Distribution Network-Distributed Generation Model
2.1. Distributed Generation Models
2.1.1. Wind Turbine Generation Power Flow Model
2.1.2. Photovoltaic Power Flow Model
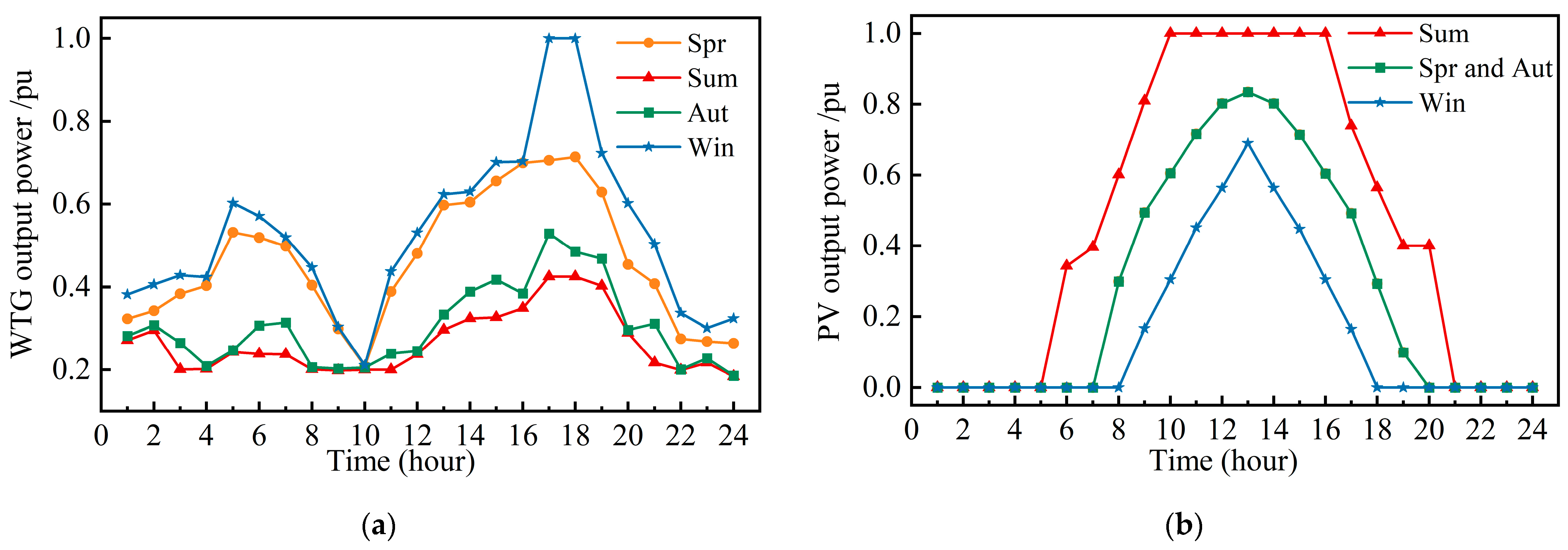
2.2. Distributed Generation Temporal Model
3. Distribution Network Load Model
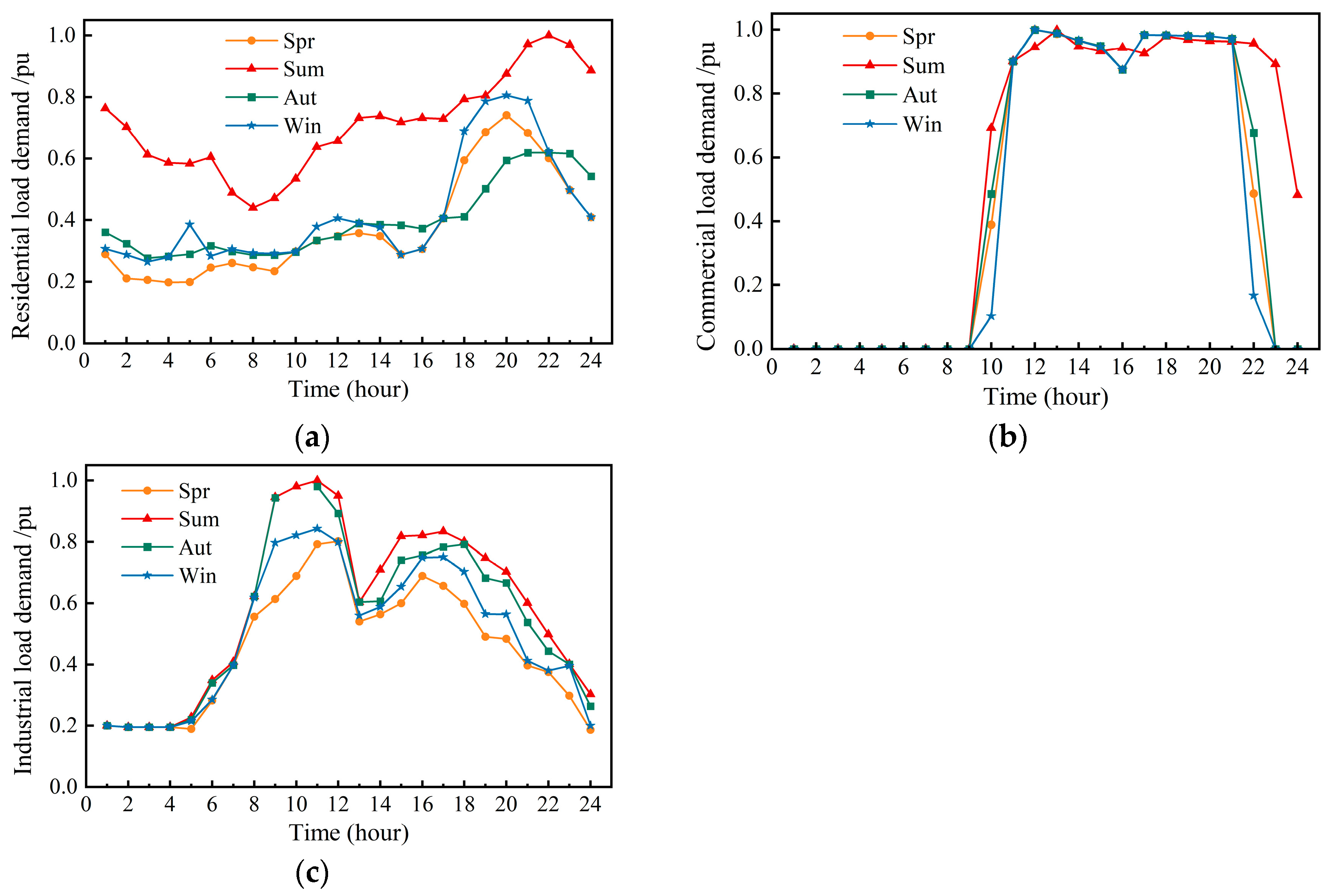
3.1. Load Temporal Characteristics
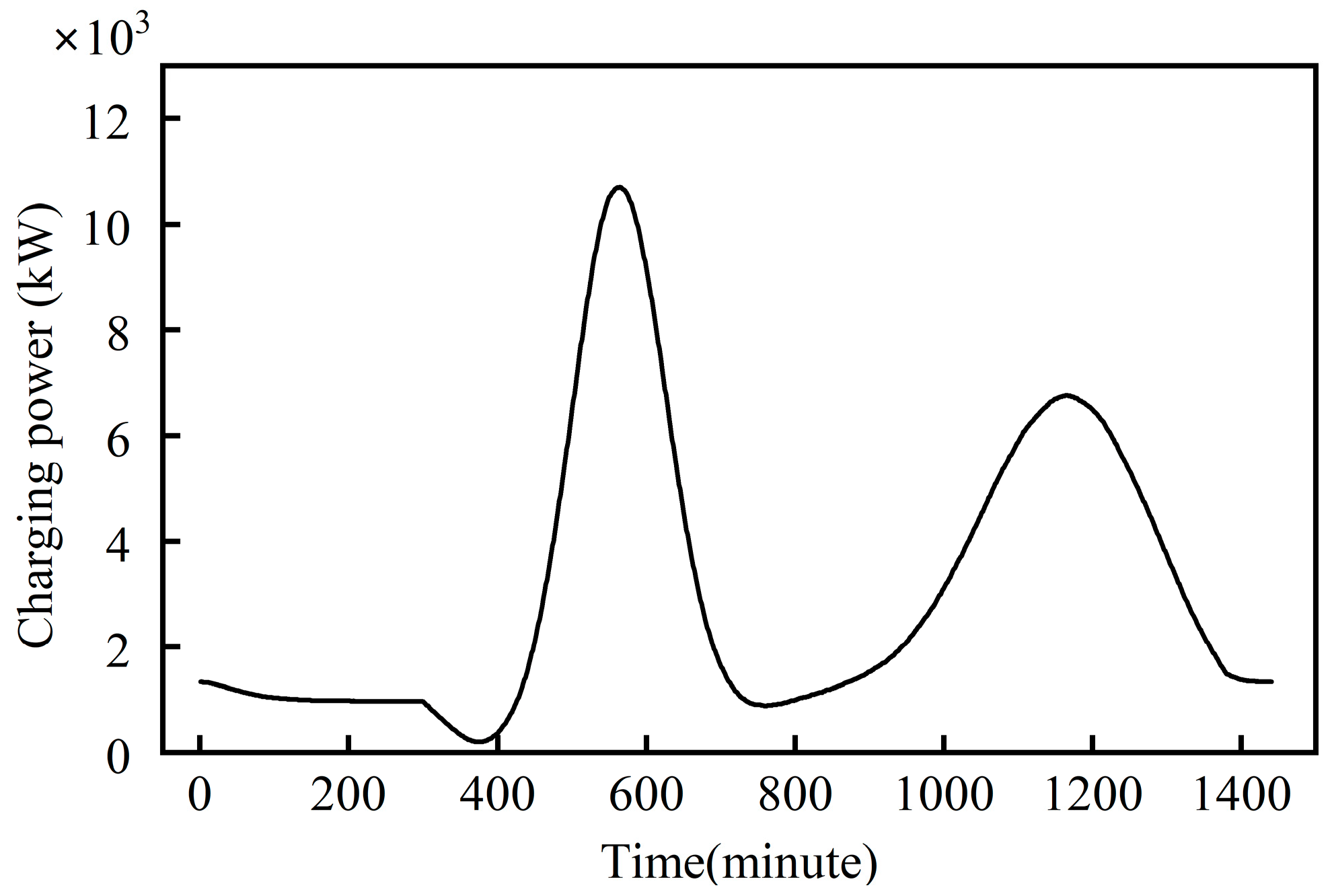
3.2. Electric Vehicle Charging Demand Model
- (1)
- EV charging behavior: single daily charge.
- (2)
- Each charging session achieves full battery replenishment.
- (3)
- Standard battery capacity is configured at 24 kwh.
4. Active Distribution Network Multi-Form Load Acceptance Capacity Assessment Method
4.1. Acceptance Capacity Assessment Model
4.2. Load Growth Pattern
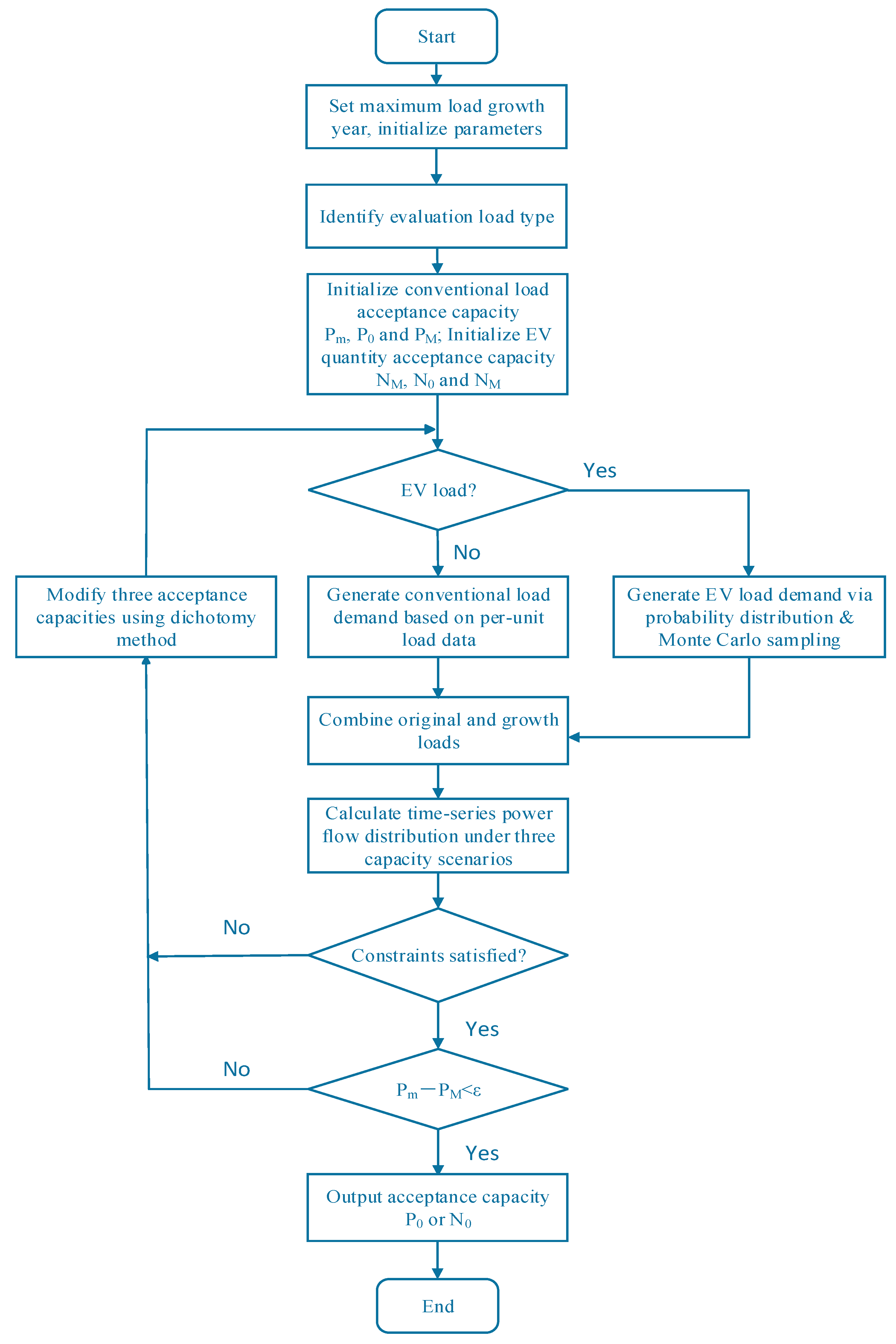
4.3. Multi-Form Load Acceptance Capacity Evaluation Process Based on Improved Repetitive Power Flow Method
5. Case Study
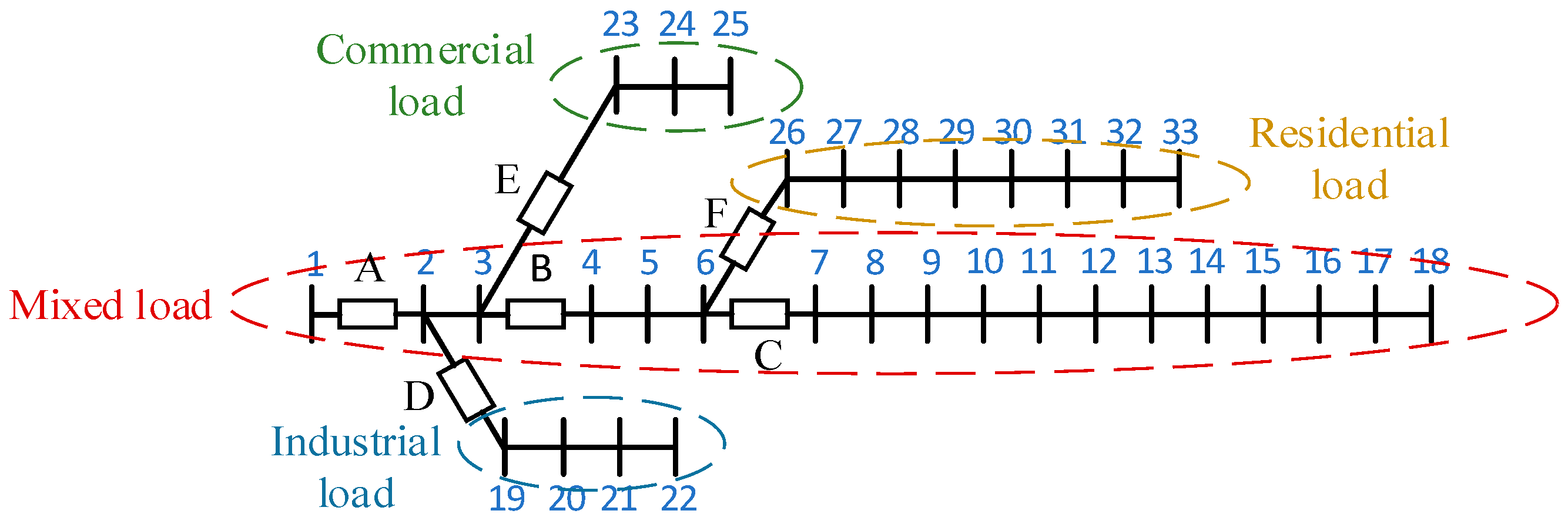
5.1. Case Study Introduction
5.2. Evaluation of Multi-Form Load Acceptance Capacity in Distribution Networks Without DG Integration
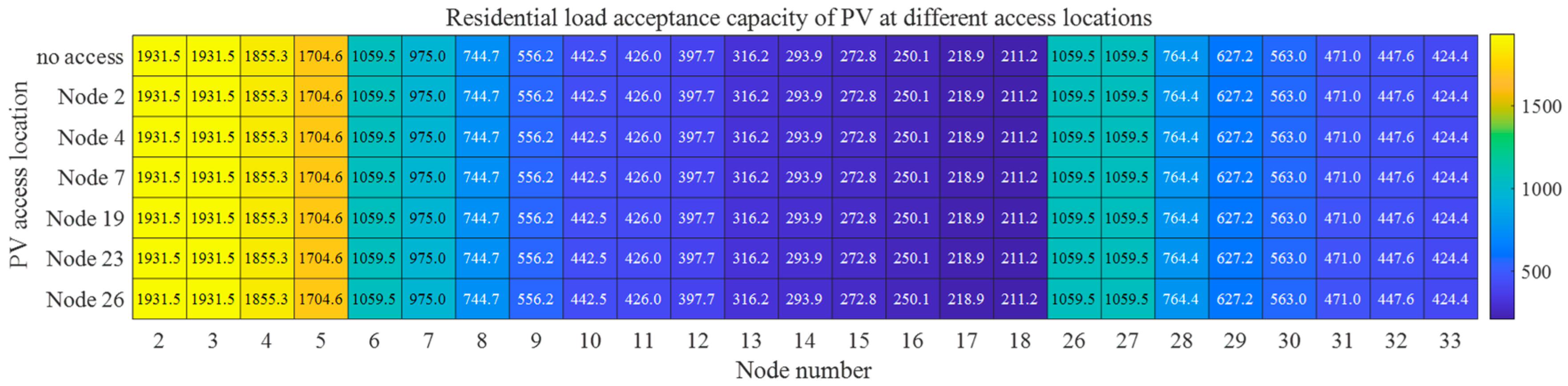
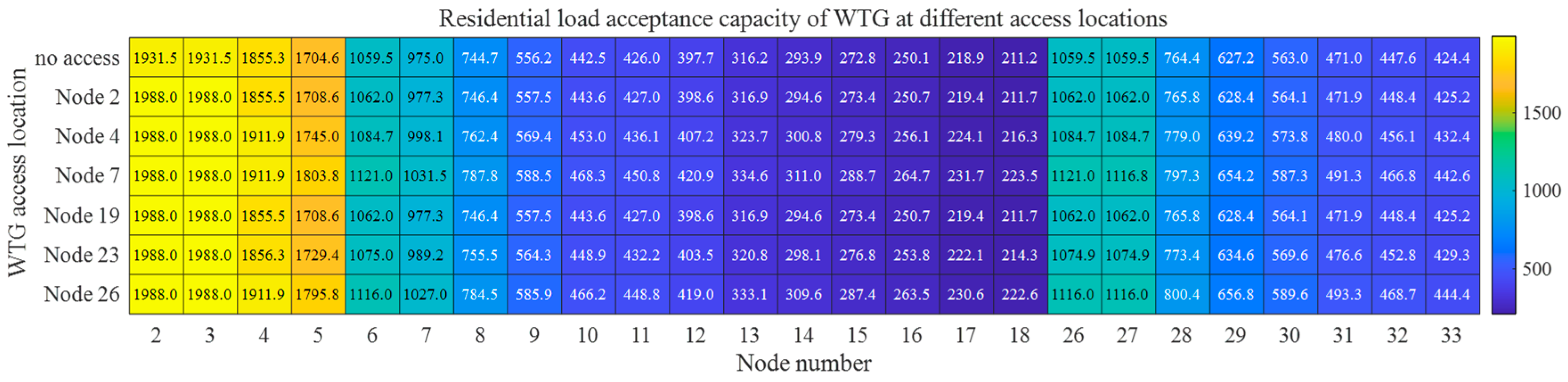
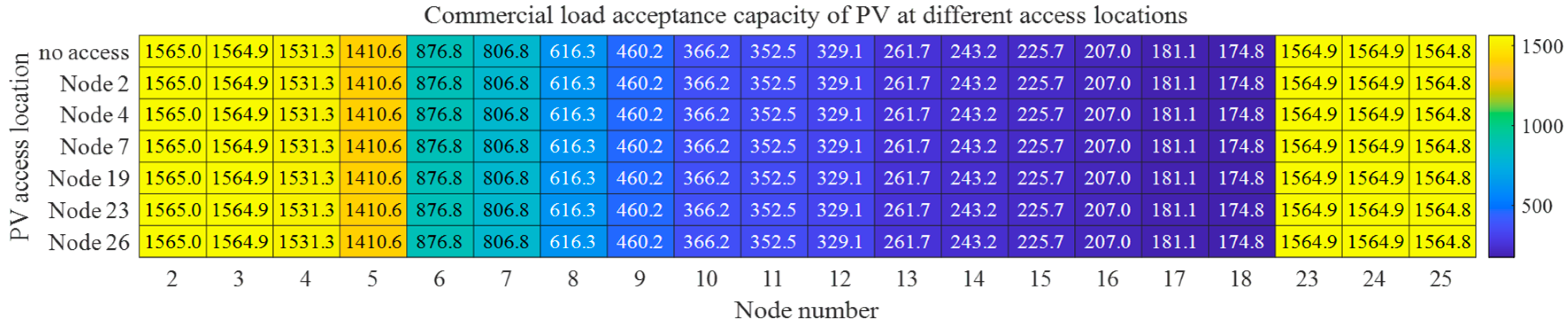
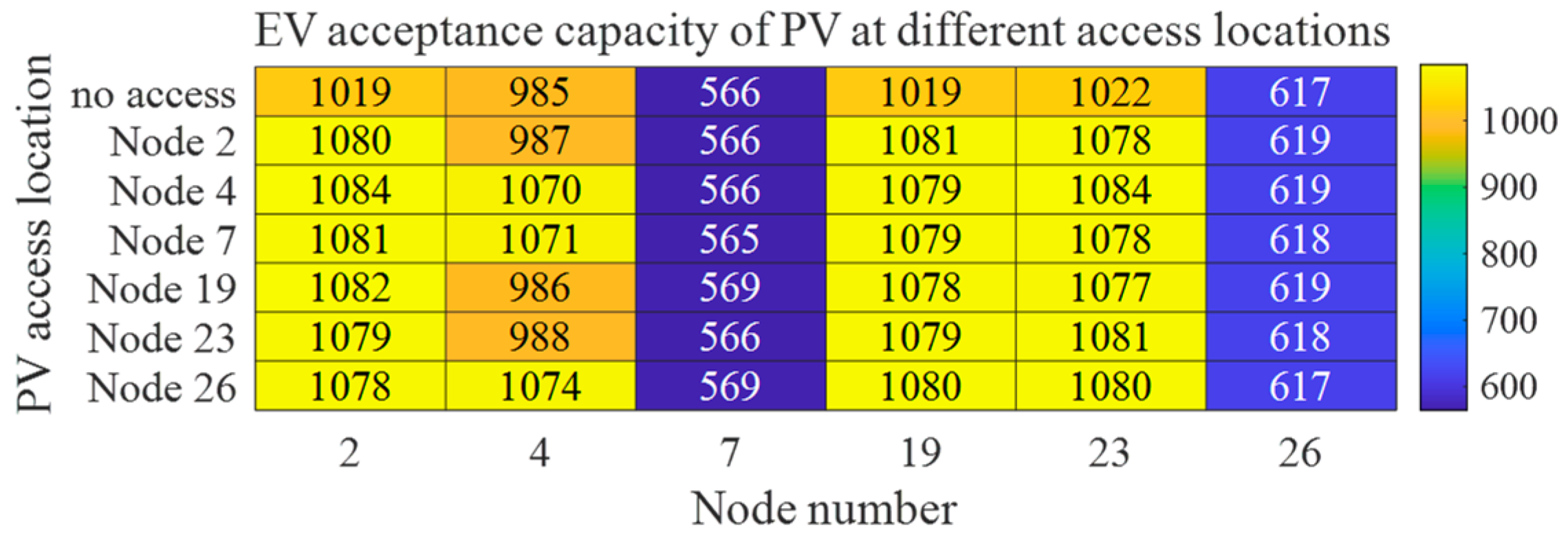
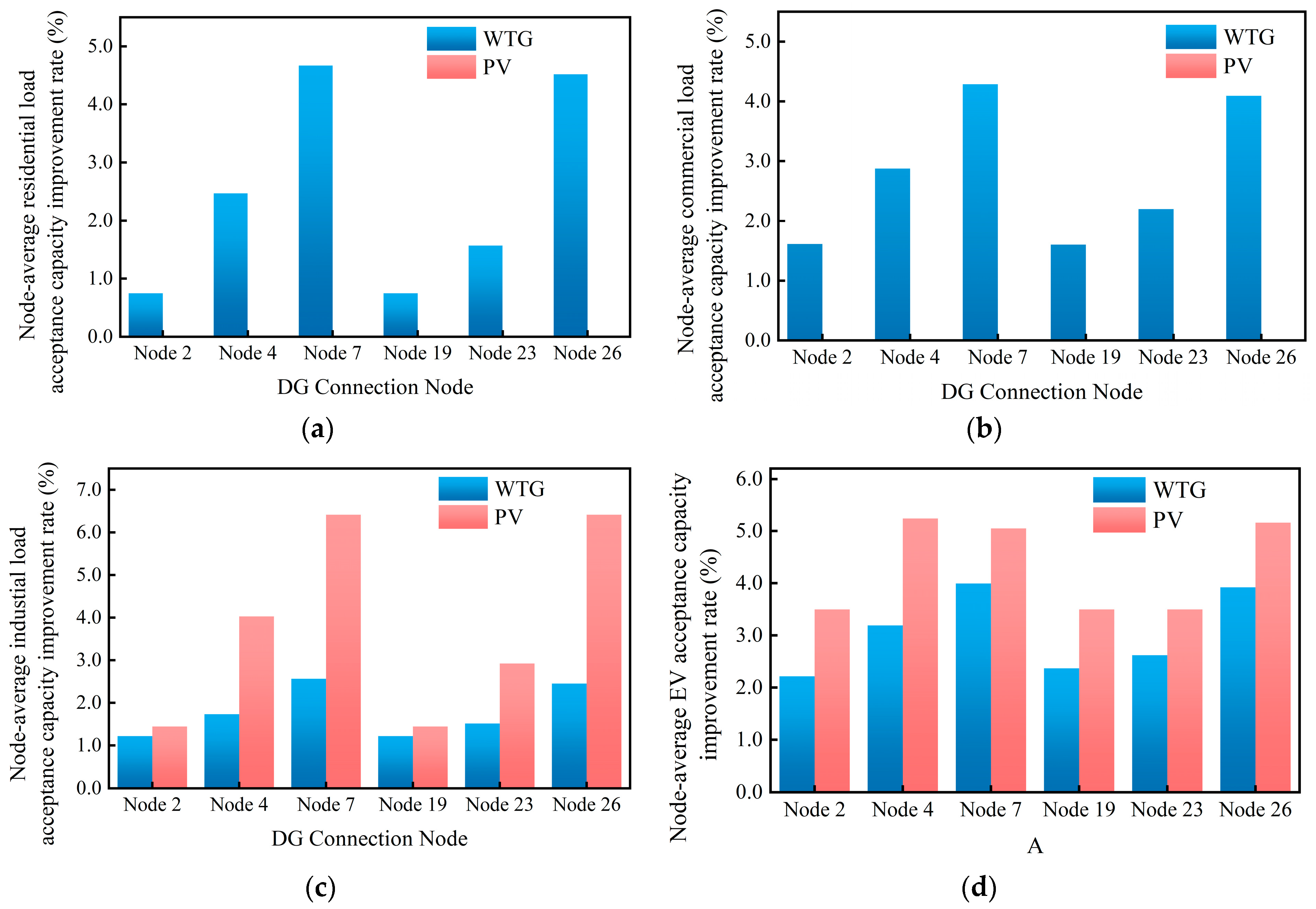
5.3. Impact of WTG and PV Integration Locations on Acceptance Capacity of Active Distribution Network
5.4. Impact of WTG-PV Ratio Variations on Acceptance Capacity
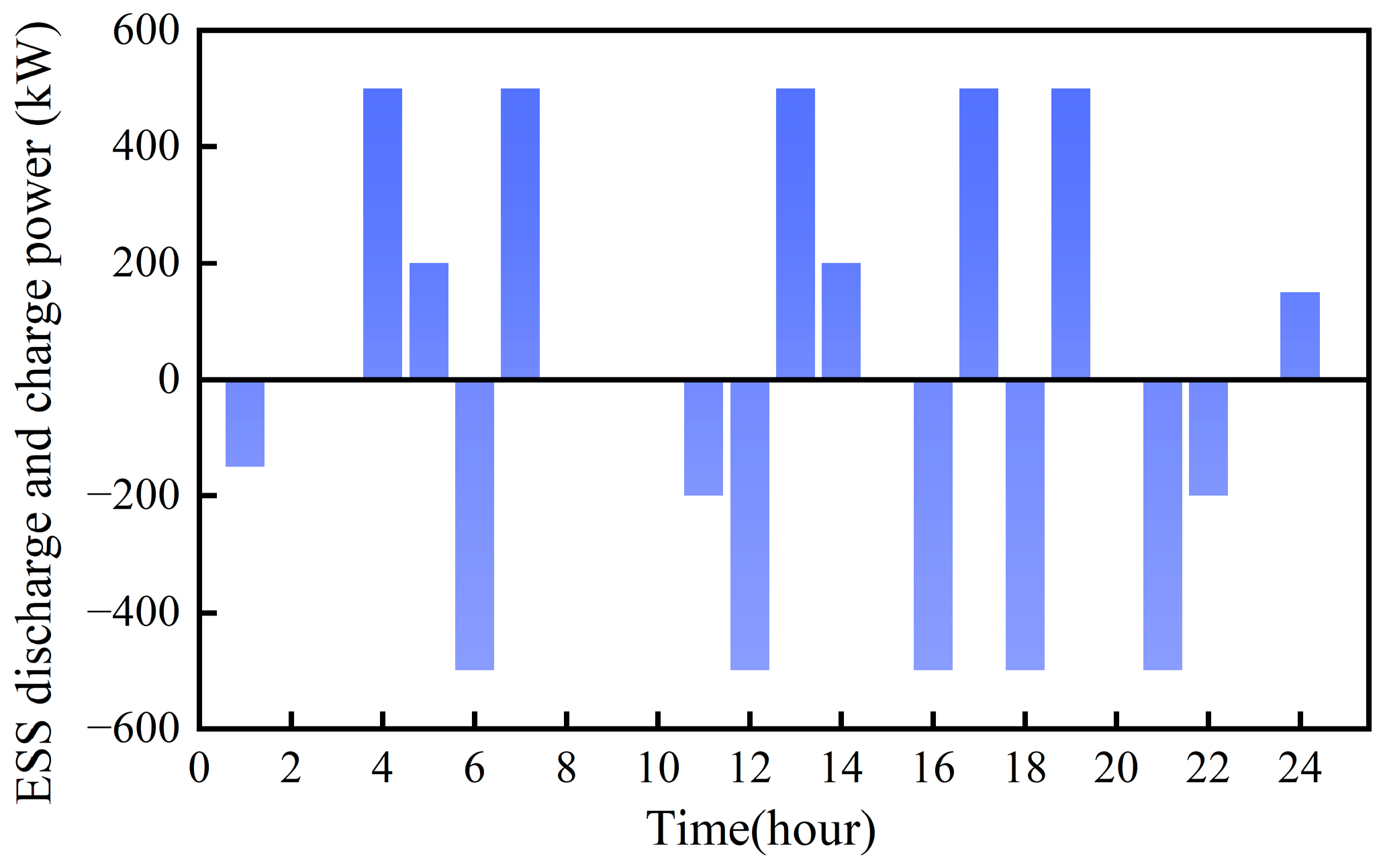
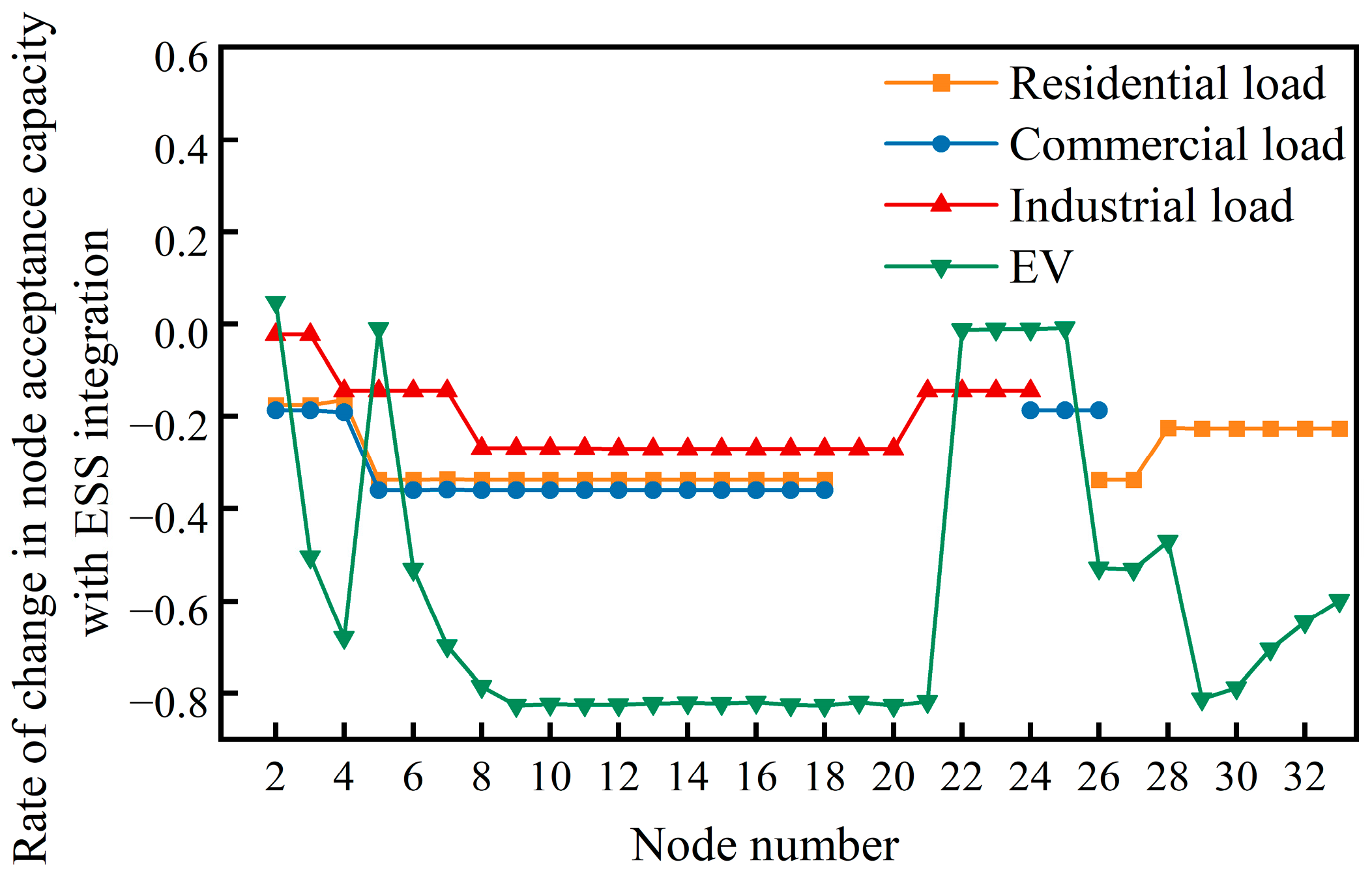
5.5. Impact of ESS Access on Acceptance Capacity of Active Distribution Network
6. Conclusions
- (1)
- The adoption of growth patterns reflecting actual load variations enables more targeted identification of practical acceptance bottlenecks, yielding assessment results with enhanced practical applicability and guidance value for subsequent load expansion planning.
- (2)
- The improved repetitive power flow evaluation methodology integrates load growth demands, multi-type load integration, and a bisection algorithm for rapid computation. Compared with conventional methods, this approach demonstrates superior capability in maximizing distribution network acceptance capacity, with its effectiveness validated through comprehensive case studies.
- (3)
- The case study demonstrates the following: ① The analysis of influencing factors under DG integration reveals that five-year original load growth induces annual acceptance capacity degradation rates of 3–5%, while mid-network DG integration (central nodes) achieves up to 5% higher acceptance capacity differentials compared to peripheral nodes. ② Spatial heterogeneity exists in optimal DG allocation, where WTG at central nodes enhances the residential/commercial load acceptance capacity by 4.27–4.29%, while PV deployment at terminal nodes maximizes the industrial load acceptance capacity improvement up to 14.7%. PV integration at node 4 achieves 5.24% maximum EV load enhancement. ③ Optimal WTG-PV ratio configurations yield differentiated benefits: a 4:1 WTG-PV ratio improves the residential/commercial load acceptance capacity by 2.18%, whereas a 1:4 ratio enhances the industrial load capacity by 6.42%. For EVs, regions closer to DG access nodes demonstrate enhanced acceptance capacity with higher WTG-PV ratios, while conversely, regions farther from DG access nodes exhibit improved performance under lower WTG-PV ratio conditions. ④ Regarding the integration behavior of user-side ESSs, the distribution network experiences a decline in acceptance capacity for different types of loads. Particularly notable is the most significant reduction in EV acceptance capacity, with the maximum node reduction rate reaching 80%. In contrast, the impact on industrial load acceptance capacity remains relatively moderate, where the maximum node acceptance capacity reduction rate is 28%.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A

Appendix B



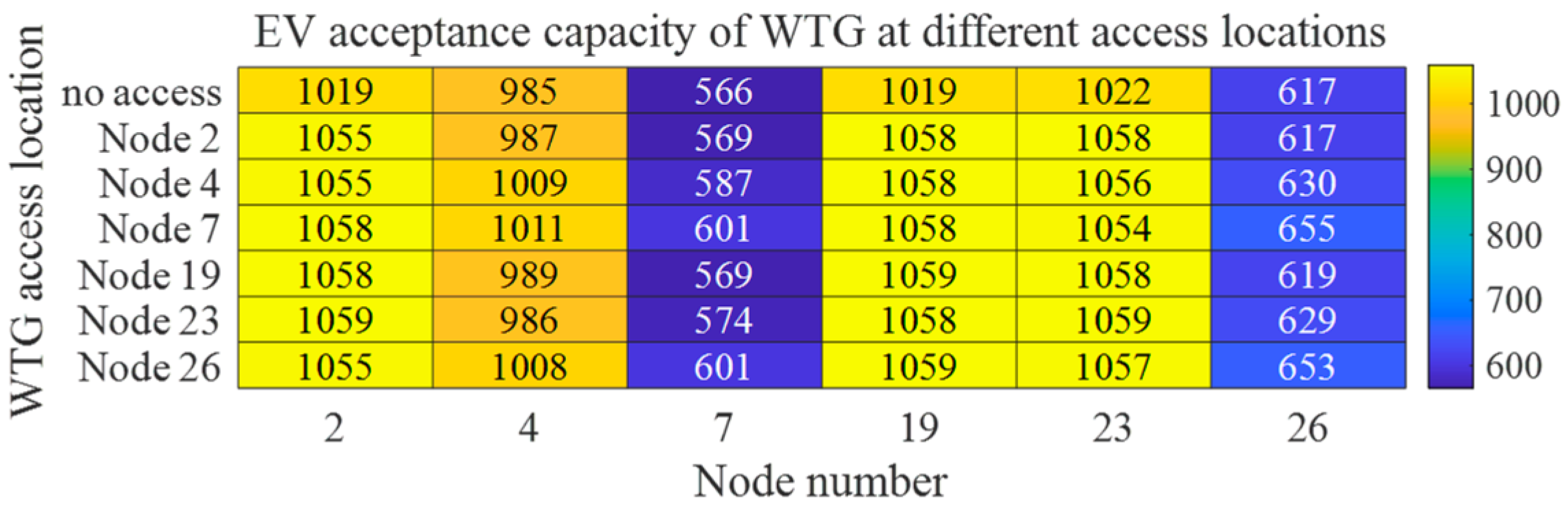
Appendix C




References
- Shafiullah; Ahmed, S.D.; Al-Sulaiman, F.A. Grid Integration Challenges and Solution Strategies for Solar PV Systems: A Review. IEEE Access 2022, 10, 52233–52257. [Google Scholar] [CrossRef]
- Rana, M.; Uddin, M.; Sarkar, R.; Meraj, S.T.; Shafiullah, G.; Muyeen, S.; Islam, A.; Jamal, T. Applications of energy storage systems in power grids with and without renewable energy integration—A comprehensive review. J. Energy Storage 2023, 68, 107811. [Google Scholar] [CrossRef]
- Kataray, T.; Nitesh, B.; Yarram, B.; Sinha, S.; Cuce, E.; Shaik, S.; Vigneshwaran, P.; Roy, A. Integration of smart grid with renewable energy sources: Opportunities and challenges—A comprehensive review. Sustain. Energy Technol. Assess. 2023, 58, 103363. [Google Scholar] [CrossRef]
- Yang, W.; Peng, H.; Chen, Y.; Zhu, L. Optimal site selection and capacity determination method for low-voltage distribution network industry expansion and installation. In Proceedings of the 2023 8th Asia Conference on Power and Electrical Engineering (ACPEE), Tianjin, China, 14–16 April 2023; pp. 2543–2548. [Google Scholar]
- Vahidinasab, V.; Tabarzadi, M.; Arasteh, H.; Alizadeh, M.I.; Beigi, M.M.; Sheikhzadeh, H.R.; Mehran, K.; Sepasian, M.S.; Mohammadbeygi, M. Overview of Electric Energy Distribution Networks Expansion Planning. IEEE Access 2020, 8, 34750–34769. [Google Scholar] [CrossRef]
- Yan, G.; Wang, Q.; Zhang, H.; Wang, L.; Wang, L.; Liao, C. Review on the Evaluation and Improvement Measures of the Carrying Capacity of Distributed Power Supply and Electric Vehicles Connected to the Grid. Energies 2024, 17, 4407. [Google Scholar] [CrossRef]
- Mahdavi, M.; Schmitt, K.E.K.; Jurado, F. Robust Distribution Network Reconfiguration in the Presence of Distributed Generation Under Uncertainty in Demand and Load Variations. IEEE Trans. Power Deliv. 2023, 38, 3480–3495. [Google Scholar] [CrossRef]
- Rodrigo, A.S.; Priyanka, V.G.C. Impact of High Penetration of EV Charging on Harmonics in Distribution Networks. In Proceedings of the 2018 Moratuwa Engineering Research Conference (MERCon), Moratuwa, Sri Lanka, 30 May–1 June 2018; pp. 340–344. [Google Scholar]
- Basnet, S.; Deschinkel, K.; Le Moyne, L.; Péra, M.C. A review on recent standalone and grid integrated hybrid renewable energy systems: System optimization and energy management strategies. Renew. Energy Focus 2023, 46, 103–125. [Google Scholar] [CrossRef]
- Chowdhury, S.; Bohre, A.K. Economic Assessment of PV Wind based HRES including Battery Storage and FC. In Proceedings of the 2023 IEEE International Conference on Power Electronics, Smart Grid, and Renewable Energy (PESGRE), Trivandrum, India, 17–20 December 2023; pp. 1–6. [Google Scholar]
- Khan, A.A.; Minai, A.F.; Pachauri, R.K.; Malik, H. Optimal Sizing, Control, and Management Strategies for Hybrid Renewable Energy Systems: A Comprehensive Review. Energies 2022, 15, 6249. [Google Scholar] [CrossRef]
- Hua, Y.-P.; Wang, S.-Q.; Han, D.; Bai, H.-K.; Wang, Y.-Y.; Li, Q.-Y. Analysis of Charging Load Acceptance Capacity of Electric Vehicles in the Residential Distribution Network. World Electr. Veh. J. 2022, 13, 214. [Google Scholar] [CrossRef]
- Ji, Y.; Zhang, J.; Li, S.; Deng, Y.; Mu, Y. Electric vehicles acceptance capacity evaluation in distribution network considering photovoltaics access. Energy Rep. 2023, 9, 602–608. [Google Scholar] [CrossRef]
- Li, X.; Liu, Y.; Liang, Y.; Zeng, S.; Li, M. Evaluation and optimization of Electric Vehicle Load Acceptance Capacity of Distribution Network. In Proceedings of the 2020 IEEE 4th Conference on Energy Internet and Energy System Integration (EI2), Wuhan, China, 30 October–1 November 2020; pp. 1890–1895. [Google Scholar]
- Huang, Y.; Zhao, L.; Qiu, W.; Xu, Y.; Gao, J.; Yan, Y.; Wu, T.; Lin, Z. Evaluation of Acceptance Capacity of Distributed Generation in Distribution Network Considering Carbon Emission. Energies 2022, 15, 4406. [Google Scholar] [CrossRef]
- He, Y.B.; Ren, D.H.; Qin, T.; Cui, H.W. Power grid optimization planning based on DG acceptance capability evaluation of hybrid AC/DC transmission system. In Proceedings of the 16th IET International Conference on AC and DC Power Transmission (ACDC 2020), Online Conference, 2–3 July 2020; pp. 404–411. [Google Scholar]
- Yang, X.; Long, C.; Ye, Y.; Li, T.; Liu, L.; Wei, J.; Liu, X.; Bai, H. Distribution Network PV Acceptance Capacity Assessment Considering Balance of Flexibility Supply and Demand. In Proceedings of the 2022 Asian Conference on Frontiers of Power and Energy (ACFPE), Chengdu, China, 21–23 October 2022; pp. 592–599. [Google Scholar]
- Wu, H.; Yuan, Y.; Zhu, J.; Qian, K.; Xu, Y. Potential Assessment of Spatial Correlation to Improve Maximum Distributed PV Acceptance capacity of Distribution Networks. Mod. Power Syst. Clean Energy 2021, 9, 800–810. [Google Scholar] [CrossRef]
- Zhang, M.; Sun, Q.; Yang, X. Research on the assessment of the capacity of urban distribution networks to accept electric vehicles based on the improved TOPSIS method. IET Gener. Transm. Distrib. 2021, 15, 2804–2818. [Google Scholar] [CrossRef]
- Bajaj, M.; Singh, A.K. Grid integrated renewable DG systems: A review of power quality challenges and state-of-the-art mitigation techniques. Int. J. Energy Res. 2020, 44, 26–69. [Google Scholar] [CrossRef]
- Meinecke, S.; Sarajlić, D.; Drauz, S.R.; Klettke, A.; Lauven, L.-P.; Rehtanz, C.; Moser, A.; Braun, M. A Benchmark Dataset of Electric Power Systems to Compare Innovative Solutions Based on Power Flow Analysis. Energies 2020, 13, 3290. [Google Scholar] [CrossRef]
- Ray, P.; Ray, P.K.; Dash, S.K. Power Quality Enhancement and Power Flow Analysis of a PV Integrated UPQC System in a Distribution Network. IEEE Trans. Ind. Appl. 2022, 58, 201–211. [Google Scholar] [CrossRef]
- Kenedy, M.; Naresh, R.; Chauhan, R. An efficient Repeated Power Flow approach to evaluate Available Transfer Capability considering power systems security. In Proceedings of the 2023 Second International Conference on Electrical. Electronics, Information and Communication Technologies (ICEEICT), Trichirappalli, India, 5–7 April 2023; pp. 1–5. [Google Scholar]
- Elgamal, M.; Korovkin, N.; Menaem, A.A.; Elmitwally, A. An algorithm for power flow analysis in isolated hybrid energy microgrid considering DG droop model and virtual impedance control loop. Sustain. Energy Grids Netw. 2022, 32, 100875. [Google Scholar] [CrossRef]
- Papadimitrakis, M.; Giamarelos, N.; Stogiannos, M.; Zois, E.; Livanos, N.-I.; Alexandridis, A. Metaheuristic search in smart grid: A review with emphasis on planning, scheduling and power flow optimization applications. Renew. Sustain. Energy Rev. 2021, 145, 111072. [Google Scholar] [CrossRef]
- Yang, J.X.; Zhang, Y.J. Optimization of charging load acceptance capacity based on ordered charging start-up mechanism and subsidy mechanism. Electr. Power Autom. Equip. 2020, 40, 122–130. [Google Scholar]
- Luo, Q.; Huang, M.X. Probabilistic load flow calculation and accommodated capacity analysis for distribution grid containing electric vehicle. J. Mech. Electr. Eng. 2015, 32, 1498–1503. [Google Scholar]
- Zhang, J.; Yan, J.; Liu, Y.; Zhang, H.; Lv, G. Daily electric vehicle charging load profiles considering demographics of vehicle users. Appl. Energy 2020, 274, 115063. [Google Scholar] [CrossRef]
- Yang, H.; Chen, Q.; Liu, Y.; Ma, Y.; Zhang, D. Demand response strategy of user-side energy storage system and its application to reliability improvement. J. Energy Storage 2024, 92, 112150. [Google Scholar] [CrossRef]


| Season | Residential Load | Commercial Load | Industrial Load | |||
|---|---|---|---|---|---|---|
| α | β | α | β | α | β | |
| Spring | 1.2 | 4.38 | 1.25 | 3.35 | 0.18 | 6.00 |
| Summer | 0.72 | 2.96 | 1.25 | 3.50 | 0.18 | 6.00 |
| Autumn | 0.98 | 3.52 | 0.99 | 3.95 | 0.18 | 6.00 |
| Winter | 1.04 | 4.19 | 1.50 | 3.15 | 0.18 | 6.00 |
| Charging Time | Daily Travel Distance |
|---|---|
| N (9, 0.882) N (19, 0.882) U (23, 5) | ln l ~ N (3.2, 0.82) |
| Partition | Medium Plan | High Plan | Low Plan | |||
|---|---|---|---|---|---|---|
| Growth Rate | Probability | Growth Rate | Probability | Growth Rate | Probability | |
| 1 | 0.050 | 0.51 | 0.065 | 0.26 | 0.04 | 0.23 |
| 2 | 0.040 | 0.55 | 0.045 | 0.22 | 0.02 | 0.23 |
| 3 | 0.060 | 0.54 | 0.08 | 0.27 | 0.046 | 0.19 |
| 4 | 0.098 | 0.57 | 0.115 | 0.21 | 0.076 | 0.22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuang, Z.; Liu, G.; Lu, H.; He, Y. Assessment and Influencing Factor Analysis of Multi-Type Load Acceptance Capacity of Active Distribution Network. Electronics 2025, 14, 1566. https://doi.org/10.3390/electronics14081566
Kuang Z, Liu G, Lu H, He Y. Assessment and Influencing Factor Analysis of Multi-Type Load Acceptance Capacity of Active Distribution Network. Electronics. 2025; 14(8):1566. https://doi.org/10.3390/electronics14081566
Chicago/Turabian StyleKuang, Zhicong, Gang Liu, Heting Lu, and Yuling He. 2025. "Assessment and Influencing Factor Analysis of Multi-Type Load Acceptance Capacity of Active Distribution Network" Electronics 14, no. 8: 1566. https://doi.org/10.3390/electronics14081566
APA StyleKuang, Z., Liu, G., Lu, H., & He, Y. (2025). Assessment and Influencing Factor Analysis of Multi-Type Load Acceptance Capacity of Active Distribution Network. Electronics, 14(8), 1566. https://doi.org/10.3390/electronics14081566







