Object Identity Reloaded—A Comprehensive Reference for an Efficient and Effective Framework for Logic-Based Machine Learning
Abstract
1. Introduction
2. Basics
- a term, representing and object, is a variable, a constant, or an n-ary function symbol applied to n terms as arguments;
- an n-ary predicate p, denoted as , is a kind of claim involving n objects;
- an atom is an n-ary predicate applied to n terms as arguments, representing a claim that can be true or false; a formula is an atom or a suitable composition of atoms using logic functions (such as negation ¬ and disjunction ∨); a theory is a set of formulas.
- A literal is an atom (positive literal) or its negation (negative literal); denotes the opposite of a literal l.
- A clause is a universal formula consisting of a finite disjunction of literals; the length of a clause C, denoted by , is the number of its literals; the empty clause □, representing a contradiction, does not contain any literal.
- Two clauses are standardized apart if they do not share variables; they are variants if they differ only in the names of variables (renaming variables in a formula does not change its meaning); in the following, clauses are always standardized apart.
- the Herbrand Universe of T, is the set of all terms that can be expressed in the language;
- the Herbrand Base of T, , is the set of all ground atoms that can be expressed in the language;
- a Herbrand Interpretation for T associates each atom in the Hebrand Universe to a truth value (true or false); it can be seen as defining the set of true atoms in .
- ;
- , ();
- .
2.1. Logic Programming
- domain restricted iff all variables occurring in its body also occur in its head;
- range restricted iff all variables occurring in its head also occur in its body;
- linked if all of its literals are; a literal is linked if at least one of its arguments is; an argument of a literal is linked if the literal is the head of the clause or if another argument of the same literal is linked [18].
2.2. Datalog
- 1.
- if C is a clause with function symbols, ;
- 2.
- if C is a flat clause, ;
- 3.
- iff .
| Algorithm 1: Algorithm for computing the set of logical consequences of a Datalog program. |
function Infer (S: finite set of Datalog clauses) : ; begin W := S while EPP can be applied to some rule and fact of W and some fact is produced do W := return /∗ all facts in W, not rules ∗/ end. |
- all the rules that define the same IDB predicate in P are in the same layer;
- contains only clauses without negated literals or whose negated literals correspond to EDB predicates;
- each contains only clauses whose negated literals are completely defined in lower level layers (i.e., layers with ).
2.3. Inductive Logic Programming
- a set of examples , where are the positive ones and are the negative ones;
- a (possibly empty) background knowledge (or BK) B.
- (completeness or sufficiency)
- ((prior or strong ) consistency) (If the calculus were complete, we could write ).
- ((prior) necessity)
- (prior consistency)
- (weak consistency).
- : C is a generalization of D, D is a specialization of C;
- : C is a proper generalization of D, D is a proper specialization of C;
- : C is an upward refinement of D, D is a downward refinement of C;
- : C is a proper upward refinement of D, D is a proper downward refinement of C.
- ρ (respectively, δ) is locally finite iff : (respectively, ) is finite and computable.
- ρ is proper iff :δ is proper iff : .
- ρ is complete iff : such that andδ is complete iff : such that and .
- ρ (respectively, δ) is ideal iff it fulfills all the above three properties.
3. Object Identity
Within a clause, terms denoted by different symbols must be distinct.
- ;
- distinct}.
| Algorithm 2: Algorithm to compute the OI equivalent of a Datalog clause |
function GenerateDatalogOIClauses (C: DatalogClause): DatalogOIClause begin := {}; for do foreach combination of k variables out of do begin Define some ordering between the k variables; foreach permutation with replacement of k constants out of do for do begin := {}; foreach partition of the remaining variables such that do begin := {}; Build a clause D by replacing the l-th () variable of the combination with the l-th constant of the permutation and all the variables belonging to with one new variable; if then Insert D in elsif there exists no renaming of D in then Insert D in end; := end; end; return end; |
4. Generalization Models
4.1. Subsumption
- ,
- are not comparable
- 1.
- ; (reflexivity)
- 2.
- and . (transitivity)
- (⇒)
- From Definition 9, substitution is such that.Since inequalities cannot occur in a Datalog clause, and are always disjoint. So, .
- 1.
- such thatσ injective .
- 2.
- .
- 3.
- iff they are variants.
- (⇒)
- If , then(by Proposition 3 extended to generic clauses). By contradiction, let , such that . By definition of ,,which is a contradiction by definition of .
| Algorithm 3: Algorithm for computing the lggOI |
Let us preliminarily define a selection under OI of two DatalogOI clauses as a pair of literals that have the same predicate symbol, sign, and arity. Given two DatalogOI clauses, is a set of DatalogOI such that for each clause ,
|
4.2. OI Implication
4.2.1. Model-Theoretic Definition
- (⇒)
- Given an OI model I for , consider the Herbrand OI interpretation having as the domain. For every n ary predicate P in , the interpretation is true if is true in I, or false otherwise.
4.2.2. Proof-Theoretic Definition
- ; thus, obviously, .
- Suppose the thesis holds for . Let be an OI derivation of C from . If ; then, the theorem is obvious. Otherwise, is an OI resolvent of some and (). By induction hypothesis, and . From Lemma 2, it follows that .
- •
- If then ;
- •
- If then .
4.2.3. Subsumption Theorem
- OI substitutions are such that .
- such that .
- ()
- such that is an instance of .
- ()
- Let be an OI derivation of from ; thus, is the resolvent of two clauses in . By induction hypothesis, OI derivation of such that is an instance of . Hence, by Lemma 4, such that is its instance.
- (⇒)
- Assume C is not a tautology. Given OI substitution that maps to new constants that do not occur in , is a non-tautological ground clause and . Thus, by Lemma 6 such that . maps variables of C to constants that are not in D because, being derived from , D cannot contain constants in . Let be a substitution such that and be the substitution obtained from by replacing in each binding the term with . Then, . Since only replaces the variables by , it follows that , i.e., .
- (⇒)
- If , by Theorem 9 such that . Since C is not self-resolvent . Hence the thesis.
- 1.
- not self-resolvent (nor ambivalent), not tautological. , , , and their supersets are the OI models for C, all of which are also OI models for D, so ; also, because . Note that under OI, and are not to be verified by the interpretations, since they would bind both X and Y onto the same constant (a or b).
- 2.
- not self-resolvent (nor ambivalent), not tautological. Interpretations , , , , , , , , are the OI models for C, and they are also OI models for D, so ; also, because . Moreover, for :and .
- 3.
- not self-resolvent (nor ambivalent), not tautological. , , , , , , , , are the OI models for C, and they are also OI models for D, so ; also, because . Note that interpretations , , , , are not OI interpretations since they would bind both X and Y onto the same constant (a or b).Moreover, forand because the empty clause subsumes everything.
4.2.4. Refutation Completeness and Compactness
- (⇒)
- If , for Theorem 9 such that . So, and thus .
- (⇐)
- Assume finite: has an OI model. Then, a Herbrand OI model can be built based on Proposition 7. The Herbrand base is in general infinite but countable: denote its elements with the sequence .Now, let be a finite set of clauses whose truth depends on . Consider a binary tree built by taking node r as the root and scuh that the successive nodes stand for the truth values of , respectively; r has two edges towards two nodes standing for the possible truth values of ; then, from each node, two edges depart towards truth values of , and so on. Clearly, a Herbrand interpretation is given by assigning the truth values encountered traversing a path in such a tree.Let be the subtree obtained by taking all finite paths that represent an OI modelfor C, . Since every has an OI model, must have arbitrarily long branches; hence, by Lemma 7, it has an infinite branch, representing an OI model for .
4.3. Decidability
- Given distinct constants not occurring in or C, is a Skolem substitution for C with respect to .The term set of by is the set of all terms occurring in .
- Given a set of terms T, the instance set of C with respect to T isThe instance set of with respect to T is .
- (⇐)
- Suppose C is not a tautology and . If , then, by Theorem 9, clause such that . Hence, since all constants in D must occur also in clauses in , can be regarded as a Skolem substitution for C with respect to D. Then, by Lemma 6, . So, we can conclude that .
- (⇒)
- Trivial when C is a tautology. If C is not a tautology, then neither is . Since by Lemma 9, from Theorem 8, it follows that is a finite set of instances of clauses in such that . For Theorem 9, there exists a derivation from of a clause E, such that . Since is made up of ground clauses, E must be ground, too; hence, . Therefore, E contains only terms from .Now, consider the ground OI substitutions that yield the clauses in from those in . new OI substitution such thatwhere is a choice of a new term from T. In this manner, every term in clauses in which is not in T is replaced with a distinct term in . Since contains ground instances of clauses in , this replacement yields a new set of clauses where each clause is a ground instance of clauses in . The term replacement involves the term set T by ; then, the existence of a derivation of E from yields a derivation of E from . Indeed, each OI resolution step in the derivation from can be transposed into an OI resolution step from , since the same terms in are replaced by the same terms in . In addition, the terms in that are not in T, replaced by , do not appear in the conclusion E of the derivation.Then, a derivation of E from exists, so we can write and hence . Now, is a set of ground instances of clauses in and all terms in are also in T; then, . Thus, .
- (⇐)
- holds, being the instance set made up of instances of clauses in . By hypothesis, , so and, by Lemma 9, .
5. Incremental Inductive Synthesis
- A theory T is inconsistent iff , is inconsistent with respect to N.
- A hypothesis H is inconsistent with respect to N iff : C is inconsistent with respect to N.
- A clause C is inconsistent with respect to N iff :
- 1.
- body(C) body(N)
- 2.
- ¬ head(C)σ = head(N)
- 3.
- constraints()σ⊆ constraints()
where and denote, respectively, the body and the head of a clause φ.
- A theory T is incomplete iff , : H is incomplete with respect to P.
- A hypothesis H is incomplete with respect to P iff ).
5.1. Refinement Operators
- when exactly one of the following conditions holds:
- 1.
- , where ;
- 2.
- , where l is an atom such that .
- when exactly one of the following conditions holds:
- 1.
- , where ;
- 2.
- , where l is an atom such that .
- , where
- , where
- where l is an atom such that and
- where l is an atom such that and
5.2. Refinement in Unrestricted Search Spaces
- •
- when exactly one of the conditions in Definition 17 and the following one holds:
- 3.
- , where , f function symbol () and ;
- •
- when exactly one of the conditions in Definition 17 and the following one holds:
- 3.
- , where , f function symbol () such that and .
- (base)
- If , then ; thus, the empty chain fulfills the lemma.
- (step)
- Assume that for some k, , there is a -chain from C to a , where is obtained from C by adding k literals contained in D. Now, let and . Since , then ; then, it can be used to refine , according to 2 in the definition of . Hence, we obtain . By inductive hypothesis, there is also a chain from C to . Thus, the lemma is satisfied for .
- (local finiteness)
- Trivial, since, by definition, a term dominated by an n-ary function () is turned into a variable (or vice versa) or a single literal is added (or removed).
- (properness)
- If , by definition of downward refinement operator, . If also , then . Hence, by 3 in Property 5 in the unrestricted space, the clauses would be variants, which is false for the construction of the operator (either C has a new term with respect to D or it is longer than D). The case is analogous for the other operator.
- (completeness)
- Let C and D be two clauses such that . We have to prove the existence of a chain from C to D (clauses equivalent to D are omitted here since they are variants). Hence, . Let . For Lemma 12, there is a -chain from C to E. By definition of E, it also holds , and by Lemma 13, there is a -chain from E to D. Thus, we have a chain from C to D, which proves that is complete. An analogous proof holds for the completeness of (Lemmas similar to 12 and 13 are needed).
5.3. Refinement Operators for OI Implication
- is a second power of C;
- is a third power of C.
5.3.1. Inverting OI Resolution
- (a)
- and or
- (b)
- and , where is a set of clauses or-introduced from C by and .
- (base)
- For , is or-introduced from . Then, of course, , ;
- (step)
- By inductive hypothesis sequence of literals, set of clauses or-introduced from by such that .By definition of linear OI resolution, is an OI resolvent of and some . Then, by Proposition 14, literal such that and .By the inductive hypothesis and by Lemma 14, set of clauses or-introduced from by such that .Thus, is a set of clauses or-introduced from by such that .
5.3.2. Expansions
- and, by Proposition 8, . So, . By Theorem 15, ; hence, .
- By Theorem 15, , i.e., , and so such that . For the properties of , . Summing up, , and by Proposition 8, , so .
- •
- iff expansion of C such that ;
- •
- iff for some n, such that .
- (—local finiteness)
- Holds by definition of and Theorem 19 ensuring the existence of an expansion, as an of a set of or-introduced clauses (a singleton, in this case);
- (—properness)
- Follows from the properness of (cf. Theorem 14);
- (—completeness)
- As for local finiteness, it comes from Theorem 19 ensuring the existence of an expansion and Proposition 12.
- (—properness)
- Like for , using again Theorem 14;
- (—local finiteness and completeness)
- The level saturation procedure [9] that computes the linear self-resolution steps is needed. Call D the specialization to be computed.For . Only a subsumption step is needed, and the ideal operator can be used.For , suppose that D has not been computed up to step and consider the case for n. A further linear OI resolution step can be computed as follows:and the ideal operator can be used to compute specializations of clauses in . The computation is non-deterministic in the choice of F.By construction, this procedure certainly finds specialization under OI implication when it exists. The computation terminates using as a halting point the condition . In fact, the cardinality of the clauses increases monotonically, both by resolution ( except when or , in which case the OI resolvent can be reached with a simple OI subsumption step) and by OI subsumption (if , then ).
6. Discussion
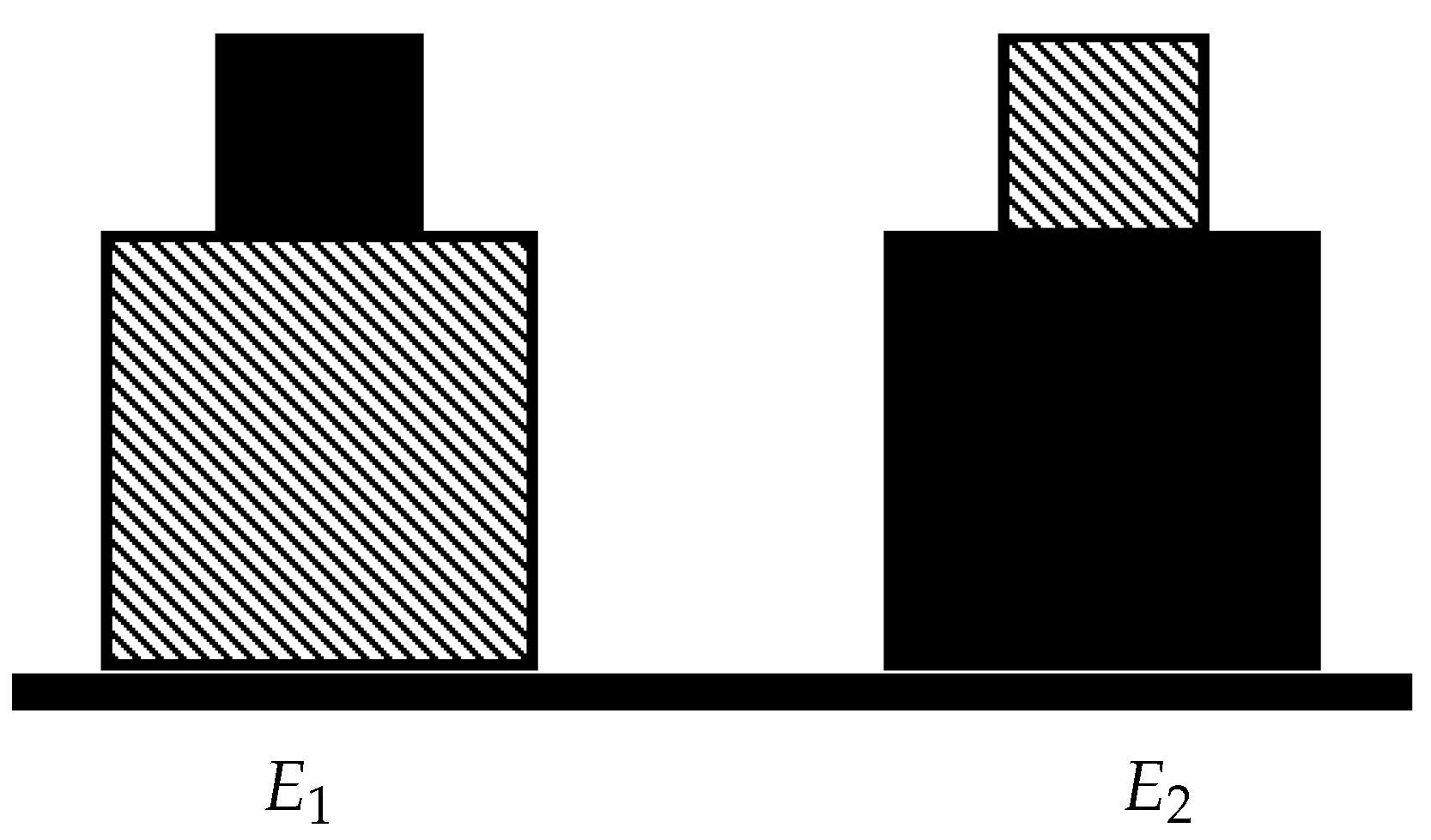
6.1. Intuition
- :
- blocks(obj1) :− part_of(obj1,p1), part_of(obj1,p2), on(p1,p2), cube(p1), cube(p2), small(p1),big(p2), black(p1), stripes(p2).
- :
- blocks(obj2) :− part_of(obj2,p3),part_of(obj2,p4), on(p3,p4), cube(p3), cube(p4), small(p3), big(p4), black(p4), stripes(p3).
- G:
- blocks(X) :− part_of(X,X1), part_of(X,X2), part_of(X,X3), part_of(X,X4), cube(X4), on(X1,X2), cube(X1), cube(X2), cube(X3), small(X1), big(X2), black(X3), stripes(X4).
- :
- blocks(X) :− part_of(X,X1), part_of(X,X2), on(X1,X2), cube(X1), cube(X2), small(X1), big(X2).
- :
- blocks(X) :− part_of(X,X1), part_of(X,X2), cube(X1), cube(X2), black(X1), stripes(X2).
6.2. Notes on Computational Complexity and Efficiency
7. Operability: Systems and Applications
7.1. OI-Based Systems
7.2. Mutagenesis
7.3. Document Image Processing
7.3.1. Scientific Papers
7.3.2. Historical Documents
7.4. Process Mining and Management
7.4.1. Complex Artificial Process Models
7.4.2. Daily Routines
| sleeping(A) | :- | true. |
| eating(A) | :- | next(_,A). |
| meal_preparation(A) | :- | next(_,A). |
| bed_to_toilet(A) | :- | next(_,A), sensor_m004(A,B), status_on(B), |
7.4.3. Process-Related Prediction
- Aruba
- described in the previous section.
- GPItaly
- reports the movements of an elderly person in the rooms of her home [64] along 253 days. Each day was a case of the process representing the movement routine.
- Chess
- consists of 400 reports of top-level matches downloaded from https://www.federscacchi.com/fsi/index.php/punteggi/archivio-partite (consulted on 29 March 2025). A case was a chess match.
8. Conclusions and Future Work
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DB | Database |
| FOL | First-Order Logic |
| iff | If and Only If |
| ILP | Inductive Logic Programming |
| LP | Logic Programming |
| ML | Machine Learning |
| OI | Object Identity |
References
- Lloyd, J.W. Foundations of Logic Programming, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1987. [Google Scholar]
- Apt, K.R. Introduction to Logic Programming. In Handbook of Theoretical Computer Science; Elsevier: Amsterdam, The Netherlands, 1990; pp. 492–574. [Google Scholar]
- Barr, A.; Feigenbaum, E. The Handbook of Artificial Intelligence; William Kaufmann: Los Altos, CA, USA, 1982. [Google Scholar]
- European Parliament and of the Council. Regulation (EU) 2024/1689 Laying Down Harmonised Rules on Artificial Intelligence and Amending Regulations (EC) No 300/2008, (EU) No 167/2013, (EU) No 168/2013, (EU) 2018/858, (EU) 2018/1139 and (EU) 2019/2144 and Directives 2014/90/EU, (EU) 2016/797 and (EU) 2020/1828 (Artificial Intelligence Act) (Text with EEA Relevance). Available online: http://data.europa.eu/eli/reg/2024/1689/oj (accessed on 13 June 2024).
- Srinivasan, A.; King, R.D.; Muggleton, S.H.; Sternberg, M.J.E. Carcinogenesis Predictions Using Inductive Logic Programming. In Intelligent Data Analysis in Medicine and Pharmacology; Lavrač, N., Keravnou, E.T., Zupan, B., Eds.; Springer: Boston, MA, USA, 1997; pp. 243–260. [Google Scholar]
- Srinivasan, A.; Muggleton, S.; King, R.; Sternberg, M. Mutagenesis: ILP experiments in a non-determinate biological domain. In Proceedings of the 4th International Workshop on Inductive Logic Programming, Bad Honnef/Bonn, Germany, 12–14 September 1994; GMD-Studien Nr. 237. pp. 217–232. [Google Scholar]
- Srinivasan, A.; Muggleton, S.; Sternberg, M.; King, R. Theories for mutagenicity: A study in first-order and feature-based induction. Artif. Intell. 1996, 85, 277–299. [Google Scholar] [CrossRef]
- Genesereth, M.; Nilsson, N. Logic Foundations of Artificial Intelligence; Morgan Kaufmann: Burlington, MA, USA, 1987. [Google Scholar]
- Nienhuys-Cheng, S.H.; de Wolf, R. Foundations of Inductive Logic Programming; Lecture Notes in Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 1997; Volume 1228. [Google Scholar]
- Khoshafian, S.N.; Copeland, G.P. Object identity. ACM Sigplan Not. 1986, 21, 406–416. [Google Scholar] [CrossRef]
- Besold, T.R.; d’Avila Garcez, A.; Bader, S.; Bowman, H.; Domingos, P.; Hitzler, P.; Kuehnberger, K.U.; Lamb, L.C.; Lima, P.M.V.; de Penning, L.; et al. Neural-symbolic learning and reasoning: A survey and interpretation. In Neuro-Symbolic Artificial Intelligence: The State of the Art; Frontiers in Artificial Intelligence and Applications; IOS Press: Amsterdam, The Netherlands, 2021; Volume 342, pp. 1–51. [Google Scholar]
- Schmidt-Schauss, M. Implication of Clauses is Undecidable. Theor. Comput. Sci. 1988, 59, 287–296. [Google Scholar] [CrossRef][Green Version]
- Garey, M.; Johnson, D. Computers and Intractability—A Guide to the Theory of NP-Completeness; Freeman: San Francisco, CA, USA, 1979. [Google Scholar]
- Robinson, J.A. A Machine-Oriented Logic Based on the Resolution Principle. J. ACM 1965, 12, 23–41. [Google Scholar] [CrossRef]
- Chang, C.; Lee, R. Symbolic Logic and Mechanical Theorem Proving; Academic Press: San Diego, CA, USA, 1973. [Google Scholar]
- Nienhuys-Cheng, S.H.; de Wolf, R. The Subsumption Theorem in Inductive Logic Programming: Facts and Fallacies. In Advances in Inductive Logic Programming; De Raedt, L., Ed.; Frontiers in Artificial Intelligence and Applications; IOS Press: Amsterdam, The Netherlands, 1996; Volume 32, pp. 265–276. [Google Scholar]
- Nienhuys-Cheng, S.H.; de Wolf, R. The Subsumption Theorem Revisited: Restricted to SLD Resolution. In Proceedings of the Computing Science in the Netherlands, Utrecht, The Netherlands, 20–22 September 1995. [Google Scholar]
- Helft, N. Inductive Generalization: A Logical Framework. In Proceedings of the 2nd European Conference on European Working Session on Learning (EWSL’87), Bled, Yugoslavia, 1 May 1987; pp. 149–157. [Google Scholar]
- van Emden, M.; Kowalski, R. The Semantics of Predicate Logic as a Programming Language. J. ACM 1976, 23, 733–742. [Google Scholar] [CrossRef]
- Ceri, S.; Gottlöb, G.; Tanca, L. Logic Programming and Databases; Springer: Berlin/Heidelberg, Germany, 1990. [Google Scholar]
- Kanellakis, P.C. Elements of Relational Database Theory. In Handbook of Theoretical Computer Science; Elsevier: Amsterdam, The Netherlands, 1990; Volume B–Formal Models and Semantics, pp. 1073–1156. [Google Scholar]
- Rouveirol, C. Extensions of Inversion of Resolution Applied to Theory Completion. In Inductive Logic Programming; Academic Press: Cambridge, MA, USA, 1992; pp. 64–90. [Google Scholar]
- Michalski, R.S. A Theory and Methodology of Inductive Learning. In Machine Learning: An Artificial Intelligence Approach; Morgan Kaufmann: Burlington, MA, USA, 1983; Volume I. [Google Scholar]
- De Raedt, L. Interactive Theory Revision—An Inductive Logic Programming Approach; Academic Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Wrobel, S. Concept Formation and Knowledge Revision; Kluwer Academic: Dordrecht, The Netherlands, 1994. [Google Scholar]
- Wrobel, S. On the proper definition of minimality in specialization and theory revision. In Machine Learning, Proceedings of the ECML-93: European Conference on Machine Learning, Vienna, Austria, 5–7 April 1993; Number 667 in Lecture Notes in Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 1993; pp. 65–82. [Google Scholar]
- Plotkin, G.D. A Note on Inductive Generalization. Mach. Intell. 1970, 5, 153–163. [Google Scholar]
- Van der Laag, P.R.J.; Nienhuys-Cheng, S.H. A Note on Ideal Refinement Operators in Inductive Logic Programming. In Proceedings of the 4th International Workshop on Inductive Logic Programming, Bad Honnef/Bonn, Germany, 12–14 September 1994; GMD-Studien Nr. 237. pp. 247–260. [Google Scholar]
- Van der Laag, P.R.J.; Nienhuys-Cheng, S.H. Existence and Nonexistence of Complete Refinement Operators. In Machine Learning, Proceedings of the ECML-94: European Conference on Machine Learning, Catania, Italy, 6–8 April 1994; Number 784 in Lecture Notes in Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 1994; pp. 307–322. [Google Scholar]
- Van der Laag, P.R.J. An Analysis of Refinement Operators in Inductive Logic Programming. Ph.D. Thesis, Erasmus University, Rotterdam, The Netherlands, 1995. [Google Scholar]
- Esposito, F.; Malerba, D.; Semeraro, G.; Brunk, C.; Pazzani, M. Traps and Pitfalls when Learning Logical Definitions from Relations. In Methodologies for Intelligent Systems, Proceedings of the 8th International Symposium, ISMIS’94, Charlotte, NC, USA, 16–19 October 1994; Number 869 in Lecture Notes in Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 1994; pp. 376–385. [Google Scholar]
- Semeraro, G.; Esposito, F.; Malerba, D.; Brunk, C.; Pazzani, M. Avoiding Non-Termination when Learning Logic Programs: A Case Study with FOIL and FOCL. In Logic Program Synthesis and Transformation—Meta-Programming in Logic, Proceedings of the 4th International Workshops, LOPSTR’94 and META’94, Pisa, Italy, 20–21 June 1994; Number 883 in Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1994; pp. 183–198. [Google Scholar]
- Esposito, F.; Laterza, A.; Malerba, D.; Semeraro, G. Locally Finite, Proper and Complete Operators for Refining Datalog Programs. In Foundations of Intelligent Systems, Proceedings of the 9th International Symposium, ISMIS’96, Zakopane, Poland, 9–13 June 1996; Number 1079 in Lecture Notes in Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 1996; pp. 468–478. [Google Scholar]
- Semeraro, G.; Esposito, F.; Malerba, D. Ideal Refinement of Datalog Programs. In Logic Program Synthesis and Transformation, Proceedings of the 5th International Workshop, LOPSTR’95, Utrecht, The Netherlands, 20–22 September 1995; Number 1048 in Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1995; pp. 120–136. [Google Scholar]
- Plotkin, G.D. Building-in Equational Theories. In Machine Intelligence; Edinburgh University Press: Edinburgh, UK, 1972; Volume 7, pp. 73–90. [Google Scholar]
- Reiter, R. Equality and domain closure in first order databases. J. ACM 1980, 27, 235–249. [Google Scholar] [CrossRef]
- Jaffar, J.; Maher, M.J. Constraint Logic Programming: A Survey. J. Log. Program. 1994, 19, 503–581. [Google Scholar] [CrossRef]
- Ferilli, S. Programmazione Logica Induttiva nella Revisione di Teorie. Laurea Degree Thesis, Dipartimento di Informatica, Università di Bari, Bari, Italy, 1996. [Google Scholar]
- Siekmann, J.H. An introduction to Unification Theory. In Formal Techniques in Artificial Intelligence—A Sourcebook; Banerji, R.B., Ed.; Elsevier Science: Amsterdam, The Netherlands, 1990; pp. 460–464. [Google Scholar]
- Semeraro, G.; Esposito, F.; Malerba, D.; Fanizzi, N.; Ferilli, S. A Logic Framework for the Incremental Inductive Synthesis of Datalog Theories. In Logic Program Synthesis and Transformation, Proceedings of the 7th International Workshop, LOPSTR’97, Leuven, Belgium, 10–12 July 1997; Number 1463 in Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1997; pp. 300–321. [Google Scholar]
- Gottlöb, G. Subsumption and Implication. Inf. Process. Lett. 1987, 24, 109–111. [Google Scholar] [CrossRef]
- Boolos, G.; Jeffrey, R. Computability and Logic, 3rd ed.; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Idestam-Almquist, P. Generalization of Clauses. Ph.D. Thesis, Stockholm University and Royal Institute of Technology, Kista, Sweden, 1993. [Google Scholar]
- Nédellec, C.; Rouveirol, C.; Adé, H.; Bergadano, F.; Tausend, B. Declarative Bias in ILP. In Advances in Inductive Logic Programming; De Raedt, L., Ed.; IOS Press: Amsterdam, The Netherlands, 1996; Volume 32, pp. 82–103. [Google Scholar]
- Komorowski, H.J.; Trcek, S. Towards Refinement of Definite Logic Programs. In Proceedings of the Methodologies for Intelligent Systems; Raś, Z.W., Zemankova, M., Eds.; Number 869 in Lecture Notes in Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 1994; pp. 315–325. [Google Scholar]
- Muggleton, S.H. Inverting Implication. In Proceedings of the 2nd International Workshop on Inductive Logic Programming, ICOT Technical Memorandum TM-1182, Tokyo, Japan, 15–20 July 1992. [Google Scholar]
- Esposito, F.; Fanizzi, N.; Ferilli, S.; Semeraro, G. A generalization model based on OI implication for ideal theory refinement. Fundam. Inform. 2001, 47, 15–33. [Google Scholar]
- Ferilli, S.; Basile, T.M.A.; Biba, M.; Mauro, N.D.; Esposito, F. A General Similarity Framework for Horn Clause Logic. Fundam. Inform. 2009, 90, 43–66. [Google Scholar] [CrossRef]
- Esposito, F.; Malerba, D.; Semeraro, G. Negation as a specializing operator. In Advances in Artificial Intelligence, Proceedings of the Third Congress of the Italian Association for Artificial Intelligence, AI* IA’93, Torino, Italy, 26–28 October 1993; Torasso, P., Ed.; Springer: Berlin/Heidelberg, Germany, 1993; pp. 166–177. [Google Scholar]
- Esposito, F.; Fanizzi, N.; Malerba, D.; Semeraro, G. Downward Refinement of Hierarchical Datalog Theories. In Proceedings of the 1995 Joint Conference on Declarative Programming, GULP-PRODE 95, Marina di Vietri, Italy, 11–14 September 1995; pp. 148–159. [Google Scholar]
- Ferilli, S. Predicate invention-based specialization in Inductive Logic Programming. J. Intell. Inf. Syst. 2016, 47, 33–55. [Google Scholar] [CrossRef]
- Esposito, F.; Malerba, D.; Semeraro, G. Multistrategy Learning for Document Recognition. Appl. Artif. Intell. Int. J. 1994, 8, 33–84. [Google Scholar] [CrossRef]
- Semeraro, G.; Esposito, F.; Fanizzi, N.; Malerba, D. Revision of logical theories. In Topics in Artificial Intelligence; Number 992 in Lecture Notes in Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 1995; pp. 365–376. [Google Scholar]
- Esposito, F.; Semeraro, G.; Fanizzi, N.; Ferilli, S. Multistrategy Theory Revision: Induction and Abduction in INTHELEX. Mach. Learn. J. 2000, 38, 133–156. [Google Scholar] [CrossRef]
- Ferilli, S. WoMan: Logic-based Workflow Learning and Management. IEEE Trans. Syst. Man Cybern. Syst. 2014, 44, 744–756. [Google Scholar] [CrossRef]
- Ferilli, S.; Angelastro, S. Activity Prediction in Process Mining using the WoMan Framework. J. Intell. Inf. Syst. 2019, 53, 93–112. [Google Scholar] [CrossRef]
- Ferilli, S. GEAR: A General Inference Engine for Automated MultiStrategy Reasoning. Electronics 2023, 12, 256. [Google Scholar] [CrossRef]
- Emde, W.; Wettschereck, D. Relational instance based learning. In Proceedings of the ICML-96; Saitta, L., Ed.; Morgan Kaufmann: Burlington, MA, USA, 1996; pp. 122–130. [Google Scholar]
- Woznica, A.; Kalousis, A.; Hilario, M. Distances and (Indefinite) Kernels for Sets of Objects. In Proceedings of the Sixth International Conference on Data Mining (ICDM’06), Hong Kong, China, 18–22 December 2006; pp. 1151–1156. [Google Scholar] [CrossRef]
- Fonseca, N.; Costa, V.S.; Rocha, R.; Camacho, R. k-RNN: K-Relational Nearest Neighbour Algorithm. In Proceedings of the SAC ’08: 2008 ACM Symposium on Applied Computing, Fortaleza, Brazil, 16–20 March 2008; ACM: New York, NY, USA, 2008; pp. 944–948. [Google Scholar] [CrossRef]
- Esposito, F.; Ferilli, S.; Fanizzi, N.; Basile, T.M.; Di Mauro, N. Incremental multistrategy learning for document processing. Appl. Artif. Intell. 2003, 17, 859–883. [Google Scholar] [CrossRef]
- Weijters, A.; van der Aalst, W. Rediscovering Workflow Models from Event-Based Data. In Proceedings of the 11th Dutch-Belgian Conference on Machine Learning (Benelearn 2001), The Hague, The Netherlands, 20 May 2011; Hoste, V., Pauw, G.D., Eds.; ACM: New York, NY, USA, 2001; pp. 93–100. [Google Scholar]
- de Medeiros, A.; Weijters, A.; van der Aalst, W. Genetic process mining: An experimental evaluation. Data Min. Knowl. Discov. 2007, 14, 245–304. [Google Scholar] [CrossRef]
- Coradeschi, S.; Cesta, A.; Cortellessa, G.; Coraci, L.; Gonzalez, J.; Karlsson, L.; Furfari, F.; Loutfi, A.; Orlandini, A.; Palumbo, F.; et al. Giraffplus: Combining social interaction and long term monitoring for promoting independent living. In Proceedings of the 2013 6th International Conference on Human System Interactions (HSI), Sopot, Poland, 6–8 June 2013; pp. 578–585. [Google Scholar]
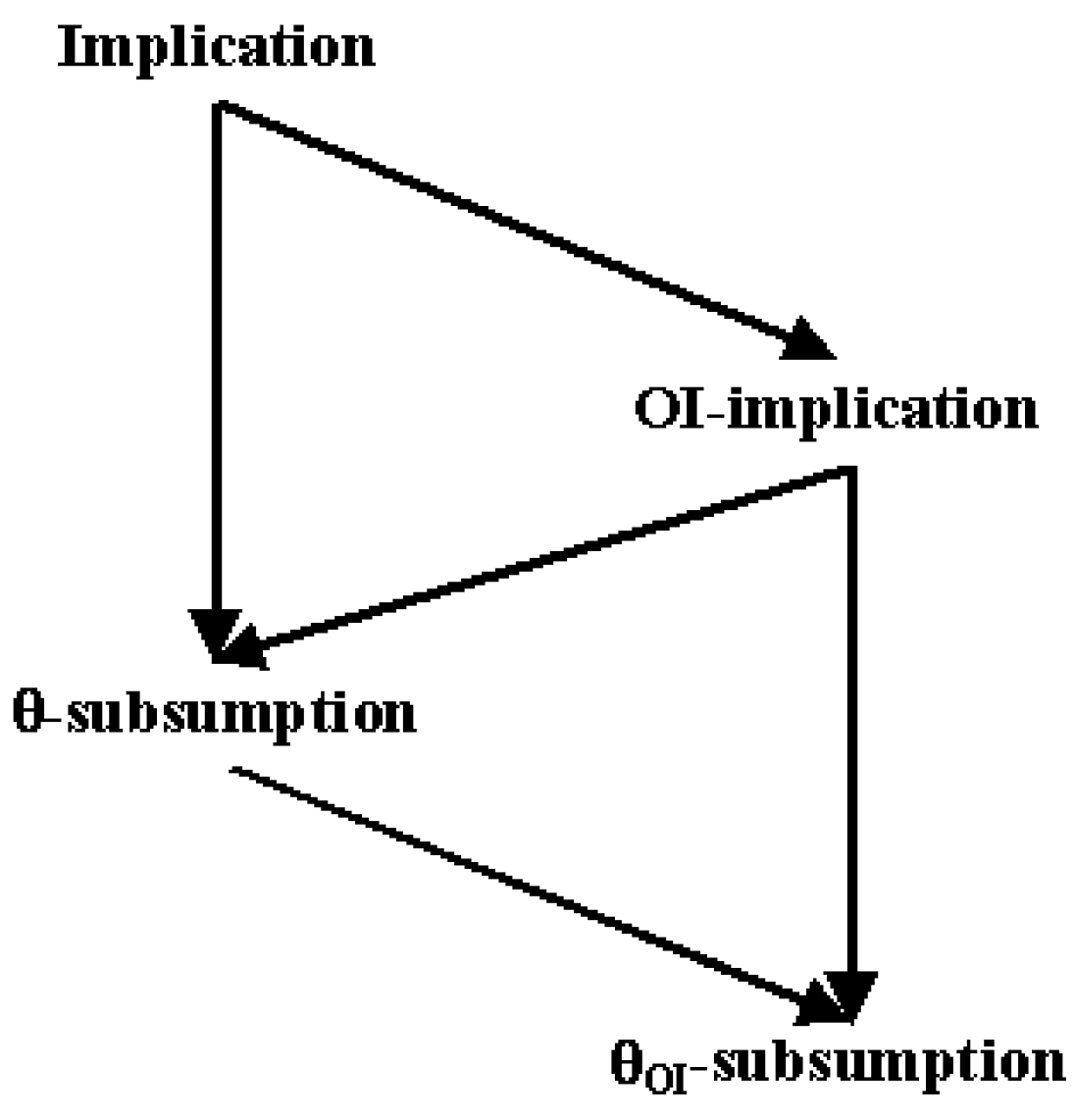

| Logics | Programming | Databases |
|---|---|---|
| predicate | procedure name | relation (table) |
| term | data structure | (atomic) value |
| clause | procedure declaration | |
| clause head | procedure heading | |
| clause body | procedure body | |
| atom in clause body | statement | |
| definite clause | sub-program | view |
| goal | execution | query |
| fact | n-tuple |
| Cl | Accuracy | F1-Measure | ||
|---|---|---|---|---|
| S | 1.9 | 0.98 | 0.97 | |
| JMLR | B | 1.9 | 0.98 | 0.97 |
| k | — | 0.90 | — | |
| S | 1 | 1.00 | 1.00 | |
| Elsevier | B | 2.1 | 0.99 | 0.97 |
| k | — | 1.00 | — | |
| S | 4.7 | 0.96 | 0.94 | |
| MLJ | B | 5.2 | 0.93 | 0.91 |
| k | — | 1.00 | — | |
| S | 2.6 | 0.98 | 0.94 | |
| SVLN | B | 3.3 | 0.97 | 0.93 |
| k | — | 0.90 | — | |
| S | 2.55 | 0.98 | 0.96 | |
| Average | B | 3.125 | 0.97 | 0.94 |
| k | — | 0.94 | — |
| Cluster | Size | Class | P (%) | R (%) |
|---|---|---|---|---|
| 1 | 65 | Elsevier | 80 | 100 |
| 2 | 65 | SVLN | 98.46 | 85.33 |
| 3 | 105 | JMLR | 90.48 | 100 |
| 4 | 118 | MLJ | 97.46 | 87.79 |
| average | 91.60 | 93.28 |
| Clauses | Length | Runtime | Accuracy | Pos | Neg | |
|---|---|---|---|---|---|---|
| faa-registration-card | 1 | 12.5 | 90.13 | 1.0 | 1.0 | 1.0 |
| dif-censorship-decision | 1.1 | 25.8 | 5761.8 | 0.963 | 0.789 | 1.0 |
| Id | Little Thumb | Genetic | Time (Genetic) |
|---|---|---|---|
| 1 | y | n | 1′ |
| 2 | y | e | >3′ |
| 3 | y | e | >1′ |
| 4 | n | y | >1′ |
| 5 | n | n | >25′ |
| 6 | n | n | >4′ |
| 7 | n | e | >30′ |
| 8 | n | e | 37″ |
| 9 | y | n | 31″ |
| 10 | y | y | 21″ |
| 11 | y | e | 30″ |
| Tasks | Transitions | |
|---|---|---|
| Recall | 91.36% | 55.49% |
| F1-measure | 95.48% | 71.37% |
| Cases | Events | Tasks | ||
|---|---|---|---|---|
| Overall | Avg | Overall | ||
| Aruba | 220 | 13,788 | 62.67 | 10 |
| GPItaly | 253 | 185,844 | 369.47 | 8 |
| White | 158 | 36,768 | 232.71 | 681 |
| Black | 87 | 21,142 | 243.01 | 663 |
| Draw | 155 | 32,422 | 209.17 | 658 |
| Folds | Pred | Recall | Rank | (Tasks) | |
|---|---|---|---|---|---|
| Aruba | 3 | 0.85 | 0.97 | 0.92 | 6.06 |
| GPItaly | 3 | 0.99 | 0.97 | 0.96 | 8.02 |
| chess | 5 | 0.54 | 0.98 | 1.0 | 11.34 |
| Folds | Pos (%) | C | A | U | W | |
|---|---|---|---|---|---|---|
| black | 5 | 0.47 | 0.20 | 0.00 | 0.15 | 0.66 |
| white | 5 | 0.70 | 0.44 | 0.00 | 0.15 | 0.40 |
| draw | 5 | 0.61 | 0.29 | 0.01 | 0.18 | 0.52 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferilli, S. Object Identity Reloaded—A Comprehensive Reference for an Efficient and Effective Framework for Logic-Based Machine Learning. Electronics 2025, 14, 1523. https://doi.org/10.3390/electronics14081523
Ferilli S. Object Identity Reloaded—A Comprehensive Reference for an Efficient and Effective Framework for Logic-Based Machine Learning. Electronics. 2025; 14(8):1523. https://doi.org/10.3390/electronics14081523
Chicago/Turabian StyleFerilli, Stefano. 2025. "Object Identity Reloaded—A Comprehensive Reference for an Efficient and Effective Framework for Logic-Based Machine Learning" Electronics 14, no. 8: 1523. https://doi.org/10.3390/electronics14081523
APA StyleFerilli, S. (2025). Object Identity Reloaded—A Comprehensive Reference for an Efficient and Effective Framework for Logic-Based Machine Learning. Electronics, 14(8), 1523. https://doi.org/10.3390/electronics14081523






