Abstract
In this study, a new sparse reconstruction algorithm based on near-field imaging is proposed to solve the grating lobe problem arising from sparse arrays. It derives the expression of the steering vector under near-field conditions and formulates the optimization problem. Moreover, the problem, by using the alternating direction method of multipliers (ADMM), is efficiently solved. Experiment results indicate that, in comparison to existing methods such as the phase coherent factor (PCF) and sum and difference beams, the proposed method significantly reduces the impact caused by grating lobes in near-field imaging. In addition, the proposed algorithm is accelerated by the ADMM, which significantly reduces the computational time. This work offers a perspective and potential solution to enhance grating lobe images.
1. Introduction
Array radar near-field imaging technology is mainly used in security detection [1]. Furthermore, with the continuous advancement of imaging technology, array imaging has been widely applied in wireless sensor networks [2], such as underground safety monitoring in coal mines [3], indoor human fall detection [4], medical imaging [5], and industrial non-destructive testing [6]. As the demand for radar applications such as high resolution, wide field of view, and low cost continues to rise, the use of array imaging becomes increasingly crucial [7].
Conventional imaging approaches, adhering to the Nyquist sampling criterion, require a substantial number of transmitting and receiving antennas to achieve enhanced angular resolution. However, these methods not only increase system costs but also introduce higher complexity, making the implementation of radar systems challenging [8].
Distributed arrays effectively reduce system costs and complexity by decreasing the number of antennas [9,10]. However, the distributed arrays, due to under-sampling in the azimuth direction, can be considered as sparse arrays, which introduce grating lobes, impacting the quality of the radar image [11].
Recently, there are two main strategies that have been used to address the grating lobe issue. One strategy involves optimizing the array design [12,13,14] to minimize the grating lobe impact on imaging quality in specific scenarios. However, this strategy increases the complexity of the array system, necessitating more stringent requirements in hardware design. Another strategy involves processing the image results, which requires no stringent hardware complexity and is easy to implement, making it gain widespread attention. In [15,16], the phase coherence factor (PCF) method was proposed. This method analyzes the phase diversity of the image information and outputs a weighted combination of the phase coherence factor and symbol coherence factor to suppress grating lobes. However, the PCF heavily relies on the coherence of the data. When the signal-to-noise ratio (SNR) is low or the target is too close, its capability to suppress grating lobes significantly decreases. Ref. [17] employed the sum and difference beams of radio frequency phase subarrays, widely used in single-pulse radar systems for target angle estimation, to eliminate grating lobes. While the sum and difference beams method does not have the limitations associated with the PCF, its effectiveness in suppressing grating lobes is limited, and it cannot achieve complete suppression. In [18], a grating lobe suppression method based on zero offset and multidiffusion under near-field conditions was proposed, which demonstrated effective suppression. However, this algorithm has strict applicability conditions and is limited to specific sparse arrays, making it lack generality.
In order to achieve better grating lobe suppression and overcome the limitations of these methods, we referred to the sparse reconstruction and compressed sensing algorithms for angle of arrival (AOA) estimation, as presented in [19]. On that basis, we extended the sparse reconstruction method to the application of grating lobe imaging and derived the steering vector for near-field conditions under sparse arrays. However, such reconstruction methods increase the computational cost [20]. Regarding this issue, using the alternating direction method of multipliers (ADMM) can accelerate the solving of optimization problems. The ADMM exploits auxiliary variables and divides the optimization problem to individual convex subproblems. Then, each subproblem is evaluated easily based on proximal operators [21].
The main contributions of this study are as follows: (1) We apply the sparse reconstruction algorithm to the grating lobe suppression of near-field imaging and provide specific optimization expressions. Simulation and experimental results demonstrate that, compared to existing grating lobe suppression algorithms, the proposed method achieves superior imaging performance under the near-field conditions. (2) We use the ADMM to accelerate the computation and provide the solution expressions for each subproblem. The results demonstrate that the ADMM significantly reduced the computation time compared to traditional optimization algorithms.
The remainder of this article is organized as follows. Section 2 elaborates on the signal model and imaging method, while Section 3 details the derivation of the proposed optimization problem and the accelerated solution strategy leveraging the ADMM. In Section 4, the numerical simulation and experimental imaging results of different algorithms are compared. Finally, Section 5 summarizes the full text.
2. Sparse Array Signal Model
2.1. Sparse Array
Considering an MIMO distributed radar imaging system, the antenna array consists of transmit–receive subarrays, as illustrated in Figure 1. In each subarray, antennas are uniformly distributed: receiving antennas with spacing d and transmitting antennas spaced at intervals of . Under far-field conditions, each transmit–receive subarray can be equivalent virtual elements. The spacing between virtual subarrays is , where , and d equals to a half-wavelength, i.e., . Thus, this array is considered to be a sparse array. Due to sparsity of the array, the spatial sampling along the array aperture fails to satisfy the Nyquist criterion, resulting in aliasing in the spatial frequency domain. It leads to the presence of grating lobes in the reconstructed image, thereby degrading the imaging quality. Addressing this issue is the primary objective of this study.
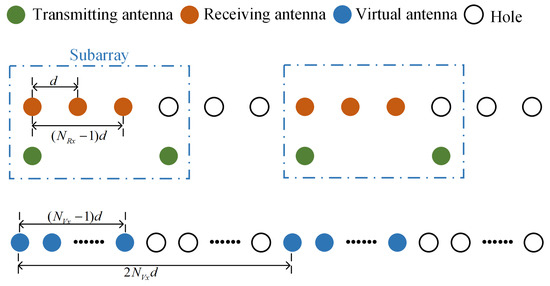
Figure 1.
Schematic depiction of the distributed array arrangement.
2.2. Array Imaging
Under far-field conditions, for the convenience of analysis, the radar transmission signal is approximated as propagating in the form of a plane wave. Consequently, each pair of transmitting and receiving signals can be approximately represented by a virtual array element. However, this approximation becomes invalid in near-field conditions. According to spherical wave propagation theory, array imaging need be computed based on the actual positions of both the transmitting and receiving elements. Therefore, in this study, a multistatic BP [22] was employed for imaging.
Taking a point target as an example, the imaging schematic is shown in Figure 2. In the Cartesian coordinate system, the linear MIMO array is along the x-axis direction. The positions of the m-th transmitting and n-th receiving antennas are denoted as and . The position of the point target is denoted as , and the reflectance is .
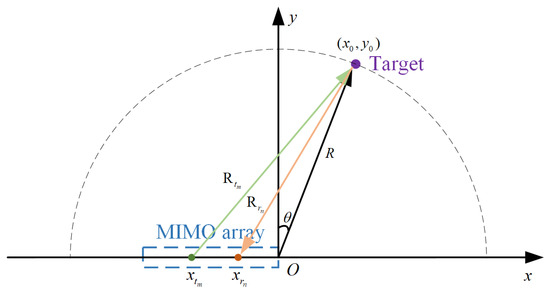
Figure 2.
Near-field MIMO array imaging model.
and represent the distances between the point target and the transmit and receive antenna elements, respectively, and they have the following relationship:
Let c represent the speed of light, and the propagation delay between transmitting and receiving antennas can be expressed as
Assume that the transmitted signal is a frequency-modulated continuous wave (FMCW), in which the frequency increases linearly with time and based on the dechirp radar system. The echo signal is dechirped by multiplying with the transmitted signal and applying a low-pass filter, converting the high-frequency into a low-frequency beat signal. And the echo data received by the n-th receiving element from the m-th transmitting antenna can be expressed as follows [23,24]:
where f represents the FMCW frequency, K represents the frequency modulation slope, and t represents the time. The Fourier transform range is applied to (3) to obtain a one-dimensional range image:
The imaging region containing the target is divided into a series of two-dimensional grids. For a certain grid point in the imaging region, the distance between the transceiver antenna and the grid point is obtained by geometric relation:
The corresponding distance propagation delay of grid points is obtained as follows:
Interpolation of the one-dimensional distance image is necessary to compensate for the mismatch between grid points. The phase term of the grid point to be compensated can be determined based on propagation delay:
Applying the phase compensation from (7) to , the compensated result can be expressed as follows:
After traversing all antennas and coherently superimposing the back projection values of the corresponding grid points, we obtain the image H.
where M and N represent the number of transmitting elements and receiving elements in the radar array, respectively; H represents the back projection value of the grid point after coherent superposition. It can be found that when the distance between the grid point and the radar is exactly equal to the distance between the target and the radar, the amplitude of the back projection value is higher, while the back projection value of the non-target region is smaller.
This study focuses on BP imaging of sparse arrays. However, the presence of grating lobes significantly reduces the imaging quality. The following section mainly discusses the sparse reconstruction method for the issue.
3. Sparse Reconstruction Issues and Solving
3.1. Optimization Problem Expression
We first introduce azimuth vectors which can be calculated based on the steering vector of the array configuration in the proposed method. Since this study addresses the near-field grating lobe image processing problem in sparse arrays, the waveform is considered as a spherical wave. And the steering vector at a distance R and angle can be expressed as
where the number of transmitting elements is , and the number of receiving elements is . denotes the transpose operation. . represents the phase term of the signal received by the n-th receiving element from the m-th transmitting element at .
Then, we introduce an overcomplete representation in terms of all possible source locations. Let be a sampling grid of all source locations of interest, where the number of potential source locations will typically be much greater than the number of targets. We construct a matrix composed of steering vectors corresponding to each potential source as its columns:
where . If the potential target azimuth angle is , the array factor can be expressed as
where . denotes the conjugate operation. Then, the azimuth vector can be expressed as
where represents the array azimuth vector for the angle . The image information h at distance R can be expressed as the summation of azimuth vectors at various possible angles, with each multiplied by a corresponding weight, as illustrated in Figure 3.
where is the corresponding weight variable for and contains the angle information of the target. represents an BP image vector at distance R. For the convenience of later analysis, noise effects in the system and transmission process were not considered.
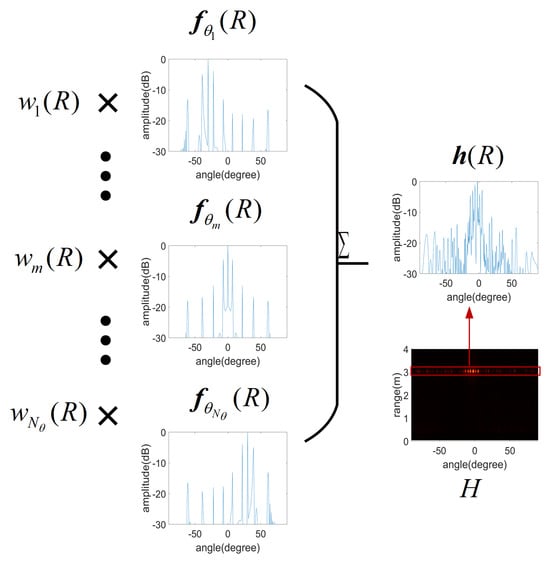
Figure 3.
Illustration depicting decomposition of image information.
Finally, we treat the solution of in (15) as a sparse reconstruction problem. The reconstruction problem for the signal is formulated as an optimization problem for the weight vector . The weight vector is expressed as
Through (14), we can obtain the matrix that includes azimuth vector for various angles.
where . Based on (15), (16), and (17), we can formulate the optimization problem. The problem for solving the weight vector can be viewed as a Lasso form:
where denotes the norm of , and denotes the norm of . can balance the reconstruction performance and sparsity as a weighting factor. The weight vector obtained after solving contains the angular information of the targets at distance R. Iterating through all distances in the image completes the sparse reconstruction of the grating lobe image.
It is worth mentioning that the choice of the parameter depends on the errors of the sparse array in practical applications. When the azimuth vector of the sparse array in practical applications deviates, it exhibits minimal deviation from the theoretical model described in (14), where . Conversely, if the deviation is significant, then . However, based on our experience, provides a good balance, as suggested by the original formula. In cases of uncertainty, it should be considered the preferred value and will be used in the later experiments.
3.2. Implementation Using ADMM
Apparently, (18) can be solved by utilizing the CVX toolbox. However, due to the slow convergence rate of the algorithms in CVX toolbox, we utilized the ADMM to accelerate solving (18) [25,26,27]. For the convenience of later analysis, let , , , and introduce an additional variable z. Then, the problem (18) can rewritten as
The augmented Lagrange function of (19) can be expressed as
where y and represent the Lagrange multiplier and penalty parameter, respectively. In theory, the value of does not affect the optimal solution of (20) within a reasonable range. However, a smaller slows convergence, while a large may degrade the solution quality. Empirically, based on our experience, setting provides an optimal tradeoff. Equation (20) can be solved through alternating iterative steps as follows:
where k represents the k-th iteration, and the expanded solution of (20) can be expressed as
Taking the derivatives with respect to x and z, we obtain closed-form solutions:
It is important to note that (19) is formulated as an -regularized least squares expression, widely utilized in compressed sensing and sparse recovery, as mentioned in [27]. Therefore, as a classical convex optimization problem, (19) is guaranteed the existence of a convergent solution and is considered to have reached convergence when the update step in (21) decreases below a specified threshold. Through an iterative solution of (23) for the weight vector at all distances, we achieve the sparse reconstruction image. The detailed instruction of the proposed method is shown in Algorithm 1.
| Algorithm 1 Sparse reconstruction algorithm. |
|
In this section, the imaging problem is treated as a convex optimization problem for sparse reconstruction. Moreover, the ADMM is employed to formulate iterative expressions, facilitating the accelerated resolution of the convex optimization problem.
4. Results
Through numerical simulations and experiments, the validity of the proposed algorithm in suppressing grating lobes for sparse array imaging was verified. To further demonstrate the performance of the proposed algorithm, we compared it with the sum and difference beams [17], which is abbreviated as SDB, and the PCF [16]. In the simulations, to illustrate the universality of the proposed algorithm, imaging results from two different arrays were considered. The topologies of the two arrays are shown in Figure 4. Therein, array I follows the same configuration as mentioned in [24]. In contrast, array II is an optimized sparse array design, as proposed in [28]. In the simulations and experiments, the classical BPA was employed for imaging. The image region and size impact the image quality and processing speed. To clearly present the experimental settings and results, Table 1 lists the radar system parameters and relevant details of the image parameters.
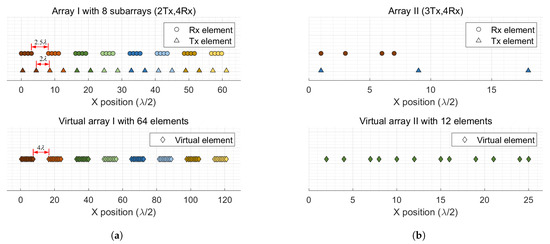
Figure 4.
The topologies of the two arrays. (a) The topology of array I. (b) The topology of array II.

Table 1.
System parameters used in the simulation and experiment setup.
4.1. Simulation Results
In the numerical simulation of array I, the positions of the two point targets are (5 m, 0°) and (5 m, −5°). Figure 5 illustrates the imaging results of the point targets for array I. To facilitate a clearer comparison, Figure 6 presents the cross-sectional results at the distance of 5 m.
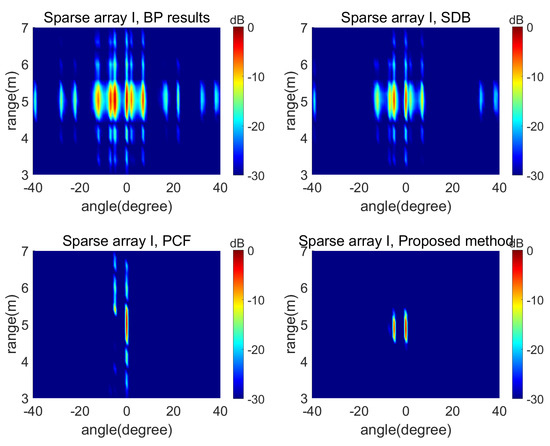
Figure 5.
The results of sparse array I.
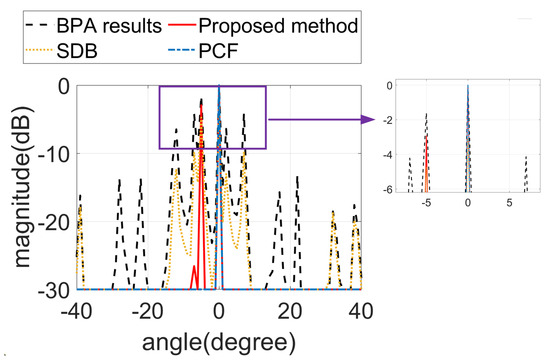
Figure 6.
The cross-sectional results of array I.
The results demonstrate that SDB offered only limited suppression of grating lobes, and the PCF, despite its significant suppression capability, obscured one of the targets. In contrast, the proposed algorithm effectively suppressed grating lobes while accurately preserving the target information.
In the numerical simulation of array II, three point targets were introduced to enhance target diversity and were positioned at (4 m, −7°), (4 m, 7°), and (6 m, 10°). The simulation results for array II are presented in Figure 7. Furthermore, Figure 8 illustrates the cross-sectional profile at 4 m for a more detailed comparison.
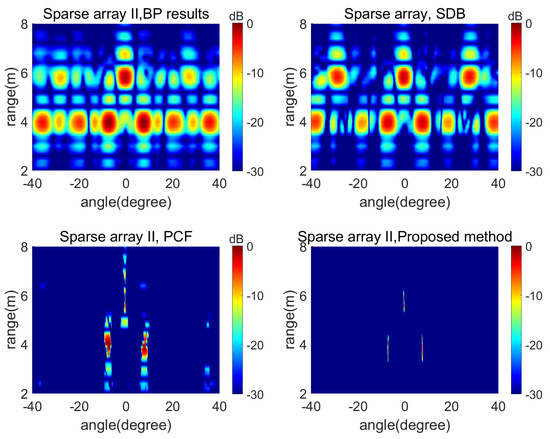
Figure 7.
The results of sparse array II.
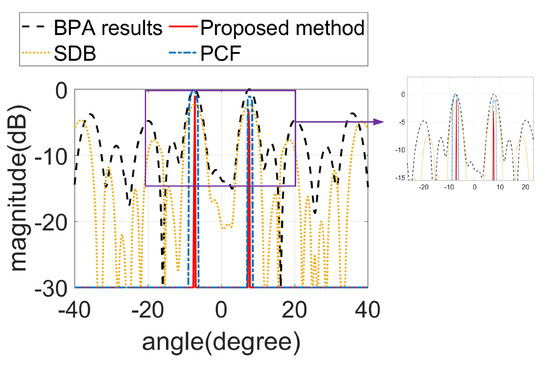
Figure 8.
The cross-sectional results of array II.
Compared to the results of array I, it can be observed that due to the wider angular separation of the targets, the PCF no longer exhibited erroneous suppression. Meanwhile, SDB and the proposed method maintained performance consistent with their results for array I. The proposed algorithm still maintained effective grating lobe suppression performance in the array II, further highlighting its versatility and broad applicability. In addition, it is worth noting that the results in Figure 5 and Figure 7 are presented with an SNR setting as 5.
To quantitatively evaluate the performance of the proposed algorithm, we used an ideal image without grating lobes as the reference and introduced the structural similarity index (SSIM), root mean square error (RMSE), and peak signal-to-noise ratio (PSNR) as evaluation metrics. A higher SSIM, lower RMSE, and higher PSNR indicate that the reconstructed image more closely resembles the reference image, demonstrating better grating lobe suppression performance.
To assess the sensitivity of each method to measurement noise and signal distortion in practical scenarios, we present the SSIM, RMSE, and PSNR results of both arrays under different SNR conditions, as shown in Figure 9. The results demonstrate that SDB exhibited relatively poor performance due to its limited capability in suppressing grating lobes. While the PCF performed well at high SNR, its effectiveness deteriorated under low-SNR conditions due to reduced signal coherence, resulting in less effective grating lobe suppression. In contrast, the proposed algorithm consistently maintained strong performance, even in low-SNR conditions.
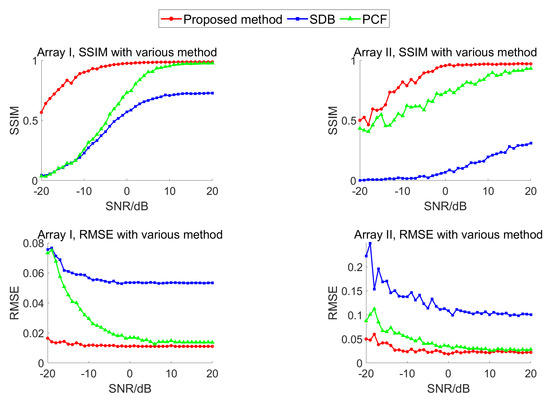
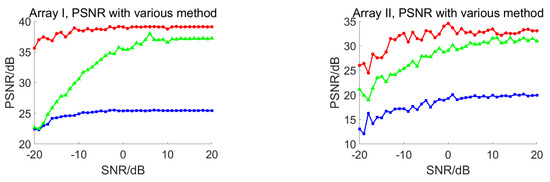
Figure 9.
The SSIM, RMSE, and PSNR results of both arrays under different SNR conditions.
4.2. Experimental Results
This section presents the results of sparse array imaging in practical scenarios, demonstrating that the proposed method significantly improves the imaging quality of sparse arrays. In the practical experiment, we employed sparse array I for imaging, and the parameters were consistent with the simulation settings. We placed two closely spaced corner reflectors at a distance of 3 m from the radar for BP imaging. The practical scenarios are shown in Figure 10. The processing effects of various methods on the images are depicted in Figure 11. To provide a clearer and more intuitive presentation of the results, we have also presented the cross-sectional at the target locations, as shown in Figure 12.

Figure 10.
Actual test scene.
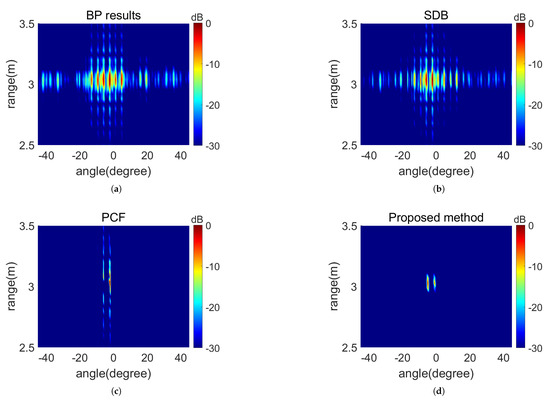
Figure 11.
(a) The original BP image. (b) Result of sum and difference beams. (c) Result of PCF. (d) Result of the proposed method.
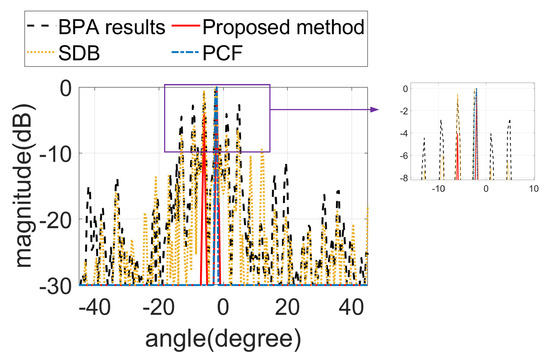
Figure 12.
The cross-sectional results of the experiment.
In the experiment, since there were no imaging results without grating lobes as benchmark, we introduced the metrics commonly used in imaging algorithms, including image entropy (IE) and image contrast (IC), to quantify the performance of various methods. In the image results, a lower IE and higher IC indicate better image quality and more effective grating lobe suppression. Table 2 presents the experimental results for image entropy and contrast across the different algorithms.

Table 2.
Performance comparison of various methods.
The experimental results demonstrate that the proposed algorithm achieved better suppression than both SDB and the PCF. Additionally, due to the proximity of target angles, the PCF erroneously treated one of the targets as a grating lobe and suppressed it. This is consistent with the simulation results, thereby highlighting the significant grating lobe suppression performance and versatility of the proposed algorithm.
4.3. Analysis of Computational Speed
In order to accelerate the computation, we applied the ADMM. Additionally, we also compared some classic optimization algorithms, such as the gradient descent [29] and proximal point algorithm (PPA) [30]. To ensure a fair comparison, we evaluated the computational time of each algorithm to obtain the results shown in Figure 11, where the gradient descent, PPA, and ADMM are shown in comparison with the results of the proposed method. Table 3 presents a comparison of runtime among different methods. The calculation time was based on an Intel Core i7-12700H at 2.3 GHz, Intel Corporation, Santa Clara, CA, USA. From the table, it can be observed that using the ADMM algorithm took only a few seconds, greatly improving computational speed compared to other optimization methods. Nevertheless, the proposed algorithm still required substantially more computational time than SDB and the PCF. This represents one of the limitations of the proposed algorithm.

Table 3.
Comparison of runtime.
5. Conclusions
This study addressed the problem of grating lobes imaging with sparse arrays and proposed a new sparse reconstruction method based on near-field conditions. The approach formulated the optimization problem based on the real array element. It transformed the problem into an optimization problem and formulated the relevant expressions. Furthermore, considering the high computational complexity, the ADMM method was employed to accelerate the solution of the problem. Experiment results demonstrate that the proposed method worked better than the existing grating lobes suppression algorithm such as sum and difference beams and the PCF. Compared to neural-network-based algorithms, the proposed method offers faster execution speed and greater convenience, avoiding extensive data training and processing. Furthermore, both theoretical analysis and simulations proved that the proposed algorithm is adaptable to any array configuration.
Despite the significant advantages of the proposed algorithm in terms of performance and versatility, it also has certain limitations. Since the algorithm performs sparse reconstruction based on different range bins, its effectiveness may not be ideal in complex target scenarios, especially when there are many targets at the same distance. Additionally, although the algorithm has been accelerated using the ADMM, it still struggles to meet the high real-time imaging requirements of certain application scenarios.
Finally, the proposed algorithm holds great potential for practical applications such as larger aperture radar arrays and less stringent real-time imaging systems. However, its performance in handling complex target scenarios and its computational speed still require further improvement. Moreover, this study focuses solely on imaging stationary targets. However, in practical applications, moving target imaging is an inevitable scenario. Based on theoretical analysis, the proposed algorithm remains applicable as long as the velocity information is known in advance or estimated beforehand. These limitations require further investigation and will be the focus of our future research.
Author Contributions
Conceptualization, J.W.; methodology, Y.W.; software, Y.W.; validation, Y.W.; formal analysis, Y.W. and G.H.; investigation, P.C.; resources, J.H.; data curation, J.H.; writing—original draft preparation, Y.W.; writing—review and editing, Y.W. and G.H.; visualization, Y.W.; supervision, P.C.; project administration, P.C.; funding acquisition, J.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Jianbing and Lingyan Key Research and Development Program of Zhejiang Province of China under Grant No. 2023C01148.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chen, D.; Nanzer, J.A. Privacy Preserving Contraband Detection Using a Millimeter-Wave Dynamic Antenna Array. IEEE Microw. Wireless Technol. Lett. 2023, 33, 915–918. [Google Scholar] [CrossRef]
- Bono, F.M.; Polinelli, A.; Radicioni, L.; Benedetti, L.; Castelli-Dezza, F.; Cinquemani, S.; Belloli, M. Wireless Accelerometer Architecture for Bridge SHM: From Sensor Design to System Deployment. Future Internet 2025, 17, 29. [Google Scholar] [CrossRef]
- Guo, T.; Wang, Y.; Xu, L.; Mei, M.; Shi, J.; Dong, L.; Xu, Y.; Huang, C. Joint communication and sensing design for multihop RIS-aided communication systems in underground coal mines. IEEE Internet Things J. 2023, 10, 19533–19544. [Google Scholar] [CrossRef]
- Shen, Z.; Nunez-Yanez, J.; Dahnoun, N. Advanced millimeter-wave radar system for real-time multiple-human tracking and fall detection. Sensors 2024, 24, 3660. [Google Scholar] [CrossRef]
- Chen, X.; Yang, Q.; Wang, H.; Zeng, Y.; Deng, B. Adaptive ADMM based high-quality fast imaging algorithm for short-range MMW MIMO-SAR systems. IEEE Trans. Antennas Propag. 2023, 71, 8925–8935. [Google Scholar] [CrossRef]
- Song, T.; Yao, X.; Wang, L.; Wang, Y.; Sun, G. Fast Factorized Kirchhoff Migration Algorithm for Near-Field Radar Imaging with Sparse MIMO Arrays. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–14. [Google Scholar] [CrossRef]
- Syeda, R.Z.; Adela, B.B.; van Beurden, M.C.; Zeijl, P.T.M.v.; Smolders, A.B. Design of a mm-wave MIMO radar demonstrator with an array of FMCW radar chips with on-chip antennas. In Proceedings of the 16th European Radar Conference, Paris, France, 2–4 October 2019; pp. 33–36. [Google Scholar]
- Qu, H.; Zhai, L. Optimization of Sparse synthesis aperture imaging array on hexagonal grids with difference basis. In Proceedings of the 2014 IEEE International Conference on Signal Processing, Communications and Computing, Guilin, China, 5–8 August 2014; pp. 544–548. [Google Scholar]
- Merlo, J.M.; Wagner, S.; Lancaster, J.; Nanzer, J.A. Fully Wireless Coherent Distributed Phased Array System for Networked Radar Applications. IEEE Microw. Wirel. Technol. Lett. 2024, 34, 837–840. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Merlo, J.M.; Mghabghab, S.R.; Schlegel, A.; Nanzer, J.A. Multiobjective Distributed Array Beamforming in the Near Field Using Wireless Syntonization. IEEE Microw. Wirel. Technol. Lett. 2023, 33, 775–778. [Google Scholar] [CrossRef]
- Zhu, J.; Lei, P.; Wang, J.; Zhang, Y.; Yuan, C. Grating Lobe Suppression and Angle Estimation Based on Virtual Antennas Filling in Sparse Array. IEEE Antennas Wirel. Propag. Lett. 2023, 22, 502–506. [Google Scholar] [CrossRef]
- Goffer, A.P.; Kam, M.; Herczfeld, P.R. Design of phased arrays in terms of random subarrays. IEEE Trans. Antennas Propag. 1994, 42, 820–826. [Google Scholar] [CrossRef]
- Alshammary, A.; Weiss, S.; Almorqi, S. Grating lobe suppression in rotationally tiled arrays. In Proceedings of the 11th European Conference on Antennas and Propagation, Paris, France, 19–24 March 2017; pp. 1158–1161. [Google Scholar]
- Feng, B.K.; Jenn, D.C. Two-way pattern grating lobe control for distributed digital subarray antennas. IEEE Trans. Antennas Propag. 2015, 63, 4375–4383. [Google Scholar] [CrossRef]
- Feng, B.K.; Jenn, D.C. Grating lobe suppression for distributed digital subarrays using virtual filling. IEEE Antennas Wirel. Propag. Lett. 2013, 12, 1323–1326. [Google Scholar] [CrossRef]
- Lv, J.; Song, Y.; Li, Z.; Wu, J. A Grating Lobe Suppression Approach for Distributed Mimo Array Radar Backprojection Algorithm. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 3444–3447. [Google Scholar]
- Han, K.; Hong, S. High-resolution phased-subarray MIMO radar with grating lobe cancellation technique. IEEE Trans. Microw. Theory Techn. 2022, 70, 2775–2785. [Google Scholar] [CrossRef]
- Zhu, R.; Zhou, J.; Jiang, G.; Cheng, B.; Fu, Q. Grating lobe suppression in near range MIMO array imaging using zero migration. IEEE Trans. Microw. Theory Techn. 2020, 68, 387–397. [Google Scholar] [CrossRef]
- Bazzi, A.; Slock, D.T.M.; Meilhac, L.; Panneerselvan, S. A comparative study of sparse recovery and compressed sensing algorithms with application to AoA estimation. In Proceedings of the 2016 IEEE 17th International Workshop on Signal Processing Advances in Wireless Communications, Edinburgh, UK, 3–6 July 2016; pp. 1–5. [Google Scholar]
- Mwisomba, C.; Abdalla, A.T.; Amour, I.; Mkemwa, F.; Maiseli, B. Fast sparse image reconstruction method in through-the-wall radars using limited memory Broyden–Fletcher–Goldfarb–Shanno algorithm. Int. J. Microw. Wirel. Technol. 2022, 14, 739–749. [Google Scholar] [CrossRef]
- Hashempour, H.R. A fast ADMM-based approach for high resolution ISAR imaging. Electron. Lett. 2020, 56, 954–957. [Google Scholar] [CrossRef]
- Dedai, M.D.; Jenkins, W.K. Convolution back-projection image reconstruction for Spotlight Mode Synthetic Aperture radar. IEEE Trans. Image Process. 1992, 1, 505–516. [Google Scholar]
- Wang, Y.; Wang, J.; He, G.; Song, T.; Zhu, J.; Zhang, C.; He, X. Enhancing 3D SAR Imaging: A Near-Field Back Projection Algorithm for Addressing Geometric Distortion. In Proceedings of the IGARSS 2024 IEEE International Geoscience and Remote Sensing Symposium, Athens, Greece, 7–12 July 2024; pp. 9648–9652. [Google Scholar]
- He, J.; Wang, J.; Yang, B.; Zhao, K.; Bao, Y.; Wang, Y.; Geng, X. Near-Field Radar Imaging Using MMIC-Based Large-Aperture Array. IEEE Sens. J. 2024, 24, 30863–30874. [Google Scholar] [CrossRef]
- Zou, H. The Adaptive Lasso and Its Oracle Properties. J. Am. Stat. Assoc. 2006, 101, 1418–1429. [Google Scholar] [CrossRef]
- Boyd, S. Distributed optimization and statistical learning via the alter-ating direction method of multipliers. Found. Trends Mach. Learn. 2010, 3, 1–122. [Google Scholar] [CrossRef]
- Kim, S.-J.; Koh, K.; Lustig, M.; Boyd, S.; Gorinevsky, D. An interior-point method for large-scale ℓ1-regularized least squares. IEEE J. Sel. Topics Signal Process. 2007, 1, 606–617. [Google Scholar] [CrossRef]
- Xu, L.; Sun, S.; We, R.; Ren, D.; Li, J. Generalized Optimization of Sparse Antenna Arrays for High-Resolution Automotive Radar Imaging. In Proceedings of the 2023 57th Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 29 October–1 November 2023; pp. 1215–1219. [Google Scholar]
- Haji, S.H.; Abdulazeez, A.M. Comparison of optimization techniques based on gradient descent algorithm: A review. PalArch’s J. Archaeol. Egypt/Egyptol. 2021, 18, 2715–2743. [Google Scholar]
- Parikh, N.; Boyd, S. Proximal algorithms. Found. Trends Optim. 2014, 1, 127–239. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).