Adaptive Selective Disturbance Elimination-Based Fixed-Time Consensus Tracking for a Class of Nonlinear Multiagent Systems

Abstract

This paper addresses the problem of fixed-time consensus tracking for a class of nonlinear multiagent systems (MASs) with disturbances. We establish a novel fixed-time consensus tracking protocol with adaptive disturbance rejection capabilities, leveraging adaptive selective disturbance elimination (ASDE) technology. This protocol consists of a distributed fixed-time observer (DFTO), a fixed-time disturbance observer (FTDO), and an adaptive selective disturbance elimination backstepping controller (ASDE) with adaptive lumped disturbance compensation abilities. The DFTO estimates the leader’s output using the communication network topology of each follower, while the FTDO rapidly observes the lumped disturbances and their derivatives. By adding disturbance indicator terms and disturbance observation attenuation terms to the control law, the beneficial and harmful effects of disturbance are distinguished. Under favorable disturbance conditions, lumped disturbances can be used to accelerate tracking speed. If disturbances are harmful, they are adaptively compensated to improve tracking accuracy. Furthermore, the fixed-time stability of each part of the protocol is analyzed using Lyapunov theory. Simulation results show that, under different initial states and command inputs, the proposed method achieves faster convergence and smaller tracking errors compared to the adaptive conditional disturbance negaton backstepping controller (ACDN), conditional disturbance negation backstepping controller (CDN), and non-smooth backstepping controller (NBCDC), verifying the effectiveness of the proposed method. The research outcomes serve as a reference for future multiagent adaptive anti-disturbance cooperative control technology.

1. Introduction

Motivated by the increasing application demands in both military and civilian domains, the distributed cooperative control of multiagent systems (MASs) has garnered considerable attention in recent years. In the realm of multiagent distributed cooperative control, the design of leader–follower consensus tracking protocols emerges as a fundamental and vital issue. Therefore, designing a consensus tracking protocol with excellent performance is crucial.

Developing consensus tracking protocols for MASs with disturbances involves two key issues. The first issue focuses on the convergence of the consensus protocols. The convergence rate is a pivotal performance specification of MASs, which reflects specifications in classical control such as rise time, settling time, overshoot, and steady-state error. Hence, it warrants primary attention. Numerous relevant studies have been conducted, broadly categorized into four types: asymptotic consensus convergence [1,2], finite-time consensus convergence [3], fixed-time consensus convergence [4,5,6,7], and predefined/prescribed-time consensus convergence [8].

The conventional linear distributed consensus tracking protocols can only achieve asymptotic consensus convergence [9,10,11,12], enabling each agent in MASs to reach consensus tracking only as the time approaches infinity, among which the representative work includes [1,2]. However, the main challenges with asymptotic consensus convergence are as follows: (1) consensus can only be attained as the time approaches infinity, limiting its applicability, and (2) if the system contains a distributed state observer, a controller, and a disturbance observer, the consensus protocol does not satisfy the “separation principle”, and its stability must be analyzed as a whole, which is difficult for MASs with complex structures. The concept of finite-time consensus convergence dates back to the 1960s and has since been introduced into MASs. Although this method demonstrates commendable control precision, robustness, and anti-disturbance ability, its estimation of settling time relies on initial conditions. Additionally, the practicality of this method is significantly constrained when the states of each agent are unmeasurable.

To address the problems associated with the aforementioned finite-time consensus/finite-time control, researchers have introduced fixed-time consensus convergence/finite-time control methods [13,14,15,16,17,18,19,20,21,22]. One distinguishing feature is the incorporation of a fractional-order non-smooth term, enabling the estimation of an upper bound on the settling time without requiring any initial condition information. The fixed-time consensus was initially discussed and defined in [14,23], respectively. The initial investigation into fixed-time consensus for MASs is presented in [24], where a nonlinear control protocol is introduced to ensure fixed-time convergence for MASs characterized by basic integrator dynamics. Additionally, Zuo and Tie [25] developed a consensus protocol for MASs. Building upon this work, Fu and Wang [26] further refined the findings of [25] by providing an upper-bound estimation. Although these methods suffer from discrepancies between estimated and actual settling times, as well as dependency on controller parameters, their excellent “separation principle” is beneficial for the theoretical proof of consensus tracking in MASs with disturbances. Moreover, recent revolutionary advancements in electronic and computer technology have substantially enhanced the computing speed of modern controllers. As a result, the challenges mentioned above can be effectively addressed through computational evolution methods. Therefore, we primarily center on addressing the fixed-time consensus challenge.

The second critical issue pertains to disturbance rejection. Disturbances are pervasive and diverse in control systems, significantly affecting the performance of the systems. For instance, when motors operate in weak-magnetic-field regions, they face parameter uncertainties and load disturbances. This introduces strong nonlinearities into the motor dynamics, negatively impacting the system’s control accuracy [27]. Consequently, anti-disturbance is a critical concern in the high-performance control. In fact, active anti-disturbance control algorithms have been widely adopted in fields such as PMSMs, robotics, and unmanned aerial vehicles. As the integration of individual systems, MASs also encounter the significant challenge of disturbance rejection. In recent research, Liu et al. [28] investigated the issue of achieving fixed-time consensus tracking in 2-order MASs in the presence of disturbances. To address this, they utilized a discontinuous sliding mode approach combined with a continuous super-twisting control strategy within the integral sliding mode (ISM) framework, ensuring disturbance compensation within an expected convergence time. However, this approach fails to accurately capture the disturbance variations, leading to imprecise compensation. Fortunately, the disturbance observer can effectively capture the dynamic changes of lumped disturbances, providing a precise basis for system compensation. And the disturbance observer-based anti-disturbance control method [29,30] exhibits superior accuracy compared to high-gain control. Disturbance observers come in various forms, with the most common being Extended State Observer (ESO) [31,32,33], disturbance observer (DOB) [34,35,36], and Generalized Proportional Integral Observer (GPIO) [37], among others. In anti-disturbance control, various uncertainties, such as unmodeled dynamics, parametric disturbances, external interferences, and nonlinear couplings, are considered as lumped disturbances. By observing the lumped disturbances and using feedforward compensation, the anti-disturbance control method exhibits superior performance compared to robust control and adaptive control. Tan and Hu [38] first proposed a fixed-time anti-disturbance nonlinear consensus tracking protocol for MASs under disturbances. By designing a distributed fixed-time state observer, disturbance observer, and non-smooth anti-disturbance backstepping controller, it has been demonstrated that utilizing disturbance feedforward compensation can improve the performance of closed-loop systems. However, the aforementioned methods all treat disturbances as detrimental factors to be completely compensated or suppressed, overlooking scenarios where disturbances can benefit the system dynamics, such as accelerating convergence speed. Fortunately, some researchers turned attention to this issue [39,40], introducing a conditional disturbance negation (CDN) technology that has been applied to omnidirectional mobile robots [41], autonomous underwater vehicles [42], and other fields. The effectiveness of the CDN-based control algorithm lies in its ability to differentiate between beneficial and detrimental disturbances, resulting in enhanced convergence and robustness.

Existing conditional disturbance negation control methods rely on the sign of the disturbance indicator to distinguish between disturbance compensation and utilization. In some cases, high-frequency switching of this sign causes ripples that degrade performance. While Sun et al. [43] proposed an adaptive conditional disturbance negation method, it reduces static performance and requires careful parameter tuning. This remains a challenge, especially for nonlinear MASs with disturbances. To tackle this, we propose a fixed-time consensus tracking protocol based on adaptive selective disturbance elimination. The method enhances tracking speed and accuracy by introducing disturbance indicators and observation attenuation terms while simplifying parameter tuning. Compared to existing works, the main innovations and contributions of this paper include three aspects:

• Unlike [43], this study introduces adaptive selective disturbance elimination in each agent’s tracking control design, incorporating disturbance indicator and disturbance observation attenuation terms in the control law. This distinguishes between beneficial and detrimental disturbances, leveraging beneficial disturbances to accelerate tracking and suppressing detrimental ones to improve tracking accuracy.
• In this study, a fixed-time disturbance observer is introduced to rapidly and accurately estimate lumped disturbances and their derivatives arising from unmodeled dynamics, parameter perturbations, external disturbances, and nonlinear couplings. Utilizing Lyapunov theory, the fixed-time stability of the disturbance observer is proven, representing a novel contribution to the field of multiagent consensus tracking.
• Additionally, an application framework for a fixed-time tracking protocol based on adaptive selective disturbance elimination is proposed. The protocol includes a distributed fixed-time observer for estimating the leader’s output under specific network topologies, a fixed-time disturbance observer for rapid estimation of lumped disturbances, and a fixed-time active anti-disturbance controller based on adaptive selective disturbance elimination, integrating the strengths of backstepping, nonlinear dynamic inversion, and conditional disturbance negation. The protocol leverages the “separation principle” and analyzes its fixed-time stability based on Lyapunov theory, demonstrating significant innovation.

This paper is organized as follows: Section 2 gives a problem formulation. Section 3 presents the technical details and theoretical proofs of the proposed fixed-time consensus tracking protocol. Simulations and analyses are given in Section 4, while some conclusions are outlined in Section 5.

2. Problem Formulation

Consider a multiagent system encompassing one leader and N followers, denoted as 0 and $i=1,2,\dots ,N$, respectively. The leader’s operational dynamics are characterized by the equations

$$\left\{\begin{array}{c}{\dot{x}}_{01}=f_{01}\left({\overline{\mathit{x}}}_{01}\right)+g_{01}\left({\overline{\mathit{x}}}_{\mathbf{01}}\right)x_{02},\hfill \\ {\dot{x}}_{02}=f_{02}\left({\overline{\mathit{x}}}_{02}\right)+g_{02}\left({\overline{\mathit{x}}}_{\mathbf{02}}\right)x_{03},\hfill \\ ⋮\hfill \\ {\dot{x}}_{0n}=f_{0n}\left({\overline{\mathit{x}}}_{0n}\right)+g_{0n}\left({\overline{\mathit{x}}}_{\mathbf{0}\mathit{n}}\right)u_0,\hfill \\ y_0=x_{01},\hfill \end{array}\right.$$

(1)

where ${\mathit{x}}_{\mathbf{0}}={[x_{01},x_{02},\dots ,x_{0n}]}^{\mathrm{T}}\in {\mathbb{R}}^n$ is the vector representing the leader’s state, while ${\overline{x}}_{0j}={[x_{01},\dots ,x_{0j}]}^{\mathrm{T}}$. The control input applied to the leader, denoted $u_0$, is a scalar, and the output produced by the leader is symbolized as $y_0$. The functions $f_{0j}(·)$ and $g_{0j}(·)$ for $j=1,2,\dots ,n$ are assumed to be continuously differentiable with locally Lipschitz derivatives.

In parallel, the dynamics of each follower are defined by the equations

$$\left\{\begin{array}{c}{\dot{x}}_{i1}=f_{i1}\left({\overline{\mathit{x}}}_{i1}\right)+g_{i1}\left({\overline{\mathit{x}}}_{\mathit{i}\mathbf{1}}\right)x_{i2}+d_{i1},\hfill \\ {\dot{x}}_{i2}=f_{i2}\left({\overline{\mathit{x}}}_{i2}\right)+g_{i2}\left({\overline{\mathit{x}}}_{\mathit{i}\mathbf{2}}\right)x_{i3}+d_{i2},\hfill \\ ⋮\hfill \\ {\dot{x}}_{in}=f_{in}\left({\overline{\mathit{x}}}_{in}\right)+g_{in}\left({\overline{\mathit{x}}}_{\mathit{in}}\right)u_i+d_{in},\hfill \\ y_i=x_{i1},\hfill \end{array}\right.$$

(2)

where ${\mathit{x}}_{\mathit{i}}={[x_{i1},\dots ,x_{in}]}^{\mathrm{T}}\in {\mathbb{R}}^n$ represents the state of the ith follower, and ${\overline{x}}_{ij}={[x_{i1},\dots ,x_{ij}]}^{\mathrm{T}}$. The scalar $u_i$ denotes the control input for the ith follower. $d_{ij}$ ($j=1,\dots ,n$) are disturbances. These disturbances consist of both model uncertainties and external factors. The functions $f_{ij}(·)$ and $g_{ij}(·)$ are pre-determined by system structure, with $g_{ij}(·)$ assumed to be non-singular entities.

The primary goal is to establish a fixed-time consensus tracking protocol, denoted by $u_i$, utilizing only localized information for each follower to achieve fixed-time coordination with the leader. In the context of multi-drone cooperative control and task execution, this protocol can achieve information sharing among drones and ensure that the entire system reaches a consistent state within a fixed time, thereby improving the reliability and efficiency of task execution. The fixed-time property ensures that for any initial conditions $y_i\left(0\right)$ with $i\in \{1,2,\dots ,N\}$, there exists a finite time interval $T_{max}$ such that

$$\left\{\begin{array}{c}\underset{t\to T_{max}}{lim}∥y_i\left(t\right)-y_0\left(t\right)∥=0,\hfill \\ y_i\left(t\right)=y_0\left(t\right),\forall t>T_{max}.\hfill \end{array}\right.$$

(3)

3. Adaptive Selective Disturbance Elimination Consensus Tracking

3.1. Distributed Fixed-Time Observer

Considering the partial accessibility of the leader’s state information to follower agents, we develop a distributed estimation framework for strict-feedback nonlinear affine systems. This architecture enables each follower to reconstruct the leader’s output, even when direct state measurement is limited to a subset of agents. Let the leader’s state vector be denoted as $x_{0,k}\in {\mathbb{R}}^n$ ($k=1,2,\dots ,n$) and its estimation generated by the ith follower as ${\widehat{x}}_{0,k}^i$. The proposed distributed fixed-time observer (DFTO) is constructed as follows:

$$\begin{array}{cc}\hfill {\dot{\widehat{x}}}_{0k}^i=& {\alpha }_k{⌈\sum _{j=1}^N{a}_{ij}({{\widehat{x}}^i}_{0k}-{{\widehat{x}}^j}_{0k})+b_i({{\widehat{x}}^i}_{0k}-x_{0k})⌋}^{1-{\displaystyle \frac{1}{\mu }}}+{\beta }_k{⌈\sum _{j=1}^N{a}_{ij}({{\widehat{x}}^i}_{0k}-{{\widehat{x}}^j}_{0k})+b_i({{\widehat{x}}^i}_{0k}-x_{0k})⌋}^{1+{\displaystyle \frac{1}{\mu }}}\hfill \\ & +f_{0k}\left({\overline{\widehat{\mathit{x}}}}_{\mathit{0}\mathit{k}}^{\mathit{i}}\right)+g_{0k}\left({\overline{\widehat{\mathit{x}}}}_{\mathit{0}\mathit{k}}^{\mathit{i}}\right){{\widehat{x}}^i}_{0k+1}+{\gamma }_k\mathrm{sign}\left[\sum _{j=1}^N{a}_{ij}({{\widehat{x}}^i}_{0k}-{{\widehat{x}}^j}_{0k})+b_i({{\widehat{x}}^i}_{0k}-x_{0k})\right]\hfill \\ & ·\sum _{m=1}^k\sum _{i=1}^N\left|\sum _{j=1}^N{a}_{ij}({{\widehat{x}}^i}_{0m}-{{\widehat{x}}^j}_{0m})+b_i({{\widehat{x}}^i}_{0m}-x_{0m})\right|,\hfill \\ \hfill k=& 1,2,\dots ,n-1,\hfill \\ & ⋮\hfill \\ \hfill {\dot{\widehat{x}}}_{0n}^i=& {\alpha }_n{⌈\sum _{j=1}^N{a}_{ij}({{\widehat{x}}^i}_{0n}-{{\widehat{x}}^j}_{0n})+b_i({{\widehat{x}}^i}_{0n}-x_{0n})⌋}^{1-{\displaystyle \frac{1}{\mu }}}+{\beta }_n{⌈\sum _{j=1}^N{a}_{ij}({{\widehat{x}}^i}_{0n}-{{\widehat{x}}^j}_{0n})+b_i({{\widehat{x}}^i}_{0n}-x_{0n})⌋}^{1+{\displaystyle \frac{1}{\mu }}}\hfill \\ & +f_{0n}\left({\overline{\widehat{\mathit{x}}}}_{\mathbf{0}\mathit{n}}^{\mathit{i}}\right)+c_n\mathrm{sign}\left[\sum _{j=1}^N{a}_{ij}({{\widehat{x}}^i}_{0n}-{{\widehat{x}}^j}_{0n})+b_i({{\widehat{x}}^i}_{0n}-x_{0n})\right]\hfill \\ & +{\gamma }_n\mathrm{sign}\left[\sum _{j=1}^N{a}_{ij}({{\widehat{x}}^i}_{0k}-{{\widehat{x}}^j}_{0k})+b_i{{\tilde{x}}^i}_{0k}\right]·\sum _{m=1}^n\sum _{i=1}^N\left|\sum _{j=1}^N{a}_{ij}({{\widehat{x}}^i}_{0m}-{{\widehat{x}}^j}_{0m})+b_i({{\widehat{x}}^i}_{0m}-x_{0m})\right|.\hfill \end{array}$$

(4)

Theorem 1.

If the observer parameters satisfy

$$\left\{\begin{array}{c}{\alpha }_k={\displaystyle \frac{\epsilon }{{\left[2{\lambda }_{min}(L+B)\right]}^{1-\frac{1}{2\mu }}}},\forall k=1,2,\dots ,n,\hfill \\ {\beta }_k={\displaystyle \frac{\epsilon ·N^{\frac{1}{2\mu }}}{{\left[2{\lambda }_{min}(L+B)\right]}^{1+\frac{1}{2\mu }}}},\forall k=1,2,\dots ,n,\hfill \\ c_n+\left|g_{0n}^{max}\left({\overline{\mathit{x}}}_{\mathbf{0}\mathit{n}}\right)u_0^{max}\right|\le 0,\hfill \\ {\gamma }_k{\lambda }_{min}(L+B)+\underset{i\in \nu }{max}∥\nabla f_{0k}^{\mathrm{T}}\left({\xi }_{\mathit{ik}}\right)∥\hfill \\ +\underset{i\in \nu }{max}∥\nabla g_{0k}^{\mathrm{T}}\left({\eta }_{\mathit{ik}}\right)∥·x_{0,k+1}^{max}\le 0,\forall k=1,2,\dots ,n-1,\hfill \\ {\gamma }_n{\lambda }_{min}(L+B)+\underset{i\in \nu }{max}∥\nabla f_{0n}^{\mathrm{T}}\left({\xi }_{\mathit{in}}\right)∥\le 0,\hfill \end{array}\right.$$

(5)

where $\epsilon <0$ and $\mu \in (0,1]$, then the observation errors of distributed observer (4) converges to zero in a fixed time bounded by

$$\begin{array}{c}\hfill T_o:={\displaystyle \frac{n\mu \pi }{\left|\epsilon \right|}}.\end{array}$$

(6)

For the corresponding definitions of the symbols and stability proofs, please refer to the paper [38].

Remark 1.

It is important to highlight that DFTO in this paper assumes a complete communication topology, where the information transmission between all followers and the leader is intact. However, in practical multiagent consensus tracking control scenarios, external noise or transmission delays may lead to incomplete information transmission in the communication network, affecting the overall control performance. In the future, research on enhancing the robustness of DFTO by addressing topology attacks will be meaningful.

3.2. Fixed-Time Disturbance Observer

Drawing upon the methodologies presented in references [38,44], this work introduces a fixed-time disturbance observer (FTDO) designed to estimate the lumped disturbances by the sliding mode technique, and its formulation is expressed as

$$\left\{\begin{array}{cc}\hfill {\dot{z}}_{ij}^1=& z_{ij}^2-k_{ij}^1{⌈z_{ij}^1-x_{ij}⌋}^{{\rho }_1}-k_{ij}^2{⌈z_{ij}^1-x_{ij}⌋}^{{\varrho }_1}+f_{ij}\left({\overline{\mathit{x}}}_{\mathit{ij}}\right)+g_{ij}\left({\overline{\mathit{x}}}_{\mathit{ij}}\right)x_{i(j+1)},\hfill \\ \hfill {\dot{z}}_{ij}^2=& z_{ij}^3-k_{ij}^3{⌈z_{ij}^1-x_{ij}⌋}^{{\rho }_2}-k_{ij}^4{⌈z_{ij}^1-x_{ij]}⌋}^{{\varrho }_2},\hfill \\ \hfill & ⋮\hfill \\ \hfill {\dot{z}}_{ij}^{l-1}=& z_{ij}^l-k_{ij}^{2l-3}{⌈z_{ij}^1-x_{ij}⌋}^{{\rho }_{l-1}}-k_{ij}^{2l-2}{⌈z_{ij}^1-x_{ij}⌋}^{{\varrho }_{l-1}},\hfill \\ \hfill {\dot{z}}_{ij}^l=& -k_{ij}^{2l-1}{⌈z_{ij}^1-x_{ij}⌋}^{{\rho }_l}-k_{ij}^{2l}{⌈z_{ij}^1-x_{ij}⌋}^{{\varrho }_l},\hfill \\ \hfill & j=1,\dots ,n-1,\hfill \end{array}\right.$$

(7)

$$\left\{\begin{array}{cc}\hfill {\dot{z}}_{in}^1=& z_{in}^2-k_{in}^1{⌈z_{in}^1-x_{in}⌋}^{{\rho }_1}-k_{in}^2{⌈z_{in}^1-x_{in}⌋}^{{\varrho }_1}+f_{in}\left({\overline{\mathit{x}}}_{\mathit{in}}\right)+g_{in}\left({\overline{\mathit{x}}}_{\mathit{in}}\right)u_i,\hfill \\ \hfill {\dot{z}}_{in}^2=& z_{in}^3-k_{in}^3{⌈z_{in}^1-x_{in}⌋}^{{\rho }_2}-k_{in}^4{⌈z_{in}^1-x_{in]}⌋}^{{\varrho }_2},\hfill \\ \hfill & ⋮\hfill \\ \hfill {\dot{z}}_{in}^{l-1}=& z_{in}^l-k_{in}^{2l-3}{⌈z_{in}^1-x_{in}⌋}^{{\rho }_{l-1}}-k_{in}^{2l-2}{⌈z_{in}^1-x_{in}⌋}^{{\varrho }_{l-1}},\hfill \\ \hfill {\dot{z}}_{in}^l=& -k_{in}^{2l-1}{⌈z_{in}^1-x_{in}⌋}^{{\rho }_l}-k_{in}^{2l}{⌈z_{in}^1-x_{in}⌋}^{{\varrho }_l},\hfill \end{array}\right.$$

(8)

where ${\rho }_m\in (0,1)$ and ${\varrho }_m>1$ for $m=1,2,\cdots ,l$ satisfy ${\rho }_i=i\rho -(i-1)$ and ${\varrho }_i=i\varrho -(i-1)$, with $\rho \in (1-{\iota }_1,1)$ and $\varrho \in (1,1+{\iota }_2)$ for sufficiently small ${\iota }_1>0$ and ${\iota }_2>0$. Observer gains $k_{ij}^g$, where $g=1,2,\cdots ,2l$, are selected such that the matrix $A_1$ and $A_2$ are Hurwitz

$$\begin{array}{cc}\hfill A_1=& \left[\begin{array}{ccccc}-k_{ij}^1& 1& 0& \cdots & 0\\ -k_{ij}^3& 0& 1& \cdots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ -k_{ij}^{2l-3}& 0& 0& \cdots & 1\\ -k_{ij}^{2l-1}& 0& 0& 0& 0\end{array}\right],A_2=\left[\begin{array}{ccccc}-k_{ij}^2& 1& 0& \cdots & 0\\ -k_{ij}^4& 0& 1& \cdots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ -k_{ij}^{2l-2}& 0& 0& \cdots & 1\\ -k_{ij}^{2l}& 0& 0& 0& 0\end{array}\right].\hfill \end{array}$$

(9)

Observer variables $z_{ij}^1,z_{ij}^2,\cdots ,z_{ij}^l$ ($j=1,2,\cdots ,n$) correspond to the estimations of $x_{ij}$, $d_{ij}$, ..., $d_{ij}^{(l-2)}$.

Remark 2.

The rate at which the observer achieves convergence plays a pivotal role in determining the overall efficacy of the control system, especially in emergency situations, where it is desirable to preset the expected convergence time of the observer. The FTDO designed in this paper is notable for its ability to estimate lumped disturbances within a finite and fixed time. In practical applications, the selection of the FTDO’s order l is critical and needs be determined based on the characteristics of the disturbed system. Note that in FTDO, the $(l-k+1)th$ order derivatives of $z_{i·}^k$($k=1,\dots l$) exist. There exists an inherent trade-off between the smoothness of disturbance estimation and the complexity of the FTDO. A fundamental compromise exists between the accuracy of disturbance estimation and the structural intricacy of the FTDO.

Theorem 2.

Considering systems described by (2), the observed values of lumped disturbances and their derivatives in the FTDO will reach a vicinity of the origin in a fixed time frame; the boundness of the convergence time can be expressed as

$$\begin{array}{c}\hfill T_{ij\_\mathrm{ob}}\le {\displaystyle \frac{{\lambda }_{max}^r\left(P_1\right)}{r_{1}r}}+{\displaystyle \frac{1}{r_2\sigma {{\rm Y}}^{\sigma }}},\end{array}$$

(10)

where $r=1-\rho$, $\sigma =\varrho -1$, $r_1={\displaystyle \frac{{\lambda }_{min}\left(Q_1\right)}{{\lambda }_{max}\left(P_1\right)}}$, $r_2={\displaystyle \frac{{\lambda }_{min}\left(Q_2\right)}{{\lambda }_{max}\left(P_2\right)}}$, positive real number ${\rm Y}\le {\lambda }_{min}\left(P_2\right)$, positive definite matrix $Q_1,Q_2\in {\mathbb{R}}^{n\times n}$ and $P_1$, $P_2$ satisfy $Q_1+P_1{A}_1+A_1^{\mathrm{T}}{P}_1=0$ and $Q_2+P_2{A}_2+A_2^{\mathrm{T}}{P}_2=0$.

Proof. 

Define the estimation errors as ${\chi }_{ij}^1=x_{ij}-z_{ij}^1,{\chi }_{ij}^2=d_{ij}-z_{ij}^2,\cdots ,{\chi }_{ij}^l=d_{ij}^{(l-2)}-z_{ij}^l$. By combining (7), (8) with (2), we can obtain

$$\left\{\begin{array}{cc}\hfill {\dot{\chi }}_1=& {\chi }_2-k_{ij}^1{⌈{\chi }_1⌋}^{{\rho }_1}-k_{ij}^2{⌈{\chi }_1⌋}^{{\varrho }_1},\hfill \\ \hfill {\dot{\chi }}_2=& {\chi }_3-k_{ij}^3{⌈{\chi }_1⌋}^{{\rho }_2}-k_{ij}^4{\left.⌈{\chi }_1\right]}^{{\varrho }_2},\hfill \\ \hfill ⋮\\ \hfill {\dot{\chi }}_{l-1}=& {\chi }_l-k_{ij}^{2l-3}{⌈{\chi }_1⌋}^{{\rho }_{l-1}}-k_{ij}^{2l-2}{⌈{\chi }_1⌋}^{{\varrho }_{l-1}},\hfill \\ \hfill {\dot{\chi }}_l=& -k_{ij}^{2l-1}{⌈{\chi }_1⌋}^{{\rho }_l}-k_{ij}^{2l}{⌈{\chi }_1⌋}^{{\varrho }_l}+d_{ij}^{(l-1)}.\hfill \end{array}\right.$$

(11)

The proof process aligns with Theorem 1 from [44], though the detailed proof is omitted here for brevity. This implies that $|{\tilde{d}}_{ij}|=|{\widehat{d}}_{ij}-d_{ij}|\le {\delta }_{ij}$. □

3.3. Adaptive Selective Disturbance Elimination Backstepping Controller

3.3.1. Adaptive Selective Disturbance Elimination Backstepping Controller Design

Define the state tracking error $e_{i1}=x_{i1}-x_{i1d}$, $e_{ij}=x_{ij}-x_{ijc}(j=2,\dots n)$ and filtering error ${\xi }_{ij}=x_{ijc}-x_{ijd}(j=2,\dots n)$, where i represents the index of the follower, and j denotes the index of the state variable. The control design process is as follows.

Step 1: We consider $x_{i2}$ as a virtual control value to make $x_{i1}$ track $x_{i1d}$. The dynamics of $e_{i1}$ can be expressed as

$$\begin{array}{c}\hfill {\dot{e}}_{i1}={\dot{x}}_{i1}-{\dot{x}}_{i1\mathrm{d},}\end{array}$$

(12)

where ${\dot{x}}_{i1\mathrm{d}}$ is the derivative of $x_{i1\mathrm{d}}$.

Then, the stabilization function $x_{i2\mathrm{d}}$ is

$$\begin{array}{cc}\hfill x_{i2\mathrm{d}}=& g_{i1}^{-1}\left({\overline{\mathit{x}}}_{\mathit{i}\mathbf{1}}\right)[-K_{i1}^1{e}_{i1}-K_{i1}^2{⌈e_{i1}⌋}^{{\mu }_1}-K_{i1}^3{⌈e_{i1}⌋}^{{\mu }_2}-f_{i1}\left({\overline{\mathit{x}}}_{\mathit{i}\mathbf{1}}\right)+{\dot{x}}_{i1\mathrm{d}}\hfill \\ \hfill & -(1-{\mathrm{e}}^{-\lambda |e_{i1}|})\mathrm{sign}\left({\widehat{d}}_{i1}{e}_{i1}\right){\widehat{d}}_{i1}-{\mathrm{e}}^{-\lambda |e_{i1}|}{\widehat{d}}_{i1}],\hfill \end{array}$$

(13)

where $\lambda \ge 0,0<{\mu }_1<1,{\mu }_2>1$, e is Euler’s number and $K_{i1}^1$, $K_{i1}^2$, $K_{i1}^3>0$.

The first command filter is designed as

$$\begin{array}{cc}\hfill {\tau }_{i2}·{\dot{x}}_{i2\mathrm{c}}=& -{\kappa }_{i2}^1{⌈x_{i2\mathrm{c}}-x_{i2\mathrm{d}}⌋}^{{\mu }_1}-{\kappa }_{i2}^2\left(x_{i2\mathrm{c}}-x_{i2\mathrm{d}}\right)-{\kappa }_{i2}^3{⌈x_{i2\mathrm{c}}-x_{i2\mathrm{d}}⌋}^{{\mu }_2}.\hfill \end{array}$$

(14)

Obviously, the dynamic of ${\xi }_{i2}$ is

$$\begin{array}{cc}\hfill {\tau }_{i2}{\dot{\xi }}_{i2}=& -{\kappa }_{i2}^1{⌈{\xi }_{i2}⌋}^{{\mu }_1}-{\kappa }_{i2}^2{\xi }_{i2}-{\kappa }_{i2}^3{⌈{\xi }_{i2}⌋}^{{\mu }_2}-{\tau }_{i2}{\dot{x}}_{i2\mathrm{d}},\hfill \end{array}$$

(15)

where ${\tau }_{i2}$ is a time constant and ${\kappa }_{i2}^1$, ${\kappa }_{i2}^2$, and ${\kappa }_{i2}^3$ are appropriate positive gains. It is assumed that ${\dot{x}}_{i2\mathrm{d}}$ is bounded, and a known positive constant $B_{i2}$ exists satisfying $B_{i2}=\sup ∥{\dot{x}}_{i2\mathrm{d}}∥$.

Combining ${\xi }_{i2}=x_{i2\mathrm{c}}-x_{i2\mathrm{d}}$ with $e_{i2}=x_{i2}-x_{i2\mathrm{c}}$ yields

$$\begin{array}{c}\hfill x_{i2}=x_{i2\mathrm{d}}+e_{i2}+{\xi }_{i2}.\end{array}$$

(16)

Considering (2) and (16), ${\dot{x}}_{i1}$ can be rewritten as

$$\begin{array}{cc}\hfill {\dot{x}}_{i1}=& f_{i1}\left({\overline{\mathit{x}}}_{i1}\right)+g_{i1}\left({\overline{\mathit{x}}}_{\mathit{i}\mathbf{1}}\right)(x_{i2\mathrm{d}}+e_{i2}+{\xi }_{i2})+d_{i1},\hfill \\ \hfill =& -K_{i1}^1{e}_{i1}-K_{i1}^2{⌈e_{i1}⌋}^{{\mu }_1}-K_{i1}^3{⌈e_{i1}⌋}^{{\mu }_2}+g_{i1}\left({\overline{\mathit{x}}}_{\mathit{i}\mathbf{1}}\right){\xi }_{i2}+g_{i1}\left({\overline{\mathit{x}}}_{\mathit{i}\mathbf{1}}\right)e_{i2}\hfill \\ \hfill & -(1-{\mathrm{e}}^{-\lambda |e_{i1}|})\mathrm{sign}\left({\widehat{d}}_{i1}{e}_{i1}\right){\widehat{d}}_{i1}-{\mathrm{e}}^{-\lambda |e_{i1}|}{\widehat{d}}_{i1}+d_{i1}+{\dot{x}}_{i1d}.\hfill \end{array}$$

(17)

Next, substituting (17) into (12) yields

$$\begin{array}{cc}\hfill {\dot{e}}_{i1}=& -K_{i1}^1{e}_{i1}-K_{i1}^2{⌈e_{i1}⌋}^{{\mu }_1}-K_{i1}^3{⌈e_{i1}⌋}^{{\mu }_2}+g_{i1}\left({\overline{\mathit{x}}}_{\mathit{i}\mathbf{1}}\right){\xi }_{i2}+g_{i1}\left({\overline{\mathit{x}}}_{\mathit{i}\mathbf{1}}\right)e_{i2}\hfill \\ \hfill & -(1-{\mathrm{e}}^{-\lambda |e_{i1}|}){\widehat{d}}_{i1}\mathrm{sign}\left({\widehat{d}}_{i1}{e}_{i1}\right)+(1-{\mathrm{e}}^{-\lambda |e_{i1}|})d_{i1}-{\mathrm{e}}^{-\lambda |e_{i1}|}({\widehat{d}}_{i1}-d_{i1}).\hfill \end{array}$$

(18)

Step j: Utilize $x_{i(j+1)},j=2,\cdots ,n-1$ to ensure $x_{ij}$ tracks $x_{ij\mathrm{c}}$. The dynamics of $e_{ij}$ can be described as

$$\begin{array}{c}\hfill {\dot{e}}_{ij}={\dot{x}}_{ij}-{\dot{x}}_{ij\mathrm{c}}.\end{array}$$

(19)

Subsequently, $x_{i(j+1)\mathrm{d}}$ can be defined as

$$\begin{array}{cc}\hfill x_{i(j+1)\mathrm{d}}=& g_{ij}^{-1}\left({\overline{\mathit{x}}}_{\mathit{ij}}\right)[-K_{ij}^1{e}_{ij}-K_{ij}^2{⌈e_{ij}⌋}^{{\mu }_1}-K_{ij}^3{⌈e_{ij}⌋}^{{\mu }_2}-f_{ij}\left({\overline{\mathit{x}}}_{\mathit{ij}}\right)\hfill \\ \hfill & -g_{i(j-1)}\left({\overline{\mathit{x}}}_{\mathit{i}(\mathit{j}-\mathbf{1})}\right)e_{i(j-1)}+{\dot{x}}_{ij\mathrm{c}}-(1-{\mathrm{e}}^{-\lambda |e_{ij}|})\mathrm{sign}\left({\widehat{d}}_{ij}{e}_{ij}\right){\widehat{d}}_{ij}-{\mathrm{e}}^{-\lambda |e_{ij}|}{\widehat{d}}_{ij}],\hfill \end{array}$$

(20)

where $K_{ij}^1$, $K_{ij}^2$ and $K_{ij}^3>0$.

Next, the command filter is designed as

$$\begin{array}{cc}\hfill {\tau }_{i(j+1)}·{\dot{x}}_{i(j+1)\mathrm{c}}=& -{\kappa }_{i(j+1)}^1{⌈x_{i(j+1)\mathrm{c}}-x_{i(j+1)\mathrm{d}}⌋}^{{\mu }_1}-{\kappa }_{i(j+1)}^2\left(x_{i(j+1)\mathrm{c}}-x_{i(j+1)\mathrm{d}}\right)\hfill \\ \hfill & -{\kappa }_{i(j+1)}^3{⌈x_{i(j+1)\mathrm{c}}-x_{i(j+1)\mathrm{d}}⌋}^{{\mu }_2}.\hfill \end{array}$$

(21)

The dynamics of ${\xi }_{i(j+1)}$ are

$$\begin{array}{cc}\hfill {\tau }_{i(j+1)}{\dot{\xi }}_{i(j+1)}=& -{\kappa }_{i(j+1)}^1{⌈{\xi }_{i(j+1)}⌋}^{{\mu }_1}-{\kappa }_{i(j+1)}^2{\xi }_{i(j+1)}-{\kappa }_{i(j+1)}^3{⌈{\xi }_{i(j+1)}⌋}^{{\mu }_2}-{\tau }_{i(j+1)}{\dot{x}}_{i(j+1)\mathrm{d}},\hfill \end{array}$$

(22)

where ${\tau }_{i(j+1)}$ represents a time constant. ${\kappa }_{i(j+1)}^1$, ${\kappa }_{i(j+1)}^2$, and ${\kappa }_{i(j+1)}^3$ are designed to be positive. We assume that ${\dot{x}}_{i(j+1)\mathrm{d}}$ is bounded, and a known positive constant $B_{i(j+1)}$ such that $B_{i(j+1)}=\sup ∥{\dot{x}}_{i(j+1)\mathrm{d}}∥$.

Combining filtering error ${\xi }_{i(j+1)}=x_{i(j+1)\mathrm{c}}-x_{i(j+1)\mathrm{d}}$ with tracking error $e_{i(j+1)}=x_{i(j+1)}-x_{i(j+1)\mathrm{c}}$ yields

$$\begin{array}{c}\hfill x_{i(j+1)}=x_{i(j+1)\mathrm{d}}+e_{i(j+1)}+{\xi }_{i(j+1)}.\end{array}$$

(23)

Considering (2) and (16), ${\dot{x}}_{i1}$ can be rewritten, and similarly, by substituting (23) into (2), we can rephrase ${\dot{x}}_{ij}$ as

$$\begin{array}{cc}\hfill {\dot{x}}_{ij}=& f_{ij}\left({\overline{\mathit{x}}}_{ij}\right)+g_{ij}\left({\overline{\mathit{x}}}_{\mathit{ij}}\right)(x_{i(j+1)\mathrm{d}}+e_{i(j+1)}+{\xi }_{i(j+1)})+d_{ij},\hfill \\ \hfill =& -K_{ij}^1{e}_{ij}-K_{ij}^2{⌈e_{ij}⌋}^{{\mu }_1}-K_{ij}^3{⌈e_{ij}⌋}^{{\mu }_2}+g_{ij}\left({\overline{\mathit{x}}}_{\mathit{ij}}\right){\xi }_{i(j+1)}+g_{ij}\left({\overline{\mathit{x}}}_{\mathit{ij}}\right)e_{i(j+1)}\hfill \\ \hfill & -(1-{\mathrm{e}}^{-\lambda |e_{ij}|})\mathrm{sign}\left({\widehat{d}}_{ij}{e}_{ij}\right){\widehat{d}}_{ij}-{\mathrm{e}}^{-\lambda |e_{ij}|}{\widehat{d}}_{ij}+d_{ij}+{\dot{x}}_{ijc}.\hfill \end{array}$$

(24)

Then, integrating (19) with (24) yields

$$\begin{array}{cc}\hfill {\dot{e}}_{ij}=& -K_{ij}^1{e}_{ij}-K_{ij}^2{⌈e_{ij}⌋}^{{\mu }_1}-K_{ij}^3{⌈e_{ij}⌋}^{{\mu }_2}+g_{ij}\left({\overline{\mathit{x}}}_{\mathit{i}\mathit{1}}\right){\xi }_{i(j+1)}+g_{ij}\left({\overline{\mathit{x}}}_{\mathit{ij}}\right)e_{i(j+1)}\hfill \\ \hfill & -g_{i(j-1)}\left({\overline{\mathit{x}}}_{\mathit{i}(\mathit{j}-\mathbf{1})}\right)e_{i(j-1)}-(1-{\mathrm{e}}^{-\lambda |e_{ij}|}){\widehat{d}}_{ij}\mathrm{sign}\left({\widehat{d}}_{ij}{e}_{ij}\right)\hfill \\ \hfill & +(1-{\mathrm{e}}^{-\lambda |e_{ij}|})d_{ij}-{\mathrm{e}}^{-\lambda |e_{ij}|}({\widehat{d}}_{ij}-d_{ij}).\hfill \end{array}$$

(25)

Step n: Unlike the previous cases, the dynamic of $e_{in}$ is

$$\begin{array}{cc}\hfill {\dot{e}}_{in}& ={\dot{x}}_{in}-{\dot{x}}_{in\mathrm{c}}=f_{in}\left({\overline{\mathit{x}}}_{in}\right)+g_{in}\left({\overline{\mathit{x}}}_{\mathit{in}}\right)u_i+d_{in}-{\dot{x}}_{in\mathrm{c}}.\hfill \end{array}$$

(26)

Finally, the $u_i$ is designed as

$$\begin{array}{cc}\hfill u_i=& g_{in}^{-1}\left({\overline{\mathit{x}}}_{\mathit{in}}\right)[-K_{in}^1{e}_{in}-K_{in}^2{⌈e_{in}⌋}^{{\mu }_1}-K_{in}^3{⌈e_{in}⌋}^{{\mu }_2}-f_{in}\left({\overline{\mathit{x}}}_{\mathit{in}}\right)-g_{i(n-1)}\left({\overline{\mathit{x}}}_{\mathit{i}(\mathit{n}-\mathbf{1})}\right)e_{i(n-1)}\hfill \\ \hfill & +{\dot{x}}_{in\mathrm{c}}-(1-{\mathrm{e}}^{-\lambda |e_{ij}|})\mathrm{sign}\left({\widehat{d}}_{ij}{e}_{ij}\right){\widehat{d}}_{ij}-{\mathrm{e}}^{-\lambda |e_{ij}|}{\widehat{d}}_{ij}],\hfill \end{array}$$

(27)

where $K_{in}^1,K_{in}^2$ and $K_{in}^3>0$.

Combining (26), (27) with (2), yields

$$\begin{array}{cc}\hfill {\dot{e}}_{in}=& -K_{in}^1{e}_{in}-K_{in}^2{⌈e_{in}⌋}^{{\mu }_1}-K_{in}^3{⌈e_{in}⌋}^{{\mu }_2}-g_{i(n-1)}\left({\overline{\mathit{x}}}_{\mathit{i}(\mathit{n}-\mathbf{1})}\right)e_{i(n-1)}\hfill \\ \hfill & -(1-{\mathrm{e}}^{-\lambda |e_{ij}|}){\widehat{d}}_{ij}\mathrm{sign}\left({\widehat{d}}_{ij}{e}_{ij}\right)+(1-{\mathrm{e}}^{-\lambda |e_{ij}|})d_{ij}-{\mathrm{e}}^{-\lambda |e_{ij}|}({\widehat{d}}_{ij}-d_{ij}).\hfill \end{array}$$

(28)

Remark 3.

During the design of control law, the derivative of the desired intermediate virtual control input $x_{ijd}(j=2,\dots ,n)$ will appear, as shown in formulas (13) and (20). The derivative of $x_{ijd}$ is difficult to obtain through analytical calculation, leading to the problem of “explosion of complexity”. To address this issue, we let $x_{ijd}$ pass through the filter to obtain $x_{ijc}$ and its derivative ${\dot{x}}_{ijc}$.

3.3.2. Analysis of System Stability

Theorem 3.

For the system (2), its closed-loop form can be derived using (13), (20) and (27) as follows:

$$\left\{\begin{array}{cc}\hfill {\dot{e}}_{i1}=& -K_{i1}^1{e}_{i1}-K_{i1}^2{⌈e_{i2}⌋}^{{\mu }_1}-K_{i1}^3{⌈e_{i1}⌋}^{{\mu }_2}+g_{i1}\left({\overline{\mathit{x}}}_{\mathit{i}\mathbf{1}}\right){\xi }_{i2}+g_{i1}\left({\overline{\mathit{x}}}_{\mathit{i}\mathbf{1}}\right)e_{i2}\hfill \\ \hfill & -(1-{\mathrm{e}}^{-\lambda |e_{i1}|}){\widehat{d}}_{i1}\mathit{sign}\left({\widehat{d}}_{i1}{e}_{i1}\right)+(1-{\mathrm{e}}^{-\lambda |e_{i1}|})d_{i1}-{\mathrm{e}}^{-\lambda |e_{i1}|}({\widehat{d}}_{i1}-d_{i1}),\hfill \\ \hfill & ⋮\hfill \\ \hfill {\dot{e}}_{ij}=& -K_{ij}^1{e}_{ij}-K_{ij}^2{⌈e_{ij}⌋}^{{\mu }_1}-K_{ij}^3{⌈e_{ij}⌋}^{{\mu }_2}+g_{ij}\left({\overline{\mathit{x}}}_{\mathit{i}\mathbf{1}}\right){\xi }_{i(j+1)}+g_{ij}\left({\overline{\mathit{x}}}_{\mathit{ij}}\right)e_{i(j+1)}\hfill \\ \hfill & -g_{i(j-1)}\left({\overline{\mathit{x}}}_{\mathit{i}(\mathit{j}-\mathbf{1})}\right)e_{i(j-1)}-(1-{\mathrm{e}}^{-\lambda |e_{ij}|}){\widehat{d}}_{ij}\mathit{sign}\left({\widehat{d}}_{ij}{e}_{ij}\right)\hfill \\ \hfill & +(1-{\mathrm{e}}^{-\lambda |e_{ij}|})d_{ij}-{\mathrm{e}}^{-\lambda |e_{ij}|}({\widehat{d}}_{ij}-d_{ij}),\hfill \\ \hfill & ⋮\hfill \\ \hfill {\dot{e}}_{in}=& -K_{in}^1{e}_{in}-K_{in}^2{⌈e_{in}⌋}^{{\mu }_1}-K_{in}^3{⌈e_{in}⌋}^{{\mu }_2}-g_{i(n-1)}\left({\overline{\mathit{x}}}_{\mathit{i}(\mathit{n}-\mathbf{1})}\right)e_{i(n-1)}\hfill \\ \hfill & -(1-{\mathrm{e}}^{-\lambda |e_{ij}|}){\widehat{d}}_{ij}\mathit{sign}\left({\widehat{d}}_{ij}{e}_{ij}\right)+(1-{\mathrm{e}}^{-\lambda |e_{ij}|})d_{ij}-{\mathrm{e}}^{-\lambda |e_{ij}|}({\widehat{d}}_{ij}-d_{ij}),\hfill \\ \hfill {\tau }_{ij}{\dot{x}}_{ij\mathrm{c}}=& -{\kappa }_{ij}^1{⌈{\xi }_{ij}⌋}^{{\mu }_1}-{\kappa }_{ij}^2⌈{\xi }_{ij}⌋-{\kappa }_{ij}^3{⌈{\xi }_{ij}⌋}^{{\mu }_2},\hfill \\ \hfill & (j=2,\cdots ,n).\hfill \end{array}\right.$$

(29)

If the control gains satisfy

$$\left\{\begin{array}{cc}\hfill {\eta }_i=& 2^{{\displaystyle \frac{1+{\mu }_1}{2}}}·\mathit{min}\left\{\underset{j\in [1,n]}{min}\{K_{ij}^2\},\underset{j\in [2,n]}{min}\{{\displaystyle \frac{{\kappa }_{ij}^1}{{\tau }_{ij}}}\}\right\}>0,\hfill \\ \hfill {\zeta }_i=& 2^{{\displaystyle \frac{1+{\mu }_2}{2}}}{(2n-1)}^{{\displaystyle \frac{1-{\mu }_2}{2}}}·\mathit{min}\left\{\underset{j\in [1,n]}{min}\{K_{ij}^3\},\underset{j\in [2,n]}{min}\{{\displaystyle \frac{{\kappa }_{ij}^3}{{\tau }_{ij}}}\}\right\}>0,\hfill \\ \hfill {\sigma }_i=& 2·\mathit{min}\{\underset{j\in [1,n-1]}{min}\{K_{ij}^1-{\displaystyle \frac{1}{2}}-{\displaystyle \frac{{\overline{g}}_{ij}\left({\overline{\mathit{x}}}_{\mathit{ij}}\right)}{2}}\},K_{in}^1-{\displaystyle \frac{1}{2}},\hfill \\ \hfill & \underset{j\in [2,n]}{min}\{{\displaystyle \frac{{\kappa }_{ij}^2}{{\tau }_{ij}}}-{\displaystyle \frac{1}{2}}-{\displaystyle \frac{{\overline{g}}_{i(j-1)}\left({\overline{\mathit{x}}}_{\mathit{i}(\mathit{j}-\mathbf{1})}\right)}{2}}\}\}=0,\hfill \end{array}\right.$$

(30)

the $e_{ij}$ and ${\xi }_{ij}$ will converge to a small neighborhood near the origin. Notably, this convergence time $T_{ic}$ is independent of the initial values of the errors, and

$$\begin{array}{c}\hfill T_{ic}=T_{i\_ob}+{\displaystyle \frac{2}{{\zeta }_i({\mu }_2-1)}}+{\displaystyle \frac{1}{{\eta }_i(2^{\frac{1+{\mu }_1}{2}}-1)}}{\displaystyle \frac{2}{1-{\mu }_1}},\end{array}$$

(31)

where $T_{i\_ob}$ is defined as the maximum value across all individual convergence times $T_{ij\_ob}$.

Proof. 

Choose the Lyapunov function

$$\begin{array}{c}\hfill W_i=\sum _{k=1}^n{\displaystyle \frac{e_{ik}^2}{2}}+\sum _{k=2}^n{\displaystyle \frac{{\xi }_{ik}^2}{2}}.\end{array}$$

(32)

The derivative with respect to time for Equation (32) is

$$\begin{array}{cc}\hfill {\dot{W}}_i=& \sum _{j=1}^n{e}_{ij}{\dot{e}}_{ij}+\sum _{j=2}^n{\xi }_{ij}{\dot{\xi }}_{ij}\hfill \\ \hfill =& \sum _{j=1}^n{e}_{ij}[-K_{ij}^1{e}_{ij}-K_{ij}^2{⌈e_{ij}⌋}^{{\mu }_1}-K_{ij}^3{⌈e_{ij}⌋}^{{\mu }_2}-(1-{\mathrm{e}}^{-\lambda |e_{ij}|}){\widehat{d}}_{ij}\mathrm{sign}\left({\widehat{d}}_{ij}{e}_{ij}\right)\hfill \\ \hfill & +(1-{\mathrm{e}}^{-\lambda |e_{ij}|})d_{ij}-{\mathrm{e}}^{-\lambda |e_{ij}|}({\widehat{d}}_{ij}-d_{ij})]+\sum _{j=1}^{n-1}{\xi }_{i(j+1)}{g}_{ij}{e}_{ij}\hfill \\ \hfill & +\sum _{j=2}^n{\xi }_{ij}\left\{-{\displaystyle \frac{{\kappa }_{ij}^1}{{\tau }_{ij}}}{⌈{\xi }_{ij}⌋}^{{\mu }_1}-{\displaystyle \frac{{\kappa }_{ij}^2}{{\tau }_{ij}}}{\xi }_{ij}-{\displaystyle \frac{{\kappa }_{ij}^3}{{\tau }_{ij}}}{⌈{\xi }_{ij}⌋}^{{\mu }_2}-{\dot{x}}_{ij\mathrm{d}}\right\}\hfill \\ \hfill =& \sum _{j=1}^n{e}_{ij}\left[-K_{ij}^1{e}_{ij}-K_{ij}^2{⌈e_{ij}⌋}^{{\mu }_1}-K_{ij}^3{⌈e_{ij}⌋}^{{\mu }_2}\right]\hfill \\ \hfill & -\sum _{j=1}^n\left\{(1-{\mathrm{e}}^{-\lambda |e_{ij}|})(|e_{ij}{\widehat{d}}_{ij}|-e_{ij}{d}_{ij})+{\mathrm{e}}^{-\lambda |e_{ij}|}{e}_{ij}{\tilde{d}}_{ij}\right\}+\sum _{j=1}^{n-1}{\xi }_{i(j+1)}{g}_{ij}{e}_{ij}\hfill \\ \hfill & +\sum _{j=2}^n{\xi }_{ij}\left\{-{\displaystyle \frac{{\kappa }_{ij}^1}{{\tau }_{ij}}}{⌈{\xi }_{ij}⌋}^{{\mu }_1}-{\displaystyle \frac{{\kappa }_{ij}^2}{{\tau }_{ij}}}{\xi }_{ij}-{\displaystyle \frac{{\kappa }_{ij}^3}{{\tau }_{ij}}}{⌈{\xi }_{ij}⌋}^{{\mu }_2}-{\dot{x}}_{ij\mathrm{d}}\right\}\hfill \\ \hfill =& \sum _{j=1}^n\left(-K_{ij}^1{e}_{ij}^2-K_{ij}^2{⌈e_{ij}⌋}^{{\mu }_1}{e}_{ij}-K_{ij}^3{⌈e_{ij}⌋}^{{\mu }_2}{e}_{ij}\right)\hfill \\ \hfill & -\sum _{j=1}^n\left\{(1-{\mathrm{e}}^{-\lambda |e_{ij}|})(|e_{ij}{\widehat{d}}_{ij}|-e_{ij}{d}_{ij})+{\mathrm{e}}^{-\lambda |e_{ij}|}{e}_{ij}{\tilde{d}}_{ij}\right\}+\sum _{j=1}^{n-1}{\xi }_{i(j+1)}{g}_{ij}{e}_{ij}\hfill \\ \hfill & +\sum _{j=2}^n\left\{-{\displaystyle \frac{{\kappa }_{ij}^1}{{\tau }_{ij}}}{⌈{\xi }_{ij}⌋}^{{\mu }_1}{\xi }_{ij}-{\displaystyle \frac{{\kappa }_{ij}^2}{{\tau }_{ij}}}{\xi }_{ij}{\xi }_{ij}-{\displaystyle \frac{{\kappa }_{ij}^3}{{\tau }_{ij}}}{⌈{\xi }_{ij}⌋}^{{\mu }_2}{\xi }_{ij}-{\dot{x}}_{ij\mathrm{d}}{\xi }_{ij}\right\},\hfill \end{array}$$

(33)

Since the following equality holds,

$$\begin{array}{cc}\hfill & (1-{\mathrm{e}}^{-\lambda |e_{ij}|})(|e_{ij}{\widehat{d}}_{ij}|-e_{ij}{d}_{ij})+{\mathrm{e}}^{-\lambda |e_{ij}|}{e}_{ij}{\tilde{d}}_{ij}\hfill \\ \hfill =& (1-{\mathrm{e}}^{-\lambda |e_{ij}|})\left[|e_{ij}{\widehat{d}}_{ij}|-e_{ij}({\widehat{d}}_{ij}-{\tilde{d}}_{ij})\right]+{\mathrm{e}}^{-\lambda |e_{ij}|}{e}_{ij}{\tilde{d}}_{ij}\hfill \\ \hfill =& (1-{\mathrm{e}}^{-\lambda |e_{ij}|})\left[(|e_{ij}{\widehat{d}}_{ij}|-e_{ij}{\widehat{d}}_{ij})+e_{ij}{\tilde{d}}_{ij}\right]+{\mathrm{e}}^{-\lambda |e_{ij}|}{e}_{ij}{\tilde{d}}_{ij}\hfill \end{array}$$

(34)

In (34), since the adaptive factor $\lambda$ is greater than 0, it follows that $0\le (1-{\mathrm{e}}^{-\lambda |e_{ij}|})<1$. Meanwhile, $|e_{ij}{\widehat{d}}_{ij}|-e_{ij}\ge 0$ always holds true, and it can be concluded that

$$\begin{array}{cc}\hfill & (1-{\mathrm{e}}^{-\lambda |e_{ij}|})(|e_{ij}{\widehat{d}}_{ij}|-e_{ij}{d}_{ij})+{\mathrm{e}}^{-\lambda |e_{ij}|}{e}_{ij}{\tilde{d}}_{ij}\hfill \\ \hfill \ge & (1-{\mathrm{e}}^{-\lambda |e_{ij}|})e_{ij}{\tilde{d}}_{ij}+{\mathrm{e}}^{-\lambda |e_{ij}|}{e}_{ij}{\tilde{d}}_{ij}\hfill \\ \hfill =& e_{ij}{\tilde{d}}_{ij}.\hfill \end{array}$$

(35)

Equation (33) can be reformulated into the subsequent expression.

$$\begin{array}{cc}\hfill {\dot{W}}_i\le & \sum _{j=1}^n\left[-K_{ij}^1{e}_{ij}^2-K_{ij}^2{\left|e_{ij}\right|}^{1+{\mu }_1}-K_{ij}^3{\left|e_{ij}\right|}^{1+{\mu }_2}-e_{ij}{\tilde{d}}_{ij}\right]+\sum _{j=1}^{n-1}{\xi }_{i(j+1)}{g}_{ij}{e}_{ij}\hfill \\ \hfill & +\sum _{j=2}^n\left\{-{\displaystyle \frac{{\kappa }_{ij}^1}{{\tau }_{ij}}}{\left|{\xi }_{ij}\right|}^{1+{\mu }_1}-{\displaystyle \frac{{\kappa }_{ij}^2}{{\tau }_{ij}}}{\xi }_{ij}^2-{\displaystyle \frac{{\kappa }_{ij}^3}{{\tau }_{ij}}}{\left|{\xi }_{ij}\right|}^{1+{\mu }_2}-{\xi }_i{\dot{x}}_{ij\mathrm{d}}\right\}\hfill \\ \hfill \le & \sum _{j=1}^n\left\{-K_{ij}^1{e}_{ij}^2-K_{ij}^2{\left|e_{ij}\right|}^{1+{\mu }_1}-K_{ij}^3{\left|e_{ij}\right|}^{1+{\mu }_2}+{\displaystyle \frac{e_{ij}^2}{2}}+{\displaystyle \frac{{\tilde{d}}_{ij}^2}{2}}\right\}+\sum _{j=1}^{n-1}{\xi }_{i(j+1)}{g}_{ij}{e}_{ij}\hfill \\ \hfill & +\sum _{j=2}^n\left\{-{\displaystyle \frac{{\kappa }_{ij}^1}{{\tau }_{ij}}}{\left|{\xi }_{ij}\right|}^{1+{\mu }_1}-{\displaystyle \frac{{\kappa }_{ij}^2}{{\tau }_{ij}}}{\xi }_{ij}^2-{\displaystyle \frac{{\kappa }_{ij}^3}{{\tau }_{ij}}}{\left|{\xi }_{ij}\right|}^{1+{\mu }_2}+{\displaystyle \frac{{\xi }_{ij}^2}{2}}+{\displaystyle \frac{{\dot{x}}_{ij\mathrm{d}}^2}{2}}\right\}\hfill \\ \hfill \le & \sum _{j=1}^n\left\{-K_{ij}^1{e}_{ij}^2-K_{ij}^2{\left|e_{ij}\right|}^{1+{\mu }_1}-K_{ij}^3{\left|e_{ij}\right|}^{1+{\mu }_2}+{\displaystyle \frac{e_{ij}^2}{2}}+{\displaystyle \frac{{\tilde{d}}_{ij}^2}{2}}\right\}+\sum _{j=1}^{n-1}{\displaystyle \frac{g_{ij}}{2}}{e}_{ij}^2\hfill \\ \hfill & +\sum _{j=2}^n\left\{-{\displaystyle \frac{{\kappa }_{ij}^1}{{\tau }_{ij}}}{\left|{\xi }_{ij}\right|}^{1+{\mu }_1}-{\displaystyle \frac{{\kappa }_{ij}^2}{{\tau }_{ij}}}{\xi }_{ij}^2-{\displaystyle \frac{{\kappa }_{ij}^3}{{\tau }_{ij}}}{\left|{\xi }_{ij}\right|}^{1+{\mu }_2}+{\displaystyle \frac{{\xi }_{ij}^2}{2}}+{\displaystyle \frac{{\dot{x}}_{ij\mathrm{d}}^2}{2}}+{\displaystyle \frac{g_{i(j-1)}}{2}}{\xi }_{ij}^2\right\}\hfill \\ \hfill =& -\sum _{j=1}^n{K}_{ij}^2{\left|e_{ij}\right|}^{1+{\mu }_1}-\sum _{j=2}^n{\displaystyle \frac{{\kappa }_{ij}^1}{{\tau }_{ij}}}{\left|{\xi }_{ij}\right|}^{1+{\mu }_1}-\sum _{j=1}^n\left(K_{ij}^1-{\displaystyle \frac{1}{2}}\right)e_{ij}^2+\sum _{j=1}^{n-1}{\displaystyle \frac{g_{ij}}{2}}{e}_{ij}^2\hfill \\ \hfill & -\sum _{j=2}^n\left({\displaystyle \frac{{\kappa }_{ij}^2}{{\tau }_{ij}}}-{\displaystyle \frac{1}{2}}-{\displaystyle \frac{g_{i(j-1)}}{2}}\right){\xi }_{ij}^2-\sum _{j=1}^n{K}_{ij}^3{\left|e_{ij}\right|}^{1+{\mu }_2}-\sum _{j=2}^n{\displaystyle \frac{{\kappa }_{ij}^3}{{\tau }_{ij}}}{\left|{\xi }_{ij}\right|}^{1+{\mu }_2}\hfill \\ \hfill & +\sum _{j=1}^n{\displaystyle \frac{{\tilde{d}}_{ij}^2}{2}}+\sum _{j=2}^n{\displaystyle \frac{{\dot{x}}_{ij\mathrm{d}}^2}{2}}\hfill \\ \hfill =& -\sum _{j=1}^n{K}_{ij}^2{\left(e_{ij}^2\right)}^{{\displaystyle \frac{1+{\mu }_1}{2}}}-\sum _{j=2}^n{\displaystyle \frac{{\kappa }_{ij}^1}{{\tau }_{ij}}}{\left({\xi }_{ij}^2\right)}^{{\displaystyle \frac{1+{\mu }_1}{2}}}-\sum _{j=1}^n\left(K_{ij}^1-{\displaystyle \frac{1}{2}}\right)e_{ij}^2+\sum _{j=1}^{n-1}{\displaystyle \frac{g_{ij}}{2}}{e}_{ij}^2\hfill \\ \hfill & -\sum _{j=2}^n\left({\displaystyle \frac{{\kappa }_{ij}^2}{{\tau }_{ij}}}-{\displaystyle \frac{1}{2}}-{\displaystyle \frac{g_{i(j-1)}}{2}}\right){\xi }_{ij}^2-\sum _{j=1}^n{K}_{ij}^3{\left(e_{ij}^2\right)}^{{\displaystyle \frac{1+{\mu }_2}{2}}}-\sum _{j=2}^n{\displaystyle \frac{{\kappa }_{ij}^3}{{\tau }_{ij}}}{\left({\xi }_{ij}^2\right)}^{{\displaystyle \frac{1+{\mu }_2}{2}}}\hfill \\ \hfill & +\sum _{j=1}^n{\displaystyle \frac{{\tilde{d}}_{ij}^2}{2}}+\sum _{j=2}^n{\displaystyle \frac{{\dot{x}}_{ij\mathrm{d}}^2}{2}}.\hfill \end{array}$$

(36)

Define $+\sum _{j=1}^n{\displaystyle \frac{{\tilde{d}}_{ij}^2}{2}}+\sum _{j=2}^n{\displaystyle \frac{{\dot{x}}_{ij\mathrm{d}}^2}{2}}$. Since $x_{ij\mathrm{d}}$ is bounded and $|{\tilde{d}}_{ij}|\le {\delta }_{ij}$ in Theorem 2, it follows that $\mathsf{\Theta }$ is positive and bounded. Applying Lemma A.2 from [45], we obtain

$$\begin{array}{cc}\hfill {\dot{W}}_i\le & -\min \left\{\underset{j\in [1,n]}{min}\{K_{ij}^2\},\underset{j\in [2,n]}{min}\{{\displaystyle \frac{{\kappa }_{ij}^1}{{\tau }_{ij}}}\}\right\}·\left[\sum _{j=1}^n{\left(e_{ij}^2\right)}^{{\displaystyle \frac{1+{\mu }_1}{2}}}+\sum _{j=2}^n{\left({\xi }_{ij}^2\right)}^{{\displaystyle \frac{1+{\mu }_1}{2}}}\right]\hfill \\ \hfill & -\min \left\{\underset{j\in [1,n]}{min}\{K_{ij}^3\},\underset{j\in [2,n]}{min}\{{\displaystyle \frac{{\kappa }_{ij}^3}{{\tau }_{ij}}}\}\right\}·\left[\sum _{j=1}^n{\left(e_{ij}^2\right)}^{{\displaystyle \frac{1+{\mu }_2}{2}}}+\sum _{j=2}^n{\left({\xi }_{ij}^2\right)}^{{\displaystyle \frac{1+{\mu }_2}{2}}}\right]\hfill \\ \hfill & -\min \left\{\underset{j\in [1,n-1]}{min}\{K_{ij}^1-{\displaystyle \frac{1}{2}}-{\displaystyle \frac{{\overline{g}}_{ij}}{2}}\},K_{in}^1-{\displaystyle \frac{1}{2}},\underset{j\in [2,n]}{min}\{{\displaystyle \frac{{\kappa }_{ij}^2}{{\tau }_{ij}}}-{\displaystyle \frac{1}{2}}-{\displaystyle \frac{{\overline{g}}_{i(j-1)}}{2}}\}\right\}\hfill \\ \hfill & ·\left[\sum _{j=1}^n{e}_{ij}^2+\sum _{j=2}^n{\xi }_{ij}^2\right]+{\mathsf{\Theta }}_i.\hfill \end{array}$$

(37)

With reference to Lemma 1 and Lemma 2 in [20], we can derive

$$\begin{array}{cc}\hfill \dot{W_i}\le & -2^{{\displaystyle \frac{1+{\mu }_1}{2}}}\min \left\{\underset{j\in [1,n]}{min}\{K_{ij}^2\},\underset{j\in [2,n]}{min}\{{\displaystyle \frac{{\kappa }_{ij}^1}{{\tau }_{ij}}}\}\right\}·{\left(\sum _{j=1}^n{e}_{ij}^2+\sum _{j=2}^n{\xi }_{ij}^2\right)}^{{\displaystyle \frac{1+{\mu }_1}{2}}}\hfill \\ \hfill & -2·\min \left\{\underset{j\in [1,n-1]}{min}\{K_{ij}^1-{\displaystyle \frac{1}{2}}-{\displaystyle \frac{{\overline{g}}_{ij}}{2}}\},K_{in}^1-{\displaystyle \frac{1}{2}},\underset{j\in [2,n]}{min}\{{\displaystyle \frac{{\kappa }_{ij}^2}{{\tau }_{ij}}}-{\displaystyle \frac{1}{2}}-{\displaystyle \frac{{\overline{g}}_{i(j-1)}}{2}}\}\right\}\hfill \\ \hfill & ·\left(\sum _{j=1}^n{e}_{ij}^2+\sum _{j=2}^n{\xi }_{ij}^2\right)\hfill \\ \hfill & -2^{{\displaystyle \frac{1+{\mu }_2}{2}}}{(2n-1)}^{{\displaystyle \frac{1-{\mu }_2}{2}}}\min \left\{\underset{j\in [1,n]}{min}\{K_{ij}^3\},\underset{j\in [1,n-1]}{min}\{{\displaystyle \frac{{\kappa }_{ij}^3}{{\tau }_{ij}}}\}\right\}·{\left(\sum _{j=1}^n{e}_{ij}^2+\sum _{j=2}^n{\xi }_{ij}^2\right)}^{{\displaystyle \frac{1+{\mu }_2}{2}}}+{\mathsf{\Theta }}_i\hfill \\ \hfill \le & -2^{{\displaystyle \frac{1+{\mu }_1}{2}}}\min \left\{\underset{j\in [1,n]}{min}\{K_{ij}^2\},\underset{j\in [2,n]}{min}\{{\displaystyle \frac{{\kappa }_{ij}^1}{{\tau }_{ij}}}\}\right\}{W_i}^{{\displaystyle \frac{1+{\mu }_1}{2}}}\hfill \\ \hfill & -2·\min \left\{\underset{j\in [1,n-1]}{min}\{K_{ij}^1-{\displaystyle \frac{1}{2}}-{\displaystyle \frac{{\overline{g}}_{ij}}{2}}\},K_{in}^1-{\displaystyle \frac{1}{2}},\underset{j\in [2,n]}{min}\{{\displaystyle \frac{{\kappa }_{ij}^2}{{\tau }_{ij}}}-{\displaystyle \frac{1}{2}}-{\displaystyle \frac{{\overline{g}}_{i(j-1)}}{2}}\}\right\}{W}_i\hfill \\ \hfill & -2^{{\displaystyle \frac{1+{\mu }_2}{2}}}{(2n-1)}^{{\displaystyle \frac{1-{\mu }_2}{2}}}\min \left\{\underset{j\in [1,n]}{min}\{K_{ij}^3\},\underset{j\in [1,n-1]}{min}\{{\displaystyle \frac{{\kappa }_{ij}^3}{{\tau }_{ij}}}\}\right\}{W_i}^{{\displaystyle \frac{1+{\mu }_2}{2}}}+{\mathsf{\Theta }}_i\hfill \\ \hfill =& -{\eta }_i{W}_i^{{\displaystyle \frac{1+{\mu }_1}{2}}}-{\zeta }_i{W}_i^{{\displaystyle \frac{1+{\mu }_2}{2}}}+{\mathsf{\Theta }}_i.\hfill \end{array}$$

(38)

According to (38), we can easily see that $W_i$ is bounded within a finite time $\left[0,T_{i\_ob}\right]$. When $t>T_{i\_ob}$, ${\mathsf{\Theta }}_i\le {\displaystyle \frac{1}{2}}\sum _{j=1}^n{\delta }_{ij}^2+{\displaystyle \frac{1}{2}}\sum _{j=2}^n{B}_{ij}^2$ can be guaranteed by Theorem 2.

Let ${\mathsf{\Xi }}_i={[e_{i1},\cdots ,e_{in},{\xi }_{i1},\cdots ,{\xi }_{i(n-1)}]}^{\mathrm{T}}$ be defined as the error vector. Theorem 2 in [44] guarantees that $\mathsf{\Xi }$ converges to an arbitrarily small neighborhood of the origin

$$\begin{array}{c}\hfill \mathsf{\Omega }=\left\{{\mathsf{\Xi }}_i\mid W_i\le {\left[{\displaystyle \frac{{\mathsf{\Theta }}_i}{{\eta }_i\left(2-2^{\frac{1+{\mu }_1}{2}}\right)}}\right]}^{{\displaystyle \frac{2}{{\mu }_1+1}}}\right\}.\end{array}$$

(39)

When ${\mathsf{\Xi }}_i\in \overline{\Omega }$, we obtain

$$\begin{array}{c}\hfill {\dot{W}}_i\le -{\eta }_i(2^{{\displaystyle \frac{1+{\mu }_1}{2}}}-1)W_i^{{\displaystyle \frac{1+{\mu }_1}{2}}}-{\zeta }_i{W}_i^{{\displaystyle \frac{1+{\mu }_2}{2}}}.\end{array}$$

(40)

The maximum limit for convergence time is

$$\begin{array}{c}\hfill T_{ic}=T_{i\_ob}+{\displaystyle \frac{2}{{\zeta }_i({\mu }_2-1)}}+{\displaystyle \frac{1}{{\eta }_i(2^{\frac{1+{\mu }_1}{2}}-1)}}{\displaystyle \frac{2}{1-{\mu }_1}},\end{array}$$

(41)

this result is independent of the initial tracking and filtering errors, thereby concluding the proof. □

Remark 4.

Although we introduce a non-negative parameter λ when constructing the disturbance feedforward compensation term, this parameter is not explicitly involved in selecting control gains (30). Superficially, it may seem that because inequality (34) ingeniously cancels out all terms containing λ mathematically, this result is not purely coincidental. Let us consider selecting $\lambda =0$, where we will pleasantly discover that Theorem 3 degenerates into a general disturbance feedforward compensation method. Conversely, as λ approaches infinity, Theorem 3 will degenerate into a conditional disturbance rejection method. Therefore, both the general form of the disturbance compensation method and the conditional disturbance rejection method are special cases of Theorem 3, and the selection of control gains and stability formula derivation results from Theorem 3 are fully applicable to these two specific scenarios.

Remark 5.

According to fixed-time convergence theory, the larger the selection of control gains, the faster the convergence speed of trajectory tracking curves. However, huge gains often lead to input saturation, introducing nonlinear uncertain factors that affect system stability. It is well known that under the same selection of control gains, the conditional disturbance rejection method can utilize beneficial disturbances to accelerate the convergence speed of the control system. When disturbances and tracking errors have the same sign, the observed values compensate entirely for the disturbances. Conversely, when disturbances and tracking errors have opposite signs, the disturbances are used to expedite the convergence speed. However, in this case, the observation of the closed-loop equations (29) reveals that the tracking accuracy is inevitably affected due to the simultaneous presence of disturbance observation values and disturbances. This issue does not exist in general disturbance feedforward compensation, eliminating all disturbances, whether beneficial or not. Therefore, by considering $\lambda \in (0,\infty )$, we can integrate the advantages of these two disturbance compensation methods. By adjusting the value of λ appropriately, we can not only accelerate the closed-loop system’s convergence speed but also significantly reduce tracking errors.

Remark 6.

We have made incremental improvements but significant enhancements to the existing control algorithm proposed by previous researchers [43]. In reference [43], only $-(1-{\mathrm{e}}^{-\lambda |e|})\widehat{d}\mathrm{sign}\left(\widehat{d}e\right)$ is used. As pointed out in the literature, excessively large values of λ will inevitably degrade tracking accuracy. When the ACDN governor behaves like the signum function, i.e., $\lambda \to +\infty$, it will rapidly switch between utilization mode and compensation mode, causing speed fluctuations and deteriorating tracking accuracy. Therefore, this method greatly restricts the range of values for λ. In comparison to the method we proposed, when the tracking error e is significant, the conditional disturbance rejection part dominates, satisfying the requirements of system robustness and rapid convergence. When the tracking error is small ($e\approx 0$), the general disturbance compensation part dominates, significantly reducing tracking errors. Moreover, if $\mathrm{sign}\left(\widehat{d}e\right)<0$, $-(1-{\mathrm{e}}^{-\lambda |e|})\widehat{d}\mathrm{sign}\left(\widehat{d}e\right)=(1-{\mathrm{e}}^{-\lambda |e|})\widehat{d}$ and $-(1-{\mathrm{e}}^{-\lambda |e|})\widehat{d}\mathrm{sign}\left(\widehat{d}e\right)-{\mathrm{e}}^{-\lambda |e|}\widehat{d}=(1-2{\mathrm{e}}^{-\lambda |e|})\widehat{d}$. If $\mathrm{sign}\left(\widehat{d}e\right)>0$, $-(1-{\mathrm{e}}^{-\lambda |e|})\widehat{d}\mathrm{sign}\left(\widehat{d}e\right)=-\widehat{d}+{\mathrm{e}}^{-\lambda |e|}\widehat{d}$ and $-(1-{\mathrm{e}}^{-\lambda |e|})\widehat{d}\mathrm{sign}\left(\widehat{d}e\right)-{\mathrm{e}}^{-\lambda |e|}\widehat{d}=-\widehat{d}$. This is why the algorithm we proposed performs better, despite only making slight modifications. Once the distributed fixed-time observer, fixed-time disturbance observer, and adaptive selective disturbance compensation-based non-smooth backstepping controller achieve convergence, the upper bound for the convergence time of the fixed-time consensus tracking protocol with adaptive selective disturbance elimination can be determined

$$\begin{array}{c}\hfill T=T_o+\underset{i\in \{1,\dots ,N\}}{max}{T}_{ic}.\end{array}$$

(42)

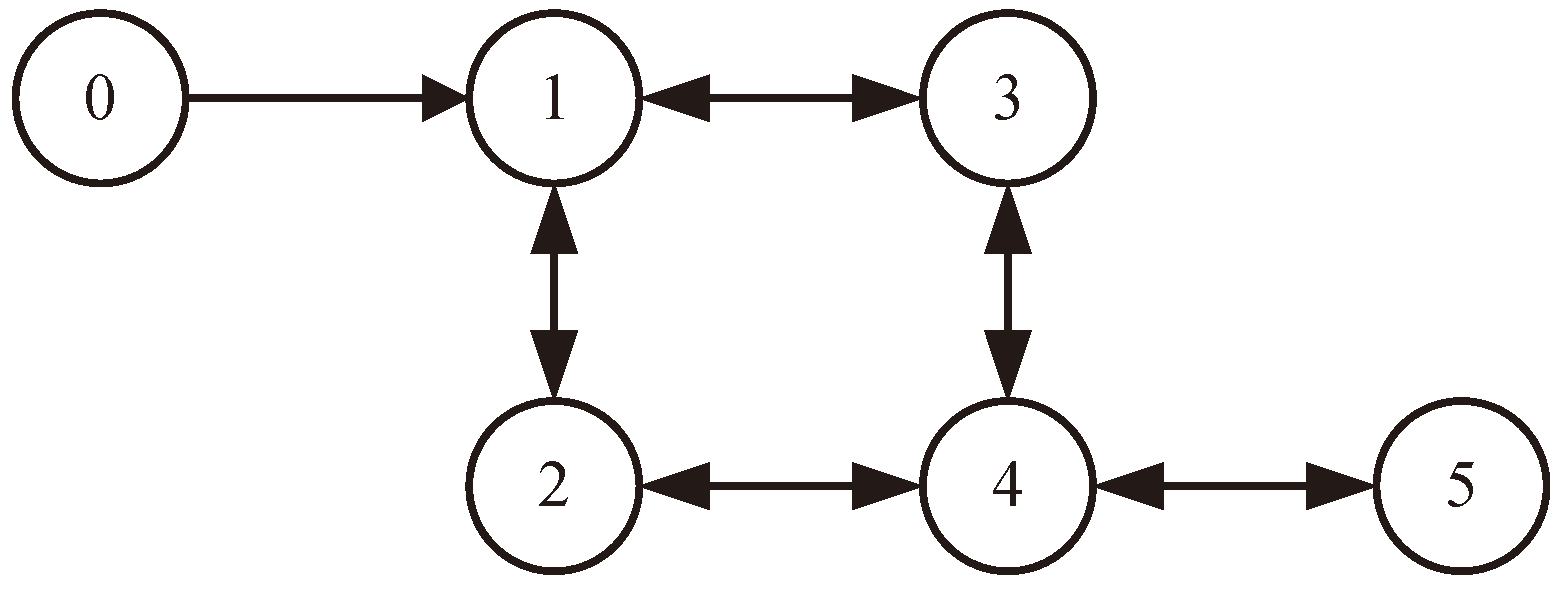
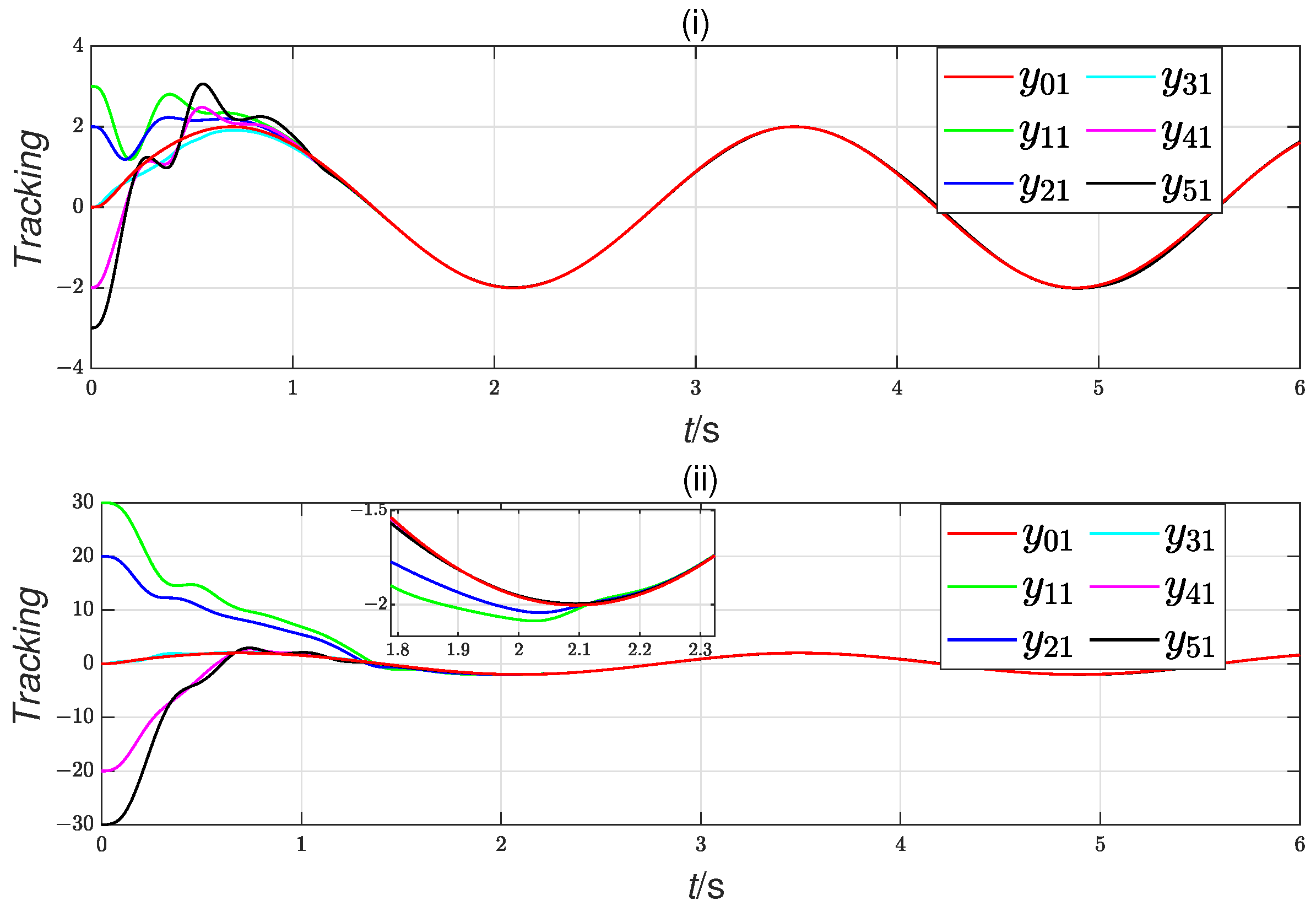
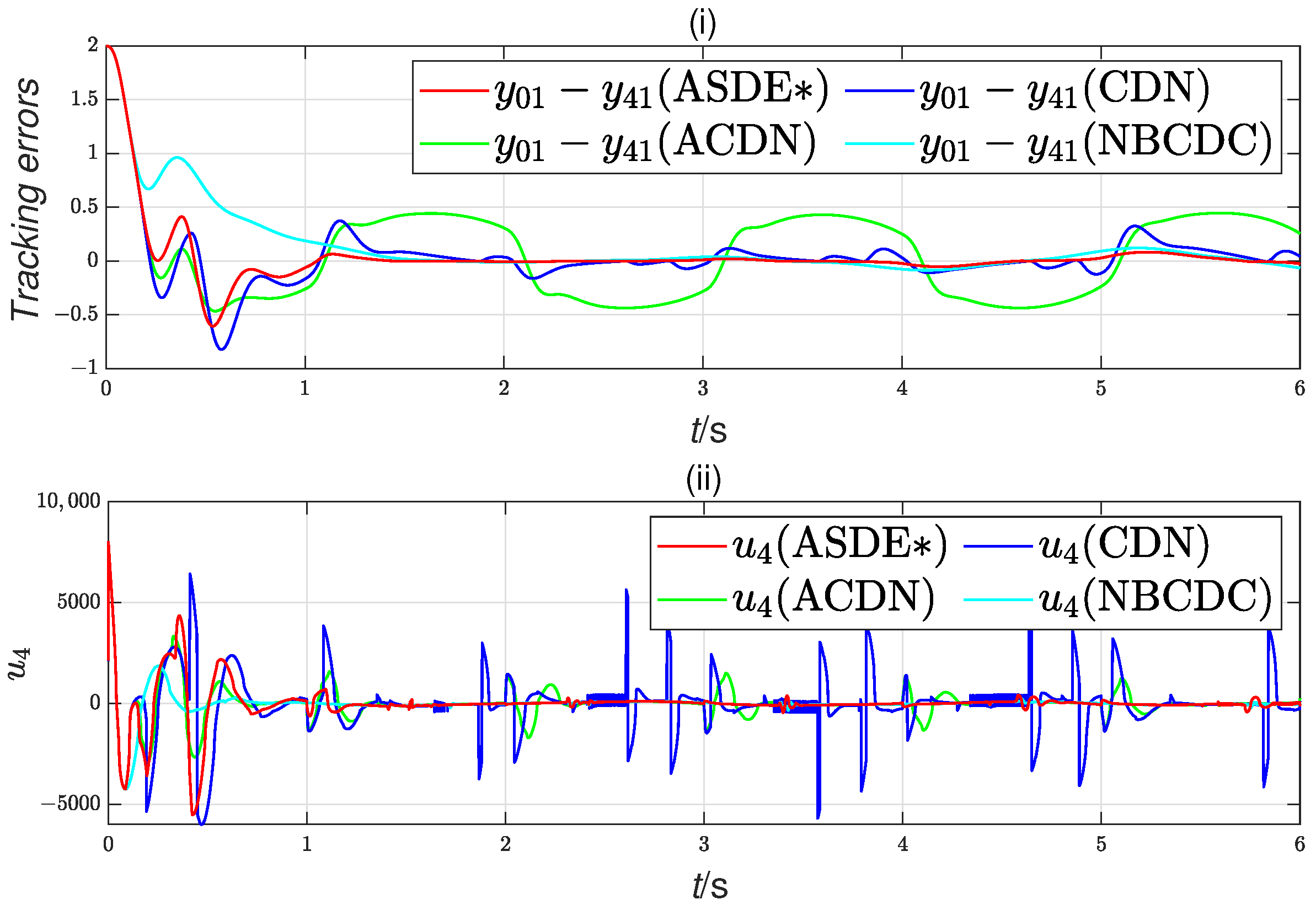
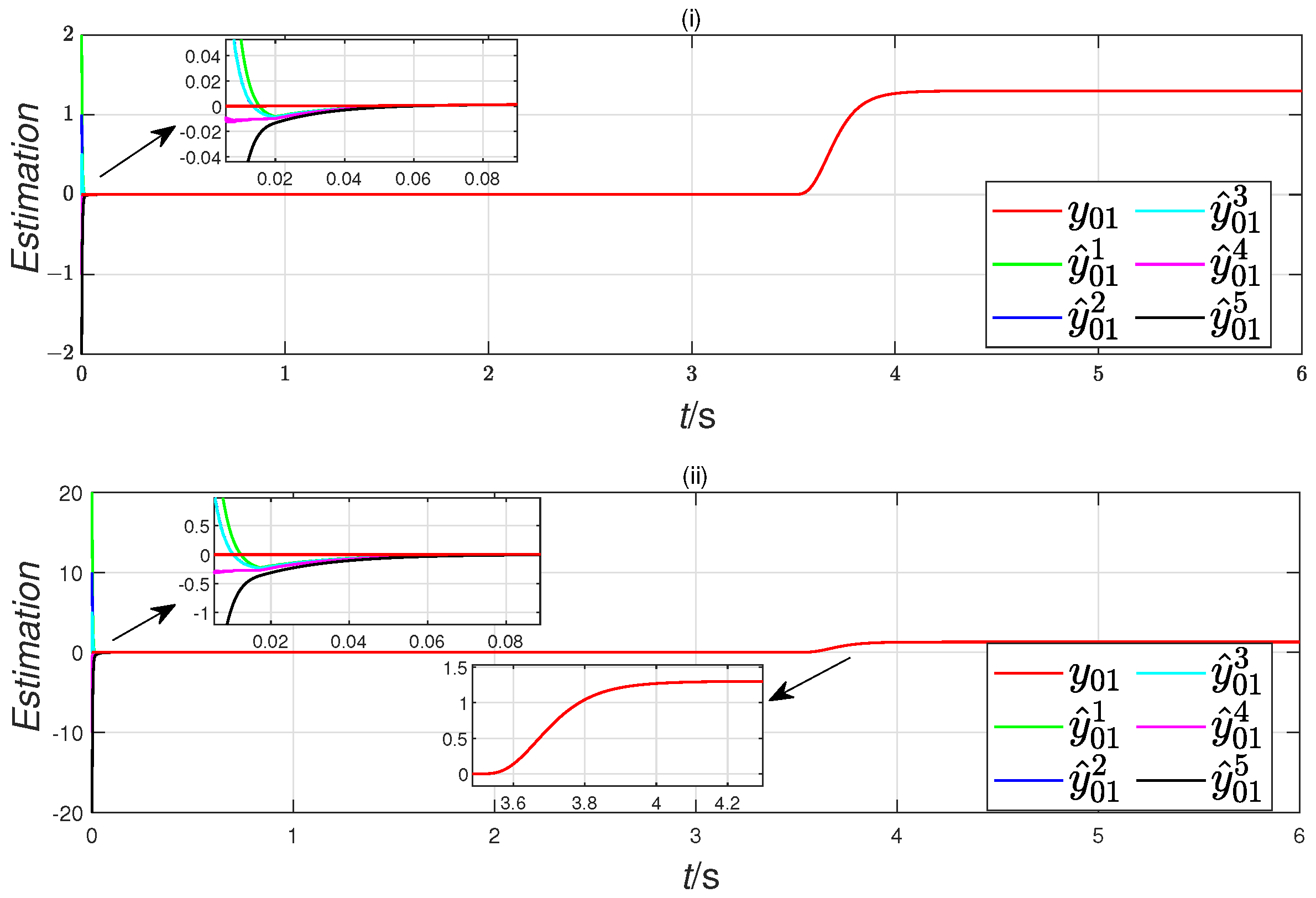
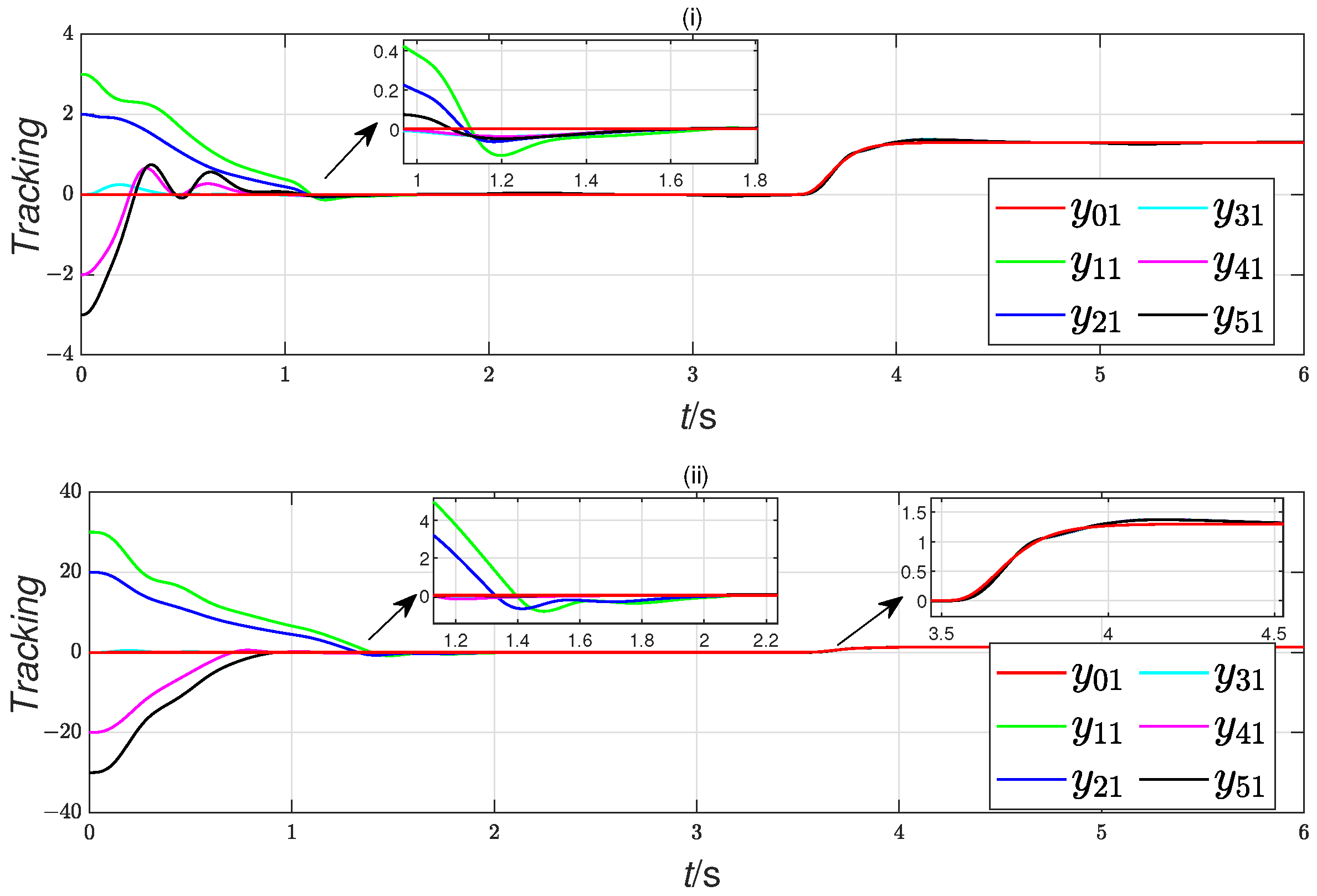
4. Simulation Results

In this section, a three-order nonlinear system is utilized to illustrate the effectiveness of the proposed protocol. The MASs used in the simulation include one leader and five followers.

The leader’s dynamic is

$$\left\{\begin{array}{c}{\dot{x}}_{01}\left(t\right)=x_{02}\left(t\right),\hfill \\ {\dot{x}}_{02}\left(t\right)=f_{02}\left({\overline{\mathit{x}}}_{02}\left(t\right)\right)+{\displaystyle \frac{1}{D}}{x}_{03}\left(t\right),\hfill \\ {\dot{x}}_{03}\left(t\right)=f_{03}\left({\overline{\mathit{x}}}_{03}\left(t\right)\right)+{\displaystyle \frac{1}{M}}{u}_0\left(t\right),\hfill \end{array}\right.$$

(43)

The models of the five followers are

$$\left\{\begin{array}{c}{\dot{x}}_{i1}\left(t\right)=x_{i2}\left(t\right)+d_{i1}\left(t\right),\hfill \\ {\dot{x}}_{i2}\left(t\right)=s_i{f}_{i2}\left({\overline{\mathit{x}}}_{i2}\left(t\right)\right)+{\displaystyle \frac{1}{D}}{x}_{i3}\left(t\right)+d_{i2}\left(t\right),\hfill \\ {\dot{x}}_{i3}\left(t\right)=s_i{f}_{i3}\left({\overline{\mathit{x}}}_{i3}\left(t\right)\right)+{\displaystyle \frac{1}{M}}{u}_i\left(t\right)+d_{i3}\left(t\right).\hfill \end{array}\right.$$

(44)

Let $x_{01},x_{02},x_{03}$, and $u_0$ denote the states and control input of the leader, while $x_{i1},x_{i2},x_{i3}$ and $u_i$$(i=1,\dots ,5)$ represent the states and control inputs of the five followers. The terms $d_{i1},d_{i2}$, and $d_{i3}$ are disturbances affecting the followers. The coefficients $s_i$ take values sequentially from 0.1 to 0.5. For the leader model, $f_{02}\left({\overline{\mathit{x}}}_{02}\left(t\right)\right)=-{\displaystyle \frac{N}{D}}sin\left(x_{01}\left(t\right)\right)-{\displaystyle \frac{B}{D}}{x}_{02}\left(t\right)$, $f_{03}\left({\overline{\mathit{x}}}_{03}\left(t\right)\right)=-{\displaystyle \frac{K_m}{M}}-{\displaystyle \frac{H}{M}}{x}_{03}\left(t\right)$, and the values of these parameters $N,B,D,M,H,K_m$ are given in [46]. Note that $f_{i2}\left({\overline{\mathit{x}}}_{i2}\left(t\right)\right),f_{i3}\left({\overline{\mathit{x}}}_{i3}\left(t\right)\right)$$(i=1,2,\dots 5)$ in the follower models use the same calculation as $f_{02}\left({\overline{\mathit{x}}}_{02}\left(t\right)\right),f_{03}\left({\overline{\mathit{x}}}_{03}\left(t\right)\right)$ in the leader’s model.

The MASs’ communication topology is depicted in Figure 1. The Laplacian matrix is

$$L=\left[\begin{array}{ccccc}2& -1& -1& 0& 0\\ -1& 2& 0& -1& 0\\ -1& 0& 2& -1& 0\\ 0& -1& -1& 3& -1\\ 0& 0& 0& -1& 1\end{array}\right],$$

(45)

the leader accessibility matrix is defined as $B=\mathrm{diag}[1,0,0,0,0]$, and we can calculate ${\lambda }_{min}(L+B)=0.1338$.

Remark 7.

Figure 1 illustrates the network topology of the MASs. Node 0 is designated as the leader, with nodes 1 to 5 functioning as the followers. Within the network topology, followers are configured to receive data from the leader, while the leader operates independently without accepting information from the followers. Additionally, the followers can communicate with each other, enabling local information exchange and coordination. This topology reflects a leader–follower hierarchy, a common structure in MASs for tasks such as formation control and distributed optimization. Excitingly, this topology exhibits scalability, enabling the integration of additional followers without altering the leader’s role, thereby extending its applicability to larger-scale multiagent systems. For more details on graph theory related to topology, please refer to [38].

To validate the effectiveness of the proposed method, we analyze two scenarios with different initial conditions for the followers. A sinusoidal command and a step command are given in scenarios 1 and 2, respectively. Furthermore, two initial conditions are assigned to each scenario:

$$\begin{array}{cc}\hfill & \left(a\right)x_0=\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right],x_1=\left[\begin{array}{c}3\\ 0\\ 0\end{array}\right],x_2=\left[\begin{array}{c}2\\ 0\\ 0\end{array}\right],x_3=\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right],x_4=\left[\begin{array}{c}-2\\ 0\\ 0\end{array}\right],x_5=\left[\begin{array}{c}-3\\ 0\\ 0\end{array}\right]\hfill \\ \hfill & {\widehat{x}}_0^1=\left[\begin{array}{c}2\\ 0\\ 0\end{array}\right],{\widehat{x}}_0^2=\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right],{\widehat{x}}_0^3=\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right],{\widehat{x}}_0^4=\left[\begin{array}{c}-1\\ 0\\ 0\end{array}\right],{\widehat{x}}_0^5=\left[\begin{array}{c}-2\\ 0\\ 0\end{array}\right]\hfill \\ \hfill & \left(b\right)x_0=\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right],x_1=\left[\begin{array}{c}30\\ 0\\ 0\end{array}\right],x_2=\left[\begin{array}{c}20\\ 0\\ 0\end{array}\right],x_3=\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right],x_4=\left[\begin{array}{c}-20\\ 0\\ 0\end{array}\right],x_5=\left[\begin{array}{c}-30\\ 0\\ 0\end{array}\right]\hfill \\ \hfill & {\widehat{x}}_0^1=\left[\begin{array}{c}20\\ 0\\ 0\end{array}\right],{\widehat{x}}_0^2=\left[\begin{array}{c}10\\ 0\\ 0\end{array}\right],{\widehat{x}}_0^3=\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right],{\widehat{x}}_0^4=\left[\begin{array}{c}-10\\ 0\\ 0\end{array}\right],{\widehat{x}}_0^5=\left[\begin{array}{c}-20\\ 0\\ 0\end{array}\right]\hfill \end{array}$$

(46)

In Scenario 1, $x_{01\mathrm{d}}=2sin\left(2.25t\right)$, $d_{i1}=10sin\left(\pi t\right)$, $d_{i2}=2sin\left(\pi t\right)$ and $d_{i3}=sin\left(\pi t\right)$.

Remark 8.

The gains of DFTO are ${\alpha }_1={\alpha }_2={\alpha }_3=-2.7,{\beta }_1={\beta }_2={\beta }_3=-7.8,$${\gamma }_1={\gamma }_2=-{\displaystyle \frac{0.1}{{\lambda }_{min}(L+B)}},{\gamma }_3=-{\displaystyle \frac{0.4}{{\lambda }_{min}(L+B)}}$, ${\mathrm{c}}_3=-10$, with the exponents in the non-smooth terms chosen as $\mu =2$. The order of the FTDO is selected as $l=4$. Its gains are selected as $k_{ij}^1=24,k_{ij}^2=24,k_{ij}^3=216,k_{ij}^4=216,k_{ij}^5=864,k_{ij}^6=864,k_{ij}^7=1296,k_{ij}^8=1296$, and the exponents in the non-smooth terms are $\rho =0.8,\varrho =1.2$. For the ASDE controller parameter design, the gains for the stable function $x_{i2d}$ are $K_{i1}^1=1.1,K_{i1}^2=0.8,K_{i1}^3=0.1$, while gains for the stable function $x_{3d}$ are designed as $K_{i2}^1=8.3,K_{i2}^2=0.8,K_{i2}^3=0.1$. The gains for the control law $u_i$ are chosen as $K_{i3}^1=0.6,K_{i3}^2=0.8,K_{i3}^3=0.1$. The gains for the filters corresponding to $x_{i2c}$ are ${\kappa }_{i2}^1=5,{\kappa }_{i2}^2=0.2,{\kappa }_{i2}^3=0.1$, and those for $x_{i3c}$ are designed as ${\kappa }_{i3}^1=5,{\kappa }_{i3}^2=0.83,{\kappa }_{i3}^3=0.1$. The time constants of the command filters are selected as ${\tau }_{i2}={\tau }_{i3}=0.1$. In the ASDE controller, the exponents of the non-smooth terms are chosen as ${\mu }_1=0.5$, ${\mu }_2=1.1$, with the adaptive term $\lambda =5$. Notably, the selected parameters satisfy the conditions specified in Theorem 1, Theorem 2, and Theorem 3.

In Scenario 2, the command is $x_{01\mathrm{d}}=\left\{\begin{array}{cc}& 0,t\le 3.5,\hfill \\ & 1.3,t>3.5.\hfill \end{array}\right.$

The disturbances and parameters, except for the ${\gamma }_1={\gamma }_2={\gamma }_3=-{\displaystyle \frac{20}{{\lambda }_{min}(L+B)}}$, $c_3=-50$, are all equal to those in Scenario 1. Prior to being sent to the leader, the command is processed through a filter, and its transfer function is ${\displaystyle \frac{1}{0.1s+1}}$.

The ITAE index is adopted to compare and analyze the performance of the aforementioned methods

$$J_{\mathrm{ITAE}}={\int }_0^{T_f}t\left|e\left(t\right)\right|dt,$$

(47)

where $e\left(t\right)$ is the error, and $T_f$ represents the simulation time.

We compared the adaptive selective disturbance elimination backstepping controller (ASDE) with the adaptive conditional disturbance negation backstepping controller (ACDN), conditional disturbance negation backstepping controller (CDN), and non-smooth backstepping controller (NBCDC). The results are illustrated in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9, and the performance results are presented in Figure 10.

Remark 9.

We have selected follower 4 as a representative example in Scenario 1, while in Scenario 2, follower 5 has been chosen as the illustrative case. The remaining followers demonstrate behavior similar to the examples provided. Figure 2 and Figure 6 illustrate that the DFTO converges within 1.2s, irrespective of the initial states, validating Theorem 1.

Remark 10.

Figure 3 and Figure 7 illustrate that all followers successfully reach convergence in less than 2.3 s, regardless of initial conditions. This observation confirms that the advanced ASDE effectively accomplished consensus tracking in a fixed time. Additionally, these results validate the assertions posited in Theorem 3.

Remark 11.

Figure 4 and Figure 8 indicate that in initial condition (a), the controller designed with ASDE demonstrates superior performance in terms of convergence speed and tracking accuracy when compared to ADCN, DCN, and NBCDC. Additionally, the proposed controller significantly improves control performance through the utilization of approximate control input. Figure 10 presents the ITAE index for each controller in the initial state (b) of two scenarios. Among the four methods evaluated, the ASDE method proposed in this paper achieves the lowest ITAE index, further highlighting its superior performance and demonstrating the effectiveness of ASDE.

Remark 12.

As illustrated in Figure 5 and Figure 9, the disturbance estimation performance of the FTDO is evaluated under two different scenarios. We can observe that the the FTDO is capable of accurately estimating lumped disturbances within a fixed time frame, regardless of the initial conditions, validating Theorem 2. Moreover, the FTDO’s insensitivity to initial conditions underscores its significant advantage in practical applications, particularly in scenarios where initial states are frequently unknown, uncertain, or unpredictable. This robustness ensures reliable performance even in the absence of precise system initialization.

Furthermore, we are surprised to observe that ACDN exhibits the worst tracking performance in Figure 3 and Figure 7. This is because when the tracking error $e_{ij}$ is very close to zero, the disturbance compensation term of ACDN, $-(1-e^{-\lambda \left|e_{ij}\right|})sign\left({\widehat{d}}_{ij}{e}_{ij}\right){\widehat{d}}_{ij}$, approaches zero. At this moment, the system still experiences disturbances (${\widehat{d}}_{ij}\ne 0$) leading to a deterioration in ACDN’s tracking performance. To address this, ASDE introduces an additional term, $-e^{-\lambda \left|e_{ij}\right|}{\widehat{d}}_{ij}$, into the existing disturbance compensation term of ACDN. When $e_{ij}$ is very close to zero, this term approximates the disturbance compensation term of NBCDC, $-{\widehat{d}}_{ij}$. As a result, ASDE is expected to exhibit tracking performance similar to that of NBCDC. Additionally, we can observe that when the tracking error crosses zero, the disturbance compensation term of CDN, $-sign\left({\widehat{d}}_{ij}{e}_{ij}\right){\widehat{d}}_{ij}$, becomes ineffective. Consequently, in the presence of disturbances, fluctuations occur in the tracking error at the zero-crossing point. In contrast, the disturbance compensation term of ASDE, $-(1-e^{-\lambda \left|e_{ij}\right|})sign\left({\widehat{d}}_{ij}{e}_{ij}\right){\widehat{d}}_{ij}-e^{-\lambda \left|e_{ij}\right|}{\widehat{d}}_{ij}$, ensures that the compensation mechanism remains active even when the tracking error crosses zero, thereby preventing fluctuations at zero-crossing points.

5. Conclusions

This study addresses the issue of fixed-time nonlinear consensus tracking in a specific type of multiagent system (MAS) affected by disturbances. By employing adaptive selective disturbance elimination techniques, we introduce an innovative protocol that ensures consensus tracking within a fixed time while adapting to reject disturbances. The framework incorporates a distributed fixed-time observer (DFTO), a fixed-time disturbance observer (FTDO), and an adaptive selective disturbance elimination backstepping controller (ASDE). Both theoretical analysis and simulation outcomes demonstrate that the newly developed DFTO expedites estimating the output of leader, achieving convergence within a fixed period. Meanwhile, the fixed-time disturbance observer efficiently detects lumped disturbances and their derivatives. The adaptive backstepping controller with selective disturbance compensation effectively differentiates between beneficial and harmful effects, achieving faster convergence and better robustness compared to existing methods. Future work will involve combining the proposed method with other controls that exhibit specific-time convergence characteristics and are less dependent on parameter design, thereby reducing the complexity of parameter tuning in fixed-time control. Additionally, further experimental validation will be carried out to assess the efficacy and real-world applicability of the proposed approach.