A Novel Fault Diagnosis and Accurate Localization Method for a Power System Based on GraphSAGE Algorithm

Abstract

Artificial intelligence (AI)-based fault diagnosis methods have been widely studied for power grids, with most research focusing on fault interval localization rather than precise fault point identification. In cases involving long-distance transmission lines or underground cables, merely locating the fault interval is insufficient. This paper presents a novel fault diagnosis and precise localization method for power systems utilizing the Graph Sample and Aggregated (GraphSAGE) algorithm. A fault diagnosis and interval localization model are developed based on the system topology, identifying k-order adjacent nodes at both ends of the fault interval. This information is then used to construct an accurate fault point localization model. Leveraging the strong inductive learning capability of GraphSAGE, the proposed method effectively captures the impact of the fault point on surrounding nodes, enabling precise fault point localization. Experimental results demonstrate that the proposed method offers high fault diagnosis accuracy, precise localization, and robust performance. The model shows significant applicability in real-world fault scenarios, maintaining strong performance and economic value across varying network topologies and incomplete data collection.

1. Introduction

Fault analysis and localization in power systems mainly involve the identification, classification, and pinpointing of faults in power lines and equipment [1,2]. Accurate and reliable fault analysis is essential for enhancing relay protection performance and ensuring the safe and stable operation of power systems [3,4,5]. Since smart grid technologies have continued to evolve, several new trends have emerged in the development of power systems: the scale of the power grid within a more complex structure has expanded; the proportion of distributed energy sources integrated into the grid has significantly increased; the trend toward power electronic systems is becoming more pronounced; and advancements in sensing technologies and information integration have led to an explosion in data volumes. These challenges, including large-scale data, intricate fault mechanisms, and diverse algorithmic models, also represent the primary obstacles to effective fault analysis and localization in modern power systems [6,7].

Traveling wave-based methods rely on the observation of both original and reflected waves generated by faults [8,9]. These methods include various approaches such as single-ended, double-ended, injection-based, and reclosing transient-based techniques [8,10]. However, when the network topology changes, the network matrix and database require reconstruction, making fault discrimination methods inflexible. Additionally, as the network structure becomes more complicated, the computational complexity increases, and the accuracy of fault detection may decrease, especially when extracting weak feature signals. With the growth of the power system scale and increasing nonlinear randomness, fault mechanism and characteristic analysis based on physical models have become more challenging. If the extracted feature quantities fail to effectively capture the distinctions between different fault signals, traditional fault analysis methods are less likely to produce satisfactory results. The key challenge in fault analysis lies in the complex nonlinear interactions among multi-time series data, multiple parameters, and multi-node coupling. In the face of massive data processing and the need to decouple complex nonlinear relationships, AI offers distinct advantages over traditional methods. The application of AI in power grid fault analysis and localization is also becoming an increasingly prevalent trend. Figure 1 illustrates the challenges associated with applying AI in power system fault diagnosis and localization.

The analysis and localization of power system faults are fundamentally classification and regression problems [11,12]. A fault diagnosis model for low-voltage intelligent distribution networks used gradient boosting trees, incorporating fixed-number interpolations to replace the measurement values of specific branches [13]. While this approach demonstrates some adaptability to changes in network topology, it fails to achieve accurate fault section localization. A Bayesian estimation algorithm was employed to accurately identify fault sections in distribution networks, demonstrating high fault tolerance [14]. Reference [15] explored the application of Convolutional Neural Networks (CNN) in machine fault diagnosis, highlighting the strong learning capabilities of CNN. Similarly, transfer learning and convolutional neural networks were leveraged to develop a fault localization model for distribution networks that remained unaffected by various fault factors [16]. However, these methods fail to simultaneously address the challenges of network topology changes while ensuring accurate fault localization.

With the advent of graph neural network (GNN) algorithms, neural network methods have been extended to the graph domain, enabling the integration of deep learning (DL) with topological graph data [17,18,19,20,21]. The most widely used GNN algorithms include graph convolutional networks (GCN), graph attention networks (GAT), and the GraphSAGE algorithm. GCN and GAT have been explored to some extent in the context of power system fault analysis. GCN was widely utilized for fault prediction in distribution networks, thoroughly considering the connections and influences between nodes. Through incorporating network topology, the accuracy and robustness of prediction models were significantly enhanced [22]. GCN was used to develop a fault localization framework for distribution networks, combining measurement data from various nodes with a network topology to achieve high discrimination accuracy [8]. However, these studies also focused less on the generalizability and practicality of the model under changes in the network topology. A high-precision fault interval localization model based on the GAT algorithm was proposed, specifically addressing topology changes in distribution networks [23]. However, the localization methods discussed in these studies mainly focus on fault interval localization, which fails to enable accurate identification of the fault point. The located fault interval can offer limited guidance for maintenance personnel; thus, accurately pinpointing the fault point in long underground cables remains a challenge.

This paper leverages the GraphSAGE algorithm to develop a fault diagnosis model that outperforms both GAT and GCN and establish an accurate fault localization model through only conventional operational data from power systems. The structure of this paper is organized as follows. Section 2 introduces the basic principles of GNN, emphasizing the advantages in learning topological information compared to other AI algorithms. Section 3 outlines the simulation data sources and settings, along with the construction of the graph structure, subgraph structure, and sub-dataset. Section 4 provides an in-depth discussion on the application of the GraphSAGE algorithm in power system fault diagnosis and accurate localization. Section 5 validates the model’s accuracy, efficiency, adaptability, and practicality across various dimensions. Section 6 offers a summary and a discussion of potential directions for future research.

2. Graph Neural Network

The core of fault diagnosis and fault interval localization in power grids involves identifying the fault type and pinpointing the section of the grid where the fault occurs [24,25]. This can be framed as a classification problem. On the other hand, accurate fault point localization is inherently a regression problem. While classic deep belief networks (DBN) and convolutional neural networks (CNN) in deep learning (DL) can address these issues, graph neural networks (GNNs) offer distinct advantages. By integrating a power grid topology with electrical feature information, GNNs enhance the ability of a network to extract relevant features through the introduction of topological relationships between nodes. This enables more efficient learning of effective features, ultimately improving both classification and regression accuracy.

In comparison, GAT and GraphSAGE enhance the efficiency of feature learning through their inherent characteristics. As demonstrated in Reference [23], GAT improves learning efficiency and fault diagnosis accuracy by introducing an attention mechanism. Both GCN and GAT require the consideration of all graph information during feature extraction, which results in significant computational demands. In contrast, GraphSAGE employs random sampling of k-order neighboring nodes during feature extraction, eliminating the need to process the entire graph, thereby reducing computational complexity. In Reference [26], Hamilton et al., the creators of the GraphSAGE algorithm, demonstrated the merits of this approach and identified a balance between the number of samplings and the size of the local sampling range. They showed that, as long as the product of the number of k-order neighboring nodes does not exceed 500, feature extraction efficiency can be enhanced. In Section 5, we also provide empirical evidence of GraphSAGE’s inductive learning capability. By randomly sampling k-order neighboring nodes, GraphSAGE addresses the efficiency issues associated with GCN and GAT, which require processing of the entire graph during feature learning. Furthermore, in the fault point localization model, GraphSAGE leverages its random sampling feature to extract richer feature representations within constrained subgraph structures, significantly improving the localization accuracy.

2.1. Graph Convolutional Neural Network

Graph convolutional networks (GCNs) leverage the convolution kernel operation from convolutional neural networks to perform convolution operations on data, incorporating the connection relationships of the power grid. The Laplacian matrix of a graph is defined as $∆=D-A$, the Laplacian matrix is normalized to ∆, and characteristic decomposition is performed on it, as shown in Equations (1) and (2):

$$∆=I-D^{-{\displaystyle \frac{1}{2}}}A{D}^{-{\displaystyle \frac{1}{2}}}$$

(1)

$$∆=U\left(\begin{array}{cccc}{\lambda }_1& 0& \cdots & 0\\ 0& {\lambda }_2& & ⋮\\ ⋮& & \ddots & 0\\ 0& \cdots & 0& {\lambda }_n\end{array}\right)U^{-1}$$

(2)

where I is the identity matrix, D is the degree matrix, A is the adjacency matrix, and $U=(\overrightarrow{u_1},\overrightarrow{u_2},\cdots ,\overrightarrow{u_n})$ and $\lambda =diag({\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n)$ are the diagonal matrices of eigenvectors and eigenvalues obtained after the decomposition of the eigenvectors.

Using U as the basis for Fourier transform on the graph, its matrix form on the spectral domain graph can be obtained, as shown in Equation (3):

$$\left\{\begin{array}{c}F\left({\lambda }_l\right)=\sum _{i=1}^{n}f\left(i\right)u_l^{*}\left(i\right)\\ F\left\{x\right\}=U^{\mathrm{T}}x\end{array}\right.$$

(3)

where $f\left(i\right)$ is the vector of the node i on the graph, $u_l^{\mathrm{*}}\left(i\right)$ is the conjugate vector of the eigenvector $u_l\left(i\right)$, and $F\left\{x\right\}$ represents the matrix form of Fourier transform.

The convolution can be expressed as the inverse transformation of the Fourier transform product of the signal function; therefore, the convolution formula on the graph can be obtained as shown in Equation (4):

$$g\times f=U(U^{\mathrm{T}}g·U^{\mathrm{T}}f)$$

(4)

where $g$ is the convolution kernel function, $f$ is the signal vector on the graph, and $U$ is the eigenvector of the Laplacian matrix of the graph.

Therefore, GCN has implemented convolution operations on the graph to extract features from data containing the structure of the power grid topology. However, since the GCN convolution kernel shares parameters in the same layer, each update requires all connection information of the power grid structure to be called, resulting in lower efficiency in learning features and a greater emphasis on extracting global features.

2.2. GraphSAGE Algorithm

GraphSAGE (Sample and AggregatE) is a graph neural network model developed by Hamilton et al. for graph node embedding learning [26,27,28,29,30]. In prior GCN models, a full-graph training approach was used, where each node updates its feature vector and the entire graph is subsequently updated. However, as the graph size increases, this method becomes highly time-consuming. The core idea of GraphSAGE is to sample a subset of neighboring nodes for each target node and then aggregate the feature information from these neighbors onto the target node. This approach reduces computational complexity while preserving the structural information of the graph.

The GraphSAGE algorithm aggregates the information of neighboring nodes onto the target node through sampling and aggregation, thereby learning the representation of nodes. The GraphSAGE algorithm operates on graph $G(E,V)$, where E is the set of edges and V is the set of nodes. The node feature of node v is represented as vector $x_v$ and the set of node feature vectors is $\{X_v,\forall v\in V\}$. The depth K represents the number of information hops of the aggregated nodes during each iteration. The differentiable aggregation function for k-order aggregation is represented as ${AGG}_k,\forall k\in \{\mathrm{1,2},\cdots ,K\}$. At the layer k, the sampling neighborhood is $N\left(v\right)$ and the aggregated information $h_{N\left(v\right)}^k$ at node v can be represented as follows:

$$h_{N\left(v\right)}^k={AGG}_k\{h_u^{k-1},\forall u\in N(v\left)\right\}$$

(5)

where $h_u^{k-1}$ is the vector representation of node u in the layer k − 1.

Connecting the aggregate vector $h_{N\left(v\right)}^k$ of the sampling neighborhood $N\left(v\right)$ with the node vector $h_v^{k-1}$ of the layer k − 1 can be expressed as follows:

$$h_v^k=\sigma (W^k·CONCAT\left(h_v^{k-1},h_{N\left(v\right)}^k\right)$$

(6)

where $W^k$ is the trainable weight matrix and $\sigma$ is the nonlinear activation function.

The final vector representation of node v obtained by layer-wise aggregation is as follows:

$$Z_v=h_v^K,\forall v\in V$$

(7)

The most commonly used aggregation functions in the GraphSAGE algorithm are as follows:

(1) Average aggregation function:

$${\mathbf{h}}_v^k\leftarrow \sigma (\mathbf{W}·MEAN({\mathrm{h}}_v^{k-1}\cup {\mathrm{h}}_u^{k-1},\forall u\in N\left(v\right)\left)\right);\mathrm{and}$$

(8)

(2) Pooling aggregation function:

$${\mathbf{A}\mathbf{G}\mathbf{G}\mathbf{R}\mathbf{E}\mathbf{G}\mathbf{A}\mathbf{T}\mathbf{E}}_{\mathit{k}}^{\mathit{p}\mathit{o}\mathit{o}\mathit{l}}=\mathrm{m}\mathrm{a}\mathrm{x}(\sigma (\mathbf{W}\mathrm{p}\mathrm{o}\mathrm{o}\mathrm{l}{\mathit{h}}_{u_i}^k+\mathrm{b}),\forall u_i\in N(v)).$$

(9)

Figure 2 shows the calculation principle of the GraphSAGE algorithm at depth K = 2.

Step 1: Sampling

The blue dot represents the target node. First, three out of five neighboring nodes are randomly selected from Layer 1. Then, from the selected neighboring nodes of Layer 1, six additional nodes from Layer 2 (those adjacent to the Layer 1 nodes) are randomly selected;

Step 2: Encoding

The input information corresponding to each node is converted into a low-dimensional feature vector through an encoder. This encoder could be a fully connected layer, a convolutional neural network, or another suitable method;

Step 3: Aggregation

The features from the red neighboring nodes of Layer 2 are aggregated to the green neighboring nodes of Layer 2. Next, the feature vectors of the Layer 1 neighboring nodes are updated and aggregated from the green nodes of Layer 1 to the blue target node, resulting in an updated feature vector for the target node.

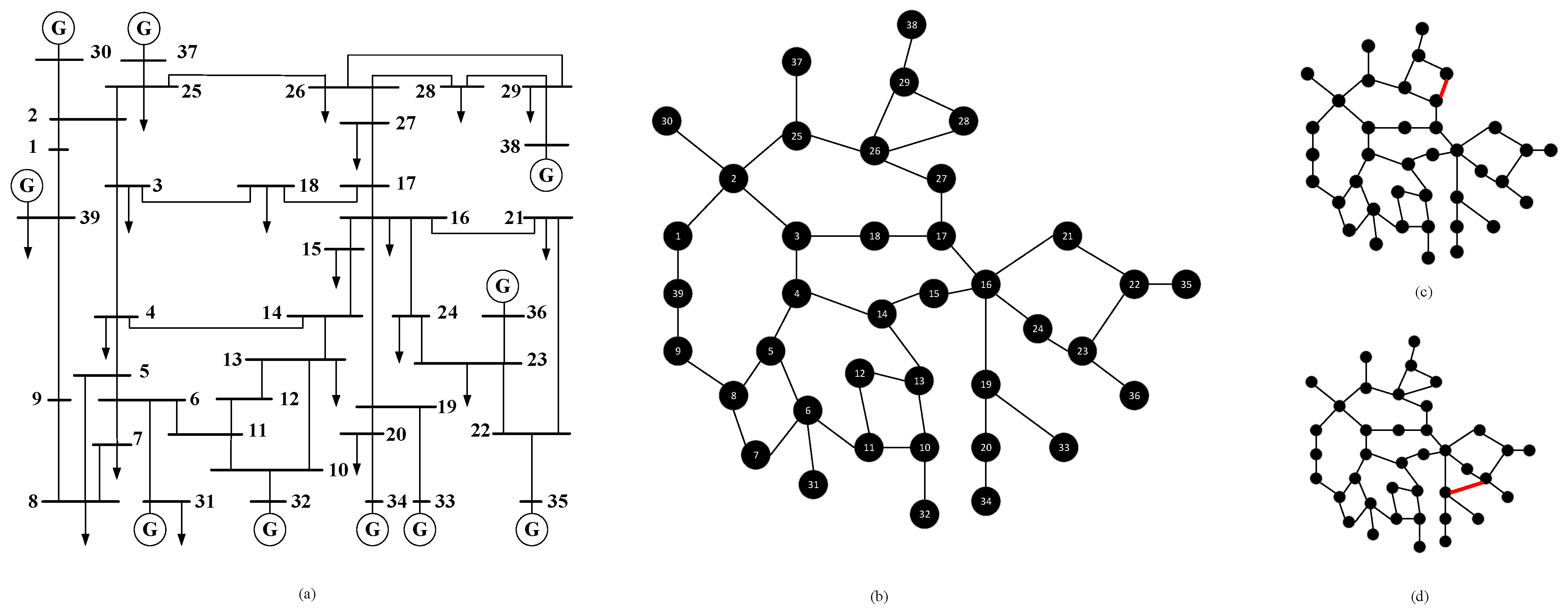
3. Database Construction

Currently, PMU (Phasor Measurement Unit) and μPMU (Micro Phasor Measurement Unit) devices are commonly used in power grids to measure data, including the voltage phase at key system nodes and the current phase of transmission lines. These data are transmitted to the monitoring master station via the communication network. The master station determines the necessary actions, such as disconnecting lines, shutting down equipment, and cutting off loads, based on the phase amplitudes at various points. Then, proper actions are taken to prevent the further spread of faults or even grid collapse. The input data for the GraphSAGE algorithm include both node features and graph information. Therefore, this paper uses the topology structure of the power grid to construct an adjacency matrix that encapsulates all relevant graph information, along with the three-phase voltage amplitude and phase angle for each node in the grid as input data. As shown in Figure 6 of Section 4, the blue section illustrates the schematic diagram for simulation data handling and graph model construction.

3.1. Fault Simulation in Power Systems

Transient faults in transmission lines can be categorized into single-phase grounding faults, two-phase short-circuit faults, two-phase grounding faults, and three-phase short-circuit faults. Common causes of these faults include lightning strikes, wind deflection, pollution, fly ash, icing, external forces, bird interference, and internal system failures. The severity of these four primary fault types varies significantly. Among them, the three-phase short-circuit fault is the most severe and serious, requiring the shortest fault clearing time to minimize system damage. While single-phase grounding faults are less harmful compared to other types, they occur most frequently, accounting for over 90% of all faults, making their management equally critical.

The IEEE 39-bus standard model utilized in this study was developed using PSD-BPA software. The parameter settings for the model are presented in

Table 1. Simulation parameter setting in PSD-BPA.

	Parameter Settings
Fault type	single-phase grounding (A-phase, B-phase, C-phase), two-phase short circuit (AB-phase, BC-phase, AC-phase), two-phase grounding (AB-phase, BC-phase, AC-phase), three-phase short circuit
Fault point position	10%, 20%, …, 90%
Load level	80%, 85%, …, 120%
Total sampling duration	40 cycles
Sampling step size	0.1 cycles
Fault start time	10th cycle
Fault end time	15th cycle
Types of sampling data	three-phase voltage amplitude three-phase voltage phase angle
Topological structure changes	connection relationship between bus1–bus2 changes to bus2–bus3 add connection relationship bus19–bus23

:

Figure 3 shows the amplitude curves of phase A voltage at all nodes where a single-phase short-circuit fault occurs at a distance of 10% from node BUS1 on the line between BUS1 and BUS2 at an 80% load level. The feature set corresponding to V in graph $G(E,V)$ presents as $\{X_v=\left(U_{va},{\theta }_{va},U_{vb},{\theta }_{vb},U_{vc},{\theta }_{vc}\right),\forall v\in V\}$. To avoid adverse effects on the subsequent training process caused by inconsistent units and differences in numerical and physical meanings and orders of magnitude, $U_{va},{\theta }_{va},U_{vb},{\theta }_{vb},U_{vc},{\theta }_{vc}$ are all taken as p.u.

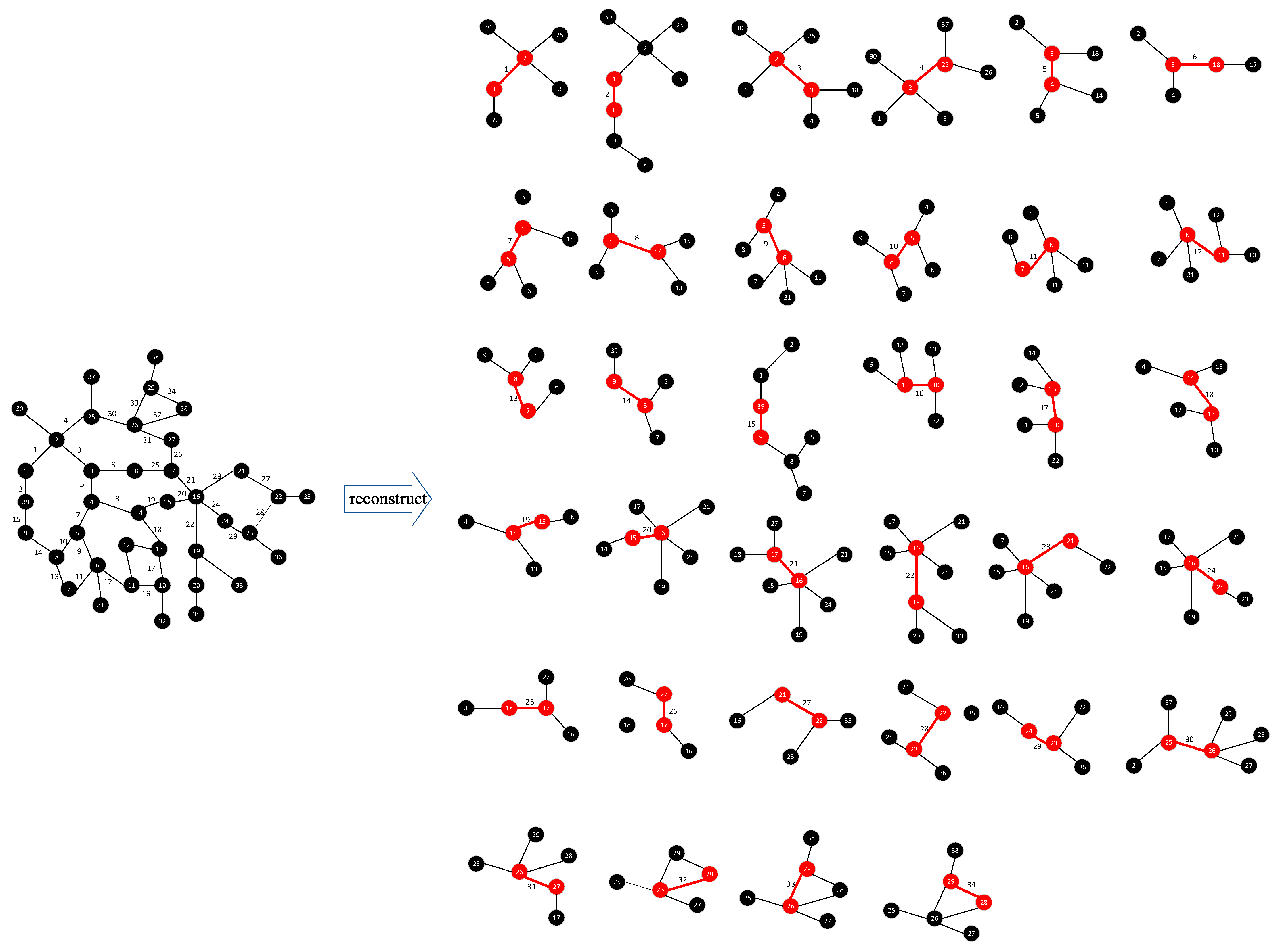
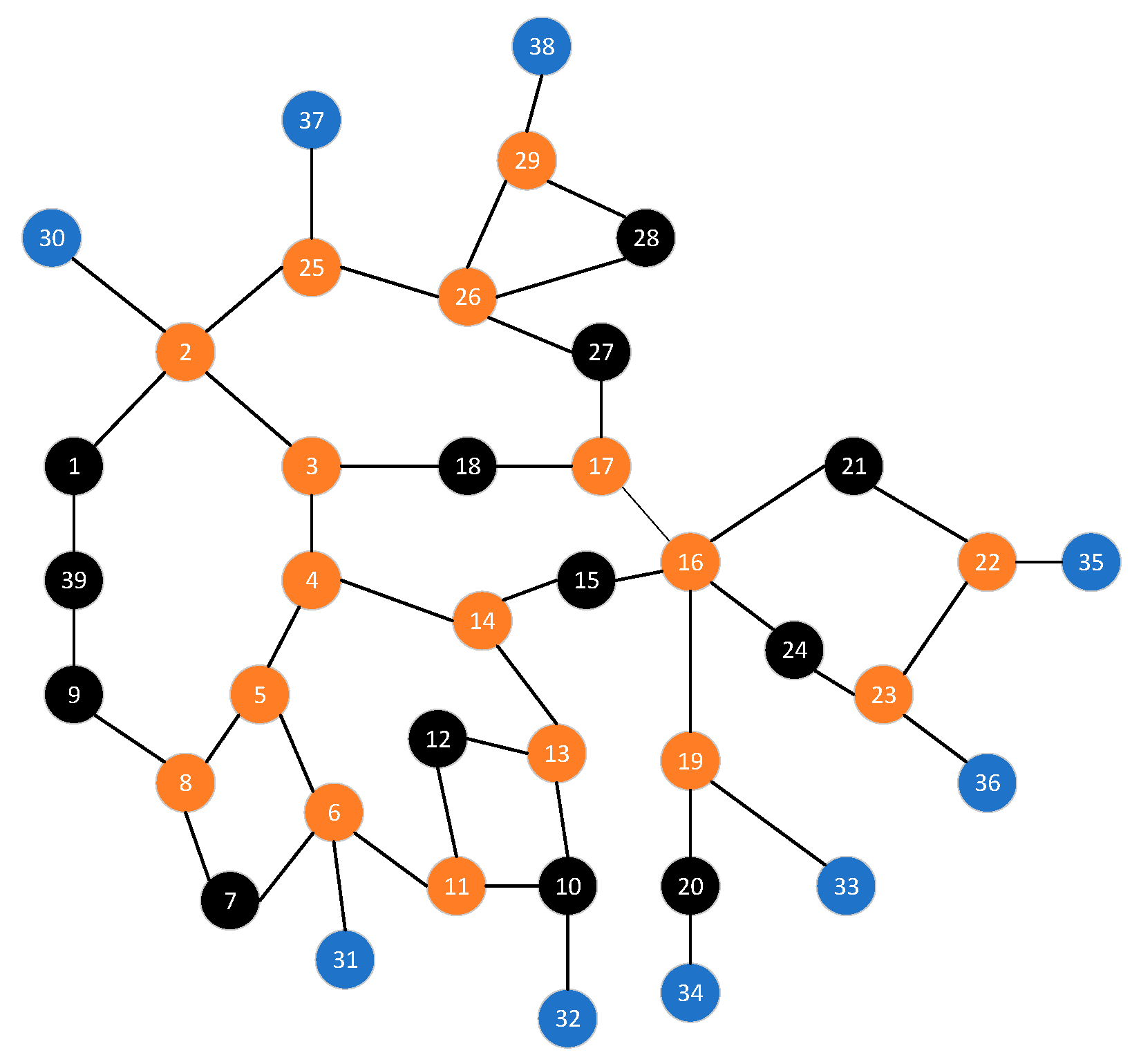
3.2. Graph Structure Construction

According to the network structure of IEEE 39-bus system, the corresponding graph structure can be constructed as shown in Figure 4:

The feature quantities used in this method exclude current information, meaning that the direction attribute is not considered. For fault type diagnosis and interval localization, the complete graph structure of the IEEE 39-bus system is sufficient to construct the GraphSAGE model. However, for accurate fault point localization, it is necessary to reconstruct the subgraph structure.

Multiple experimental results have demonstrated that utilizing whole graph structures for accurate fault point localization is not effective. In this paper, a subgraph structure is reconstructed based on k-order adjacent nodes at the endpoints of the fault interval, as shown in Figure 5. Taking the interval bus1–bus2 as an example, the first-order adjacent node set of bus1 is {bus2, bus39}, and the first-order adjacent node set of bus2 is {bus1, bus3, bus25, bus30}. The new structure of graph can be described as follows:

$$G_{bus1-bus2}(E,V)$$

(10)

where

$$E=\left[\begin{array}{cccccc}0& 1& 0& 0& 0& 1\\ 1& 0& 1& 1& 1& 0\\ 0& 1& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0\\ 1& 0& 0& 0& 0& 0\end{array}\right]$$

$$V=\{bus1,bus2,bus3,bus25,bus30,bus39\}$$

The adjacency matrix E is typically represented using the sequence of starting nodes and the sequence of target nodes, as follows:

starting nodes = {0,0,1,1,1,1,2,3,4,5}

target nodes = {1,5,0,2,3,4,1,1,1,0}

The corresponding node feature dataset can be described as follows:

$$\left\{X_v=\left(U_{va},{\theta }_{va},U_{vb},{\theta }_{vb},U_{vc},{\theta }_{vc}\right)\right\}$$

(11)

where

$$\forall v\in \{bus1,bus2,bus3,bus25,bus30,bus39\}$$

4. Fault Diagnosis and Accurate Localization Model of Power System Based on GraphSAGE Algorithm

As previously mentioned, the essence of power system fault diagnosis lies in solving a classification problem, while accurate fault point localization is fundamentally a regression problem. Initially, a classification model for the entire system is constructed using the GraphSAGE algorithm to address fault diagnosis and interval localization. Guided by this high-precision classification model, a subgraph structure and database were created based on the endpoints of the identified fault interval. The inductive learning capability of the GraphSAGE algorithm was then utilized to develop a regression model for accurate fault point localization.

As illustrated in Figure 6, the input consists of the adjacency matrix of the IEEE 39-bus system, while the feature matrix is formed by concatenating the three-phase voltage amplitude sequence and the three-phase voltage phase angle sequence for each node. This can be expressed as follows:

$$X=\left(U_{va},{\theta }_{va},U_{vb},{\theta }_{vb},U_{vc},{\theta }_{vc}\right)$$

(12)

Labels based on fault types and interval information are established as follows:

$$label=\left\{\begin{array}{c}0,three-phasebetweenbus1-bus2\\ 1,three-phasebetweenbus1-bus39\\ \begin{array}{c}⋮\\ 339,C-phrase-Gbetweenbus28-bus29\end{array}\end{array}\right.$$

(13)

In Figure 6, the yellow part represents the fault diagnosis model. The feature extraction part adopts three layers of GraphSAGE; each layer connects a TopKPooling layer and a ReLU layer in series and a GAP layer is connected in parallel. The TopKPooling layer is used to reduce the number of nodes and retain important node information. The ReLU layer is used to enhance the non-linear expression ability of the model and the GAP layer is used to transform the feature matrix into a feature vector containing global information. The three global features are combined to form the final feature vector. Then, the classifier used for fault type diagnosis and interval localization comprises three fully connected layers followed by a softmax function.

The model parameters are fully described in Section 4. The following parameter settings were used for training: an initial learning rate of 0.0001; the Adam optimizer; a batch size of 128, and the cross-entropy loss function. The model was trained for 500 epochs or until convergence.

In Figure 6, the green part represents the fault localization model. Subgraphs are selected based on the classification results, and corresponding new sub-databases are constructed as inputs. These sub-databases are labeled with fault point location information. The feature extraction process utilizes one or two layers of GraphSAGE, depending on the number of nodes in the subgraph. An equivalent number of TopKPooling layers, ReLU layers, and GAP layers are employed to obtain the feature vector. Finally, two or three fully connected layers are connected to determine the accurate location of the fault point.

Figure 6. Method framework diagram.

Figure 6. Method framework diagram.

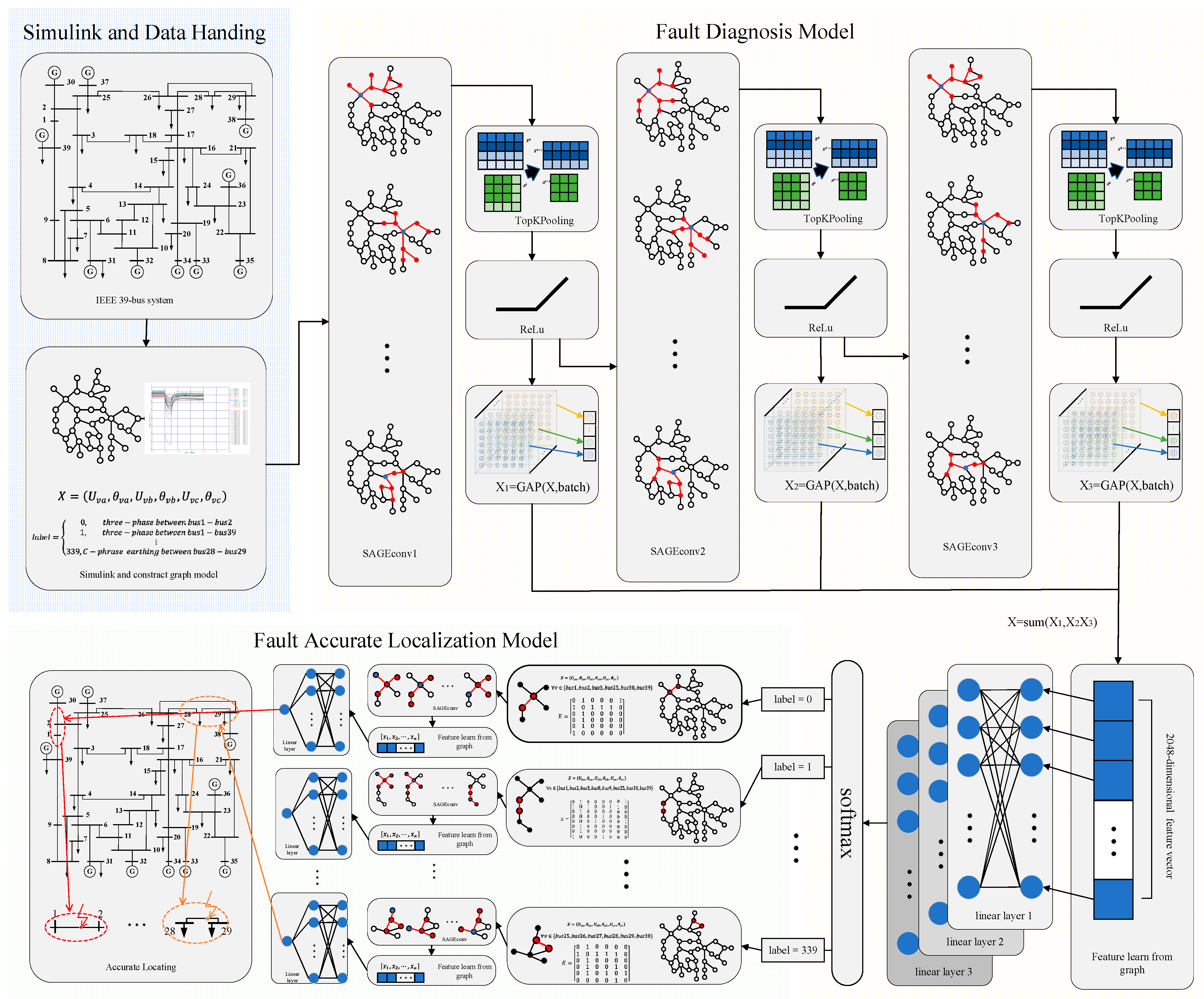
5. Validation Experiments

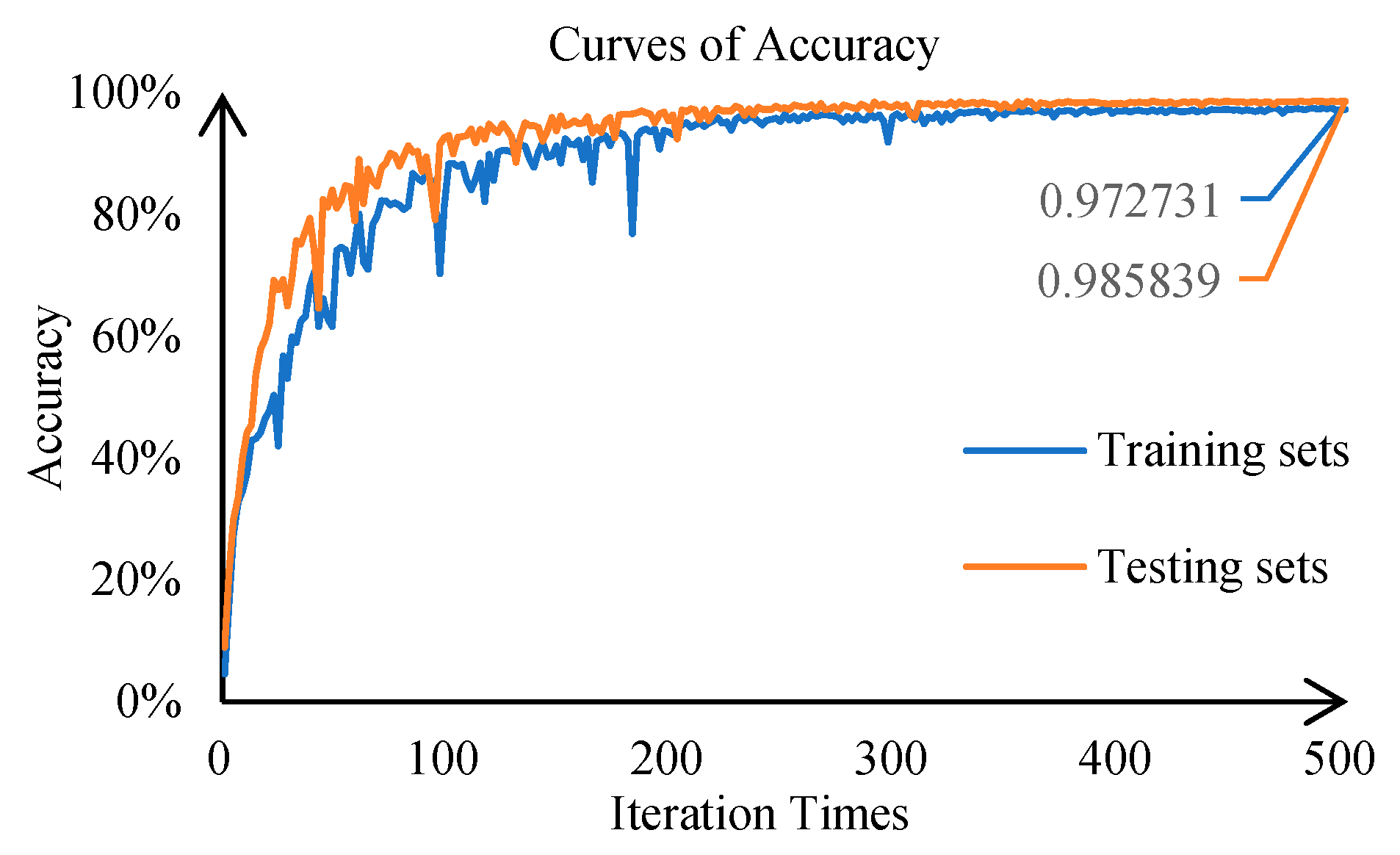
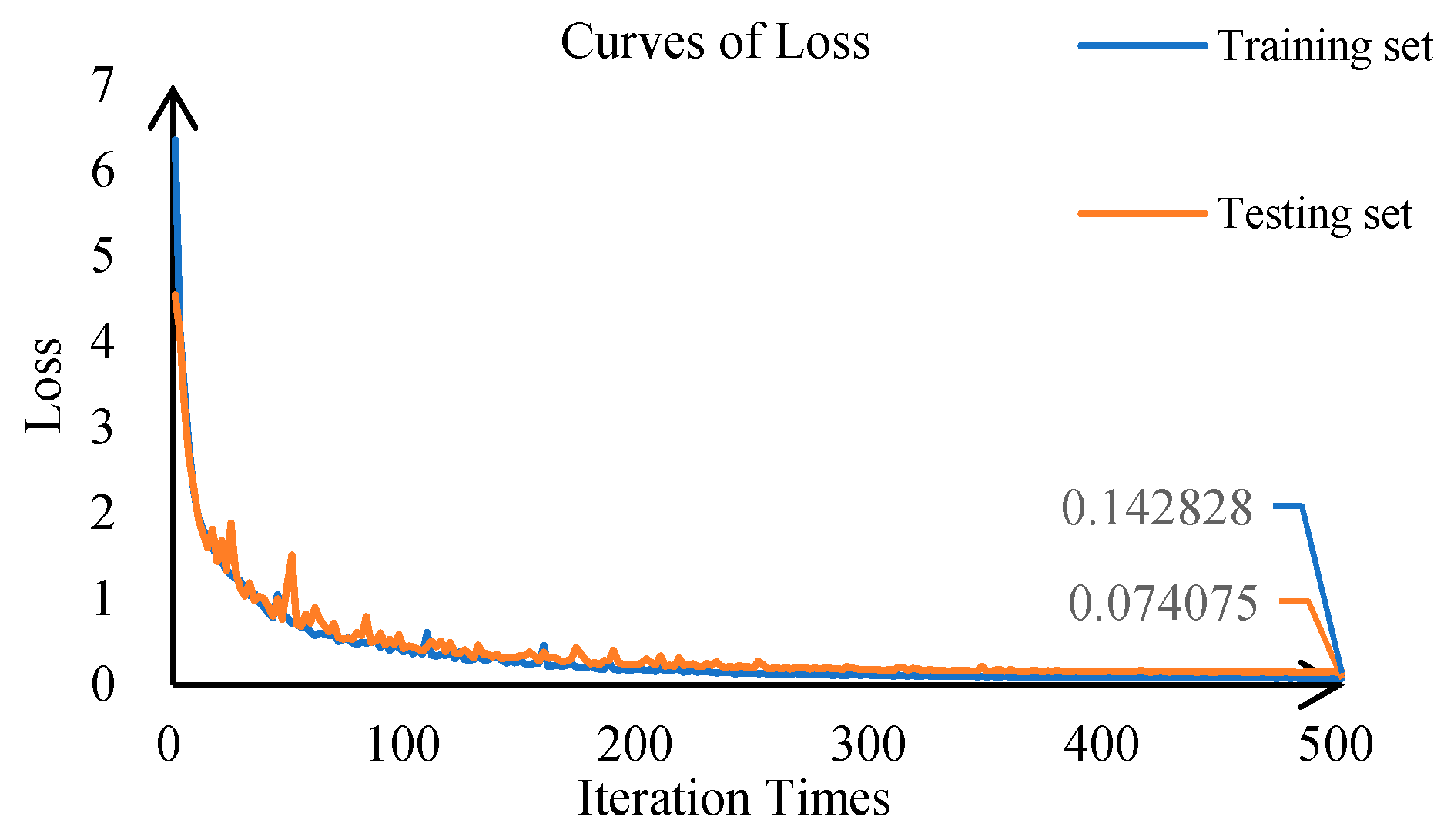
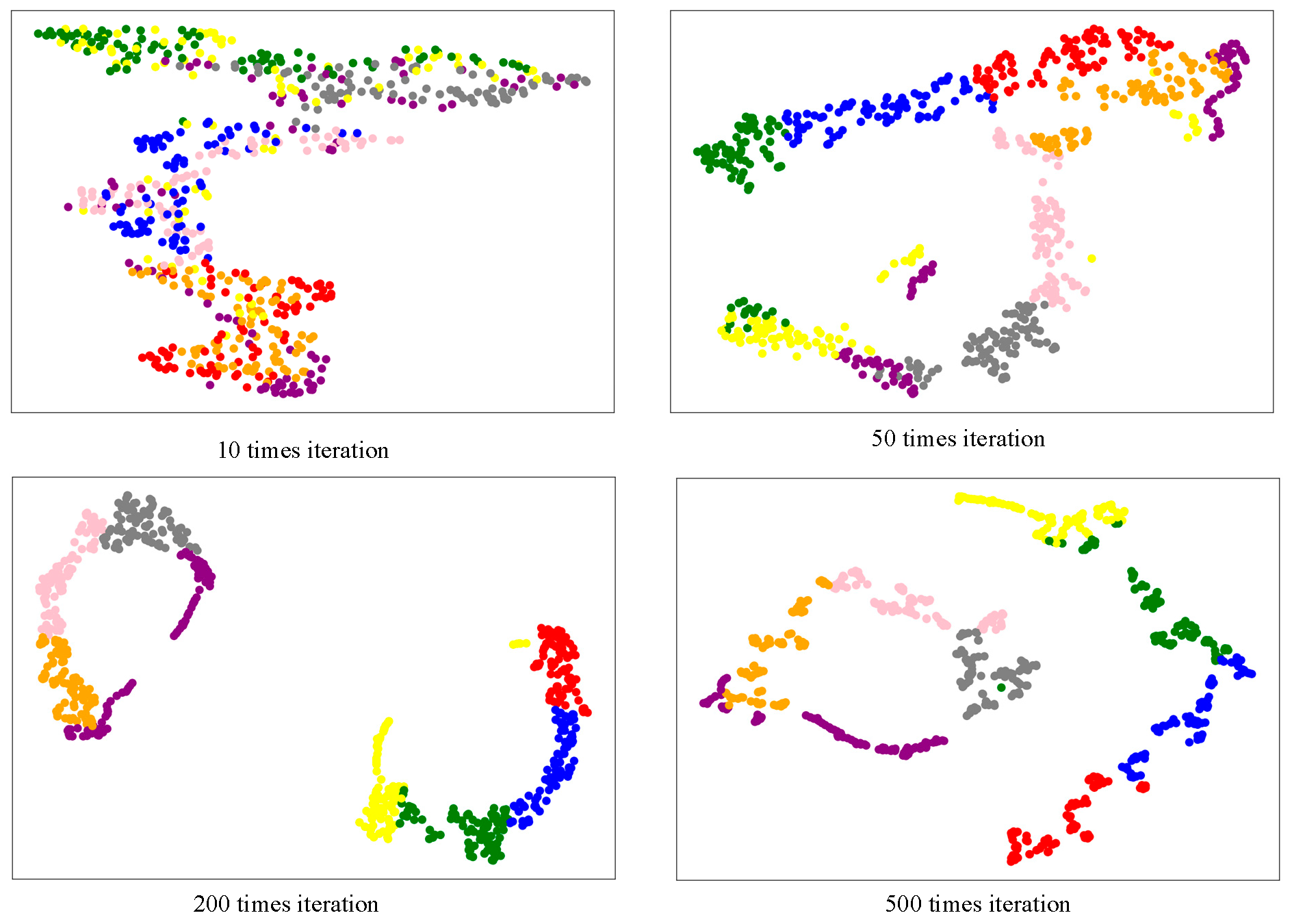
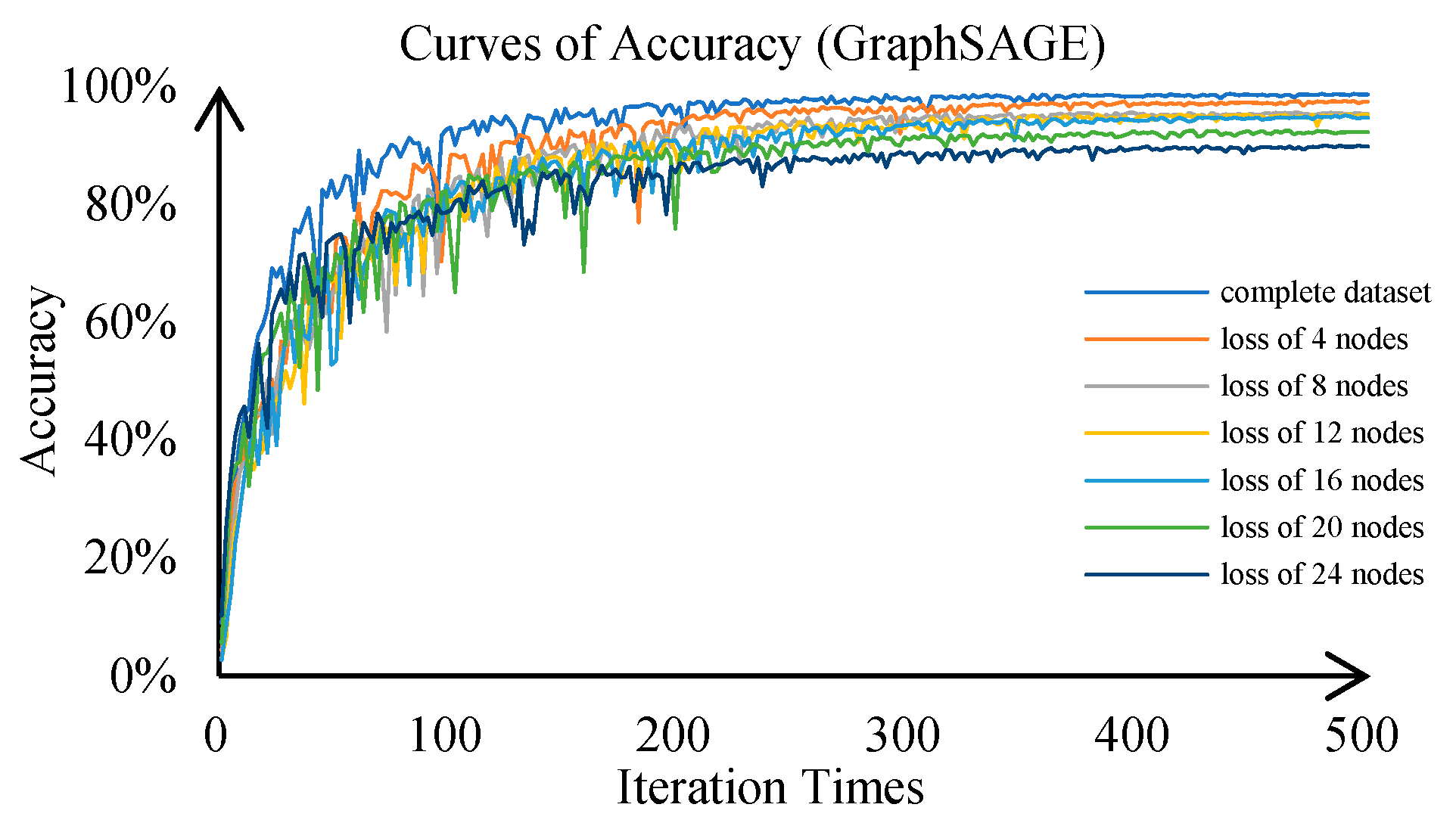
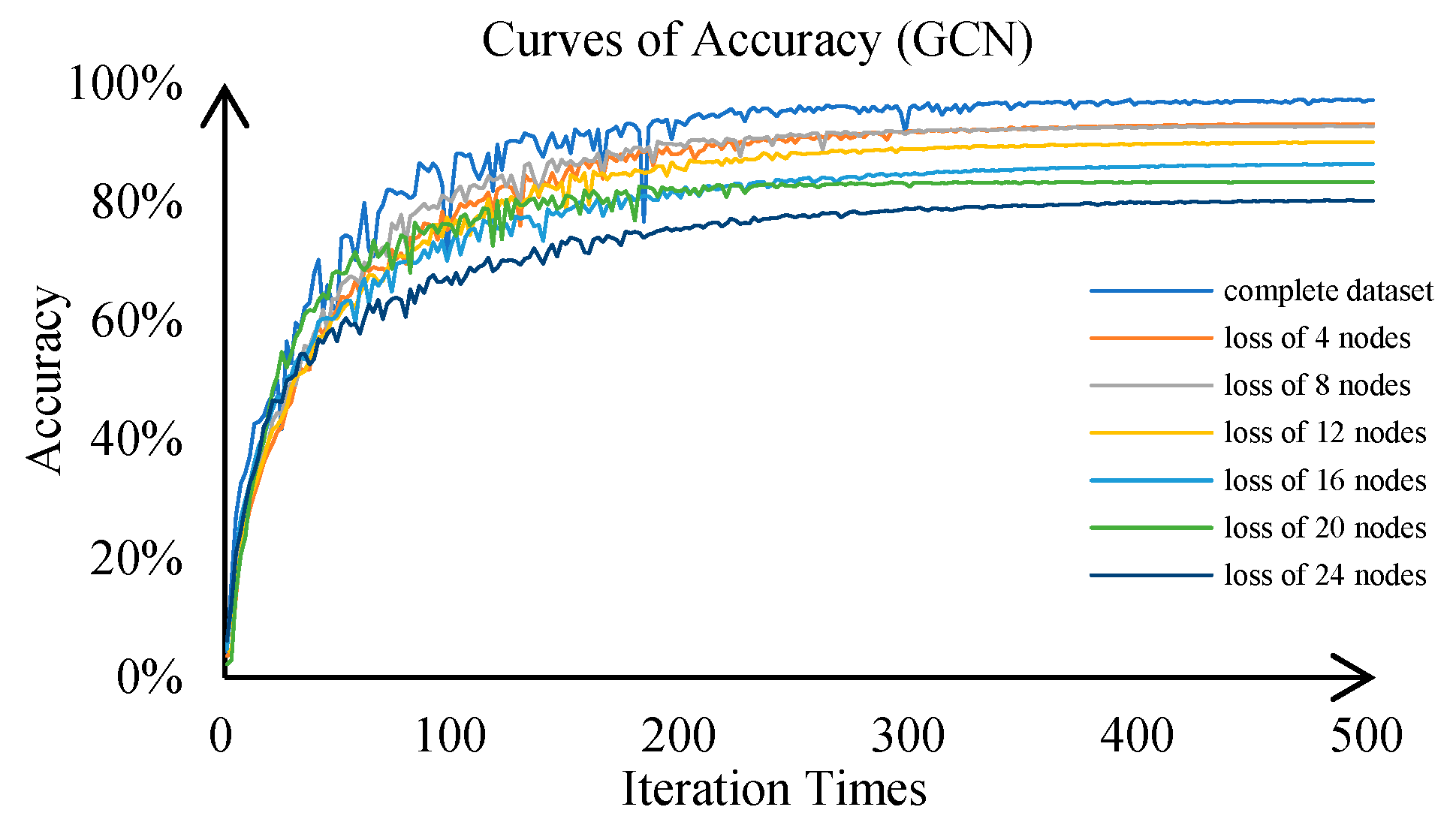
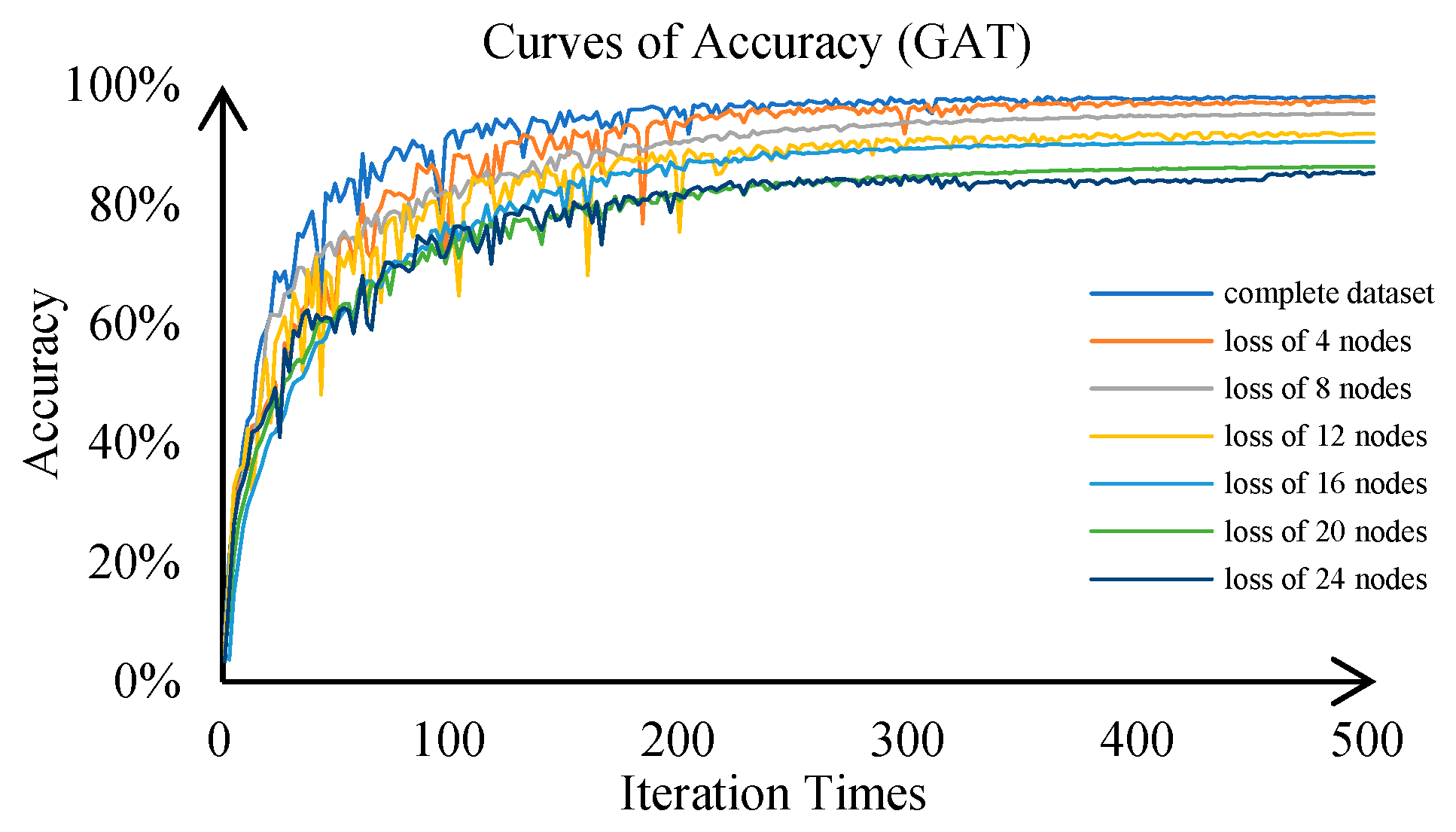
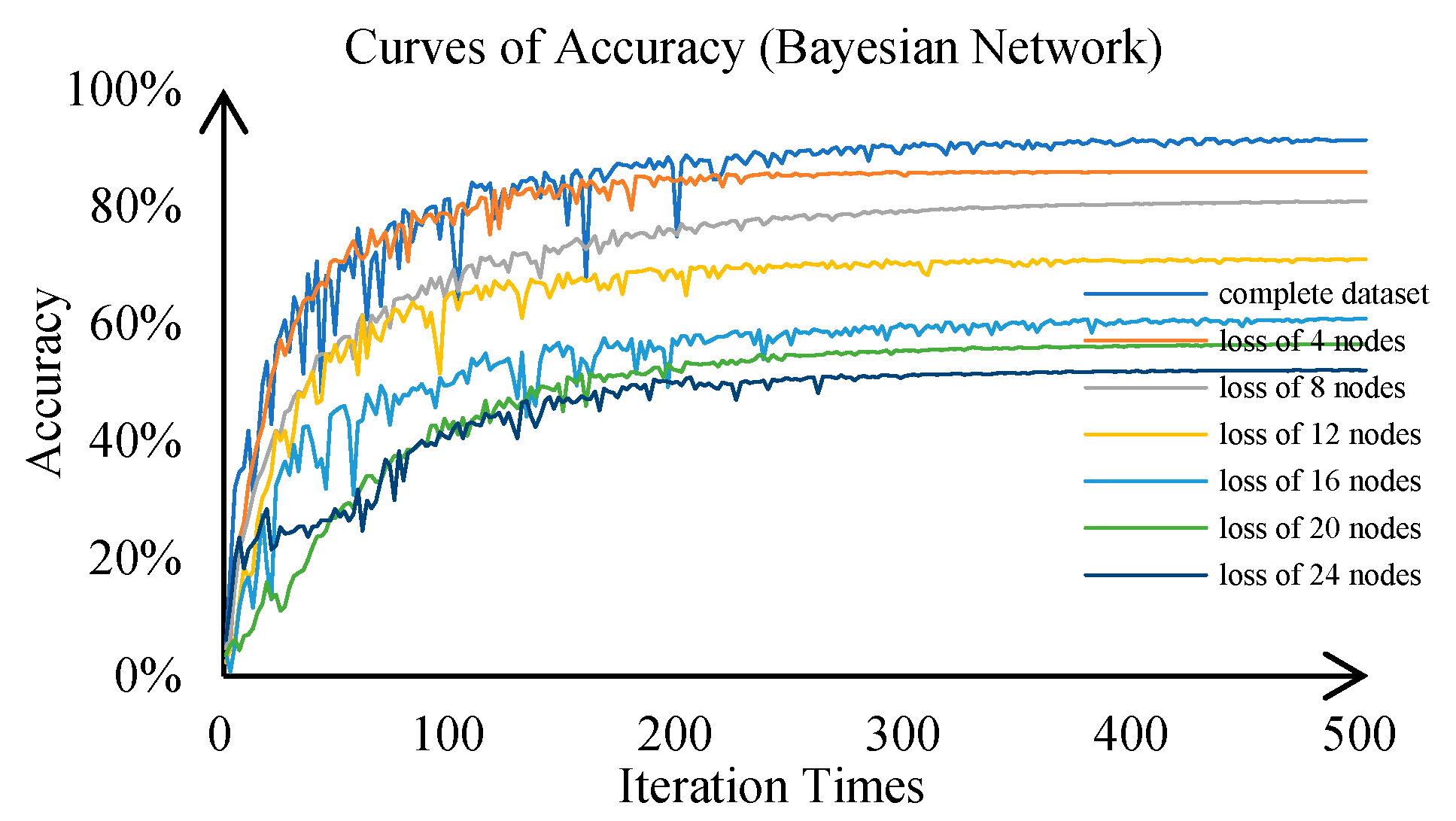
5.1. Diagnosis Model Validation

Fault data were simulated using PSD-BPA software(v4.2), considering the most common types of faults: three-phase short circuit, two-phase short circuit (AB-phase, BC-phase, CA-phase), two-phase grounding (AB-phase-G, BC-phase-G, CA-phase-G), and single-phase grounding (A-phase-G, B-phase-G, C-phase-G). A total of 34 fault lines (excluding busbars) were defined, with 9 fault points on each line spaced from 10% to 90% of the line length. To account for load fluctuations, simulations were performed at 9 load levels ranging from 80% to 120%, generating a total of 27,540 (9 (load levels) × 9 (fault points) × 34 (lines) × 10 (fault types)) data samples.

For each node, feature quantities were organized based on the phase A voltage and phase A voltage phase angle. The sampling length was 40 cycles, with a sampling step of 0.1 cycle. Due to the characteristics of the PSD-BPA simulation software, two sampling values were generated at the moments of fault occurrence and fault clearance. As a result, each feature produced 402 sampling points, leading to a total of 2412 feature points per node. The data for all 39 nodes were arranged row-wise to form a feature matrix of size 39 × 2412. The adjacency matrix was constructed as described and discussed in Section 3.2, with the topology of the 39-node system represented as a 2 ∗ 92 matrix. The database was divided into training and testing sets at a 9:1 ratio.

GraphSAGE, GCN, GAT, CNN, and the Bayesian network were individually tested on different datasets while keeping all other parameters the same, as follows: Step 1: Test the standard model using the complete dataset

Step 2: Simulate data loss or data collection failure, randomly delete data from 4 nodes, 8 nodes, 12 nodes, 16 nodes, 20 nodes, and 24 nodes for testing.

Step 3: Test the adaptability of GraphSAGE, GCN, GAT, CNN and Bayesian network to the new network when the topology changes.

Figure 7 shows the fault diagnosis accuracy curves for both training and test sets, while Figure 8 displays the error curves for both training and test sets. The output results of the test set are not used to update the network parameters; they only record the network’s performance on the test set during the training process. From Figure 7 and Figure 8, it is obvious that there is no overfitting during the iterations and that the network exhibits good robustness. Here, only the comparison curves of the training set and the test set for the GraphSAGE algorithm are shown. In the following sections, only the results of the test set will be presented.

As shown in Figure 9, the GraphSAGE algorithm achieves the highest accuracy when validated on the full dataset. Figure 10 shows the scatter distribution of the data after dimensionality reduction using t-SNE. Since there is a large number of sample categories (340 in total), only eight categories are selected for display. In the first seven rows of

Table 2. Performance testing under different models.

Models	GraphSAGE	GCN	GAT	CNN	Bayesian Network
Complete dataset	98.59%	97.15%	98.08%	95.38%	91.32%
Loss of 4 nodes	97.35%	93.13%	97.25%	92.33%	85.93%
Loss of 8 nodes	95.32%	92.81%	95.24%	89.42%	80.89%
Loss of 12 nodes	95.13%	90.07%	91.89%	84.5%	71.01%
Loss of 16 nodes	94.67%	86.42%	90.57%	79.18%	60.83%
Loss of 20 nodes	92.19%	83.36%	86.42%	73.49%	56.52%
Loss of 24 nodes	89.79%	80.24%	85.35%	66.31	52.13%
Connection relationship changes from bus26–bus28 to bus27–bus28	97.86%	94.75%	96.37%	91.42%	86.13%
Add connection relationship bus19–bus23	97.63%	94.28%	95.84%	91.14%	84.75%

, the CNN algorithm achieves a fault diagnosis accuracy of 95.38% when tested on the complete dataset. However, when 24 nodes are missing, its accuracy drops to 66.31%, a decrease of 29.07%. The Bayesian network algorithm achieves an accuracy of 91.32% on the complete dataset; however, this drops to 52.13% when 24 nodes are missing, a decrease of 39.19%. In contrast, GraphSAGE, GCN, and GAT experience decreases of 8.8%, 16.91%, and 12.73%, respectively.

It is evident that graph neural networks, which incorporate topological information and update feature representations from neighboring nodes, exhibit stronger representation capabilities and are less sensitive to missing data. Among these, the GraphSAGE algorithm, with its random sampling characteristic, can acquire more feature information through multiple random sampling processes under the same conditions, resulting in the highest fault diagnosis accuracy.

Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15 display the accuracy curves of GraphSAGE, GCN, GAT, CNN, and Bayesian network algorithms on the complete dataset and datasets with varying degrees of missing data. These figures clearly show that the GraphSAGE algorithm is the least affected by missing data, while the Bayesian network is the most affected. Rows 8 and 9 of Table 2 show the fault diagnosis accuracy of the five algorithms when the topology of the power system changes. GNNs consider that the system topology will achieve higher fault diagnosis accuracy compared to classical deep learning and machine learning algorithms. GAT, due to its attention mechanism, achieves higher accuracy than GCN, a conclusion that was validated in Reference [13].

However, GraphSAGE outperforms GAT in tests on the same dataset. While the advantage is marginal on the complete dataset (only 0.51% higher than GAT), the benefits of GraphSAGE become more pronounced as the number of missing nodes increases. Specifically, when 20 nodes and 24 nodes are missing, GraphSAGE’s accuracy is 5.77% and 4.44%, respectively. This highlights that the random sampling characteristic of GraphSAGE offers a greater advantage in solving power system fault diagnosis problems.

Notably, as is shown in Table 2, the accuracy difference under three scenarios (losing 8 nodes, 12 nodes, and 16 nodes) reveals an interesting trend. The accuracy decreased by only 0.65% from losing 8 nodes to losing 16 nodes but dropped by 3.27% when transitioning from the complete dataset to losing 8 nodes.

This finding appears counterintuitive. Further investigation revealed that the accuracy reduction depends on the location of the missing nodes. As shown in Figure 16, nodes with lower degrees (e.g., the blue node with a degree of 2) have a smaller impact on accuracy compared to nodes with higher degrees (e.g., the orange nodes, all with degrees of at least 4).

When all the data for the blue nodes are lost, the accuracy can still be maintained at 98.04%. Furthermore, if only the data for the 17 orange nodes are reserved, the accuracy can still be maintained at 95.13%, as shown in Figure 17.

In Table 2, through the last two rows of data, it is obvious that GraphSAGE has stronger adaptability and higher accuracy when the power grid topology changes.

5.2. Accurate Localization Model Validation

To simplify the model, the following two assumptions were made when constructing the subgraph model:

Assumption 1: Locality of Fault Influence. We assumed that the impact of a fault point is predominantly localized within its k-order neighboring nodes. This assumption is based on the observation that electrical disturbances typically diminish as they propagate through the network. Therefore, constructing subgraphs centered around the k-order neighborhood efficiently captures relevant fault features while reducing computational complexity;

Assumption 2: Static Topology During Fault Occurrence. We assumed that the power system topology remains static during the fault occurrence and diagnosis process. This assumption simplifies the model construction by avoiding dynamic changes in node connectivity, which may otherwise introduce additional noise in the graph representation.

In Section 3, Figure 6 shows all the subgraphs. Based on the results of the diagnosis model, a new sub-dataset is constructed corresponding to the identified subgraph model. The sub-dataset and subgraph serve as new inputs, with the fault point location information used as the new labels. The samples are divided into sub-training sets and sub-testing sets at a 9:1 ratio. The output of the model is the predicted location of the fault point. Thus, the localization error can be calculated as follows:

$$error=\left|outputs\times 100\%-labelvalue\right|$$

(14)

Figure 18 illustrates the error distribution for locating three-phase short-circuit faults, with similar trends observed across other fault types. The subgraph structure used in the model plays a crucial role in determining the accuracy of fault location. For instance, as depicted in Figure 19, the output of the fault diagnosis model is 14, corresponding to a three-phase short-circuit fault between bus9 and bus39. Two subgraphs are constructed for comparison: the first includes only first-order adjacent nodes of the interval endpoints, while the second incorporates second-order adjacent nodes. Models trained on these subgraphs yield significantly different results. Figure 19 corresponds to the results within the red square in Figure 18, the model using the first-order subgraph achieves a maximum locating error of less than 3.5%, whereas the second-order subgraph model exhibits errors exceeding 14%. These findings highlight that the size and structure of the subgraph are critical to fault localization accuracy. Experimental validation confirms that subgraphs containing at least six nodes consistently limit the maximum fault localization error to below 3.5%.

We conducted the same tests on these two types of subgraphs using the GAT and GCN algorithms; the test results are shown in Figure 20 and Figure 21. When the subgraph structure selects the first-order subgraph, the maximum localization error of GAT and GCN exceeds 17.5%. However, when the subgraph structure selects the second-order subgraph, the maximum localization errors of GAT and GCN decrease to approximately 8% and 9%, respectively.

Comparing these results with those in Figure 19, the accurate localization error of the GraphSAGE algorithm is significantly lower than those of the GAT and GCN algorithms. This validation result can be easily explained. Although GAT introduces an attention mechanism compared to GCN, both GAT and GCN algorithms focus on learning features using global graph information. For subgraphs with a relatively simple structure, the attention mechanism introduced by GAT has a limited effect. In contrast, the random sampling characteristic of GraphSAGE enables it to capture richer feature information and demonstrate stronger representation capabilities, leading to a more accurate localization performance.

Table 3. Fault localization error distribution.

Range	Number	Proportion
[0, 0.5%)	185	6.72%
[0.5%, 1%)	552	20.04%
[1%, 1.5%)	639	23.20%
[1.5%, 2%)	784	28.47%
[2%, 2.5%)	335	12.16%
[2.5%, 3%)	201	7.30%
[3%, 3.5%)	45	1.63%
[3.5%, 4%)	13	0.47%

further underscores the effectiveness of the proposed approach: 78.43% of test samples achieve a prediction error of less than 2% and 99.53% of test samples achieve a prediction error of less than 3.5%. These results consistently demonstrate the robustness and precision of the subgraph-based fault localization method, forcefully emphasizing the importance of subgraph design in achieving accurate results.

Regarding the selection of subgraph size, it is certain that a bigger size does not always result in a better performance. Using the entire graph for fault point localization can lead to significant errors. This phenomenon can also be easily explained: a line fault has a limited impact on the entire power grid, with a greater effect on nearby nodes. If the entire graph structure is used for localization, the nodes minimally affected by the fault can skew the final diagnosis results. Figure 5 illustrates all the subgraph structures used, with the maximum error not exceeding 4%.

Compared to the traditional method of fault location using traveling waves, where the sampling interval of traveling wave measurement devices is 1 millisecond, the fault location is determined by the time difference of traveling waves detected at both ends. The basic principle is that the propagation speed of traveling waves in power lines is close to the speed of light. The error source is solely the time difference caused by the sampling interval, typically resulting in a maximum error of no more than 30 km/s (speed of light) × 1 ms (measurement error) = 300 m.

The proposed method achieves a maximum error of no more than 4% of the line length. Therefore, for lines shorter than 7.5 km, this method has a certain advantage over the traveling wave method. However, for longer transmission lines, the localization error of this method is larger than that of the traveling wave method. Nevertheless, this method has obvious advantages over the traveling wave method. Since PMU and μPMU are already widely deployed in power grids, the required data can be directly obtained. In contrast, traveling wave measurement devices are expensive and are only installed in higher-voltage transmission networks. Thus, this method offers certain economic benefits compared to the traveling wave method and aligns more closely with the future development trends of smart grids.

6. Conclusions

This manuscript used the GraphSAGE algorithm to develop a fault diagnosis and accurate fault localization model for power systems. The feasibility and performance of the proposed method were validated across multiple dimensions, as follows:

(1)

While some studies have used GCN, GAT, classical deep learning (CNN), and machine learning (Bayesian network) methods to address fault type classification and fault interval localization in power grids. Few studies have also established an AI-based model for accurate fault localization. This article introduces an innovative approach by using GraphSAGE to build an accurate fault localization model, leveraging its inductive learning capability and fully utilizing topological information to realize accurate fault localization;

(2)

Extensive validation data demonstrate that the higher the degree of a node, the more effectively it can learn features from neighboring nodes. This property allows for the identification of key nodes when processing large-scale power grid data, thereby reducing the complexity of the model while maintaining accuracy;

(3)

In simulations involving topology changes in the power grid, GraphSAGE consistently outperforms GCN and GAT, with an accuracy improvement of about 3% and 2%. This demonstrates its strong adaptability to topology variations and excellent practical applicability;

(4)

In the accurate localization model, the random sampling characteristic and inductive learning capability of the GraphSAGE algorithm can achieve significantly higher localization accuracy compared to GAT and GCN;

(5)

When the line length does not exceed 7.5 km, this method offers certain advantages over the traveling wave method. Moreover, this method offers greater economic practicality compared to the traveling wave method.

The fault diagnosis and accurate localization model developed in this study is suitable for power grids with moderate topology changes. However, due to the significant differences in power grid structures, further research is also essential. Techniques, such as transfer learning and reinforcement learning, could optimize the proposed model, enabling it to handle scenarios with substantial topological changes and improving its generalization and practical performance.

Microgrids and hybrid AC-DC grids are also becoming widely prevalent. In these networks, the optimization of feature representations may be necessary, especially for hybrid AC–DC grids. Since current simulations are based on AC grids, further research is needed to determine how to select node feature representations for DC components. In further research, noise signals can also be incorporated into the database construction to simulate and testify the sampling noise. Additionally, if feasible, real power grid data should be obtained to further validate the practicality and applicability of this method.