Analysis of Circuit Configurations Suitable for Self-Supplied AC-DC Converters Using Thin-Film Piezoelectric Generators and Multilayer Energy Storage Supercapacitors
Abstract
1. Introduction
2. Thin-Film Piezoelectric Generators for Wearable Power Supplies
3. Multiplayer Supercapacitors, Designed for Piezoelectric Energy Harvesters
4. Electronic Circuits Used to Convert AC to DC Voltage
4.1. Circuit Configurations with Discrete Components
4.1.1. Standard Diode Bridge Rectifier
4.1.2. Voltage Doubler Rectifier
4.2. Circuit Configurations with Integrated Components
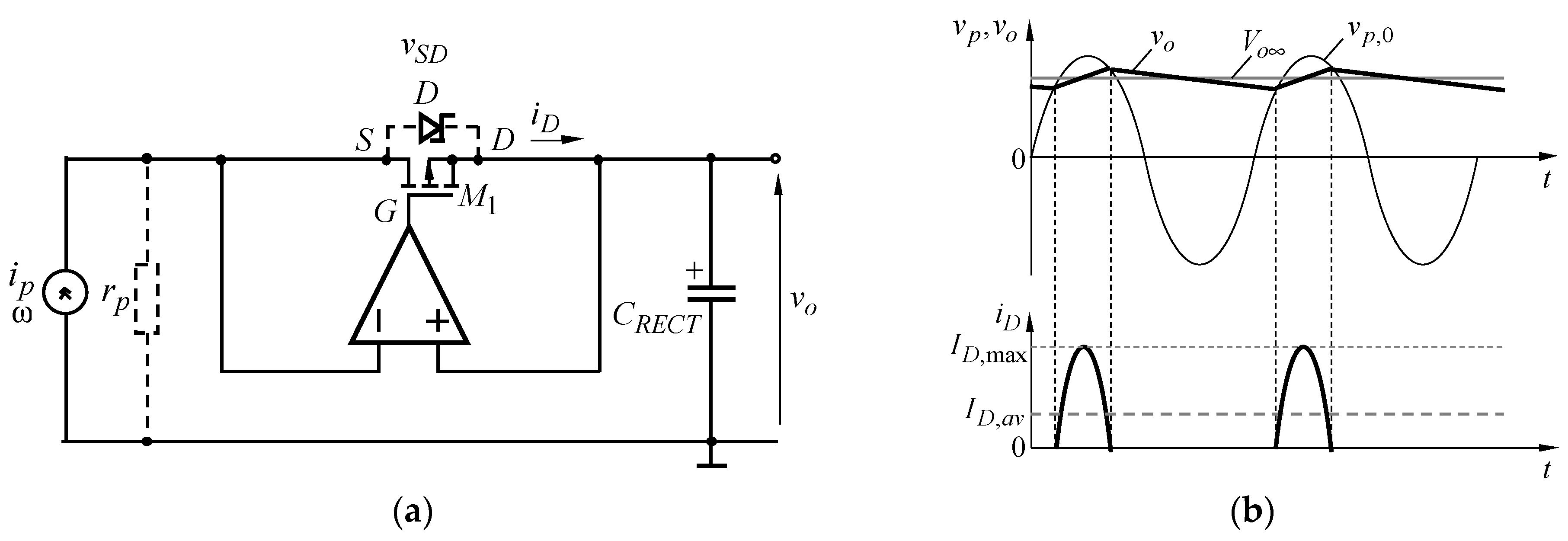
4.2.1. Bridge Rectifier Using MOSFETs
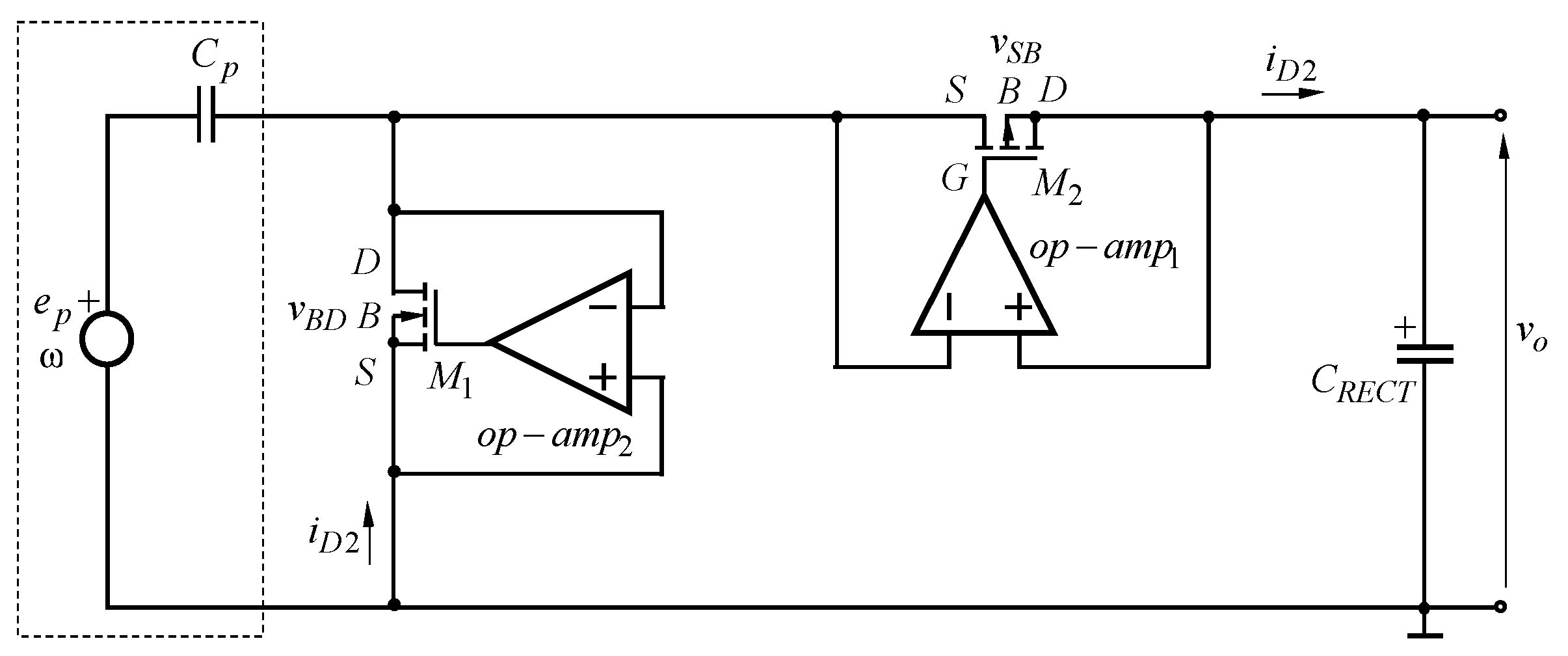
4.2.2. Active Rectifiers
4.2.3. Voltage Doubler AC-DC Converters
4.3. Parameter Study for Different Rectifier Stages Topologies of Reported Piezoelectric Energy Harvesting Systems
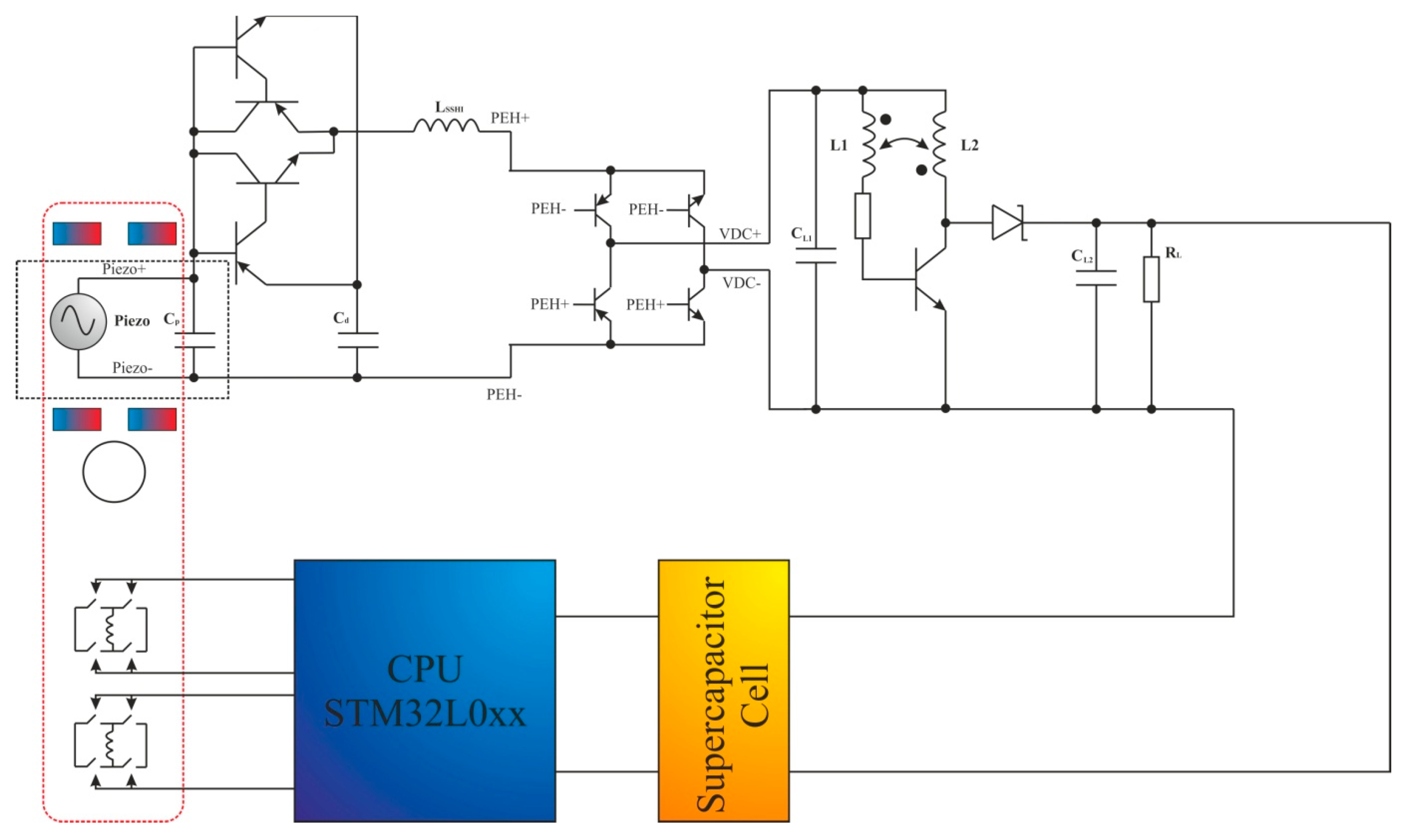
5. SSHI (Synchronized Switch Harvesting on Inductor) Based Energy Harvesting Circuits
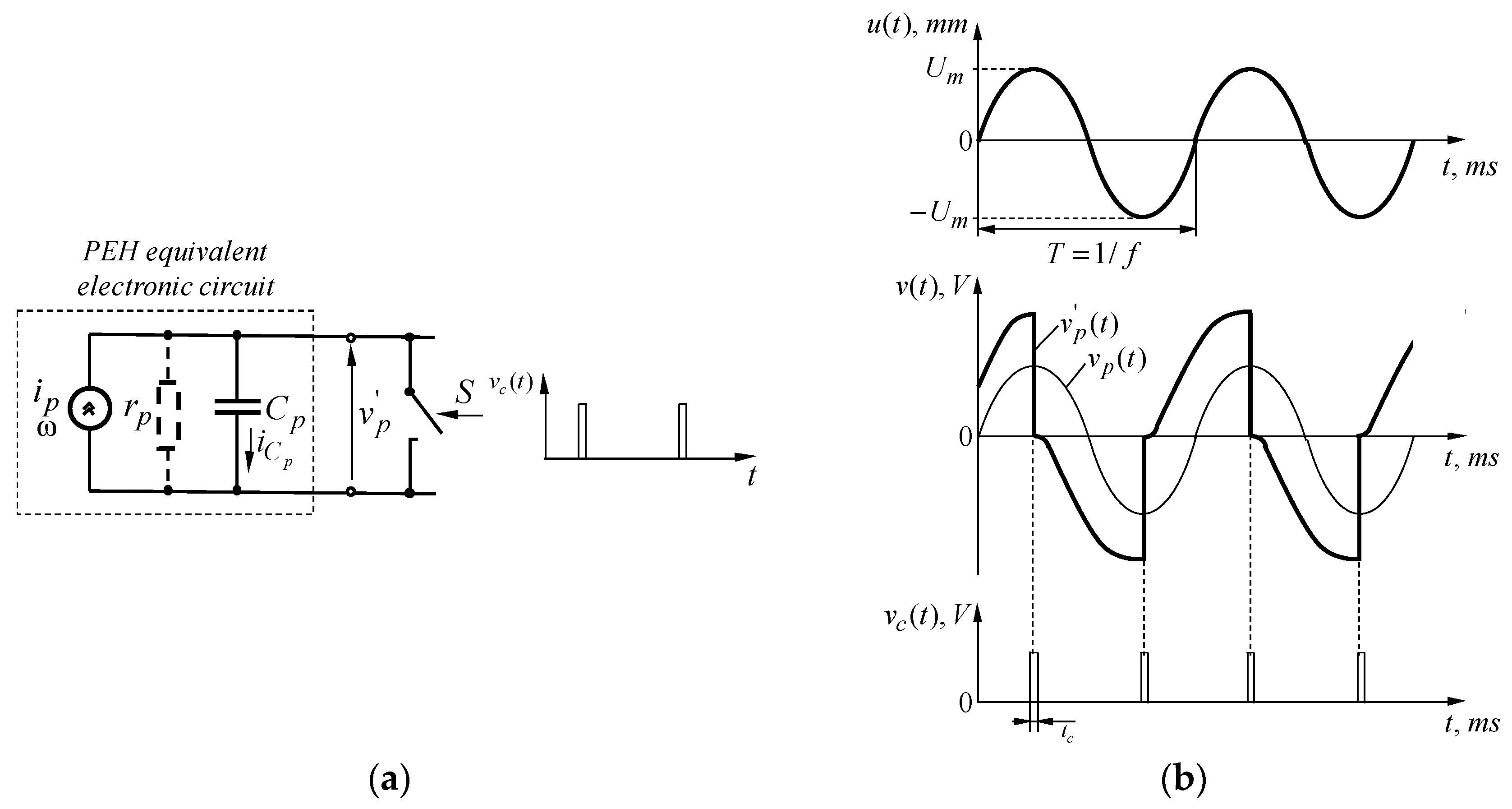
5.1. General Principle of a SSHI Technique
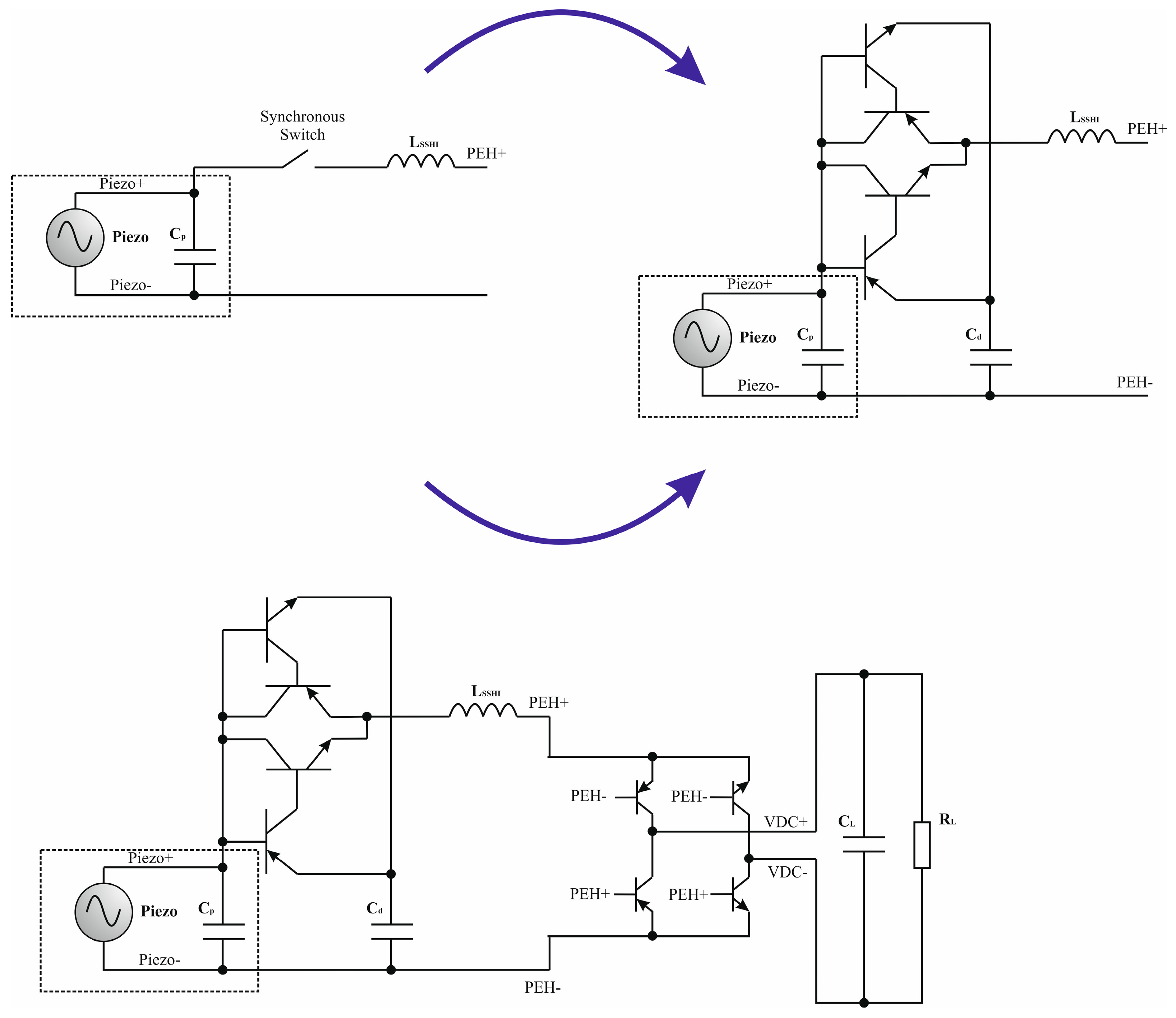
5.2. Parallel SSHI Technique—Basic Functional Circuit and Operational Principle
5.3. Series SSHI Technique—Basic Functional Circuit and Operational Principle
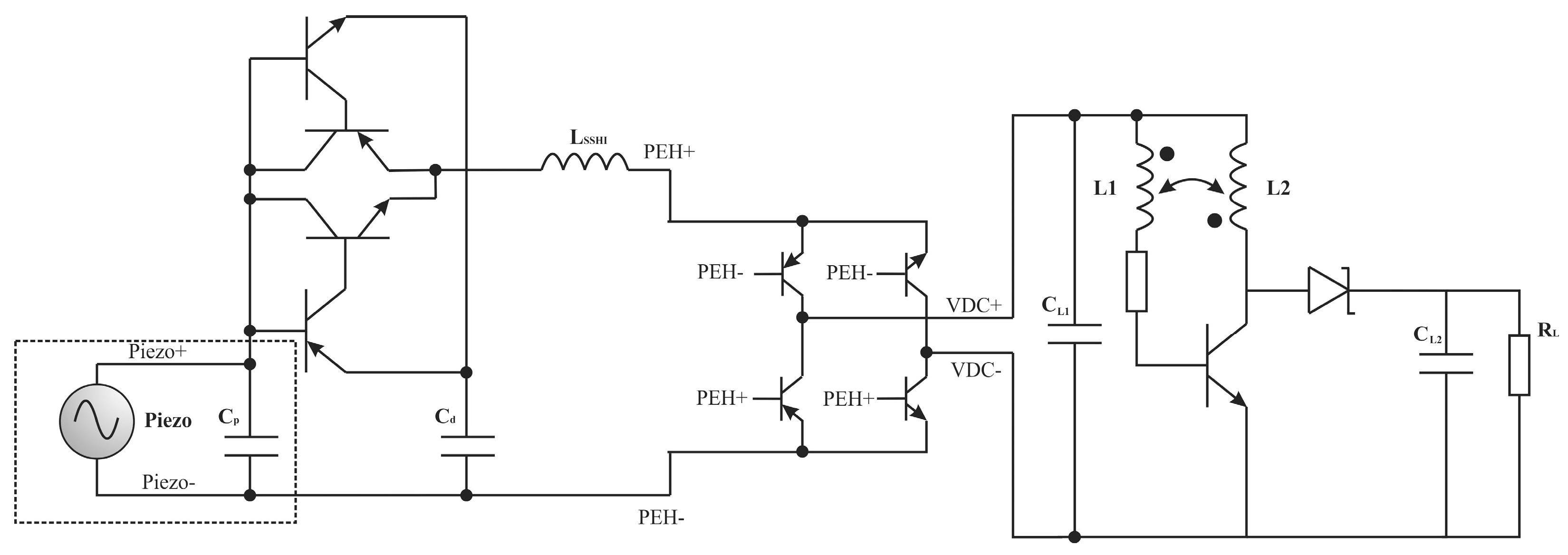
5.4. Structure and Operational Principle of a Basic Resonant Rectifier Circuits
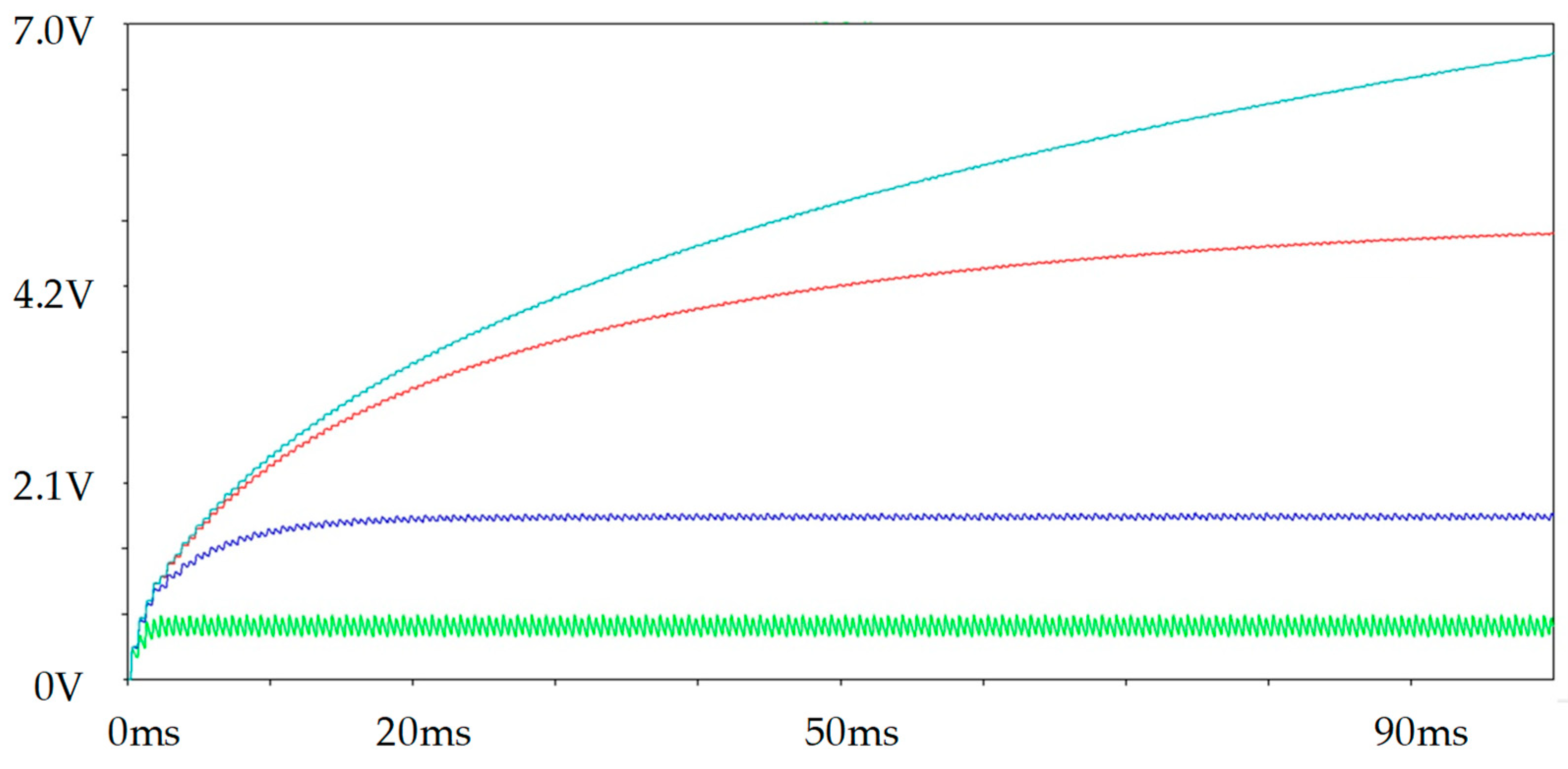
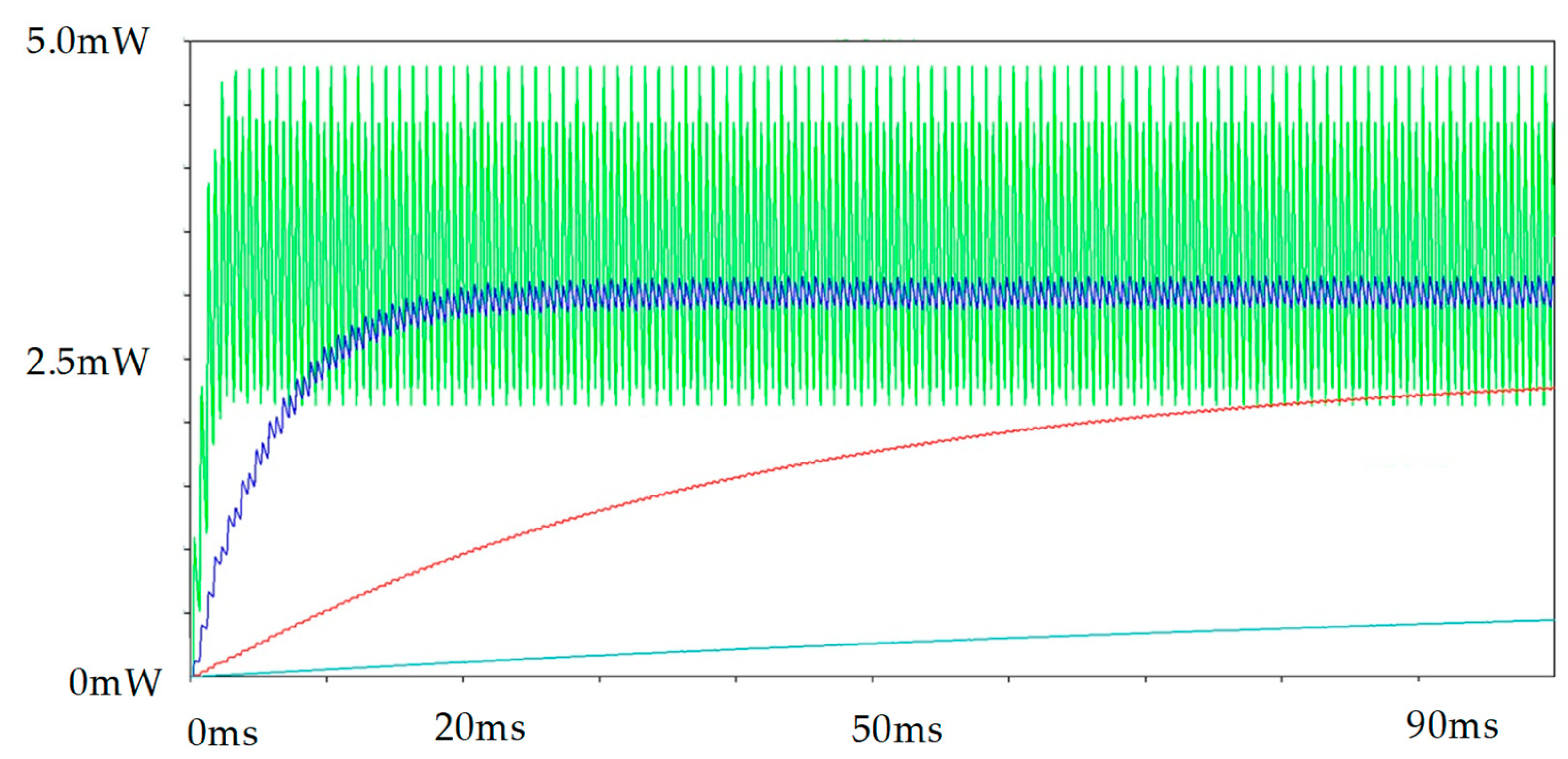
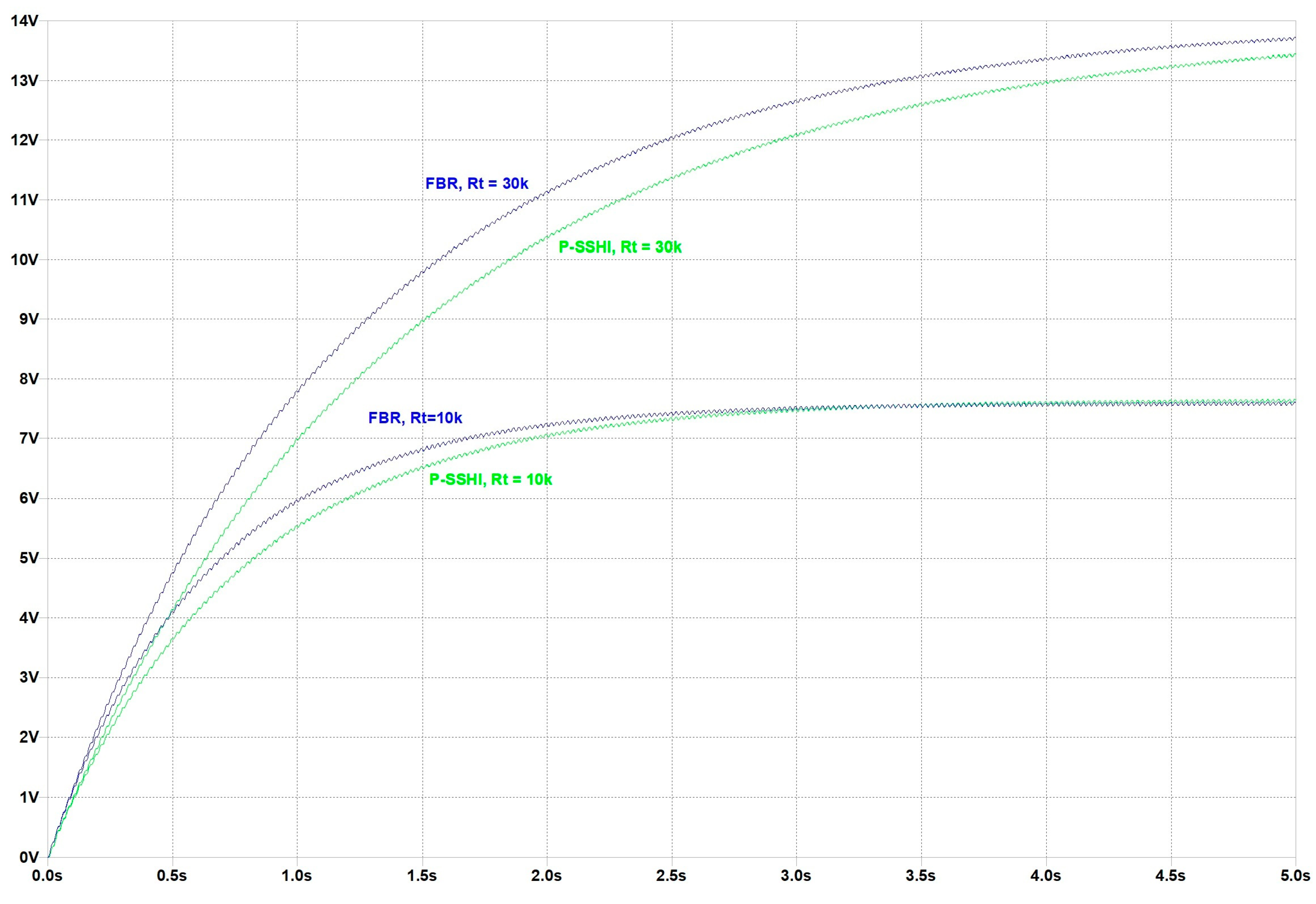
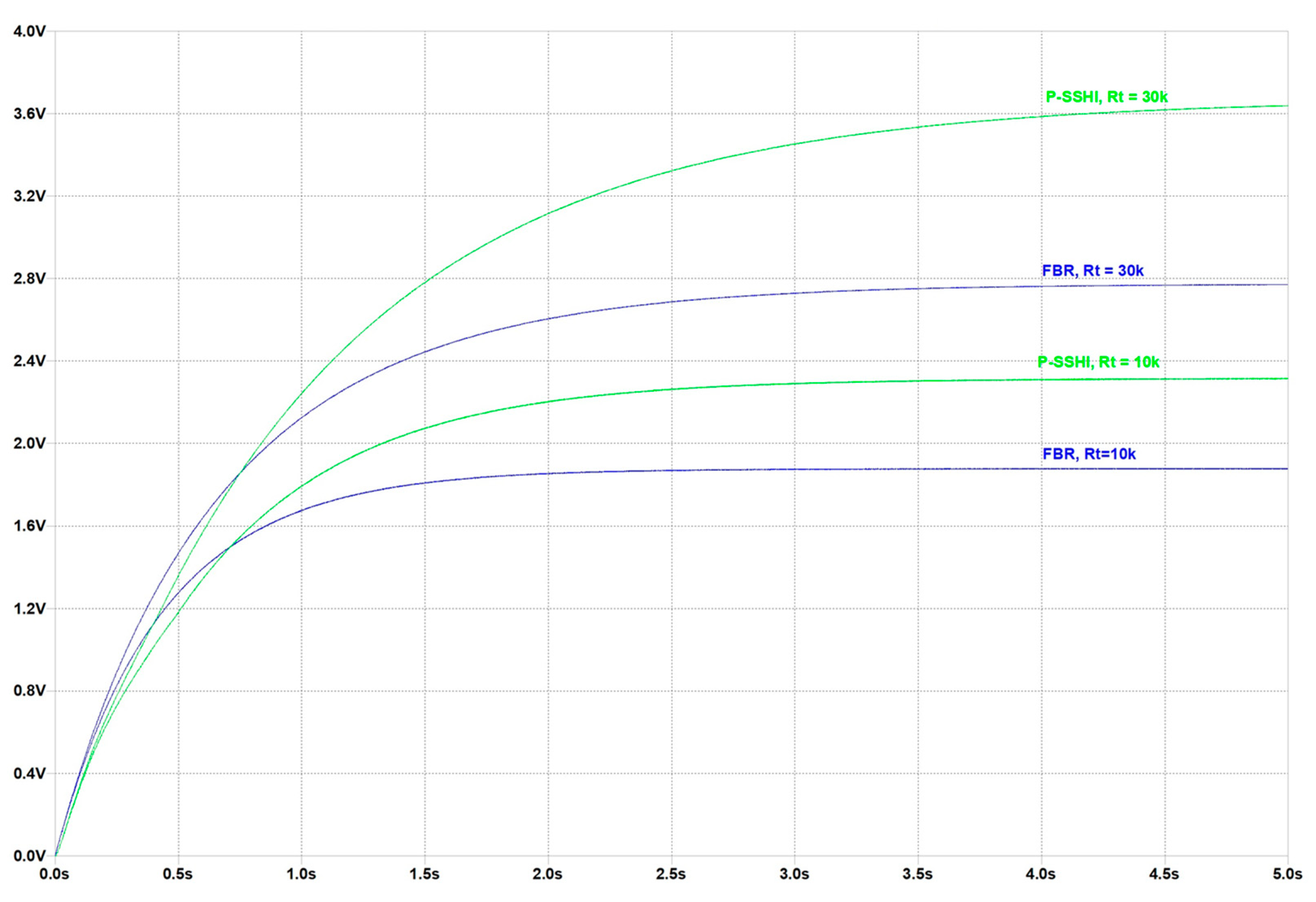
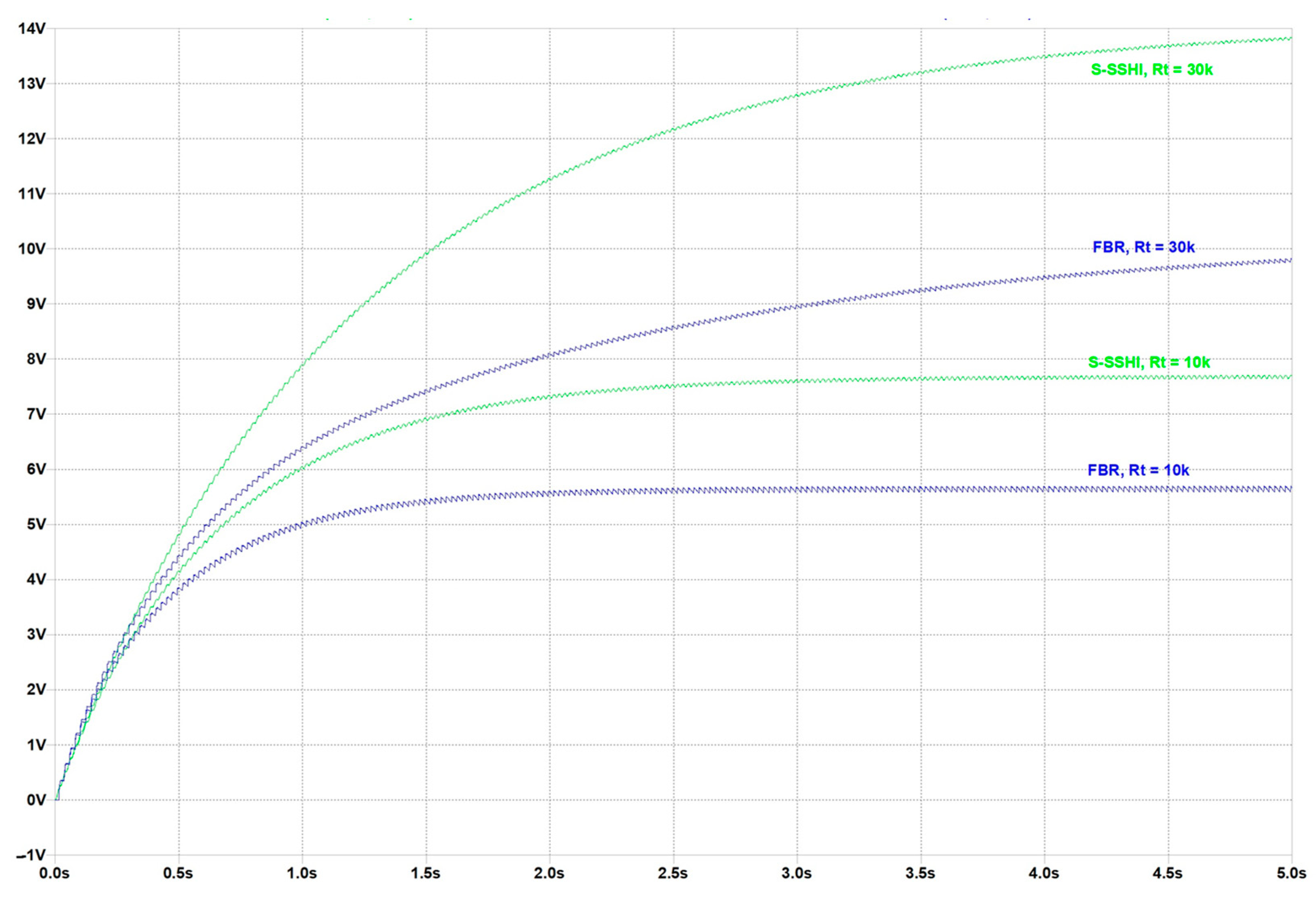
5.4.1. Simulation Testing and Discussions on Resonant Rectifier Circuit, Employing Parallel SSHI Technique
5.4.2. Simulation Testing and Discussions on Resonant Rectifier Circuit, Employing Series SSHI Technique
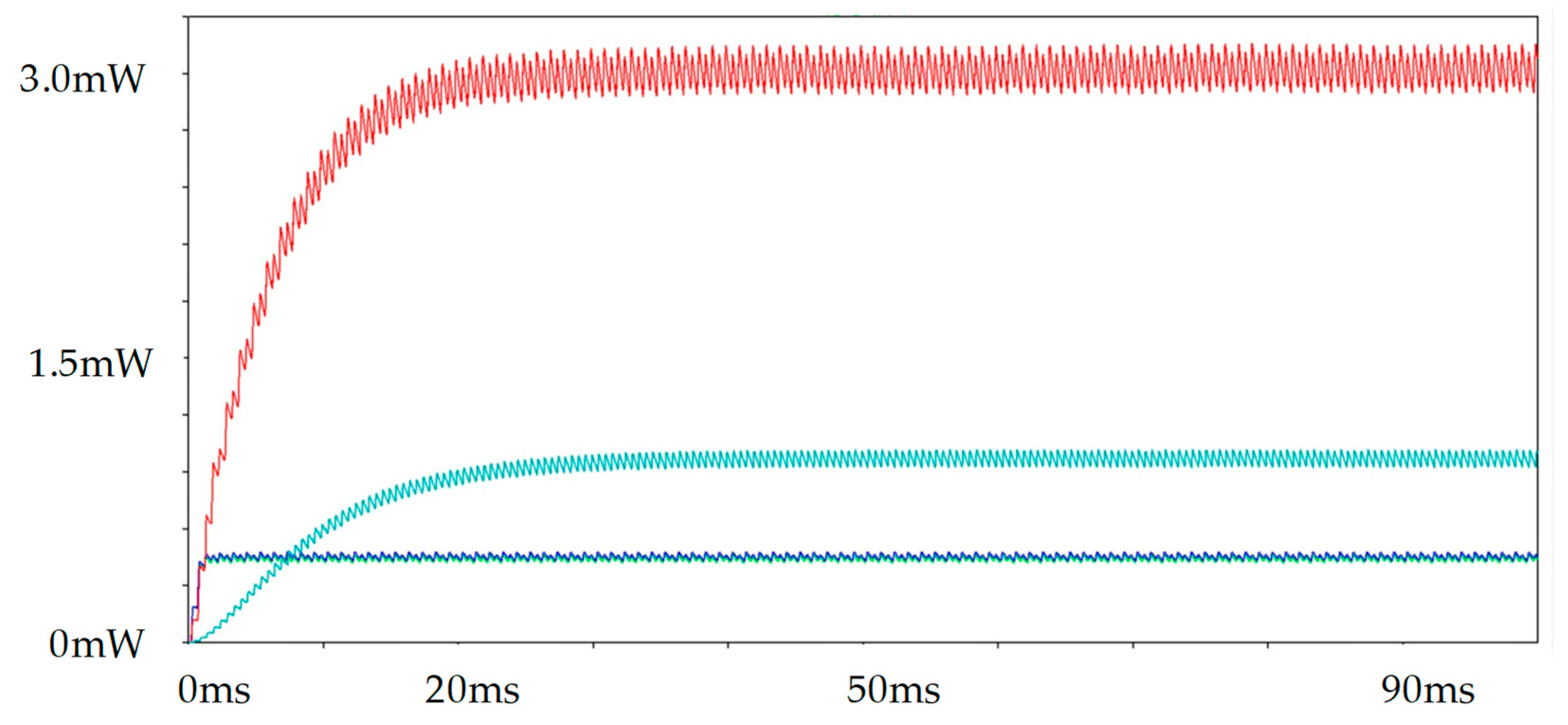
5.4.3. Simulation Results and Discussions on s-SSHI and p-SSHI Circuits, Employing a Model of Commercially Available Multilayer Piezoelectric Generator
5.5. Piezoelectric Harvester Resonant Frequency Matching and Tuning
- (1)
- Positioning a set of constant magnets over the vibrating structure;
- (2)
- Adjusting the length of the cantilever;
- (3)
- Protruding the tip’s inertial mass.
5.6. Summary of Key Advances in SSHI Techniques for Piezoelectric Energy Harvesting Applications
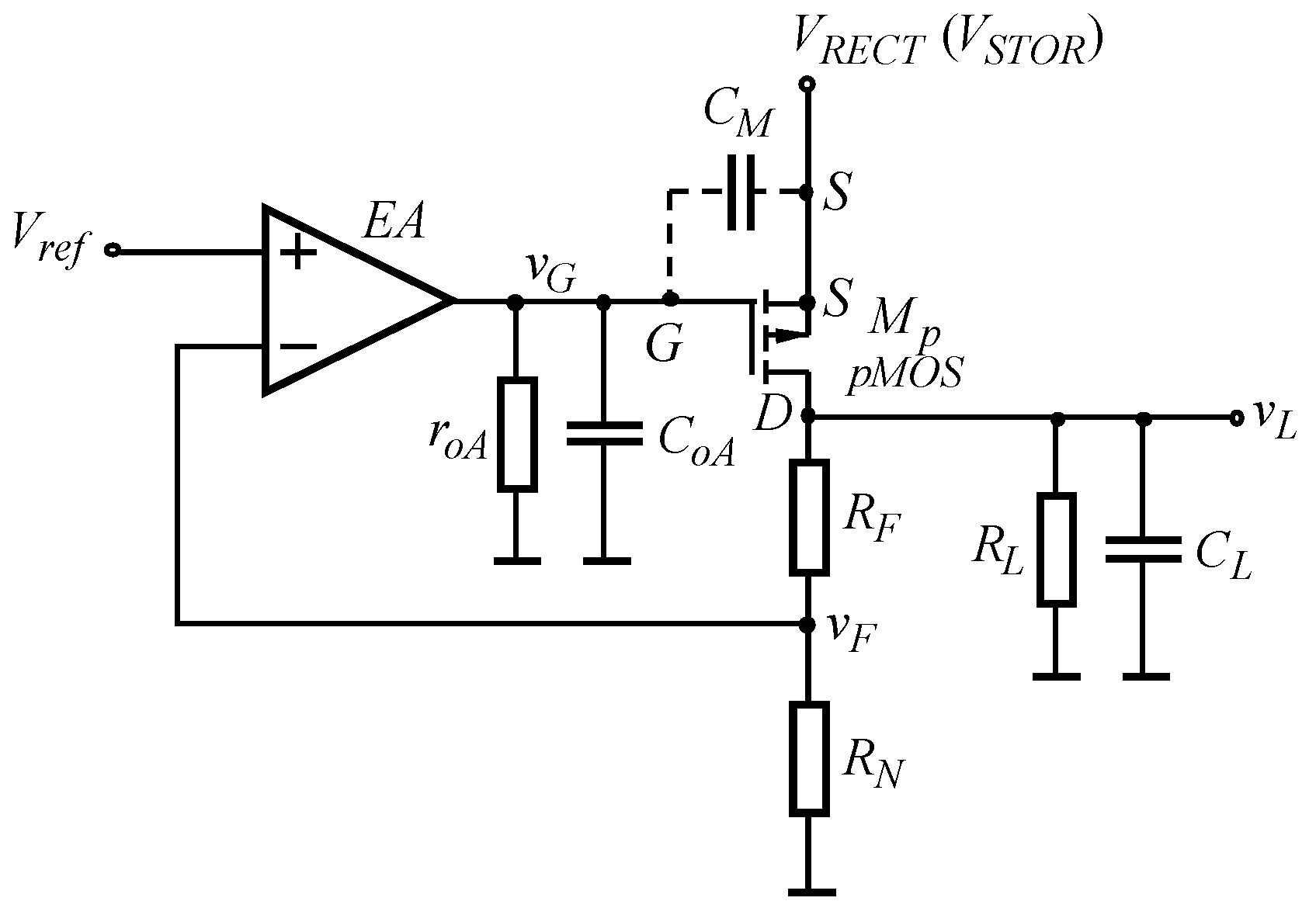
6. Low-Dropout (LDO) Regulators for Piezoelectric Energy Harvesting Applications: Basic Parameters of Commercially Available ICs of LDO Regulators
6.1. Typical Circuit Diagram of an LDO. Parameter Definition
6.2. Recent Advances of LDOs. Comparative Analysis
6.3. Commercially Available IC of LDOs
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kang, M.; Yeo, W.-H. Advances in Energy Harvesting Technologies for Wearable Devices. Micromachines 2024, 15, 884. [Google Scholar] [CrossRef] [PubMed]
- Kong, T.; Hedayatipour, A. Oximeter for All: An Innovative Look in Inclusive Physiological Monitoring. IEEE Circuits Syst. Mag. 2024, 24, 43–44. [Google Scholar] [CrossRef]
- Durbha, R.; Koomson, V. ChromaSense-Empowering Health, Empowering You. IEEE Circuits Syst. Mag. 2024, 24, 45–46. [Google Scholar] [CrossRef]
- Nangobi, Z.; Rodgers, M.; Nadunga, C. Your Health Application. IEEE Circuits Syst. Mag. 2024, 24, 47–48. [Google Scholar] [CrossRef]
- Fu, H.; Jiang, J.; Hu, S.; Rao, J.; Theodossiades, S. A multi-stable ultra-low frequency energy harvester using a nonlinear pendulum and piezoelectric transduction for self-powered sensing. Mech. Syst. Signal Process. 2023, 189, 110034. [Google Scholar] [CrossRef]
- Shuvo, M.M.H.; Titirsha, T.; Amin, N.; Islam, S.K. Energy Harvesting in Implantable and Wearable Medical Devices for Enduring Precision Healthcare. Energies 2022, 15, 7495. [Google Scholar] [CrossRef]
- Friebe, M. Innovation design for the future of health. In Novel Innovation Design for the Future of Health: Entrepreneurial Concepts for Patient Empowerment and Health Democratization; Springer: Cham, Switzerland, 2022; Chapter 1; pp. 1–13. ISBN 978-3-031-08190-3. [Google Scholar]
- Song, Y.; Min, J.; Yu, Y.; Wang, H.; Yang, Y.; Zhang, H.; Gao, W. Wireless Battery-Free Wearable Sweat Sensor Powered by Human Motion. Sci. Adv. 2020, 6, eaay9842. [Google Scholar] [CrossRef]
- Li, C.; Jiang, F.; Liu, C.; Liu, P.; Xu, J. Present and Future Thermoelectric Materials Toward Wearable Energy Harvesting. Appl. Mater. Today 2019, 15, 543–557. [Google Scholar] [CrossRef]
- Todaro, M.T.; Guido, F.; Algieri, L.; Mastronardi, V.M.; Desmaële, D.; Epifani, G.; De Vittorio, M. Biocompatible, Flexible, and Compliant Energy Harvesters Based on Piezoelectric Thin Films. IEEE Trans. Nanotechnol. 2018, 17, 220–230. [Google Scholar] [CrossRef]
- Khalifa, S.; Lan, G.; Hassan, M.; Seneviratne, A.; Das, S.K. HARKE: Human Activity Recognition from Kinetic Energy Harvesting Data in Wearable Devices. IEEE Trans. Mob. Comput. 2018, 17, 1353–1368. [Google Scholar] [CrossRef]
- Seneviratne, S.; Hu, Y.; Nguyen, T.; Lan, G.; Khalifa, S.; Thilakarathna, K. A Survey of Wearable Devices and Challenges. IEEE Commun. Surv. Tutor. 2017, 19, 2573–2620. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.C. Wearable Sensors for Human Activity Monitoring: A Review. IEEE Sens. J. 2014, 15, 1321–1330. [Google Scholar] [CrossRef]
- Wang, Z.-q.; Huang, Z.-h. Wearable health status monitoring device for electricity workers using ZigBee-based wireless sensor network. In Proceedings of the 2014 7th International Conference on Biomedical Engineering and Informatics, Dalian, China, 14–16 October 2014; pp. 602–606. [Google Scholar] [CrossRef]
- Maciuca, A.; Popescu, D.; Strutu, M.; Stamatescu, G. Wireless sensor network based on multilevel femtocells for home monitoring. In Proceedings of the 2013 IEEE 7th International Conference on Intelligent Data Acquisition and Advanced Computing Systems (IDAACS), Berlin, Germany, 12–14 September 2013; pp. 499–503. [Google Scholar] [CrossRef]
- Wearable Technology Market. September 2024. Available online: https://www.precedenceresearch.com/wearable-technology-market (accessed on 8 March 2025).
- Hannan, M.A.; Mutashar, S.; Samad, S.A.; Hussain, A. Energy harvesting for the implantable biomedical devices: Issues and challenges. Biomed. Eng. Online 2014, 13, 79. [Google Scholar] [CrossRef] [PubMed]
- Bandodkar, A.J.; Wang, J. Wearable Biofuel Cells: A Review. Electroanalysis 2016, 28, 1188–1200. [Google Scholar] [CrossRef]
- Yu, Y.; Nassar, J.; Xu, C.; Min, J.; Yang, Y.; Dai, A.; Doshi, R.; Huang, A.; Song, Y.; Gehlhar, R.; et al. Biofuel-Powered Soft Electronic Skin with Multiplexed and Wireless Sensing for Human-Machine Interfaces. Sci. Robot. 2020, 5, eaaz7946. [Google Scholar] [CrossRef]
- Gao, W.; Emaminejad, S.; Nyein, H.Y.Y.; Challa, S.; Chen, K.; Peck, A.; Fahad, H.M.; Ota, H.; Shiraki, H.; Kiriya, D.; et al. Fully Integrated Wearable Sensor Arrays for Multiplexed in Situ Perspiration Analysis. Nature 2016, 529, 509–514. [Google Scholar] [CrossRef]
- Wu, F.; Li, C.; Yin, Y.; Cao, R.; Li, H.; Zhang, X.; Zhao, S.; Wang, J.; Wang, B.; Xing, Y.; et al. A Flexible, Lightweight, and Wearable Triboelectric Nanogenerator for Energy Harvesting and Self-Powered Sensing. Adv. Mater. Technol. 2019, 4, 1800216. [Google Scholar] [CrossRef]
- Zou, Y.; Raveendran, V.; Chen, J. Wearable Triboelectric Nanogenerators for Biomechanical Energy Harvesting. Nano Energy 2020, 77, 105303. [Google Scholar] [CrossRef]
- Yin, L.; Kim, K.N.; Trifonov, A.; Podhajny, T.; Wang, J. Designing Wearable Microgrids: Towards Autonomous Sustainable on-Body Energy Management. Energy Environ. Sci. 2022, 15, 82–101. [Google Scholar] [CrossRef]
- Choi, Y.-M.; Lee, M.G.; Jeon, Y. Wearable Biomechanical Energy Harvesting Technologies. Energies 2017, 10, 1483. [Google Scholar] [CrossRef]
- Mendez-Lira, O.; Spinelli, E.M.; Gonzalez-Landaeta, R. Battery-Less Power Management Circuit Powered by a Wearable Piezoelectric Energy Harvester. Energy Technol. 2021, 9, 2100520. [Google Scholar] [CrossRef]
- Haider, S.T.; Shah, M.A.; Lee, D.-G.; Hur, S. A Review of the Recent Applications of Aluminum Nitride-Based Piezoelectric Devices. IEEE Access 2023, 11, 58779–58795. [Google Scholar] [CrossRef]
- Liu, H.; Fu, H.; Sun, L.; Lee, C.; Yeatman, E.M. Hybrid Energy Harvesting Technology: From Materials, Structural Design, System Integration to Applications. Renew. Sustain. Energy Rev. 2021, 137, 110473. [Google Scholar] [CrossRef]
- Jinno, H.; Fukuda, K.; Xu, X.; Park, S.; Suzuki, Y.; Koizumi, M.; Yokota, T.; Osaka, I.; Takimiya, K.; Someya, T. Stretchable and Waterproof Elastomer-Coated Organic Photovoltaics for Washable Electronic Textile Applications. Nat. Energy 2017, 2, 780–785. [Google Scholar] [CrossRef]
- Almarri, N.; Chang, J.; Song, W.; Jiang, D.; Demosthenous, A. Piezoelectric energy harvesting and ultra-low-power management circuits for medical devices. Nano Energy 2024, 13, 110196. [Google Scholar] [CrossRef]
- Horie, K.; Al Farisi, M.S.; Hasegawa, Y.; Matsushima, M.; Kawabe, T.; Shikida, M. Proof-of-Concept Quantitative Monitoring of Respiration Using Low-Energy Wearable Piezoelectric Thread. Electronics 2024, 13, 4577. [Google Scholar] [CrossRef]
- Tarhan, E.; Hoseyni, S.M.; Aghakhani, A.; Basdogan, I. Investigation of networked SSHI configurations for plate-based piezoelectric energy harvesters. J. Intell. Mater. Syst. Struct. 2025, 36, 327–339. [Google Scholar] [CrossRef]
- Ali, A.; Iqbal, S.; Chen, X. Recent advances in piezoelectric wearable energy harvesting based on human motion: Materials, design, and applications. Energy Strategy Rev. 2024, 53, 101422. [Google Scholar] [CrossRef]
- Verma, P.; Naval, S.; Mallick, D.; Jain, A. Hybrid Piezoelectric-Triboelectric Biomechanical Harvesting System for Wearable Applications. IEEE Trans. Circuits Syst. II Express Briefs 2024, 71, 1914–1918. [Google Scholar] [CrossRef]
- Ali, A.; Shaukat, H.; Bibi, S.; Altabey, W.A.; Noori, M.; Kouritem, S.A. Recent Progress in Energy Harvesting Systems for Wearable Technology. Energy Strat. Rev. 2023, 49, 101124. [Google Scholar] [CrossRef]
- Ren, W.; Sun, Y.; Zhao, D.; Aili, A.; Zhang, S.; Shi, C.; Zhang, J.; Geng, H.; Zhang, J.; Zhang, L.; et al. High-Performance Wearable Thermoelectric Generator with Self-Healing, Recycling, and Lego-like Reconfiguring Capabilities. Sci. Adv. 2021, 7, eabe0586. [Google Scholar] [CrossRef]
- Yuan, J.; Zhu, R. A Fully Self-Powered Wearable Monitoring System with Systematically Optimized Flexible Thermoelectric Generator. Appl. Energy 2020, 271, 115250. [Google Scholar] [CrossRef]
- Chodankar, N.; Padwal, C.; Pham, H.D.; Ostrikov, K.K.; Jadhav, S.; Mahale, K.; Yarlagadda, P.K.; Huh, Y.S.; Han, Y.K.; Dubal, D. Piezo-supercapacitors: A new paradigm of self-powered wellbeing and biomedical devices. Nano Energy 2021, 90 Pt A, 106607. [Google Scholar] [CrossRef]
- Sayed, D.M.; Allam, N.K. All-solid-state, self-powered supercapacitors: State-of-the-art and future perspectives. J. Energy Storage 2022, 56 Pt A, 105882. [Google Scholar] [CrossRef]
- Park, Y.; Cho, K.; Kim, S. Vertical all-in-one energy systems constructed with thermoelectric generators and microsupercapacitors. J. Power Sources 2021, 510, 230402. [Google Scholar] [CrossRef]
- Aktakka, E.E.; Najafi, K. A Micro Inertial Energy Harvesting Platform with Self-Supplied Power Management Circuit for Autonomous Wireless Sensor Nodes. IEEE J. Solid-State Circuits 2014, 49, 2017–2029. [Google Scholar] [CrossRef]
- Sanchez, D.A.; Leicht, J.; Jodka, E.; Fazel, E.; Manoli, Y. 21.2 A 4µW-to-1mW parallel-SSHI rectifier for piezoelectric energy harvesting of periodic and shock excitations with inductor sharing, cold start-up and up to 681% power extraction improvement. In Proceedings of the IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 31 January–4 February 2016. [Google Scholar] [CrossRef]
- Dell’Anna, F.; Dong, T.; Li, P.; Wen, Y.; Yang, Z.; Casu, M.R.; Azadmehr, M.; Berg, Y. State-of-the-Art Power Management Circuits for Piezoelectric Energy Harvesters. IEEE Circuits Syst. Mag. 2018, 18, 27–48. [Google Scholar] [CrossRef]
- Chamanian, S.; Muhtaroğlu, A.; Külah, H. A Self-Adapting Synchronized-Switch Interface Circuit for Piezoelectric Energy Harvesters. IEEE Trans. Power Electron. 2020, 35, 901–912. [Google Scholar] [CrossRef]
- Chamanian, S.; Çiftci, B.; Muhtaroğlu, A.; Külah, H. A Self-Powered and Area Efficient SSHI Rectifier for Piezoelectric Harvesters. IEEE Access 2021, 9, 117703–117713. [Google Scholar] [CrossRef]
- Ben Ammar, M.; Sahnoun, S.; Fakhfakh, A.; Viehweger, C.; Kanoun, O. Self-Powered Synchronized Switching Interface Circuit for Piezoelectric Footstep Energy Harvesting. Sensors 2023, 23, 1830. [Google Scholar] [CrossRef]
- Costanzo, L.; Lo Schiavo, A.; Vitelli, M. A Self-Supplied Power Optimizer for Piezoelectric Energy Harvesters Operating under Non-Sinusoidal Vibrations. Energies 2023, 16, 4368. [Google Scholar] [CrossRef]
- Ghandi, S.; Janaideh, M.A.; Zhang, L. State of the Art on Power Conditioning for Piezoelectric Energy Harvesters. IEEE Trans. Power Electron. 2024, 39, 3724–3737. [Google Scholar] [CrossRef]
- LTC3588-1 Nanopower Energy Harvesting Power Supply—Datasheet. Analog Devices, Norwood, MA, USA. 2023. Available online: https://www.analog.com/en/products/ltc3588-1.html (accessed on 14 September 2024).
- ADP5092 Ultralow Power Energy Harvester PMU with MPPT and Charge Management—Datasheet. Analog Devices, Norwood, MA, USA. 2023. Available online: https://www.analog.com/en/products/adp5092.html (accessed on 14 September 2024).
- MAX20361 Small, Single-/Multi-Cell Solar Harvester with MPPT and Harvest Counter—Datasheet. Analog Devices, Norwood, MA, USA. 2023. Available online: https://www.analog.com/en/products/max20361.html (accessed on 14 September 2024).
- TPSM365R6RDNR 3-V to 65-V Input, 1-V to 13-V Output, 0.6-A Synchronous Buck Converter Power Module—Datasheet; Texas Instruments: Dallas, TX, USA, 2023; Available online: https://www.ti.com/product/TPSM365R6/part-details/TPSM365R6RDNR (accessed on 14 September 2024).
- Li, W.; Lin, K.; Chen, L.; Yang, D.; Ge, Q.; Wang, Z. Self-Powered Wireless Flexible Ionogel Wearable Devices. ACS Appl. Mater. Interfaces 2023, 15, 14768–14776. [Google Scholar] [CrossRef] [PubMed]
- Hao, D.; Gong, Y.; Wu, J.; Shen, Q.; Zhang, Z.; Zhi, J.; Zou, R.; Kong, W.; Kong, L. A Self-Sensing and Self-Powered Wearable System Based on Multi-Source Human Motion Energy Harvesting. Small 2024, 20, 2311036. [Google Scholar] [CrossRef]
- Mahapatra, A.; Ajimsha, R.S.; Deepak, D.; Misra, P. Tuning ZnO-based piezoelectric nanogenerator efficiency through n-ZnO/p-NiO bulk interfacing. Nature 2024, 14, 11871. [Google Scholar] [CrossRef]
- Lv, P.; Zhan, H.; Xin, L.; Zhang, S.; Wang, J.; Li, R.; Li, C.; Ren, L.; Zhang, M.; Cheng, X. Flexible, bilayered piezoelectric composite based on large-scale inorganic PZT film and organic P(VDF-TrFE) membrane for mechanical energy harvesting. Surf. Interfaces 2024, 51, 104623. [Google Scholar] [CrossRef]
- Ali, T.A.; Pilz, J.; Schäffner, P.; Kratzer, M.; Teichert, C.; Stadlober, B.; Coclite, A.M. Piezoelectric Properties of Zinc Oxide Thin Films Grown by Plasma-Enhanced Atomic Layer Deposition. Phys. Status Solidi A 2020, 217, 2000319. [Google Scholar] [CrossRef]
- Putra, P.P.; Akasaka, S.; Konosu, Y.; Zhang, S.; Tanioka, A.; Matsumoto, H. Structure–Piezoelectric Property Relationships of Thin Films Composed of Electrospun Aligned Poly(vinylidene fluoride) Nanofibers. Nanomaterials 2024, 14, 491. [Google Scholar] [CrossRef]
- Ali, I.; Dulal, M.; Karim, N.; Afroj, S. 2D Material-Based Wearable Energy Harvesting Textiles: A Review. Small Struct. 2024, 5, 2300282. [Google Scholar] [CrossRef]
- Li, P.; Zhang, Z. Self-Powered 2D Material-Based pH Sensor and Photodetector Driven by Monolayer MoSe2 Piezoelectric Nanogenerator. ACS Appl. Mater. Interfaces 2020, 12, 58132–58139. [Google Scholar] [CrossRef]
- Zhiqiang, S.; Rongxi, H.; Feng, J. Recent progress in piezoelectric thin films as self-powered devices: Material and application. Front. Mater. 2024, 11, 1373040. [Google Scholar] [CrossRef]
- Bairagi, S.; Kumar, C.; Babu, A.; Aliyana, A.K.; Stylios, G.; Pillai, S.C.; Mulvihill, D.M. Wearable nanocomposite textile-based piezoelectric and triboelectric nanogenerators: Progress and perspectives. Nano Energy 2023, 118 Pt B, 108962. [Google Scholar] [CrossRef]
- Maestri, G.; Ferreira, L.B.; Bachmann, P.; Paim, A.A.; Merlini, C.; Steffens, F. Recent advances in piezoelectric textile materials: A brief literature review. J. Eng. Fibers Fabr. 2023, 18, 15589250231151242. [Google Scholar] [CrossRef]
- Ju, B.J.; Oh, J.H.; Yun, C.; Park, C.H. Development of a superhydrophobic electrospun poly (vinylidene fluoride) web via plasma etching and water immersion for energy harvesting applications. RSC Adv. 2018, 8, 28825–28835. [Google Scholar] [CrossRef] [PubMed]
- Mokhtari, F.; Spinks, G.M.; Sayyar, S.; Cheng, Z.; Ruhparwar, A.; Foroughi, J. Highly Stretchable Self-Powered Wearable Electrical Energy Generator and Sensors. Adv. Mater. Technol. 2021, 6, 2000841. [Google Scholar] [CrossRef]
- Zhen, L.; Lu, L.; Yao, Y.; Liua, J.; Yang, B. Flexible inorganic piezoelectric functional films and their applications. J. Adv. Ceram. 2023, 12, 433–462. [Google Scholar] [CrossRef]
- Yeo, H.G.; Xue, T.; Roundy, S.; Ma, X.; Rahn, C.; Trolier-McKinstry, C. Strongly (001) Oriented Bimorph PZT Film on Metal Foils Grown by rf-Sputtering for Wrist-Worn Piezoelectric Energy Harvesters. Adv. Funct. Mater. 2018, 28, 1801327. [Google Scholar] [CrossRef]
- Chen, C.; Feng, J.; Li, J.; Guo, Y.; Shi, X.; Peng, H. Functional Fiber Materials to Smart Fiber Devices. Chem. Rev. 2023, 123, 613–662. [Google Scholar] [CrossRef]
- Liu, Y.; Li, H.; Feng, Q.; Su, H.; Li, D.; Shang, Y.; Chen, H.; Li, B.; Dong, H. A Three-Dimensional-Printed Recyclable, Flexible, and Wearable Device for Visualized UV, Temperature, and Sweat pH Sensing. ACS Omega 2022, 7, 9834–9845. [Google Scholar] [CrossRef]
- Güçlü, H.; Kasım, H.; Yazici, M. Investigation of the optimum vibration energy harvesting performance of electrospun PVDF/BaTiO3 nanogenerator. J. Compos. Mater. 2023, 57, 409–424. [Google Scholar] [CrossRef]
- Bairagi, S.; Ali, S.W. Influence of High Aspect Ratio Lead-Free Piezoelectric Fillers in Designing Flexible Fibrous Nanogenerators: Demonstration of Significant High Output Voltage. Energy Technol. 2019, 7, 1900538. [Google Scholar] [CrossRef]
- Sheng, T.; He, Q.; Cao, Y.; Dong, Z.; Gai, Y.; Zhang, W.; Zhang, D.; Chen, H.; Jiang, Y. Research on energy harvesting using piezoelectric materials. ACS Appl. Mater. Interfaces 2023, 15, 39570–39577. [Google Scholar] [CrossRef]
- Wang, S.; Khan, A.A.; Teale, S.; Xu, J.; Parmar, D.H.; Zhao, R.; Grater, L.; Serles, P.; Zou, Y.; Filleter, T.; et al. Large piezoelectric response in a Jahn-Teller distorted molecular metal halide. Nat. Commun. 2023, 14, 1852. [Google Scholar] [CrossRef] [PubMed]
- Yea, J.; Ha, J.; Lim, K.S.; Lee, H.; Oh, S.; Jekal, J.; Yu, T.S.; Jung, H.H.; Park, J.U.; Lee, T.; et al. Research on novel nanostructures for enhanced performance. ACS Nano 2024, 18, 34096–34106. [Google Scholar] [CrossRef]
- Kim, S.; Towfeeq, I.; Dong, Y.; Gorman, S.; Rao, A.M.; Koley, G. P(VDF-TrFE) Film on PDMS Substrate for Energy Harvesting Applications. Appl. Sci. 2018, 8, 213. [Google Scholar] [CrossRef]
- Subasinghage, K.; Gunawardane, K. Supercapacitor-Assisted Energy Harvesting Systems. Energies 2024, 17, 3853. [Google Scholar] [CrossRef]
- Jalal, N.I.; Ibrahim, R.I.; Oudah, M.K. A review on Supercapacitors: Types and components. J. Phys. Conf. Ser. 2021, 1973, 012015. [Google Scholar] [CrossRef]
- Krishnamoorthy, K.; Pazhamalai, P.; Manoharan, S.; Ali, N.; Kim, S.-J. Recent trends, challenges, and perspectives in piezoelectric-driven self-chargeable electrochemical supercapacitors. Carbon Energy 2022, 4, 833–855. [Google Scholar] [CrossRef]
- Kasprzak, D.; Mayorga-Martinez, C.C.; Alduhaish, O.; Pumera, M. Wearable and Flexible All-Solid-State Supercapacitor Based on MXene and Chitin. Energy Technol. 2023, 11, 2201103. [Google Scholar] [CrossRef]
- Shimada, T.; Takenaka, N.; Ando, Y.; Otani, M.; Okubo, M.; Yamada, A. Relationship between Electric Double-Layer Structure of MXene Electrode and Its Surface Functional Groups. Chem. Mater. 2022, 34, 2069–2075. [Google Scholar] [CrossRef]
- Zhang, Y.; Cao, J.; Yuan, Z.; Zhao, L.; Wang, L.; Han, W. Assembling Co3O4 Nanoparticles into MXene with Enhanced electrochemical performance for advanced asymmetric supercapacitors. J. Colloid Interface Sci. 2021, 599, 109–118. [Google Scholar] [CrossRef]
- Ahmad, F.; Zahid, M.; Jamil, H.; Khan, M.A.; Atiq, S.; Bibi, M.; Shahbaz, K.; Adnan, M.; Danish, M.; Rasheed, F.; et al. Advances in graphene-based electrode materials for high-performance supercapacitors: A review. J. Energy Storage 2023, 72, 108731. [Google Scholar] [CrossRef]
- NK, P.S.; Jeong, S.M.; Rout, C.S. MXene–carbon based hybrid materials for supercapacitor applications. Energy Adv. 2024, 3, 341–365. [Google Scholar] [CrossRef]
- Singh, P. Composites Based on Conducting Polymers and Carbon Nanotubes for Supercapacitors. In Conducting Polymer Hybrids; Kumar, V., Kalia, S., Swart, H., Eds.; Springer Series on Polymer and Composite Materials; Springer: Cham, Switzerland, 2017; pp. 1–23. [Google Scholar] [CrossRef]
- Lu, Y.; Jiang, Y.; Lou, Z.; Shi, R.; Chen, D.; Shen, G. Wearable supercapacitor self-charged by P(VDF-TrFE) piezoelectric separator. Prog. Nat. Sci. Mater. Int. 2020, 30, 174–179. [Google Scholar] [CrossRef]
- Arenas, L.F.; Ponce de León, C.; Walsh, F.C. Three-dimensional porous metal electrodes: Fabrication, characterisation and use. Curr. Opin. Electrochem. 2019, 16, 1–9. [Google Scholar] [CrossRef]
- Areir, M.; Xu, Y.; Harrison, D.; Fyson, J. 3D printing of highly flexible supercapacitor designed for wearable energy storage. Mater. Sci. Eng. B 2017, 226, 29–38. [Google Scholar] [CrossRef]
- Aleksandrova, M.; Pandiev, I. Printed Piezoelectric Harvester for Integration in a Wearable Energy Storage Device. In Proceedings of the 2024 47th International Spring Seminar on Electronics Technology (ISSE), Prague, Czech Republic, 15–19 May 2024; pp. 1–4. [Google Scholar] [CrossRef]
- Aleksandrova, M.; Pandiev, I. Synergistic integration of energy harvesters and supercapacitors for enhanced performance. Helyion 2025, 11, e42808. [Google Scholar] [CrossRef]
- Zhao, X.; Cao, H.; Coleman, B.J.; Tan, Z.; Echols, I.J.; Pentzer, E.B.; Lutkenhaus, J.L.; Radovic, M.; Green, M.J. Role of Antioxidant Structure in Mitigating Oxidation in Ti3C2Tx and Ti2CTx MXenes. Adv. Mater. Interf. 2022, 9, 2200480. [Google Scholar] [CrossRef]
- Swain, N.; Balasubramaniam, S.; Ramadoss, A. High energy density supercapattery empowered by efficient binder-free three-dimensional carbon coated NiCo2O4/Ni battery and Fe3S4@NiCo pseudocapacitive electrodes. J. Energy Storage 2023, 58, 106220. [Google Scholar] [CrossRef]
- Wang, W.; Cao, J.; Yu, J.; Tian, F.; Luo, X.; Hao, Y.; Huang, J.; Wang, F.; Zhou, W.; Xu, J.; et al. Flexible Supercapacitors Based on Stretchable Conducting Polymer Electrodes. Polymers 2023, 15, 1856. [Google Scholar] [CrossRef] [PubMed]
- Balboni, R.; Maron, G.; Masteghin, M.; Tas, M.; Rodrigues, L.; Gehrke, V.; Alano, J.; Andreazza, R.; Carreño, N.; Silva, S. An easy to assemble PDMS/CNTs/PANI flexible supercapacitor with high energy-to-power density. Nanoscale 2022, 14, 2266–2276. [Google Scholar] [CrossRef]
- Railanmaa, A.; Soltani, A.; Lehtimäki, S.; Pournoori, N.; Keskinen, J.; Hokka, M.; Lupo, D. Skin-conformable printed supercapacitors and their performance in wear. Sci. Rep. 2020, 10, 15194. [Google Scholar] [CrossRef] [PubMed]
- Thomas, S.A.; Cherusseri, J.; Rajendran, D.N. A Minireview on Polyurethane-Based Flexible Electrodes for Wearable Supercapacitors: Strategies. Synth. Electrochem. Perform. Eval. Energy Fuels 2025, 39, 2–18. [Google Scholar] [CrossRef]
- Wen, Y.; Chen, H.; Wu, M.; Li, C. Vertically oriented MXene bridging the frequency response and capacity density gap for AC-filtering pseudocapacitors. Adv. Funct. Mater. 2022, 32, 2111613. [Google Scholar] [CrossRef]
- Pathak, M.; Bhatt, D.; Bhatt, R.C.; Bohra, B.S.; Tatrari, G.; Rana, S.; Arya, M.C.; Sahoo, N.G. High Energy Density Supercapacitors: An Overview of Efficient Electrode Materials, Electrolytes, Design, and Fabrication. Chem. Rec. 2024, 24, e202300236. [Google Scholar] [CrossRef]
- Dar, M.A.; Majid, S.R.; Satgunam, M.; Batoo, K.M.; Kalpana, S.; Arularasan, P.; Sheik Fareed, S.; Moholkar, A.V.; Shembade, U.V. Electrochemical performance of Fe-doped SnSe material electrodes for supercapacitors. J. Energy Storage 2024, 94, 112403. [Google Scholar] [CrossRef]
- Yao, L.; Liu, J.; Eedugurala, N.; Mahalingavelar, P.; Adams, D.J.; Wang, K.S.; Mayer, K.S.; Azoulay, J.D.; Ng, T.N. Ultrafast high-energy micro-supercapacitors based on open-shell polymer-graphene composites. Cell Rep. Phys. Sci. 2022, 3, 100792. [Google Scholar] [CrossRef]
- Gautham Prasad, G.; Shetty, N.; Thakur, S.; Rakshitha; Bommegowda, K.B. Supercapacitor technology and its applications: A review. IOP Conf. Ser. Mater. Sci. Eng. 2019, 561, 012105. [Google Scholar] [CrossRef]
- Sezer, N.; Koç, M. A comprehensive review on the state-of-the-art of piezoelectric energy harvesting. Nano Energy 2021, 80, 105567. [Google Scholar] [CrossRef]
- Ottman, G.K.; Hofmann, H.F.; Bhatt, A.C.; Lesieutre, G.A. Adaptive piezoelectric energy harvesting circuit for wireless remote power supply. IEEE Trans. Power Electron. 2002, 17, 669–676. [Google Scholar] [CrossRef]
- Tabesh, A.; Frechette, L.G. A Low-Power Stand-Alone Adaptive Circuit for Harvesting Energy from a Piezoelectric Micropower Generator. IEEE Trans. Ind. Electron. 2010, 57, 840–849. [Google Scholar] [CrossRef]
- Tietze, V.; Schenk, C. Power Supplies. In Electronic Circuits, 2nd ed.; Springer: New York, NY, USA, 2008; Chapter 16; pp. 885–928. ISBN 978-3-540-00429-5. [Google Scholar]
- Ben-Yaakov, S.; Krihely, N. Resonant rectifier for piezoelectric sources. In Proceedings of the Twentieth Annual IEEE Applied Power Electronics Conference and Exposition, Austin, TX, USA, 6–10 March 2005; Volume 1, pp. 249–253. [Google Scholar] [CrossRef]
- Song, H.J.; Choi, Y.-T.; Wereley, N.M.; Purekar, A.S. Energy Harvesting Devices Using Macro-Fiber Composite Materials. J. Intell. Mater. Syst. Struct. 2010, 21, 647–658. [Google Scholar] [CrossRef]
- Elfrink, R.; Renaud, M.; Kamel, T.M.; de Nooijer, C.; Jambunathan, M.; Goedbloed, M.; Hohlfeld, D.; Matova, S.; Pop, V.; Caballero, L.; et al. Vacuum-packaged piezoelectric vibration energy harvesters: Damping contributions and autonomy for a wireless sensor system. J. Micromech. Microeng. 2010, 20, 104001. [Google Scholar] [CrossRef]
- Liu, W.; Wang, Z.; Qu, S.; Luo, R. Vibration energy harvesting and management for wireless sensor networks in bridge structural monitoring. In Proceedings of the 2015 IEEE SENSORS, Busan, Republic of Korea, 1–4 November 2015. [Google Scholar] [CrossRef]
- Du, S.; Jia, Y.; Zhao, C.; Amaratunga, G.A.J.; Seshia, A.A. A Fully Integrated Split-Electrode SSHC Rectifier for Piezoelectric Energy Harvesting. IEEE J. Solid-State Circuits 2019, 54, 1733–1743. [Google Scholar] [CrossRef]
- Pandiev, I.; Aleksandrova, M.; Kolev, G. Design and Implementation of Interface Circuits Intended for Printed Piezoelectric Micropower Harvesters on Flexible Substrates. IOP Conf. Ser. Mater. Sci. Eng. 2020, 876, 012007. [Google Scholar] [CrossRef]
- Çiftci, B.; Chamanian, S.; Koyuncuoğlu, A.; Muhtaroğlu, A.; Külah, H. A Low-Profile Autonomous Interface Circuit for Piezoelectric Micro-Power Generators. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 1458–1471. [Google Scholar] [CrossRef]
- Stefanov, N. Special rectifiers, and Power rectifiers. In Power Supply Devices; Tehnika: Sofia, Bulgaria, 2002; Chapter 2 and Chapter 4; pp. 43–68, 84–96. ISBN 954-03-0564-0. [Google Scholar]
- Seifart, M. Stromversorgung. In Analoge Schaltungen, 6th ed.; Verlag Technik: Berlin, Germany, 2003; Chapter 22; pp. 591–639. ISBN 3-341-01298-2. [Google Scholar]
- Pandiev, I.; Tomchev, N.; Kurtev, N.; Aleksandrova, M. Analysis of the Methods for Realization of Low-Power Piezoelectric Energy Harvesting Circuits for Wearable Battery-Free Power Supply Devices. Appl. Sci. 2024, 14, 4792. [Google Scholar] [CrossRef]
- Sedra, A.; Smith, K.; Carusone, T.; Gaudet, V. MOS Field-Effect Transistors (MOSFETs). In Microelectronic Circuits, 8th ed.; Oxford University Press: Oxford, NY, USA, 2020; Chapter 5; pp. 246–303. [Google Scholar]
- Dallago, E.; Miatton, D.; Venchi, G.; Frattini, G.; Ricotti, G. Self-Supplied Integrable Active High-Efficiency AC-DC Converter for Piezoelectric Energy Scavenging Systems. In Proceedings of the 2007 IEEE International Symposium on Circuits and Systems (ISCAS), New Orleans, LA, USA, 27–30 May 2007; pp. 1633–1636. [Google Scholar] [CrossRef]
- Dallago, E.; Miatton, D.; Venchi, G.; Bottarel, V.; Frattini, G.; Ricotti, G.; Schipani, M. Active self-supplied AC-DC converter for piezoelectric energy scavenging systems with supply independent bias. In Proceedings of the 2008 IEEE International Symposium on Circuits and Systems (ISCAS), Seattle, WA, USA, 18–21 May 2008; pp. 1448–1451. [Google Scholar] [CrossRef]
- Dong, Z.; Allen, P.E. Low-voltage, supply independent CMOS bias circuit. In Proceedings of the 2002 45th Midwest Symposium on Circuits and Systems, MWSCAS-2002, Tulsa, OK, USA, 4–7 August 2002; p. III. [Google Scholar] [CrossRef]
- Hehn, T.; Hagedorn, F.; Maurath, D.; Marinkovic, D.; Kuehne, I.; Frey, A. A Fully Autonomous Integrated Interface Circuit for Piezoelectric Harvesters. IEEE J. Solid-State Circuits 2012, 47, 2185–2198. [Google Scholar] [CrossRef]
- Ghovanloo, M.; Najafi, K. Fully integrated wideband high-current rectifiers for inductively powered devices. IEEE J. Solid-State Circuits 2004, 39, 1976–1984. [Google Scholar] [CrossRef]
- Godinho, A.; Yang, Z.; Dong, T.; Gonçalves, L.; Mendes, P.; Wen, Y.; Li, P.; Jiang, Z. A Dynamic Threshold Cancellation Technique for a High-Power Conversion Efficiency CMOS Rectifier. Sensors 2021, 21, 6883. [Google Scholar] [CrossRef]
- Frick, V.; Wassouf, L.; Jamshidpour, E. Voltage Flip Efficiency Enhancement for Piezo Energy Harvesting. Electronics 2021, 10, 2400. [Google Scholar] [CrossRef]
- Edla, M.; Lim, Y.Y.; Padilla, R.V.; Deguchi, M. An Improved Rectifier Circuit for Piezoelectric Energy Harvesting from Human Motion. Appl. Sci. 2021, 11, 2008. [Google Scholar] [CrossRef]
- Yuen, P.W.; Chong, G.; Ramiah, H. A high efficient dual-output rectifier for piezoelectric energy harvesting. Int. J. Electron. Commun. (AEÜ) 2019, 111, 152922. [Google Scholar] [CrossRef]
- Yang, H.; Huang, M.; Ren, M.; Li, X. Piezoelectric energy harvesting interface circuit for small area and low power consumption—A review. Measurement 2024, 242, 116051. [Google Scholar] [CrossRef]
- Richard, C.; Guyomar, D.; Audigier, D.; Ching, G. Semi Passive Damping using Continuous Switching of a Piezoelectric Device. In Proceedings of the SPIE Smart Structures and Materials 1999: Passive Damping and Isolation, Newport Beach, CA, USA, 1–2 March 1999; SPIE: San Diego, CA, USA, 1999. [Google Scholar]
- Guyomar, D.; Richard, C.; Lefeuvre, E.; Petit, L. Piezoelectric Non-linear Systems for Standalone Vibration Control and Energy Reclamation; AC’04: Hildesheim, Germany, 2004. [Google Scholar]
- Badel, A.; Guyomar, D.; Lefeuvre, E.; Richard, C. Efficiency enhancement of a piezoelectric energy harvesting device in pulsed operation by synchronous charge inversion. J. Intell. Mater. Syst. Struct. 2005, 16, 889–901. [Google Scholar] [CrossRef]
- Dicken, J.; Mitcheson, P.D.; Stoianov, I.; Yeatman, E.M. Increased power output from piezoelectric energy harvesters by pre-biasing. In Proceedings of the 9th International Workshop on Micro and Nanotechnology for Power Generation and Energy Conversion Applications (PowerMEMS), Washington, DC, USA, 1–4 December 2009; pp. 75–78. [Google Scholar]
- Fang, S.; Xia, H.; Xia, Y.; Ye, Y.; Shi, G.; Wang, X.; Chen, Z. An efficient piezoelectric energy harvesting circuit with series-SSHI rectifier and FNOV-MPPT control technique. IEEE Trans. Ind. Electron. 2021, 68, 7146–7155. [Google Scholar] [CrossRef]
- Chew, Z.J.; Zhu, M. Adaptive Self-Configurable Rectifier for Extended Operating Range of Piezoelectric Energy Harvesting. IEEE Trans. Ind. Electron. 2020, 67, 3267–3276. [Google Scholar] [CrossRef]
- Badel, A.; Benayad, A.; Lefeuvre, E.; Lebrun, L.; Richard, C.; Guyomar, D. Single crystals and nonlinear process for outstanding vibration-powered electrical generators. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2006, 53, 673–684. [Google Scholar] [CrossRef]
- Younas, O.; Li, P.; Wen, Y. A compact self-powered inductor-less piezoelectric energy harvesting circuit using gyrator. Smart Mater. Struct. 2024, 33, 065013. [Google Scholar] [CrossRef]
- Song, H.C.; Kim, S.W.; Kim, H.S.; Lee, D.G.; Kang, C.Y.; Nahm, S. Piezoelectric energy harvesting design principles for materials and structures: Material figure-of-merit and self-resonance tuning. Adv. Mater. 2020, 32, 2002208. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.S.; Kim, J.H.; Kim, J. A review of piezoelectric energy harvesting based on vibration. Int. J. Precis. Eng. Manuf. 2011, 12, 1129–1141. [Google Scholar] [CrossRef]
- Liu, Y.; Tian, G.; Wang, Y.; Lin, J.; Zhang, Q.; Hofmann, H.F. Active piezoelectric energy harvesting: General principle and experimental demonstration. J. Intell. Mater. Syst. Struct. 2009, 20, 575–585. [Google Scholar] [CrossRef]
- Koniavitis, K.; Alimisis, V.; Uzunoglu, N.; Sotiriadis, P.P. An Analog Integrated Multiloop LDO: From Analysis to Design. Electronics 2024, 13, 3602. [Google Scholar] [CrossRef]
- Sun, M.; Wang, L.; Huang, T.; Xu, M. A Fast Transient Response Capacitor-Less LDO with Transient Enhancement Technology. Micromachines 2024, 15, 299. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Bailón, J.; Calvo, B.; Medrano, N. A Fully-Integrated 180 nm CMOS 1.2 V Low-Dropout Regulator for Low-Power Portable Applications. Electronics 2021, 10, 2108. [Google Scholar] [CrossRef]
- Khan, D.; Basim, M.; Ain, Q.u.; Shah, S.A.A.; Shehzad, K.; Verma, D.; Lee, K.-Y. Design of a Power Regulated Circuit with Multiple LDOs for SoC Applications. Electronics 2022, 11, 2774. [Google Scholar] [CrossRef]
- Gao, M.; Cai, X.; Gao, Y.; Xia, R.; Li, B. Fully Integrated 1.8 V Output 300 mA Load LDO with Fast Transient Response. Electronics 2023, 12, 1409. [Google Scholar] [CrossRef]
- Serrano-Reyes, A.; Sanz-Pascual, M.T.; Calvo-López, B. Three-Stage CMOS LDO with Optimized Power and Dynamic Performance for Portable Devices. Electronics 2023, 12, 4638. [Google Scholar] [CrossRef]
- Seo, U.-Y.; Kwon, S.-W.; Kim, D.-H.; Oh, J.-Y.; Kim, M.-S.; Koo, Y.-S. Design of High-Reliability Low- Dropout Regulator Combined with Silicon Controlled Rectifier-Based Electrostatic Discharge Protection Circuit Using Dynamic Dual Buffer. Electronics 2024, 13, 3016. [Google Scholar] [CrossRef]
- Christos, K.; Thomas, U. A Nano-Power 0.5 V Event-Driven Digital-LDO with Fast Start-Up Burst Oscillator for SoC-IoT. J. Low Power Electron. Appl. 2020, 10, 41. [Google Scholar] [CrossRef]
- Texas Instruments. TPS7A16A-Q1 Ultra-Low Power, High Voltage LDO Regulator Datasheet, February 2019. Available online: https://www.ti.com (accessed on 8 March 2025).
- Torex Semiconductor. XC620 Series LDO Voltage Regulator Datasheet. Available online: https://www.torexsemi.com (accessed on 8 March 2025).
- STMicroelectronics. STLQ015 Ultra-Low Power Linear Regulator Datasheet. Available online: https://www.st.com (accessed on 8 March 2025).
- Analog Devices. MAX15007 Low Quiescent Current LDO Regulator Datasheet. Available online: https://www.analog.com (accessed on 8 March 2025).
- Microchip Technology. MIC5365 Ultra-Low Quiescent Current Regulator Datasheet. Available online: https://www.microchip.com (accessed on 8 March 2025).
- Texas Instruments. LP5907 Ultra-Low Noise LDO Regulator Datasheet. Available online: https://www.ti.com (accessed on 8 March 2025).

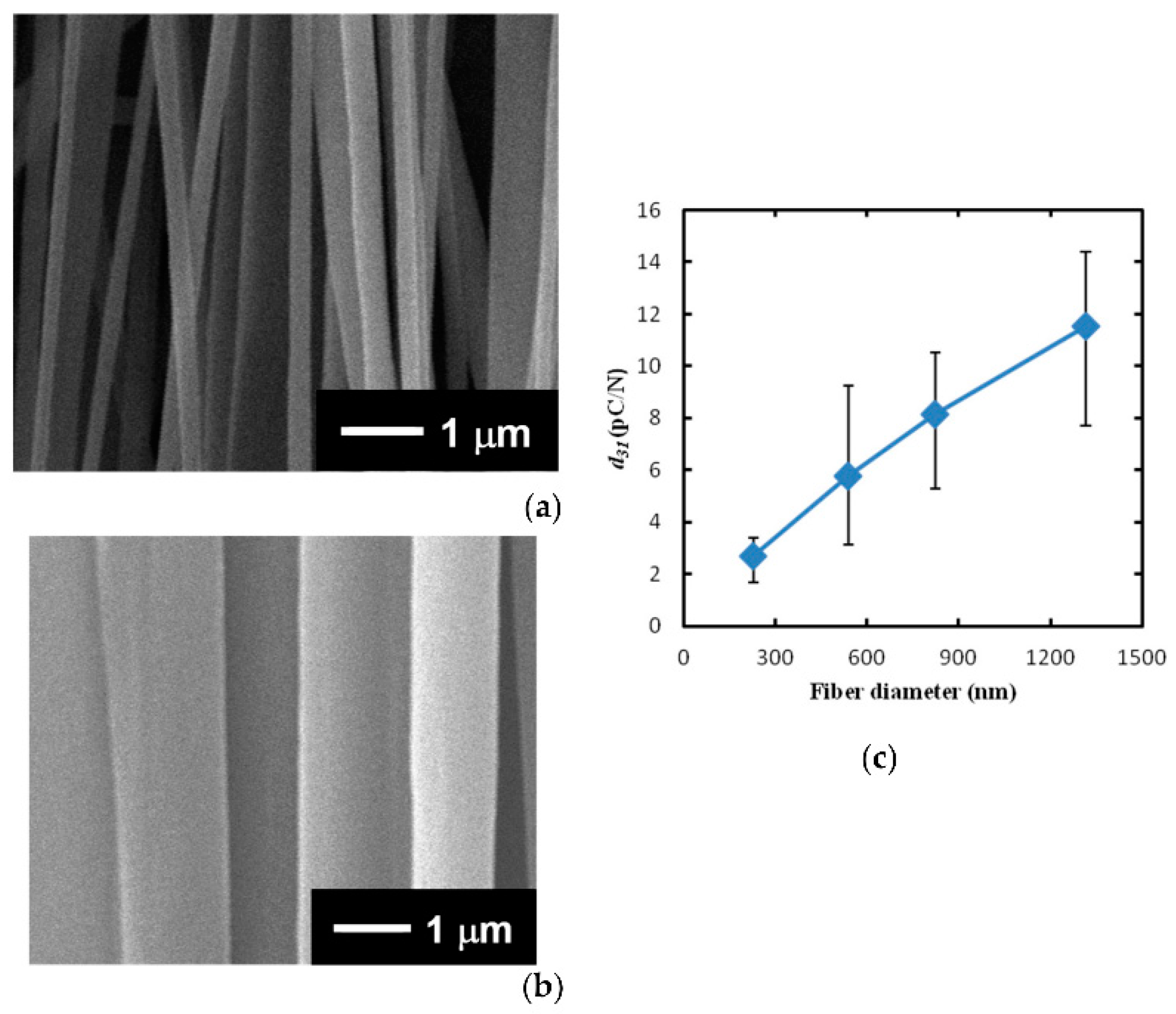
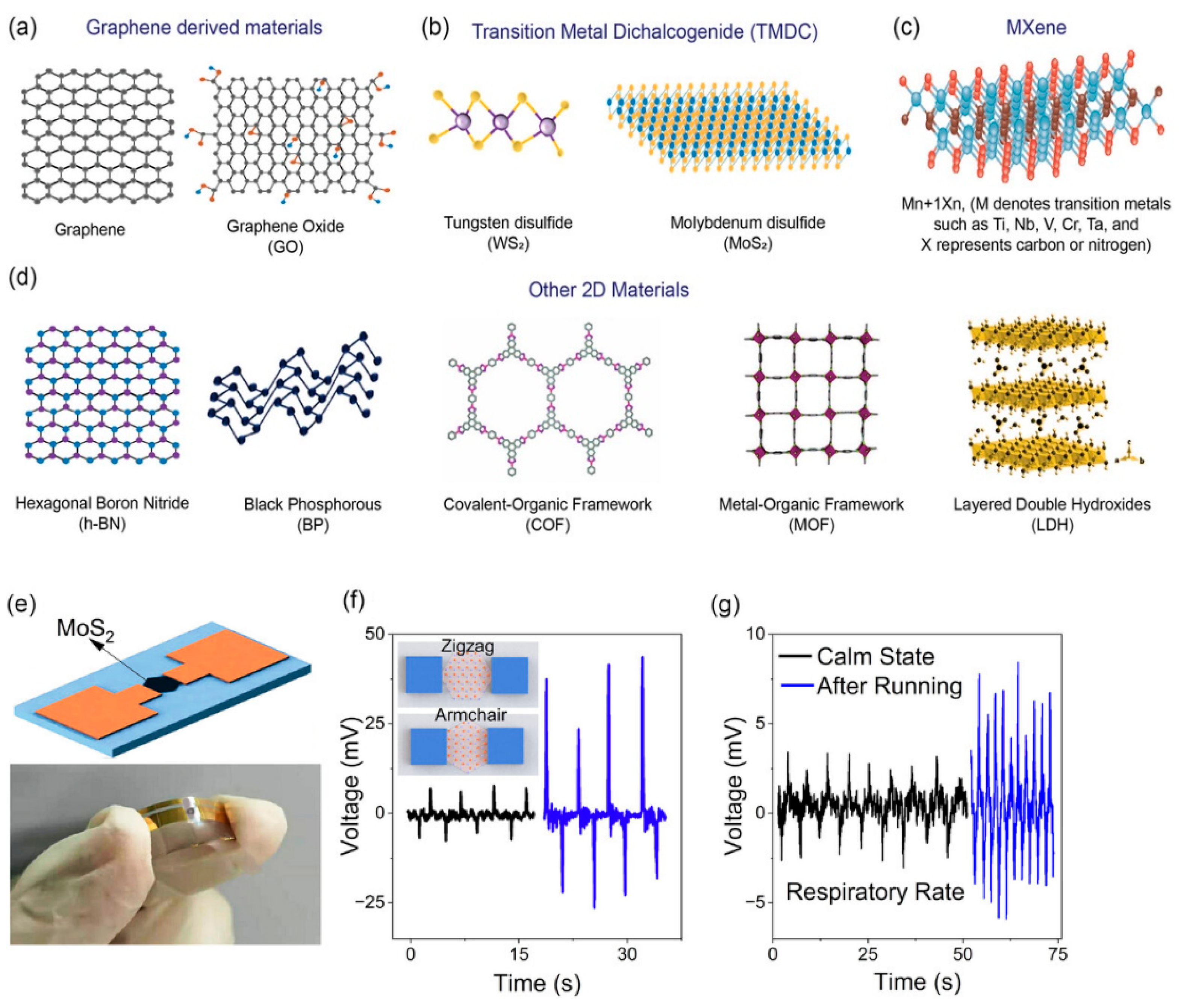
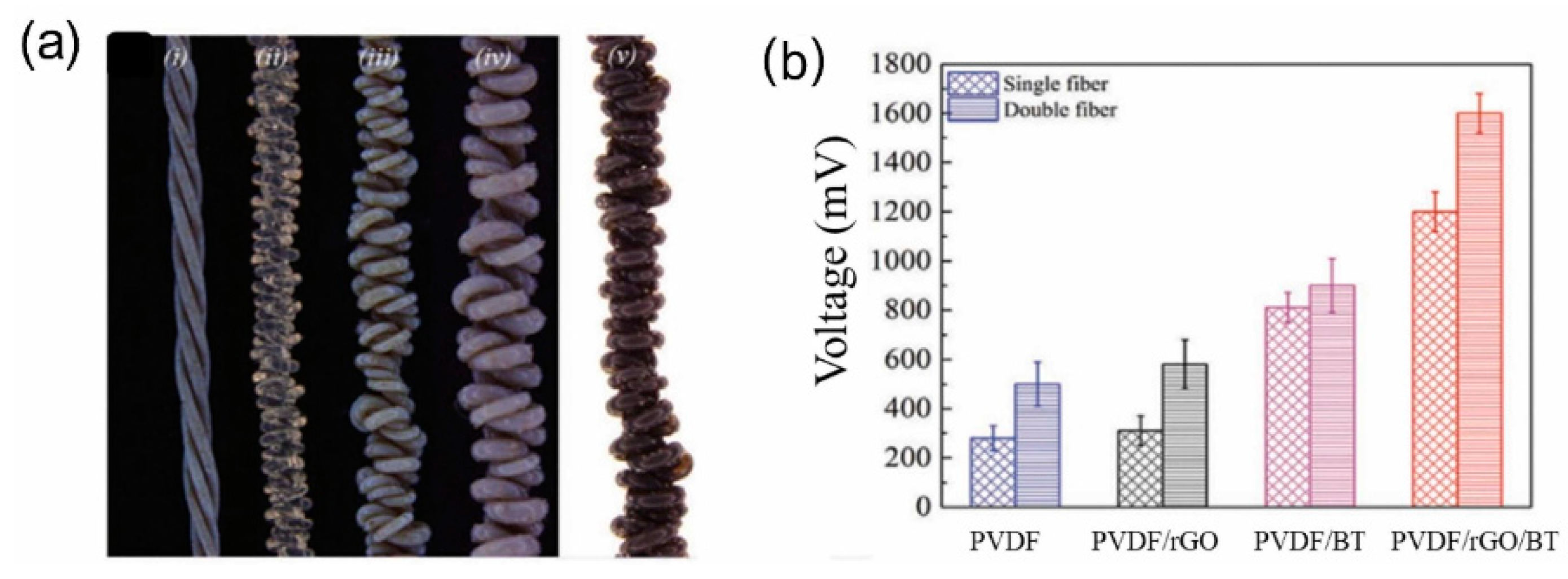


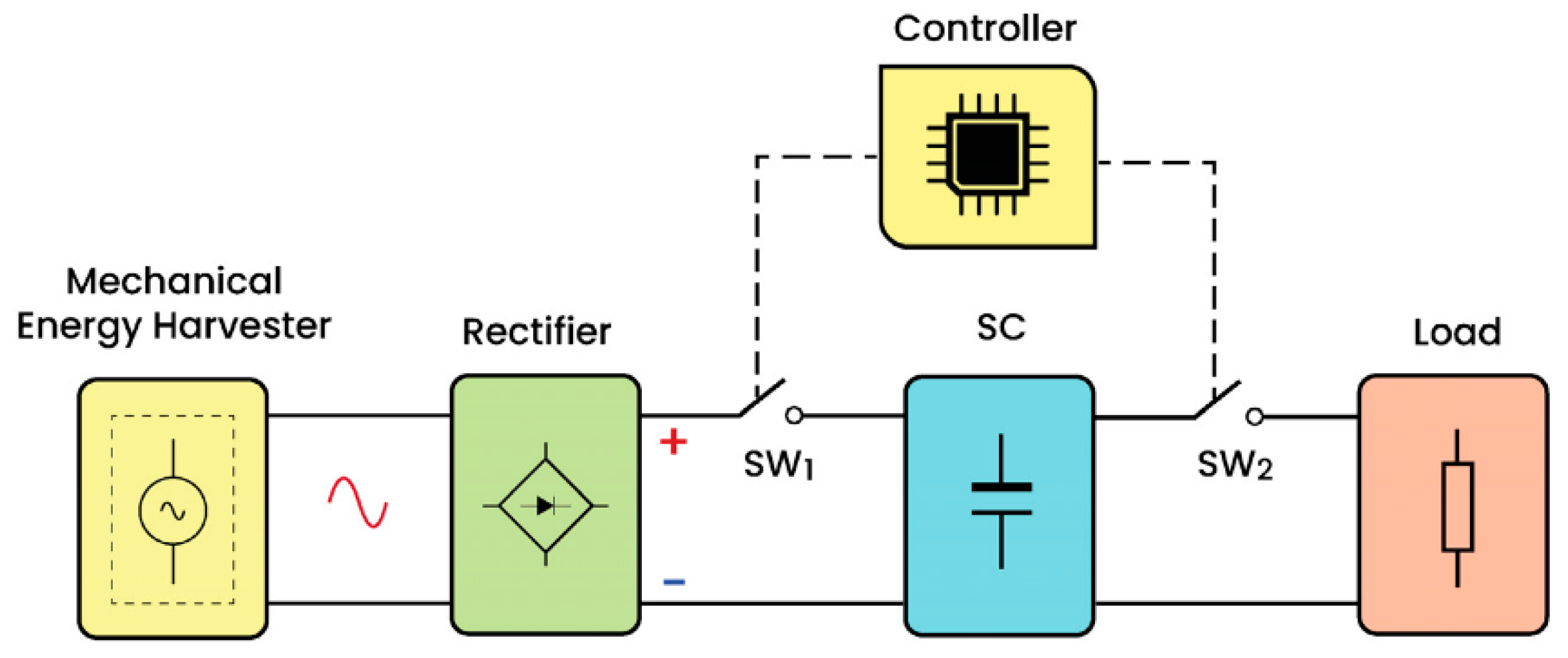
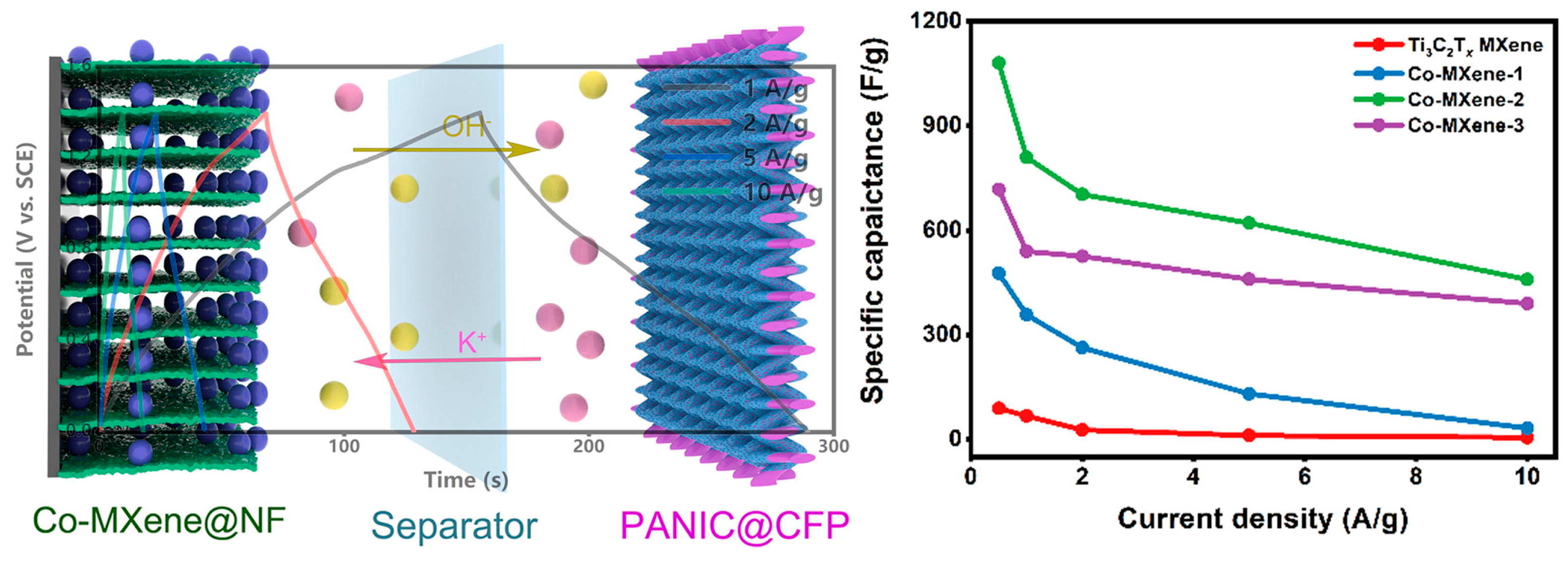


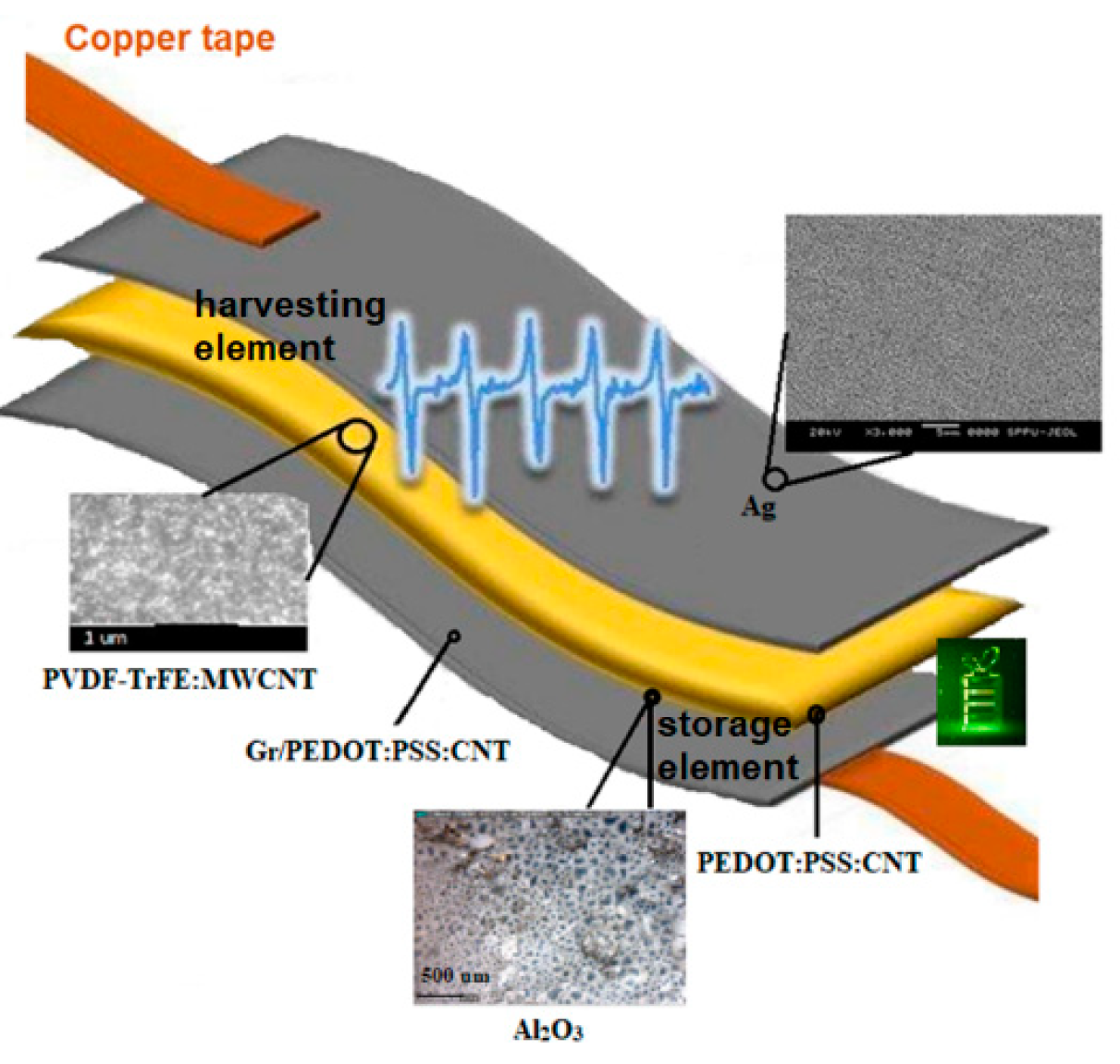


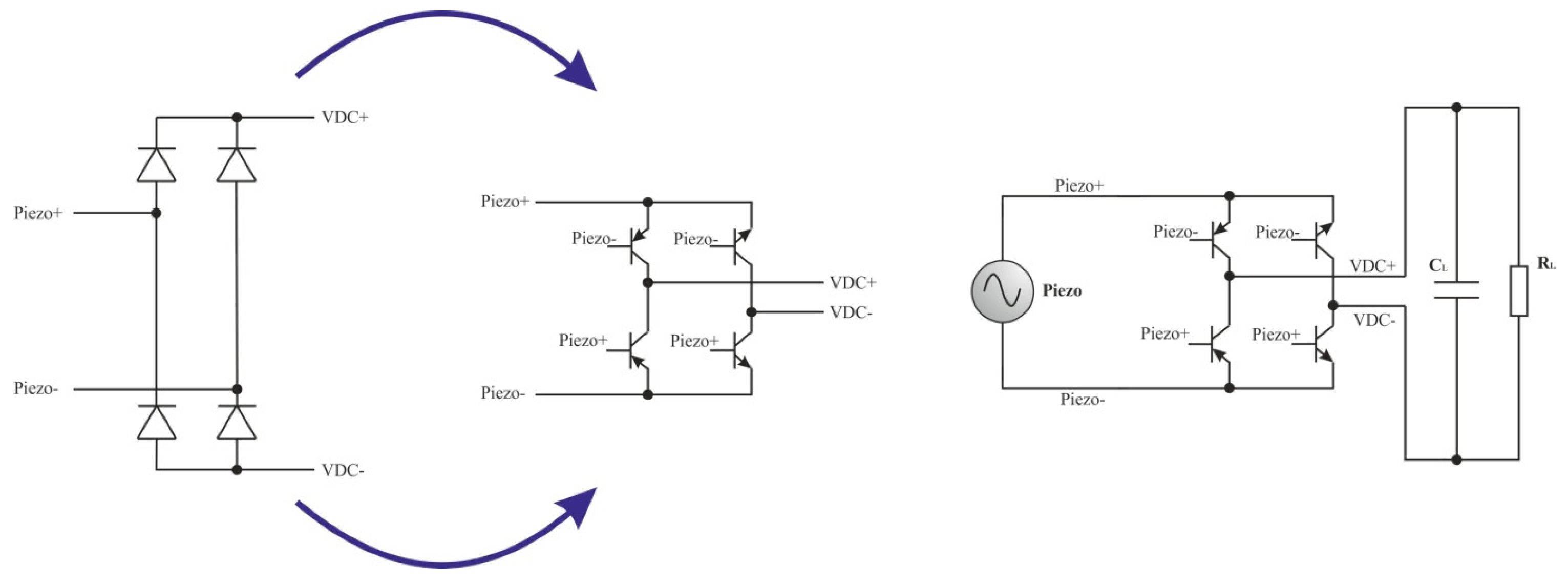
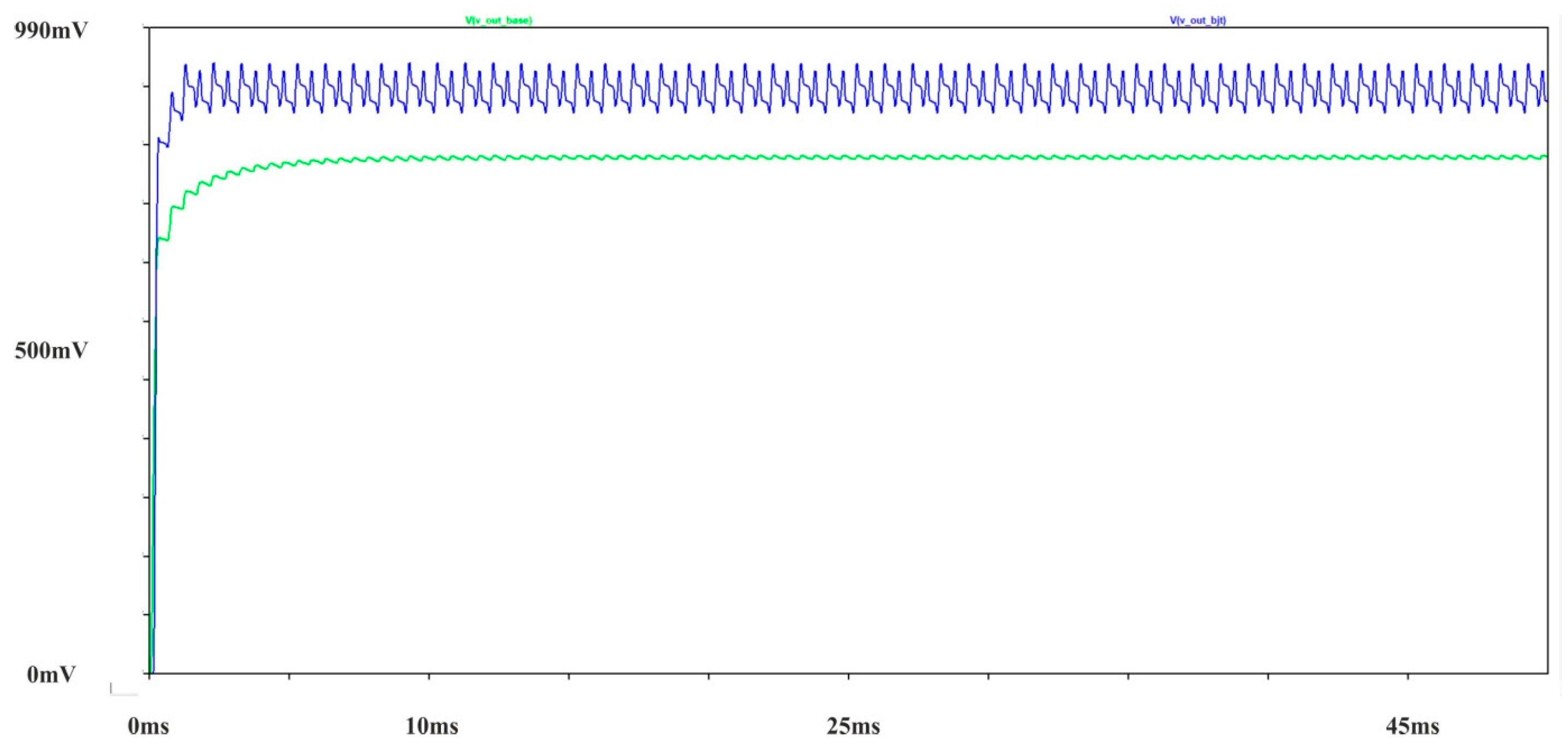
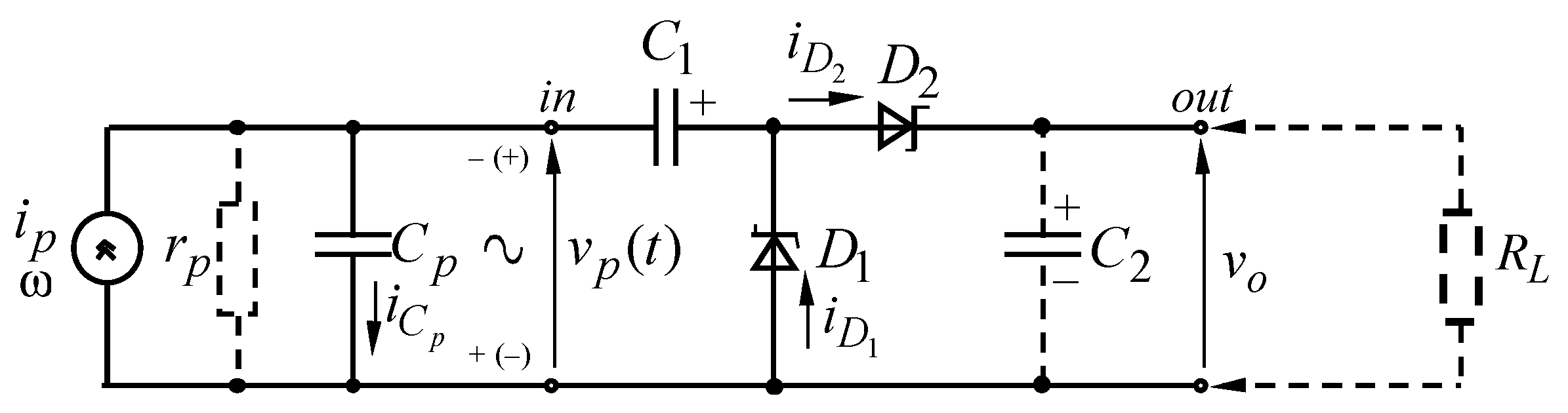




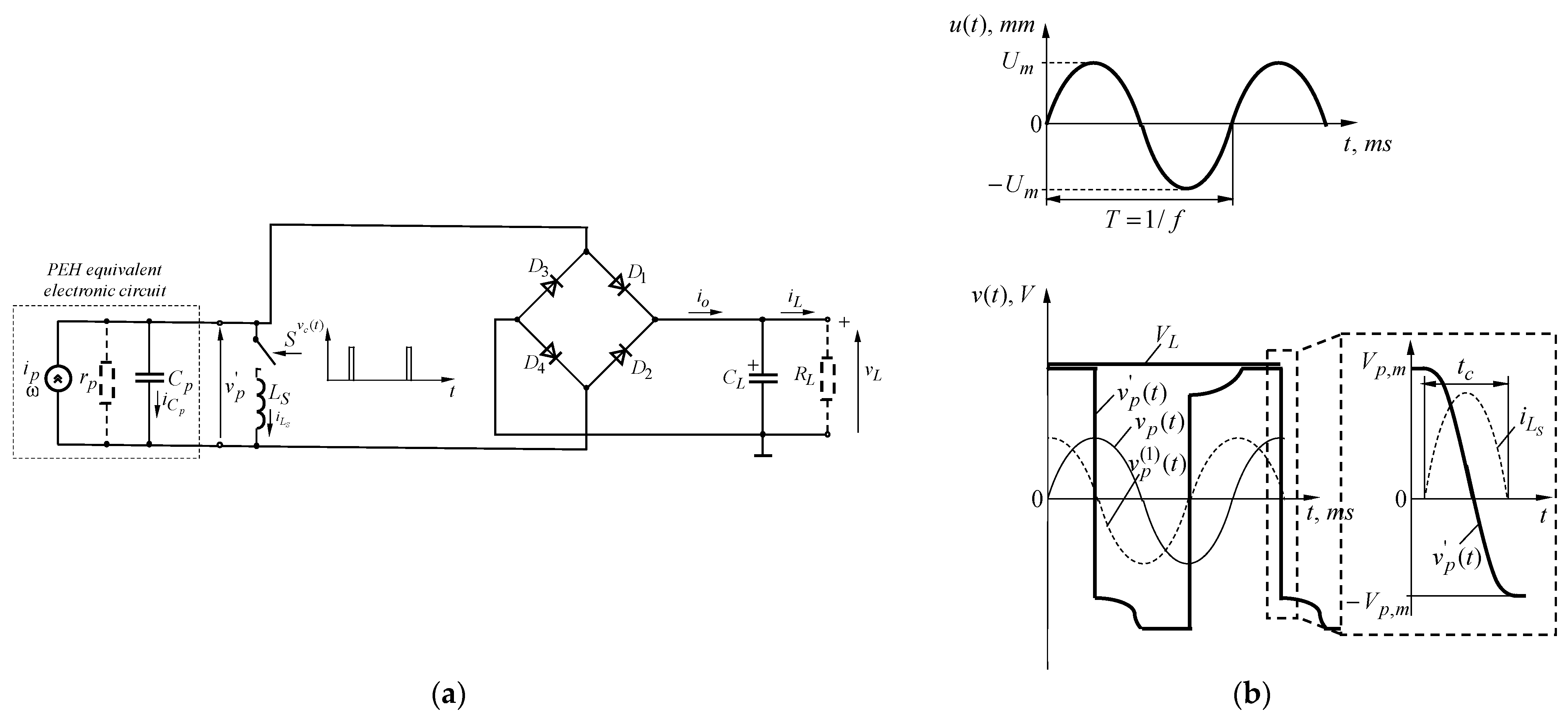

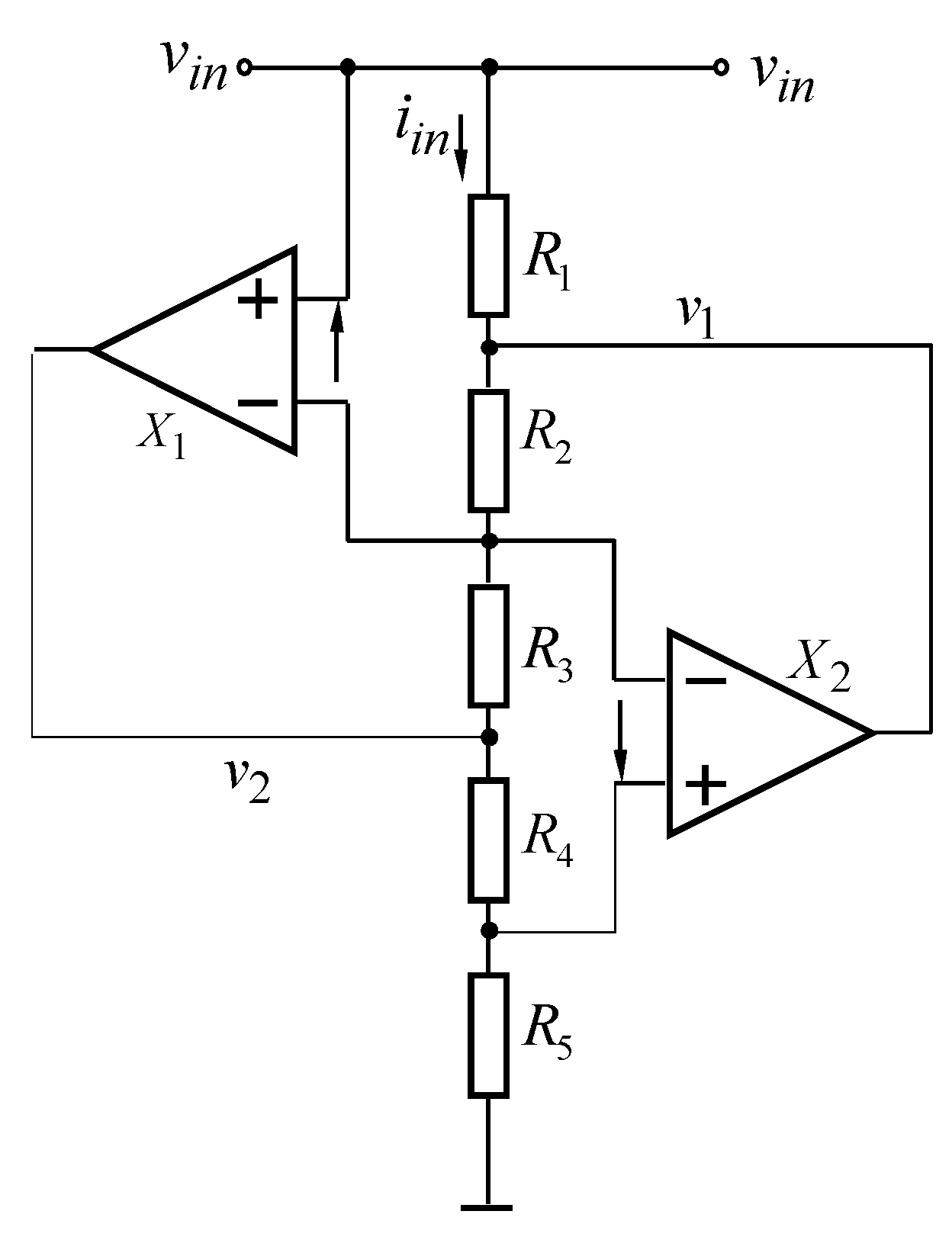
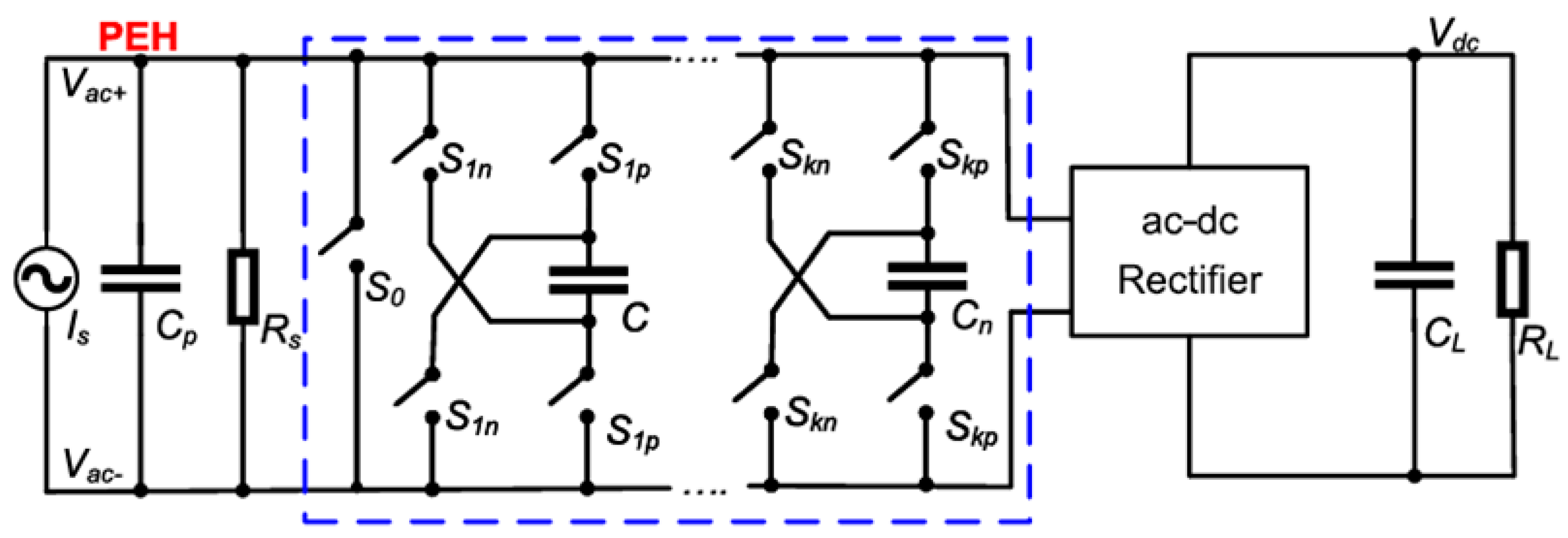

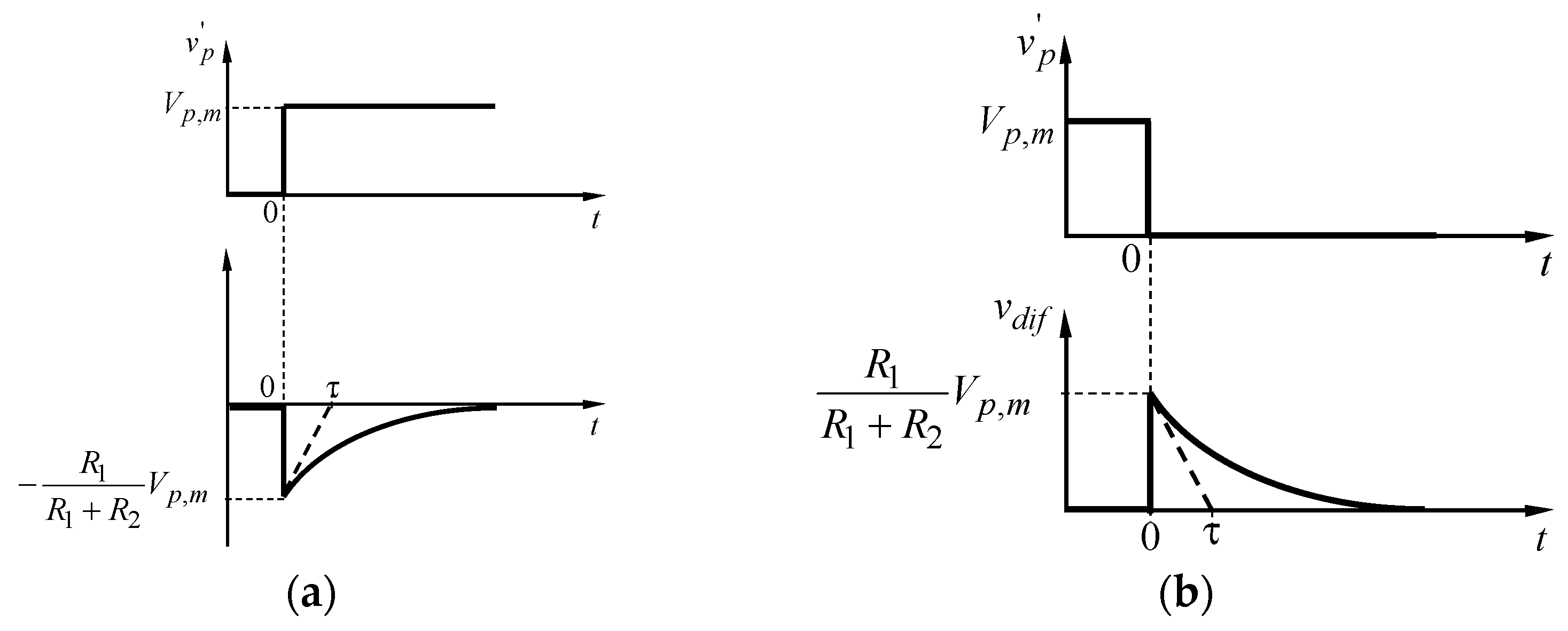
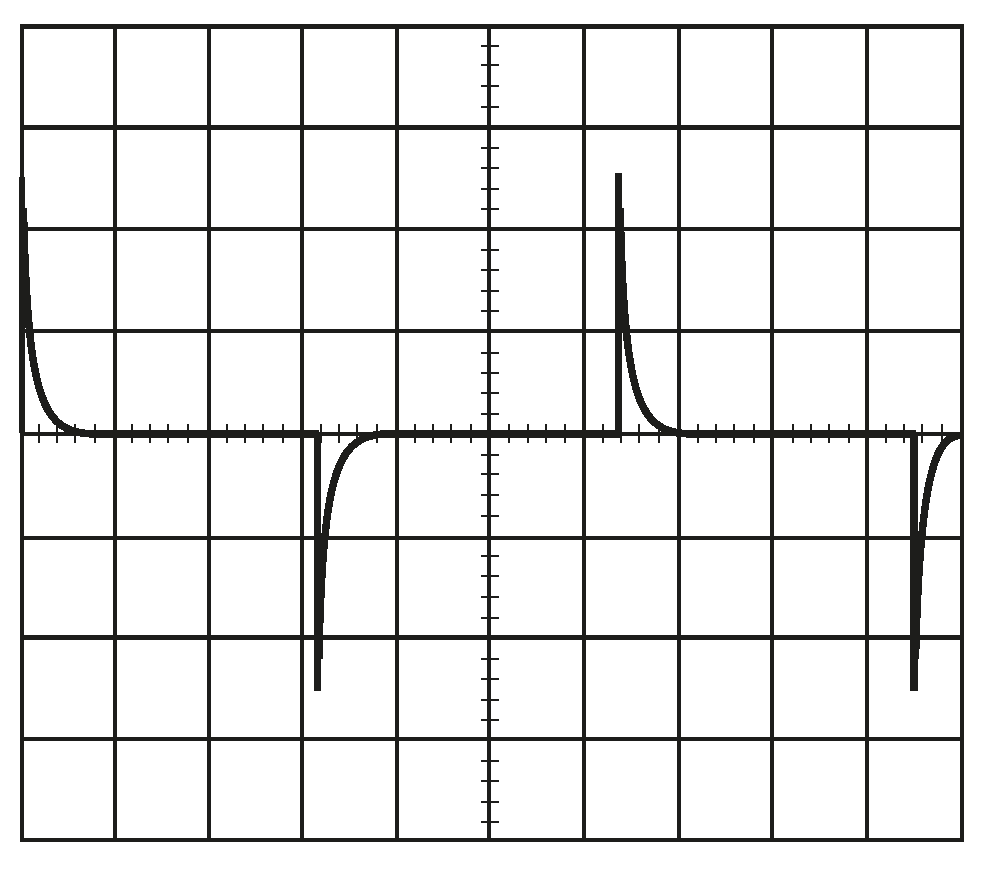

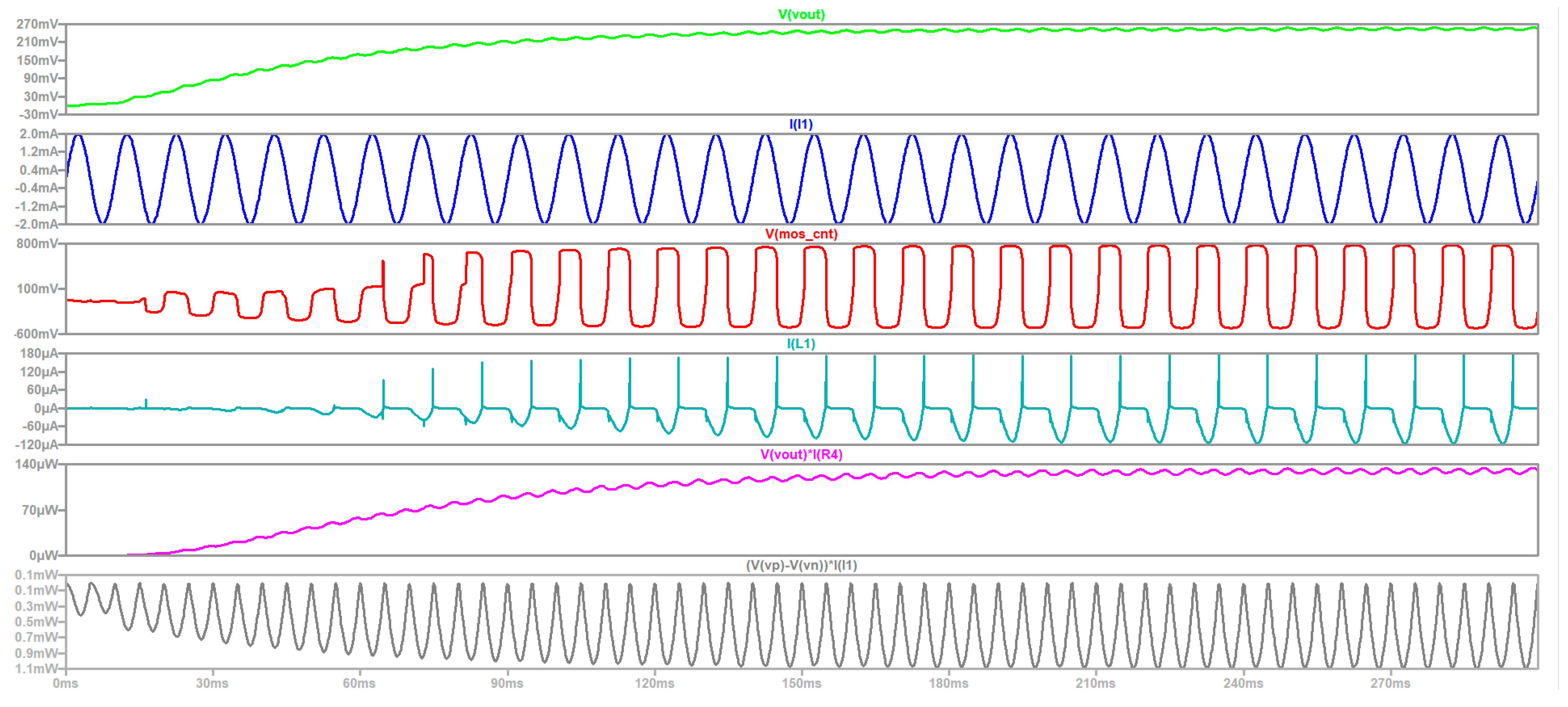
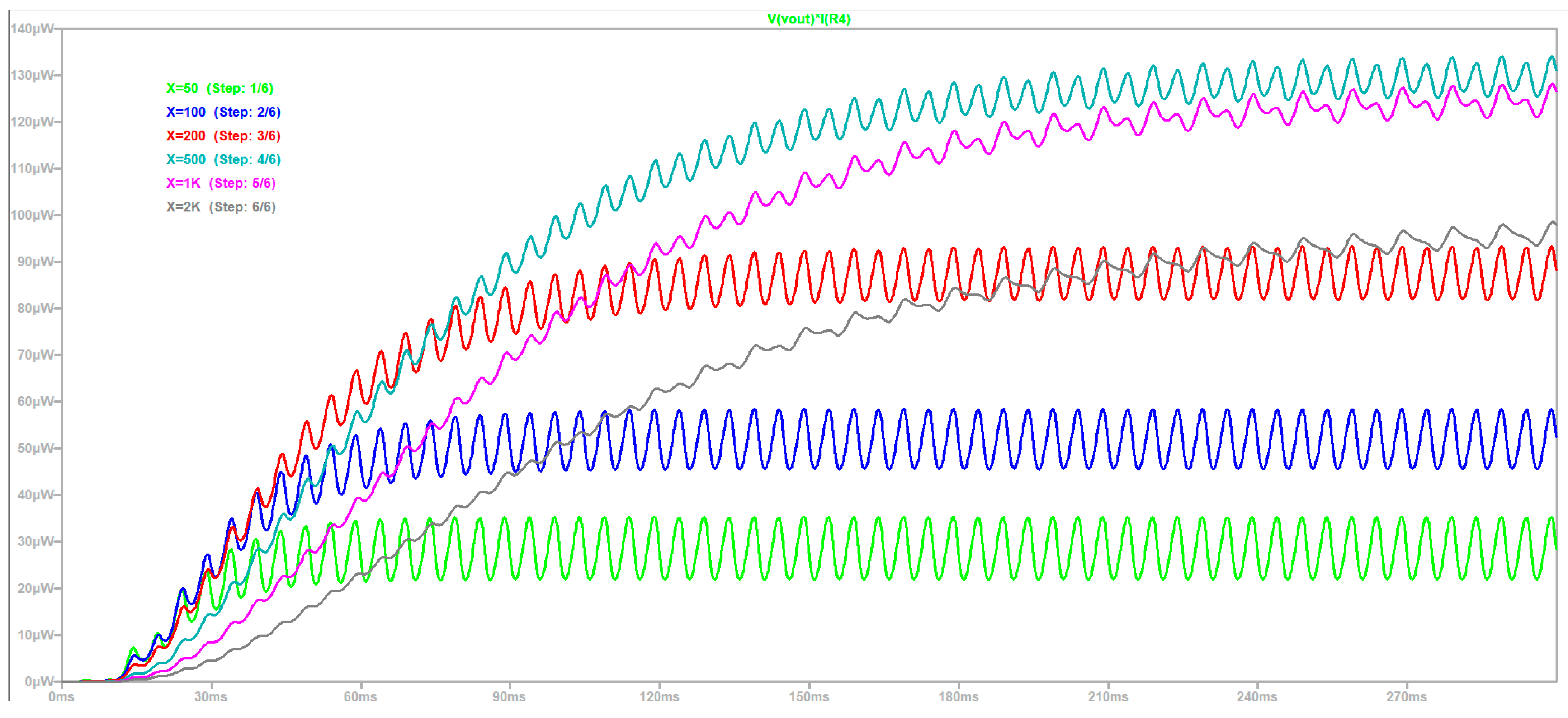
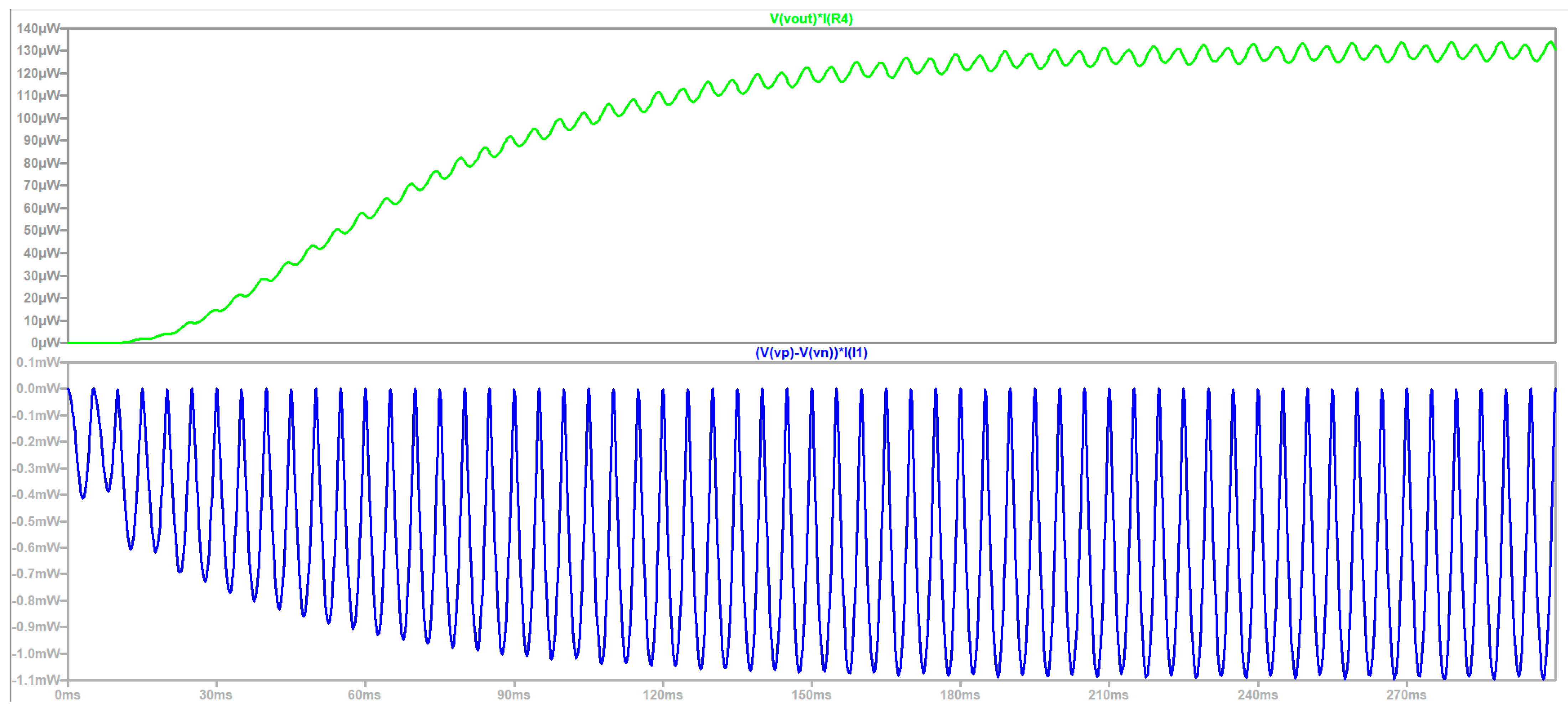


| Parameter/Ref. | [69] | [70] | [71] | [72] | [54] | [73] | [74] |
|---|---|---|---|---|---|---|---|
| Power Generation Capability (mW) | 243 | 22.8 | 2.3 | 43 | 37.9 | 8.34 | 6.62 |
| Thickness (µm) | 50 | 235 | 2 | 100 | 6 | 0.5 | 7 |
| Force/Mass Loading | 0.5 N vibration | 10 N pressure | 1% strain | 15 N | 30 N | 30 kg | 1.75 g |
| Material Used | PVDF/ BaTiO3 | PVDF/ KNN | Nb0.02Pb (Zr0.6Ti0.4)O3 | EDABCO-CuCl4@PVDF | NiO: ZnO | PZT | PVDF-TrFE |
| Fabrication Techniques | Electro-spinning | Electro-spinning | Spin-coating | Spin-coating | Spin-coating | Sputte-ring | Spin-coating |
| Frequency (Hz) | 15.7 | 7 | 1 | 5 | 4 | 2 | 5 |
| Metric | Typical Values | Most Recent Reference |
|---|---|---|
| Gravimetric capacitance | 100–600 F/g | [90,95] |
| Energy Density | 1 to 50 Wh/kg | [96] |
| Power Density | 10 to 10,000 W/kg | [97] |
| Cycle Life | 50,000 to 110,000 cycles | [98] |
| Internal Resistance | <1 Ω | [99] |
| Operating Voltage Range | 2.5 to 5 V | [99] |
| Charge/Discharge Time | Seconds to minutes | [99] |
| Parameter | Godinho, A. et al. [120] | Frick, V. et al. [121] | Edla, M. et al. [122] | Yuen, P. W. et al. [123] | Kamran, M. et al. [124] |
|---|---|---|---|---|---|
| Technology | CMOS 130 nm | CMOS 0.35 μm | Discrete components | CMOS 65 nm | Discrete components |
| Frequency | 3.2 kHz | 100 Hz | 2 Hz | 120 Hz | 5 Hz |
| Output voltage | 0.45–1 V | 1 V | 3.8 V | 1.21 V | 18 V |
| Power Conversion Efficiency (PCE) | 84% | n.a. | n.a. | 84% | 72.3% |
| Power Conversion Efficiency (VCE) | 99% | n.a. | n.a. | 98% | n.a. |
| Cost | high | medium | low | high | low |
| Complexity | high | medium | medium | low | low |
| Year | 2021 | 2021 | 2021 | 2019 | 2023 |
| Parameter | Sanchez, D.A. et al. [41] | Chamanian, S. et al. [44] | Ben Ammar, M.B. et al. [45] | Du, S. et al. [108] | Çiftci, B. et al. [110] | Fang, S. et al. [129] | Chew, Z. et al. [130] |
|---|---|---|---|---|---|---|---|
| Topology | Parallel-SSHI | E-SSHI | P-SSHI | SE-SSHC | SSCHI | Series-SSHI | Topology Switching |
| Piezoelectric Harvester | MIDE V21B and V22B | AB4113B-LW100-R | AB4113B-LW100-R | Custom MEMS | Custom MEMS | Custom PE | MFC8528-P2 |
| Piezoelectric Capacitance | 9–26 nF | 4.66 nF | n.a. | 1.94 nF | 2 nF | 180 nF | n.a. |
| Operating Frequency | 134.6–229.2 Hz | 208 Hz | 1 Hz | 219 Hz | 415 Hz | n.a. | n.a. |
| Output Voltage | 0.7–5 V | 0.87 V | 3.6 V | 2.5 V | 1.02 V | n.a. | 1.2–20 V |
| Inductance Value | n.a. | 68–820 μH | n.a. | n.a. | 68–100 μH | 1.5 mH | n.a. |
| Efficiency | 94% (V22B), 89% (V21B) | 86% (68 μH) 93% (820 μH) | n.a. | n.a. | 78.7% (68 μH), 83% (100 μH) | 50% | 93–98% |
| FOM Factor | 4.4 (res), 6.81 (off-res) | 3.69 (68 μH) 5.23 (820 μH) | n.a. | 3.6–8.2 | 4.56 (68 μH), 5.44 (100 μH) | 2.68 | n.a. |
| Device type | Discrete components | Integrated circuit | Discrete Components | Integrated circuit | Integrated circuit | Discrete Components | Discrete Components |
| Parameter | Koniavitis, K. et al. [136] | Sun, M. et al. [137] | Pérez-Bailón, J. et al. [138] | Khan, D. et al. [139] | Gao, M. et al. [140] | Serrano- Reyes, A. et al. [141] | Seo, U.-Y. et al. [142] | Christos K. et al. [143] |
|---|---|---|---|---|---|---|---|---|
| Technology | 90 nm CMOS | 180 nm CMOS | 180 nm CMOS | 180 nm CMOS | 180 nm CMOS | 180 nm CMOS | 55 nm CMOS | 55 nm CMOS |
| Output Voltage | 1 V | 1 V | 1.2 V | 1.8 V | 1.8 V | 1.8 V | 1.0 V | 0.5 V |
| Dropout Voltage | 0.4 V | 0.2 V | 0.6 V | 0.1 V | 0.2 V | 0.1 V | 0.1 V | 0.05 V |
| Quiescent Current | 100 µA | 47 µA | 8.6 µA | 13.8 µA | 66.4 µA | 158 µA | 12 µA | 558 nA |
| Load Regulation | 10 µV/mA | 25 µV/mA | 5 µV/mA | 1.94 µV/mA | 6 µV/mA | 5.7 µV/mA | 0.6 µV/mA | 1 µV/mA |
| PSRR | 85 dB | 60 dB | n.a. | 95 dB | 65 dB | 85 dB | n.a. | n.a. |
| Settling Time | n.a. | 0.2 µs | n.a. | 0.2 µs | n.a. | n.a. | n.a. | 0.3 µs |
| Main advantage | Multiloop design for low noise | Capacitor-less, fast transient response | Compact, temperature robust design | High gain, three-stage design | Enhanced transient response | Reverse Nested Miller Compensation | Electrostatic discharge protection | Event-driven, fast startup oscillator |
| Year | 2024 | 2024 | 2021 | 2022 | 2023 | 2023 | 2024 | 2020 |
| Parameter | TPS7A16A-Q1 [144] | XC6206J [145] | STLQ015 [146] | MAX15007 [147] | MIC5365 [148] | LP5907 [149] |
|---|---|---|---|---|---|---|
| Input voltage | 3–60 V | 1.5–6.0 V | 1.5–5.5 V | 4.0–40 V | 2.5–5.5 V | 2.2–5.5 V |
| Output voltage | 2.5–6.5 V | 0.9–4.0 V | 0.8–3.3 V | 3.3 V | 1.5–5.0 V | 1.2–4.5 V |
| Quiescent current | 25 µA | 1 µA | 1.4 µA | 91 µA | 29 µA | 12 µA |
| Dropout voltage | 300 mV | 200 mV | 60 mV | 400 mV | 80 mV | 120 mV |
| Max output current | 100 mA | 200 mA | 150 mA | 350 mA | 150 mA | 250 mA |
| Main advantage | Wide input range, excellent PSRR | Ultra-low power, portable-friendly | Nano-power, optimized for IoT and wearables | Automotive reliability, industrial-grade | Compact design, ultra-low power | High PSRR, noise-sensitive applications |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pandiev, I.; Aleksandrova, M.; Kurtev, N.; Rizanov, S. Analysis of Circuit Configurations Suitable for Self-Supplied AC-DC Converters Using Thin-Film Piezoelectric Generators and Multilayer Energy Storage Supercapacitors. Electronics 2025, 14, 1083. https://doi.org/10.3390/electronics14061083
Pandiev I, Aleksandrova M, Kurtev N, Rizanov S. Analysis of Circuit Configurations Suitable for Self-Supplied AC-DC Converters Using Thin-Film Piezoelectric Generators and Multilayer Energy Storage Supercapacitors. Electronics. 2025; 14(6):1083. https://doi.org/10.3390/electronics14061083
Chicago/Turabian StylePandiev, Ivaylo, Mariya Aleksandrova, Nikolay Kurtev, and Stefan Rizanov. 2025. "Analysis of Circuit Configurations Suitable for Self-Supplied AC-DC Converters Using Thin-Film Piezoelectric Generators and Multilayer Energy Storage Supercapacitors" Electronics 14, no. 6: 1083. https://doi.org/10.3390/electronics14061083
APA StylePandiev, I., Aleksandrova, M., Kurtev, N., & Rizanov, S. (2025). Analysis of Circuit Configurations Suitable for Self-Supplied AC-DC Converters Using Thin-Film Piezoelectric Generators and Multilayer Energy Storage Supercapacitors. Electronics, 14(6), 1083. https://doi.org/10.3390/electronics14061083








