An Index of Refraction Adaptive Neural Refractive Radiance Field for Transparent Scenes
Abstract
1. Introduction
1.1. Three-Dimensional Reconstruction Methods for Transparent Objects
1.2. Radiance Field Reconstruction Methods
1.3. Radiance Field Reconstruction Methods for Transparent Object Scene
- A framework for scene reconstruction and novel view synthesis that only relies on a set of multi-view transparent object scene images or videos without any other prior knowledge.
- An IOR estimation algorithm that can automatically search for the best IOR during the process of radiance field training, which ensures the accuracy of subsequent radiance field training without the need for an accurate IOR value.
- We correct the inaccurate calculation method of the refractive effect in NeRRF, enabling us to render the phenomenon of the foreground darkening caused by refraction more accurately, especially at the edges.
- A mask-based ray-tracing acceleration algorithm that can reduce the training time by approximately 60% and rendering time by 75%.
- Our method performs complete inverse rendering on the scene to obtain relatively accurate ambient light, transparent object geometry, and IOR, enabling various downstream tasks such as object editing, environment editing, and IOR editing.
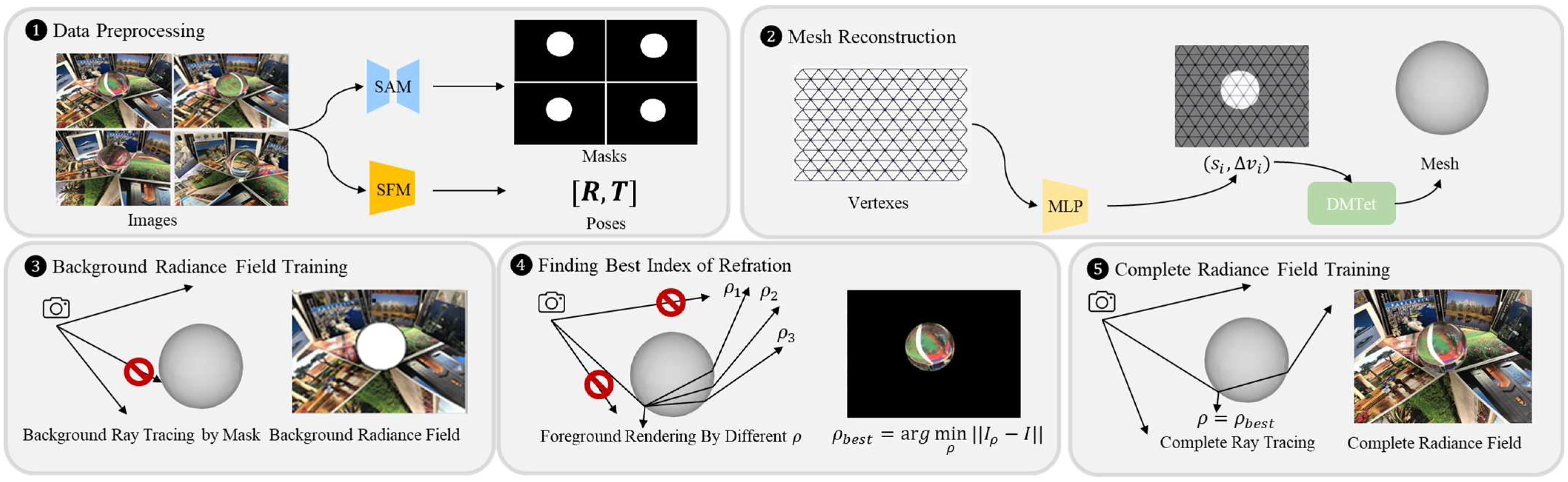
2. IOR-Adaptive Refraction Scene Reconstruction Method
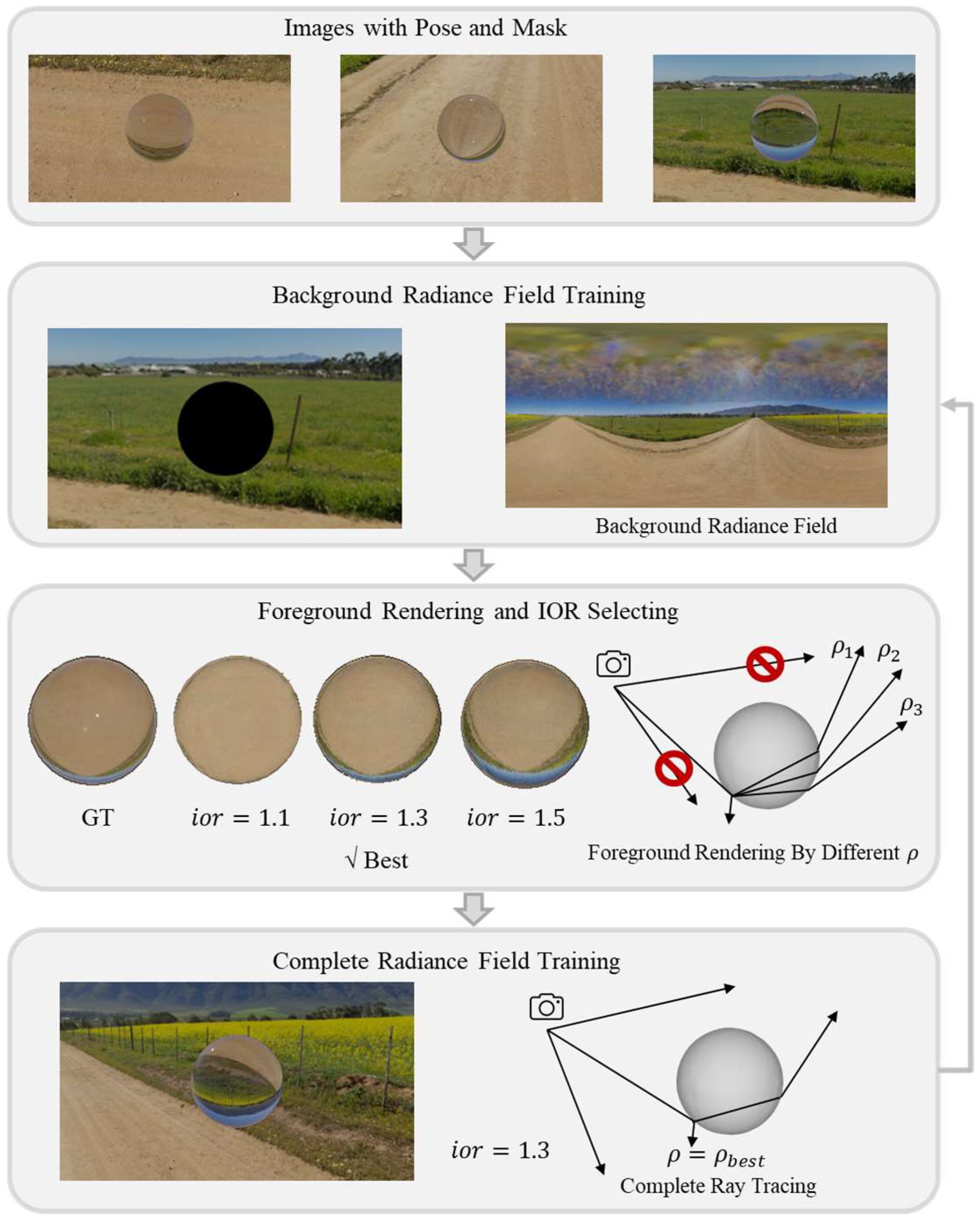
2.1. Data Preprocessing
2.2. Mesh Reconstruction
2.3. Radiance Field Training and IOR Optimization Based on Ray Tracing
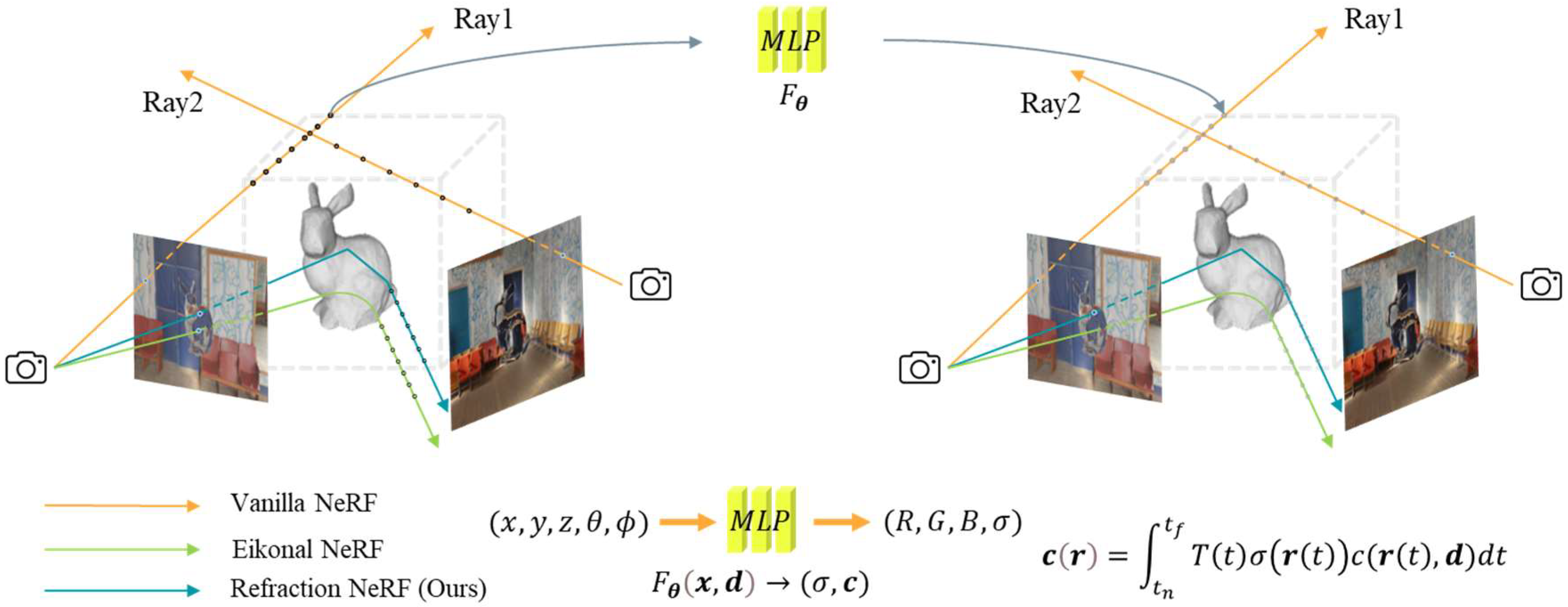
2.3.1. Neural Radiance Field
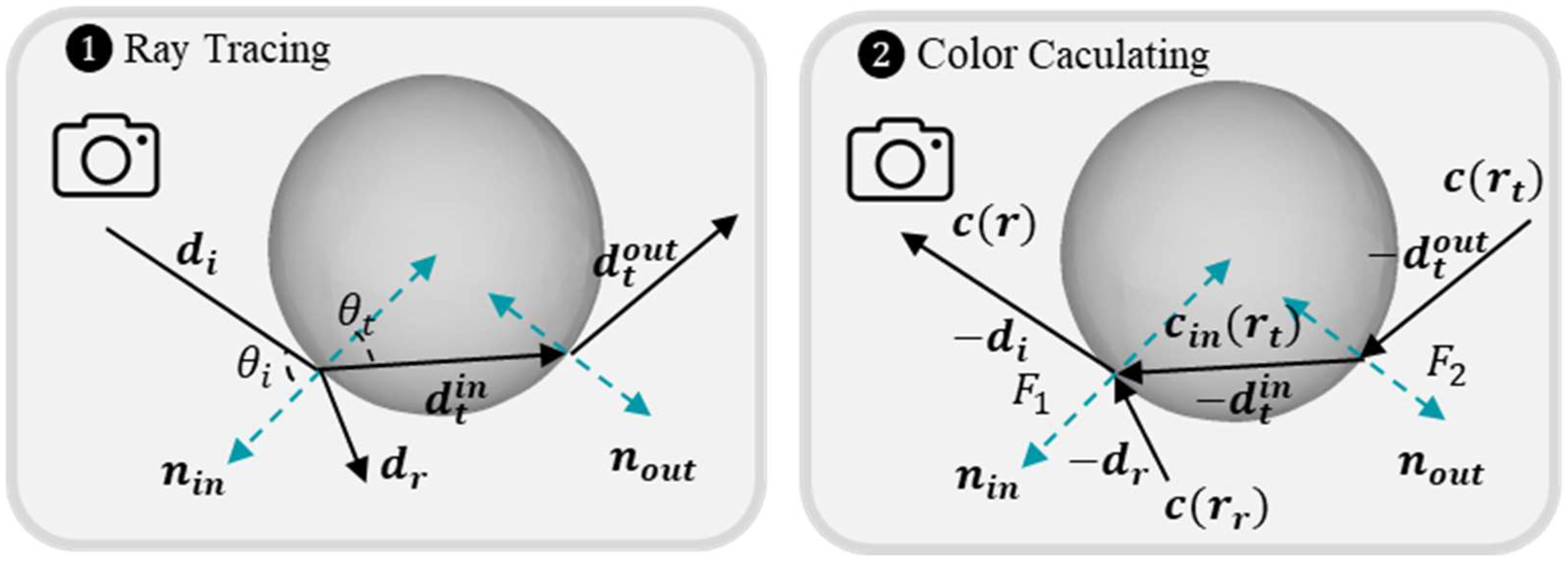
2.3.2. Refraction Radiance Field
2.3.3. IOR Optimization
| Algorithm 1 Optimal IOR searching. |
| Input: A MLP , IOR range , the number of IOR search segments , transparent object mesh , foreground camera rays , foreground pixel color . |
| Output: Optimal IOR . |
| 1: Divide the IOR range into equal parts . |
| 2: Init , |
| 3: for () do 4: 5: Calculate the emergent light rays after refraction . 6: Render color of each pixel by Equation (5), . 7: Calculate 8: if then 9: 10: end if 11: end for 12: new IOR range 13: Set the IOR range for the next search. |
| 14: return |
3. Experiments and Results
3.1. Experiment Settings
3.1.1. Dataset
3.1.2. Evaluation
3.1.3. Experimental Details
- 1.
- Details of Surface Reconstruction
- 2.
- Details of Radiance Field Reconstruction
3.2. Experiment Results
3.2.1. Geometric Reconstruction Results
3.2.2. Results of Novel View Synthesis and IOR Optimization
3.2.3. Supplementary Experiments
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhuang, S.F.; Tu, D.W.; Zhang, X. Research on Corresponding Point Matching and 3D Reconstruction of Underwater Binocular Stereo Vision. Chin. J. Sci. Instrum. 2022, 43, 147–154. [Google Scholar]
- Weinmann, M.; Klein, R. Advances in Geometry and Reflectance Acquisition (Course Notes). In Proceedings of the SIGGRAPH Asia 2015 Courses, Kobe, Japan, 2–6 November 2015; pp. 1–71. [Google Scholar]
- Zhang, Z.; Liu, X.; Guo, Z.; Gao, N.; Meng, X. Shape Measurement of Specular/Diffuse Complex Surface Based on Structured Light. Infrared Laser Eng. 2020, 49, 0303015. [Google Scholar] [CrossRef]
- Bai, X.F.; Zhang, Z.H. 3D Shape Measurement Based on Colour Fringe Projection Techniques. Chin. J. Sci. Instrum. 2017, 38, 1912–1925. [Google Scholar]
- Huang, S.; Shi, Y.; Li, M.; Qian, J.; Xu, K. Underwater 3D Reconstruction Using a Photometric Stereo with Illuminance Estimation. Appl. Opt. 2023, 62, 612–619. [Google Scholar] [CrossRef]
- Aberman, K.; Katzir, O.; Zhou, Q.; Luo, Z.; Sharf, A.; Greif, C.; Chen, B.; Cohen-Or, D. Dip Transform for 3D Shape Reconstruction. ACM Trans. Graph. (TOG) 2017, 36, 1–11. [Google Scholar] [CrossRef]
- Trifonov, B.; Bradley, D.; Heidrich, W. Tomographic Reconstruction of Transparent Objects. In ACM SIGGRAPH 2006 Sketches; Association for Computing Machinery: New York, NY, USA, 2006; pp. 55–es. [Google Scholar]
- Hullin, M.B.; Fuchs, M.; Ihrke, I.; Seidel, H.-P.; Lensch, H. Fluorescent Immersion Range Scanning. In Proceedings of the ACM SIGGRAPH 2008, Los Angeles, CA, USA, 11–15 August 2008; ACM: New York, NY, USA, 2008; pp. 87.1–87.10. [Google Scholar]
- Baihe, Q.; Yang, Q.; Xinyang, X.U. Surface Profile Reconstruction of Inhomogeneous Object Based on Direct Light Path Method. J. Chang. Univ. Sci. Technol. (Nat. Sci. Ed.) 2018, 41, 33–36+51. [Google Scholar]
- Ji, Y.; Xia, Q.; Zhang, Z. Fusing Depth and Silhouette for Scanning Transparent Object with RGB-D Sensor. Int. J. Opt. 2017, 2017, 9796127. [Google Scholar] [CrossRef]
- He, K.; Sui, C.; Huang, T.; Dai, R.; Lyu, C.; Liu, Y.-H. 3D Surface Reconstruction of Transparent Objects Using Laser Scanning with LTFtF Method. Opt. Lasers Eng. 2022, 148, 106774. [Google Scholar] [CrossRef]
- Eren, G.; Aubreton, O.; Meriaudeau, F.; Sanchez Secades, L.A.; Fofi, D.; Teoman Naskali, A.; Truchetet, F.; Ercil, A. Scanning from Heating: 3D Shape Estimation of Transparent Objects from Local Surface Heating. Opt. Express 2009, 17, 11457–11468. [Google Scholar] [CrossRef]
- Meriaudeau, F.; Secades, L.A.S.; Eren, G.; Erçil, A.; Truchetet, F.; Aubreton, O.; Fofi, D. 3-D Scanning of Nonopaque Objects by Means of Imaging Emitted Structured Infrared Patterns. IEEE Trans. Instrum. Meas. 2010, 59, 2898–2906. [Google Scholar] [CrossRef]
- Rantoson, R.; Stolz, C.; Fofi, D.; Meriaudeau, F. Optimization of Transparent Objects Digitization from Visible Fluorescence Ultraviolet Induced. Opt. Eng. 2012, 51, 033601. [Google Scholar] [CrossRef]
- Kutulakos, K.N.; Steger, E. A Theory of Refractive and Specular 3D Shape by Light-Path Triangulation. Int. J. Comput. Vis. 2008, 76, 13–29. [Google Scholar] [CrossRef]
- Atcheson, B.; Ihrke, I.; Heidrich, W.; Tevs, A.; Bradley, D.; Magnor, M.; Seidel, H.-P. Time-Resolved 3D Capture of Non-Stationary Gas Flows. ACM Trans. Graph. (TOG) 2008, 27, 1–9. [Google Scholar] [CrossRef]
- Wu, B. Image-based Modeling and Rendering of Transparent Objects. Doctoral Thesis, University of Chinese Academy of Sciences (Shenzhen Institutes of Advanced Technology Chinese Academy of Sciences), Shenzhen, China, 2019. [Google Scholar]
- Hao, Z.; Liu, Y. Transparent Object Shape Measurement Based on Deflectometry. Proceedings 2018, 2, 548. [Google Scholar] [CrossRef]
- Zongker, D.E.; Werner, D.M.; Curless, B.; Salesin, D.H. Environment Matting and Compositing. In Seminal Graphics Papers: Pushing the Boundaries; University of Washington: Seattle, WA, USA, 2023; Volume 2, pp. 537–546. [Google Scholar]
- Chuang, Y.-Y.; Zongker, D.E.; Hindorff, J.; Curless, B.; Salesin, D.H.; Szeliski, R. Environment Matting Extensions: Towards Higher Accuracy and Real-Time Capture. In Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques, New York, NY, USA, July 23–28 2000; pp. 121–130. [Google Scholar]
- Ihrke, I.; Kutulakos, K.N.; Lensch, H.P.; Magnor, M.; Heidrich, W. Transparent and Specular Object Reconstruction. In Proceedings of the Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2010; Volume 29, pp. 2400–2426. [Google Scholar]
- Xu, X.; Lin, Y.; Zhou, H.; Zeng, C.; Yu, Y.; Zhou, K.; Wu, H. A Unified Spatial-Angular Structured Light for Single-View Acquisition of Shape and Reflectance. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 206–215. [Google Scholar]
- Liu, I.; Chen, L.; Fu, Z.; Wu, L.; Jin, H.; Li, Z.; Wong, C.M.R.; Xu, Y.; Ramamoorthi, R.; Xu, Z. Openillumination: A Multi-Illumination Dataset for Inverse Rendering Evaluation on Real Objects. Adv. Neural Inf. Process. Syst. 2024, 36, 36951–36962. [Google Scholar]
- Mildenhall, B.; Srinivasan, P.P.; Tancik, M.; Barron, J.T.; Ramamoorthi, R.; Ng, R. Nerf: Representing Scenes as Neural Radiance Fields for View Synthesis. Commun. ACM 2021, 65, 99–106. [Google Scholar] [CrossRef]
- Barron, J.T.; Mildenhall, B.; Tancik, M.; Hedman, P.; Martin-Brualla, R.; Srinivasan, P.P. Mip-Nerf: A Multiscale Representation for Anti-Aliasing Neural Radiance Fields. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2021; pp. 5855–5864. [Google Scholar]
- Barron, J.T.; Mildenhall, B.; Verbin, D.; Srinivasan, P.P.; Hedman, P. Mip-Nerf 360: Unbounded Anti-Aliased Neural Radiance Fields. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 5470–5479. [Google Scholar]
- Chen, Z.; Funkhouser, T.; Hedman, P.; Tagliasacchi, A. Mobilenerf: Exploiting the Polygon Rasterization Pipeline for Efficient Neural Field Rendering on Mobile Architectures. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 16569–16578. [Google Scholar]
- Qin, S.; Xiao, J.; Ge, J. Dip-NeRF: Depth-Based Anti-Aliased Neural Radiance Fields. Electronics 2024, 13, 1572. [Google Scholar] [CrossRef]
- Srinivasan, P.P.; Deng, B.; Zhang, X.; Tancik, M.; Mildenhall, B.; Barron, J.T. Nerv: Neural Reflectance and Visibility Fields for Relighting and View Synthesis. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 7495–7504. [Google Scholar]
- Boss, M.; Jampani, V.; Braun, R.; Liu, C.; Barron, J.; Lensch, H. Neural-Pil: Neural Pre-Integrated Lighting for Reflectance Decomposition. Adv. Neural Inf. Process. Syst. 2021, 34, 10691–10704. [Google Scholar]
- Jin, H.; Liu, I.; Xu, P.; Zhang, X.; Han, S.; Bi, S.; Zhou, X.; Xu, Z.; Su, H. Tensoir: Tensorial Inverse Rendering. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 165–174. [Google Scholar]
- Li, Z.; Wang, L.; Cheng, M.; Pan, C.; Yang, J. Multi-View Inverse Rendering for Large-Scale Real-World Indoor Scenes. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 12499–12509. [Google Scholar]
- Wang, P.; Liu, L.; Liu, Y.; Theobalt, C.; Komura, T.; Wang, W. Neus: Learning Neural Implicit Surfaces by Volume Rendering for Multi-View Reconstruction. arXiv 2021, arXiv:2106.10689. [Google Scholar]
- Yao, Y.; Zhang, J.; Liu, J.; Qu, Y.; Fang, T.; McKinnon, D.; Tsin, Y.; Quan, L. Neilf: Neural Incident Light Field for Physically-Based Material Estimation. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 700–716. [Google Scholar]
- Liu, Y.; Wang, P.; Lin, C.; Long, X.; Wang, J.; Liu, L.; Komura, T.; Wang, W. Nero: Neural Geometry and Brdf Reconstruction of Reflective Objects from Multiview Images. ACM Trans. Graph. (TOG) 2023, 42, 1–22. [Google Scholar] [CrossRef]
- Zeng, C.; Chen, G.; Dong, Y.; Peers, P.; Wu, H.; Tong, X. Relighting Neural Radiance Fields with Shadow and Highlight Hints. In Proceedings of the ACM SIGGRAPH 2023 Conference Proceedings, Los Angeles, CA, USA, 6–10 August 2023; pp. 1–11. [Google Scholar]
- Sainz, M.; Pajarola, R. Point-Based Rendering Techniques. Comput. Graph. 2004, 28, 869–879. [Google Scholar] [CrossRef]
- Grossman, J.P.; Dally, W.J. Point Sample Rendering. In Proceedings of the Rendering Techniques’98: Proceedings of the Eurographics Workshop, Vienna, Austria, 29 June—1 July 1998; Springer: Berlin/Heidelberg, Germany, 1998; pp. 181–192. [Google Scholar]
- Schütz, M.; Kerbl, B.; Wimmer, M. Software Rasterization of 2 Billion Points in Real Time. Proc. ACM Comput. Graph. Interact. Tech. 2022, 5, 1–17. [Google Scholar] [CrossRef]
- Kerbl, B.; Kopanas, G.; Leimkühler, T.; Drettakis, G. 3D Gaussian Splatting for Real-Time Radiance Field Rendering. ACM Trans. Graph. 2023, 42, 1–14. [Google Scholar] [CrossRef]
- Gao, J.; Gu, C.; Lin, Y.; Li, Z.; Zhu, H.; Cao, X.; Zhang, L.; Yao, Y. Relightable 3D Gaussians: Realistic Point Cloud Relighting with Brdf Decomposition and Ray Tracing. In Proceedings of the European Conference on Computer Vision, Paris, France, 26–27 March 2025; Springer: Berlin/Heidelberg, Germany, 2025; pp. 73–89. [Google Scholar]
- Shi, Y.; Wu, Y.; Wu, C.; Liu, X.; Zhao, C.; Feng, H.; Liu, J.; Zhang, L.; Zhang, J.; Zhou, B. Gir: 3D Gaussian Inverse Rendering for Relightable Scene Factorization. arXiv 2023, arXiv:2312.05133. [Google Scholar]
- Jiang, Y.; Tu, J.; Liu, Y.; Gao, X.; Long, X.; Wang, W.; Ma, Y. Gaussianshader: 3D Gaussian Splatting with Shading Functions for Reflective Surfaces. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 5322–5332. [Google Scholar]
- Bemana, M.; Myszkowski, K.; Revall Frisvad, J.; Seidel, H.-P.; Ritschel, T. Eikonal Fields for Refractive Novel-View Synthesis. In Proceedings of the ACM SIGGRAPH 2022 Conference Proceedings, Vancouver, BC, Canada, 7–11 August 2022; pp. 1–9. [Google Scholar]
- Pan, J.-I.; Su, J.-W.; Hsiao, K.-W.; Yen, T.-Y.; Chu, H.-K. Sampling Neural Radiance Fields for Refractive Objects. In Proceedings of the SIGGRAPH Asia 2022 Technical Communications, Daegu, Republic of Korea, 6–9 December 2022; pp. 1–4. [Google Scholar]
- Sun, J.-M.; Wu, T.; Yan, L.-Q.; Gao, L. NU-NeRF: Neural Reconstruction of Nested Transparent Objects with Uncontrolled Capture Environment. ACM Trans. Graph. (TOG) 2024, 43, 1–14. [Google Scholar] [CrossRef]
- Chen, X.; Liu, J.; Zhao, H.; Zhou, G.; Zhang, Y.-Q. Nerrf: 3D Reconstruction and View Synthesis for Transparent and Specular Objects with Neural Refractive-Reflective Fields. arXiv 2023, arXiv:2309.13039. [Google Scholar]
- Shen, T.; Gao, J.; Yin, K.; Liu, M.-Y.; Fidler, S. Deep Marching Tetrahedra: A Hybrid Representation for High-Resolution 3D Shape Synthesis. Adv. Neural Inf. Process. Syst. 2021, 34, 6087–6101. [Google Scholar]
- Kirillov, A.; Mintun, E.; Ravi, N.; Mao, H.; Rolland, C.; Gustafson, L.; Xiao, T.; Whitehead, S.; Berg, A.C.; Lo, W.-Y. Segment Anything. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–3 October 2023; pp. 4015–4026. [Google Scholar]
- Schonberger, J.L.; Frahm, J.-M. Structure-from-Motion Revisited. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4104–4113. [Google Scholar]
- Gropp, A.; Yariv, L.; Haim, N.; Atzmon, M.; Lipman, Y. Implicit Geometric Regularization for Learning Shapes. arXiv 2020, arXiv:2002.10099. [Google Scholar]
- Müller, T.; Evans, A.; Schied, C.; Keller, A. Instant Neural Graphics Primitives with a Multiresolution Hash Encoding. ACM Trans. Graph. (TOG) 2022, 41, 1–15. [Google Scholar] [CrossRef]
- Metashape. Available online: https://www.agisoft.com/ (accessed on 7 October 2023).
- Sarvestani, A.S.; Zhou, W.; Wang, Z. Perceptual Crack Detection for Rendered 3D Textured Meshes. In Proceedings of the 2024 16th International Conference on Quality of Multimedia Experience (QoMEX), Karlshamn, Sweden, 18–20 June 2024; pp. 1–7. [Google Scholar]
- Zhang, Z.; Sun, W.; Min, X.; Wang, T.; Lu, W.; Zhai, G. No-Reference Quality Assessment for 3D Colored Point Cloud and Mesh Models. IEEE Trans. Circuits Syst. Video Technol. 2022, 32, 7618–7631. [Google Scholar] [CrossRef]
- Barron, J.T.; Mildenhall, B.; Verbin, D.; Srinivasan, P.P.; Hedman, P. Zip-Nerf: Anti-Aliased Grid-Based Neural Radiance Fields. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–3 October 2023; pp. 19697–19705. [Google Scholar]



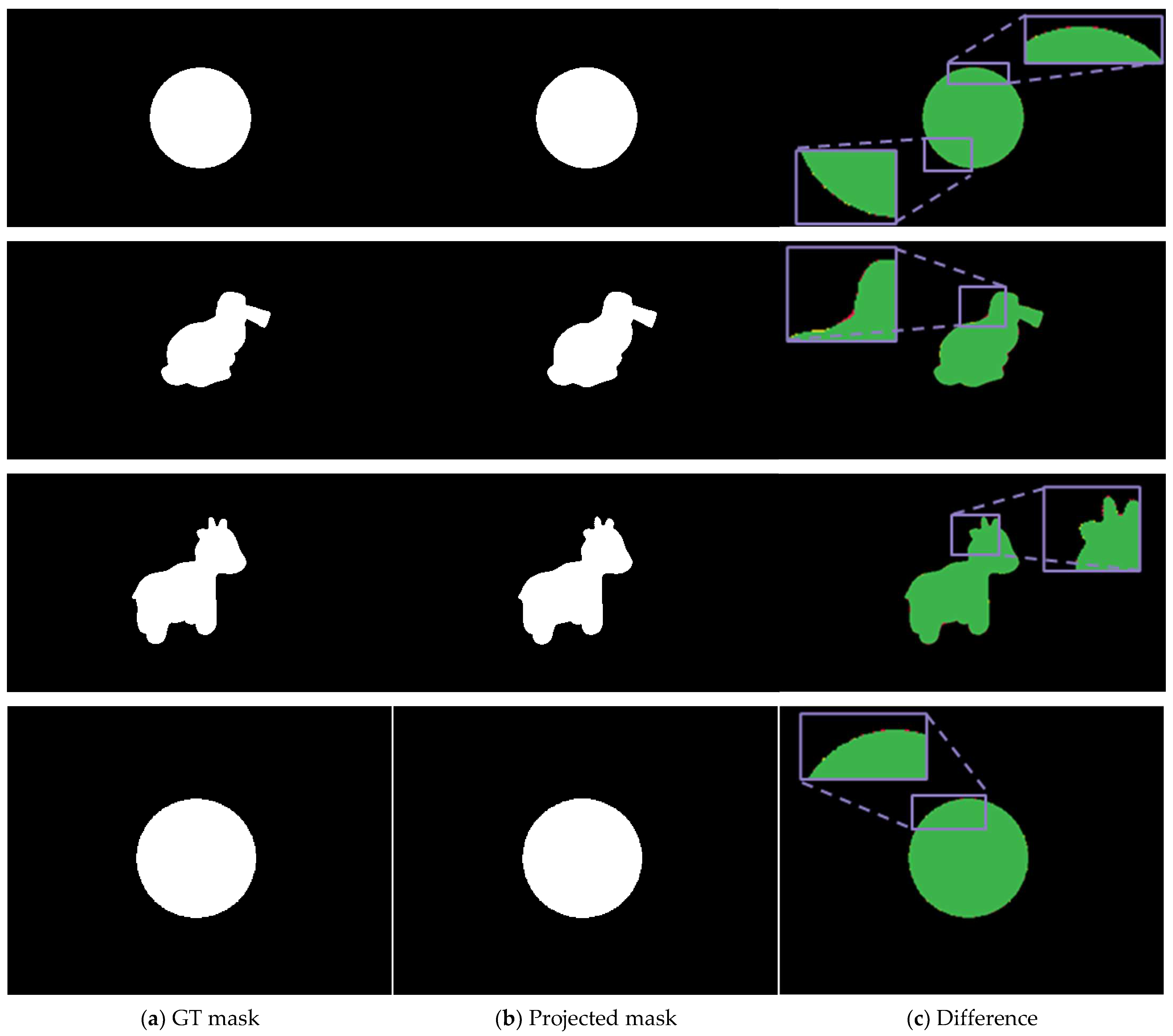








| Datasets | Ball | Bunny | Cow | Glass |
|---|---|---|---|---|
| IoU | 0.995 | 0.984 | 0.987 | 0.994 |
| Methods | ||||||
|---|---|---|---|---|---|---|
| Comp. | Forg. | Comp. | Forg. | Comp. | Forg. | |
| NeRF [52] | 23.63 | 17.35 | 0.752 | 0.276 | 0.202 | 0.091 |
| NeRRF [47] | 26.72 | 17.53 | 0.830 | 0.404 | 0.123 | 0.092 |
| NeRFRO 1 [45] | 23.77 | — | 0.756 | — | 0.379 | — |
| Ours | 27.14 | 18.20 | 0.830 | 0.408 | 0.121 | 0.092 |
| Methods | ||||||
|---|---|---|---|---|---|---|
| Comp. | Forg. | Comp. | Forg. | Comp. | Forg. | |
| NeRF [52] | 16.90 | 14.00 | 0.505 | 0.254 | 0.313 | 0.211 |
| NeRRF [47] | 17.23 | 15.90 | 0.497 | 0.286 | 0.312 | 0.179 |
| Mip-NeRF 1 [25] | 16.29 | — | 0.523 | — | 0.418 | — |
| NeRFRO 1 [45] | 17.62 | — | 0.491 | — | 0.275 | — |
| Eikonal 1 [44] | 18.38 | — | 0.583 | — | 0.239 | — |
| Ours | 17.19 | 15.57 | 0.497 | 0.288 | 0.312 | 0.183 |
| Datasets | Ball | Bunny | Cow | Glass |
|---|---|---|---|---|
| IOR-GT | 1.30 | 1.20 | 1.20 | 1.50 |
| IOR-predicted | 1.31 | 1.15 | 1.19 | 1.47 |
| Ball | Bunny | Cow | Glass | |||||
|---|---|---|---|---|---|---|---|---|
|
Training Time↓ |
Training Time↓ |
Training Time↓ |
Training Time↓ | |||||
| Complete | 5 h 07 min | 0.008 | 5 h 42 min | 0.007 | 4 h 55 min | 0.007 | 18 h 03 min | 0.003 |
| Mask-Based (Ours) | 1 h 45 min | 0.033 | 1 h 33 min | 0.029 | 1 h 21 min | 0.030 | 7 h 49 min | 0.011 |
| Methods | ||||||
|---|---|---|---|---|---|---|
| Comp. | Forg. | Comp. | Forg. | Comp. | Forg. | |
| Full Model | 27.14 | 18.20 | 0.830 | 0.408 | 0.121 | 0.092 |
| w/o Physical Constraints | 26.64 | 17.14 | 0.811 | 0.385 | 0.129 | 0.097 |
| w/o IOR Optimization | 23.28 | 13.26 | 0.783 | 0.319 | 0.173 | 0.137 |
| Methods | ||||||
|---|---|---|---|---|---|---|
| Comp. | Forg. | Comp. | Forg. | Comp. | Forg. | |
| Full Model | 17.19 | 15.57 | 0.497 | 0.288 | 0.312 | 0.183 |
| w/o Physical Constraints | 17.11 | 15.28 | 0.487 | 0.272 | 0.332 | 0.239 |
| w/o IOR Optimization | 17.04 | 13.07 | 0.461 | 0.212 | 0.344 | 0.252 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, J.; Yue, Z.; Li, S.; Cheng, Z.; Lian, Z.; Song, M.; Cheng, Y.; Zhao, H. An Index of Refraction Adaptive Neural Refractive Radiance Field for Transparent Scenes. Electronics 2025, 14, 1073. https://doi.org/10.3390/electronics14061073
Wei J, Yue Z, Li S, Cheng Z, Lian Z, Song M, Cheng Y, Zhao H. An Index of Refraction Adaptive Neural Refractive Radiance Field for Transparent Scenes. Electronics. 2025; 14(6):1073. https://doi.org/10.3390/electronics14061073
Chicago/Turabian StyleWei, Jiangnan, Ziyi Yue, Shuai Li, Zhiqi Cheng, Zhouhui Lian, Mengxiao Song, Yinqian Cheng, and Hongying Zhao. 2025. "An Index of Refraction Adaptive Neural Refractive Radiance Field for Transparent Scenes" Electronics 14, no. 6: 1073. https://doi.org/10.3390/electronics14061073
APA StyleWei, J., Yue, Z., Li, S., Cheng, Z., Lian, Z., Song, M., Cheng, Y., & Zhao, H. (2025). An Index of Refraction Adaptive Neural Refractive Radiance Field for Transparent Scenes. Electronics, 14(6), 1073. https://doi.org/10.3390/electronics14061073





