Multi-Agent Reinforcement Learning-Based Control Method for Pedestrian Guidance Using the Mojiko Fireworks Festival Dataset
Abstract
1. Introduction
2. Related Work
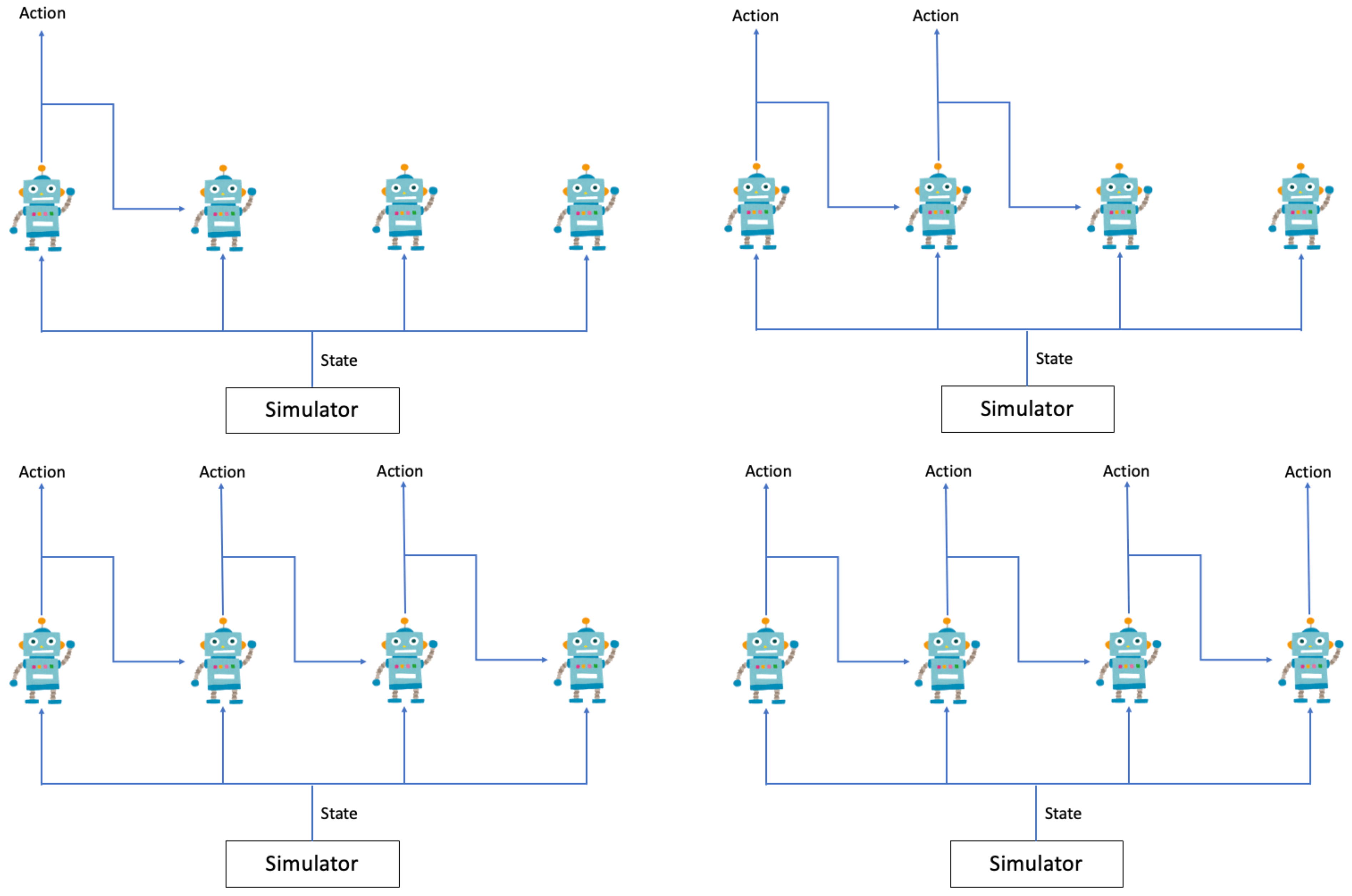
2.1. Multi-Agent Reinforcement Learning Framework
2.2. MA-DDPG
2.3. Cooperative Multi-Agent Reinforcement Learning
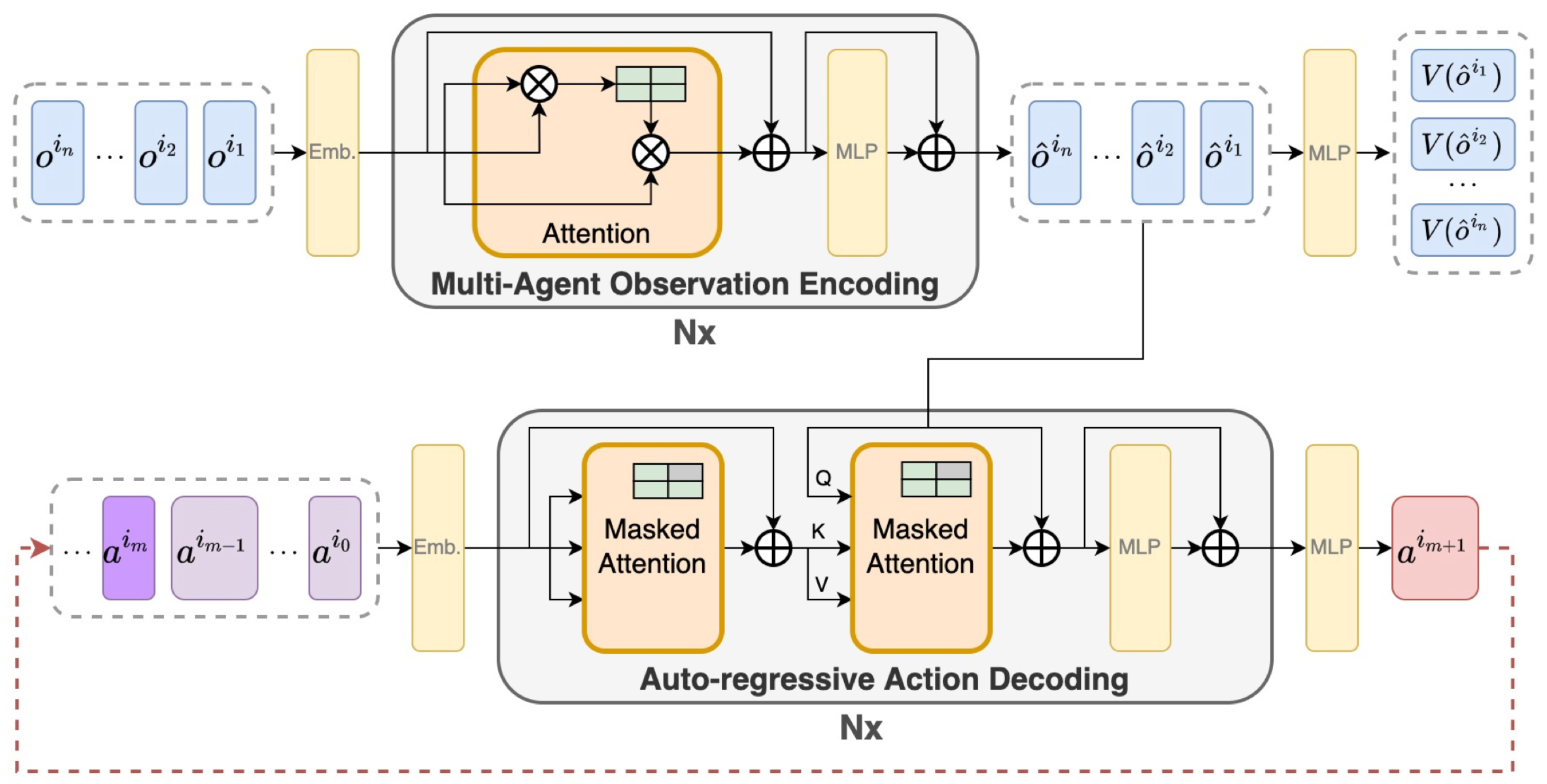
2.4. MAT
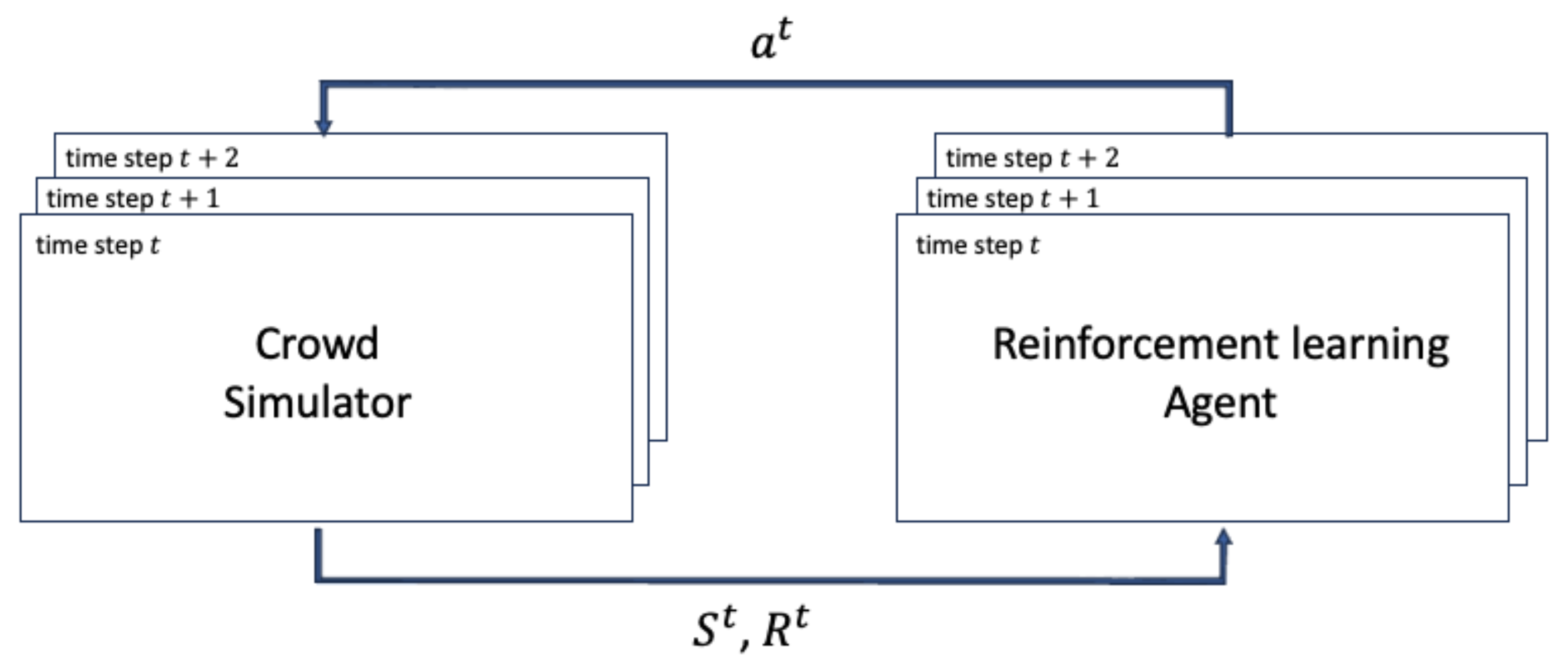
3. Methodology
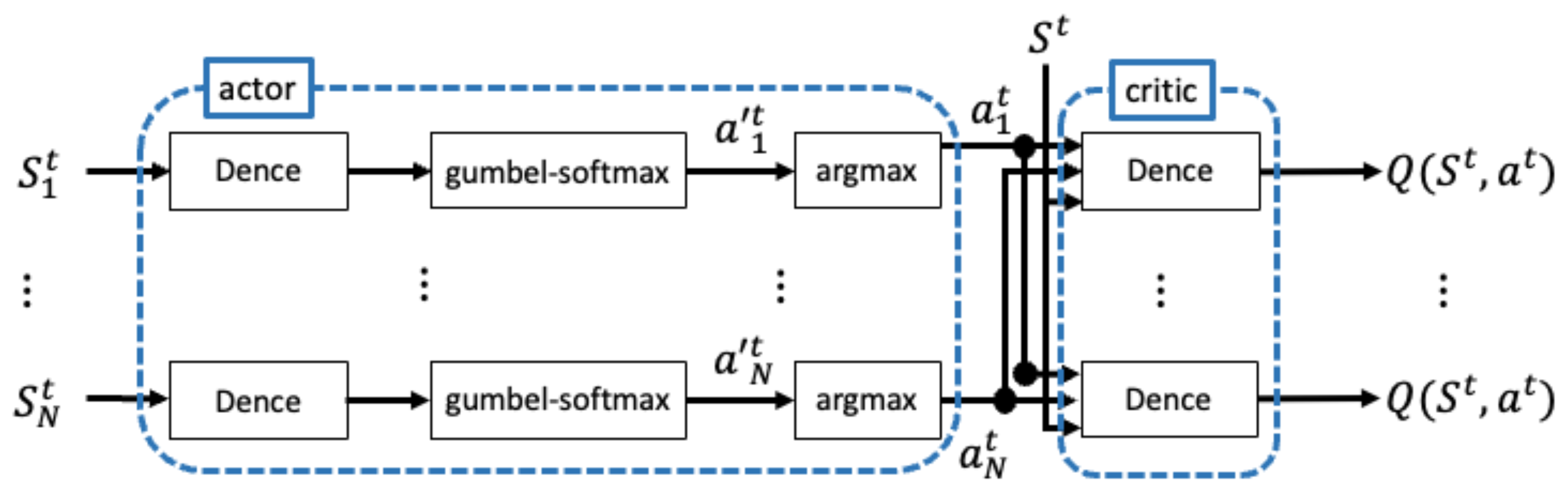
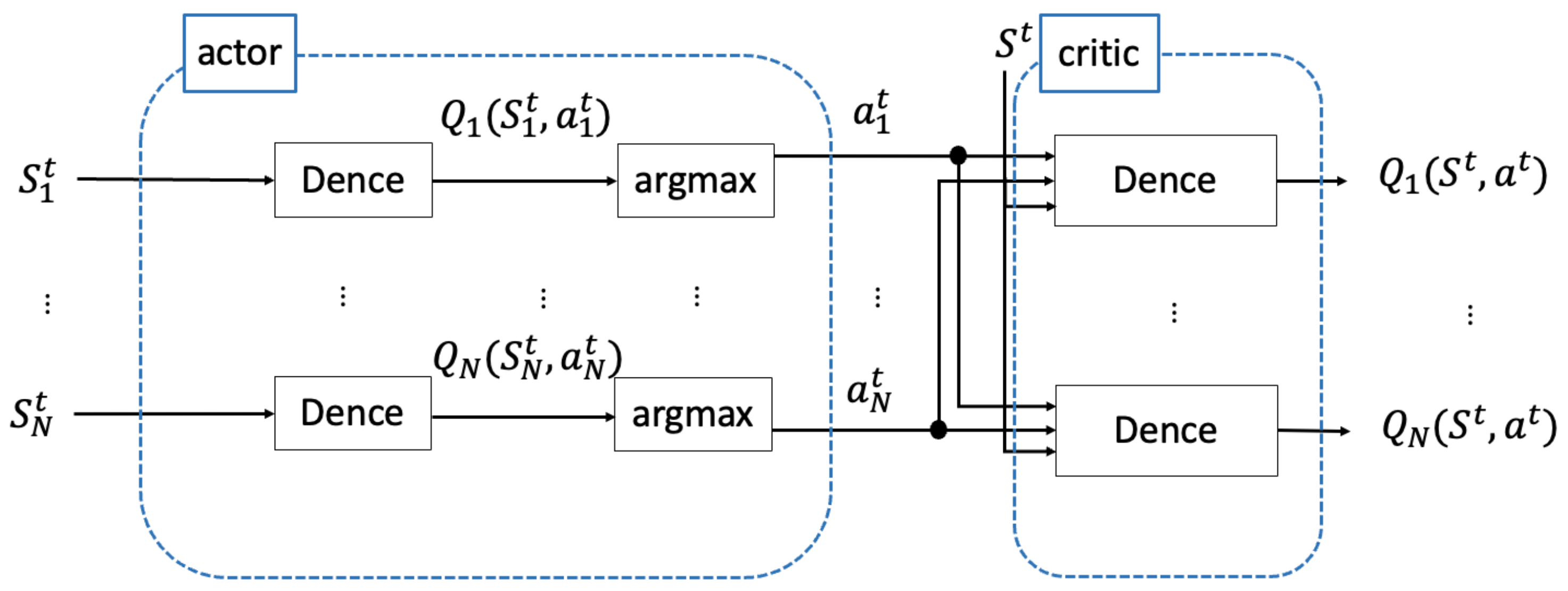
3.1. Actor–Critic Structure
3.2. Exploration
4. Experimental Environment
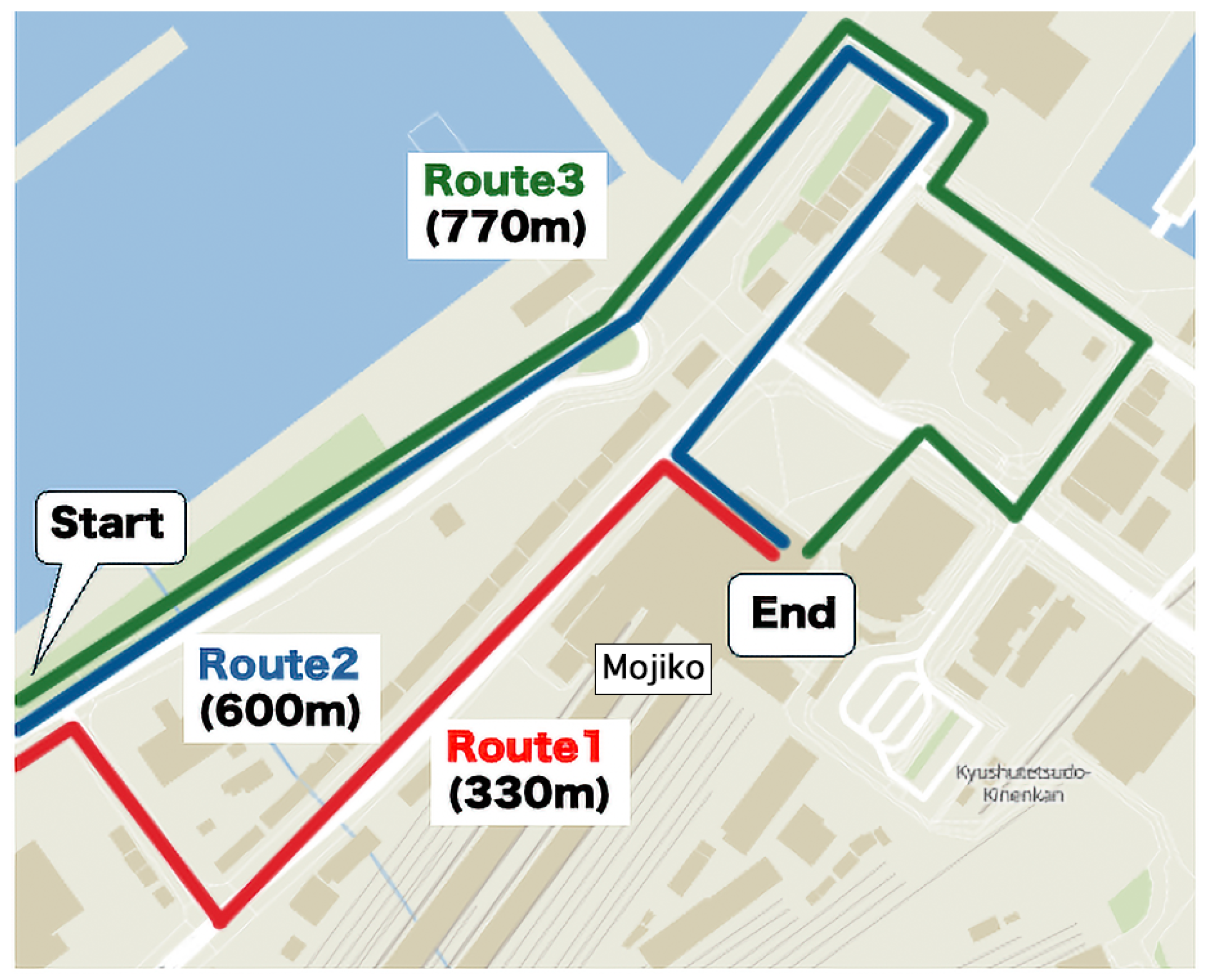
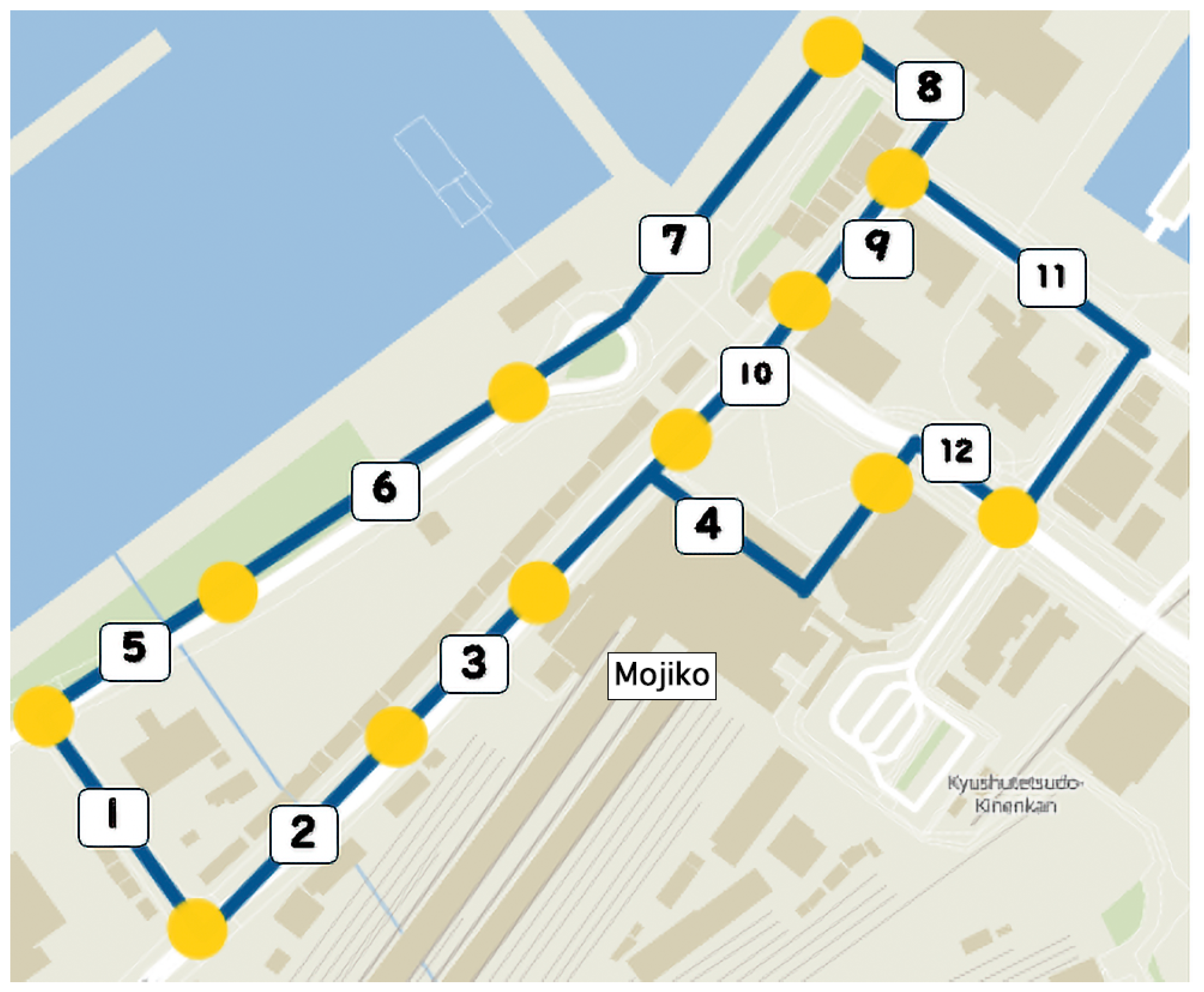
4.1. Dataset
4.2. Evaluation Metrics
4.3. State and Reward in Reinforcement Learning
4.4. Hyperparameters
5. Results and Discussion
5.1. Comparison with MA-DDPG
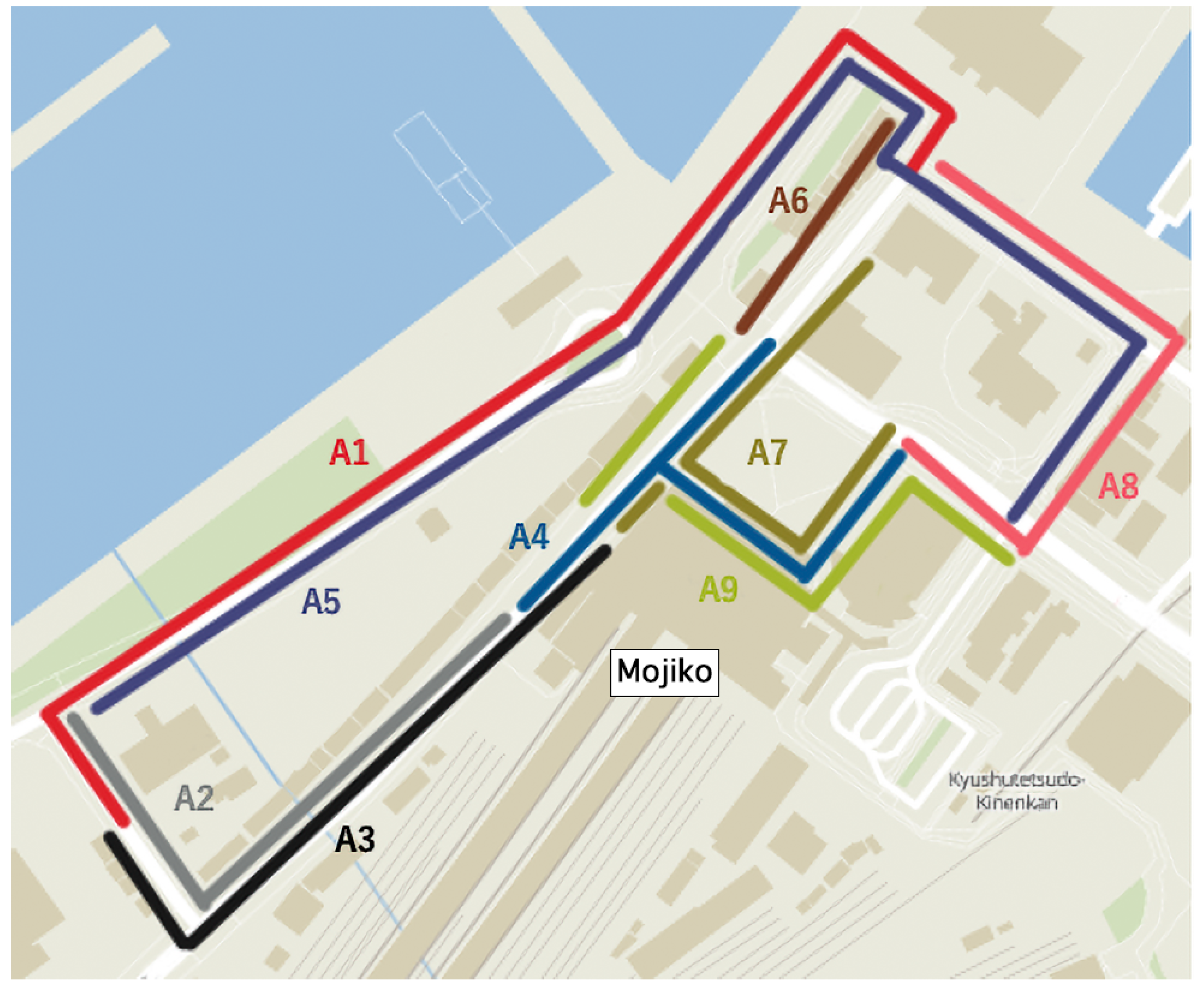
5.2. Analysis of Route Confluence Points
5.3. Comparison with MAT
6. Conclusions
- A detailed analysis of computational requirements and optimization remains an important direction.
- These findings must be validated with real-world pedestrian data or controlled field experiments to assess model performance under truly dynamic crowd behaviors, extreme congestion situations, safety risk, and unpredictable factors not fully captured in simulations.
- Future deployment must address ethical concerns including privacy implications of sensor systems, potential biases in crowd management algorithms, and clear responsibility frameworks for safety outcomes.
- Alternative exploration strategies must be explored beyond -greedy, such as Gumbel-Softmax, to potentially enhance the learning process and convergence properties of our approach.
- The social force model has limitations in its ability to perfectly reproduce actual pedestrian behavior, which may affect the results. Therefore, we explore a more sophisticated model [29].
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pang, Y.; Kashiyama, T.; Yabe, T.; Tsubouchi, K.; Sekimoto, Y. Development of people mass movement simulation framework based on reinforcement learning. Transp. Res. Part C Emerg. Technol. 2020, 117, 102706. [Google Scholar] [CrossRef]
- Miyazaki, K.; Amagasaki, M.; Kiyama, M.; Okamoto, T. Acceleration of data assimilation for Large-scale human flow data. IEICE Tech. Rep. 2022, 122, 178–183. [Google Scholar]
- Shigenaka, S.; Onishi, M.; Yamashita, T.; Noda, I. Estimation of Large-Scale Pedestrian Movement Using Data Assimilation. IEICE Trans. 2018, J101-D, 1286–1294. [Google Scholar]
- Matsubayasi, T.; Kiyotake, H.; Koujima, H.; Toda, H.; Tanaka, Y.; Mutou, Y.; Shiohara, H.; Miyamoto, M.; Shimizu, H.; Otsuka, T.; et al. Data Assimilation and Preliminary Security Planning for People Crowd. IEICE Trans. 2019, 34, 1–11. [Google Scholar]
- Kalman, R.E. A new approach to linear filtering and prediction problems. Trans. ASME J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Gordon, N.J.; Salmond, D.J.; Smith, A.F.M. Novel approach to nonlinear/non-Gaussian Bayesian state estimation. Radar Signal Process. 1993, 140, 107–113. [Google Scholar] [CrossRef]
- Chen, H.; Zendehdel, N.; Leu, M.C.; Yin, Z. Fine-grained activity classification in assembly based on multi-visual modalities. J. Intell. Manuf. 2024, 35, 2215–2233. [Google Scholar] [CrossRef]
- Kaelbling, L.P.; Littman, M.L.; Moore, A.W. Reinforcement Learning: A Survey. J. Articial Intell. Res. 1996, 4, 237–285. [Google Scholar] [CrossRef]
- Chen, C.; Wei, H.; Xu, N.; Zheng, G.; Yang, M.; Xiong, Y.; Xu, K.; Li, Z. Toward A Thousand Lights: Decentralized Deep Reinforcement Learning for Large-Scale Traffic Signal Control. Proc. Assoc. Adv. Artif. Intell. Conf. Artif. Intell. 2020, 34, 3414–3421. [Google Scholar] [CrossRef]
- Li, Z.; Yu, H.; Zhang, G.; Dong, S.; Xu, C.Z. Network-wide traffic signal control optimization using a multi-agent deep reinforcement learning. Transp. Res. Part C Emerg. Technol. 2021, 125, 103059. [Google Scholar] [CrossRef]
- Silver1, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; Driessche, G.V.D.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef] [PubMed]
- Antonoglou, I.; Schrittwieser, J.; Ozair, S.; Hubert, T.; Silver, D. Planning in stochastic environments with a learned model. In Proceedings of the 10th International Conference on Learning Representations, Virtual, 25 April 2022. [Google Scholar]
- Gao, R.; Zha, A.; Shigenaka, S.; Onishi, M. Hybrid Modeling and Predictive Control of Large-Scale Crowd Movement in Road Network. In Proceedings of the 24th International Conference on Hybrid Systems: Computation and Control, Nashville, TN, USA, 19–21 May 2021; pp. 1–7. [Google Scholar]
- Richalet, J.; Eguchi, G.; Hashimoto, Y. Why Predictive Control? J. Soc. Instrum. Control. Eng. 2004, 43, 654–664. [Google Scholar]
- Tan, M. Multi-Agent Reinforcement Learning: Independent vs. Cooperative Agents. In Proceedings of the Tenth International Conference on International Conference on Machine Learning, Amherst, MA, USA, 27–29 July 1993; pp. 330–337. [Google Scholar]
- Foerster, J.N.; Assael, Y.M.; Freitas, N.D.; Whiteson, S. Learning to Communicate with Deep Multi-Agent Reinforcement Learning. In Proceedings of the 30th International Conference on Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 2145–2153. [Google Scholar]
- Lowe, R.; Wu, Y.; Tamar, A.; Harb, J.; Abbeel, P.; Mordatch, I. Multi-Agent Actor-Critic for Mixed Cooperative-Competitive Environments. In Proceedings of the 31st Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 6382–6393. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. In Proceedings of the 4th International Conference on Learning Representations, San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Silver, D.; Lever, G.; Heess, N.; Degris, T.; Wierstra, D.; Riedmiller, M. Deterministic Policy Gradient Algorithms. In Proceedings of the 31st International Conference on Machine Learning, Beijing, China, 21–26 June 2014; Volume 32, pp. I-387–I-395. [Google Scholar]
- Wen, M.; Kuba, J.G.; Lin, R.; Zhang, W.; Wen, Y.; Wang, J.; Yang, Y. Multi-Agent Reinforcement Learning is A Sequence Modeling Problem. arXiv 2022, arXiv:2205.14953. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Shusuke, S.; Shunki, T.; Shuhei, W.; Yuki, T.; Yoshihiko, O.; Masaki, O. MAS-Bench: Parameter Optimization Benchmark for Multi-Agent Crowd Simulation. In Proceedings of the 20th International Conference on Autonomous Agents and MultiAgent Systems, Virtual, 3–7 May 2021; pp. 1652–1654. [Google Scholar]
- Helbing, D.; Molnar, P. Social force model for pedestrian dynamics. Phys. Rev. E 1995, 51, 4282. [Google Scholar] [CrossRef] [PubMed]
- Nishida, R.; Shigenaka, S.; Kato, Y.; Onishi, M. Recent Advances in Crowd Movement Space Design and Control using Crowd Simulation. Jpn. Soc. Artif. Intell. 2022, 37, 1–16. [Google Scholar] [CrossRef]
- Fruin, J.J. Designing for pedestrians:A level-of-service concept. In Proceedings of the 50th Annual Meeting of the Highway Research Board, No.HS-011999, Washington, DC, USA, 18–22 January 1971. [Google Scholar]
- Abdelghany, A.; Abdelghany, K.; Mahmassani, H.; Alhalabi, W. Modeling framework for optimal evacuation of large-scale crowded pedestrian facilities. Eur. J. Oper. Res. 2014, 237, 1105–1118. [Google Scholar] [CrossRef]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A Next-generation Hyperparameter Optimization Framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2623–2631. [Google Scholar]
- Charalambous, P.; Pettre, J.; Vassiliades, V.; Chrysanthou, Y.; Pelechano, N. GREIL-Crowds: Crowd Simulation with Deep Reinforcement Learning and Examples. ACM Trans. Graph. (TOG) 2023, 42, 1–15. [Google Scholar] [CrossRef]
| LOS | Pedestrian Density |
|---|---|
| A | <0.31 |
| B | 0.31–0.43 |
| C | 0.43–0.72 |
| D | 0.72–1.08 |
| E | 1.08–2.17 |
| F | >2.17 |
| Reward | Pedestrian Density |
|---|---|
| 1.0 | <0.31 |
| 0.6 | 0.31–0.43 |
| 0.2 | 0.43–0.72 |
| −0.2 | 0.72–1.00 |
| Parameter | Value |
|---|---|
| buffer size | 10,000,000 |
| actor lr | 5.00 |
| critic lr | 5.00 |
| gamma | 0.99 |
| batch size | 40 |
| optimizer | Adam |
| ppo clip | 0.05 |
| ppo epochs | 10 |
| entropy coef | 0.001 |
| Reward | −5 when Pedestrian Density > 1 |
| Parameter | Value |
|---|---|
| buffer size | 100,000 |
| actor lr | 0.01 |
| hidden layer dim in actor | (64, 8) |
| critic lr | 0.01 |
| hidden layer dim in critic | (64, 8) |
| gamma | 0.99 |
| batch size | 1024 |
| optimizer | Adam |
| update frequency of the target network | 30 |
| soft-update | 0.1 |
| Parameter | Value |
|---|---|
| buffer size | 100,000 |
| actor lr | 0.01 |
| hidden layer dim in actor | (128, 32) |
| critic lr | 0.01 |
| hidden layer dim in critic | (128, 32) |
| gamma | 0.99 |
| batch size | 1024 |
| optimizer | Adam |
| update frequency of the target network | 30 |
| 0.1 | |
| 0 | |
| 800 |
| Section | MAT | MA-DDPG | Ours |
|---|---|---|---|
| Section 1 | 0.27 | 0.33 | 0.27 |
| Section 2 | 0.45 | 0.29 | 0.25 |
| Section 3 | 0.71 | 0.36 | 0.30 |
| Section 4 | 0.50 | 0.57 | 0.21 |
| Section 5 | 0.22 | 0.34 | 0.24 |
| Section 6 | 0.26 | 0.34 | 0.24 |
| Section 7 | 0.26 | 0.34 | 0.24 |
| Section 8 | 0.26 | 0.29 | 0.24 |
| Section 9 | 0.38 | 0.51 | 0.03 |
| Section 10 | 0.66 | 0.48 | 0.04 |
| Section 11 | 0.09 | 0.24 | 0.26 |
| Section 12 | 0.14 | 0.42 | 0.23 |
| Agent | MA-DDPG | Ours |
|---|---|---|
| Agent 1 | 1176.2 | 1188.0 |
| Agent 2 | 1175.8 | 1188.0 |
| Agent 3 | 1130.2 | 1188.0 |
| Agent 4 | 1125.8 | 1188.0 |
| Agent 5 | 1165.8 | 1188.0 |
| Agent 6 | 1169.8 | 1188.0 |
| Agent 7 | 1167.8 | 1188.0 |
| Agent 8 | 1164.6 | 1188.0 |
| Agent 9 | 1167.4 | 1188.0 |
| MAT | MA-DDPG | Ours | |
|---|---|---|---|
| Average travel time (s) | 489 | 538 | 530 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kiyama, M.; Amagasaki, M.; Okamoto, T. Multi-Agent Reinforcement Learning-Based Control Method for Pedestrian Guidance Using the Mojiko Fireworks Festival Dataset. Electronics 2025, 14, 1062. https://doi.org/10.3390/electronics14061062
Kiyama M, Amagasaki M, Okamoto T. Multi-Agent Reinforcement Learning-Based Control Method for Pedestrian Guidance Using the Mojiko Fireworks Festival Dataset. Electronics. 2025; 14(6):1062. https://doi.org/10.3390/electronics14061062
Chicago/Turabian StyleKiyama, Masato, Motoki Amagasaki, and Toshiaki Okamoto. 2025. "Multi-Agent Reinforcement Learning-Based Control Method for Pedestrian Guidance Using the Mojiko Fireworks Festival Dataset" Electronics 14, no. 6: 1062. https://doi.org/10.3390/electronics14061062
APA StyleKiyama, M., Amagasaki, M., & Okamoto, T. (2025). Multi-Agent Reinforcement Learning-Based Control Method for Pedestrian Guidance Using the Mojiko Fireworks Festival Dataset. Electronics, 14(6), 1062. https://doi.org/10.3390/electronics14061062






