Optimized Watermelon Scion Leaf Segmentation Model Based on Hungarian Algorithm and Information Theory
Abstract
1. Introduction
2. Materials and Methods
2.1. Image Dataset
2.2. Experimental Setup and Environment
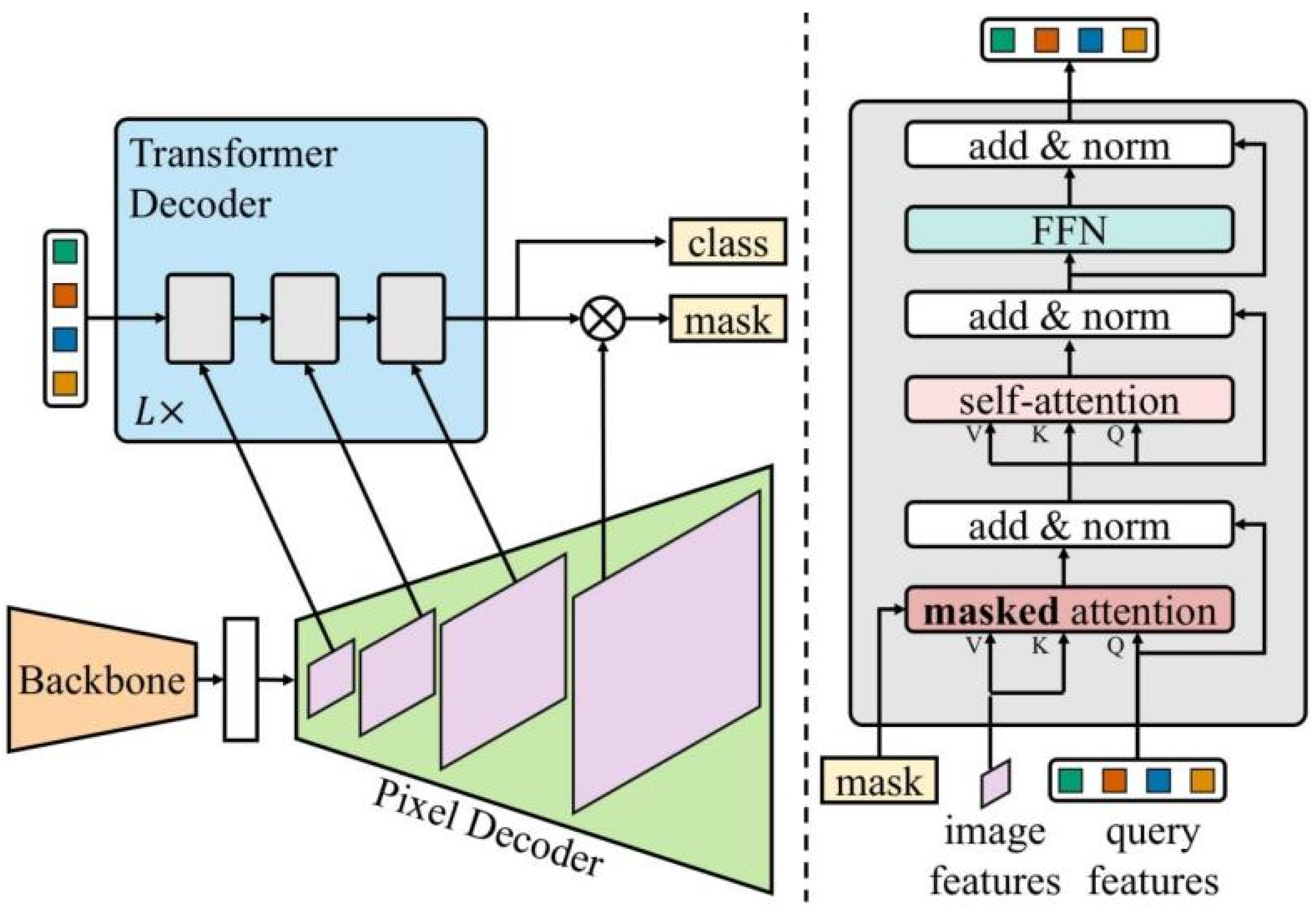
2.3. Mask2Former Model
2.4. Model Improvement
2.4.1. Optimal Feature Re-Ranking (OFR)
- Row-wise minimum subtraction: Subtract the minimum value of each row from all elements in that row. The formula for this is as follows:
- Column-wise minimum subtraction: Subtract the minimum value of each column from all elements in that column. The formula for this is as follows:
- Find and mark zero elements: Identify the zero elements and mark them. The formula for this is as follows:
- Cover zero elements: Draw the minimum number of lines to cover all zero elements in the matrix. If the number of covering lines L is less than N, adjust the matrix as follows:
- Compute the minimum value m among the uncovered elements. The calculation formula for this is as follows:
- Then, adjust the matrix using the following strategy:
2.4.2. Dynamic Information Modulation (DIM)
- Dimensional Consistency: The interpolated feature map has the same dimensions as , ensuring consistency in size and facilitating the subsequent information discrepancy calculation. This alignment simplifies the comparison of information between the two feature maps and enables seamless integration in the model’s processing pipeline.
- Information Retention and Detail Reconstruction: Compared to other interpolation methods, bilinear interpolation better preserves surrounding information during the upsampling process, minimizing information loss. For semantic segmentation, maintaining the smoothness of spatial information aids in more accurately segmenting edges and fine details. When upsampling feature maps, bilinear interpolation can reconstruct details without distortion, which is crucial for segmentation tasks, as they require precise delineation of object boundaries and subtle features.
3. Experiments and Results
3.1. Evaluation Metrics
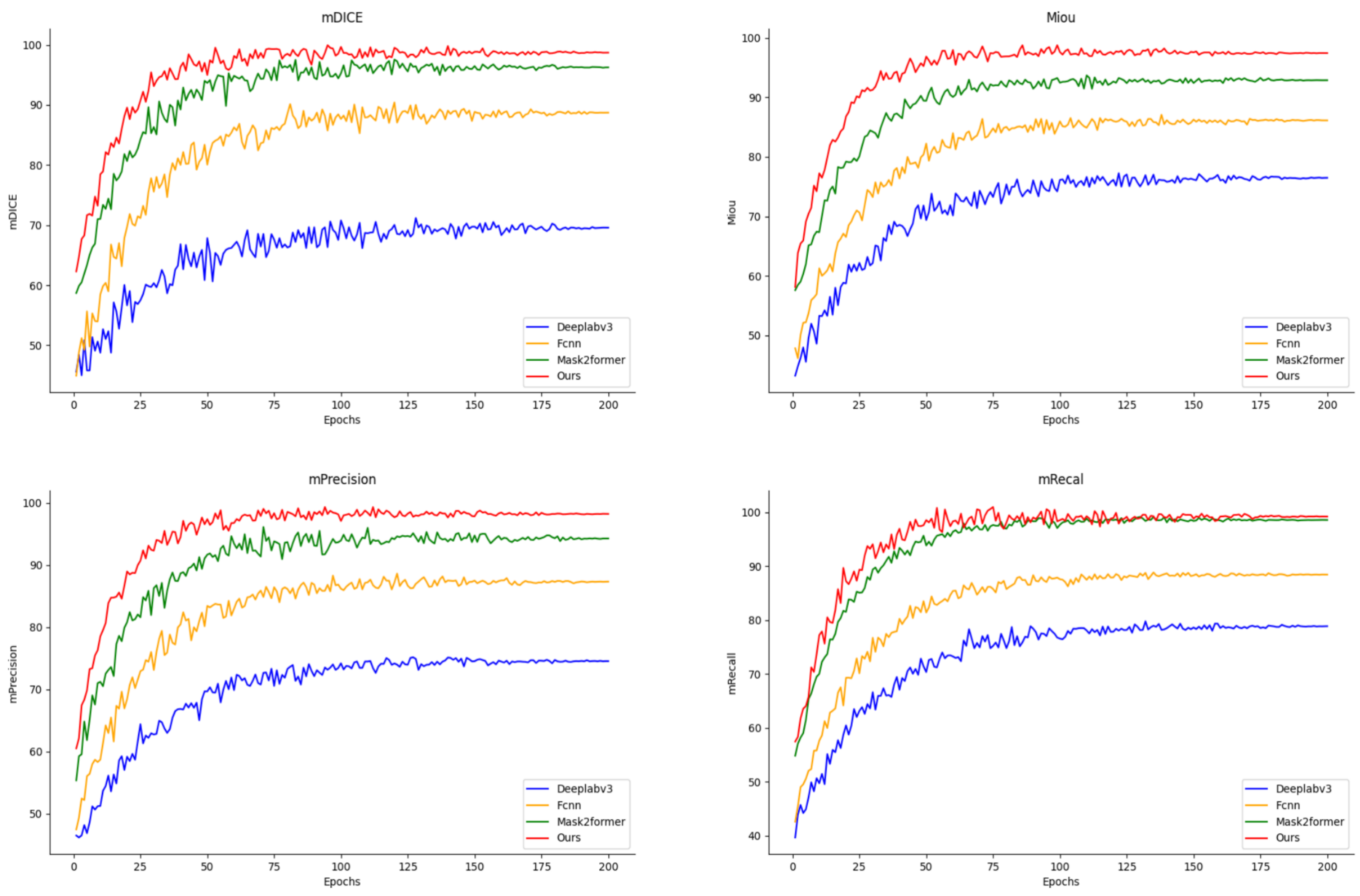
3.2. Ablation Experiments
3.3. Comparison Experiments
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huang, H.; Fu, D.G.; Li, W.X.; Rong, W.; Li, C.Y.; Feng, Z.Y.; Min, D.X. A Comparative Analysis of Rootstock, Seedling Age, and Anatomical and Physiological Studies for Watermelon Grafting. Preprints 2024, 2024120885. [Google Scholar] [CrossRef]
- Sahoo, B.; Lenka, S.; Meher, S.; Satpathy, B.; Munshi, R.; Mishra, N.; Sahoo, K. The art of grafting: Elevating vegetable production to new height. e-planet 2024, 22, 24–39. [Google Scholar]
- Yadav, S.K.; Singh, A. Vegetable Grafting: A New Approach to Increase Yield and Quality in Vegetables. Pharma Innov. J. 2023, 12, 407–411. [Google Scholar]
- Li, J. Effect of different types of rootstock grafting on watermelon fruit quality. Agric. Eng. 2024, 14, 50–54. [Google Scholar]
- Ilakiya, T.; Parameswari, E.; Davamani, V.; Yazhini, G.; Singh, S. Grafting Mechanism in Vegetable Crops. Res. J. Chem. Environ. Sci. 2021, 9, 1–9. [Google Scholar]
- Raza, M. Grafting in Vegetables: Transforming Crop Production with Cutting-Edge Techniques. Kashmir J. Sci. 2024, 3, 1–9. [Google Scholar]
- Liang, H.; Zhu, J.; Ge, M.; Wang, D.; Liu, K.; Zhou, M.; Sun, Y.; Zhang, Q.; Jiang, K.; Shi, X. A Comparative Analysis of the Grafting Efficiency of Watermelon with a Grafting Machine. Horticulturae 2023, 9, 600. [Google Scholar] [CrossRef]
- Abbasi, R.; Martinez, P.; Ahmad, R. The digitization of agricultural industry–a systematic literature review on agriculture 4.0. Smart Agric. Technol. 2022, 2, 100042. [Google Scholar] [CrossRef]
- Zhang, K.L.; Chu, J.; Zhang, T.Z.; Yin, Q.; Kong, Y.S.; Liu, Z. Development Status and Analysis of Automatic Grafting Technology for Vegetables. Nongye Jixie Xuebao/Transactions Chin. Soc. Agric. Mach. 2017, 48, 1–13. [Google Scholar]
- Yu, Q.; Zhang, J.; Xia, C. Design and Experiment of Automatic Grafting Device for Grafting Machine Based on Vision Driven. In Proceedings of the 2017 International Conference on Computer Technology, Electronics and Communication (ICCTEC), Dalian, China, 19–21 December 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1169–1172. [Google Scholar]
- Olivar-Jiménez, C.V.; Aguilar-Orduña, M.A.; Sira-Ramírez, H.J. Semi-automatic grafting machine prototype for tomato seedlings. In Proceedings of the 2023 20th International Conference on Electrical Engineering, Computing Science and Automatic Control (CCE), Mexico City, Mexico, 25–27 October 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–6. [Google Scholar]
- Yan, G.; Feng, M.; Lin, W.; Huang, Y.; Tong, R.; Cheng, Y. Review and prospect for vegetable grafting robot and relevant key technologies. Agriculture 2022, 12, 1578. [Google Scholar] [CrossRef]
- Valliammal, N.; Geethalakshmi, S. Plant leaf segmentation using non linear K means clustering. Int. J. Comput. Sci. Issues (IJCSI) 2012, 9, 212. [Google Scholar]
- Li, D.; Cao, Y.; Shi, G.; Cai, X.; Chen, Y.; Wang, S.; Yan, S. An overlapping-free leaf segmentation method for plant point clouds. IEEE Access 2019, 7, 129054–129070. [Google Scholar] [CrossRef]
- Xia, C.; Wang, L.; Chung, B.K.; Lee, J.M. In situ 3D segmentation of individual plant leaves using a RGB-D camera for agricultural automation. Sensors 2015, 15, 20463–20479. [Google Scholar] [CrossRef] [PubMed]
- Yang, K.; Zhong, W.; Li, F. Leaf segmentation and classification with a complicated background using deep learning. Agronomy 2020, 10, 1721. [Google Scholar] [CrossRef]
- Guo, R.; Qu, L.; Niu, D.; Li, Z.; Yue, J. LeafMask: Towards greater accuracy on leaf segmentation. In Proceedings of the CVF International Conference on Computer Vision Workshops (ICCVW), Virtual, 11–17 October 2021; pp. 1249–1258. [Google Scholar]
- Bhagat, S.; Kokare, M.; Haswani, V.; Hambarde, P.; Kamble, R. Eff-UNet++: A novel architecture for plant leaf segmentation and counting. Ecol. Inform. 2022, 68, 101583. [Google Scholar] [CrossRef]
- Vaswani, A. Attention is all you need. arXiv 2017, arXiv:1706.03762v7. [Google Scholar]
- Dosovitskiy, A. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Cheng, B.; Misra, I.; Schwing, A.G.; Kirillov, A.; Girdhar, R. Masked-attention mask transformer for universal image segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 1290–1299. [Google Scholar]
- Cheng, B.; Schwing, A.; Kirillov, A. Per-pixel classification is not all you need for semantic segmentation. Adv. Neural Inf. Process. Syst. 2021, 34, 17864–17875. [Google Scholar]
- Mills-Tettey, G.A.; Stentz, A.; Dias, M.B. The Dynamic Hungarian Algorithm for the Assignment Problem with Changing Costs; Technical Report CMU-RI-TR-07-27; Robotics Institute: Pittsburgh, PA, USA, 2007. [Google Scholar]
- Rényi, A. On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Contributions to the Theory of Statistics, 20 June–30 July 1960; University of California Press: Berkeley, CA, USA, 1961; Volume 4, pp. 547–562. [Google Scholar]
- Lin, J. Divergence measures based on the Shannon entropy. IEEE Trans. Inf. Theory 1991, 37, 145–151. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Garcia-Garcia, A.; Orts-Escolano, S.; Oprea, S.; Villena-Martinez, V.; Garcia-Rodriguez, J. A review on deep learning techniques applied to semantic segmentation. arXiv 2017, arXiv:1704.06857. [Google Scholar]
- Powers, D.M. Evaluation: From precision, recall and F-measure to ROC, informedness, markedness and correlation. arXiv 2020, arXiv:2010.16061. [Google Scholar]
- Bertels, J.; Eelbode, T.; Berman, M.; Vandermeulen, D.; Maes, F.; Bisschops, R.; Blaschko, M.B. Optimizing the dice score and jaccard index for medical image segmentation: Theory and practice. In Proceedings of the Medical Image Computing and Computer Assisted Intervention–MICCAI 2019: 22nd International Conference, Shenzhen, China, 13–17 October 2019; Proceedings, Part II 22. Springer: Berlin/Heidelberg, Germany, 2019; pp. 92–100. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Schroff, F.; Adam, H. Rethinking atrous convolution for semantic image segmentation. arXiv 2017, arXiv:1706.05587. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]





| Model | mIoU | mDICE | mPrecision | mRecall |
|---|---|---|---|---|
| Mask2Former | 92.88 | 96.25 | 94.25 | 98.58 |
| Mask2Former + OFR | 96.22 | 98.06 | 97.18 | 98.98 |
| Mask2Former + DIM | 96.22 | 98.06 | 97.18 | 98.98 |
| Enhanced-Mask2Former | 97.44 | 98.70 | 98.20 | 99.21 |
| Model | mIoU | mDICE | mPrecision | mRecall |
|---|---|---|---|---|
| Deeplabv3 | 76.52 | 69.61 | 74.55 | 78.93 |
| FCNN | 86.14 | 88.73 | 87.32 | 88.46 |
| Mask2Former | 92.88 | 96.25 | 94.25 | 98.58 |
| Enhanced-Mask2Former | 97.44 | 98.70 | 98.20 | 99.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Yu, Q.; Xu, Z. Optimized Watermelon Scion Leaf Segmentation Model Based on Hungarian Algorithm and Information Theory. Electronics 2025, 14, 620. https://doi.org/10.3390/electronics14030620
Zhu Y, Yu Q, Xu Z. Optimized Watermelon Scion Leaf Segmentation Model Based on Hungarian Algorithm and Information Theory. Electronics. 2025; 14(3):620. https://doi.org/10.3390/electronics14030620
Chicago/Turabian StyleZhu, Yi, Qingcang Yu, and Zihao Xu. 2025. "Optimized Watermelon Scion Leaf Segmentation Model Based on Hungarian Algorithm and Information Theory" Electronics 14, no. 3: 620. https://doi.org/10.3390/electronics14030620
APA StyleZhu, Y., Yu, Q., & Xu, Z. (2025). Optimized Watermelon Scion Leaf Segmentation Model Based on Hungarian Algorithm and Information Theory. Electronics, 14(3), 620. https://doi.org/10.3390/electronics14030620






