Multithreaded and GPU-Based Implementations of a Modified Particle Swarm Optimization Algorithm with Application to Solving Large-Scale Systems of Nonlinear Equations
Abstract
1. Introduction
2. Background and Related Work
2.1. Particle Swarm Optimization Algorithm
| Algorithm 1 Pseudocode for standard PSO |
|
2.2. PSO for Solving SNEs
| Algorithm 2 Pseudocode for PPSO |
|
2.3. Related Work
3. Algorithm Implementations
3.1. Sequential Algorithm
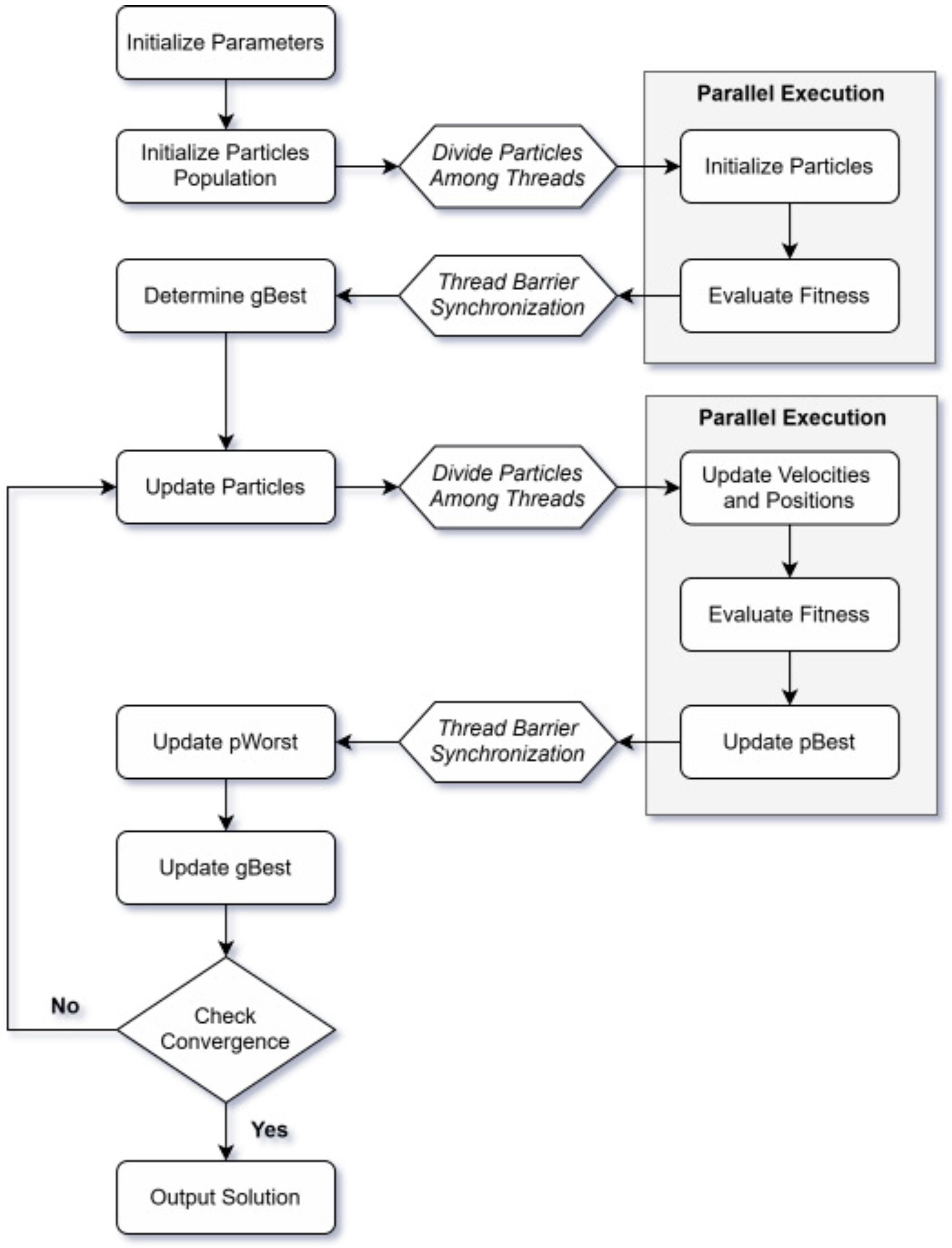
3.2. Multithreaded Design
| Algorithm 3 Pseudocode for multithreaded PPSO |
|
| Algorithm 4 Multithreaded particles initialization |
|
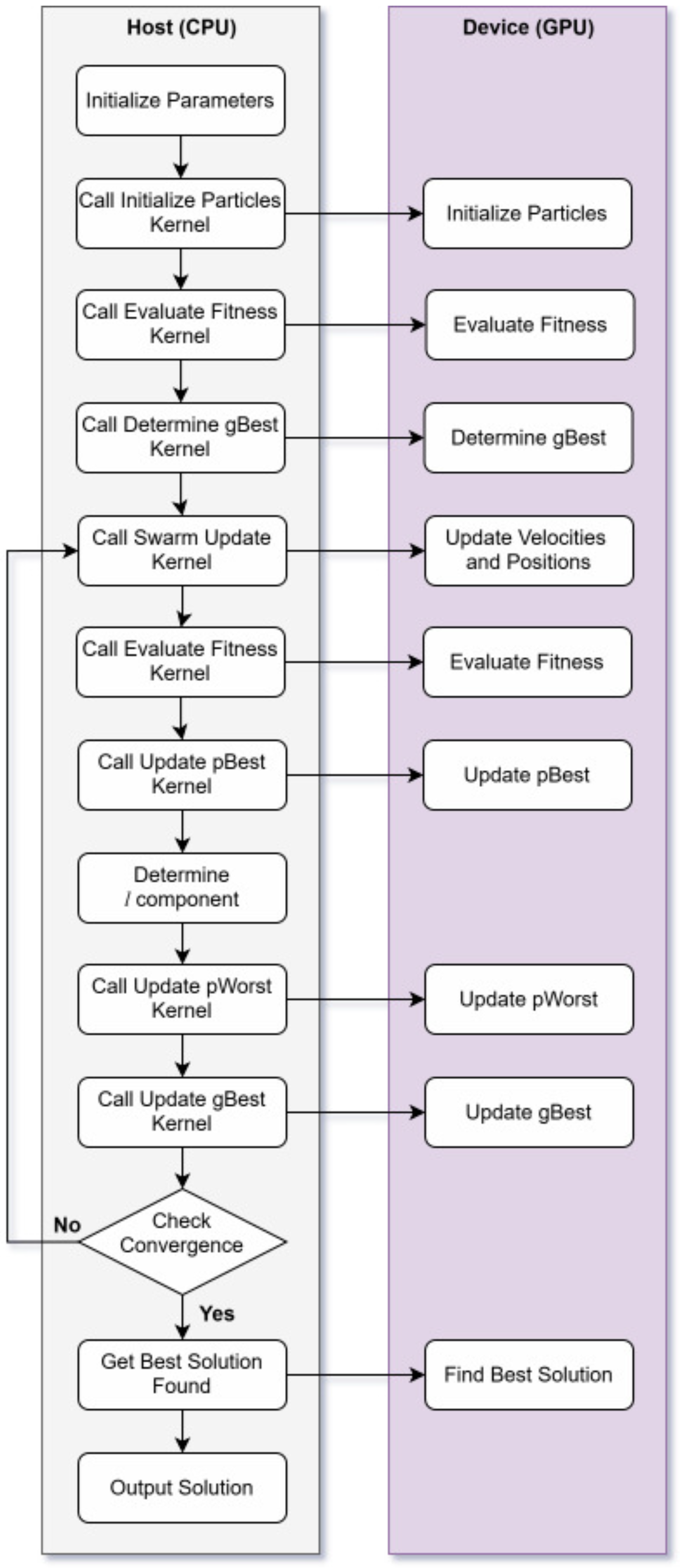
3.3. GPU Parallelization
3.3.1. CUDA Programming Fundamentals
3.3.2. GPU-Based PPSO
| Algorithm 5 Pseudocode for GPU-based PPSO |
|
| Algorithm 6 Kernel for particle initialization |
|
| Algorithm 7 Kernel for swarm updating |
|
| Algorithm 8 Kernel for updating |
|
| Algorithm 9 Kernel for determining |
|
| Algorithm 10 Kernel for updating |
|
4. Computational Experiments
4.1. Experimental Setup
4.2. Test Problems
5. Results and Discussion
5.1. Sequential Codebase Evaluation
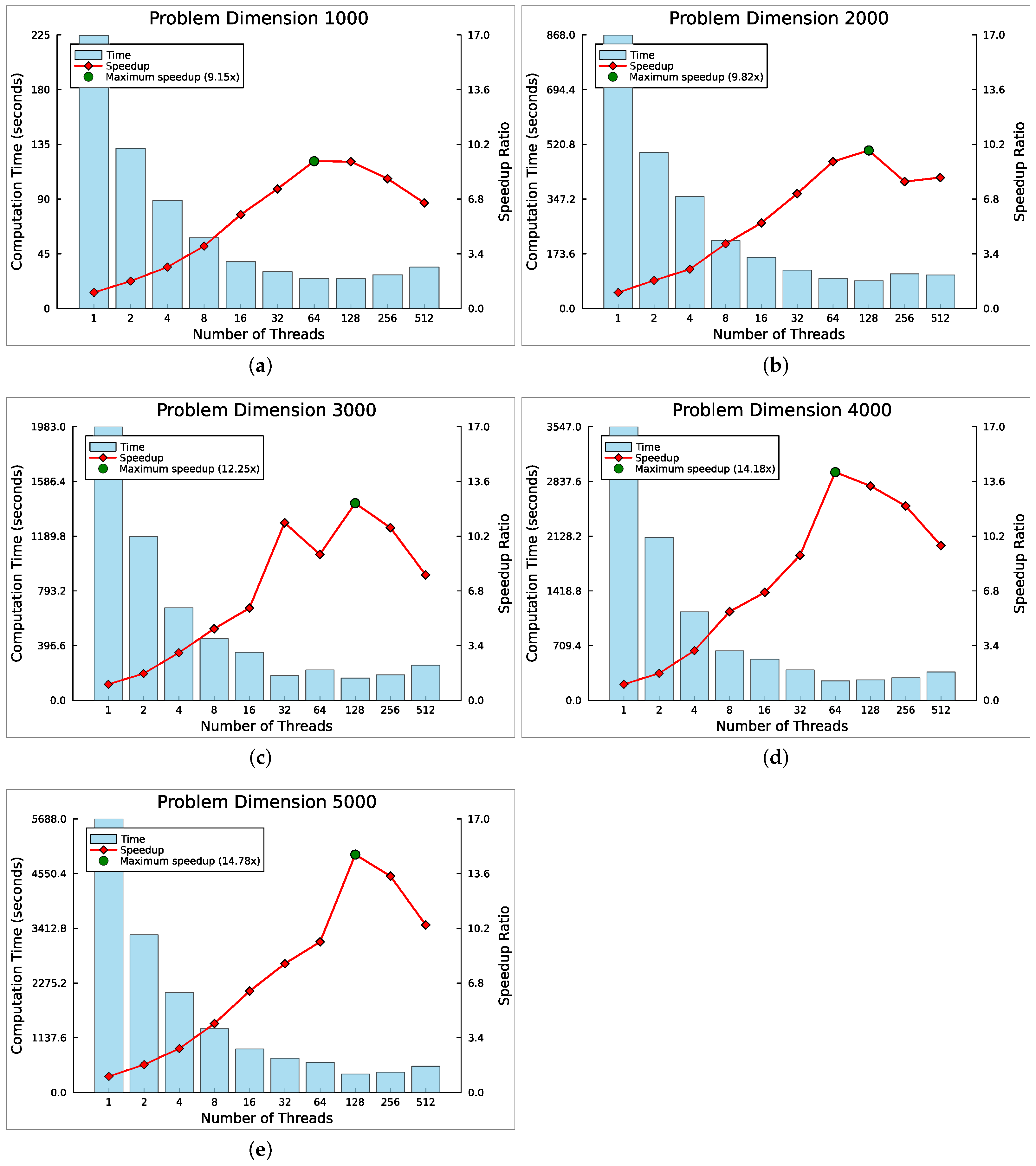
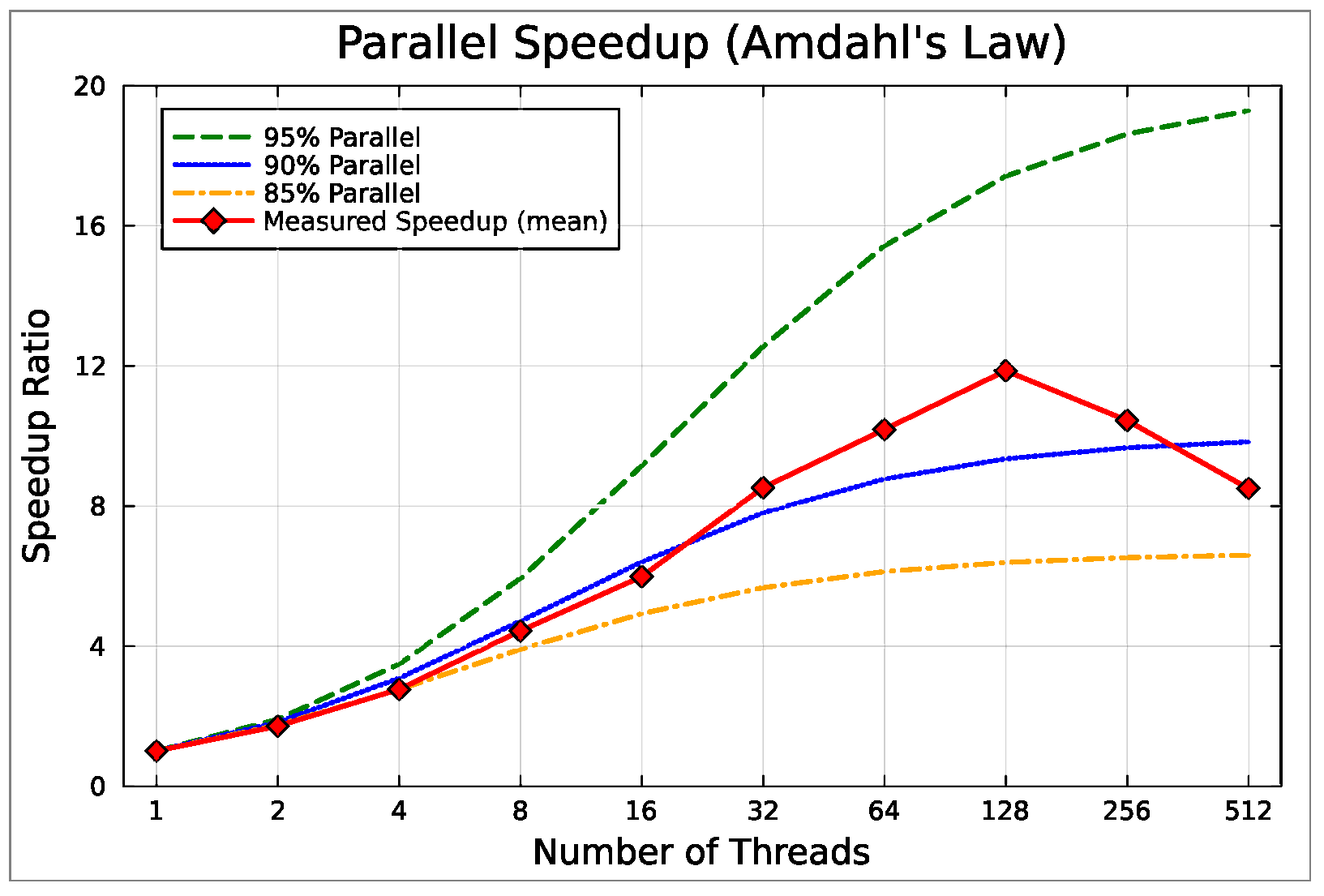
5.2. Multithreaded Speedup Analysis
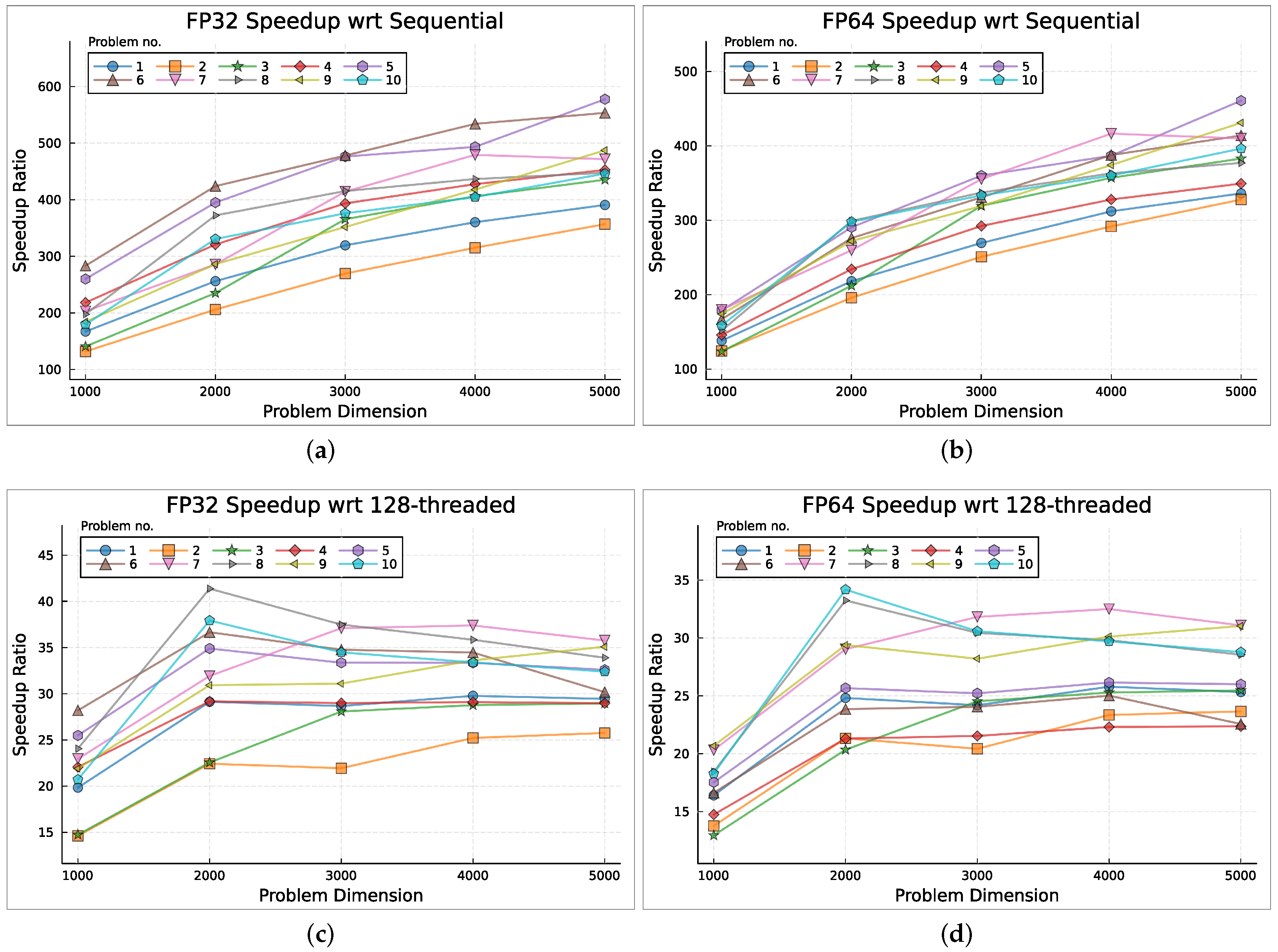
5.3. GPU Parallelization
5.4. Parallelization Impact on Solution Quality
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95–International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Zaini, F.A.; Sulaima, M.F.; Razak, I.A.W.A.; Zulkafli, N.I.; Mokhlis, H. A review on the applications of PSO-based algorithm in demand side management: Challenges and opportunities. IEEE Access 2023, 11, 53373–53400. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar] [CrossRef]
- Storn, R. Differential Evolution—A Simple and Efficient Adaptive Scheme for Global Optimization over Continuous Spaces; Technical Report 11; International Computer Science Institute: Berkeley, CA, USA, 1995. [Google Scholar]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Shami, T.M.; El-Saleh, A.A.; Alswaitti, M.; Al-Tashi, Q.; Summakieh, M.A.; Mirjalili, S. Particle swarm optimization: A comprehensive survey. IEEE Access 2022, 10, 10031–10061. [Google Scholar] [CrossRef]
- Jaberipour, M.; Khorram, E.; Karimi, B. Particle swarm algorithm for solving systems of nonlinear equations. Comput. Math. Appl. 2011, 62, 566–576. [Google Scholar] [CrossRef]
- Kotsireas, I.S.; Pardalos, P.M.; Semenov, A.; Trevena, W.T.; Vrahatis, M.N. Survey of methods for solving systems of nonlinear equations, Part I: Root-finding approaches. arXiv 2022. [Google Scholar] [CrossRef]
- Li, Y.; Wei, Y.; Chu, Y. Research on solving systems of nonlinear equations based on improved PSO. Math. Probl. Eng. 2015, 2015, 727218. [Google Scholar] [CrossRef]
- Choi, H.; Kim, S.D.; Shin, B.C. Choice of an initial guess for Newton’s method to solve nonlinear differential equations. Comput. Math. Appl. 2022, 117, 69–73. [Google Scholar] [CrossRef]
- Zhang, G.; Allaire, D.; Cagan, J. Taking the guess work out of the initial guess: A solution interval method for least-squares parameter estimation in nonlinear models. J. Comput. Inf. Sci. Eng. 2020, 21, 021011. [Google Scholar] [CrossRef]
- Dattner, I. A model-based initial guess for estimating parameters in systems of ordinary differential equations. Biometrics 2015, 71, 1176–1184. [Google Scholar] [CrossRef] [PubMed]
- Gong, W.; Liao, Z.; Mi, X.; Wang, L.; Guo, Y. Nonlinear equations solving with intelligent optimization algorithms: A survey. Complex Syst. Model. Simul. 2021, 1, 15–32. [Google Scholar] [CrossRef]
- Verma, P.; Parouha, R.P. Solving systems of nonlinear equations using an innovative hybrid algorithm. Iran. J. Sci. Technol. Trans. Electr. Eng. 2022, 46, 1005–1027. [Google Scholar] [CrossRef]
- Tawhid, M.A.; Ibrahim, A.M. An efficient hybrid swarm intelligence optimization algorithm for solving nonlinear systems and clustering problems. Soft Comput. 2023, 27, 8867–8895. [Google Scholar] [CrossRef]
- Ribeiro, S.; Silva, B.; Lopes, L.G. Solving systems of nonlinear equations using Jaya and Jaya-based algorithms: A computational comparison. In Algorithms for Intelligent Systems, Proceedings of the International Conference on Paradigms of Communication, Computing and Data Analytics (PCCDA 2023), New Delhi, India, 22–23 April 2023; Yadav, A., Nanda, S.J., Lim, M.H., Eds.; Springer: Singapore, 2023; pp. 119–136. [Google Scholar] [CrossRef]
- Silva, B.; Lopes, L.G.; Mendonça, F. Parallel GPU-acceleration of metaphorless optimization algorithms: Application for solving large-scale nonlinear equation systems. Appl. Sci. 2024, 14, 5349. [Google Scholar] [CrossRef]
- Tiwari, P.; Mishra, V.N.; Parouha, R.P. Modified differential evolution to solve systems of nonlinear equations. OPSEARCH 2024, 61, 1968–2001. [Google Scholar] [CrossRef]
- Lalwani, S.; Sharma, H.; Satapathy, S.C.; Deep, K.; Bansal, J.C. A survey on parallel particle swarm optimization algorithms. Arab. J. Sci. Eng. 2019, 44, 2899–2923. [Google Scholar] [CrossRef]
- Hussain, M.M.; Fujimoto, N. GPU-based parallel multi-objective particle swarm optimization for large swarms and high dimensional problems. Parallel Comput. 2020, 92, 102589. [Google Scholar] [CrossRef]
- Wang, C.C.; Ho, C.Y.; Tu, C.H.; Hung, S.H. cuPSO: GPU parallelization for particle swarm optimization algorithms. In Proceedings of the 37th ACM/SIGAPP Symposium on Applied Computing, Virtual, 25–29 April 2022; ACM: New York, NY, USA, 2022; pp. 1183–1189. [Google Scholar] [CrossRef]
- Wang, H.; Luo, X.; Wang, Y.; Sun, J. Identification of heat transfer coefficients in continuous casting by a GPU-based improved comprehensive learning particle swarm optimization algorithm. Int. J. Therm. Sci. 2023, 190, 108284. [Google Scholar] [CrossRef]
- Chraibi, A.; Ben Alla, S.; Touhafi, A.; Ezzati, A. Run time optimization using a novel implementation of Parallel-PSO for real-world applications. In Proceedings of the 2020 5th International Conference on Cloud Computing and Artificial Intelligence: Technologies and Applications (CloudTech), Marrakesh, Morocco, 24–26 November 2020; pp. 1–7. [Google Scholar] [CrossRef]
- Kumar, L.; Pandey, M.; Ahirwal, M.K. Implementation and testing of parallel PSO to attain speedup on general purpose computer systems. Multimed. Tools Appl. 2024, 83. [Google Scholar] [CrossRef]
- Liao, S.; Liu, B.; Cheng, C.; Li, Z.; Wu, X. Long-term generation scheduling of hydropower system using multi-core parallelization of particle swarm optimization. Water Resour. Manag. 2017, 31, 2791–2807. [Google Scholar] [CrossRef]
- Engelbrecht, A. Particle swarm optimization: Velocity initialization. In Proceedings of the 2012 IEEE Congress on Evolutionary Computation, Brisbane, QLD, Australia, 10–15 June 2012; pp. 1–8. [Google Scholar] [CrossRef]
- Bezanson, J.; Edelman, A.; Karpinski, S.; Shah, V.B. Julia: A fresh approach to numerical computing. SIAM Rev. 2017, 59, 65–98. [Google Scholar] [CrossRef]
- Gao, K.; Mei, G.; Piccialli, F.; Cuomo, S.; Tu, J.; Huo, Z. Julia language in machine learning: Algorithms, applications, and open issues. Comput. Sci. Rev. 2020, 37, 100254. [Google Scholar] [CrossRef]
- Besard, T.; Foket, C.; De Sutter, B. Effective extensible programming: Unleashing Julia on GPUs. IEEE Trans. Parallel Distrib. Syst. 2019, 30, 827–841. [Google Scholar] [CrossRef]
- Moré, J.J.; Garbow, B.S.; Hillstrom, K.E. Testing unconstrained optimization software. ACM Trans. Math. Softw. 1981, 7, 17–41. [Google Scholar] [CrossRef]
- Friedlander, A.; Gomes-Ruggiero, M.A.; Kozakevich, D.N.; Martínez, J.M.; Santos, S.A. Solving nonlinear systems of equations by means of quasi-Newton methods with a nonmonotone strategy. Optim. Methods Softw. 1997, 8, 25–51. [Google Scholar] [CrossRef]
- Bodon, E.; Del Popolo, A.; Lukšan, L.; Spedicato, E. Numerical Performance of ABS Codes for Systems of Nonlinear Equations; Technical Report DMSIA 01/2001; Universitá degli Studi di Bergamo: Bergamo, Italy, 2001. [Google Scholar]
- Ziani, M.; Guyomarc’h, F. An autoadaptative limited memory Broyden’s method to solve systems of nonlinear equations. Appl. Math. Comput. 2008, 205, 202–211. [Google Scholar] [CrossRef]
- Kelley, C.T.; Qi, L.; Tong, X.; Yin, H. Finding a stable solution of a system of nonlinear equations. J. Ind. Manag. Optim. 2011, 7, 497–521. [Google Scholar] [CrossRef]
- Amdahl, G.M. Validity of the single processor approach to achieving large scale computing capabilities. In Proceedings of the Spring Joint Computer Conference, New York, NY, USA, 18–20 April 1967; pp. 483–485. [Google Scholar] [CrossRef]

| Dim. | Codebase A | Codebase B | Codebase C | |||
|---|---|---|---|---|---|---|
| Time | Mem. Alloc. | Time | Mem. Alloc. | Time | Mem. Alloc. | |
| 1000 | 39.40 | 91.31 | 25.97 | 23.17 | 15.53 | 23.17 |
| 2000 | 190.71 | 362.25 | 131.21 | 91.93 | 60.42 | 91.93 |
| 3000 | 591.18 | 812.32 | 388.96 | 206.29 | 165.73 | 206.29 |
| 4000 | 1046.19 | 1442.42 | 646.16 | 366.24 | 282.66 | 366.24 |
| 5000 | 1860.78 | 2252.52 | 1123.96 | 571.80 | 451.98 | 571.80 |
| Dim. (Pop.) | Prob. No. | Sequential | 2 Threads | 4 Threads | 8 Threads | 16 Threads | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Time | Time | Speedup | Time | Speedup | Time | Speedup | Time | Speedup | ||
| 1000 (10,000) | 1 | 201.41 | 120.91 | 1.67 | 90.15 | 2.23 | 51.74 | 3.89 | 33.66 | 5.98 |
| 2 | 216.32 | 115.79 | 1.87 | 76.07 | 2.84 | 45.38 | 4.77 | 38.49 | 5.62 | |
| 3 | 234.27 | 140.83 | 1.66 | 89.69 | 2.61 | 56.81 | 4.12 | 40.35 | 5.81 | |
| 4 | 249.61 | 150.81 | 1.66 | 129.61 | 1.93 | 64.23 | 3.89 | 38.86 | 6.42 | |
| 5 | 261.86 | 159.72 | 1.64 | 92.97 | 2.82 | 64.18 | 4.08 | 40.66 | 6.44 | |
| 6 | 260.06 | 147.47 | 1.76 | 99.19 | 2.62 | 62.88 | 4.14 | 41.28 | 6.30 | |
| 7 | 212.39 | 117.39 | 1.81 | 76.26 | 2.79 | 60.18 | 3.53 | 41.37 | 5.13 | |
| 8 | 198.72 | 116.87 | 1.70 | 64.44 | 3.08 | 56.80 | 3.50 | 35.67 | 5.57 | |
| 9 | 201.59 | 120.13 | 1.68 | 80.06 | 2.52 | 57.38 | 3.51 | 41.26 | 4.89 | |
| 10 | 208.11 | 127.47 | 1.63 | 89.40 | 2.33 | 61.94 | 3.36 | 33.94 | 6.13 | |
| 2000 (20,000) | 1 | 767.34 | 460.99 | 1.66 | 320.42 | 2.39 | 202.56 | 3.79 | 147.12 | 5.22 |
| 2 | 790.30 | 457.53 | 1.73 | 373.53 | 2.12 | 230.84 | 3.42 | 144.54 | 5.47 | |
| 3 | 922.04 | 511.71 | 1.80 | 386.10 | 2.39 | 241.97 | 3.81 | 159.45 | 5.78 | |
| 4 | 984.43 | 543.32 | 1.81 | 374.24 | 2.63 | 226.54 | 4.35 | 175.02 | 5.62 | |
| 5 | 1029.65 | 558.05 | 1.85 | 417.97 | 2.46 | 209.94 | 4.90 | 179.61 | 5.73 | |
| 6 | 1032.13 | 535.42 | 1.93 | 381.07 | 2.71 | 247.36 | 4.17 | 178.52 | 5.78 | |
| 7 | 776.92 | 477.41 | 1.63 | 361.04 | 2.15 | 189.00 | 4.11 | 159.37 | 4.87 | |
| 8 | 784.83 | 460.56 | 1.70 | 297.90 | 2.63 | 199.57 | 3.93 | 155.47 | 5.05 | |
| 9 | 801.32 | 504.44 | 1.59 | 330.48 | 2.42 | 218.60 | 3.67 | 157.27 | 5.10 | |
| 10 | 785.91 | 445.81 | 1.76 | 312.49 | 2.52 | 192.38 | 4.09 | 172.37 | 4.56 | |
| 3000 (30,000) | 1 | 1748.95 | 1111.85 | 1.57 | 620.75 | 2.82 | 361.14 | 4.84 | 371.09 | 4.71 |
| 2 | 1814.80 | 1170.25 | 1.55 | 702.31 | 2.58 | 428.42 | 4.24 | 322.14 | 5.63 | |
| 3 | 2135.45 | 1253.57 | 1.70 | 766.84 | 2.78 | 491.18 | 4.35 | 305.04 | 7.00 | |
| 4 | 2296.83 | 1323.15 | 1.74 | 706.72 | 3.25 | 509.21 | 4.51 | 323.22 | 7.11 | |
| 5 | 2400.22 | 1328.41 | 1.81 | 629.89 | 3.81 | 470.68 | 5.10 | 399.22 | 6.01 | |
| 6 | 2286.73 | 1354.65 | 1.69 | 706.57 | 3.24 | 441.18 | 5.18 | 341.90 | 6.69 | |
| 7 | 1762.67 | 1068.86 | 1.65 | 655.59 | 2.69 | 392.28 | 4.49 | 352.98 | 4.99 | |
| 8 | 1786.70 | 1139.72 | 1.57 | 553.59 | 3.23 | 460.88 | 3.88 | 347.58 | 5.14 | |
| 9 | 1825.84 | 1091.53 | 1.67 | 723.73 | 2.52 | 484.34 | 3.77 | 348.35 | 5.24 | |
| 10 | 1771.69 | 1029.75 | 1.72 | 648.64 | 2.73 | 434.49 | 4.08 | 371.13 | 4.77 | |
| 4000 (40,000) | 1 | 3155.91 | 2138.04 | 1.48 | 1050.57 | 3.00 | 625.43 | 5.05 | 428.97 | 7.36 |
| 2 | 3271.58 | 2026.97 | 1.61 | 1100.51 | 2.97 | 631.93 | 5.18 | 511.64 | 6.39 | |
| 3 | 3730.62 | 2444.81 | 1.53 | 1206.68 | 3.09 | 646.50 | 5.77 | 618.50 | 6.03 | |
| 4 | 4046.10 | 2322.71 | 1.74 | 1239.92 | 3.26 | 683.88 | 5.92 | 593.46 | 6.82 | |
| 5 | 4081.88 | 2317.78 | 1.76 | 1248.15 | 3.27 | 715.32 | 5.71 | 483.43 | 8.44 | |
| 6 | 4246.33 | 2329.60 | 1.82 | 1399.72 | 3.03 | 648.33 | 6.55 | 546.88 | 7.76 | |
| 7 | 3349.56 | 1831.52 | 1.83 | 996.56 | 3.36 | 620.19 | 5.40 | 562.44 | 5.96 | |
| 8 | 3184.82 | 1856.79 | 1.72 | 1151.81 | 2.77 | 628.52 | 5.07 | 448.32 | 7.10 | |
| 9 | 3234.49 | 1932.52 | 1.67 | 1025.79 | 3.15 | 606.86 | 5.33 | 544.59 | 5.94 | |
| 10 | 3164.82 | 1918.81 | 1.65 | 1050.31 | 3.01 | 616.30 | 5.14 | 603.06 | 5.25 | |
| 5000 (50,000) | 1 | 5021.38 | 2844.10 | 1.77 | 1904.56 | 2.64 | 1325.81 | 3.79 | 949.56 | 5.29 |
| 2 | 5299.68 | 3060.97 | 1.73 | 2006.01 | 2.64 | 1312.41 | 4.04 | 823.62 | 6.43 | |
| 3 | 5863.39 | 3258.24 | 1.80 | 2197.87 | 2.67 | 1331.35 | 4.40 | 877.68 | 6.68 | |
| 4 | 6378.36 | 3632.83 | 1.76 | 2276.32 | 2.80 | 1307.49 | 4.88 | 970.52 | 6.57 | |
| 5 | 7109.06 | 3727.13 | 1.91 | 2206.63 | 3.22 | 1434.24 | 4.96 | 854.76 | 8.32 | |
| 6 | 6593.87 | 3920.42 | 1.68 | 2195.36 | 3.00 | 1278.81 | 5.16 | 906.08 | 7.28 | |
| 7 | 5055.14 | 3143.65 | 1.61 | 2070.81 | 2.44 | 1331.02 | 3.80 | 967.73 | 5.22 | |
| 8 | 4975.48 | 3074.87 | 1.62 | 1941.05 | 2.56 | 1316.31 | 3.78 | 915.10 | 5.44 | |
| 9 | 5334.54 | 3236.17 | 1.65 | 2023.51 | 2.64 | 1312.60 | 4.06 | 926.00 | 5.76 | |
| 10 | 5242.86 | 2899.70 | 1.81 | 1940.35 | 2.70 | 1325.12 | 3.96 | 869.98 | 6.03 | |
| Dim. (Pop.) | Prob. No. | 32 Threads | 64 Threads | 128 Threads | 256 Threads | 512 Threads | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Time | Speedup | Time | Speedup | Time | Speedup | Time | Speedup | Time | Speedup | ||
| 1000 (10,000) | 1 | 27.92 | 7.21 | 22.78 | 8.84 | 23.91 | 8.42 | 26.94 | 7.48 | 33.40 | 6.03 |
| 2 | 28.03 | 7.72 | 22.93 | 9.44 | 23.97 | 9.02 | 27.40 | 7.89 | 33.59 | 6.44 | |
| 3 | 30.25 | 7.74 | 27.78 | 8.43 | 24.53 | 9.55 | 27.92 | 8.39 | 34.95 | 6.70 | |
| 4 | 28.44 | 8.78 | 24.34 | 10.25 | 25.25 | 9.89 | 28.95 | 8.62 | 35.45 | 7.04 | |
| 5 | 29.43 | 8.90 | 25.94 | 10.09 | 25.68 | 10.20 | 29.35 | 8.92 | 35.78 | 7.32 | |
| 6 | 36.90 | 7.05 | 24.75 | 10.51 | 25.88 | 10.05 | 29.05 | 8.95 | 35.16 | 7.40 | |
| 7 | 31.79 | 6.68 | 26.96 | 7.88 | 24.01 | 8.85 | 27.02 | 7.86 | 33.03 | 6.43 | |
| 8 | 31.05 | 6.40 | 23.08 | 8.61 | 24.18 | 8.22 | 27.18 | 7.31 | 33.14 | 6.00 | |
| 9 | 28.53 | 7.07 | 22.56 | 8.94 | 23.97 | 8.41 | 26.80 | 7.52 | 33.75 | 5.97 | |
| 10 | 30.69 | 6.78 | 24.44 | 8.52 | 24.02 | 8.66 | 26.85 | 7.75 | 33.05 | 6.30 | |
| 2000 (20,000) | 1 | 129.92 | 5.91 | 93.91 | 8.17 | 87.30 | 8.79 | 115.24 | 6.66 | 103.14 | 7.44 |
| 2 | 118.60 | 6.66 | 102.17 | 7.74 | 86.04 | 9.19 | 113.60 | 6.96 | 101.68 | 7.77 | |
| 3 | 125.61 | 7.34 | 82.16 | 11.22 | 88.47 | 10.42 | 112.39 | 8.20 | 107.80 | 8.55 | |
| 4 | 120.85 | 8.15 | 109.58 | 8.98 | 89.55 | 10.99 | 107.42 | 9.16 | 111.42 | 8.84 | |
| 5 | 120.09 | 8.57 | 93.49 | 11.01 | 91.00 | 11.32 | 108.69 | 9.47 | 111.83 | 9.21 | |
| 6 | 136.40 | 7.57 | 97.54 | 10.58 | 89.24 | 11.57 | 107.76 | 9.58 | 111.47 | 9.26 | |
| 7 | 117.39 | 6.62 | 94.47 | 8.22 | 86.84 | 8.95 | 104.51 | 7.43 | 104.26 | 7.45 | |
| 8 | 104.04 | 7.54 | 87.01 | 9.02 | 87.24 | 9.00 | 109.28 | 7.18 | 101.79 | 7.71 | |
| 9 | 131.42 | 6.10 | 90.95 | 8.81 | 86.58 | 9.26 | 109.85 | 7.29 | 103.70 | 7.73 | |
| 10 | 114.04 | 6.89 | 104.57 | 7.52 | 90.16 | 8.72 | 113.84 | 6.90 | 106.12 | 7.41 | |
| 3000 (30,000) | 1 | 167.15 | 10.46 | 220.41 | 7.93 | 157.03 | 11.14 | 182.99 | 9.56 | 258.71 | 6.76 |
| 2 | 183.91 | 9.87 | 243.53 | 7.45 | 147.74 | 12.28 | 183.46 | 9.89 | 226.33 | 8.02 | |
| 3 | 169.17 | 12.62 | 240.12 | 8.89 | 164.02 | 13.02 | 186.65 | 11.44 | 253.86 | 8.41 | |
| 4 | 190.38 | 12.06 | 224.11 | 10.25 | 169.21 | 13.57 | 189.96 | 12.09 | 264.32 | 8.69 | |
| 5 | 183.40 | 13.09 | 208.84 | 11.49 | 168.15 | 14.27 | 188.92 | 12.70 | 257.03 | 9.34 | |
| 6 | 192.63 | 11.87 | 230.44 | 9.92 | 166.35 | 13.75 | 186.48 | 12.26 | 258.85 | 8.83 | |
| 7 | 173.75 | 10.14 | 220.78 | 7.98 | 157.87 | 11.17 | 181.32 | 9.72 | 250.56 | 7.03 | |
| 8 | 178.76 | 10.00 | 226.44 | 7.89 | 161.30 | 11.08 | 182.41 | 9.79 | 250.76 | 7.13 | |
| 9 | 187.34 | 9.75 | 159.95 | 11.41 | 161.41 | 11.31 | 181.39 | 10.07 | 265.72 | 6.87 | |
| 10 | 168.93 | 10.49 | 238.39 | 7.43 | 162.53 | 10.90 | 181.93 | 9.74 | 259.03 | 6.84 | |
| 4000 (40,000) | 1 | 381.39 | 8.27 | 242.53 | 13.01 | 260.82 | 12.10 | 290.97 | 10.85 | 366.04 | 8.62 |
| 2 | 378.23 | 8.65 | 238.70 | 13.71 | 261.82 | 12.50 | 289.19 | 11.31 | 358.13 | 9.14 | |
| 3 | 357.62 | 10.43 | 254.85 | 14.64 | 264.31 | 14.11 | 293.43 | 12.71 | 364.70 | 10.23 | |
| 4 | 409.03 | 9.89 | 244.19 | 16.57 | 275.37 | 14.69 | 302.41 | 13.38 | 381.04 | 10.62 | |
| 5 | 350.41 | 11.65 | 383.72 | 10.64 | 275.99 | 14.79 | 298.89 | 13.66 | 371.79 | 10.98 | |
| 6 | 462.64 | 9.18 | 250.30 | 16.96 | 274.12 | 15.49 | 300.29 | 14.14 | 367.62 | 11.55 | |
| 7 | 374.81 | 8.94 | 232.30 | 14.42 | 261.46 | 12.81 | 291.79 | 11.48 | 358.15 | 9.35 | |
| 8 | 414.10 | 7.69 | 223.61 | 14.24 | 261.54 | 12.18 | 289.36 | 11.01 | 373.34 | 8.53 | |
| 9 | 384.84 | 8.40 | 243.35 | 13.29 | 260.32 | 12.43 | 290.12 | 11.15 | 381.78 | 8.47 | |
| 10 | 449.09 | 7.05 | 221.43 | 14.29 | 261.20 | 12.12 | 286.27 | 11.06 | 364.99 | 8.67 | |
| 5000 (50,000) | 1 | 688.06 | 7.30 | 620.70 | 8.09 | 378.51 | 13.27 | 416.26 | 12.06 | 543.04 | 9.25 |
| 2 | 679.29 | 7.80 | 689.92 | 7.68 | 382.58 | 13.85 | 418.82 | 12.65 | 525.77 | 10.08 | |
| 3 | 687.51 | 8.53 | 706.20 | 8.30 | 390.09 | 15.03 | 423.05 | 13.86 | 554.37 | 10.58 | |
| 4 | 745.23 | 8.56 | 459.96 | 13.87 | 408.44 | 15.62 | 431.74 | 14.77 | 573.91 | 11.11 | |
| 5 | 802.39 | 8.86 | 711.26 | 10.00 | 401.30 | 17.71 | 435.18 | 16.34 | 561.62 | 12.66 | |
| 6 | 731.70 | 9.01 | 671.43 | 9.82 | 359.64 | 18.33 | 429.11 | 15.37 | 533.68 | 12.36 | |
| 7 | 594.42 | 8.50 | 672.33 | 7.52 | 383.46 | 13.18 | 415.23 | 12.17 | 545.24 | 9.27 | |
| 8 | 712.45 | 6.98 | 687.94 | 7.23 | 376.80 | 13.20 | 417.81 | 11.91 | 555.96 | 8.95 | |
| 9 | 664.33 | 8.03 | 402.47 | 13.25 | 384.21 | 13.88 | 421.06 | 12.67 | 522.12 | 10.22 | |
| 10 | 811.77 | 6.46 | 671.32 | 7.81 | 380.80 | 13.77 | 415.60 | 12.62 | 546.21 | 9.60 | |
| Dim. | 2 T | 4 T | 8 T | 16 T | 32 T | 64 T | 128 T | 256 T | 512 T | Mean |
|---|---|---|---|---|---|---|---|---|---|---|
| 1000 | 1.71 | 2.58 | 3.88 | 5.83 | 7.43 | 9.15 | 9.13 | 8.07 | 6.56 | 6.04 |
| 2000 | 1.75 | 2.44 | 4.02 | 5.32 | 7.13 | 9.13 | 9.82 | 7.88 | 8.14 | 6.18 |
| 3000 | 1.67 | 2.97 | 4.44 | 5.73 | 11.03 | 9.07 | 12.25 | 10.73 | 7.79 | 7.30 |
| 4000 | 1.68 | 3.09 | 5.51 | 6.71 | 9.02 | 14.18 | 13.32 | 12.07 | 9.62 | 8.35 |
| 5000 | 1.73 | 2.73 | 4.28 | 6.30 | 8.00 | 9.36 | 14.79 | 13.44 | 10.41 | 7.89 |
| Mean | 1.71 | 2.76 | 4.43 | 5.98 | 8.52 | 10.18 | 11.86 | 10.44 | 8.50 |
| Dim. (Pop.) | Prob. No. | Single Precision (FP32) | Double Precision (FP64) | ||||
|---|---|---|---|---|---|---|---|
| Time | Speedup (Seq.) | Speedup (128 T) | Time | Speedup (Seq.) | Speedup (128 T) | ||
| 1000 (10,000) | 1 | 1.21 | 167.12 | 19.84 | 1.46 | 138.20 | 16.41 |
| 2 | 1.64 | 131.88 | 14.62 | 1.74 | 124.25 | 13.77 | |
| 3 | 1.66 | 140.76 | 14.74 | 1.89 | 123.69 | 12.95 | |
| 4 | 1.14 | 218.23 | 22.07 | 1.71 | 145.82 | 14.75 | |
| 5 | 1.01 | 259.87 | 25.49 | 1.47 | 178.71 | 17.53 | |
| 6 | 0.92 | 283.33 | 28.20 | 1.56 | 166.96 | 16.62 | |
| 7 | 1.05 | 203.06 | 22.95 | 1.18 | 179.77 | 20.32 | |
| 8 | 1.00 | 197.74 | 24.06 | 1.31 | 151.62 | 18.45 | |
| 9 | 1.09 | 184.21 | 21.90 | 1.16 | 173.94 | 20.68 | |
| 10 | 1.16 | 179.53 | 20.72 | 1.31 | 158.45 | 18.29 | |
| 2000 (20,000) | 1 | 3.00 | 256.08 | 29.13 | 3.52 | 218.13 | 24.82 |
| 2 | 3.84 | 206.01 | 22.43 | 4.03 | 195.91 | 21.33 | |
| 3 | 3.92 | 235.11 | 22.56 | 4.35 | 212.13 | 20.35 | |
| 4 | 3.07 | 320.82 | 29.18 | 4.20 | 234.23 | 21.31 | |
| 5 | 2.61 | 394.92 | 34.90 | 3.54 | 290.52 | 25.67 | |
| 6 | 2.43 | 423.95 | 36.66 | 3.74 | 275.97 | 23.86 | |
| 7 | 2.72 | 285.67 | 31.93 | 2.99 | 259.66 | 29.03 | |
| 8 | 2.11 | 372.25 | 41.38 | 2.62 | 299.05 | 33.24 | |
| 9 | 2.80 | 286.23 | 30.93 | 2.95 | 271.99 | 29.39 | |
| 10 | 2.38 | 330.61 | 37.93 | 2.64 | 298.00 | 34.18 | |
| 3000 (30,000) | 1 | 5.48 | 319.39 | 28.68 | 6.49 | 269.47 | 24.19 |
| 2 | 6.73 | 269.50 | 21.94 | 7.23 | 250.92 | 20.43 | |
| 3 | 5.84 | 365.62 | 28.08 | 6.69 | 319.35 | 24.53 | |
| 4 | 5.84 | 393.45 | 28.99 | 7.86 | 292.37 | 21.54 | |
| 5 | 5.04 | 476.24 | 33.36 | 6.67 | 360.03 | 25.22 | |
| 6 | 4.78 | 477.99 | 34.77 | 6.91 | 330.76 | 24.06 | |
| 7 | 4.26 | 414.23 | 37.10 | 4.96 | 355.27 | 31.82 | |
| 8 | 4.30 | 415.28 | 37.49 | 5.30 | 337.17 | 30.44 | |
| 9 | 5.19 | 351.76 | 31.10 | 5.72 | 319.12 | 28.21 | |
| 10 | 4.71 | 375.97 | 34.49 | 5.31 | 333.39 | 30.58 | |
| 4000 (40,000) | 1 | 8.76 | 360.28 | 29.78 | 10.11 | 312.02 | 25.79 |
| 2 | 10.38 | 315.14 | 25.22 | 11.21 | 291.72 | 23.35 | |
| 3 | 9.19 | 406.13 | 28.77 | 10.45 | 357.02 | 25.29 | |
| 4 | 9.46 | 427.51 | 29.10 | 12.34 | 327.86 | 22.31 | |
| 5 | 8.27 | 493.30 | 33.35 | 10.56 | 386.72 | 26.15 | |
| 6 | 7.95 | 533.98 | 34.47 | 10.95 | 387.63 | 25.02 | |
| 7 | 6.99 | 479.16 | 37.40 | 8.04 | 416.37 | 32.50 | |
| 8 | 7.30 | 436.51 | 35.85 | 8.77 | 362.99 | 29.81 | |
| 9 | 7.74 | 417.75 | 33.62 | 8.64 | 374.19 | 30.12 | |
| 10 | 7.82 | 404.63 | 33.40 | 8.79 | 360.02 | 29.71 | |
| 5000 (50,000) | 1 | 12.85 | 390.67 | 29.45 | 14.94 | 336.03 | 25.33 |
| 2 | 14.85 | 356.81 | 25.76 | 16.17 | 327.77 | 23.66 | |
| 3 | 13.47 | 435.29 | 28.96 | 15.31 | 382.90 | 25.47 | |
| 4 | 14.09 | 452.57 | 28.98 | 18.26 | 349.28 | 22.37 | |
| 5 | 12.31 | 577.46 | 32.60 | 15.43 | 460.66 | 26.00 | |
| 6 | 11.92 | 553.32 | 30.18 | 15.93 | 413.86 | 22.57 | |
| 7 | 10.72 | 471.57 | 35.77 | 12.33 | 409.87 | 31.09 | |
| 8 | 11.12 | 447.59 | 33.90 | 13.20 | 377.03 | 28.55 | |
| 9 | 10.95 | 487.26 | 35.09 | 12.38 | 430.97 | 31.04 | |
| 10 | 11.75 | 446.12 | 32.40 | 13.23 | 396.30 | 28.78 | |
| Dim. | CPU | GPU | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2 T | 4 T | 8 T | 16 T | 32 T | 64 T | 128 T | 256 T | 512 T | FP64 | |
| 1000 | 1.16 | −0.21 | −0.21 | −0.09 | 0.30 | −3.41 | 2.63 | 4.69 | −0.18 | −1.03 |
| 2000 | 0.36 | 2.19 | 2.19 | 2.33 | −0.61 | 1.17 | 0.10 | −0.12 | −0.70 | 1.50 |
| 3000 | −0.51 | −0.09 | −0.09 | 0.57 | 0.73 | 2.13 | 1.24 | 1.12 | 1.46 | −1.94 |
| 4000 | 1.98 | 0.58 | 0.58 | 2.30 | 4.09 | 0.82 | 2.17 | 3.34 | 2.32 | 2.50 |
| 5000 | −0.11 | −0.12 | −0.12 | −0.29 | 1.51 | −0.97 | −1.62 | −0.13 | 2.14 | −0.63 |
| Mean | 0.58 | 0.47 | 0.47 | 0.96 | 1.21 | −0.05 | 0.90 | 1.78 | 1.01 | 0.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silva, B.; Lopes, L.G.; Mendonça, F. Multithreaded and GPU-Based Implementations of a Modified Particle Swarm Optimization Algorithm with Application to Solving Large-Scale Systems of Nonlinear Equations. Electronics 2025, 14, 584. https://doi.org/10.3390/electronics14030584
Silva B, Lopes LG, Mendonça F. Multithreaded and GPU-Based Implementations of a Modified Particle Swarm Optimization Algorithm with Application to Solving Large-Scale Systems of Nonlinear Equations. Electronics. 2025; 14(3):584. https://doi.org/10.3390/electronics14030584
Chicago/Turabian StyleSilva, Bruno, Luiz Guerreiro Lopes, and Fábio Mendonça. 2025. "Multithreaded and GPU-Based Implementations of a Modified Particle Swarm Optimization Algorithm with Application to Solving Large-Scale Systems of Nonlinear Equations" Electronics 14, no. 3: 584. https://doi.org/10.3390/electronics14030584
APA StyleSilva, B., Lopes, L. G., & Mendonça, F. (2025). Multithreaded and GPU-Based Implementations of a Modified Particle Swarm Optimization Algorithm with Application to Solving Large-Scale Systems of Nonlinear Equations. Electronics, 14(3), 584. https://doi.org/10.3390/electronics14030584








