Designing Spiking Neural Network-Based Reinforcement Learning for 3D Robotic Arm Applications

Abstract

This study investigates a novel approach to robotic arm control through integrating spiking neural networks with the twin delayed deep deterministic policy gradient reinforcement learning algorithm. Specifically, it presents the first application of spiking neural networks-based twin delayed deep deterministic policy gradient in 3D robotic manipulation, demonstrating its extension from traditional 2D tasks to complex 3D target-reaching scenarios with improved energy efficiency and stability. Additionally, with the inertial measurement unit data the system successfully mimics human arm movements, achieving a success rate of 0.95 among 50 trials and enabling an intuitive and accurate human–robot interaction system. This pioneering attempt highlights the feasibility of combining the biologically inspired spiking neural networks with the reinforcement learning algorithm to address the real-time challenges in high-dimensional robotic environments and advance the field of human–robot interaction systems.

1. Introduction

A robotic system consists of hardware and software components interacting with its environment to perform given tasks autonomously [1]. This system is utilized across various applications and increasingly adopts biologically inspired mechanisms to improve its efficiency and adaptability, aiming to implement human-like capabilities [2]. In particular, robotic arms that mimic human hand gestures and arm movements hold significant potential in various human–robot interface (HRI) fields, including assistive devices, rehabilitation therapy, and human–robot collaboration technologies [3,4]. To mimic human arm movements, camera-based systems are often utilized to generate smooth motion trajectories of human movement recorded through motion capture [5]. However, traditional camera-based systems face limitations in tasks requiring real-time control and flexibility due to environmental constraints such as lighting and obstacles [6]. In contrast, the inertial measurement unit (IMU) captures real-time orientation (roll, pitch, yaw) of a human arm, enabling intuitive and responsive control by providing robust and efficient data necessary for determining the movement speed and direction of robotic arms, regardless of environmental conditions. Furthermore, combining IMU data with EMG (electromyography) enables more precise control [7]. IMU measures the real-time orientation of the human arm to guide the robotic arm’s movement speed and direction, while EMG data are used to analyze hand gestures for controlling the robotic arm’s gripper.

Robotic arms can perform a variety of tasks, such as pick-and-place, assembly, and object alignment [8,9]. Accurate target reaching, which involves positioning the robotic arm’s end-effector precisely at a specific goal point, is essential for the successful execution of these tasks and serves as a critical operation for many applications [10]. Traditionally, inverse kinematics (IK) has been employed to compute joint movements based on the target position [11]. During this process, IMU provides initial conditions and orientation data required for IK calculations by measuring the real-time orientation of the human arm. IK demonstrates the strength in calculating joint movements to achieve a target end position of the robotic arm [12].

However, it has significant limitations in complex robotic systems. As the degrees of freedom (DoF) in robotic arms increase, the state and action spaces expand exponentially, making it difficult to identify the optimal joint configuration for achieving a specific target position [13]. This is a major drawback making it difficult for the traditional control method to respond in real time. Furthermore, the IK-based approach encounters difficulties in adapting to non-linear system dynamics and changes in complex working environments, limiting its ability to handle the dynamic environmental conditions and task scenarios [14,15]. Consequently, such constraints could significantly reduce the flexibility and scalability of the robotic systems.

To address these challenges, reinforcement learning (RL) has recently gained attention as an alternative to robotic arm control. RL could learn optimal control policies through the interaction with the environment and input data without explicit system models [16]. This enables the exploration of high-dimensional state and action spaces in systems with high DoF and provides adaptability to changes in the operating environment. RL overcomes the challenges of IK by leveraging its learning ability through interaction with the environment, eliminating the need for explicit mathematical models or iterative solvers. Traditional IK methods often struggle with issues such as computational inefficiency, sensitivity to singularities, and difficulties in generalizing to dynamic or high-dimensional scenarios [17]. RL, however, directly maps the relationship between an end-effector’s target pose and joint configurations through trial-and-error learning, guided by a reward mechanism. This allows RL to adaptively explore complex state-action spaces, find stable solutions even in singular configurations, and continuously refine its control policies based on the environmental feedback. Moreover, RL provides a framework for real-time, robust decision-making that could generalize across diverse tasks and workspaces, enabling efficient and accurate solutions for both position and orientation requirements in robotic systems [18,19,20,21,22,23]. These attributes make RL a promising approach for solving major challenges in robotic arm control, such as the complex motion planning, environmental adaptation, and real-time control [24]. Indeed, deep reinforcement learning (DRL), which applies deep neural networks (DNNs) to RL structure, has demonstrated remarkable results in high-dimensional problems, particularly in the fields like smooth motion planning and robotic navigation tasks using deep deterministic policy gradient (DDPG) [25,26,27].

However, the DNN-based RL models consume enormous computational resources during the learning and inference process due to the complex structure of DNNs [28]. This high computational cost is a major limitation for robots to use limited onboard resources, such as mobile robots powered by batteries or small embedded systems. High energy consumption shortens battery life, limiting the operating time. Additionally, the computational complexity of DRL hinders immediate responses to rapidly changing environments, reducing the reliability and stability of robotic arms, particularly in high-speed or unpredictable scenarios [29,30]. To overcome these limitations, spiking neural networks (SNNs), a biologically inspired third-generation neural network, have emerged as a promising alternative [31]. SNNs were designed based on the biological basis that humans perform information processing in the form of spikes, and could provide low energy consumption and fast calculation speed when combined with a neuromorphic hardware [32]. These properties could make SNNs a promising solution for energy-efficient AI applications in robotics, low-power IoT devices, and real-time control systems [33,34,35].

In particular, research has increasingly focused on the integration of SNNs with RL to improve energy efficiency, including the studies combining DDPG with SNNs for the robotic arm control, known as spiking DDPG (SDDPG) [36,37,38]. SDDPG has demonstrated its energy efficiency and performance of the robotic arm tasks such as reaching target positions, grasping objects, and transporting them by utilizing a camera-based system combining the structures of SNNs and DRL. However, the main drawbacks of DDPG include Q-value overestimation, reduced learning stability, unstable policy updates, and low exploration efficiency in continuous control environments. To address these shortcomings, twin delayed deep deterministic policy gradient (TD3) was proposed in DRL [39]. TD3 mitigates Q-value overestimation by employing two critic networks and improves the learning stability and performance with delaying policy updates. SNN architecture is also applied to TD3, and recent studies have validated its performance in OpenAI gym tasks [30,40].

To our best knowledge, this study represents the first attempt to mimic human arm movements using SNN-based RL, incorporating IMU data, and achieves the first implementation of 3D target-reaching tasks using SNN-based TD3 [41].

The contributions of this study are summarized as follows:

• The first attempt to mimic human arm movements using SNN-based RL.
• The first implementation of 3D target-reaching tasks using SNN-based TD3.

2. Related Work

In the study of robotic arms mimicking human arm movements, research has actively explored both IK methods and learning-based approaches utilizing neural networks, aiming to achieve natural and efficient control [3]. IK is a traditional method to control the robotic arms, enabling the computation of joint movements required for the arm to reach a target position [11]. Particularly, as the DoF of a robotic arm increase—allowing for more versatile movements—appropriate motion modelling becomes crucial [5], which helps the robot to be controlled efficiently while maintaining its natural posture. From this perspective, researchers have applied IK to optimize the criteria such as minimum jerk, energy efficiency, and collision avoidance, thereby generating smooth trajectories that resemble human movements [42,43,44,45]. However, IK-based approaches face several limitations in complex dynamic environments, leading to growing interest in learning-based methods as potential solutions [14,46]. Among these, approaches utilizing DNNs and DRL have gained significant attention for overcoming such challenges [15,24,47]. These methods often utilize human motion data obtained from motion capture systems or inertial measurement units (IMUs) to train models that could generate human-like movements [48]. In particular, reinforcement learning-based control has shown strengths in optimizing trajectories and learning human movement patterns through trial and error in simulation or real environments [49]. Such approaches enable more natural and efficient control in various applications, including humanoid robots, rehabilitation, and human–robot interaction (HRI). Consequently, their recent advancements have allowed robotic arms to autonomously learn and discover optimal motions in diverse environments.

With the development of these learning-based approaches, SNNs have recently received attention to solve the target-reaching problem of robotic arms [50,51,52,53]. While traditional IK-based methods have high computational complexity and modeling limitations, SNNs have the advantage of low energy consumption and excellent temporal information processing ability by imitating the operating principles of biological neural networks [46]. Therefore, SNNs could overcome the problems of the IK-based methods through a learning-based approach [54]. For example, SNNs dynamically learn the complex relationships between robotic joint movement and target position using biologically plausible learning rules like spike-timing-dependent plasticity (STDP) [50]. Zahra et al. [55] proposed a method inspired by the motor babbling process observed in human infants during early motor learning stages, focusing on simple target-reaching tasks in simulation without utilizing camera-based or IMU data. This approach generates the joint information in the stages of learning, enabling immediate control commands to be generated without pre-planning paths to target points [55]. Additionally, Polykretis et al. developed a model to mimic natural human movement trajectories by generating bell-shaped velocity profiles, allowing for smoother and more efficient motions, aiming to achieve target-reaching tasks within a simulation environment [56]. These approaches enable robots to operate effectively in environments involving human interaction or dynamic workspaces, generating movement trajectories that are more natural than those produced by traditional methods. Therefore, it enables robots to autonomously adapt and achieve goals in various environments and enables efficient and natural control beyond the traditional computational models based on mathematical methods.

The aforementioned DRL has been widely utilized as a robust learning-based approach for solving the target-reaching problem in robotic arms. However, it also faces limitations such as high computational costs and a lack of energy efficiency like the IK-based approach. To address these challenges, a hybrid approach combining SNNs and DRL, known as spiking DDPG (SDDPG), has been proposed [36,37,38]. By taking advantage of the energy efficiency, fast inference capability, and real-time learning potential of SNNs, which mimic the operation of the biological neurons, its combination with DRL effectively reduces computational costs and improves energy efficiency [57,58]. As a result, SDDPG enables autonomous and efficient learning in complex workspaces [36]. SDDPG adopts an actor–critic structure, where the actor network is implemented with SNNs and the critic network uses DNNs. The spiking actor network (SAN) is responsible for generating actions as a policy, while the deep critic network (DCN) evaluates the actions of the SAN using value functions or Q-values [37,38]. To address the non-differentiable nature of SNNs [59], SAN is trained using the surrogate gradient descent learning algorithm, achieving fast learning and high accuracy. During the testing stage, DCN is utilized to evaluate the actor network but is not employed during the testing stage. Consequently, after training, SAN could operate independently on neuromorphic hardware. This enables SAN to perform real-time control with limited onboard resources, effectively solving high-DoF robotic arms detecting objects using a camera-based system and reaching target points in diverse simulation environments. It has demonstrated superior reaching accuracy and trajectory optimization compared to the conventional DDPG models [38].

Although SDDPG successfully combines the advantages of DRL and SNNs to enable energy-efficient and stable robotic control in complex environments, it inherits limitations such as Q-value overestimation and policy instability from DDPG, which could impact the learning stability of SNN-based systems [60]. To overcome these issues, TD3 has been proposed, and when combined with SNNs, it shows potential to simultaneously stabilize Q-values and improve exploration efficiency [39].

This study represents the first attempt to mimic human arm movements through SNN-based reinforcement learning, incorporating IMU data. Furthermore, we implement 3D target-reaching tasks using SNN-based TD3 for the first time, demonstrating that the fusion of DRL and SNNs enables energy-efficient and stable control in complex environments. Following up on the achievements of previous research, this approach emphasizes the effectiveness of combining SNNs and DRL for high-dimensional problems such as robotic arm control.

3. Materials and Methods

We performed the target-reaching task using a 3-Dof robotic arm that independently implemented using the OpenAI gymnasium [61,62], SpyTorch [63] developed as an extension of the widely used PyTorch deep learning library framework and the Mujoco physics simulator [64]. As shown in Figure 1, Mujoco’s Reacher-v4 environment was customized by extending the joint structure, modifying the target position configuration, and adjusting the reward structure. The newly designed environment expands the task from 2D space to 3D, enabling reinforcement learning agents to perform the target-reaching task in more complex environments.

The robotic arm in the complex 3D space was successfully controlled by adopting the existing method that applies SAN in the actor–critic framework of the TD3 algorithm based on DRL, and the surrogate gradient approach was utilized to address the continuous control problems [41]. This approach is illustrated in Figure 2. The two-neuron encoder for the input environmental state values, introduced by Pérez-Carrasco et al. [65], was employed to encode the input values into binary neurons [41]. This method converts the negative input values into spike signals, expanding the n dimension of states to 2n. Each state value is mapped to two neurons: one activates when the state value is positive, while the other activates when it is negative. Consequently, for any given state value, the neuron representing the other state remains inactive, ensuring the independent firing between the two neurons. Therefore, this method has the advantage of providing a stable learning process for the SNNs without directly converting the input value to spikes, and its significant performance has been proven even in a complex reinforcement learning environment combining DRL and SNNs [41,65,66]. The encoded spikes are passed to the hidden layers of the SNNs, which consist of integrate-and-fire (IF) neurons [67]. These neurons process their input currents over time, updating the membrane potentials. When the membrane potential surpasses a threshold due to their accumulated currents, a spike signal is emitted to stimulate subsequent neurons. A membrane potential decoder [41] interprets the cumulative membrane potential of the output layer neurons over time, and the continuous robot arm control movements are generated based on this. To enhance the stability in continuous robot arm control, we adopted the approach proposed by Akl et al. [41], disabling the spiking mechanism in the output neurons by setting their firing threshold to infinity. This approach allows the membrane potentials to be accumulated without spike firing, and the final values, calculated as the weighted sum of incoming spikes with no decay, are directly utilized as continuous actions. Additionally, the decoded membrane potentials are scaled to fit within the joint torque limits of the robotic arm, ensuring compatibility with the physical system constraints.

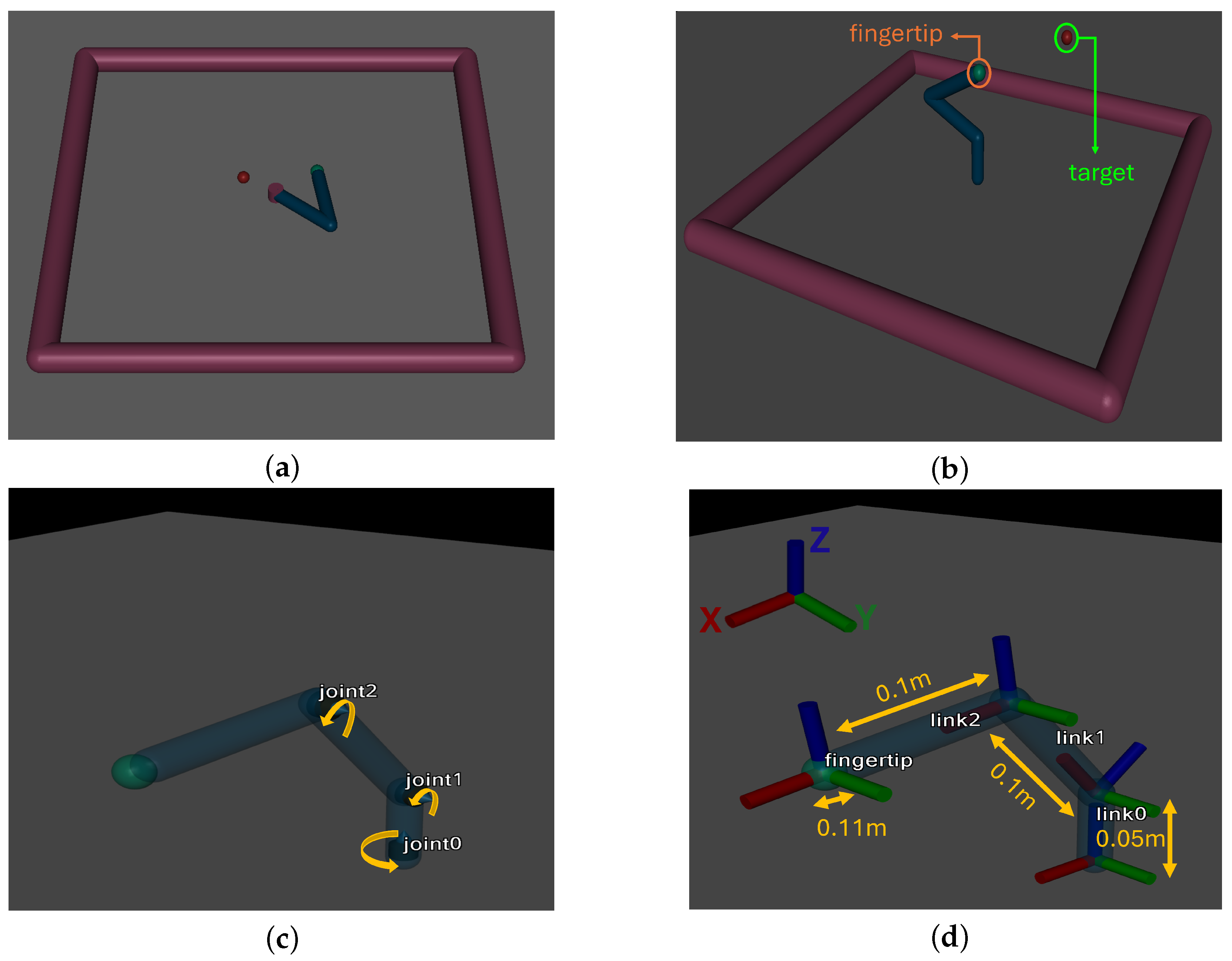
3.1. Robotic Arm Design

The robotic arm consists of three hinge joints, each performing rotational movements:

• Joint 1: Rotation in the Z-axis (vertical axis).
• Joint 2, 3: Rotation in the Y-axis (horizontal axis).

A robotic manipulator consisting of three links and a fingertip that serves as the end-effector. The total arm length is approximately 0.35 m, including:

• A vertical base link of 0.05 m.
• Two horizontal links of 0.1 m in length.
• A fingertip with a diameter of 0.11 m.

All joints are controlled with torques in the range between −1.0 and 1.0. The fingertip is equipped with a contact detection sensor designed to identify its interaction with target objects.

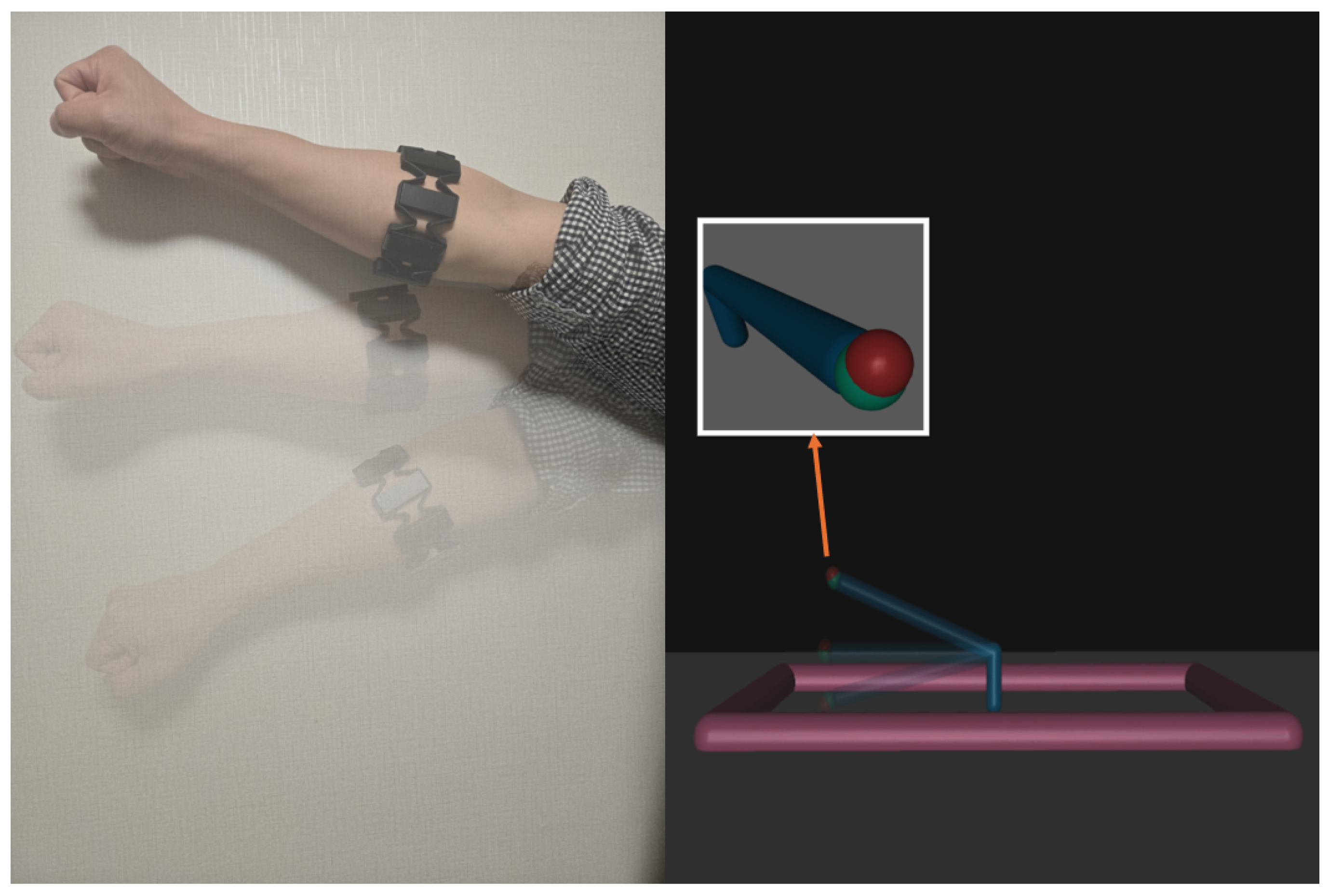
3.2. Simulation Environment

In this study, to overcome the limitation where the existing 2-DoF robot arm could only move in a plane, we designed it to operate in 3D space by expanding it to a 3-DoF robot arm. The target position is randomly generated using a spherical coordinate system in the workspace of the robot arm, and is set to be placed at a certain distance from the floor. In addition, the target location was limited to be created within the maximum reach of the robot arm to increase learning efficiency. The reward structure was designed corresponding to the distance from the goal, the feedback of collision, and the proximity to the goal, and the goal reaching, where the reward was applied with a weight considering the robot arm’s collision. Additionally, a collision handling logic was implemented to detect the collision between the ground and the robot’s links, as well as between the links themselves. Penalties were applied based on these collisions, improving the stability of the robot’s learning process. Figure 3 shows the details of the simulation environment. This customization contributed to improving the performance of the robotic arm and enabling learning in more complex 3D work environments. The simulation environment was customized based on Mujoco’s 2-DoF Reacher-v4 environment with the following modifications:

• DoF Expansion: The arm was redesigned for 3D movements adding an additional degree of freedom.
• Target Positioning: The target points are randomly generated within the workspace using spherical coordinates and are positioned to remain within the robot arm’s maximum reach.
• Reward System: Distance-based rewards are refined to vary based on the distance to the target, with additional weighted adjustments applied upon reaching the target depending on collision status and proximity.
• Collision Logic: Collisions between the ground and the robot arm’s links, as well as between the links themselves, are detected and penalized accordingly.

The simulation environment was set to gravity $-9.81{\mathrm{m}/\mathrm{s}}^2$ and a time interval of $0.01$ s, and the state values were as follows:

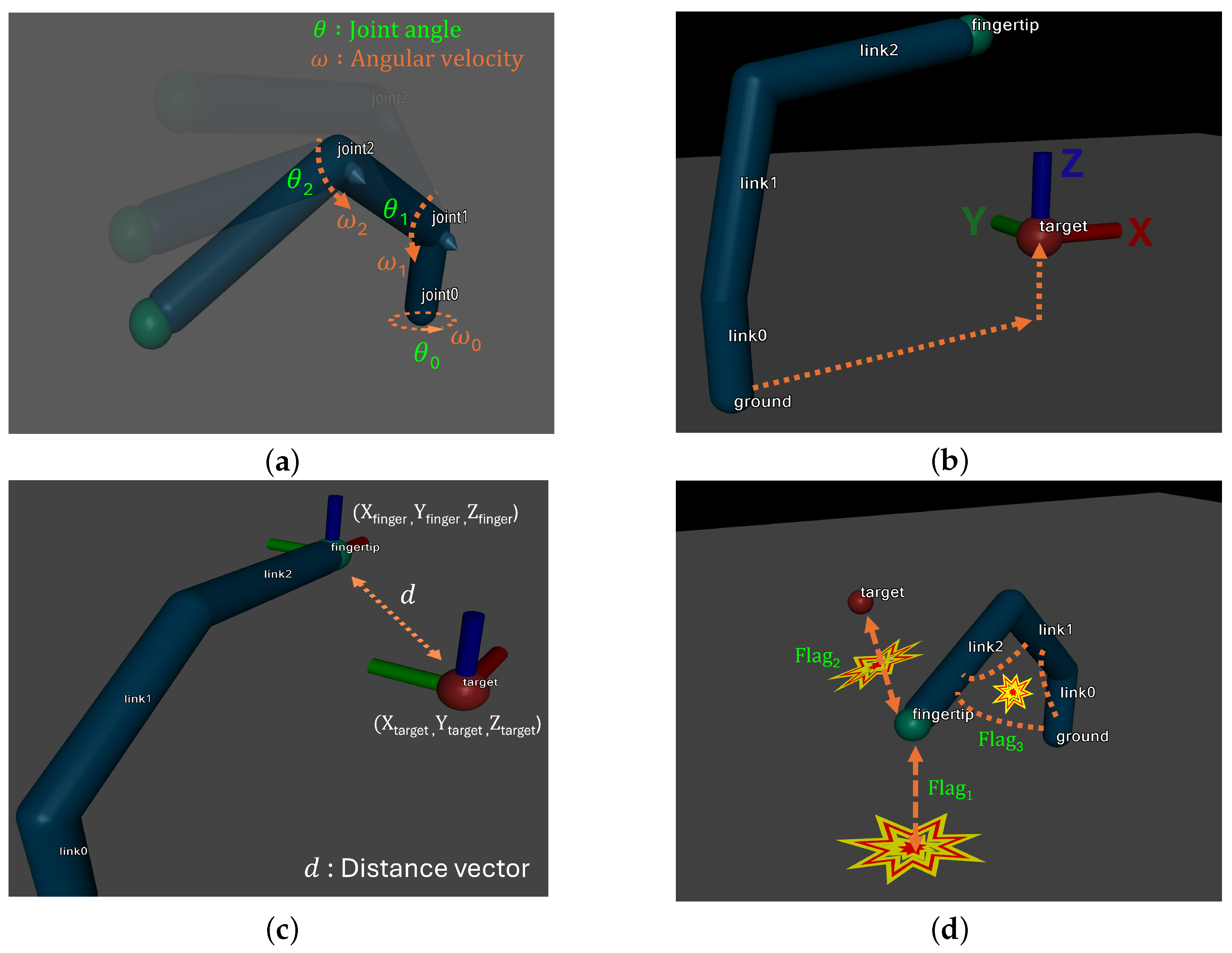
• Cosine and sine of joint angles.
• Joint angular velocities.
• Target’s x, y, and z coordinates.
• Distance vector between the fingertip and the target.
• Flag indicating collision with the ground.
• Flag indicating collision between links.
• Flag indicating whether the goal has been reached.

A three-dimensional decision vector is utilized to control the robotic arm, enabling adjustments to the angles of its three joints, ${\theta }_i$. The three-dimensional decision vector is defined as follows:

$$\mathrm{Action}=[{\alpha }_0,{\alpha }_1,{\alpha }_2]$$

where ${\theta }_i$ represents the angle of the i-th joint, where $i\in \{0,1,2\}$. By modifying these three joint angles, the end effector of the robotic arm can be positioned at the desired location.

3.3. Reward Function Design for Target Reaching

In reinforcement learning, the structure of the reward function is a key factor in determining policy performance [68]. The existing reacher environment’s reward function focuses only on distance and control penalties, neglecting factors like collision handling and stability after reaching the goal. Inspired by the integration of the collision penalties in reciprocal velocity obstacle-based rewards [69] and stage-based guidance in dense reward functions for robotic trajectory planning [70], we expanded the reward function of the existing reacher environment and designed a more sophisticated reward function to improve agent learning and performance. Unlike the original reward structure, which primarily focused on distance and control penalties, our design includes collision penalties and stage-based rewards determined by how close the fingertip is to the target.

The reward function used in the existing reacher environment consists of two components: distance rewards and control rewards. The distance reward is calculated as the negative value of the distance between the robot’s fingertip and the target, offering higher rewards as the fingertip approaches the target. The control reward penalizes the magnitude of movements to prevent excessive motion. However, the existing reward function has the following limitations:

• Ignoring collisions: The existing reward function does not account for collisions between the robot and other objects in the environment (e.g., the ground or its own links), which might undermine the robot’s stability in realistic scenarios.
• Lack of clarity in goal achievement: The reward function lacks clear criteria for determining whether the goal has been successfully reached, leading to potential instability in learning even after the goal is achieved.

To address these limitations and better reflect the real-world robot control scenarios, we designed a new reward function by incorporating the collision penalties and target-reaching rewards. The structure of the new reward function is detailed below:

• Collision Reward: To detect and address collisions, the system identifies collision states within the environment and applies penalties or rewards accordingly. Penalties are imposed when the robot collides with the ground or when self-collisions occur between links, thereby reinforcing the stability of the robot’s movements.
• Target-reaching Reward: Rewards are assigned proportionally based on the distance to the target, with higher rewards provided for closer proximity. After reaching the target, additional rewards or penalties are applied depending on the presence or absence of collisions, ensuring the robot maintains a stable state after achieving the goal.

4. Experimental Results

In this section, we present the results of the experiments evaluating the performance of the robot arm’s target-reaching task using the SNN-based TD3 model. The experiment analyzed the variations in the averaged reward received by the agent during a total of 40,000 learning episodes, and evaluated the success rate of reaching the target point provided through the IMU in the simulation. The model was trained based on randomly generated target points in the simulation environment. Figure 4 illustrates examples of the agent’s success and failure trials for the target-reaching tasks. In this experiment, the changes in rewards during the training process and the success rate of the target-reaching tasks are mainly investigated.

4.1. Experimental Settings

In the previous session, we described the Mujoco 3-DoF robotic arm environment designed for target-reaching tasks. The input state values consist of 18 elements: 6 values representing the cosine and sine of the 3 joints, 3 joint angular velocities, 3 target coordinates, a distance vector between the fingertip and the target coordinates, 2 flags indicating collisions with the ground and between links, and 1 flag indicating whether the target has been reached. Through a two-neuron encoder, the model’s input values are expanded to 36. However, since the DCN evaluates the value of specific states and actions, the three action values corresponding to the joints are added, resulting in a total of 39 inputs. Our networks consist of two hidden layers, where 256 IF neurons are implemented. The SAN is a policy network determining the agent’s actions and has three outputs, while the DCN learns the Q-values and has one output. The neuron’s threshold for SAN is set to 1. Other parameters (e.g., memory buffer size, target update interval, discount factor, noise, etc.) are identical to those used by Akl et al. [41].

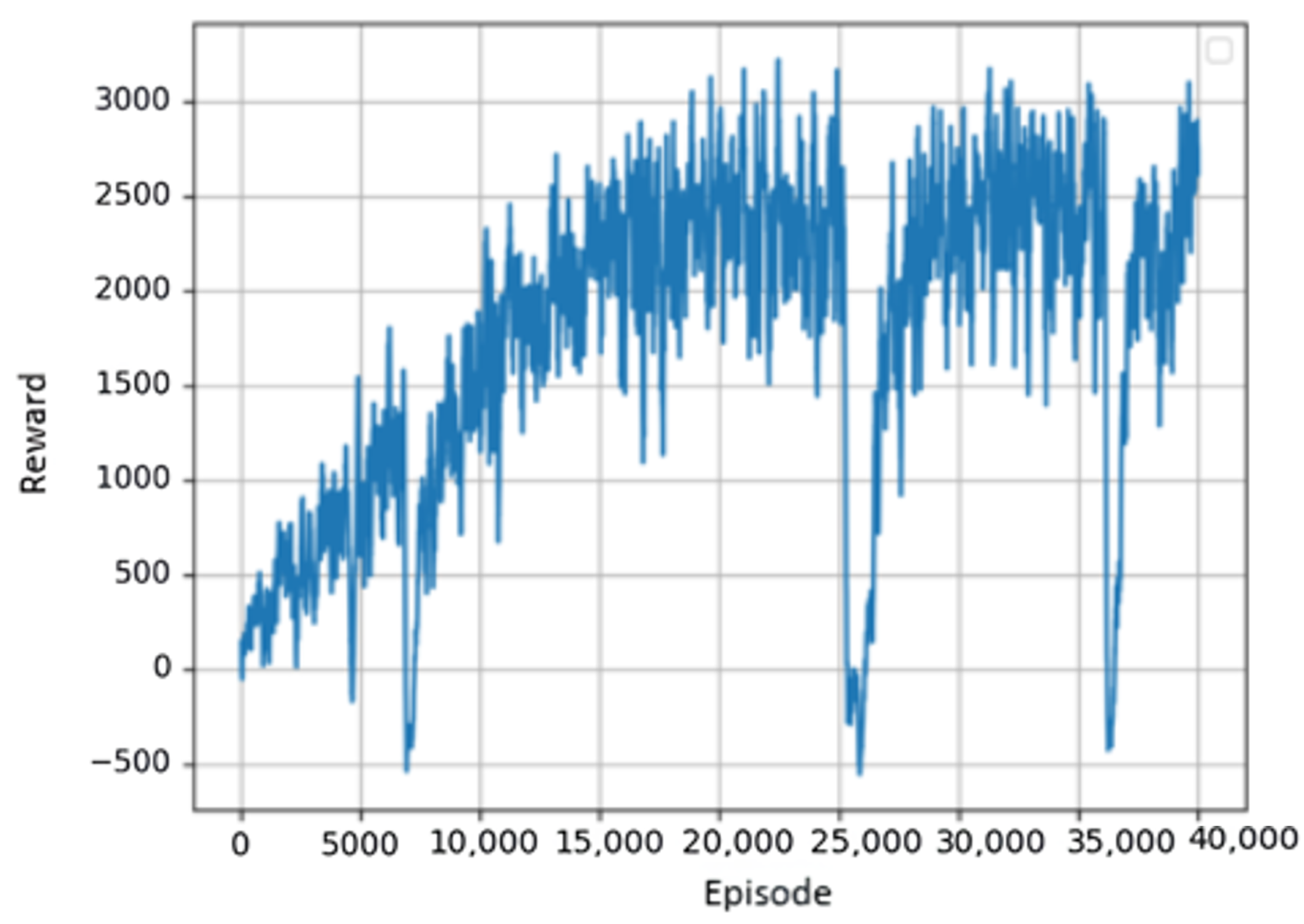
4.2. Training and Testing Results for the Target-Reaching Task

Figure 5 shows the results of the SNN-based TD3 model trained in a customized environment, with each episode set to a maximum of 500 steps. In the early episodes, the averaged rewards exhibited low values and significant fluctuation. However, as the training process progressed, the averaged reward gradually increased. In the later episodes of the training, the rewards were stabilized within a range between 2500 and 3000, indicating the model’s high success rate in performing the target-reaching tasks. However, a sharp decrease in reward was observed around 25,000th and 30,000th episodes, which could be interpreted as a case where the model is not sufficiently generalized to a specific situation. This phenomenon aligns with the well-known issue of catastrophic forgetting in reinforcement learning [71], where the model might forget the previously learned policies while adapting to new data, such as the random target positions. Despite these challenges, the agent’s performance improved consistently, with the rewards gradually rising and stabilizing after 37,000 episodes. The trained model demonstrated excellent policy optimization, accurately handling various target positions in the simulation environment and achieving outstanding performance in the target-reaching task.

To test the arm movement target-reaching task, IMU data were recorded using the Myo armband developed by Thalmic Labs [72]. The user’s arm movements and posture were tracked in real time through the gyroscope and accelerometer obtained using the IMU sensor in the armband, and converted into the target points in the Mujoco’s Reacher-v4 environment. Although the gyroscope produces accurate posture information, there is a problem in that errors are accumulated and diverge over time [73]. On the other hand, the posture obtained with an accelerometer has the advantage that the error does not increase over time and is limited to a certain range [74]. Since the data from these two sensors are complementary, they were integrated. Additionally, the Kalman filter was applied to reduce noise and improve the accuracy of the estimated posture [75]. This minimized the error and uncertainty of the IMU data, enabling the user’s arm movements to be accurately mapped to the target points in the virtual environment.

As shown in Figure 6, the robotic arm, controlled through the trained SAN agent, followed the target points and effectively mimicked the arm movement target-reaching task. In the experiment, the target-reaching tasks were defined when the distance between the target point and the fingertip of the robot arm was less than 5 mm, and the success rate was calculated based on this. As a result, the target tasks were successfully reached with a success rate of 0.95 among 50 trials, as shown in

Table 1. The performances of the target-reaching tasks.

	Success Rate	Execution Time (ms)
Training Performance	$0.95\pm 0.043$	$0.224\pm 0.062$
Testing Performance	$0.95\pm 0.037$	$0.231\pm 0.054$

, which also summarizes the execution time and performance metrics for both training and testing. SAN showed high adaptability to the target point in the robot arm control and enabled precise control that followed the user’s movements in real time. This approach utilizes the advantages of reinforcement learning to provide high accuracy and stability even in complex environments, and enables an intuitive and efficient interface between users and robots.

5. Discussion

The implementation of the SNN-based TD3 for the 3D target-reaching tasks demonstrates significant advancements in robotic arm control. The experimental results show stable performance in controlling the 3-DoF robotic arm through the extension of Mujoco’s Reacher-v4 environment to handle the 3D movements and incorporating an SNN-based TD3 algorithm. The spiking actor network learned accurate and stable control policies over 40,000 training episodes, achieving a 95% success rate in target-reaching trials with a precision threshold less than 5 mm.

The integration of the IMU data for the arm movement target-reaching task fundamental limitations of camera-based systems. The IMU-based approach provides robust performance regardless of environmental conditions such as lighting or obstacles, enabling real-time control capabilities. Additionally, the successful implementation of TD3 with SNNs for the 3D target-reaching effectively solves the limitations of the previous SDDPG implementations, particularly in handling the Q-value overestimation problem.

The SNN-based approach demonstrates promising potential for future robotic applications based on the simulation results. Previous studies have shown that SNNs, when implemented on neuromorphic hardware, could achieve significant power consumption benefits compared to the traditional neural networks [32,33]. While our simulation demonstrates the effectiveness of combining SNNs with TD3 for the robotic control, the actual energy efficiency benefits would need to be validated through hardware implementation. The integration of the IMU data enables direct human–robot interfaces, suggesting potential applications in the prosthesis technologies and industrial automation once validated on physical systems.

Despite these outstanding performances, several limitations require attention. Training and evaluation of the proposed SNN algorithm were performed in the simulation environment, necessitating the validation under real-world conditions that include unmodeled friction, mechanical tolerances, and sensor noise. The reward function primarily incentivized the target-reaching and collision avoidance without addressing more complex tasks such as path planning around obstacles. The reliance on the IMU signals for the target position inference, while allowing the real-time interaction, might reduce the accuracy during abrupt arm motions or sensor drift without more advanced filtering or calibration strategies. Performances of the computational and energy efficiency require validation on actual neuromorphic hardware to confirm the hardware-level advantages of the SNN-based methods.

The application of the spiking actor networks within the TD3 framework effectively solves the higher-dimensional robotic arm tasks, expanding the possibilities of real-time and low-power motion control. The incorporation of the IMU data as a direct means of teleoperation advances the human–robot interaction capabilities. These findings suggest that an SNN-based TD3 control scheme could serve as the foundation for future applications requiring human-like fluidity, robustness, and low-latency control. Further investigations into domain adaptation, transfer learning from simulation to hardware, and more complex multi-step tasks would extend the potential of this method. The deployment of SNN-based reinforcement learning on the neuromorphic devices for real-world robotic arms would enable the energy-efficient, adaptive, and safer robots for human assistance in daily activities and specialized tasks such as rehabilitation and telepresence.

6. Conclusions

This study demonstrated the successful implementation of the SNN-based TD3 for the 3D target-reaching tasks mimicking human arm movements. The integration of SNNs with TD3 reinforcement learning achieved stable performance in controlling a 3-DoF robotic arm, with a 95% success rate in target-reaching trials. The system effectively combined the neuromorphic computing principles with an advanced reinforcement learning algorithm to achieve precise and efficient robot control. The integration of the IMU data provided robust performance regardless of the environmental conditions, overcoming the limitations of the conventional camera-based systems.