Automated Scattering Media Estimation in Peplography Using SVD and DCT
Abstract
1. Introduction
2. Automating the Process of Estimating Scattering Media Information
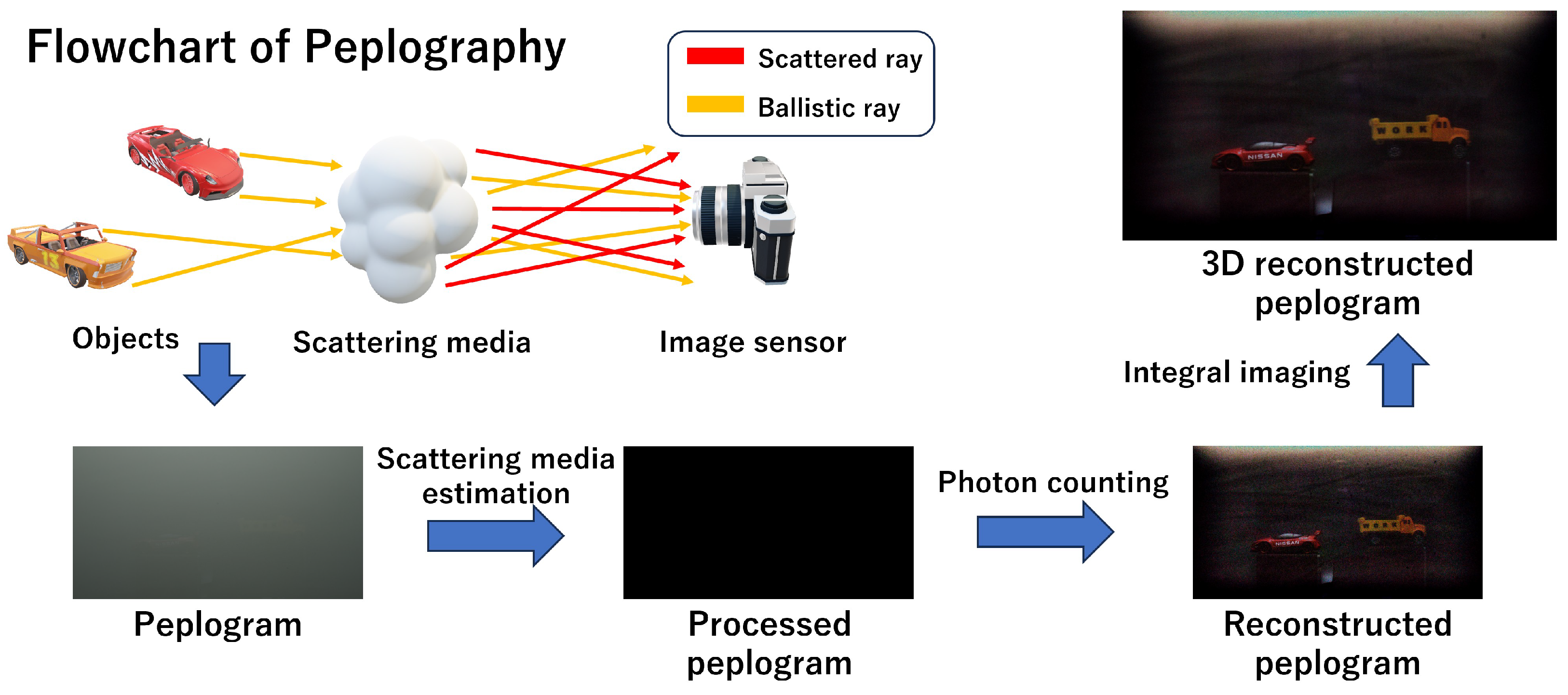
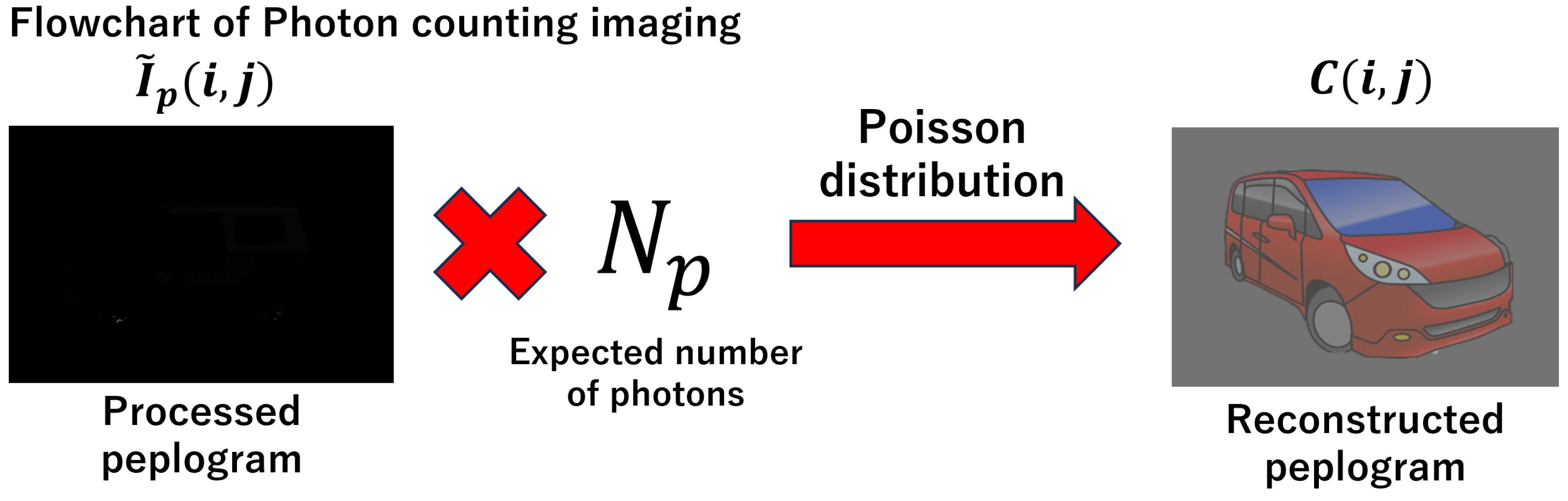
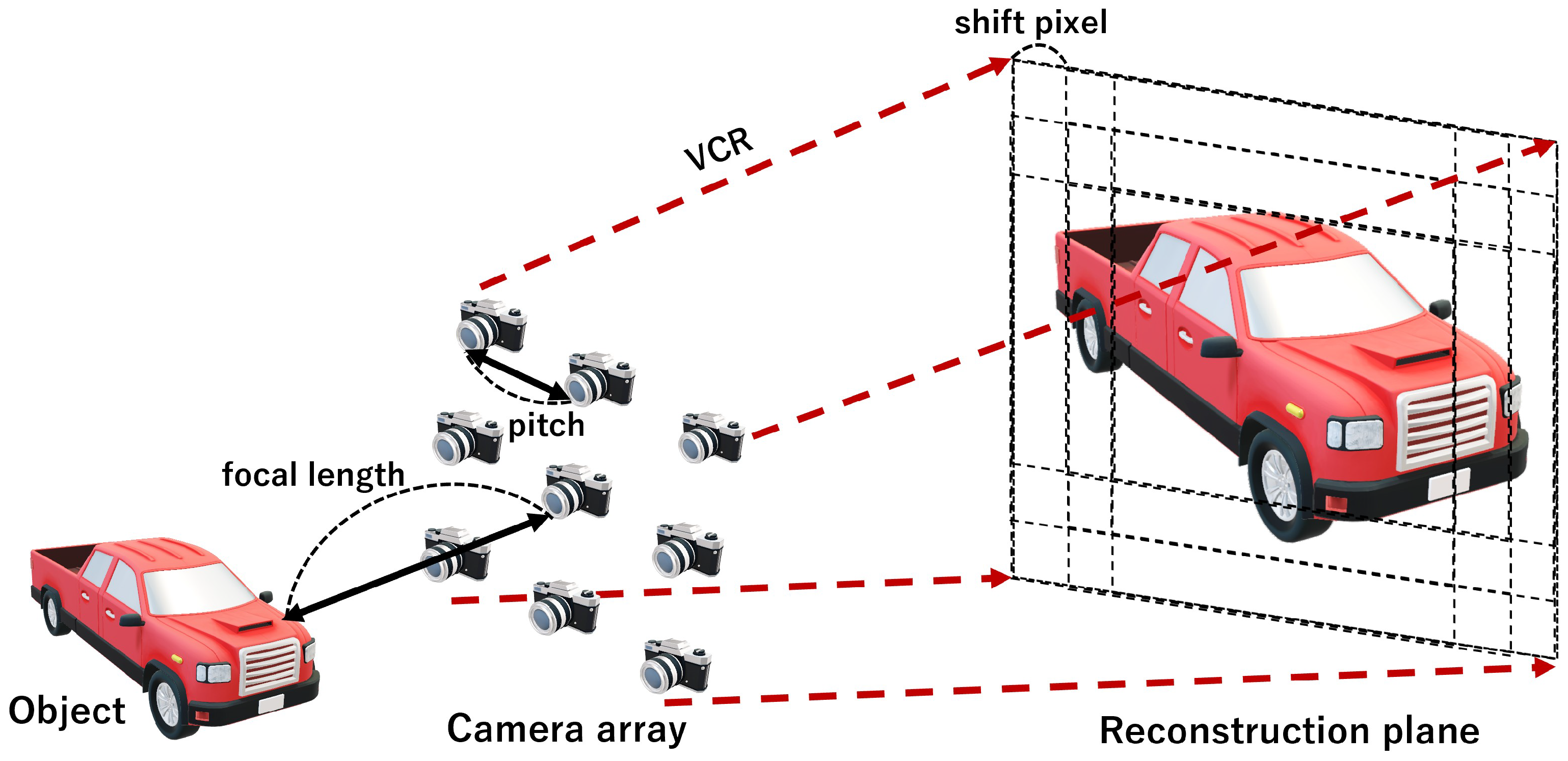
2.1. Peplography
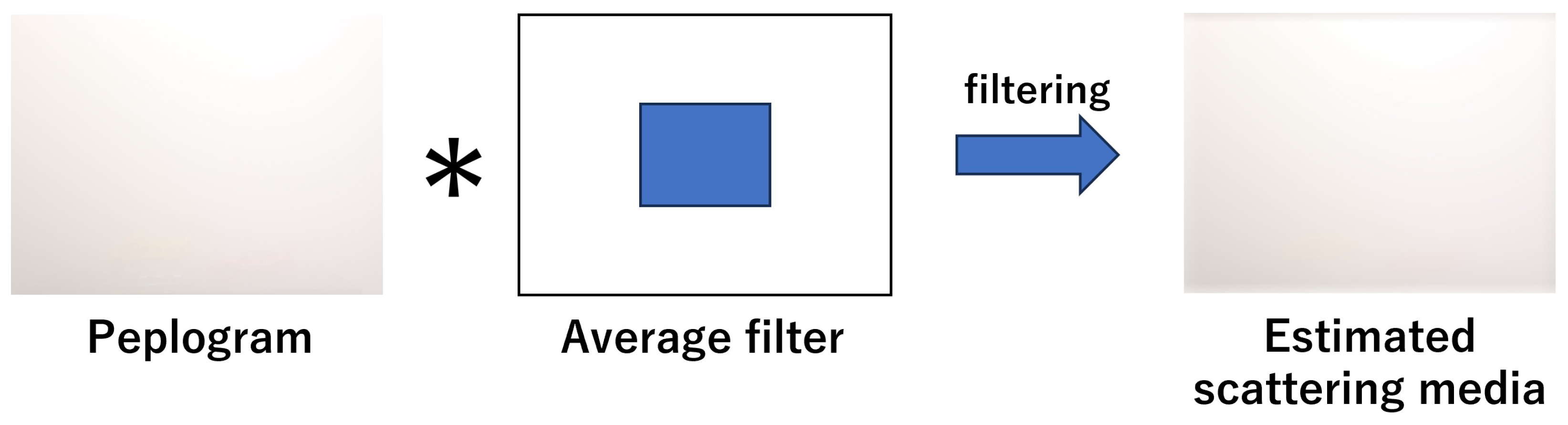
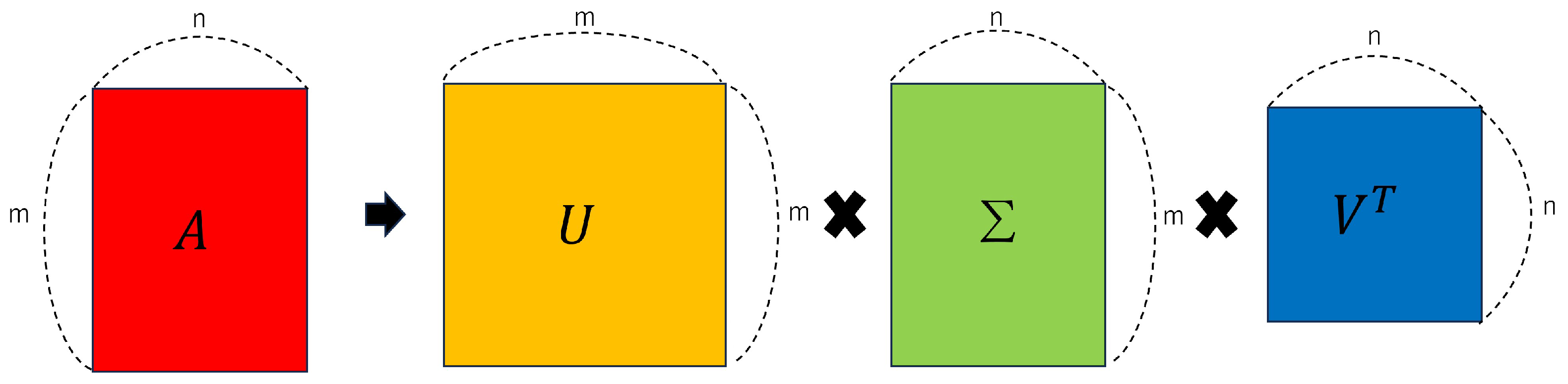
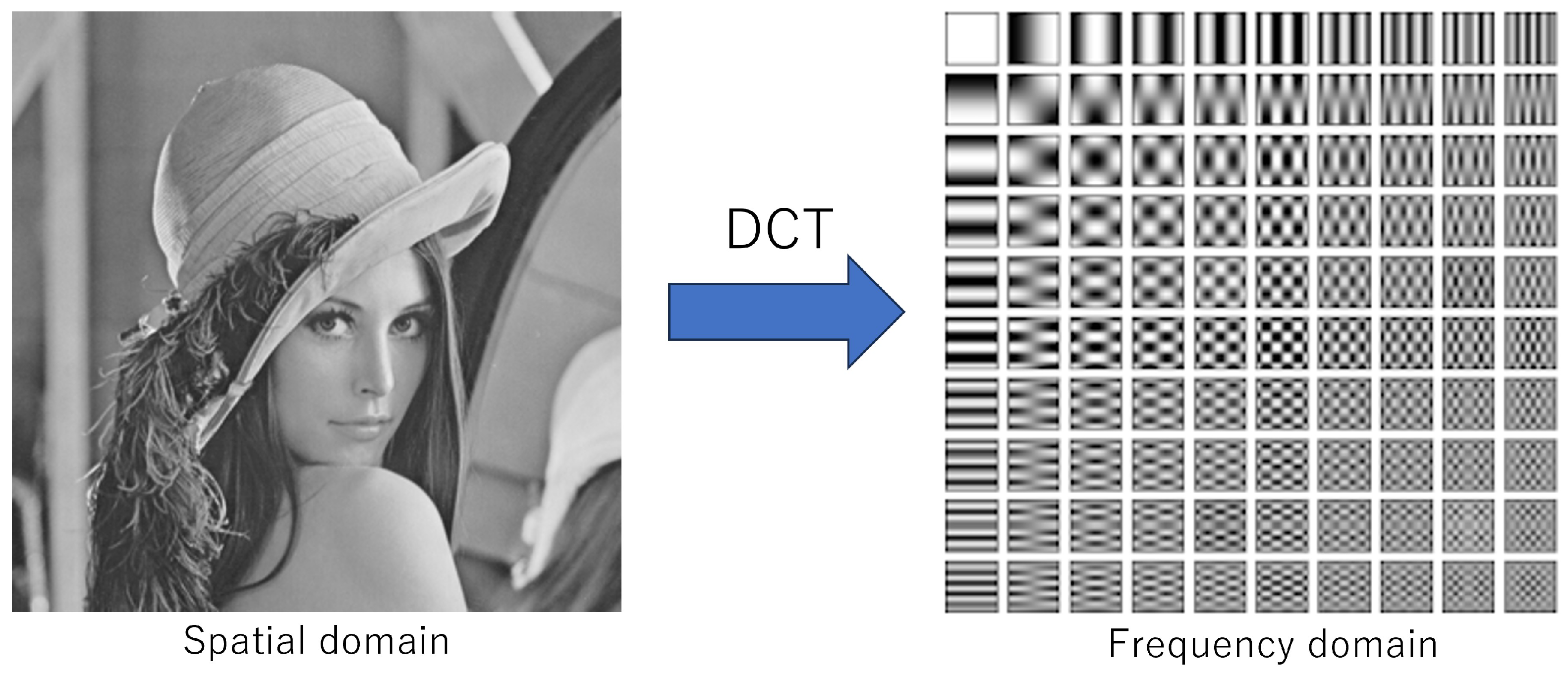
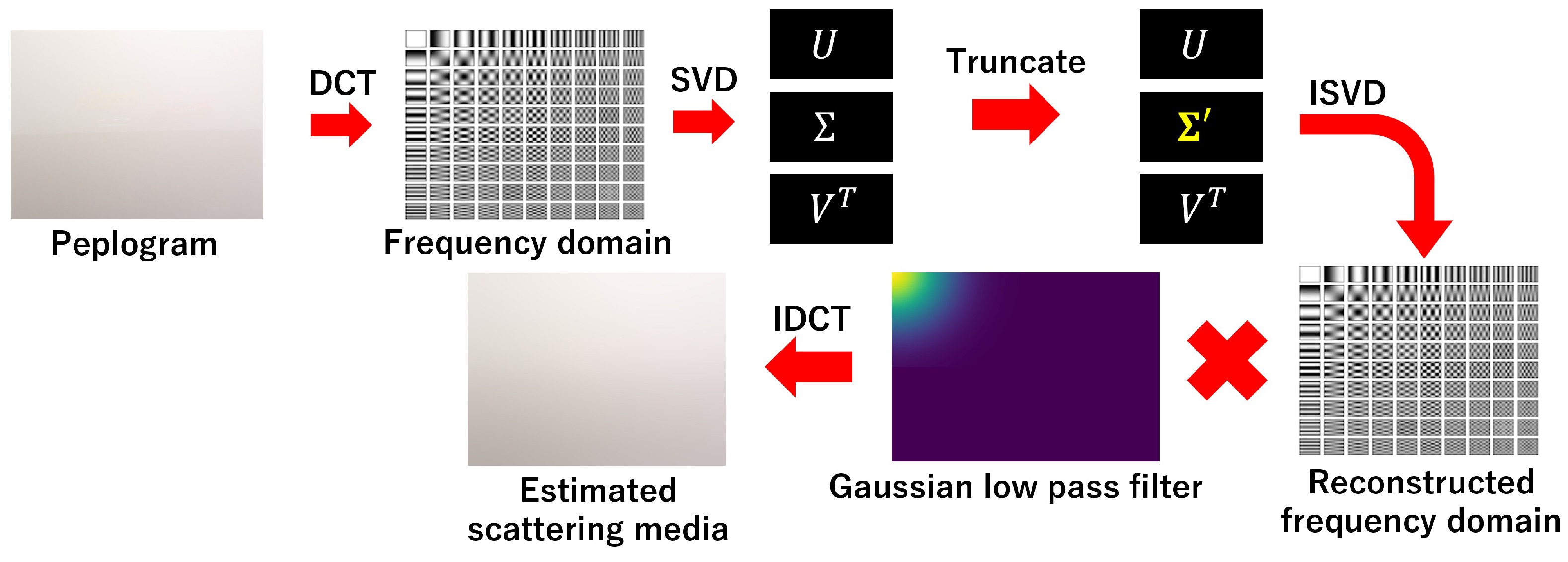
2.2. Proposed Method
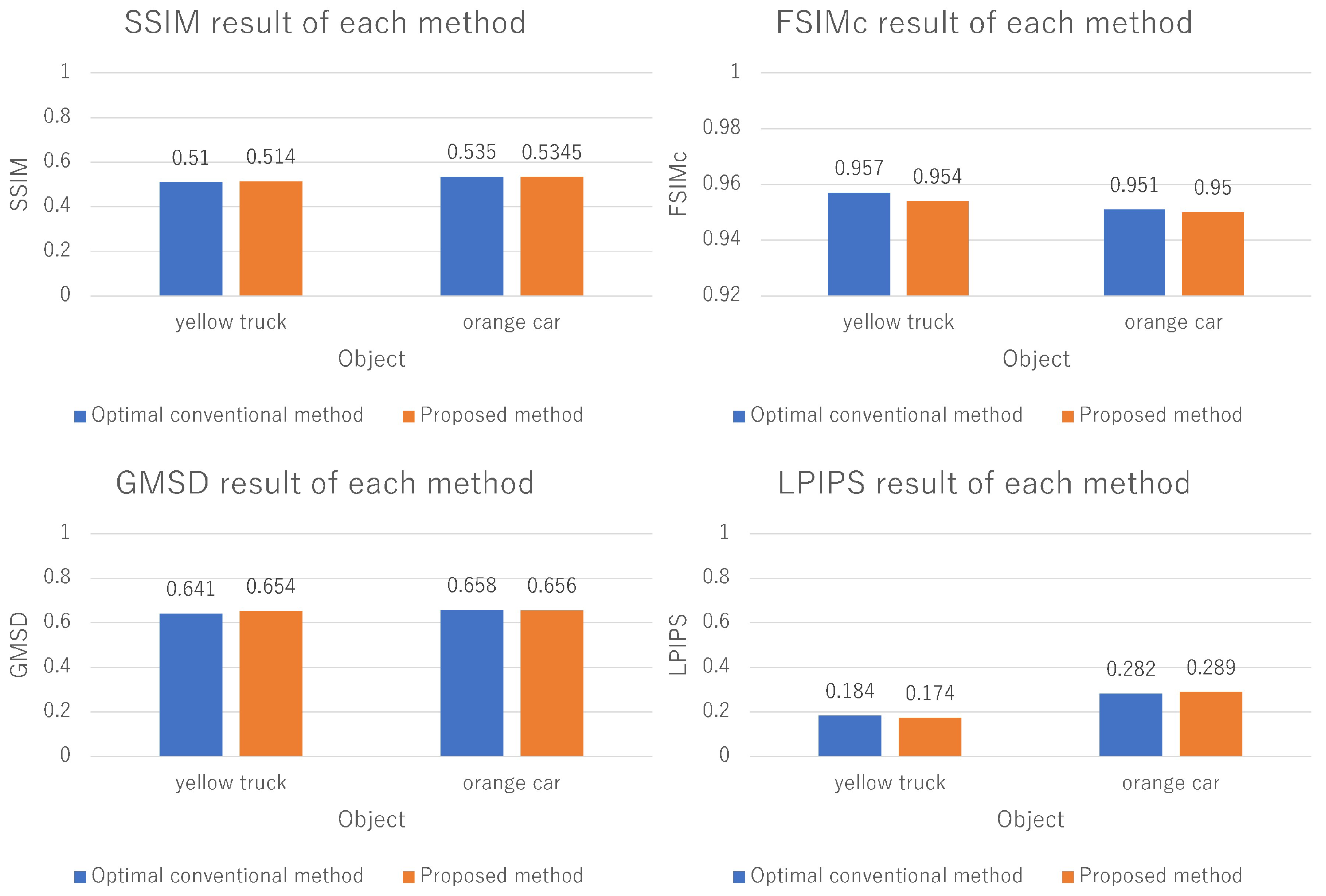
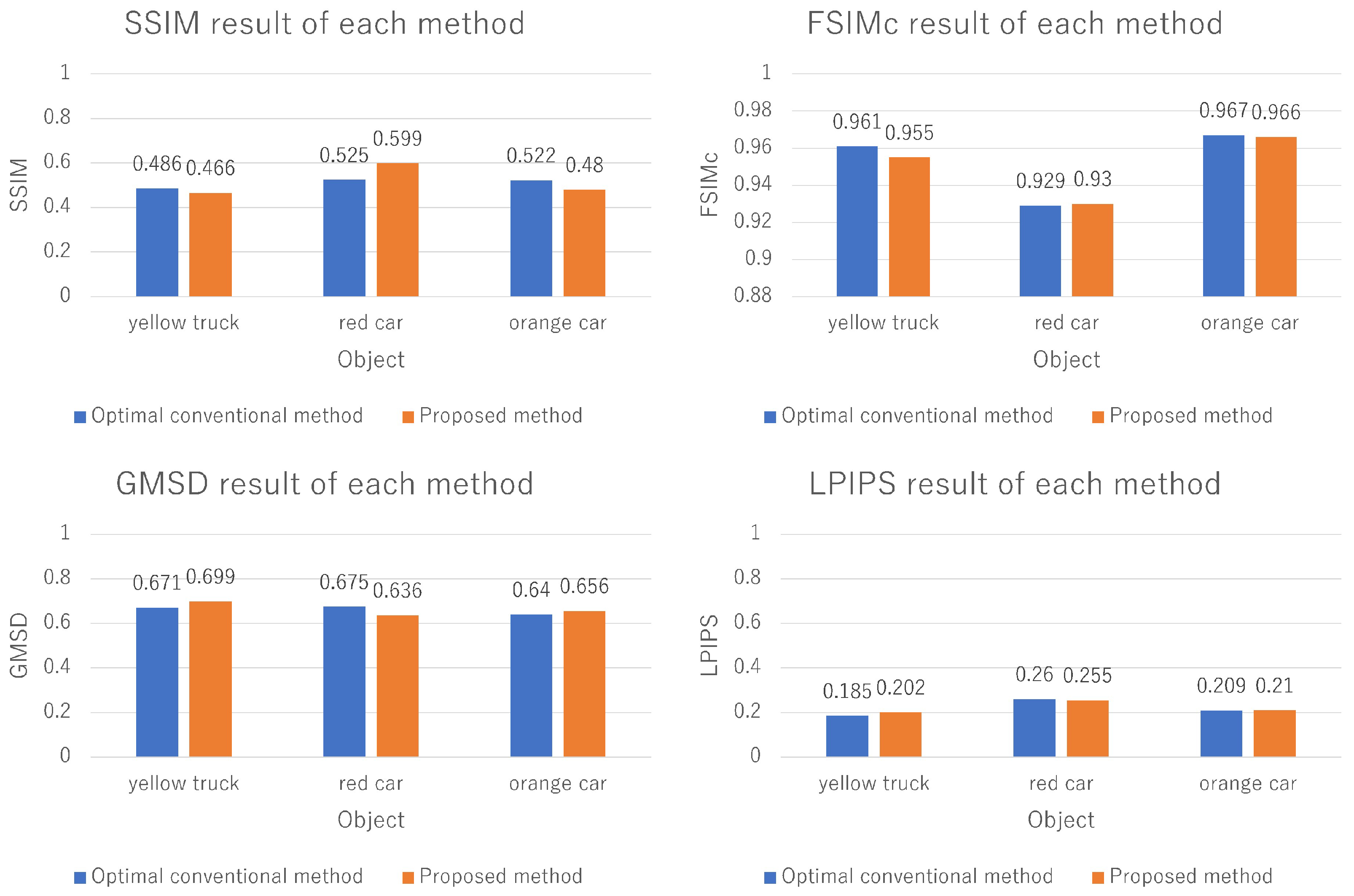
3. Experimental Setup and Results
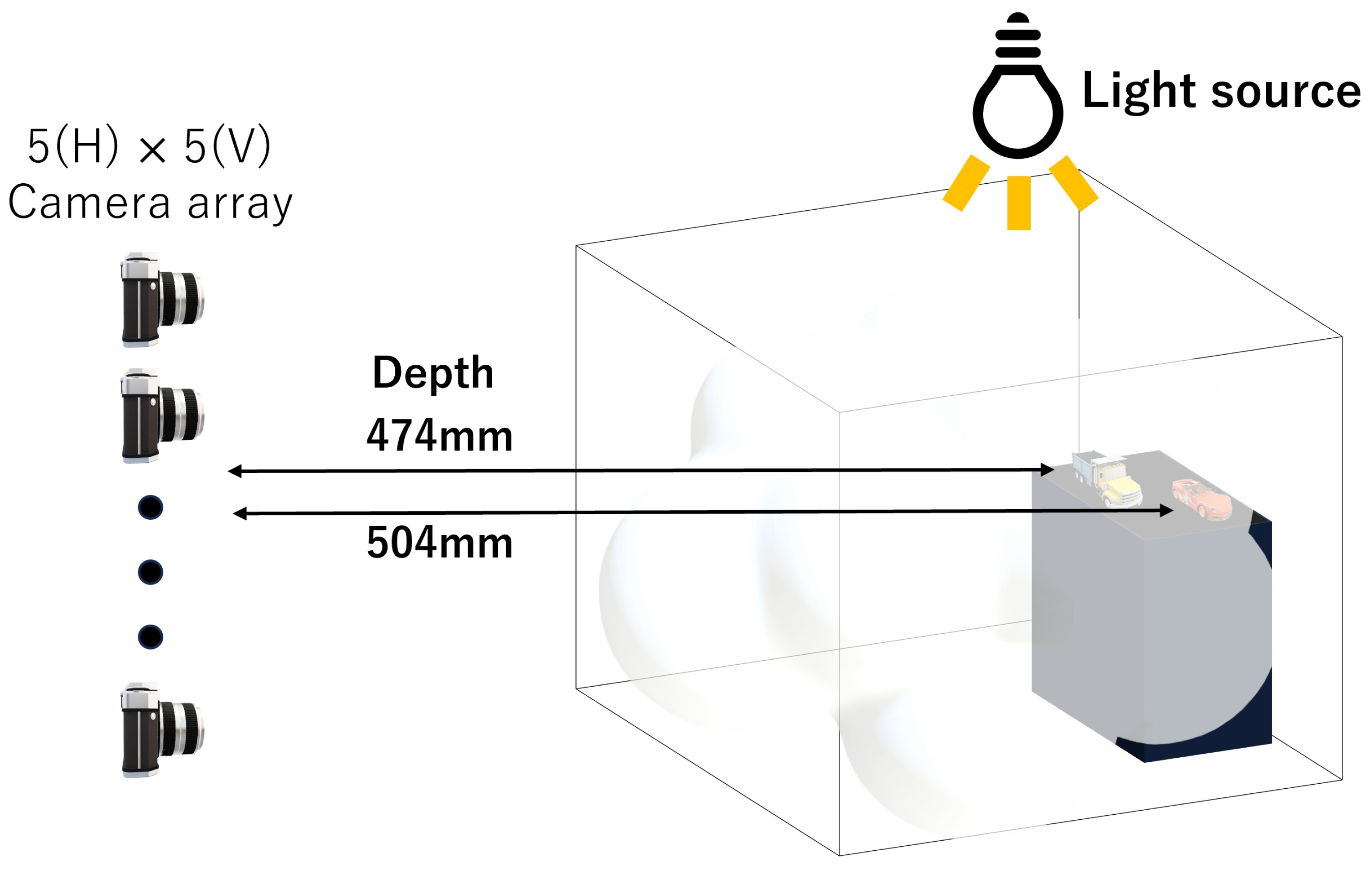
Experimental Setup
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, J.; Wang, S.; Wang, X.; Ju, M.; Zhang, D. A review of remote sensing image dehazing. Sensors 2021, 21, 3926. [Google Scholar] [CrossRef] [PubMed]
- Tan, Y.; Zhu, Y.; Huang, Z.; Tan, H.; Chang, W. Brief Industry Paper: Real-Time Image Dehazing for Automated Vehicles. In Proceedings of the 2023 IEEE Real-Time Systems Symposium (RTSS), Taipei, Taiwan, 5–8 December 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 478–483. [Google Scholar]
- Wang, Y.; Chao, W.L.; Garg, D.; Hariharan, B.; Campbell, M.; Weinberger, K.Q. Pseudo-lidar from visual depth estimation: Bridging the gap in 3d object detection for autonomous driving. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 8445–8453. [Google Scholar]
- Li, Y.; Ibanez-Guzman, J. Lidar for autonomous driving: The principles, challenges, and trends for automotive lidar and perception systems. IEEE Signal Process. Mag. 2020, 37, 50–61. [Google Scholar] [CrossRef]
- Schechner, Y.Y.; Narasimhan, S.G.; Nayar, S.K. Instant dehazing of images using polarization. In Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), Kauai, HI, USA, 8–14 December 2001; IEEE: Piscataway, NJ, USA, 2001; Volume 1, p. 1. [Google Scholar]
- He, K.; Sun, J.; Tang, X. Single image haze removal using dark channel prior. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 2341–2353. [Google Scholar] [PubMed]
- Zhu, Q.; Mai, J.; Shao, L. A fast single image haze removal algorithm using color attenuation prior. IEEE Trans. Image Process. 2015, 24, 3522–3533. [Google Scholar]
- Cai, B.; Xu, X.; Jia, K.; Qing, C.; Tao, D. Dehazenet: An end-to-end system for single image haze removal. IEEE Trans. Image Process. 2016, 25, 5187–5198. [Google Scholar] [CrossRef]
- Zhang, H.; Sindagi, V.; Patel, V.M. Multi-scale single image dehazing using perceptual pyramid deep network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Salt Lake City, UT, USA, 14–19 June 2018; pp. 902–911. [Google Scholar]
- Dong, H.; Pan, J.; Xiang, L.; Hu, Z.; Zhang, X.; Wang, F.; Yang, M.H. Multi-Scale Boosted Dehazing Network With Dense Feature Fusion. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Virtual, 14–19 June 2020; pp. 2157–2167. [Google Scholar]
- Agrawal, S.C.; Jalal, A.S. A comprehensive review on analysis and implementation of recent image dehazing methods. Arch. Comput. Methods Eng. 2022, 29, 4799–4850. [Google Scholar] [CrossRef]
- Wang, Y.; Yan, X.; Wang, F.L.; Xie, H.; Yang, W.; Zhang, X.P.; Qin, J.; Wei, M. Ucl-dehaze: Towards real-world image dehazing via unsupervised contrastive learning. IEEE Trans. Image Process. 2024, 33, 1361–1374. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Fu, W.; Yu, H.; Zhang, Y. Effective polarization-based image dehazing through 3D convolution network. Signal Image Video Process. 2024, 18 (Suppl. S1), 1–12. [Google Scholar] [CrossRef]
- Cho, M.; Javidi, B. Peplography—A passive 3D photon counting imaging through scattering media. Opt. Lett. 2016, 41, 5401–5404. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Cho, M.; Lee, M.C. 3D visualization of objects in heavy scattering media by using wavelet peplography. IEEE Access 2022, 10, 134052–134060. [Google Scholar] [CrossRef]
- Ono, S.; Kim, H.W.; Cho, M.; Lee, M.C. A research on scattering removal technology using compact GPU machine for real-time visualization. In Proceedings of the 2023 23rd International Conference on Control, Automation and Systems (ICCAS), Yeosu, Republic of Korea, 17–20 October 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1460–1464. [Google Scholar]
- Tavakoli, B.; Javidi, B.; Watson, E. Three dimensional visualization by photon counting computational integral imaging. Opt. Express 2008, 16, 4426–4436. [Google Scholar] [CrossRef] [PubMed]
- Moon, I.; Javidi, B. Three-dimensional recognition of photon-starved events using computational integral imaging and statistical sampling. Opt. Lett. 2009, 34, 731–733. [Google Scholar] [CrossRef]
- Aloni, D.; Stern, A.; Javidi, B. Three-dimensional photon counting integral imaging reconstruction using penalized maximum likelihood expectation maximization. Opt. Express 2011, 19, 19681–19687. [Google Scholar] [CrossRef] [PubMed]
- Xiao, X.; Javidi, B. 3D photon counting integral imaging with unknown sensor positions. JOSA A 2012, 29, 767–771. [Google Scholar] [CrossRef]
- Lee, C.G.; Moon, I.; Javidi, B. Photon-counting three-dimensional integral imaging with compression of elemental images. JOSA A 2012, 29, 854–860. [Google Scholar] [CrossRef] [PubMed]
- Jung, J.; Cho, M.; Dey, D.K.; Javidi, B. Three-dimensional photon counting integral imaging using Bayesian estimation. Opt. Lett. 2010, 35, 1825–1827. [Google Scholar] [CrossRef]
- Kim, H.W.; Lee, M.C.; Cho, M. Three-Dimensional Image Visualization under Photon-Starved Conditions Using N Observations and Statistical Estimation. Sensors 2024, 24, 1731. [Google Scholar] [CrossRef] [PubMed]
- Morton, G. Photon counting. Appl. Opt. 1968, 7, 1–10. [Google Scholar] [CrossRef]
- Srinivas, M.D.; Davies, E.B. Photon counting probabilities in quantum optics. Int. J. Opt. 1981, 28, 981–996. [Google Scholar] [CrossRef]
- Goodman, J.W. Statistical Optics; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Watson, E.A.; Morris, G.M. Comparison of infrared upconversion methods for photon-limited imaging. J. Appl. Phys. 1990, 67, 6075–6084. [Google Scholar] [CrossRef]
- Tsuchiya, Y.; Inuzuka, E.; Kurono, T.; Hosoda, M. Photon-counting imaging and its application. In Advances in Electronics and Electron Physics; Elsevier: Amsterdam, The Netherlands, 1986; Volume 64, pp. 21–31. [Google Scholar]
- Lippmann, G. La photographie integrale. Comptes-Rendus 1908, 146, 446–451. [Google Scholar]
- Jang, J.S.; Javidi, B. Three-dimensional synthetic aperture integral imaging. Opt. Lett. 2002, 27, 1144–1146. [Google Scholar] [CrossRef] [PubMed]
- Hong, S.H.; Jang, J.S.; Javidi, B. Three-dimensional volumetric object reconstruction using computational integral imaging. Opt. Express 2004, 12, 483–491. [Google Scholar] [CrossRef] [PubMed]
- Park, J.H.; Hong, K.; Lee, B. Recent progress in three-dimensional information processing based on integral imaging. Appl. Opt. 2009, 48, H77–H94. [Google Scholar] [CrossRef] [PubMed]
- Javidi, B.; Carnicer, A.; Arai, J.; Fujii, T.; Hua, H.; Liao, H.; Martínez-Corral, M.; Pla, F.; Stern, A.; Waller, L.; et al. Roadmap on 3D integral imaging: Sensing, processing, and display. Opt. Express 2020, 28, 32266–32293. [Google Scholar] [CrossRef]
- Lee, J.; Usmani, K.; Javidi, B. Polarimetric 3D integral imaging profilometry under degraded environmental conditions. Opt. Express 2024, 32, 43172–43183. [Google Scholar] [CrossRef]
- Inoue, K.; Cho, M. Visual quality enhancement of integral imaging by using pixel rearrangement technique with convolution operator (CPERTS). Opt. Lasers Eng. 2018, 111, 206–210. [Google Scholar] [CrossRef]
- Kahu, S.; Rahate, R. Image compression using singular value decomposition. Int. J. Adv. Res. Technol. 2013, 2, 244–248. [Google Scholar]
- Gavish, M.; Donoho, D.L. The optimal hard threshold for singular values is 4/√3. IEEE Trans. Inf. Theory 2014, 60, 5040–5053. [Google Scholar] [CrossRef]
- Donoho, D.; Gavish, M.; Romanov, E. ScreeNOT: Exact MSE-optimal singular value thresholding in correlated noise. Ann. Stat. 2023, 51, 122–148. [Google Scholar] [CrossRef]
- Pascal, N.; Ele, P.; Basile, K.I. Compression approach of EMG signal using 2D discrete wavelet and cosine transforms. Am. J. Signal Process. 2013, 3, 10–16. [Google Scholar]
- Raid, A.; Khedr, W.; El-Dosuky, M.A.; Ahmed, W. Jpeg image compression using discrete cosine transform-A survey. arXiv 2014, arXiv:1405.6147. [Google Scholar]
- Zhang, L.; Zhang, L.; Mou, X.; Zhang, D. FSIM: A feature similarity index for image quality assessment. IEEE Trans. Image Process. 2011, 20, 2378–2386. [Google Scholar] [CrossRef]
- Xue, W.; Zhang, L.; Mou, X.; Bovik, A.C. Gradient magnitude similarity deviation: A highly efficient perceptual image quality index. IEEE Trans. Image Process. 2013, 23, 684–695. [Google Scholar] [CrossRef]
- Zhang, R.; Isola, P.; Efros, A.A.; Shechtman, E.; Wang, O. The unreasonable effectiveness of deep features as a perceptual metric. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 586–595. [Google Scholar]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, S.; Kim, H.-W.; Cho, M.; Lee, M.-C. Automated Scattering Media Estimation in Peplography Using SVD and DCT. Electronics 2025, 14, 545. https://doi.org/10.3390/electronics14030545
Song S, Kim H-W, Cho M, Lee M-C. Automated Scattering Media Estimation in Peplography Using SVD and DCT. Electronics. 2025; 14(3):545. https://doi.org/10.3390/electronics14030545
Chicago/Turabian StyleSong, Seungwoo, Hyun-Woo Kim, Myungjin Cho, and Min-Chul Lee. 2025. "Automated Scattering Media Estimation in Peplography Using SVD and DCT" Electronics 14, no. 3: 545. https://doi.org/10.3390/electronics14030545
APA StyleSong, S., Kim, H.-W., Cho, M., & Lee, M.-C. (2025). Automated Scattering Media Estimation in Peplography Using SVD and DCT. Electronics, 14(3), 545. https://doi.org/10.3390/electronics14030545





