Automatic Generation Strategy for Standard Cell Layout in DTCO Process Based on Reinforcement Learning

Abstract

DTCO (Design–Technology Co-optimization) facilitates communication between the design and process flows, thereby expediting the cycle of the chip development pipeline. Within the DTCO framework, the development of a standard cell library, which entails the rapid generation of standard cell layouts, constitutes a crucial aspect in enhancing the efficiency of digital integrated circuit development. In light of the issue of the substantial time consumption associated with manual layout design prevalent in the industry, a novel method for the automatic generation of standard cell layouts, leveraging reinforcement learning for placement and the Dijkstra algorithm for routing, is proposed. Compared with traditional automatic layout algorithms, the proposed methodology exhibits enhanced adaptability. When accounting for the influence of technological node variations on design alterations, the device information and key design rule parameters are configured as adjustable variables to accommodate the migration across different processes. It is demonstrated that the proposed method can accelerate the DTCO cycle and enable the migration of the standard cell layout from the 55 nm process to the 28 nm process of a specific foundry. It is anticipated that this approach can offer novel perspectives for the advancement of EDA tools dedicated to the automatic generation of standard cell layouts.

1. Introduction

With the advent of the use of semiconductor technology in deep submicron and nanometer regimes, the demand for high-performance and efficient chips within novel process nodes has witnessed a significant upsurge. Conventional design methodologies, however, fall short in fulfilling these escalating requirements. In response to this predicament, DTCO (Design–Technology Co-optimization) strategies have been proposed. These strategies are designed to effect a synergistic optimization of both the process technology and chip design, facilitating a profound integration between the two. Consequently, they enable the creation of chip products that exhibit enhanced performance, reduced power consumption, and improved cost-effectiveness at new process nodes [1,2].

The standard cell library constitutes a crucial module within the DTCO integrated circuit design process. It contains a collection of pre-designed and character-based basic functional cells such as logic gates, triggers, IO ports, etc. [3,4]. These cells have fixed layout designs and sizes, which can be combined into complex digital circuits like building blocks [5,6,7]. The generation of standard cell layouts occupies a central position in DTCO, as it directly affects the quality of the standard cell library. At present, placement and routing in the generation of the standard cell library still rely heavily on manual drawing and debugging, which not only exhibits inefficiency but also struggles to satisfy the demands of chip iteration within the DTCO workflow. The problems with manual methods include the time consumption, high cost, difficulty in adapting to changes in new processes, and potential under-optimization issues [8,9].

Therefore, in order to accelerate the generation process of the standard cell library, the industry has long been in urgent need of an automated method for generating standard cell layouts. Over the past two decades, scholars have been delving into this area. In 2004, Ma Qi et al. harnessed the simulated annealing algorithm to optimize the area and delay of the cell layout, which can handle circuits not limited to static series–parallel structures [10]. In 2006, Lazzari C et al. employed the Euler algorithm for layout planning and explored the shortest path for routing [11]. In 2014, Ziesemer A et al. utilized mixed linear programming (MILP) for the layout and optimized the layout area [12]. In 2021, Hao Rui et al. adopted deep learning algorithms for the layout and roughly completed the overall layout of deployable linear actuators [13]. Nevertheless, these methods failed to account for design rule constraints and thus were not applied in practical engineering projects. In the domain of layout design, consideration must be given to design rules that pertain to the manufacturability in chip production. In 2019, Kyeongrok Jo et al. from Seoul National University utilized graph theory methods to lay out transistors based on design rules [14]. In 2020, Daereal Lee et al. from the University of California put forward a satisfiability model theory that dynamically allocates pins to solve position and path issues [15]. Although design rule constraints were taken into consideration, the DRC detection situation could not be presented, leaving designers in the dark about error details. In 2024, Gao Xiaohan et al. from the School of Computer Science at Peking University studied the existing standard cell layouts and constructed a model that can migrate the standard cells to different driving strengths but cannot achieve migration between different process nodes [16]. In 2021, Haoxing Ren et al. utilized reinforcement learning to generate single-node standard cell layouts and fix some DRCs, but their method could not meet the requirements of layout migration under multiple processes [17].

In order to address these challenges, a novel approach predicated on reinforcement learning for the placement of standard cells and the Dijkstra algorithm for routing has been devised. This approach exhibits better adaptability and is capable of diminishing the rework induced by process alterations via the DTCO strategy. Consequently, it effectively curtails the development cycle of standard cell layouts across different process nodes, as illustrated in Figure 1.

The remaining sections will provide detailed descriptions of the proposed method. In the Section 2, the layout of transistors will be elaborated. The Section 3 focuses on algorithm analysis, covering research into the standard cell layout based on reinforcement learning, as well as layout routing with the Dijkstra algorithm. The Section 4 presents the results of the proposed method and verifies its migration. The Section 5 presents a summary of the entire text.

2. Analysis of Standard Cell Layout

The layout design of a standard cell needs to meet multiple design specifications such as source–drain sharing and a minimum area. At the same time, there are various design scenarios, such as differences in the circuit module layout and an irregular transistor size [18,19,20,21]. A reinforcement learning-based standard cell automatic placement method is proposed for this multi-constraint objective optimization problem, which extracts the layout features of standard cells and sets the design criteria as a reward function under a reinforcement learning framework. As an intelligent agent, the transistor unit interacts directly with the layout scene, accumulates different circuit placement and corresponding reward values, and autonomously learns movement strategies based on this, thereby achieving the automatic optimization of the standard cell layout under multiple constraint conditions.

In standard cell layouts, the area is often wasted due to the diversity of transistor sizes, particularly in highly restricted cells. To address this issue, folding technology is employed to divide and arrange large transistors in parallel horizontally, thereby reducing the routing complexity. A transistor pair, consisting of PMOS and NMOS transistors, is utilized with the goal of minimizing the number of chains to optimize the cell width. When creating the layout, consideration must be given to the relative position and placement direction of the chains to alleviate routing difficulties and enhance the routing rate. The order and flipping of the chains must be determined in the layout, and a 180° flipping decision should be made based on the principle of source–drain sharing. Dummy gates are to be inserted between MOS transistors that do not share, in order to maximize source–drain sharing. The optimization objective involves the use of reinforcement learning algorithms to learn rules and achieve optimal transistor sorting while adhering to height constraints, ultimately yielding the unit with the most optimal area.

The transformation from the input of the transistor netlist to the generation of a standard cell placement in the JSON format predominantly encompasses the following patterns:

• The standard cell placement includes two rows of horizontal diffusion bars, P-type and N-type, with all PMOS transistors located on the P-type bars and NMOS transistors located on the N-type bars.
• A pair of PMOS and NMOS transistors with a common gate are vertically aligned and share a polycrystalline gate. This pair of PMOS and NMOS transistors is called a transistor pair, while a pair of PMOS and NMOS transistors with a non-common gate but that are vertically aligned are also called a transistor pair [22].
• If the source and drain regions of MOS transistors connected in a circuit are adjacent, they are connected by diffusion regions, which is called source–drain sharing. Multiple MOS transistors arranged continuously with source–drain sharing are called diffusion chains. Since MOS transistors are often arranged in pairs of P and N, diffusion chains are also called transistor pair chains [23].
• The power supply VSS/ground wire VDD are arranged in parallel outside the two rows of horizontal bars.
• The wire mesh outside of the power supply VSS/ground VDD is arranged between the P-type and N-type horizontal bars.

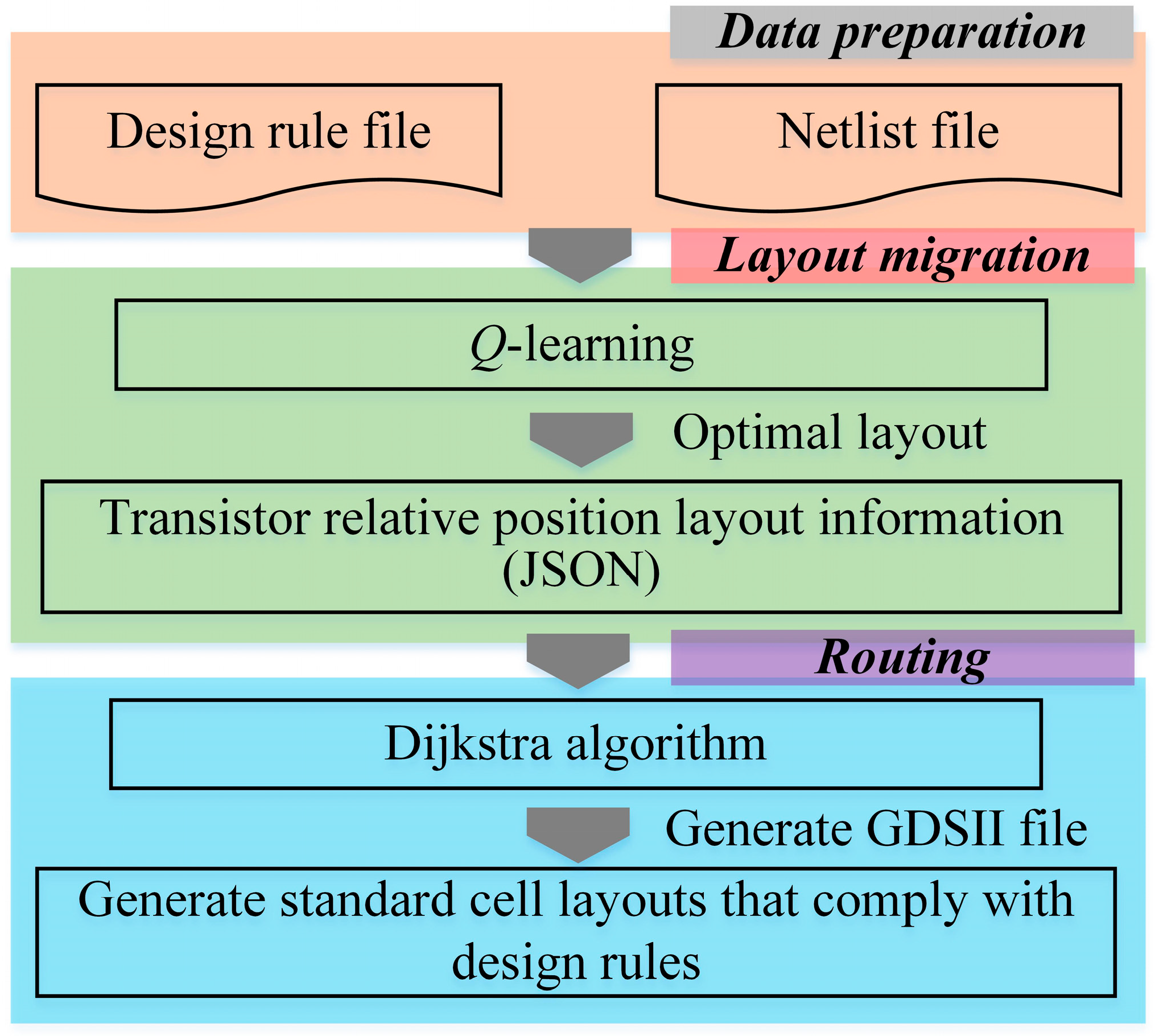
3. Algorithm Design

This section is divided into the design of the placement algorithms and routing algorithms to achieve the automatic generation of standard cell layouts.

3.1. Placement Algorithm

The Q-learning algorithm is a reinforcement learning algorithm based on value iteration, which can solve optimal policy problems in discrete states and action spaces without the need to know the state transition model of the environment in advance [24]. The main idea is that search and rescue robots interact with their surrounding environment, making multiple attempts at each possible state and action, continuously learning and optimizing a value function, Q (s,a), to achieve autonomous learning.

In the process of using the Q-learning algorithm for a standard cell layout, there are three important elements: s_t (state), a_t (action), and r_t (reward). Through continuous information exchange with the environment, the algorithm constructs a Q-table based on actions and states and stores the state values of each state in the table, abbreviated as a Q-value. During the layout process, in the current state s, we can select a_t (action), and through the influence of the environment, form a new state (s_t + 1), generating a reward or punishment (r_t + 1).

After the design of the front-end standard cell circuit is completed and the netlist is exported, the transistors in the netlist can be randomly placed or placed based on experience as the initial layout input model. The transistor pair chain serves as an agent. At step t, the observed value of the environment is s_t, and the current reward value r_t is calculated based on the settings of the constraint conditions. Reinforcement learning outputs an action strategy, a_t, based on the current observed value, and obtains a new layout observation value, s_t+1, by moving the position information of the current agent. The current environment, action strategy, reward value, and new environment are combined into a quadruple (s_t, a_t, r_t, s_t+1) and stored in the transistor layout experience pool, continuously accumulating experience of different layouts to train the reinforcement learning network for self-learning and self-optimization, gradually finding a standard cell circuit layout that meets the constraint conditions and is more optimal, realizing an automatic design model for the standard cell circuit layout that meets multiple constraint conditions and can be used for multiple process nodes. The overall framework of the automatic layout method for a standard cell layout is shown in Figure 2.

The main process of the Q-learning algorithm is as follows:

• State space: When transistors act as intelligent agents moving in a scene, they will determine the next action to be executed based on the observed layout scene. The interaction between intelligent agents and layout scenarios is the foundation of and key to reinforcement learning for autonomous learning and training. Of these, the layout scenario refers to the transistor element pool environment in which the intelligent agent exists and interacts. Therefore, the state space observed by intelligent agents and the action strategies executed need to be designed and represented in a reasonable layout. The state space s observed by intelligent agents is defined as

$$s=[v_x,v_y,x-x_i,y|\left\{0,1\right\}]$$

(1)

In the formula, $v_x$ and $v_y$ represent the current action speed of the intelligent agent, $x_i$ represents the current position information of the intelligent agent, $x=\left\{x_1,x_2,\dots ,x_N\right\}$ represents the position information of all transistors in the standard cell circuit layout, and y = 0 or 1, respectively, represents the location of the transistors in the N or P region.

• Action space design: The movement of the intelligent agent is a deterministic behavior, and purpose of the action space of the intelligent agent is mainly to exchange the source and drain under fixed gate conditions and search for sharing situations. For each transistor in the current group, check if its source is in the drain list of any transistor in the previous group.
• Reward function design: Create an array that includes the “source drain sharing” situation to count the maximum number of sources and drains shared and reward them. If the drain of the current transistor is the same as the source of the next transistor and their y-coordinates are the same and the x-coordinate of the current transistor plus 1 equals the x-coordinate of the next transistor, then these two transistors are considered “shared” with a reward value of r_t + 1.

$$\left\{\begin{array}{c}Current\_Transistor[drain]=Next\_Transistor[source]\\ Current\_Transistor[y]=Next\_Transistor[y]\\ Current\_Transistor[x]+1=Next\_Transistor[x]\end{array}\right.$$

(2)

If the above three equations are satisfied, the situation is judged as source–drain sharing and has the reward value r_t + 1. In addition to source–drain sharing, the congestion and density are also considered as placement optimization targets, as shown in Equation (3).

$$r(s,a,s^{\prime })={\omega }_1\cdot r_{congestion}(s,a,s^{\prime })+{\omega }_2\cdot r_{density}(s,a,s^{\prime })$$

(3)

Among these values, $r(s,a,s^{\prime })$ represents the reward for taking action a in state s and transitioning to state s^′. ${\omega }_1$ and ${\omega }_2$ are the weights of the congestion and density, respectively, which jointly influence the routing path. A higher congestion weight will prompt the algorithm to evade high-congestion regions, thus enhancing the distributability of the path. Simultaneously, a higher density weight will impel the algorithm to avoid high-density areas, thereby improving the feasibility of placement and ultimately having an impact on the layout performance. Consequently, a balance must be struck between congestion reduction and density control.

• Update the Q-value: Update the Q-value according to the Q-learning formula:

$$Q(s_t,a_t)\leftarrow Q(s_t,a_t)+\alpha [r_{t+1}+\gamma \underset{a^{\prime }\in A(s_t)}{\max }Q(s_{t+1},a^{\prime })-Q(s_t,a_t)]$$

(4)

Through such a reciprocating movement, the exploration of diverse states, and the attainment of rewards, it can be discerned that the greater the reward value r_t, the higher the proportion of source–drain sharing. Concurrently, through the judicious output of congestion and density weights, the optimal layout can be procured.

Among these elements, action forms the strategy of the core of the transistor layout. In step t, the input is the environmental state matrix s_t, and the determined action value a_t is output. A critic takes the solution value function as the core, inputs the action value a_t and the state value s_t, and outputs the evaluation value Q for a series of layout action strategies in the current round. Therefore, the training process is the learning process of judging the quality of action strategies, and through training, a series of layout action strategies with the highest Q value are obtained.

In each training round, each gate is moved in a fixed sequence until the last gate is switched, and then it is reset to the initial layout to start a new round. The collected samples (s_t, a_t, r_t, s_t+1) from each step are input into the main network for training, and the sampling results are stored in the layout experience pool. The data in the layout experience pool are continuously updated. Samples are randomly selected from the local experience pool to serve as inputs for the target network. The parameters of the main network are updated through round-based updating. After several rounds, the parameters of the main network are assigned to the target network for the parameter updating of the target network. The algorithm structure is shown in Figure 3.

3.2. Routing Algorithm

After completing the optimal layout design, the next step is routing, which requires the connection of the same connection points based on the output JSON format layout content. This process involves the routing work of the metal layer and via layer. The accuracy of routing is evaluated by considering the degree of deviation from the routing guidance and the cost in specific metal layers. According to the current process rules, the routing work uses metal 1 to connect the corresponding pins. If there is a pin overlap, it needs to be routed on the second metal layer (metal 2), usually involving two layers of metal wires.

In the routing stage, an improved Dijkstra algorithm was proposed to achieve the shortest path and an obstacle avoidance routing strategy. The Dijkstra algorithm steps are as follows:

• Initialization: Set the shortest path estimation value d[u] for all identical Net nodes to infinity (indicating that the actual path has not been found yet), except for the source point s, whose value is initialized to 0 (the distance from the source point to itself).

  $$d[s]=0,d[v]=\infty ,\forall v\ne s$$

  (5)
• Node selection: Select the node with the shortest distance from the source point as the current processing node u. This choice is based on a greedy strategy to ensure that each step processes the node with the shortest known path.

  $$u=\arg {\min }_{v\in V}d[v]$$

  (6)
• Relaxation operation: Perform a relaxation operation on each adjacent unprocessed node, v, of the current processing node u, attempting to update the shortest path estimation of the adjacent nodes through the current node. The core of the relaxation operation is to check whether there is a shorter path to reach adjacent nodes. If $d[u]+w(u,v)<d[v]$, then $d[v]=d[u]+w(u,v)$. Among these values, $d[u]$ represents the currently known shortest path length from the source point to node $u$, and $w(u,v)$ represents the weight of the edge from node $u$ to $v$.
• Update operation: If the path length from node $u$ to node $v$ is less than the known path length $d[u]$ from the source point to $v$, then update $d[u]$ to the path length from $u$ to $v$. Repeat the above steps until all nodes have been processed, that is, the shortest path to all reachable nodes has been found.

When routing, the routing path needs to be preprocessed. For the highest density routing network, the path needs to be adjusted to comply with the design rules, as shown in Figure 4. In the highest density routing network (red box area), move points a and b on line ② to adjacent grids to obtain the points a’ and b’ and re-plan to add point c. This can effectively avoid overlapping or routing congestion between metal wires.

4. Results

The proposed method is implemented based on the 55 nm process of a certain foundry. For the standard cell netlist obtained from the front-end design, a Q-learning optimization layout is used to obtain the relative position information of transistor routing (stored in a JSON format). Then, based on the optimal layout, the Dijkstra algorithm is used to perform path optimization with the aim of minimizing the use of metal lines for routing. The implementation process is shown in Figure 5, taking AN2D0 as an example.

The proposed method uses a 55 nm process from a certain foundry to demonstrate the effect of automatically generated standard cell layouts. The geometric results are listed in

Table 1. Comparison of 55 nm standard cell layouts based on a certain foundry.

Cell	Cell Info		Area (μm2)		Design Time		Norm.Delay (ns)		Norm.Power (μW)		DRVs
	Num.T	Num.Nets	Manual	Ours	Manual	Ours	Manual	Ours	Manual	Ours	Manual	Ours
AND	6	9	1.40	1.40	10–15 min	3–5 s	0.542	0.538	0.053	0.52	0	0
NAND	8	12	1.40	140	10–15 min	3–5 s	0.538	0.535	0.056	0.054	0	0
AO	10	13	1.96	1.95	10–15 min	3–5 s	0.431	0.428	0.049	0.045	0	0
DQH	26	17	5.88	5.86	40–50 min	5–10 s	0.421	0.419	0.041	0.040	0	0
CLK	12	13	1.40	1.40	10–15 min	3–5 s	0.562	0.553	0.039	0.037	0	0
INV	2	6	0.84	0.82	10–15 min	3–5 s	0.521	0.518	0.036	0.035	0	0
BUF	4	7	1.12	1.10	10–15 min	3–5 s	0.481	0.465	0.032	0.029	0	0
MUX	12	12	3.08	3.06	10–15 min	3–5 s	0.461	0.458	0.025	0.023	0	0

, considering standard cells with different numbers of transistors (“# T”) and networks (“# Net”), from simple combinational logic cells to more complex sequential logic cells, in terms of the generation time, delay, power consumption, and DRC violation counting. The proposed method can generate DRC cleaning solutions while maintaining consistency with the manual layout area, and the metal routing is more reasonable, and the automatically generated layout has the effect of a lower delay and power consumption.

The proposed layout algorithm sets the device information (the transistor channel length L_G) and design rule information (the standard cell height H_STD, the line width length W_v, the via width W_v, the gate-to-gate distance D_G, the VDD/VSS metal strip height H_VDD/H_VSS, the distance from the outermost gate to the edge D_og, and the distance between metal D_w) as adjustable variable parameters and integrates them into the Dijkstra algorithm (the automatic generation method of the standard cell layout is shown in Figure 5d), which facilitates the routing migration of different design rules at different process nodes.

The proposed method was validated for feasibility through migration using a 28 nm process from a certain foundry. Figure 6a,b show the circuit layouts of the 55 nm and 28 nm D flip-flops, respectively. The front-end netlists of the different processes may have slight differences, resulting in differences in the generated layouts. The proposed Q-learning algorithm can generate an optimal placement to adapt to these differences. The Dijkstra algorithm for routing can meet the shortest distance requirements based on specific design rules. Moreover, as the 28 nm process requires the addition of a dummy gate on both sides of each standard cell to balance the density, the proposed method can also meet this requirement. It was indicated that the proposed method could effectively achieve standard cell layout migration between different processes without violating DRC and achieve routing resource utilization similar to that of a manual layout.

5. Conclusions

A novel standard cell automatic generation method based on reinforcement learning for placement and the Dijkstra algorithm for routing is proposed which solves the problem of difficult DRC through the uncoordinated design of the standard cell placement and routing. In terms of the placement, the method sets up reward objectives such as source–drain sharing and a minimum area for layout specifications, unifying various constraints and optimization goals within the same framework. The state space, action space, and reward function were designed according to actual scenarios to construct a reinforcement learning algorithm model for the automatic optimization of the standard cell layout. For routing, the Dijkstra algorithm performs path planning for Net nodes in the optimal layout, using a backward search approach to find the optimal path. When considering the impact of process differences on design variations, the device information and key information of the design rules were set as adjustable variable parameters, achieving migration between different processes and realizing a fast chain for DTCO (Design–Technology Co-optimization). It has been proven that the method can migrate standard cell layouts from a 55 nm process to a 28 nm process. The proposed method effectively addresses the problems of the high time consumption and suboptimal layout quality associated with manual layout drawing. It is expected to be applied in the development of EDA tools for the automatic generation of standard cell layouts. To achieve this goal, the proposed method needs to be developed into an EDA point tool and embedded into the DTCO platform for application by writing an interface program. This requires comprehensive consideration of the design rule compatibility, integration with existing tools, validation and testing, the user interface, and the experience. In real-world scenarios, automatically generated layouts can effectively optimize their power consumption and latency. However, due to the fixed distance size in design rules, the degree of optimization for their area may be limited.