Enhanced Monte Carlo Simulations for Electron Energy Loss Mitigation in Real-Space Nanoimaging of Thick Biological Samples and Microchips
Abstract
1. Introduction
2. Results
2.1. Implementing MC Simulation with EELS Capability
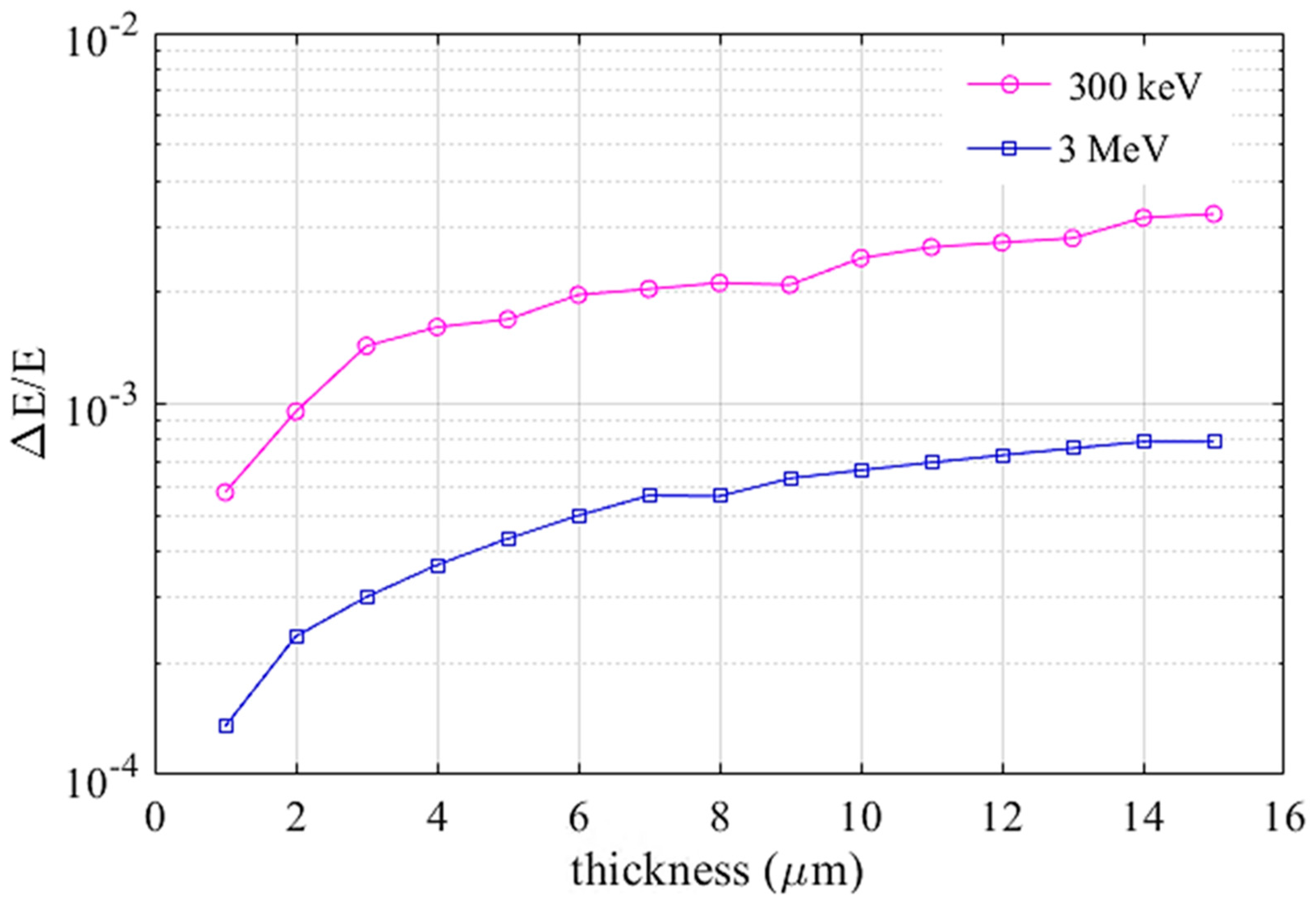
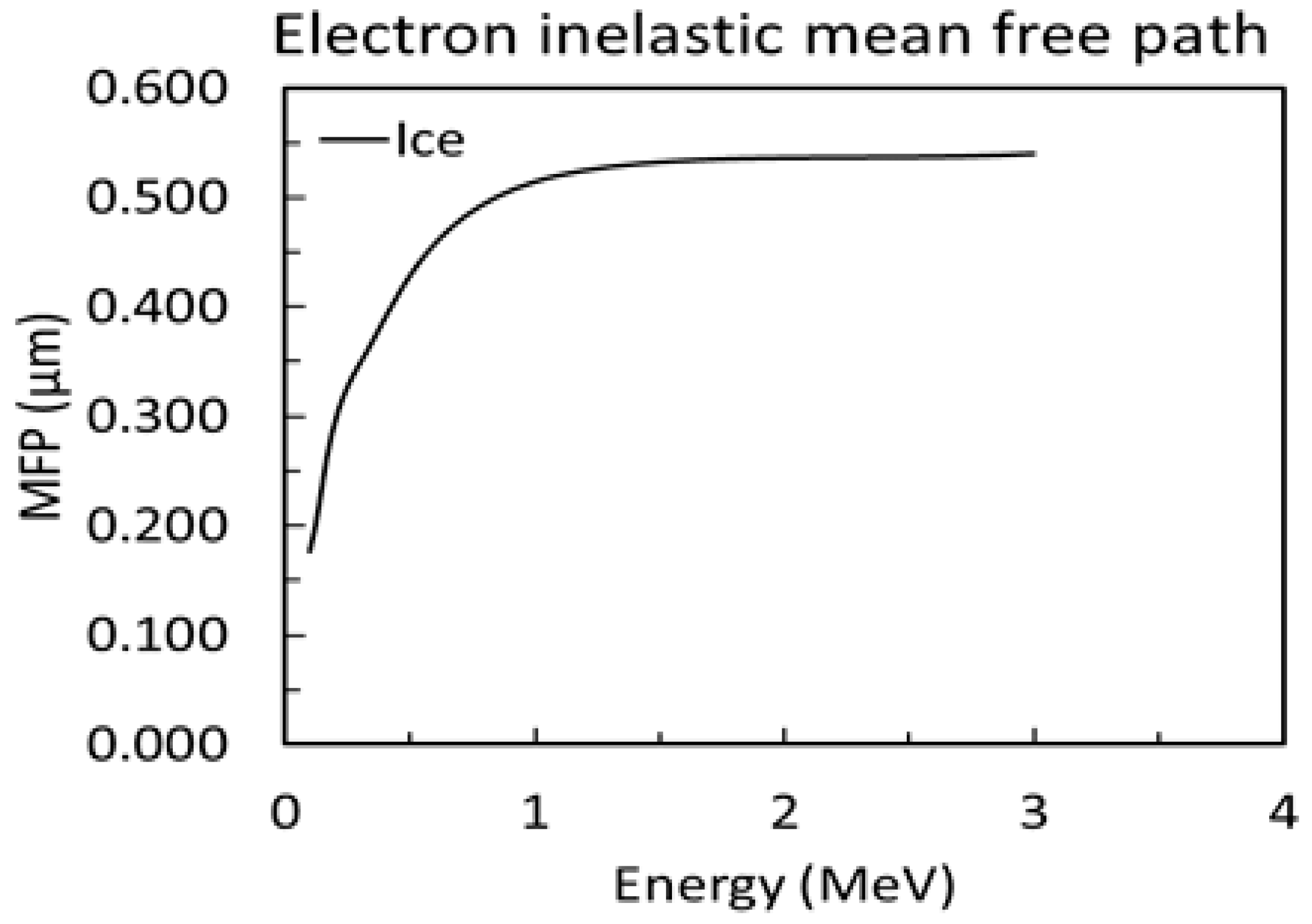
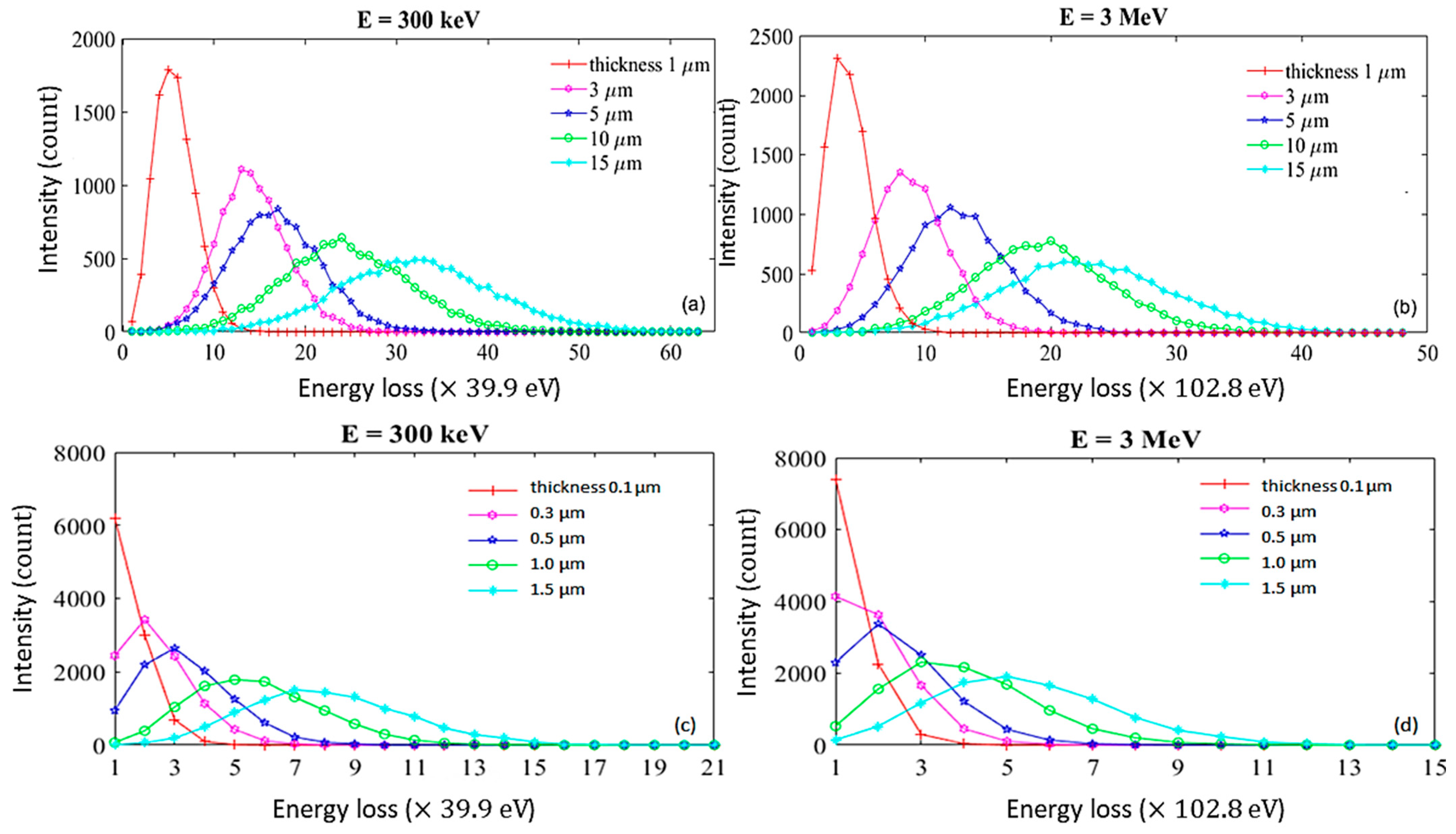
2.2. Simulating EELS
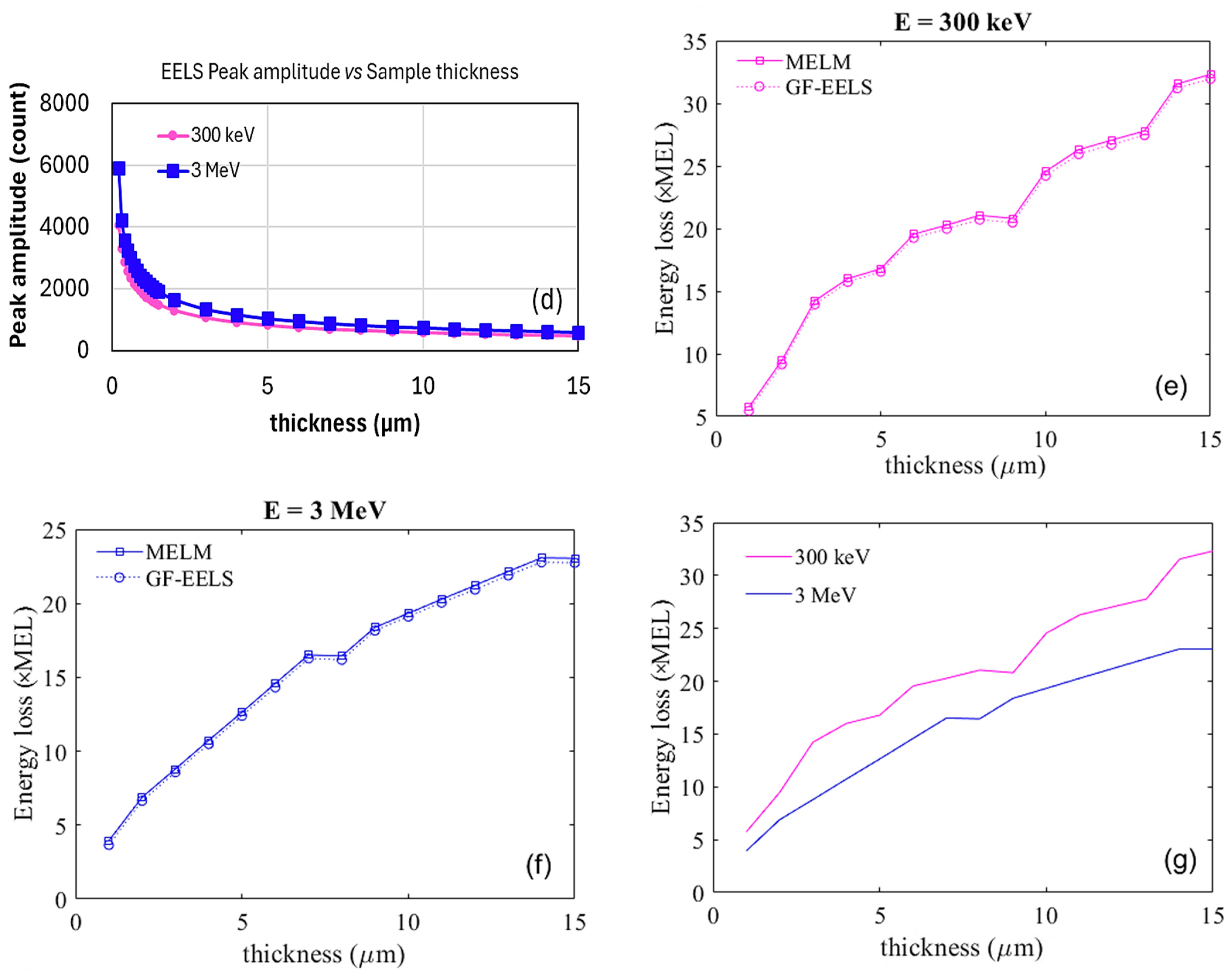
2.3. Analyzing EELS via Two Methods
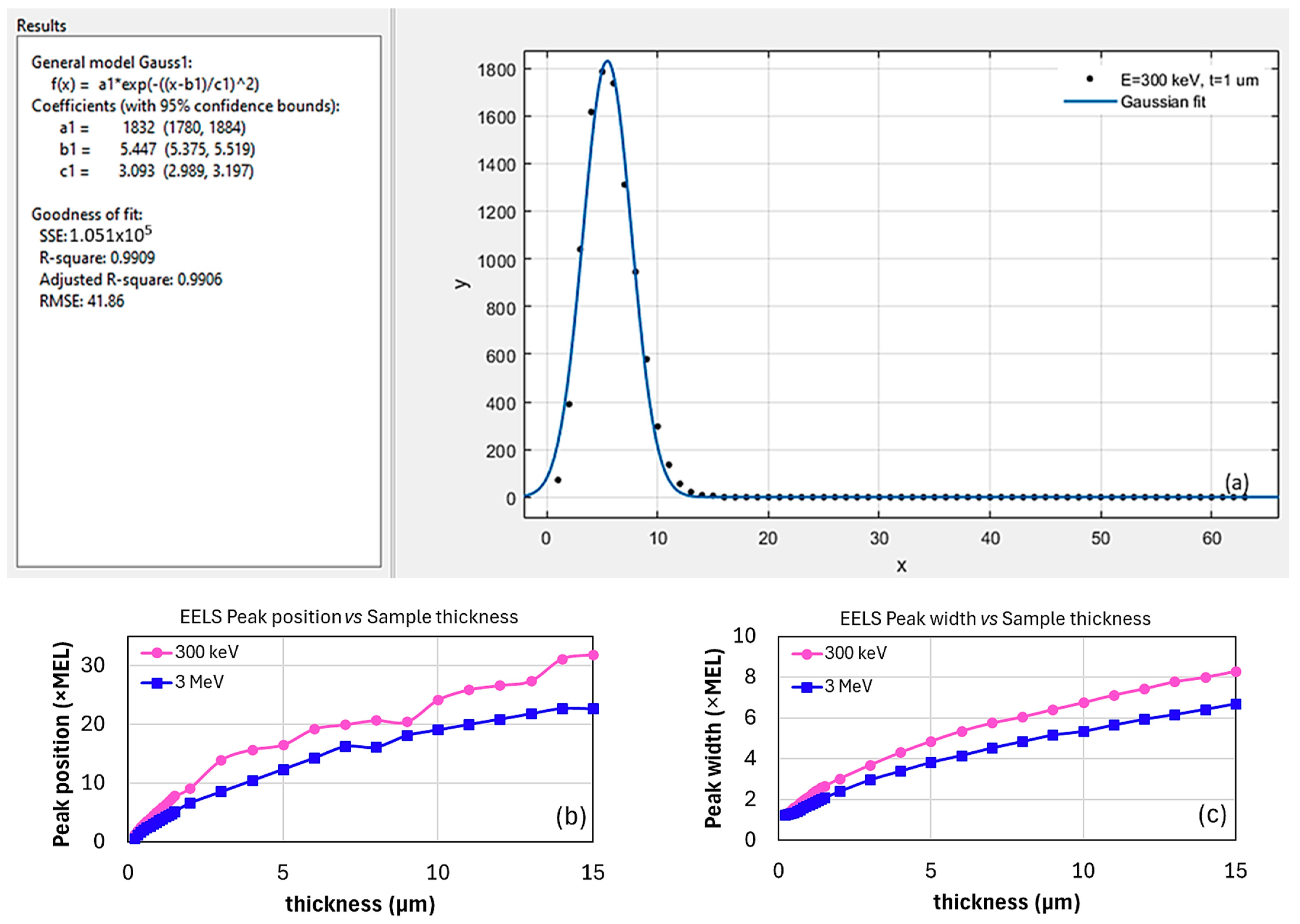
2.3.1. Method 1: Gaussian Fitting
2.3.2. Method 2: Analytical Estimation of Energy Loss
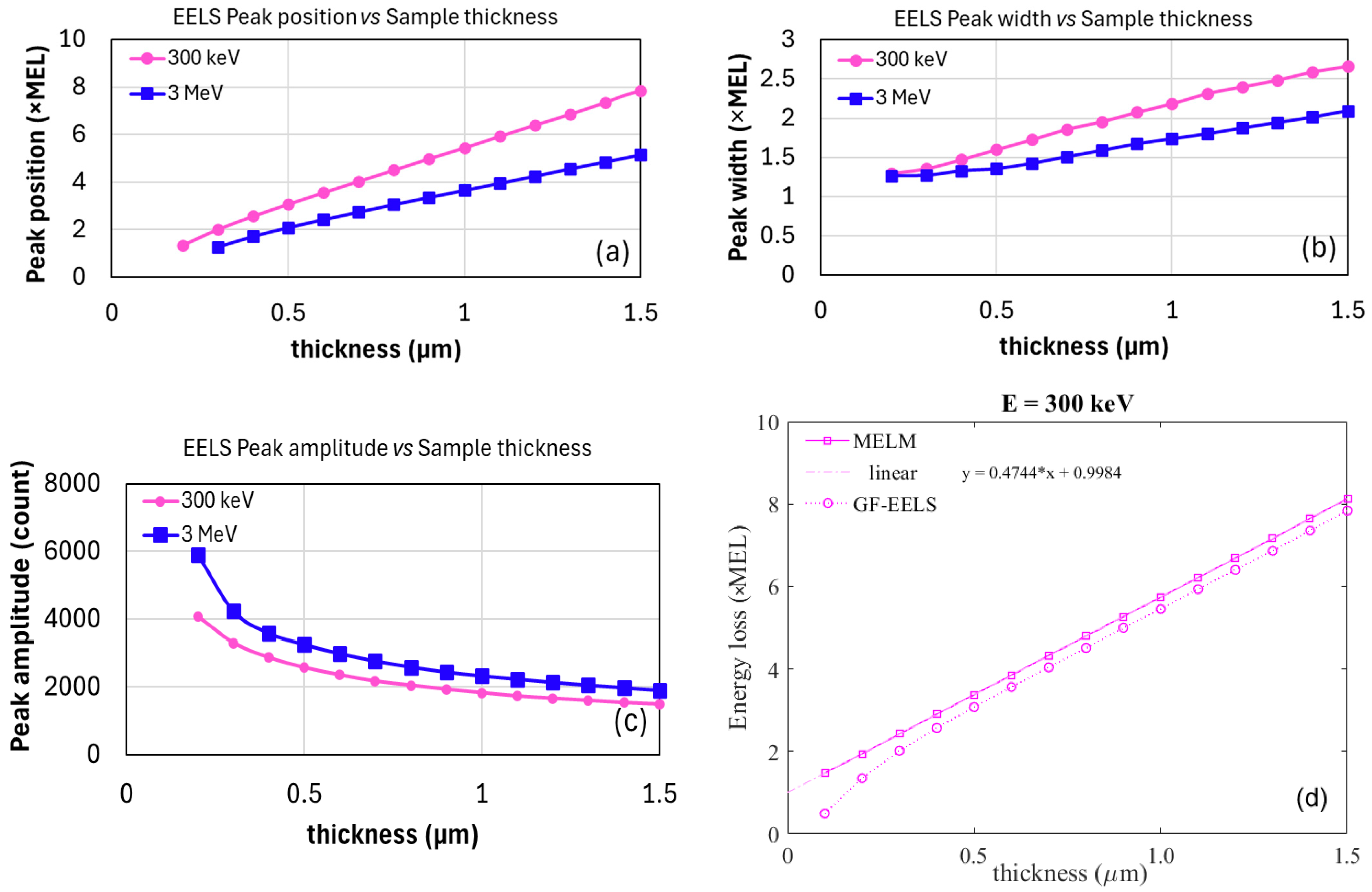
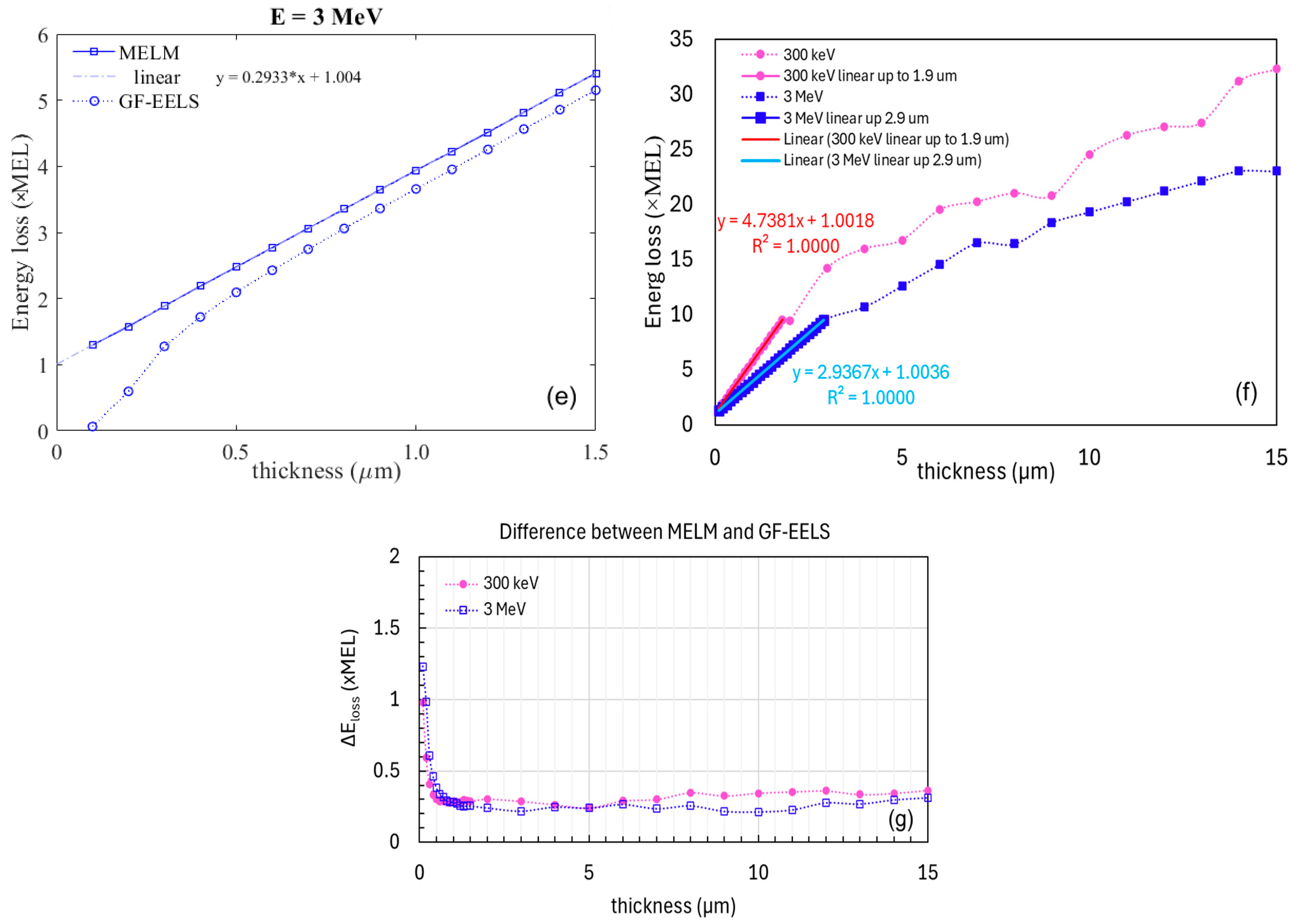
2.4. Simulating EELS for Thin Samples
2.5. Differentiating Elastic and Inelastic Scattering via a Dipole Spectrometer
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Beam Energy Spread Influence on TEM Resolution
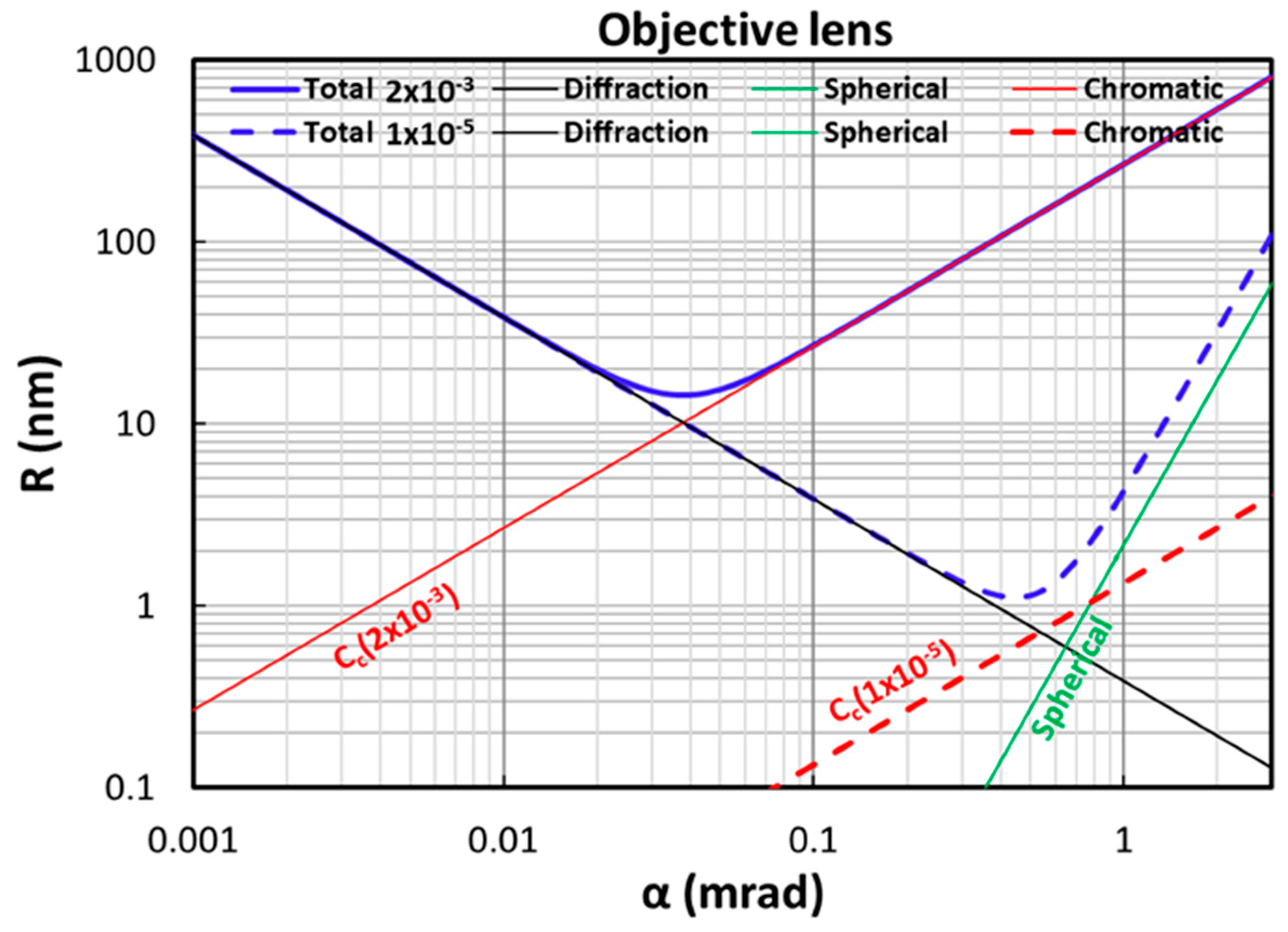
Appendix A.2. Derivation of the Equivalence Between Two Methods: Gaussian Fitting and Direct Analysis
References
- Weiner, E.; Pinskey, J.M.; Nicastro, D.; Otegui, M.S. Electron microscopy for imaging organelles in plants and algae. Plant Physiol. 2022, 188, 713–725. [Google Scholar] [CrossRef] [PubMed]
- Böhning, J.; Bharat TA, M. Towards high-throughput in situ structural biology using electron cryotomography. Prog. Biophys. Mol. Biol. 2021, 160, 97–103. [Google Scholar] [CrossRef] [PubMed]
- Oikonomou, C.M.; Jensen, G.J. Cellular Electron Cryotomography: Toward Structural Biology In Situ. Annu. Rev. Biochem. 2017, 86, 873–896. [Google Scholar] [CrossRef]
- Otegui, M.S.; Pennington, J.G. Electron tomography in plant cell biology. Microscopy 2019, 68, 69–79. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Wang, L.; Maxson, J.; Bartnik, A.C.; Kaemingk, M.; Wan, W.; Cultrera, L.; Wu, L.; Smaluk, V.; Shaftan, T.; et al. Towards Construction of a Novel Nanometer-resolution MeV-STEM for Imaging of Thick Frozen Biological Samples. Photonics 2024, 11, 252. [Google Scholar] [CrossRef]
- Yang, X.; Wang, L.; Smaluk, V.; Shaftan, T. Optimize electron beam energy toward in-situ imaging of large thick frozen bio-samples with nanometer resolution. Nanomaterials 2024, 14, 803. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Yang, X. Monte Carlo Simulation of Electron Interactions in an MeV-STEM for Thick Frozen Biological Sample Imaging. Appl. Sci. 2024, 14, 1888. [Google Scholar] [CrossRef]
- Wan, W.; Chen, F.R.; Zhu, Y. Design of compact ultrafast microscopes for single- and multi-shot imaging with MeV electrons. Ultramicroscopy 2018, 194, 143–153. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Smaluk, V.; Shaftan, T.; Wang, L.; McSweeney, S.; Yu, L.; Tiwari, G.; Hidaka, Y.; Wang, G.; Doom, L.; et al. Current Status of Developing Ultrafast Mega-Electron-Volt Electron Microscope; NSLSII-TN-ASD-383; Brookhaven National Laboratory (BNL): Upton, NY, USA, 2022. [Google Scholar]
- Wolf, S.G.; Shimoni, E.; Elbaum, M.; Houben, L. STEM Tomography in Biology. In Cellular Imaging: Electron Tomography and Related Technique; Hanssen, E., Ed.; Springer International Publishing: Cham, Switzerland, 2018; pp. 33–60. [Google Scholar]
- Reimer, L.; Kohl, H. Transmission Electron Microscopy, 5th ed.; Springer Science + Business Media, LLC.: New York, NY, USA, 2008. [Google Scholar]
- Henderson, R. The potential and limitations of neutrons, electrons and X-rays for atomic resolution microscopy of unstained biological molecules. Q. Rev. Biophys. 1995, 28, 171–193. [Google Scholar] [CrossRef] [PubMed]
- Peet, M.J.; Henderson, R.; Russo, C.J. The energy dependence of contrast and damage in electron cryomicroscopy of biological molecules. Ultramicroscopy 2019, 203, 125–131. [Google Scholar] [CrossRef]
- Langmore, J.P.; Smith, M.F. Quantitative energy-filtered electron-microscopy of biological molecules in ice. Ultramicroscopy 1992, 46, 349–373. [Google Scholar] [CrossRef] [PubMed]
- Jacobsen, C.; Medenwaldt, R.; Williams, S. X-Ray Microscopy and Spectromicroscopy: Status Report from the Fifth International Conference, Würzburg, August 19–23, 1996; Thieme, J., Schmahl, G., Rudolph, D., Umbach, E., Eds.; Springer: Berlin/Heidelberg, Germany, 1998; pp. 197–206. [Google Scholar]
- Du, M.; Jacobsen, C. Relative merits and limiting factors for X-ray and electron microscopy of thick, hydrated organic materials. Ultramicroscopy 2018, 184, 293–309. [Google Scholar] [CrossRef] [PubMed]
- Egerton, R.F. Choice of operating voltage for a transmission electron microscope. Ultramicroscopy 2014, 145, 85–93. [Google Scholar] [CrossRef]
- Tanaka, N. Electron Nano-Imaging, 1st ed.; Springer: Tokyo, Japan, 2017. [Google Scholar]
- Pante, I.; Cucinotta, F.A. Cross sections for the interactions of 1 eV–100 MeV electrons in liquid water and application to Monte-Carlo simulation of HZE radiation tracks. New J. Phys. 2009, 11, 063047. [Google Scholar] [CrossRef]
- Quintard, B.; Yang, X.; Wang, L. Quantitative Modeling of High-Energy Electron Scattering in Thick Samples Using Monte Carlo Techniques. Appl. Sci. 2025, 15, 565. [Google Scholar] [CrossRef]
- Photoelectron Generated Amplified Spontaneous Radiation Source (PEGASUS). Available online: http://pbpl.physics.ucla.edu/pages/pegasus.html (accessed on 20 October 2024).
- Yang, X.; Wang, L.; Smaluk, V.; Shaftan, T.; Wang, T.; Bouet, N.; D’Amen, G.; Wan, W.; Musumeci, P. Simulation Study of High-Precision Characterization of MeV Electron Interactions for Advanced Nano-Imaging of Thick Biological Samples and Microchips. Nanomaterials 2024, 14, 1797. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.; Manshaii, F.; Xiao, X.; Chen, J. Artificial intelligence assisted nanogenerator applications. J. Mater. Chem. A 2025, 13, 832. [Google Scholar] [CrossRef]

| E | dsam | α | ∆E/E | ϵgeo |
|---|---|---|---|---|
| MeV | nm | mrad | pm·rad | |
| 3.0 | 2 | 1 | <10−4 | 2 |
| Elastic Cross-Section (nm2) | Inelastic Cross-Section (nm2) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Detector Collection Angle | Detector Collection Angle | |||||||||
| Electron energy (eV) | θ0 (mrad) | 0–10 mrad | 10–50 mrad | 50–100 mrad | Total | θE (mrad) | 0–10 mrad | 10–50 mrad | 50–100 mrad | Total |
| 300,000 | 11.8 | 2.1 × 10−5 | 2.6 × 10−5 | 2.6 × 10−6 | 5.0 × 10−5 | 0.080 | 9.4 × 10−5 | 6.8 × 10−6 | 3.4 × 10−7 | 1.0 × 10−4 |
| 3,000,000 | 2.1 | 2.9 × 10−5 | 1.3 × 10−6 | 5.5 × 10−8 | 3.1 × 10−5 | 0.011 | 4.1 × 10−5 | 1.7 × 10−7 | 6.9 × 10−9 | 4.1 × 10−5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Smaluk, V.; Shaftan, T.; Wang, L. Enhanced Monte Carlo Simulations for Electron Energy Loss Mitigation in Real-Space Nanoimaging of Thick Biological Samples and Microchips. Electronics 2025, 14, 469. https://doi.org/10.3390/electronics14030469
Yang X, Smaluk V, Shaftan T, Wang L. Enhanced Monte Carlo Simulations for Electron Energy Loss Mitigation in Real-Space Nanoimaging of Thick Biological Samples and Microchips. Electronics. 2025; 14(3):469. https://doi.org/10.3390/electronics14030469
Chicago/Turabian StyleYang, Xi, Victor Smaluk, Timur Shaftan, and Liguo Wang. 2025. "Enhanced Monte Carlo Simulations for Electron Energy Loss Mitigation in Real-Space Nanoimaging of Thick Biological Samples and Microchips" Electronics 14, no. 3: 469. https://doi.org/10.3390/electronics14030469
APA StyleYang, X., Smaluk, V., Shaftan, T., & Wang, L. (2025). Enhanced Monte Carlo Simulations for Electron Energy Loss Mitigation in Real-Space Nanoimaging of Thick Biological Samples and Microchips. Electronics, 14(3), 469. https://doi.org/10.3390/electronics14030469





