An NTRU-Based Key Encapsulation Scheme for Underwater Acoustic Communication

Abstract

With the increasing emphasis on safeguarding maritime sovereignty and developing marine resources, the security of underwater acoustic communication has risen to a new level of importance. Given the complex environmental challenges faced by underwater acoustic channels, this paper proposes an NTRU-based key encapsulation scheme designed to ensure secure and reliable underwater data transmission, while maintaining privacy and integrity. In the public–private key pair generation phase, a ring sampling technique is employed to generate a compact NTRU trapdoor, which not only guarantees security but also effectively reduces the communication overhead. During the encapsulation phase, underwater acoustic channel characteristics during communication are introduced as temporary identity information to ensure the confidentiality and reliability of the key encapsulation mechanism. Furthermore, the traditional key encapsulation mechanism is extended by integrating a digital signature process, where the encapsulated ciphertext is signed. The use of digital signature technology verifies the authenticity and integrity of the transmitted data, ensuring that communication data remain secure and unaltered in complex underwater acoustic environments. Finally, we conduct a rigorous correctness analysis and security proofs, demonstrating that the proposed scheme achieves chosen ciphertext security, while meeting the demands of low bandwidth and limited computational capacity in underwater acoustic communication.

1. Introduction

With the growing global demand for maritime sovereignty protection and the exploitation of underwater resources, underwater acoustic communication technology has become a critical means of ocean information transmission and monitoring [1,2]. However, underwater acoustic communication faces numerous challenges, such as low bandwidth, high latency, frequency-selective fading, and the highly dynamic and complex channel environment, making the assurance of data transmission security and integrity a pressing issue [3]. In harsh underwater acoustic environments, traditional encryption mechanisms struggle to ensure the security of communication [4,5]. They have a high computational overhead, while lacking an efficient key encapsulation mechanism and being unable to resist quantum attacks. To address the security challenges of underwater acoustic communication, numerous studies have focused on two key aspects: encryption algorithms, and key management mechanisms [6,7]. Symmetric encryption algorithms, such as the Advanced Encryption Standard (AES), are widely adopted for their efficiency; however, their security relies heavily on key distribution and management, making them vulnerable to eavesdropping and man-in-the-middle attacks [8]. While symmetric encryption algorithms, such as AES, are widely adopted for their efficiency, their security depends on key distribution and management, making them vulnerable to eavesdropping and man-in-the-middle attacks; in contrast, asymmetric cryptographic algorithms, such as Rivest–Shamir–Adleman (RSA) and elliptic curve cryptography (ECC), offer higher security, but their computational complexity makes them unsuitable for resource-constrained underwater acoustic communication environments [9,10]. Meenakshi et al. [11] improved ECC and optimized it for underwater environments, significantly reducing the computational overhead. However, performance bottlenecks still exist under high-noise conditions and low signal-to-noise ratios, and this method is unable to resist quantum attacks.

Recently, post-quantum cryptography has garnered widespread attention for its ability to resist quantum computing attacks. Among these, lattice-based cryptography has emerged as a research hotspot due to its high level of security and efficiency [12,13,14]. F. Nisha et al. [15] discussed the advantages and disadvantages of NTRU encryption, NTRU signature, ring–lizard, and Kyber algorithms, providing an in-depth analysis of their performance in various application scenarios. Use of the NTRU encryption scheme helps reduce computational and storage overhead. The NTRU public key encryption scheme proposed by Jonghyun et al. [16], with its smaller key size and faster computational performance, has been proven suitable for resource-constrained communication scenarios.In 2023, Piljoo et al. [17] proposed a lightweight polynomial multiplication accelerator based on NTRU, which significantly reduced the overhead associated with key generation and transmission. Eros et al. [18] further validated the security and computational efficiency of NTRU in embedded devices, demonstrating its suitability for dynamic environments. In [19], Alexandr et al. proposed a code-based key encapsulation scheme, achieving significant progress in resisting quantum attacks. In [20], Joohee et al. proposed a post-quantum key encapsulation scheme for IoT devices, which ensures security, while reducing the time consumption for key encapsulation and decryption. Therefore, post-quantum key encapsulation schemes can help optimize computational efficiency and reduce overhead, making them suitable for resource-constrained underwater communication.

In recent years, physical layer security techniques have been proposed as an effective approach to counter eavesdropping attacks. By leveraging the random characteristics of underwater acoustic channels, such as channel state information (CSI), as a source of randomness for key generation, these techniques inherently provide information-theoretic security [21,22]. Pan et al. [23] proposed a lightweight key agreement method, which demonstrated strong robustness in complex underwater environments. Yicong et al. [24] proposed an accurate and efficient key generation method, which encapsulates the CSI with a confusion matrix using circular convolution, thereby enhancing communication accuracy and efficiency. However, such schemes lack integration with post-quantum cryptographic mechanisms and are therefore unable to resist quantum attack threats.

However, designing a key encapsulation method based on NTRU and applying it to underwater acoustic communication still faces the following challenges: (1) how to reduce the communication overhead to accommodate the bandwidth limitations of underwater acoustic channels; and (2) how to integrate underwater channel characteristics to enhance the dynamism and security of key encapsulation.

To address the aforementioned issues, this paper proposes an NTRU-based key encapsulation scheme for underwater acoustic communication. By integrating underwater channel characteristics into a post-quantum cryptographic framework, the scheme aims to achieve efficient and secure key management and data transmission. The following are the main contributions of this paper:

(a).

In the key generation phase, a compact NTRU trapdoor is generated using ring sampling techniques and used as the private key.

(b).

Based on this, underwater acoustic channel characteristics are integrated as temporary identity information to generate the encapsulated key.

(c).

The traditional key encapsulation mechanism is extended by incorporating a digital signature phase.

(d).

Under the random oracle model, the proposed scheme was proven to achieve security against chosen ciphertext attacks, while significantly reducing the communication bandwidth requirements, making it suitable for complex underwater acoustic communication environments.

The organization of this paper is as follows: Section 2 provides a brief introduction to NTRU, KEM (key encapsulation mechanism), digital signatures, and related concepts. Section 3 describes the conventional NTRU trapdoor generation algorithm and the ring sampling algorithm adopted in this paper. Section 4 introduces the model of the underwater acoustic channel and presents the proposed NTRU-based key encapsulation scheme for underwater communication. Section 5 provides a security proof under the random oracle model and compares the proposed scheme with other advanced methods. The paper concludes with Section 6, where the primary findings are recapped.

2. Preliminaries

2.1. Lattices

Lattices are a fundamental concept in both mathematics and cryptography. In cryptography, lattices represent a mathematical structure with significant applications. Below are some definitions of lattices:

Definition 1 (Lattices).

In an m-dimensional vector space ${\mathbb{R}}^m$, $\mathbb{Z}$ represents the set of integers. There is a set of linearly independent vectors $V_1,V_2,\cdots ,V_n\in {\mathbb{R}}^m$ (where $m\ge n$), then the lattice is defined as

$$\Lambda =\left\{\sum _{i=1}^n{x}_i{v}_i:x_i\in \mathbb{Z},i=1,2,\dots ,n\right\}$$

(1)

Vectors $V_1,V_2,\dots ,V_n$ form the basis for the lattice $\mathbf{\Lambda }$, where m is the dimension of the lattice $\mathbf{\Lambda }$, and n is the rank of the lattice $\mathbf{\Lambda }$. Before introducing the NTRU lattice, a definition of the anticirculant matrix is first given.

Lemma 1

([25]). Given an n-dimensional lattice Λ, for any $\epsilon >0$, Gaussian parameter $\sigma >2{\eta }_{\epsilon }(\Lambda )$, and center $c\in {\mathbb{R}}^n$, we have $D_{\Lambda ,\sigma ,c}\left(x\right)\le \left({\displaystyle \frac{1-\epsilon }{1+\epsilon }}\right)·2^{-n}.$ If $\epsilon <1/3$, the minimum value of $D_{\Lambda ,\sigma ,c}\left(x\right)$ is at least $n-1$.

$D_{\Lambda ,\sigma ,c}\left(x\right)$ is used to describe the probability at the point x, and ${\eta }_{\epsilon }(\Lambda )$ represents a bound. Lemma 1 provides both the upper and lower bounds for the function $D_{\Lambda ,\sigma ,c}\left(x\right)$.

Lemma 2.

For any real number $\sigma >0$ and positive integer $\mathrm{m}$, there exists

$$Pr[x\leftarrow D_{\sigma }^1:\mid x\mid >12\sigma ]<2^{-100};Pr[x\leftarrow D_{\sigma }^m:\parallel x\parallel >2\sigma \sqrt{m}]<2^{-m}$$

(2)

In a Gaussian distribution, as the dimensions m and $\sigma$ increase, the probability of drawing a vector whose norm exceeds a certain threshold rapidly becomes very small.

Definition 2 (Anti-circulant matrix).

The N-dimensional anticirculant matrix of $\mathrm{f}$ is defined as the Toeplitz matrix provided below:

$$\begin{array}{c}{A}_N\left(f\right)=\left[\begin{array}{cccc}{f}_0& f_1& \cdots & f_{N-1}\\ -f_{N-1}& f_0& \cdots & f_{N-2}\\ ⋮& ⋮& ⋮& ⋮\\ -f_1& -f_2& \cdots & -f_0\end{array}\right]=\left[\begin{array}{c}f\\ (x\ast f)\\ ⋮\\ x^{N-1}\ast f\end{array}\right]\end{array}$$

(3)

In general, an anti-circulant matrix can be denoted as $\mathrm{A}\left(\mathrm{f}\right)$, which satisfies the following addition and multiplication properties: $A_n\left(f\right)+A_n\left(g\right)=A_n(f+g)$ and $A_n\left(f\right)A_n\left(g\right)=A_n\left(fg\right)$.

Definition 3 (NTRU Lattices).

Let $\mathrm{N}$ be a power of 2, $\mathrm{q}$ be a positive integer, and $f,g\in \mathbb{R}$. Calculate $h=g·f^{-1}modq$. The NTRU lattice Λ can be represented as

$${\Lambda }_{NTRU}=\left\{(u,v)\in R^2\mid u+\nu \ast h=0modq\right\}$$

(4)

The lattice ${\Lambda }_{NTRU}$ is a full-rank lattice in ${\mathbb{Z}}^2$, generated by the matrix ${\mathbf{A}}_{h,q}=\left(\begin{array}{cc}-{\mathcal{A}}_N\left(h\right)& I_N\\ q·I_N& O_N\end{array}\right)$. Due to the poor orthogonality of ${\mathbf{A}}_{h,q}$, it cannot be used as the basis for the trapdoor in the key encapsulation scheme of NTRU. Ducas et al. [26] proposed another method for generating short bases $\mathrm{B}=\left[\begin{array}{cc}g& G\\ -f& -F\end{array}\right]$, which can generate the same lattice as ${\mathbf{A}}_{h,q}$.

Similarly to the NTRU lattice, we define the $\mathrm{q}$-ary lattice.

Definition 4 ($\mathbf{q}$-ary lattice).

Let $n,m,q\in \mathbb{Z}$, $\mathbf{A}\in {\mathbb{Z}}_q^{n\times m}$, and $\mathbf{u}\in {\mathbb{Z}}_q^n$, satisfying $\mathbf{Ax}=\mathbf{u}modq$. The definition is given as follows:

$$\begin{array}{cc}& {\Lambda }^{\perp }\left(A\right)=\{\mathit{y}\in {\mathbb{Z}}^m:\mathit{A}\mathit{y}=\mathbf{0}modq\}\hfill \\ & {\Lambda }_u^{\perp }\left(A\right)=\{\mathit{y}\in {\mathbb{Z}}^m:\mathit{A}\mathit{y}=\mathit{u}modq\}={\Lambda }^{\perp }\left(\mathit{A}\right)+x\hfill \end{array}$$

(5)

where ${\mathbf{\Lambda }}_u^{\perp }\left(\mathbf{A}\right)$ is a coset of ${\mathbf{\Lambda }}^{\perp }\left(\mathbf{A}\right)$.

2.2. Gaussian Functions and Distributions on Lattices

Definition 5 (Discrete Gaussian Function).

For any $c\in {\mathbb{R}}^n$ and $s>0$, the Gaussian function on ${\mathbb{R}}^n$ is defined as

$${\rho }_{s,c}\left(x\right)=e^{-{\pi \parallel x\parallel }^2/s^2}$$

(6)

Lemma 3

([27]). For any vector $v\in {\mathbb{Z}}^m$ and any positive real number α, if $\sigma =\omega (\parallel v\parallel \sqrt{logm})$:

$$Pr[x\leftarrow D_{\sigma }^m:D_{\sigma }^m\left(x\right)/D_{\nu ,\sigma }^m\left(x\right)=O\left(1\right)]=1-2^{-\omega (logm)}$$

(7)

Definition 6 (Discrete Gaussian Distribution).

We can define a discrete Gaussian distribution $D_{\Lambda +c,s}$ on any lattice $\Lambda \in {\mathbb{R}}^N$, centered at c with the parameter s:

$$\forall x\in \Lambda +c,D_{\Lambda +c,s}\left(x\right)={\displaystyle \frac{{\rho }_s\left(x\right)}{{\rho }_s\left(\Lambda +c\right)}}$$

(8)

When $c=0$, it can be simplified as ${\rho }_s\left(x\right)$ and $D_{\Lambda ,s}\left(x\right)$.

2.3. Key Encapsulation Mechanism

The key encapsulation mechanism consists of three polynomial-time algorithms, denoted as $KEM=(KeyGen,Encaps,Decaps)$. Let the security parameter be $\lambda$, the key space be $\mathbf{K}$, and the ciphertext space be $\mathrm{C}$. The following describes the three algorithms:

(1) Key Generation Algorithm $(pk,sk)$←$KeyGen$($1^{\lambda }$):

Input the security parameter, and output a pair of public and private keys $(pk,sk)$.

(2) Key Encapsulation Algorithm $(c,K)\leftarrow Encaps\left(pk\right)$:

Input the public key $\mathrm{pk}$, output the temporary encapsulated key $\mathrm{K}$ and the corresponding ciphertext $\mathrm{c}$, where c $\in \mathrm{C}$.

(3) Decapsulation Algorithm $K^{\prime }\leftarrow Decaps(sk,c)$:

Input the private key $\mathrm{sk}$ and the ciphertext $\mathrm{c}$, output the temporary encapsulated key $K^{\prime }$. Here, $K^{\prime }$ can be ⊥, which indicates a decapsulation failure.

Definition 7 (The correctness of KEM).

The probability of key decapsulation failure is defined as

$$Pr\left[Decaps\right(sk,c)\ne K:(c,K)\leftarrow Encaps(pk)<\delta ]$$

(9)

That is, if $K^{\prime }=K$ holds for any security parameter $\lambda$, the encapsulation scheme is considered correct. A $\mathrm{KEM}$ scheme is said to satisfy indistinguishability under chosen ciphertext attack (IND-CCA) security if, for any polynomial-time adversary A, the attacker’s advantage satisfies

$$Ad{\nu }_{\mathrm{A},KEM}^{IND-CCA}\left(\lambda \right)=Pr\left[\begin{array}{c}\left(pk,sk\right)\leftarrow KeyGen\left(1^{\lambda }\right);\\ \left(c^{\ast },K_0\right)\leftarrow Encaps\left(pk\right);\\ K_1\leftarrow \mathbf{K};b\leftarrow \{0,1\};\\ b^{\prime }\leftarrow {\mathrm{A}}^{Dec(\ast )}\left(pk,c^{\ast },K_b\right);\\ b^{\prime }=b\end{array}\right]\le -{\displaystyle \frac{1}{2}}$$

(10)

2.4. Digital Signature

The digital signature scheme comprises three distinct algorithms, denoted as $Sig=(Gen,Sign,Ver)$. Let $\mathbf{M}$ be the message space, $\mathbf{S}$ be the signature space, and $\lambda$ be the security parameter. Below are the definitions of the three algorithms:

(1) Key Generation Algorithm $(pk,sk)$←$Gen$($1^{\lambda }$):

Given the security parameter $\lambda$, the algorithm outputs a public and private key pair $(pk,sk)$.

(2) Signature Algorithm s = ${\mathrm{Sign}}_{sk}\left(m\right)$:

Input the message m, where $m\in M$, and the private key $sk$; output the signature s, where $s\in S$.

(3) Verification Algorithm $Ve{r}_{pk}\left(m,s\right)$:

Given the public key $pk$, the message m, and the signature s, the signature is considered valid if $Ve{r}_{pk}(m,s)=1$; otherwise, it is deemed invalid.

Definition 8 (Unforgeability of Digital Signatures).

For a digital signature scheme $Sig=(Gen,Sign,Ver)$ for any polynomial-time adversary $\mathbf{A}$, there exists a non-negligible function $\mathrm{negl}$ such that the following condition is satisfied:

$$Pr\left[Ver\left(\lambda ,s,pk\right)=m\right]=1-negl\left(\lambda \right)$$

(11)

One might conclude that the digital signature scheme exhibits robust resistance to adaptive chosen-message attacks.

Definition 9 (The confidentiality of digital signatures).

In the context of anonymous identity-based cryptography under the multi-user adaptive chosen ciphertext attack (MU-IND-CCA) security model, if no adversary can win the MU-IND-CCA game with a non-negligible advantage in polynomial time, then the digital signature scheme possesses strong secrecy.

Lemma 4

([28]). Forking Lemma. Suppose A is a probabilistic polynomial-time Turing machine that can generate a valid signature σ for a given message m and a random oracle output h with a non-negligible probability. If A is run again with the same random seed but a different random oracle, it will, with non-negligible probability, produce a second valid forgery ${\sigma }^{\prime }$ for the same message m, corresponding to a different random oracle output $h^{\prime }$, where $h\ne h^{\prime }$.

2.5. Hardness Assumption

The following section introduces the related hard problems concerning the lattices and NTRU lattices involved in the proposed scheme.

Definition 10 (The R-SIS_q,m,β problem).

Given a random vector $\overrightarrow{a}\in {\mathbb{R}}_q^m$ and a real number $\beta >0$, the problem is to find a non-zero vector $\overrightarrow{z}\in {\mathbb{R}}^m$ such that $\parallel \overrightarrow{z}\parallel \le \beta$ and ${\sum }_{i=1}^m{a}_i·z_i=0(modq),$ where ${(z_1,\dots ,z_m)}^T\in {\mathbb{R}}^m$.

Definition 11 (The $\mathit{SIS}$ problem on the NTRU lattice).

Given a prime q, a real number β, and two small polynomials $f,g\in \mathbb{R}$, let $A_{h,q}=\left(\begin{array}{c}h,1\end{array}\right)\in {\mathbb{R}}_{1_q\times 2}$, where $h={\displaystyle \frac{g}{f}}$. The SIS problem on the NTRU lattice is to find a vector $\left(\begin{array}{c}{z}_1,z_2\end{array}\right)\in {\mathbb{R}}_{2_q\times 1}$ that satisfies the following two conditions: 1. $A_{h,q}{\left(\begin{array}{c}{z}_1,z_2\end{array}\right)}^T=0(modq)$, 2. $∥\left(\begin{array}{c}{z}_1,z_2\end{array}\right)∥\le \beta$.

Definition 12 (The NTRU One-Wayness Assumption).

NTRU one-way hardness refers to the difficulty of computing $(r,e)$ given the public key h and the ciphertext c.

3. Trapdoor Generation Algorithm on NTRU Lattices

3.1. TrapGen

Given a security parameter $\lambda$, a prime $q=\mathrm{poly}\left(\lambda \right)$, and a Gaussian parameter $\sigma >\omega \left(\sqrt{log\left(2\lambda \right)}\right))$, there exists a probabilistic polynomial-time (PPT) algorithm ${\mathrm{TrapGen}}_{\mathrm{NTRU}}$ that takes $1^{\lambda }$ as input and outputs an NTRU lattice ${\Lambda }_{h,q}$ with a trapdoor basis ${\mathbf{B}}_{f,g}$ and a polynomial $h=g·f^{-1}modq$, satisfying $\parallel (f,g)\parallel \le 2\sigma \sqrt{\lambda }$. Let ${\mathcal{R}}_q^{\times }$ represent all invertible elements modulo q in the polynomial ring $\mathcal{R}=\mathbb{Z}\left[x\right]/(x^n+1)$, and let ${\mathcal{D}}_{\sigma }^n$ denote the n-dimensional discrete Gaussian distribution with parameter $\sigma$. For the set D, denote $f\leftarrow D$ as selecting f uniformly at random from D. The specific steps of the algorithm are as follows: Algorithm 1 [29].

Algorithm 1 ${\mathrm{TrapGen}}_{\mathrm{NTRU}}$($1^{\lambda }$)

Input:  $\lambda ,q,\sigma .q=\mathrm{ploy}\left(\lambda \right),\sigma >\omega \left(\sqrt{log\left(2\lambda \right)}\right)$

Output:  ${\mathit{B}}_{f,g},h.h=g·f^{-1}modq$

1: Sample $f\leftarrow {\mathcal{D}}_{\sigma }^n$, $g\leftarrow {\mathcal{D}}_{\sigma }^n$. If $fmodq\notin {\mathcal{R}}_q^{\times }$ and $gmodq\notin {\mathcal{R}}_q^{\times }$, or $\parallel f\parallel >\sigma \sqrt{\lambda }$ and $\parallel g\parallel >\sigma \sqrt{\lambda }$, resample. 2: If $⟨f,g⟩\ne \mathcal{R}$, restart. 3: Compute $F_1,G_1\in \mathcal{R}$ such that $f{G}_1-g{F}_1=1$. Then set $F_q=q{F}_1$ and $G_q=q{G}_1$. 4: Compute $F,G\in \mathcal{R}$, where for $k\in \mathbb{Z}$, $(F,G)=(F_q,G_q)-k(f,g)$. 5: If $∥\left(F,G\right)∥>\lambda \sigma$, restart. 6: Return $B_{f,g}$, $h=g·f^{-1}modq$.

3.2. Annular NTRU Trapdoor Generation

Common $\mathrm{NTRU}$ trapdoor generation algorithms (for example, Algorithm 1) typically obtain the desired quality polynomial pair $(\mathrm{f},\mathrm{g})$ by repeatedly sampling until a random polynomial pair $(\mathrm{f},\mathrm{g})$ has been generated. Although this method appears to be straightforward, it has shortcomings in terms of efficiency and security. In our approach, to adapt to the underwater acoustic communication environment, we propose a ring-based uniform sampling method based on a hybrid sampler, suitable for generating trapdoor bases $B_{f,g}$.

Our approach embeds a quality target ${\phi }_i$ into the hybrid sampler and directly performs uniform sampling from quality targets that meet the conditions. Figure 1 shows the ring uniform sampling. The specific implementation is as follows: Algorithm 2.

Algorithm 2 Ring Trapdoor Generation Algorithm

Input: Ring order n, modulus q, target quality coefficient $\alpha$ and ring region $A^{+}(r,R)$, where $0<r<R$.

Output:  ${\mathit{B}}_{f,g},h.h=g·f^{-1}modq$

1: repeat 2: $for1\le i\le n/2do$ 3: $u\leftarrow U\left(\left[r^2,R^2\right]\right),\rho \leftarrow \sqrt{u},\theta \leftarrow U\left([0,\pi /2]\right)$ 4: $\left(z,z^{\prime }\right)\leftarrow \left(x·e^{i\nu },y·e^{i{\nu }^{\prime }}\right)$ end for 5: $\tilde{f}\leftarrow {\phi }^{-1}(z_1,\cdots ,z_{n/2}),\tilde{g}\leftarrow {\phi }^{-1}(w_1,\cdots ,w_{n/2})$ 6: $f\leftarrow \tilde{f},g\leftarrow \tilde{g}$ 7: Until $\forall i=1,\cdots ,n/2,\left(\left|{\phi }_i\left(f\right)\right|+\left|{\phi }_i\left(g\right)\right|\right)\in A^{+}\left(\sqrt{q}/\alpha ,\alpha \sqrt{q}\right)$ 8: Return $B_{f,g}$, $h=g·f^{-1}modq$

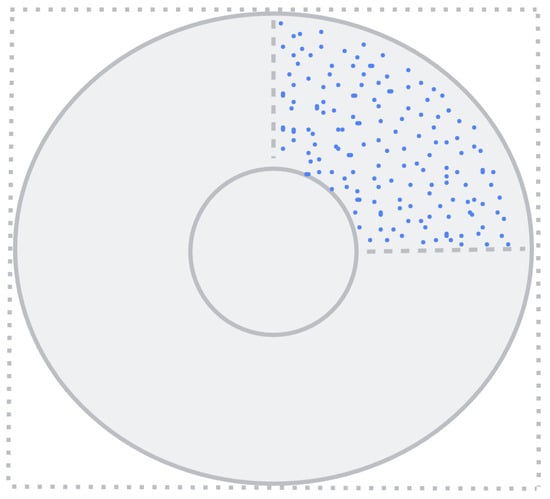
Figure 1. Sampled uniformly in $A^{+}(r,R)$.

The process from $\tilde{f}$, $\tilde{g}$ to $B_{f,g}$ is omitted after Step 7 in Algorithm 2, as it is the same as in Algorithm 1. Since the polynomials $\tilde{f}$ and $\tilde{g}$ generated using the inverse Fourier transform typically do not have integer coefficients and thus do not meet the requirements of the NTRU trapdoor, this paper effectively addresses this issue by applying a coefficient-by-coefficient rounding method [30] which maximally preserves the original properties of the polynomials.

4. Syntax and Model

4.1. Underwater Acoustic Channel Model

The over-the-air (OTA) model is commonly used to describe the process of transmitting and aggregating information through wireless channels, particularly in mobile communication and sensor networks. This model is also applicable to underwater acoustic communication. However, due to factors such as signal attenuation, propagation speed variations, and noise in the underwater environment, the characteristics of underwater acoustic communication differ from those of aerial channels. Therefore, in this paper, we reference relevant literature [31,32] and propose improvements and adaptations to the existing underwater acoustic channel model based on prior research. The following is a detailed introduction to the underwater acoustic channel model adopted in this study.

It is assumed that Alice and Bob, the two parties participating in the underwater acoustic communication, are both legitimate, while the third-party attacker (Eve) is the adversary. In the proposed NTRU-based underwater acoustic communication key encapsulation scheme, Alice is responsible for generating the temporary key, performing the key encapsulation, signing the encapsulated ciphertext, and finally transmitting the data to Bob via the underwater acoustic channel. Bob is responsible for verifying the signature and performing the decapsulation operation to ensure that the received data are legitimate and have not been tampered with. The communication model is shown in Figure 2.

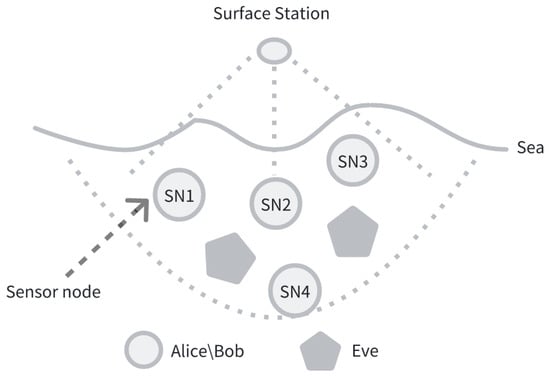
Figure 2. The Communication Model.

The underwater acoustic channel is a complex, random, spatiotemporal, and frequency-varying channel, and its transmission quality is severely affected by multipath and Doppler effects. Due to the complexity of the shallow water environment, underwater acoustic signals undergo refraction and reflection when interacting with the seabed, sea surface, or marine organisms during transmission. As a result, the underwater acoustic signals sent by Alice do not reach Bob simultaneously, leading to multipath effects.

Let $\mathrm{P}$ be the number of paths, ${\tau }_p$ be the delay of the p-th path, $h_p$ be the channel gain of the p-th path, and $n\left(t\right)$ be the noise in the channel. The multipath channel can be represented as

$$h\left(t\right)=\sum _{i=1}^P{h}_p\left(t\right)s\left(t-{\tau }_p\right)+n\left(t\right)$$

(12)

where $h\left(t\right)$ is the transmitted signal and $s\left(t\right)$ is the received signal.

In underwater communication, the relative positions of Alice and Bob are typically in a state of relative motion, so the impact of the Doppler effect must be considered. Furthermore, as the underwater acoustic signals travel along different paths to the receiver, the incident angles will vary, resulting in different Doppler factors for each path. By substituting ${\tau }_p\left(t\right)={\tau }_p+g_{i}t$ into the above equation, the multipath channel with Doppler effect can be expressed as

$$h\left(\begin{array}{c}t\end{array}\right)=\sum _{i=1}^P{h}_p\left(\begin{array}{c}t\end{array}\right)s\left(\begin{array}{c}t-{\tau }_p-g_{p}t\end{array}\right)+n\left(\begin{array}{c}t\end{array}\right)$$

(13)

where $g_p$ is the Doppler factor.

In the proposed scheme of this paper, a joint channel model is developed for the underwater acoustic channel, which can be expressed as

$$h(t,f)=\sum _{i=1}^L{a}_i{e}^{j2\pi \Delta f_{i}t}\delta \left(t-{\tau }_p\right)$$

(14)

Based on this, a two-dimensional Gaussian distribution is constructed, where the mean and covariance matrices represent the distribution characteristics of the multipath delay and Doppler shift, respectively. The joint distribution can be expressed as

$$P(\tau ,\Delta f)={\displaystyle \frac{1}{2\pi {\sigma }_{\tau }{\sigma }_f}}exp\left(-{\displaystyle \frac{{\left(\tau -{\mu }_{\tau }\right)}^2}{2{\sigma }_{\tau }^2}}-\left({\displaystyle \frac{\Delta f-{\mu }_f^2}{2{\sigma }_f^2}}\right)\right)$$

(15)

For simplicity, we assume that the received signal undergoes a Fourier transform to obtain its frequency domain representation $H\left(f\right)$. Based on the joint distribution $P(\tau ,\Delta f)$, a channel compensation matrix $C(f,\tau )$ is constructed, where the complex compensation factor for each path can be expressed as $C_i=e^{-j\left(2\pi \Delta f_i{\tau }_i\right)}$. By calculation, the joint compensation for multipath and Doppler can be obtained as follows

$$Y\left(f\right)=H\left(f\right)·C(f,\tau )$$

(16)

In the key encapsulation process, applying the joint compensation of the complex compensation factors to the ciphertext helps improve the integrity and security of transmission over the underwater acoustic channel under the influence of multipath and Doppler effects. In our scheme, the unique characteristics of the underwater acoustic channel are leveraged to enhance the security of the encapsulation.

4.2. Scheme Definition

In this section, we will describe a key encapsulation scheme suitable for underwater acoustic secure communication.

Our scheme involves 6-tuples of algorithms: Setup, Key-Gen, Key-Encaps, Sign, Verify, and Key-Decaps.

Setup. Alice takes the security parameter $\lambda$ as input and selects the appropriate parameters required for the system.

Key-Gen. Alice runs the trapdoor generation algorithm to output the public and private key pair.

Key-Encaps. Alice uses the private key to perform the encapsulation operation, taking into account the characteristics of the underwater acoustic channel, and outputs the encapsulated key K and ciphertext $CT$.

Sign. Alice generates a signature private key based on the characteristics of the underwater acoustic channel, signs the encapsulated ciphertext $CT$, and sends the signature $sig$ and the ciphertext $CT$ to Bob.

Verify. Bob uses the public key to verify the received signature $sig$.

Key-Decaps. Bob uses the private key to decapsulate the ciphertext $CT$ after the signature verification is successful, and outputs the message m and the encapsulated key K.

4.3. Security Model

This section outlines the security model for our scheme, focusing primarily on two key dimensions.

Existential Unforgeability: Ensure that in the complex underwater acoustic communication environment, the legitimate receiver receives the signed ciphertext as authentic and complete, thereby ensuring that the decapsulated key K is correct and error-free.

Confidentiality: Ensure that no one, other than the legitimate recipient, can extract any meaningful information from the ciphertext and thereby break the encapsulated key K.

4.4. Construction of the Scheme in This Paper

The NTRU-based underwater acoustic communication key encapsulation scheme proposed in this paper is introduced below, denoted as UA-NTRU.

(1) Setup. Given a security parameter $\lambda$. Let the polynomial ring be $R_q=\mathbb{Z}\left[x\right]/⟨x^n+1⟩$, where n is the degree of the polynomial and q is the modulus. Choose a positive integer p such that $gcd(p,q)=1$. Let the plaintext space be $\mathcal{M}\in {\{0,1\}}^k$, the key encapsulation space be ${\{0,1\}}^{\nu }$, and the Gaussian parameter $\sigma >\omega \left(\sqrt{log\left(2n\right)}\right)$, $x=\tilde{\Omega }\left(n^{3/2}\sigma \right)$. Let $H:{\{0,1\}}^{\ast }\to {\{0,1\}}^k$ be a hash function.

(2) Key-Gen. Run Algorithm 2 to obtain $h=g·f^{-1}modq$, where $h\in R_q$. And obtain $B_{f,g}=\left[\begin{array}{cc}g& G\\ -f& -F\end{array}\right]\in R_q^{2\times 2}$. The private key is $sk=B_{f,g}$, and the public key is $pk=h$.

(3) Key-Encaps. This step is divided into two parts: generating the encapsulated key K and the encapsulated ciphertext $CT$ by combining the characteristics of the underwater acoustic channel. Alice first dynamically obtains the channel characteristics $\left(\begin{array}{c}\Delta f,\tau ,L\end{array}\right)$ from the underwater acoustic sensor. For the sake of simplicity, it is assumed that the obtained channel characteristics are normalized and then combined into a feature vector $F=\left(\begin{array}{c}\Delta f,\tau ,L\end{array}\right)$. Use a hash function to map H to the polynomial ring: T = H$\left(F\right)\in {\left\{0,1\right\}}^{{\nu }_1}$.

Input message $m\in \mathcal{M}$, public key $pk$. Randomly select $K^{\prime }\in {\{0,1\}}^{{\nu }_2}$, Compute the encapsulated key $K=T\parallel K^{\prime }$, $v=v_1+v_2$. Randomly select $r,e_0,e_1\leftarrow {\{-1,0,1\}}^{\ast }$, and compute $c_1=m\otimes H\left(K\right)$, $c_2=rh+e_0$, $c_3=rK+e_1+⌊{\displaystyle \frac{q}{2}}⌉·K.$ Here, $c_2,c_3\in R_q$, ⌊⌉ represents the rounding function. Considering the computational efficiency of the nodes in the underwater acoustic environment, we perform the following operation on $c_3$, $c_3=2^b·⌊{\displaystyle \frac{1}{2^b}}·c_3⌋$. Where $\lceil {log}_{2}q\rceil -3\ge b$.

Output the ciphertext $CT=(c_1,c_2,c_3)$, and the encapsulated key is K.

(4) Sign. In this stage, the generated ciphertext $CT$ is signed to produce the signature $Sig$. The signing process, combined with underwater acoustic communication, follows the same procedure as described above. Run the Gaussian sampling algorithm to obtain $(x_1,x_2)=(T,0)-SampleD({\mathit{B}}_{\mathit{f},\mathit{g}},x,(T,0))$. Where $x_1$ and $x_2$ satisfy $\left\{\begin{array}{c}{x}_1+x_2·h=T\end{array}\right\}.$ Output the signature private key $s{k}_{sig}=(x_1,x_2)$. Select polynomials $a_1,a_2\in D_{\sigma }^n$. Compute $u=H^{\prime }(a_1+h·a_2,CT)$. For $i=1,2$, compute $z_i=a_i+x_i·u$. Output the signature $sig=(z_1,z_2,u)$.

(5) Verify. Input the signature $sig$, ciphertext $CT$, and channel characteristics F. The verifier outputs “1” if and only if $H^{\prime }(h\ast z_2+z_1-H\left(F\right)\ast u,CT)=u$, where it must satisfy $\parallel (z_1,z_2)\parallel \le 2\sigma \sqrt{2n}$.

(6) Key-Decaps. After step 4, verification is passed, Bob uses the private key $B_{f,g}$ to perform the decryption operation on the ciphertext $CT=(c_1,c_2,c_3)$. Compute $S_{f,g}=\left(1,-B_{f,g}\right)$ and $f=⟨c_3,S_{f,g}⟩$. Compute $K=⌊{\displaystyle \frac{2}{q}}·f⌉$. If the parsed result is $K=T\parallel K^{\prime }$, the encapsulation is successful, and output the encapsulated key K; otherwise, output ⊥.

4.5. Correctness Analysis

Let us first consider the correctness of the digital signature in our scheme. In the step Verify, it can be seen that

$$\begin{array}{c}h\ast z_2+z_1-H\left(F\right)\ast u\hfill \\ =h\ast (a_2+x_2\ast u)+(a_1+x_1\ast u)-T\ast u\hfill \\ =h\ast (a_2+x_2\ast u)+(a_1+x_1\ast u)-(x_2\ast h+x_1)\ast u\hfill \\ =a_1+a_2\ast h\hfill \end{array}$$

(17)

Therefore, we have $H^{\prime }(h\ast z_2+z_1-H\left(F\right)\ast u,CT)=H^{\prime }(a_1+a_2\ast h)=u$, which satisfies the first condition for the correctness of the signature. Based on Lemmas 1–3 and the rejection sampling technique [33], it can be concluded that $\parallel z_1\parallel \le 2\sigma \sqrt{n}$ and $\parallel z_2\parallel \le 2\sigma \sqrt{n}$ with a probability of at least $1-2^{-\omega (logn)}$. Therefore, it can be satisfied that $\parallel (z_1,z_2)\parallel$ with overwhelming probability satisfies $\parallel (z_1,z_2)\parallel \le 2\sigma \sqrt{2n}$. In conclusion, it can be deduced that the digital signature scheme in our proposal satisfies correctness.

After ensuring the correctness of Steps 3–4, the verification process of the underwater acoustic communication-based key encapsulation scheme in this paper is as follows: Through $c_1$, Bob can compute $m=c_1\oplus H\left(K\right)$ to recover the original message m. In our scheme, for any $(pk,sk)\leftarrow \mathrm{Key-Gen}\left(1^{\lambda }\right)$ and the encapsulated key $K\in {\{0,1\}}^v$. Satisfy $Pr\left\{\mathrm{Key-Decaps}\left(\mathrm{Key-Encaps}(pk,T)\right)=T\Vert K^{\prime }\right\}=1$. To ensure that the key K can be correctly decapsulated, assume that the noise follows a zero-mean Gaussian distribution with a variance of ${\displaystyle \frac{2}{3}}\left(\parallel B_{f,g}{\parallel }^2+1\right)$, where $\parallel B_{f,g}\parallel$ is the norm of Bob’s private key. The following correctness condition can be derived: $q\ge {\displaystyle \frac{32\sqrt{\lambda ln2}}{3\sqrt{3}}}·\parallel {\mathsf{B}}_{f,g}\parallel$. It is important to note that bit loss may lead to decryption errors. However, when $\lceil {log}_{2}q\rceil -3\ge b$, this does not significantly affect the correct decapsulation of the scheme.

5. Security Proof

5.1. Existential Unforgeability

This section demonstrates that the proposed NTRU-based key encapsulation scheme for underwater acoustic communication achieves unforgeability within the random oracle framework.

Theorem 1.

Assuming that the small integer solution (R-SIS) problem on rings is hard, the NTRU-based underwater acoustic communication key encapsulation scheme proposed in this paper satisfies unforgeability in the random oracle model.

Proof. 

If there exists a PPT adversary $\mathcal{A}$ that can forge a signature in Step 3 of the scheme with a non-negligible probability $\epsilon$, then we can construct a challenger $\mathcal{C}$ that, by interacting with $\mathcal{A}$, can solve the R-SIS problem with the same non-negligible probability. The game simulation between the adversary $\mathcal{A}$ and the challenger $\mathcal{C}$ is as follows:

(1) The challenger $\mathcal{C}$ takes the security parameter $\lambda$ as input and randomly selects two hash functions $H:{\{0,1\}}^{\ast }\to {\mathbb{Z}}_q^n$ and $H^{\prime }:{\{0,1\}}^{\ast }\to {\mathbb{Z}}_q^n$. Then, $\mathcal{C}$ sends the system’s master private key $B_{f,g}$, the master public key h, and the public parameters $\mathrm{PP}=\{H,H^{\prime }\}$ to the adversary $\mathcal{A}$.

(2) The adversary $\mathcal{A}$ can adaptively make the following queries to the challenger $\mathcal{C}$ in polynomial time, assuming that $\mathcal{A}$ does not make duplicate queries.

$H_1$ query: $\mathcal{C}$ maintains a list $L_1=\{F,H\left(F\right),s{k}_{f,g}\}$, initially empty. When the adversary $\mathcal{A}$ sends the channel characteristic F for the $H_1$ query, $\mathcal{C}$ first searches the list $L_1$. If $H\left(F\right)$ is found, $\mathcal{C}$ returns $H\left(F\right)$ to the adversary $\mathcal{A}$. Otherwise, $\mathcal{C}$ uniformly randomly selects polynomials $x_1,x_2\in D_x^n$, computes $H\left(F\right)=x_1+h·x_2$, and stores it in $L_1$. Finally, $\mathcal{C}$ sends $H\left(F\right)$ to the adversary $\mathcal{A}$.

$H_2$ query: When the adversary $\mathcal{A}$ sends the channel characteristic F to the oracle for a key extraction query, $\mathcal{C}$ searches in $L_1$ and sends the corresponding $s{k}_{\mathrm{sig}}$ to the adversary $\mathcal{A}$.

Signature query: To obtain a signature for the ciphertext CT, the adversary $\mathcal{A}$ sends $(F,\mathrm{CT})$ for a signature query. Upon receiving the query, $\mathcal{C}$ first looks up the corresponding $s{k}_{\mathrm{sig}}$ in $L_1$, then randomly selects polynomials $a_1,a_2\in D_{\sigma }^n$ and a polynomial $u\in D_{H^{\prime }}$. Let $u=H^{\prime }(a_1+h·a_2,\mathrm{CT})$. Next, for $i=1,2$, $\mathcal{C}$ computes $z_i=a_i+x_i·u$, obtaining the signature $\mathrm{sig}=(z_1,z_2,u)$. Finally, $\mathcal{C}$ stores $\{\mathrm{sig}=(z_1,z_2,u),F,\mathrm{CT},a_1,a_2\}$ at the corresponding position in $L_1$, and sends the signature sig to the adversary $\mathcal{A}$.

$H^{\prime }$ query: When the adversary $\mathcal{A}$ sends $(\mathrm{CT},a_1,a_2)$ for an $H^{\prime }$ query, $\mathcal{C}$ searches in $L_1$ for $(\mathrm{CT},a_1,a_2)$ and sends the corresponding polynomial u to the adversary $\mathcal{A}$.

The adversary $\mathcal{A}$ outputs a forged signature ${\mathrm{sig}}^{\prime }=(z_1^{\prime },z_2^{\prime },u^{\prime })$ for $(F^{\prime },{\mathrm{CT}}^{\prime })$ with a non-negligible probability.

According to Lemma 4, $\mathcal{A}$ outputs a new forged signature ${\mathrm{sig}}^{\ast }=(z_1^{\ast },z_2^{\ast },u^{\ast })$ for $(F^{\prime },C{T}^{\prime })$ with non-negligible probability, such that $z_1^{\prime }+z_2^{\prime }·h-H\left(F^{\prime }\right)·u^{\prime }=z_1^{\ast }+z_2^{\ast }·h-H\left(F^{\prime }\right)·u^{\ast }=y_1^{\prime }+h·y_2^{\prime }$, where $u^{\ast }\ne u^{\prime }$, so we have $[z_1^{\prime }-z_1^{\ast }-x_1^{\prime }(u^{\prime }-u^{\ast })]+[z_2^{\prime }-z_2^{\ast }+x_2^{\prime }(u^{\prime }-u^{\ast })]·h=0$. According to Lemmas 1 and 2, we have $\Vert z_1^{\prime }-z_1^{\ast }-x_1^{\prime }(u^{\prime }-u^{\ast })\Vert \le \Vert z_1^{\prime }\Vert +\Vert z_1^{\ast }\Vert +\Vert x_1^{\prime }{u}^{\prime }\Vert +\Vert x_1^{\prime }{u}^{\ast }\Vert \le (4\sigma +2\lambda x)\sqrt{n}$, which holds with overwhelming probability. Similarly, $\Vert z_2^{\prime }-z_2^{\ast }+x_2^{\prime }(u^{\prime }-u^{\ast })\Vert \le \Vert z_2^{\prime }\Vert +\Vert z_2^{\ast }\Vert +\Vert x_2^{\prime }{u}^{\prime }\Vert +\Vert x_2^{\prime }{u}^{\ast }\Vert \le (4\sigma +2\lambda x)\sqrt{n}$.

Based on the preimage minimum distance property of the trapdoor function on the NTRU lattice, it is highly probable that there exists a new signing key $s{k}_{f,g}^{\ast }=(x_1^{\ast },x_2^{\ast })$, where the new signature differs from $(x_1^{\prime },x_2^{\prime })$ only in the i-th coefficient, and satisfies $x_1^{\ast }+x_2^{\ast }·h=H\left(F^{\prime }\right)$. If $x_1^{\prime }\ne x_1^{\ast }$, then we have $[z_1^{\prime }-z_1^{\ast }-x_1^{\prime }(u^{\prime }-u^{\ast })]-[z_1^{\prime }-z_1^{\ast }-x_1^{\ast }(u^{\prime }-u^{\ast })]=(x_1^{\ast }-x_1^{\prime })(u^{\prime }-u^{\ast })\ne 0.$ Therefore, if $z_1^{\prime }-z_1^{\ast }-x_1^{\ast }(u^{\prime }-u^{\ast })=0$, it follows that $z_1^{\prime }-z_1^{\ast }-x_1^{\prime }(u^{\prime }-u^{\ast })\ne 0$. Similarly, if $x_2^{\prime }\ne x_2^{\ast }$, the same reasoning holds, and we omit the detailed description here. Based on the above considerations, it can be concluded that $([z_1^{\prime }-z_1^{\ast }-x_1^{\prime }(u^{\prime }-u^{\ast })],[z_2^{\prime }-z_2^{\ast }+x_2^{\prime }(u^{\prime }-u^{\ast })])\ne 0$ holds with at least $3/4$ probability.

So, if it satisfies $\beta \ge (4\sigma +2\lambda x)\sqrt{2n}$, $([z_1^{\prime }-z_1^{\ast }-x_1^{\prime }(u^{\prime }-u^{\ast })],[z_2^{\prime }-z_2^{\ast }+x_2^{\prime }(u^{\prime }-u^{\ast })])$ is called the solution of the SIS problem on the NTRU lattice in this paper.

Certificate completed. □

5.2. Confidentiality

The following will prove that our proposed NTRU-based key encapsulation scheme for underwater acoustic communication is IND-CCA secure, based on the NTRU hardness assumption.

Before that, let us first discuss the indistinguishability under chosen plaintext attack (IND-CPA) security of the UA-NTRU scheme.

Theorem 2.

For every probabilistic polynomial-time adversary $\mathcal{A}$, one can construct a probabilistic polynomial-time adversary $\mathcal{B}$ with a runtime similar to $\mathcal{A}$, such that

$${\mathit{Adv}}_{\mathrm{UA}-\mathrm{NTRU}}^{\mathrm{IND}-\mathrm{CPA}}\left(\mathcal{A}\right)\le {\mathit{Adv}}^{\mathrm{NTRU}-\mathrm{OW}}\left(\mathcal{B}\right).$$

(18)

where $\mathcal{A}$ is a classical adversary, and the hash function $\mathcal{H}$ is modeled as a classical random oracle.

$$Ad{v}_{\mathrm{UA}-\mathrm{NTRU}}^{\mathrm{IND}-\mathrm{CPA}}\left(\mathcal{A}\right)\le 2d_{\mathcal{H}}\sqrt{Ad{v}^{\mathrm{NTRU}-\mathrm{OW}}\left(\mathcal{B}\right)}$$

(19)

where $\mathcal{A}$ is a quantum adversary, the hash function $\mathcal{H}$ is modeled as a quantum random oracle, and $d_{\mathcal{H}}$ denotes the depth of $\mathcal{A}$’s queries to $\mathcal{H}$.

Proof. 

Suppose there exists a probabilistic polynomial-time adversary $\mathcal{A}$ that can win the game $G_1$, with the output satisfying $CT=C{T}^{\ast }$. We can then construct a probabilistic polynomial-time adversary $\mathcal{B}$ that solves the NTRU one-way hardness problem. Specifically, $\mathcal{B}$ receives the public key h and the challenge ciphertext $C{T}^{\ast }$ from $\mathcal{A}$ running in the game $G_1$. The goal of adversary $\mathcal{B}$ is to output a pair $(r,e)$ such that $C{T}^{\ast }=rh+e$. Adversary $\mathcal{B}$ takes h and $C{T}^{\ast }$ as input and runs the adversary $\mathcal{A}$. Adversary $\mathcal{A}$ outputs a pair $(r,e)$, which is then used by $\mathcal{B}$ as its output. If adversary $\mathcal{B}$ successfully simulates the game $G_1$, this means that the pair $(r,e)$ output by $\mathcal{A}$ satisfies $C{T}^{\ast }=rh+e$, i.e., adversary $\mathcal{A}$ wins the game $G_1$. Thus, it follows that adversary $\mathcal{B}$ can successfully solve the NTRU one-way function problem with the pair $(r,e)$ as output. Conversely, if the pair $(r,e)$ output by adversary $\mathcal{A}$ does not satisfy $C{T}^{\ast }=rh+e$, then adversary $\mathcal{B}$, using this pair $(r,e)$ as its output, will not be able to successfully solve the NTRU one-way function problem. In conclusion, the advantage of adversary $\mathcal{A}$ winning the game $G_1$ is equal to the advantage of adversary $\mathcal{B}$ in solving the NTRU one-way function problem, i.e.,

$$\mathrm{Pr}\left[{\mathrm{Win}}_{G_1}\right]={\mathrm{Adv}}^{\mathrm{NTRU-OW}}\left(\mathcal{B}\right).$$

(20)

Theorem 3.

If the adversary $\mathcal{A}$ can break the IND-CCA security of the UA-NTRU scheme, then there exists an adversary $\mathcal{B}$ that can break the IND-CPA security of UA-NTRU, such that

$$Ad{v}_{\mathrm{UA}-\mathrm{NTRU}}^{\mathrm{IND}-\mathrm{CCA}}\left(\mathcal{A}\right)\le 2\left(Ad{v}_{\mathrm{UA}-\mathrm{NTRU}}^{\mathrm{IND}-\mathrm{CPA}}\left(\mathcal{B}\right)+{\displaystyle \frac{q_{\mathcal{H}}}{\left|\mathcal{M}\right|}}\right)+{\displaystyle \frac{q_{\mathrm{D}}}{2^{\gamma }}}+q_{\mathcal{H}}\mathrm{l}$$

(21)

where $q_{\mathcal{H}}$ is the number of queries to the random oracle, $q_{\mathcal{D}}$ is the number of queries to the decapsulation algorithm and challenge queries, γ is the length of the private key, and $\mathrm{l}$ is the entropy of $F\left(pk\right)$. In summary, based on the NTRU hardness assumption, the NTRU-based key encapsulation scheme for underwater acoustic communication proposed in this paper is IND-CCA secure.

Certificate completed. □

5.3. Summary

In the context of underwater communication, for instance, when two underwater sensing devices need to exchange critical data (such as detection signals, positioning information, etc.), existential unforgeability ensures that these data cannot be impersonated or altered by intermediary attackers, thereby preventing erroneous decisions and potential security risks. At the same time, confidentiality ensures that the transmitted data are accessible only to authorized users, effectively protecting the privacy and sensitive information in underwater communication. The scheme proposed in this paper, through rigorous security proofs, is able to fully satisfy the aforementioned security requirements.

6. Comparison and Conclusions

6.1. Comparison

The key encapsulation mechanism is a crucial component in encryption protocols. Common examples include those based on the RSA public-key encryption algorithm [34] and the Diffie–Hellman [35] key exchange protocol. These mechanisms were designed based on the integer factorization problem and the discrete logarithm problem, respectively. With the rapid development of quantum computers, their powerful parallel computing capabilities pose significant security challenges to traditional key encapsulation mechanisms. This paper proposes an NTRU-based key encapsulation scheme for underwater acoustic communication, leveraging the algebraic structure of NTRU, which can achieve quantum-resistant security in underwater acoustic communication. The scheme offers advantages such as small storage space, low computational cost, and fulfillment of IND-CCA security. To reduce the storage space in underwater acoustic communication, this scheme uses the trapdoor basis $B_{f,g}$ obtained through ring sampling as the system’s private key. Water acoustic channel characteristics are incorporated into the key encapsulation process to provide authenticity to the scheme. Additionally, a short-length digital signature is introduced, ensuring the integrity of data transmission in the underwater acoustic environment, without compromising the overall computational efficiency.

In Table 1, we present a comparison of the security strengths of different schemes. In this paper, the proposed scheme incorporates underwater acoustic channel characteristics during the key encapsulation process, effectively introducing identity information, which enables the scheme to resist forgery attacks such as message replay and information reorganization. In contrast, Refs. [36,37] do not introduce relevant identity information and, therefore, cannot defend against message replay attacks. Additionally, the proposed scheme ensures unforgeability and CCA security due to the integration of a digital signature mechanism in the NTRU-based key encapsulation scheme. Ref. [36], based on the ring learning with errors (R-LWE) problem, does not satisfy CCA security and lacks unforgeability. Although Ref. [37] is also an NTRU-based key encapsulation scheme that satisfies CCA security, it lacks unforgeability.

Table 1. Comparison of security strength.

Scheme	CCA	Replay Attack	Unforgeability
Our scheme	✓	✓	✓
Ref. [36]	×	×	×
Ref. [37]	✓	×	×

As shown in Table 2, the private key generated by the ring sampling algorithm in this paper requires less storage space compared to [37]. Additionally, the storage space for the ciphertext is also smaller than that in [37], and the storage space for the added signature is also relatively small. Compared with [36], the proposed scheme has a slightly larger storage space for various aspects. However, Ref. [36] does not have quantum-resistant capabilities. Considering the complexity of the underwater acoustic communication environment and the need to ensure communication security, the proposed scheme is more suitable for underwater acoustic communication.

Table 2. Comparison of storage space (unit:KB).

Scheme	System Private Key	Signature Generation	Ciphertext Size
Our scheme	462	217	892
Ref. [36]	226	-	489
Ref. [37]	663	-	1220

Table 3 presents a comparison of the time overheads between the proposed scheme and those in [36,37]. Although the proposed scheme includes an additional signature step, its time overhead is similar to that of [37] and far superior to that of [36]. Without significantly increasing the overhead, our scheme offers better security, making it well-suited for challenging underwater acoustic communication environments.

Table 3. Comparison of time overheads (unit: $\mathsf{\mu }$s).

Scheme	Key-Gen	Key-Encaps	Key-Decaps
Our scheme	22.8	31.1	43.0
Ref. [36]	57.90	54.86	35.39
Ref. [37]	23.4	30.5	41.3

6.2. Conclusions

In this paper, we proposed an NTRU-based key encapsulation scheme for underwater acoustic communication. The scheme leverages a trapdoor basis generated by the ring sampling algorithm as the private key, while incorporating the characteristics of underwater acoustic channels into the key encapsulation process. Additionally, by introducing a signature step, the scheme overcomes the limitations of traditional key encapsulation mechanisms. Experimental results showed that our scheme ensures IND-CCA security, while offering reduced storage requirements and improved computational efficiency. However, in extreme underwater acoustic environments with high noise and low signal-to-noise ratios, the current scheme may still face performance bottlenecks, particularly in terms of the computational overhead during key generation and encapsulation. Future work will focus on improving the operational efficiency of the key encapsulation algorithm to meet the computational constraints of underwater communication systems. Furthermore, we will explore how to adapt the scheme for different underwater communication scenarios, to enhance its flexibility and robustness. Given the potential threats posed by quantum computing, strengthening the post-quantum resilience of the scheme and integrating it with other cryptographic mechanisms will be a key direction for future research.