Denoising Method for Injected Geoelectric Current Field Signals Based on CEEMDAN-IWT

Abstract

To address the issue of weak geoelectric current field signals that are severely affected by noise and cannot be directly used for geological structure analysis in injected geoelectric current field detection technology, this study proposes a complete ensemble empirical mode decomposition with adaptive noise and improved wavelet thresholding collaborative denoising (CEEMDAN-IWT) method to enhance the interpretation accuracy of geoelectric current signals. The method performs signal decomposition through CEEMDAN and selects the effective intrinsic mode function (IMF) components based on the variance contribution criterion for preliminary denoising. It then combines the improved wavelet thresholding function for further fine denoising and reconstruction, obtaining high signal-to-noise ratio (SNR) electrical data. Simulation and real-world data validation show that in a simulation experiment with an initial SNR of −5 dB, the method improves the $SNR$ to 18.65 dB, and the SNR enhancement is superior to traditional methods under various noise intensities. In practical applications, the normalized cross-correlation (NCC) between the denoised signal and the original injected signal reaches as high as 0.9254, significantly outperforming traditional methods. At the same time, it balances the preservation of signal features with noise suppression, offering significant application value for improving the reliability of injected geoelectric current field detection data.

1. Introduction

Injected geoelectric current field signal detection technology, as a key technological method in the field of geophysical exploration, constructs an artificial geoelectric current field by injecting controllable currents into the earth. This allows for the acquisition of information on the distribution of subsurface electrical property parameters, thereby enabling geological structure analysis [1,2]. This technology has been widely applied in fields such as geological exploration [3], mineral resource exploration [4], underground construction safety monitoring [5], and ground-penetrating communication [6]. The core objective of data acquisition is to accurately extract the effective field signals induced by the artificial source, providing a reliable data foundation for the inversion of subsurface electrical property parameters.

However, in practical detection, the non-ideal channel characteristics of the earth lead to severe signal attenuation during transmission, significantly reducing the effective signal strength at the receiving end [7]. At the same time, the observation system suffers from composite interference from multiple noise sources: earth intrinsic noise, industrial electromagnetic interference, and environmental random noise [8], which collectively result in measured data exhibiting three major characteristics: weak effective signals, high noise intensity, and significantly low signal-to-noise ratio ($SNR$). This severely limits the accuracy of electrical property parameter inversion and the interpretability of the data [9]. Therefore, developing efficient geoelectric current field signal denoising methods to obtain high $SNR$ detection data has become a research focus in this field [10].

The denoising methods of traditional injected current field signal detection technology are limited by the defects of the technical paradigm, typically targeting only specific types of noise, making it difficult to achieve comprehensive suppression of multi-source noise. Existing weak signal denoising methods can be classified into five categories: time-domain methods (such as correlation detection [11] and time-domain averaging [12]) are simple to implement but have poor noise robustness; frequency-domain methods (such as adaptive filtering [13]) have high computational efficiency but suffer from threshold sensitivity, making it difficult to set appropriate noise thresholds; in time-frequency analysis methods, wavelet transform lacks adaptability, relying on the selection of wavelet parameters, and is prone to mistakenly removing valid coefficients at low signal-to-noise ratios [14,15]; empirical mode decomposition (EMD) and its improved algorithm complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN) can decompose signals adaptively, but the former suffers from modal aliasing and endpoint effects [16], while the latter still faces incomplete decomposition in low signal-to-noise ratio scenarios [17]; emerging learning methods (such as neural networks [18]) break through the limitations of traditional prior knowledge but rely on large amounts of training data, and their physical mechanisms are difficult to explain. All of the above methods face inherent limitations of a single denoising strategy, making it challenging to balance denoising performance and signal fidelity, with insufficient ability to suppress transient noise and poor adaptability. This significantly limits the improvement of the data quality in injected current field detection.

In the field of geophysical signal processing, existing research has focused on improving EMD-based methods and integrating multiple techniques. For example, Xu et al. used EMD-wavelet hard thresholding to denoise electrical imaging logging data [19]. Liu et al. proposed an EMD-adaptive interval threshold seismic denoising method, which was validated through field measurements to enhance the signal-to-noise ratio [20]. Xu et al. applied EMD-ICA to separate noise from induced polarization data [21]. Cheng et al. used the EEMD-SVD-LWT method to optimize lidar signal denoising by selecting effective components with SVD [16]. Although these methods are effective for specific signal denoising tasks, the mode mixing issue of EMD and EEMD still leads to the loss of valid information in low signal-to-noise ratio geoelectric field signals. Rao et al.’s VMD-improved wavelet threshold algorithm enhances signal extraction ability under strong interference, but the number of modes in VMD must be preset manually, lacking adaptability to the signal attenuation characteristics of geological media [22]. Wang et al.’s CEEMDAN-traditional wavelet thresholding method does not optimize the threshold function for multi-source noise in low signal-to-noise ratio geoelectric fields and lacks quantification criteria for selecting IMF components [14]. In summary, existing research still has room for improvement in terms of multi-source noise adaptability, quantification standards for selecting effective components, and targeted optimization of threshold functions, making it difficult to meet the collaborative requirements of preserving weak signals, suppressing multi-source noise, and performing adaptive decomposition for injected geoelectric field signals.

To address the above issues, this study combines the advantages of complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN) with an improved wavelet thresholding (IWT) denoising algorithm and proposes a CEEMDAN-IWT collaborative denoising method. The method first utilizes CEEMDAN for adaptive signal decomposition, taking advantage of its noise-assisted characteristics to overcome the modal aliasing issue of EMD, and decomposes the complex mixed signal into IMF components with different frequencies. Next, IMF components are selected based on the variance contribution rate, achieving precise separation of effective components from multi-source noise. To address the residual noise in the selected components, an improved wavelet thresholding (IWT) function is introduced and parameter optimization is performed based on the characteristics of the ground electric field signal. This further enhances residual noise suppression while preserving weak signal details. Finally, high-quality denoised ground electric field signals are obtained through inverse summation reconstruction of the effective components. Compared to traditional methods, the CEEMDAN-IWT denoising method not only fully utilizes the adaptive separation advantage of CEEMDAN but also achieves detail preservation through scene-specific optimization of the threshold function. The research results significantly improve the quality of the ground electric field signals while retaining the details of weak effective signals. The denoising performance is far superior to conventional methods, greatly enhancing the quality of injected current field detection data and providing a reliable data foundation for underground electrical parameter inversion.

2. Signal Characteristics Analysis

The Injected geoelectric current field signal detection lies in extracting the effective signals induced by artificial sources. However, during the actual data acquisition process, the signals received by the sensors inevitably mix with the Earth’s inherent noise, as well as electromagnetic interference caused by the operation of industrial equipment, disturbances in the power system, and random environmental factors. Such interference can severely degrade the weak artificial ground current field signals, leading to a sharp decline in the signal-to-noise ratio of the collected data, with the effective signals being masked. This directly restricts the accuracy and reliability of subsequent data analysis. To clarify the characteristics of the Injected geoelectric current field signal, a signal characteristic analysis is conducted based on the measured data collected by the sensors.

Figure 1 shows the original signal of the injected geoelectric current field collected by the sensor under normal environmental conditions. As can be seen from Figure 1, the signal contains a large number of randomly distributed spike pulses, with amplitude values ranging from −0.1 mV to 0.1 mV. From the time-domain analysis, the noise persists throughout the entire collection period, with the waveform envelope fluctuating sharply. The sample points are densely distributed and exhibit a repetitive spike pattern, demonstrating strong randomness and transient burst characteristics. This is primarily due to inherent noise sources such as electromagnetic disturbances from nature and dynamic changes in underground media, reflecting the fundamental interference effect of ground noise on effective signal collection.

To investigate the influence mechanism of external interference sources on the sensor output signal, time-sensitive transient activities such as vehicle movement and the operation of a power drill were introduced during the testing process to simulate typical human-made interference scenarios. Figure 2 shows the measured data collected by the sensor after the introduction of external interference sources. Compared with conventional scenarios without artificial interference, the time-domain characteristics of the signal exhibit a significantly increased waveform disorder, with numerous small-amplitude fluctuations and dense spikes. This indicates that the electromagnetic interference generated by time-sensitive transient activities superimposes on the geoelectric current field signal, further increasing the complexity of the signal.

Comprehensive measured analysis indicates that the output signal interference sources of the injected geoelectric current field sensor exhibit a multi-layered superimposed characteristic, simultaneously affected by both natural inherent noise and human activity interference. Among them, natural inherent noise primarily takes the form of geomagnetic disturbances and dynamic polarization of underground media, characterized by wide time-domain distribution and random fluctuation. Human activity interference, triggered by industrial equipment operation, power system disturbances, and environmental random factors, is manifested in strong transient and impulsive features. The effective signal artificially generated attenuates after propagation through the geoelectric medium, with its amplitude generally ranging from microvolts to millivolts, making it highly vulnerable to interference. As engineering applications continue to expand, the actual working environment is becoming increasingly complex, which not only intensifies the complexity of interference scenarios but also increases the difficulty of extracting weak signals. This poses a core challenge to traditional denoising methods. Traditional denoising techniques struggle to achieve a dynamic balance between “noise suppression” and “feature preservation,” and are incapable of comprehensively and effectively suppressing multi-type composite noise.

3. Methodology

3.1. CEEMDAN Signal Decomposition Algorithm

CEEMDAN is an improved signal decomposition method based on the EMD algorithm. By repeatedly adding and averaging noise, it effectively suppresses noise and improves the accuracy and reliability of signal decomposition [23]. The core idea of EMD is to decompose complex signals adaptively into a set of intrinsic mode functions (IMF) and a residual component, based on the signal’s inherent time-scale characteristics, without relying on predefined basis functions. The IMF components must satisfy two conditions: (1) the number of extreme points (local maxima and minima) in the entire data sequence is equal to the number of zero-crossings, or at most differs by one; (2) at any moment, the average of the upper envelope formed by local maxima and the lower envelope formed by local minima is zero. The specific implementation of EMD is as follows: First, all extreme points of the original signal are identified, and the upper and lower envelopes are fitted using cubic spline interpolation. The mean of the envelopes is then calculated, and the original signal is subtracted from the mean to obtain a proto-IMF. The proto-IMF is then iteratively filtered until it satisfies the IMF criteria. The residual signal after removing the first IMF becomes the new original signal, and the process is repeated until the residual component becomes a monotonic function that cannot be decomposed further. However, EMD has notable drawbacks: mode mixing (i.e., components of different time scales are mixed within the same IMF, or the same component is distributed across multiple IMFs) and endpoint effects (envelope fitting at the signal endpoints is inaccurate, leading to decomposition errors), which seriously affect the quality of decomposition.

CEEMDAN (complete ensemble empirical mode decomposition with adaptive noise) was proposed as an improved algorithm to solve the problems of mode mixing and endpoint effects in EMD. It essentially enhances the decomposition accuracy and reliability by introducing adaptive Gaussian white noise and leveraging statistical averaging effects within the EMD framework. Compared to EMD, CEEMDAN retains the core advantage of “adaptive decomposition based on the signal’s inherent characteristics” while optimizing the noise injection method and decomposition iteration strategy. This effectively suppresses mode mixing and endpoint effects, significantly improving the accuracy and stability of signal decomposition. The specific processing approach and decomposition process are as follows [24]:

(1) A series of adaptive white noise ${\tau }_0{Z}_{(t)}^i$ is added to the original geoelectric current field signal $Y_{(t)}$, as shown in Equation (1):

$$Y_{(t)}^i=Y_{(t)}+{\tau }_0{Z}_{(t)}^i$$

(1)

where $Y_{(t)}^i$ is the geoelectric current field signal after the $i$-th addition of adaptive white noise; $Y_{(t)}$ is the original geoelectric current field signal; ${\tau }_0$ is the Gaussian white noise coefficient; $Z_{(t)}^i$ is the white noise added in the $i$-th iteration; and $i$ is the iteration number.

(2) Perform EMD on $Y_{(t)}^i$ to obtain the first intrinsic mode function $IM{F}_1(t)$, as shown in Equation (2).

$$IM{F}_1(t)={\displaystyle \frac{1}{I}}\sum _{t=1}^I{E}_1\left[Y_{(t)}^i\right]$$

(2)

where $IM{F}_1(t)$ is the first intrinsic mode function; $E_1$ is the operator that obtains the first intrinsic mode function from the EMD of the signal to be processed; and $I$ is the number of decompositions of the signal to be processed using the EMD method.

(3) Calculate the residual after removing the first mode component, as shown in Equation (3).

$$r_1(t)=Y(t)-IM{F}_1(t)$$

(3)

where $r_1(t)$ is the residual component of $IM{F}_1(t)$.

(4) Add adaptive white noise ${\tau }_0{Z}_{(t)}^i$ to $r_1(t)$ to obtain a new signal. Perform EMD on the new signal to obtain $IM{F}_2(t)$, as shown in Equation (4). Then, calculate the residual after removing the second mode component, which is $r_2(t)$, as shown in Equation (5).

$$IM{F}_2\left(t\right)={\displaystyle \frac{1}{I}}\sum _{k=1}^I{E}_1\left\{r_1\left(t\right)+{\tau }_1{E}_1\left[Z_{(t)}^i\right]\right\}$$

(4)

$$r_2(t)=r_1(t)-IM{F}_2(t)$$

(5)

where $IM{F}_2\left(t\right)$ is the second intrinsic mode component; ${\tau }_1$ is the white noise coefficient from the second EMD; and $r_2(t)$ is the residual component of $IM{F}_2(t)$.

(5) Repeat the above steps until the resulting residual signal is a monotonic function and can no longer be decomposed. At this point, the original geoelectric current field signal is decomposed as shown in Equation (6).

$$Y_{(t)}=R\left(i\right)+\sum _{k=1}^{L}IM{F}_k(t)$$

(6)

where $R\left(i\right)$ is the final residual component; $L$ is the number of intrinsic mode components; and $IM{F}_k(t)$ is the $k$-th intrinsic mode component.

The advantage of CEEMDAN lies in its ability to significantly suppress the mode mixing phenomenon through the noise injection and ensemble averaging strategy mentioned above. It also reduces the issue of non-uniqueness in decomposition results caused by the randomness of noise, thereby providing cleaner and more physically meaningful mode components for subsequent denoising processes based on IMF components.

3.2. IWT Signal Denoising Method

In the wavelet denoising process, the core role of the threshold is to distinguish between the effective signal components and the noise components in the wavelet coefficients. Noise typically corresponds to wavelet coefficients with smaller magnitudes, while the effective signal usually corresponds to wavelet coefficients with larger magnitudes. By setting a reasonable threshold to filter or modify the wavelet coefficients, a balance between noise suppression and signal fidelity can be achieved. The noise in the injected geoelectric field signal mainly consists of inherent terrestrial noise, industrial electromagnetic interference, and environmental random noise. This type of noise has a multi-source composite characteristic, with its intensity and distribution dynamically changing according to the detection environment, making it difficult to establish an accurate prior model. At the same time, the signal exhibits non-stationary characteristics after being transmitted through the Earth, with low-frequency effective components easily blending with the noise, further increasing the difficulty of noise suppression. To address this issue, the SURE (Stein Unbiased Risk Estimate) threshold and BayesShrink threshold show clear adaptation limitations: the SURE threshold determines the threshold by minimizing the unbiased risk estimate, which requires strict signal stationarity. When processing non-stationary geoelectric field signals, the risk estimation model is easily affected by signal fluctuations, leading to bias and causing excessive noise residuals or loss of effective signal. The BayesShrink threshold, based on the Bayesian estimation framework, assumes Gaussian noise distribution by default. However, non-Gaussian noise such as industrial equipment pulse interference significantly reduces the accuracy of variance estimation, making it unsuitable for complex noise scenarios. Therefore, this study selects the Visushrink threshold. The Visushrink threshold does not rely on prior knowledge of specific signal types [25]. Instead, it adaptively calculates the threshold based on the statistical characteristics of the wavelet coefficients and noise levels, making it suitable for different scenarios with varying noise intensities in the electric current field signals. This approach avoids the drawbacks of traditional empirical thresholds that require repeated tuning, and effectively removes noise while preserving useful signals. As shown in Equation (7).

$$\lambda =\sigma \sqrt{2\ln N}$$

(7)

$$\sigma ={\displaystyle \frac{median(|w_{1,k}|)}{0.6745}}$$

(8)

where $N$ is the length of the wavelet coefficients, $\sigma$ is the estimate of the noise level, $w_{1,k}$ is the coefficient after the first wavelet transform, and $k$ is the position parameter.

Wavelet transform denoising has multi-scale analysis capability, which allows it to remove noise while preserving the details of the signal [26]. In the denoising of injected geoelectric current field signals, it is crucial to process the signal with an appropriate threshold function to ensure optimal denoising results. Common threshold methods include hard thresholding and soft thresholding [27]. However, the hard threshold function has a discontinuity problem, which may introduce discontinuities during signal reconstruction, leading to insufficient denoising effects in practical geoelectric current field signals [28]. On the other hand, the soft threshold function has continuity at the decomposition points, and thus, compared to hard thresholding, the denoised waveform is smoother. However, it introduces a constant bias, which causes distortion in the reconstructed geoelectric current field signal, affecting its reconstruction [29]. Therefore, to achieve the best denoising effect, selecting the appropriate thresholding method requires a balance based on denoising needs and signal characteristics. This is the key factor in achieving optimal denoising results. The processing functions for hard thresholding and soft thresholding are shown in Equations (9) and (10).

$${\widehat{W}}_{j,k}\left\{\begin{array}{cc}{W}_{j,k}& \left|W_{j,k}\right|\ge \lambda \\ 0& \left|W_{j,k}\right|<\lambda \end{array}\right.$$

(9)

$${\widehat{W}}_{j,k}\left\{\begin{array}{cc}sign\left(W_{j,k}\right)\left(\left|W_{j,k}\right|-\lambda \right)& \left|W_{j,k}\right|\ge \lambda \\ 0& \left|W_{j,k}\right|<\lambda \end{array}\right.$$

(10)

where ${\widehat{W}}_{j,k}$ is the wavelet coefficient of the geoelectric current field detection signal after thresholding, $W_{j,k}$ is the wavelet coefficient of the geoelectric current field detection signal at the $j$-th wavelet coefficient on the $k$-th scale before thresholding, and $\lambda$ is the critical threshold value.

In order to overcome the issues encountered in both hard thresholding and soft thresholding methods as much as possible, and to improve the performance of geoelectric current field signal denoising, this study refers to and adopts the improved threshold function from reference [30], which is expressed as follows:

$${\widehat{W}}_{j,k}\left\{\begin{array}{cc}sign\left(W_{j,k}\right)\left(\left|W_{j,k}\right|-\lambda \left(1-e^{{\displaystyle \frac{-\ln (a+1)}{\left|W_{j,k}\right|-\lambda }}}\right)\right)& \left|W_{j,k}\right|>\lambda \\ 0& \left|W_{j,k}\right|\le \lambda \end{array}\right.$$

(11)

where $a$ is the adjustment factor, ranging from [0, 3.5), used to control the shrinkage characteristics of the threshold function. This function is optimized through a parameter-adjustable exponential continuous transition mechanism, addressing the discontinuity problem of hard thresholds and the constant bias of soft thresholds, as described below:

(1)

Eliminated the discontinuity of the hard threshold

The hard thresholding function exhibits a discontinuity at $\left|W_{j,k}\right|=\lambda$, which introduces a breakpoint. In the improved thresholding function, $1-e^{{\displaystyle \frac{-\ln (a+1)}{\left|W_{j,k}\right|-\lambda }}}$ serves as an adjustment term. When $\left|W_{j,k}\right|$ approaches ${\lambda }^{+}$, the exponential term approaches 0, and ${\widehat{W}}_{j,k}$ approaches 0; when $\left|W_{j,k}\right|$ approaches infinity, the exponential term approaches 1, and ${\widehat{W}}_{j,k}$ approaches $W_{j,k}$. This allows the function to achieve a smooth transition at the threshold point, retaining the non-shrinking property of the hard threshold for large signal coefficients while eliminating the discontinuity.

(2)

Mitigated the constant bias of the soft thresholding.

The soft thresholding applies a fixed subtraction to coefficients above the threshold, which introduces a constant bias. In contrast, the proposed function replaces the fixed operation with an exponential term. When $\left|W_{j,k}\right|$ approaches infinity, ${\widehat{W}}_{j,k}$ approaches $W_{j,k}$, eliminating the constant bias. When $W_{j,k}$ approaches $\lambda$, the degree of shrinkage is adaptively adjusted by $a$, balancing noise suppression and signal fidelity.

Therefore, this thresholding function demonstrates greater flexibility compared to traditional wavelet thresholding functions. As $a$ approaches 0, the function converges to the hard thresholding function; when $a$ approaches 3.5, the function nearly coincides with the soft thresholding function, as detailed in reference [30]. To better meet the denoising requirements of injected electric field signals, the range of $a$ is narrowed to between 1.5 and 2.5. This improved thresholding function can adaptively adjust the shrinkage strategy, achieving a better balance between noise suppression and signal detail preservation. Its mathematical continuity and asymptotic unbiasedness are the fundamental reasons for its superior performance.

3.3. CEEMDAN-IWT Signal Denoising Method

In the detection of injected electric current field signals, the signal undergoes significant attenuation and becomes extremely weak after transmission through the ground, while being subject to interference from multiple noise sources. Traditional processing methods struggle to balance noise suppression from multiple sources with the preservation of weak signals. While CEEMDAN can adaptively decompose the signal and separate noise across different frequency bands, its ability to suppress residual random noise in high-frequency Intrinsic Mode Function (IMF) components is limited. Traditional wavelet threshold denoising allows for multi-scale signal processing but lacks adaptive decomposition capability, which can lead to misjudgment of valid components in low $SNR$ scenarios.

To address this issue, this paper proposes a collaborative denoising method combining CEEMDAN and an Improved Wavelet Threshold (IWT). Through a cascade strategy of adaptive decomposition, component selection, refined denoising, and signal reconstruction, the method achieves a balance between efficient noise suppression and signal feature preservation. The overall method process consists of four main parts: Signal decomposition, Component selection, Fine denoising, and Signal reconstruction. The specific process is shown in Figure 3.

(1)

CEEMDAN Adaptive Decomposition

As a core preprocessing step in the denoising process, CEEMDAN adaptive decomposition is first applied to the noisy geoelectric field signal collected. By adding Gaussian white noise to the original signal and performing multiple iterations of selection, the complex noisy signal is adaptively decomposed into a set of intrinsic mode functions (IMFs) with different time scales and good orthogonality. This decomposition process essentially represents a frequency domain, time-domain joint pre-classification of the signal and noise, laying the physical foundation for subsequent precise selection of effective components. Compared to traditional wavelet transform, CEEMDAN does not require manually setting the wavelet basis function or decomposition level. Instead, it adaptively matches the inherent features of the signal for decomposition, and the iterative selection mechanism significantly suppresses the mode mixing problem commonly found in the EMD method, providing high-quality processed objects for subsequent quantitative selection and fine denoising. This is the premise and core guarantee for achieving efficient and robust denoising.

(2)

Effective IMF Selection Based on Variance Contribution Rate

After CEEMDAN adaptive decomposition, it is necessary to distinguish which IMFs are dominated by the effective signal and which are dominated by noise. The Variance Contribution Rate ($VCR$) represents the proportion of the energy of an IMF component relative to the total energy of the original signal. After the noisy geoelectric field signal is iteratively decomposed by CEEMDAN with added white noise, the IMFs dominated by noise have a very low $VCR$, while those dominated by the effective signal have a significantly higher $VCR$. This paper abandons the reliance on subjective observation methods and introduces $VCR$ as an objective, quantitative screening criterion. This allows for the identification and extraction of the signal-dominated components from the noise-dominated IMFs, avoiding human subjectivity and significantly enhancing adaptability and robustness to unknown noise environments. This step is key to achieving automated denoising. The variance contribution rate ($VCR$) of the $i$-th IMF component is defined as [31]:

$$VC{R}_{(i)}={\displaystyle \frac{D(IM{F}_i)}{{\displaystyle \sum _{i=1}^{I}D}(IM{F}_i)}}$$

(12)

where $IM{F}_i$ is the $i$-th mode, $I$ is the total number of modes, and $D(IM{F}_i)$ is the variance of the $i$-th IMF component.

(3)

Multi-Scale Fine Denoising of Effective Components Based on IWT

Even after the selection of effective IMFs, some noise may still overlap with the signal’s frequency band. To address this, the study employs the improved wavelet threshold function (IWT) described in Section 3.2 to perform independent denoising for each selected IMF component. In this stage, the multi-resolution analysis characteristics of IWT are fully utilized: for each IMF, wavelet transform further decomposes it into finer time-frequency scales, and the IWT threshold function adjusts the coefficients adaptively at different scales based on a preset threshold strategy. Compared to direct wavelet denoising on the original signal, the advantages of this step are: First, the objective is clearer—only the signal-dominated components that have been initially selected are denoised, reducing the risk of mistakenly affecting global coefficients. Second, the scale is more appropriately matched, allowing the selection of the most suitable wavelet basis and decomposition level for different IMF components with varying central frequencies, achieving customized fine denoising. Third, IWT’s adjustable parameters facilitate a smooth transition between soft and hard thresholding, with continuity at the threshold points effectively suppressing the reconstruction oscillations caused by hard thresholding. Its asymptotic unbiasedness overcomes the constant bias inherent in soft thresholding, maximizing the suppression of residual noise while excellently preserving weak effective signal features.

(4)

Signal Reconstruction

All effective IMF components after fine denoising by IWT are reconstructed through a joint inverse CEEMDAN transform and inverse wavelet transform. By summing the components, a high signal-to-noise ratio ($SNR$) clean geoelectric field signal is restored, completing the denoising process. During reconstruction, the orthogonality of CEEMDAN decomposition and the coefficient fidelity of IWT processing ensure that traditional methods’ suppression or distortion of weak effective features during denoising is avoided. Ultimately, a clean geoelectric field signal with a high $SNR$ is obtained, enabling effective denoising of the electrical detection data. This provides reliable data for the inversion of subsurface electrical parameters.

In summary, the CEEMDAN-IWT method proposed in this study addresses the core challenge of balancing noise suppression and effective signal feature retention in traditional injected geoelectric field signal processing techniques, particularly in low signal-to-noise ratio ($SNR$) and multi-source noise interference scenarios. This method, through the adaptive decomposition of CEEMDAN and the variance contribution rate selection mechanism, reduces the reliance on prior knowledge of noise typically required by traditional methods, while overcoming the limitations of wavelet transform basis function selection sensitivity, thereby achieving a synergistic enhancement of denoising performance. On the other hand, it also mitigates or alleviates some of the inherent limitations of the CEEMDAN algorithm. Although this method involves multiple decompositions and iterative computations, which leads to higher computational complexity and insufficient real-time performance, the complexity issue does not pose a significant obstacle in practical applications of injected geoelectric field detection. This is due to the complexity of the detection environment, the trend toward portable, miniaturized equipment design, and the fact that data processing is mostly conducted in laboratories for offline analysis. Therefore, the computational complexity does not present a major barrier to practical application. In conclusion, while the proposed method increases computational load to some extent, it significantly improves signal fidelity and reliability. Its two-level collaborative processing architecture minimizes signal distortion and enhances processing accuracy, providing high-quality data support for subsequent underground electrical parameter inversion and geological structure analysis.

4. Simulation Experiment Verification Results and Discussion

4.1. Simulation Signal Construction IWT

This study conducts an effectiveness verification experiment of the CEEMDAN-IWT denoising method based on a simulation platform. The injected geoelectric current field signal has a duration of 15 s, with the first 5 s representing a Minimum Shift Keying ($MSK$) modulated signal, which provides synchronization and initial calibration functions to ensure accurate signal capture. The remaining 10 s consist of a sinusoidal signal with an amplitude of 100 μV, matching the weak amplitude characteristics of actual geoelectric current field signals, with a frequency of 10 Hz, effectively suppressing the signal attenuation effect in the Earth’s medium. To address the composite noise problem of background random noise and multi-source electromagnetic interference in the injected geoelectric current field signal, a three-level noise modeling strategy is adopted: (1) A Gaussian white noise model is used to characterize the statistical properties of environmental random noise; (2) Random pulse noise is used to simulate the transient pulse noise caused by natural phenomena or external environmental interference during the detection process, representing abrupt temporal changes; (3) A 50 Hz power line interference noise is used to simulate the periodic characteristics of electromagnetic coupling interference from power frequency in actual measurement environments. The final constructed geoelectric current field detection signal simulation model is shown in Equation (13). This model accurately simulates the injected geoelectric current field detection signal in a real environment, providing a more comprehensive evaluation of the denoising performance.

$$y_{(t)}=x_{(t)}+n_{(t)}+{\epsilon }_{(t)}+h(t)$$

(13)

where $y(t)$ represents the simulated noisy geoelectric current field signal, $x(t)$ is the ideal geoelectric current field signal, $n(t)$ is Gaussian white noise, $\epsilon (t)$ is random pulse noise, and $h(t)$ is the 50 Hz power frequency interference.

The paper selected a noise background with a signal-to-noise ratio ($SNR$) of −5 dB to verify the denoising effect of the proposed method. Figure 4a shows the waveform of the ideal geoelectric current field signal, and Figure 4b shows the waveform of the simulated noisy geoelectric current field signal.

It can be seen that noise significantly interferes with the quality of the injection-type geoelectric current field signal detection data, causing numerous spikes and making the ideal signal features blurred and difficult to distinguish, which is consistent with the statistical analysis results of the measured data.

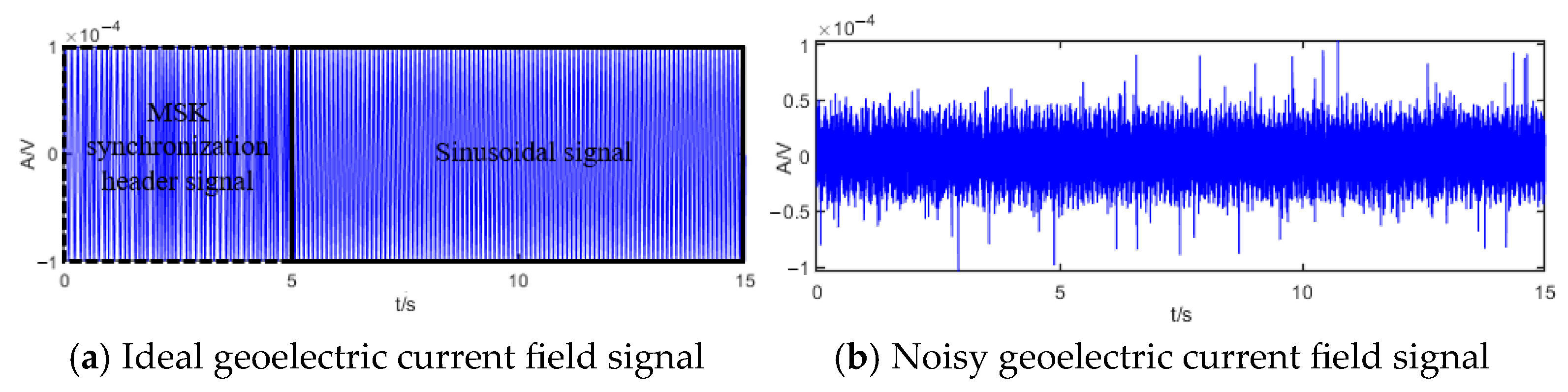
4.2. CEEMDAN-IWT Denoising Results and Discussion

First, the injected geoelectric current field signal needs to be decomposed using CEEMDAN. Considering both accuracy and efficiency, the specific parameters for the CEEMDAN denoising algorithm in this study, obtained through multiple experiments, are as follows: the noise standard deviation is 0.2, the number of noise additions is 100, and the maximum number of iterations is 1000. The signal is decomposed into 13 intrinsic mode functions (IMFs), as shown in Figure 5.

There are significant differences in the noise levels of different intrinsic mode functions (IMFs), and the reasonable setting of threshold parameters directly affects the IMF component selection effect. A threshold that is too low may result in the residual noise-dominated modes, while a threshold that is too high may lead to the loss of valid components. This paper references the work of Peng et al. [31] and adopts the IMF component selection criterion based on the $VCR$, setting the threshold to ≤0.01. When $VCR$ ≤ 0.01, the IMF component carries less than 1% of the original signal information and mainly reflects the random fluctuation characteristics of the noise. This judgment does not depend on the specific type of the signal but is based on the inherent difference in variance contribution between noise and valid signals. Furthermore, $VCR$ is a dimensionless parameter that is unaffected by the absolute strength of the signal and can adapt to original signal scenarios with different amplitudes. At the same time, the ensemble averaging strategy of CEEMDAN has already preliminarily reduced the interference of noise in the decomposition results, and the thresholding of $VCR$ can further precisely remove residual minor noise. Compared to other parameter selection criteria, it demonstrates stronger robustness to scene changes. Figure 6 shows the variance contribution rate calculation results for the 13 IMF decomposition components. According to the calculation results, the variance contribution rates of IMF7–IMF13 are all ≤0.01 and are removed. The total variance contribution rate of the selected IMF components is 0.9749, indicating that IMF1–IMF6 have completed the preliminary denoising while largely preserving the geoelectric current field signal characteristics.

To achieve optimal denoising performance, this paper uses the signal-to-noise ratio ($SNR$) as a quantitative evaluation metric to assess the denoising effect. When calculating the $SNR$, the first step is to perform a sliding correlation calculation between the denoised signal and the $MSK$ synchronization header template signal, as shown in Equation (14). The sampling point that maximizes the sliding correlation coefficient is identified. The $MSK$ synchronization header lasts for 5 s, and starting from the end of the synchronization header, a 10 s signal is extracted as the valid window. The valid signal segment within this window is used for the $SNR$ calculation, effectively excluding the transient interference from the $MSK$ synchronization header.

$$r_{MSKi}={\displaystyle \frac{{\displaystyle \sum _{n=i}^{i+l_{MSK}-1}(tb{t}_{MSKn}-\overline{tb{t}_{MSK}})(s_n-\overline{s})}}{\sqrt{\left[{\displaystyle \sum _{n=i}^{i+l_{MSK}-1}{(tb{t}_{MSKn}-\overline{tb{t}_{MSK}})}^2}\right]\left[{\displaystyle \sum _{n=i}^{i+l_{MSK}-1}{(s_n-\overline{s})}^2}\right]}}}$$

(14)

where $s$ represents the denoised signal, $tb{t}_{MSK}$ is the $MSK$ synchronization header signal, and $tb{t}_{MSK}$ has $l_{MSK}$ sampling points, $r_{MSKi}$ is the $i$-th sliding correlation coefficient.

The expression for the signal-to-noise ratio is:

$$SNR=10\lg {\displaystyle \frac{P_S}{P_N}}=10\lg {\displaystyle \frac{\frac{1}{L}{\displaystyle {\sum }_{k=m}^{m+L-1}{x}^2(k)}}{\frac{1}{L}{\displaystyle {\sum }_{k=m}^{m+L-1}{\left[s(k)-x(k)\right]}^2}}}$$

(15)

where $P_S$ is the power of the useful signal, and $P_N$ is the power of the noise, $x(k)$ is the sampled value of the pure signal, $s(k)$ is the sampled value of the denoised signal, $m$ is the index of the starting sampling point of the valid window, $L$ is the number of sampling points in the valid window.

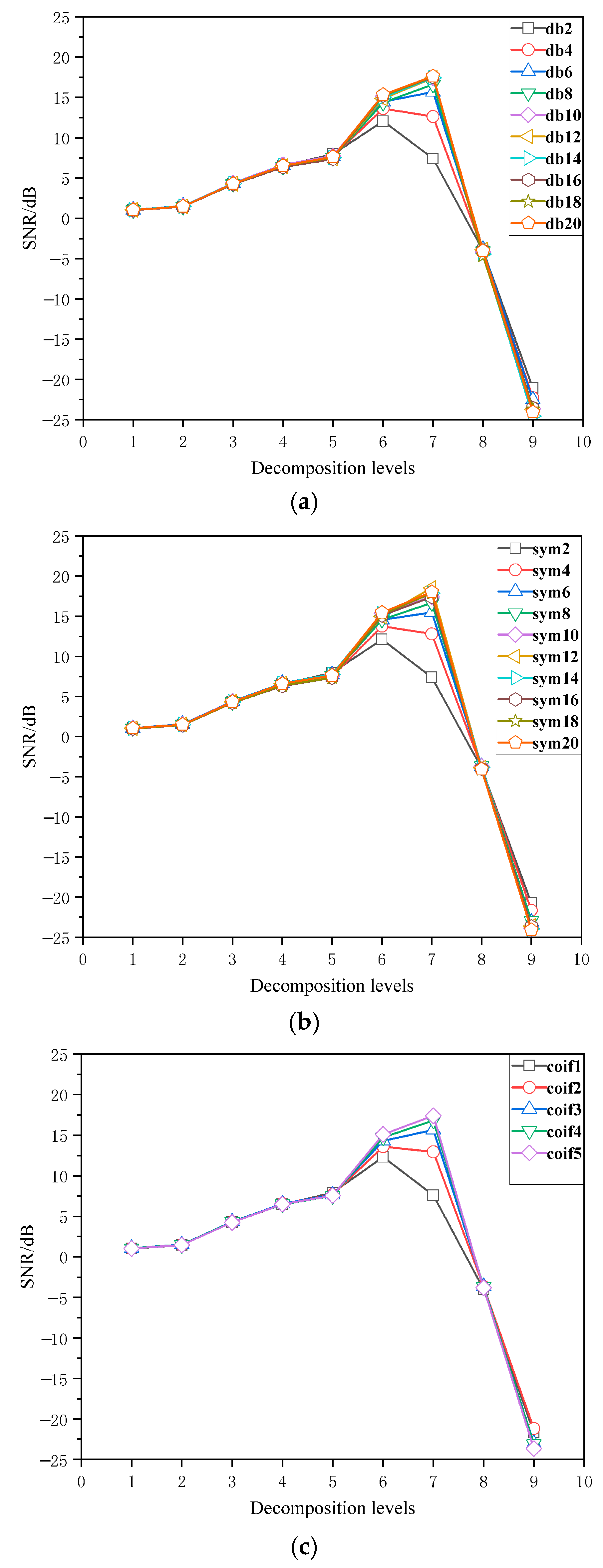
Experiments on denoising of geoelectric current field signals were conducted for different wavelet basis functions and decomposition layer combinations to select the optimal wavelet parameter combination. The experimental results indicate that the signal-to-noise ratio reaches its maximum value of 18.65 dB when the sym12 wavelet basis is used with 7 decomposition layers, as shown in Figure 7. Based on this, the sym12 wavelet basis and 7-layer decomposition are determined as the optimal parameter combination to ensure the best denoising effect

To verify the rationality of the “$VCR$ ≤ 0.01” IMF filtering threshold proposed in this study and evaluate its impact on the denoising effect, a sensitivity analysis was conducted. In the simulation scenario with an initial $SNR$ of −5 dB, thresholds of 0.005, 0.01, and 0.02 were set. The performance differences were quantified by comparing the denoised signal’s signal-to-noise ratio ($SNR$) and normalized cross-correlation ($NCC$). The results are shown in

Table 1. Denoising performance comparison with different $VCR$ thresholds.

$\mathit{V}\mathit{C}\mathit{R}$ Threshold	$\mathit{S}\mathit{N}\mathit{R}$ (dB)	$\mathit{N}\mathit{C}\mathit{C}$
0.005	18.05	0.9586
0.01	18.65	0.9611
0.02	17.51	0.9527

, and the expression for the $NCC$ is given in Equation (16).

$$NCC={\displaystyle \frac{{\displaystyle {\sum }_{i=1}^L(s(k)x(k))}}{\sqrt{{\displaystyle {\sum }_i^L{s}^2(k){\displaystyle {\sum }_{n=1}^L{x}^2(k)}}}}}$$

(16)

The above results indicate that when the $VCR$ threshold is set to 0.01, both the $SNR$ and $NCC$ reach their highest levels, achieving the best denoising effect. When the threshold is set to 0.005, the selection criterion is too loose, which leads to the residual presence of some noise-dominant IMF components due to insufficient filtering. Although a small amount of noise is suppressed, the proportion of residual noise increases, resulting in a decrease in both $SNR$ and $NCC$. On the other hand, when the threshold is raised to 0.02, the filtering becomes too strict, leading to excessive elimination of IMF components and thus causing the loss of effective signal, which results in the lowest $SNR$ and $NCC$ values. In conclusion, the effective energy of the injected electric field signal is mainly concentrated in a few mid-to-high frequency IMF components, while the variance contribution of the noise components is generally low. The threshold of 0.01 effectively removes most noise components without excessively losing the effective signal, achieving an optimal balance between noise suppression and signal fidelity.

To preliminarily verify the denoising effect of the proposed method, a visual analysis is first conducted through waveform comparison. The proposed method is compared with wavelet hard thresholding, soft thresholding, Improvement thresholding, CEEMDAN-hard thresholding, and CEEMDAN-soft thresholding, with a focus on the ability of each method to restore details at characteristic points. The denoising effect comparisons are shown in Figure 8a–f. The figure also presents a waveform comparison between the ideal current field signal and the denoised signal in the 9–11 s time interval, along with local enlarged details at three key characteristic positions to highlight the detail retention of different methods.

The experimental results show that all six denoising methods effectively eliminate most of the noise in the simulated noisy geoelectric current field signal. However, the CEEMDAN-IWT method proposed in this study demonstrates a significant advantage in detail preservation: As seen from the detail comparisons in the local zoomed-in regions A, B, and C, this method not only removes the noise but also preserves the waveform characteristics and the amplitude-phase relationships of the original signal to a greater extent. In contrast, when using hard threshold wavelet or soft threshold wavelet individually, the signal details deviate significantly, and the denoising effect is poorer. Although the other methods can also effectively denoise, they still exhibit some minor deviations. The experimental results validate the synergistic improvement effect of the CEEMDAN-IWT method in adaptive noise separation and weak signal fidelity.

The waveform comparison above preliminarily demonstrates the advantage of the proposed method in terms of detail preservation. To further validate the effectiveness and superiority of the proposed method, this study conducts a comprehensive comparison between the proposed method and existing typical denoising methods using the simulated signal dataset with a signal-to-noise ratio of −5 dB synthesized in Section 4.1 (sampling duration: 15 s). The specific parameter settings are shown in

Table 2. Parameter configuration.

Baselines	Parameter	Metrics
Correlation detection	correlation window size	500 samples
	step size	512 samples
	window function type	hamming window
Adaptive filtering	filter order	32
	adaptive step size	0.01
Wavelet hard thresholding	wavelet type	sym12
	decomposition levels	7
	threshold selection rule	visushrink
CEEMDAN	noise standard deviation	0.2
	ensemble size	100
	maximum number of iterations	1000
IWT	wavelet type	sym12
	decomposition levels	7
	threshold selection rule	visushrink
CEEMDAN-IWT	noise standard deviation	0.2
	ensemble size	100
	maximum number of iterations	1000
	wavelet type	sym12
	decomposition levels	7
	threshold selection rule	visushrink

.

To objectively quantify the overall performance, the $SNR$, $NCC$, and root mean square error ($RMSE$) are selected as evaluation metrics, with the $RMSE$ calculation formula shown in Equation (17). The results are presented in

Table 3. Performance comparison of different denoising methods.

Method Category	Representative Methods	$\mathit{S}\mathit{N}\mathit{R}$ (dB)	$\mathit{N}\mathit{C}\mathit{C}$	$\mathit{R}\mathit{M}\mathit{S}\mathit{E}$
Time-domain	correlation detection	10.35	0.8715	0.0178
Frequency-domain	adaptive filtering	9.92	0.8261	0.0211
Time-frequency domain	wavelet hard thresholding	12.53	0.9021	0.0117
	CEEMDAN	12.14	0.8838	0.0135
	IWT	15.02	0.9244	0.0095
Proposed method in this study	CEEMDAN-IWT	18.65	0.9611	0.0015

. Although learning-based methods have shown strong potential in the field of signal processing, their application in practical geoelectric field detection faces two key challenges: first, these methods typically require a large number of labeled “noise-clean” signal pairs for supervised training, which is difficult to obtain in actual exploration environments where pure reference signals are scarce; second, their decision-making process lacks physical interpretability, making it challenging to meet the need for clear physical mechanisms in the interpretation of geoelectric field data. Therefore, to better align with the requirements of robustness, practicality, and transparency of mechanisms in geoelectric field detection, this study does not include such methods in the comparative analysis.

$$RMSE=\sqrt{{\displaystyle \frac{1}{L}}{\displaystyle \sum _{i=1}^L{\left[s(k)-x(k)\right]}^2}}$$

(17)

According to the results in Table 3, the CEEMDAN-IWT method significantly outperforms other comparative methods in overall denoising performance. Although traditional time-domain and frequency-domain methods possess some denoising capability, their overall metrics are relatively poor. adaptive filtering achieved $SNR$ = 9.92 dB, $NCC$ = 0.8261, $RMSE$ = 0.0211; correlation detection achieved $SNR$ = 10.35 dB, $NCC$ = 0.8715, $RMSE$ = 0.0178. This indicates that traditional methods struggle to effectively preserve signal features under strong noise conditions, resulting in noticeable distortion and residual noise. Time–frequency analysis methods perform better overall than traditional methods. Among them, the improved wavelet thresholding (IWT) performs the best, achieving $SNR$ = 15.02 dB, $NCC$ = 0.9244, $RMSE$ = 0.0095, surpassing traditional wavelet hard thresholding ($SNR$ = 12.53 dB) and CEEMDAN-only denoising ($SNR$ = 12.14 dB), demonstrating the advantage of multi-scale analysis.

The method proposed in this study, through the synergistic effect of CEEMDAN adaptive decomposition and fine denoising via IWT, further optimizes denoising performance, achieving $SNR$ = 18.65 dB, $NCC$ = 0.9611, $RMSE$ = 0.0015, and attaining a better balance between noise suppression and signal fidelity.

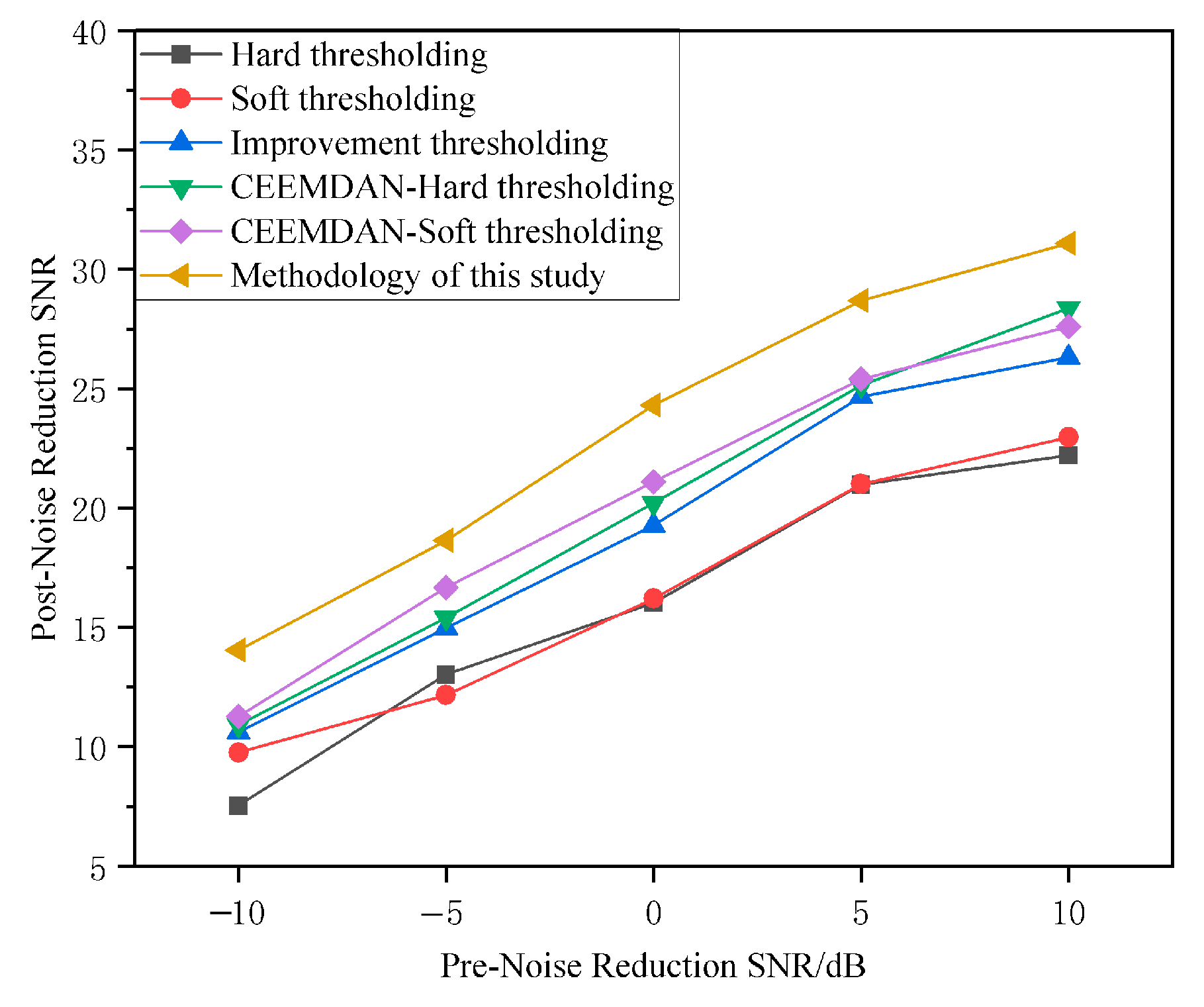
To further explore the denoising performance of the CEEMDAN-IWT method under different noise conditions, denoising analysis was conducted on signals mixed with noise at various $SNR$. The experimental results demonstrate that the CEEMDAN-IWT denoising method outperforms the other six methods, significantly improving the $SNR$ in various noise environments. It effectively separates the characteristic signal and reduces noise interference, enabling more effective signal extraction and noise suppression, thereby significantly enhancing the signal quality, The results are shown in Figure 9. This validates the strong robustness and adaptability of the method.

The robustness results under different noise intensities have already demonstrated the advantages of the method, but a single experiment may be influenced by the randomness of the noise. To ensure the statistical reliability of the conclusions, 45 independent noise realization experiments were conducted under each $SNR$ condition to quantify the stability of the results. The output $SNR$ and $RMSE$ are presented in the form of Mean ± Std, with the results shown in

Table 4. Simulation Experiment Performance Results under Multiple Input $SNR$.

Pre-Denoising $\mathit{S}\mathit{N}\mathit{R}$ (dB)	Post-Denoising $\mathit{S}\mathit{N}\mathit{R}$ (dB)	$\mathit{R}\mathit{M}\mathit{S}\mathit{E}$
−10	14.05 ± 1.08	0.0049 ± 0.00043
−5	18.53 ± 1.06	0.0019 ± 0.00015
0	24.87 ± 1.05	0.0009 ± 0.00011
5	28.36 ± 1.03	0.0006 ± 0.00006
10	30.85 ± 0.97	0.0002 ± 0.00004

.

As the input $SNR$ increases from −10 dB to 10 dB, the output $SNR$ increases from 14.05 dB to 30.85 dB, with the standard deviation remaining ≤ 1.08 dB. The $RMSE$ decreases from 0.0049 to 0.0002 as the input $SNR$ improves, with the standard deviation ≤ 0.00043. These results validate the robustness of the method to changes in noise intensity, and the results demonstrate statistical reliability.

To quantitatively evaluate the computational efficiency and resource consumption of the CEEMDAN-IWT method, this study conducted a computational complexity analysis experiment. The running time and memory usage of the method were measured under different signal lengths (N) and ensemble numbers (I), with the results shown in

Table 5. Computational efficiency and resource consumption.

N	I	Runtime (s)	Memory Usage (KB)
1500	50	1.616	865.1328
	100	3.0208	869.4375
	200	5.9338	878.0312
3750	50	4.1382	1246.3984
	100	7.6857	1251.0859
	200	14.6022	1291.3281
7500	50	8.3893	1925.7031
	100	16.0796	1979.6172
	200	31.7238	1996.0234
15,000	50	20.7799	3444.8594
	100	41.3003	3462.4375
	200	77.9286	3568.6953

.

As can be seen from Table 5, the runtime of the CEEMDAN-IWT method increases approximately linearly with both signal length (N) and ensemble size (I). Under the same I, when N increases from 1500 to 15,000 (a 10-fold increase), the runtime rises by about 12–14 times; under the same N, when I increases from 50 to 200 (a 4-fold increase), the runtime increases by approximately 3.6–3.9 times. The memory usage shows a moderate upward trend with the growth of N (when N increases 10-fold, memory rises from 865 KB to 3569 KB), but remains basically stable with changes in I, indicating that memory consumption is mainly determined by the signal decomposition scale.

From the perspective of practical application scenarios, this method has certain applicability on embedded platforms under the conditions of medium-length signals (N ≤ 7500) and moderate ensemble sizes (I = 50–100). At this point, the memory requirement is less than 2 MB and the runtime is controlled within 16 s, which can match the resource constraints of portable geoelectric field detection equipment. For scenarios with large N (e.g., 15,000) or large I (e.g., 200), offline processing is recommended to balance performance and resource consumption.

The above research results indicate that the method proposed in this study, through the synergistic effect of CEEMDAN and improved wavelet threshold denoising, not only better preserves the key information of the geoelectric current field signal, preventing the loss of critical information in geological analysis, but also significantly outperforms traditional methods in terms of various precise quantitative indicators and environmental adaptability. This achieves the optimal balance between noise suppression and signal fidelity. Although this method slightly increases the computational load, it significantly enhances signal fidelity and reliability. Its two-level synergistic processing framework minimizes signal distortion and improves processing accuracy, providing high-quality data support for subsequent underground electrical parameter inversion and geological structure analysis.

5. Field Measurement Experiment Verification Results and Discussion

5.1. Experiment Data Collection

Injecting geoelectric current fields is a method used to construct a geoelectric current field by injecting current into the ground, thereby enabling geological exploration. It is widely applied in geological surveys and underground information detection. This technology uses a pair of grounding electrodes to inject an alternating current signal of a specific frequency into the ground medium. The current diffuses and propagates in the underground medium according to Ohm’s law, ultimately forming an artificial source geoelectric current field, which is a key parameter reflecting underground geological information. The detection of the injected geoelectric current field involves collecting the geoelectric current field response signals through buried sensors distributed at different locations. The output signal from the sensors contains both effective response components and multi-source noise.

To verify the practical application effect of the CEEMDAN-IWT denoising method, this study conducted an injection-type geoelectric current field construction and data collection experiment near Henan Zhai Village, close to the Shengshuitou Jinwu Silver Mine in Miyun County. There are electrical property differences between the mineral body and the surrounding rock in the underground area, and the geoelectric current field response signal can effectively reflect this difference, which is consistent with the core application scenario of the injected geoelectric current field technology. The experimental area measures 150 m in length and 80 m in width. The data collection process faced three types of noise interference: (1) Vibration from construction machinery superimposed with environmental random noise; (2) Electromagnetic interference from residential areas and high-voltage power lines; (3) Geoelectric field background noise caused by volcanic activity in the mining area. The noise environment is representative. The overall situation of the experimental area is shown in Figure 10.

In this study, a geoelectric current field was constructed by applying a geoelectric current field signal to a pair of buried electrodes. The amplitude of the geoelectric current field injection signal was 50 V, with a frequency of 10 Hz, composed of $MSK$ and sine waves. The sine wave signal served as the effective signal, while the $MSK$ signal functioned as the synchronizing head. The electrodes were made of hard aluminum hollow tube structure, with a length of 100 cm, a diameter of 30 mm, and a burial depth of 70 cm. The distance between the electrodes was 5 m. Figure 11a and Figure 11b, respectively, show the electrode arrangement at the signal injection end and the signal detection end.

The geoelectric field construction and detection equipment is shown in Figure 12, including the self-developed geoelectric current mobile injection terminal and the self-developed geoelectric current field WeChat detection device.

A signal injection point is set up in the experimental area to construct the artificial source geoelectric current field. Due to the attenuation of the geoelectric current field signal and its anisotropic characteristics, 9 detection points are arranged along the experimental area. The RTK positioning system is used to calibrate the coordinates of all measurement points and convert them into a local rectangular coordinate system, as shown in Figure 13. Multi-directional signal acquisition provides comprehensive data samples for the verification of the CEEMDAN-IWT denoising method.

5.2. Denoising Performance Evaluation Metrics

This study addresses the objective limitation that actual environmental noise cannot be completely eliminated and pure reference signals cannot be obtained. The correlation coefficient (r) and noise-to-noise ratio (NNR) are used to quantify the signal feature retention and noise suppression effectiveness, respectively. Under the constraint of not having a pure reference signal, this method constructs a dual evaluation system for feature fidelity and noise suppression, providing a quantifiable basis for analyzing the denoising performance of the injected geoelectric current field measurement signals.

The normalized cross-correlation ($NCC$) directly quantifies the degree of feature retention by calculating the time-domain correlation between the denoised signal and the original injected signal. A sliding correlation calculation is performed between the $MSK$ synchronization header template signal and the denoised signal to find the sampling point where the sliding correlation coefficient is maximized. At this point, a sine wave signal segment is extracted. Then, by calculating the amplitude and initial phase of the extracted signal, a standard sine wave signal is constructed, and a correlation calculation is performed between the extracted signal and the standard sine wave signal., as shown in Equation (14).

The Noise-to-Noise Ratio (NNR) indirectly reflects the noise suppression effectiveness by the ratio of the environmental noise energy to the energy of the denoised signal [32]. The expression is as follows:

$$NNR={\log }_{10}[{\displaystyle \frac{{\displaystyle \sum _{i=1}^L{h}^2(k)}}{{\displaystyle \sum _{i=1}^L{(y(k)-s(k))}^2}}}]$$

(18)

In the equation, $L$ represents the data length, $s(k)$ is the denoised signal sequence, $h(k)$ is the environmental noise sequence, and $y(k)$ is the noisy signal sequence.

5.3. CEEMDAN-IWT Denoising Results and Discussion

In this study, to preliminarily verify the effectiveness of the proposed method, the CEEMDAN-IWT denoising method was applied to process the measurement signals from nine geoelectric current field measurement points. Taking the J₅ detection point as an example, which is located in the middle of the experimental area and is close to construction machinery vibrations and residential areas, where noise interference is significant, the collected signal for this detection point was first adaptively decomposed using the CEEMDAN method. The noise standard deviation was set to 0.2, the number of noise additions to 100, and the maximum number of iterations to 1000. As a result, the original signal was decomposed into 15 intrinsic mode function (IMF) components and 1 residual component. The specific decomposition results are shown in Figure 14.

After the CEEMDAN adaptive decomposition, the variance contribution rate of each IMF component was calculated. Components with a variance contribution rate less than 0.01 were determined to be noise-dominated invalid components and discarded. After filtering, the valid IMF components IMF1 to IMF7 were retained. For the residual noise in each valid component, an improved wavelet threshold function was used for independent denoising. The denoised valid components were then reconstructed, ultimately obtaining the desired injected geoelectric current field signal. The processing results are shown in Figure 15.

The collected signals from the remaining eight detection points were processed following the same procedure, and the processing results are shown in Figure 16.

Comparative analysis shows that the measured data is significantly affected by environmental noise, with noise almost covering the entire collection range. Similarly to the simulation signal scenario, the effective signal is drowned out by noise and cannot be used directly. After processing with the denoising method proposed in this study, the signal amplitude decreases noticeably, the waveform smoothness improves, and the identification of the injected geoelectric current field signal features is significantly enhanced. The experimental results validate that this method maintains good adaptability to multi-level noise environments, effectively restores feature information, and significantly improves signal fidelity. Figure 12 shows the comparison of the measured data before and after denoising at nine test locations, along with the visualization results of the extracted segments.

In order to comprehensively and deeply assess the performance of the CEEMDAN-IWT denoising algorithm, this section will analyze it from two key dimensions: first, signal feature fidelity, which quantifies the similarity between the denoised signal and the original injected signal in terms of waveform using the $NCC$, directly reflecting the algorithm’s ability to retain effective geological information; and second, noise suppression effectiveness, which measures the algorithm’s ability to suppress complex environmental noise (such as mechanical vibration, power-frequency interference, and geoelectric background noise) using the NNR. It is important to note that the performance of any geoelectric field signal processing method is constrained by multiple factors, including transmission distance, surface electrical structure, and the intensity and type of environmental noise. The core advantage of the collaborative denoising strategy proposed in this study lies in overcoming the limitations of single denoising methods when dealing with non-stationary, multi-source complex noise, through the adaptive decomposition of CEEMDAN. Moreover, the use of an improved wavelet threshold function achieves a better balance between noise suppression and the preservation of weak signal details, thereby enhancing the algorithm’s adaptability and stability in changing underground environments and noisy fields. The following will verify this through specific data. In this study, six denoising methods, including wavelet hard and soft thresholding denoising methods, IWT denoising method, CEEMDAN-hard threshold denoising method, CEEMDAN-soft threshold denoising method, and the proposed denoising method in this study, were applied sequentially to the measured signals from nine measurement points. The performance was quantified by calculating the correlation coefficient and noise-to-noise ratio before and after denoising. The experimental results show that the CEEMDAN-IWT method performs optimally in the synergistic optimization of feature preservation and noise suppression. The specific results are shown in

Table 6. Quantitative indicators for denoising performance.

Measurement Points		J1	J2	J3	J4	J5	J6	J7	J8	J9
$NCC$	wavelet hard threshold	0.8361	0.8373	0.8388	0.8403	0.8341	0.8398	0.8372	0.8346	0.8351
	wavelet soft threshold	0.8382	0.8396	0.8365	0.8438	0.8315	0.8422	0.8413	0.8321	0.8378
	IWT	0.8665	0.8682	0.8678	0.8742	0.8603	0.8733	0.8717	0.8632	0.8652
	CEEMDAN-hard threshold	0.8932	0.8952	0.8926	0.8953	0.8829	0.8922	0.8894	0.8841	0.8885
	CEEMDAN-soft threshold	0.8942	0.8957	0.8935	0.8968	0.8864	0.8946	0.8903	0.8873	0.8895
	The denoising method in this study	0.9236	0.9253	0.9227	0.9254	0.9109	0.9241	0.9196	0.9124	0.9164
NNR	wavelet hard threshold	1.1244	1.1412	1.1511	1.1877	1.1589	1.2785	1.0860	1.1731	1.0321
	wavelet soft threshold	1.1468	1.0820	1.1172	1.0266	1.1535	1.2021	1.0563	1.1893	1.0210
	IWT	1.1099	0.9536	1.0872	0.9495	1.1113	1.1558	0.9975	1.1627	0.9372
	CEEMDAN-hard threshold	0.5037	0.5324	0.7249	0.4976	0.7713	1.0739	0.6361	0.9325	0.2822
	CEEMDAN-soft threshold	0.7132	0.4631	0.4937	0.3692	0.7352	0.9819	0.6340	0.9564	0.2633
	The denoising method in this study	0.1053	0.0537	0.1146	0.0237	0.1531	0.0811	0.1323	0.1405	0.1385

.

This study validates the denoising performance from two dimensions: signal feature retention and noise suppression. In terms of signal fidelity, the closer the absolute value of the $NCC$ is to 1, the higher the consistency in shape between the denoised signal and the original signal. In terms of noise suppression efficiency, the closer the absolute value of the NNR is to 0, the less residual noise energy remains. The quantitative results in Table 6 clearly indicate that the CEEMDAN-IWT method proposed in this study achieves a synergistic optimization of feature preservation and noise suppression across all nine measurement points, with overall denoising performance significantly outperforming the other five conventional methods. In terms of signal fidelity, the $NCC$ of this method ranges from 0.9109 to 0.9254, the closest to 1 among all methods, indicating the highest waveform consistency between the denoised signal and the original injected signal. This demonstrates that the method effectively smooths noise while maximally preserving signal detail features. Regarding noise suppression efficiency, its NNR values range only from 0.0237 to 0.1531, much lower than those of other methods, indicating that the residual noise energy after denoising is minimal and that the suppression of multi-source complex noise is more thorough.

Further analysis of the indicators at each measurement point reveals that the denoising performance indicators ($NCC$ value relatively low, NNR absolute value relatively high) for points J₅, J₇, J₈, and J₉ show a slight decline compared to the other points. This phenomenon is closely related to the spatial distribution of the measurement points and the actual environmental interference. Referring to the measurement point layout in Figure 13, it is evident that points J₇, J₈, and J₉ are the farthest from the signal injection source. When the injected electric field signal propagates through the underground medium, it undergoes significant attenuation with increasing distance, leading to the weakest received signal strength at these points. When combined with environmental noise, the signal-to-noise ratio further decreases, posing a greater challenge to the denoising algorithm. While point J₅ is not the farthest, it is significantly affected by the background electric field noise, surrounding residential areas, and high-voltage power lines, resulting in complex electromagnetic interference. There may also be local variations in the medium’s electrical properties, creating unfavorable conditions with signal attenuation and strong noise interference, making it the location with the poorest denoising performance among all the measurement points. Thus, the advantages of the proposed method are not unconditional, as its performance is also constrained by factors such as distance and geological background conditions. When the distance between the measurement point and the signal injection source exceeds a certain threshold, signal attenuation intensifies sharply, resulting in extremely weak signal strength. Furthermore, the background noise of the injected electric field signal is jointly influenced by the Earth’s background noise and environmental random noise. If the signal strength falls below the critical noise intensity threshold, even with CEEMDAN’s adaptive decomposition and refined denoising via the improved wavelet thresholding, it remains challenging to fully separate the mixed components of noise and valid signals. This not only limits the improvement of the correlation coefficient but also hinders further reduction in residual noise energy. Fundamentally, this limitation is determined by the propagation characteristics of electric field signals and the attenuation effects of underground media, which constitutes a common challenge for all denoising methods in injected electric field detection technology.

However, even under these unfavorable conditions, the performance of the CEEMDAN-IWT method remains consistently superior to all the comparison methods. This highlights its core advantage: traditional single denoising methods (such as wavelet thresholding) have fixed parameters and poor adaptability, which can easily lead to distortion of the valid signal or excessive residual noise when facing severe signal attenuation and complex noise mixing due to distance. In contrast, the CEEMDAN-IWT method, through adaptive decomposition and selection, can perform differentiated and fine-grained processing according to the characteristics of each IMF component, thereby exhibiting stronger robustness when handling signals with different signal-to-noise ratios and noise compositions. It reduces the dependence on prior knowledge of transmission distance and environmental noise. This adaptive processing mechanism, based on the inherent characteristics of the signal itself, is the fundamental reason for its ability to maintain excellent performance in changing underground environments, maximizing data quality within the detectable range where the signal has not been completely obliterated.

6. Conclusions

This study addresses the issue that weak geoelectric current signals are severely interfered with by noise in the injection-type geoelectric current field signal detection technology, making them unsuitable for direct geological structure analysis. A CEEMDAN and improved wavelet thresholding collaborative denoising method is proposed to remove background noise from the geoelectric current field data and improve signal interpretation accuracy. The method adaptively decomposes the signal using CEEMDAN, selects the effective intrinsic mode function (IMF) components based on the variance contribution rate, and then applies improved wavelet thresholding for multi-scale refinement processing of the IMF components, balancing noise suppression and weak signal feature retention capabilities. The high-quality denoised signal is then reconstructed.

In simulation experiments, under the condition of an initial $SNR$ of −5 dB, the method improved the $SNR$ to 18.65 dB. More importantly, as illustrated in Figure 9, the $SNR$ enhancement effect of the proposed method under different noise intensity conditions (ranging from −10 dB to 10 dB) is significantly superior to that of traditional methods such as wavelet hard thresholding, wavelet soft thresholding, IWT, CEEMDAN-hard thresholding, and CEEMDAN-soft thresholding. This fully verifies the strong robustness of the method against variable noise environments.

In field measurement experiments, to comprehensively evaluate the denoising performance from the dual dimensions of signal feature retention and noise suppression, the $NCC$ and NNR were adopted as quantitative evaluation indicators. As shown in Table 6, after processing with the proposed method, the data from nine signal measurement points significantly outperforms other traditional denoising methods in terms of performance evaluation indicator $NCC$; the correlation coefficient between the denoised geoelectric current field signal and the ideal injected signal reaches up to 0.9254, indicating that the method demonstrates enhanced robustness against the dual interference of distance attenuation and complex environmental noise.

The CEEMDAN-IWT collaborative strategy effectively mitigates the limitations of conventional single denoisers, which are highly sensitive to specific noise types and stationary assumptions, offering a more reliable data processing approach for scenarios with variable channel characteristics and multi-source noise. The method achieves optimal noise suppression while maximizing the retention of signal feature details. The research findings provide a reliable and advanced data processing method for geological exploration, underground construction safety monitoring, ground-penetrating communication, and other fields, and have significant implications for personnel safety in underground construction, coal mining, emergency communication, and related areas.