Study on the Transient Temperature Evolution Characteristics of Three-Phase Co-Box Type GIS and Inversion Method for Busbar Temperature
Abstract
1. Introduction
2. GIS Busbar Temperature Rise Test
2.1. Test Prototype and Equipment
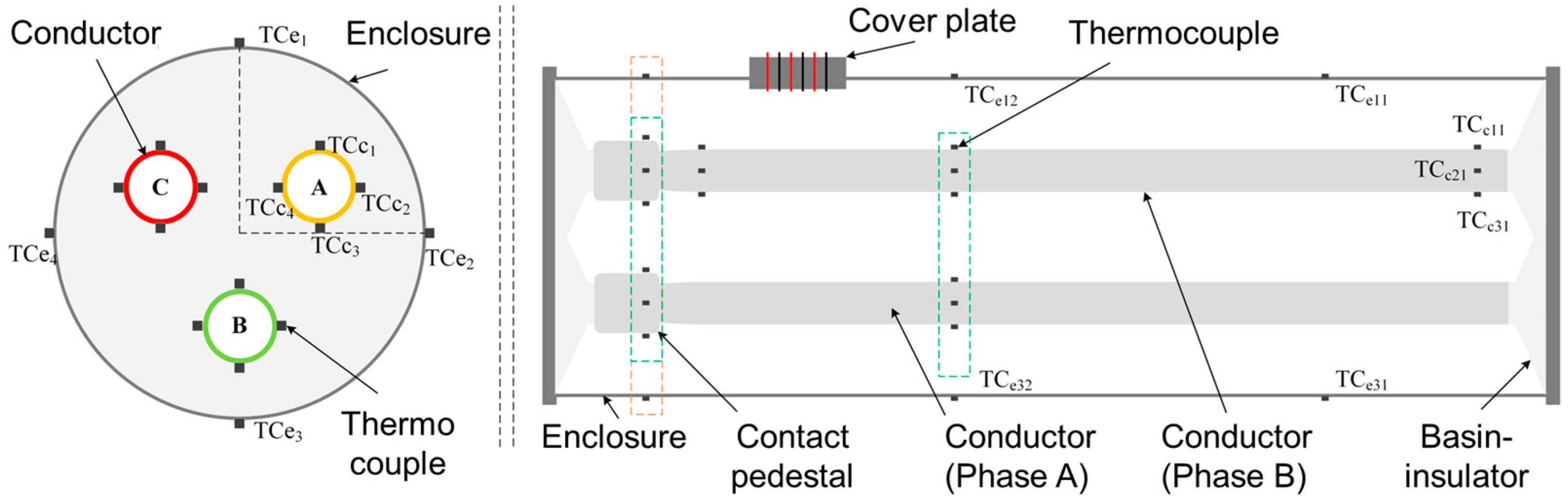
2.2. Thermocouple Layout Scheme
2.3. Temperature Rise Test
3. Transient Temperature Evolution Analysis
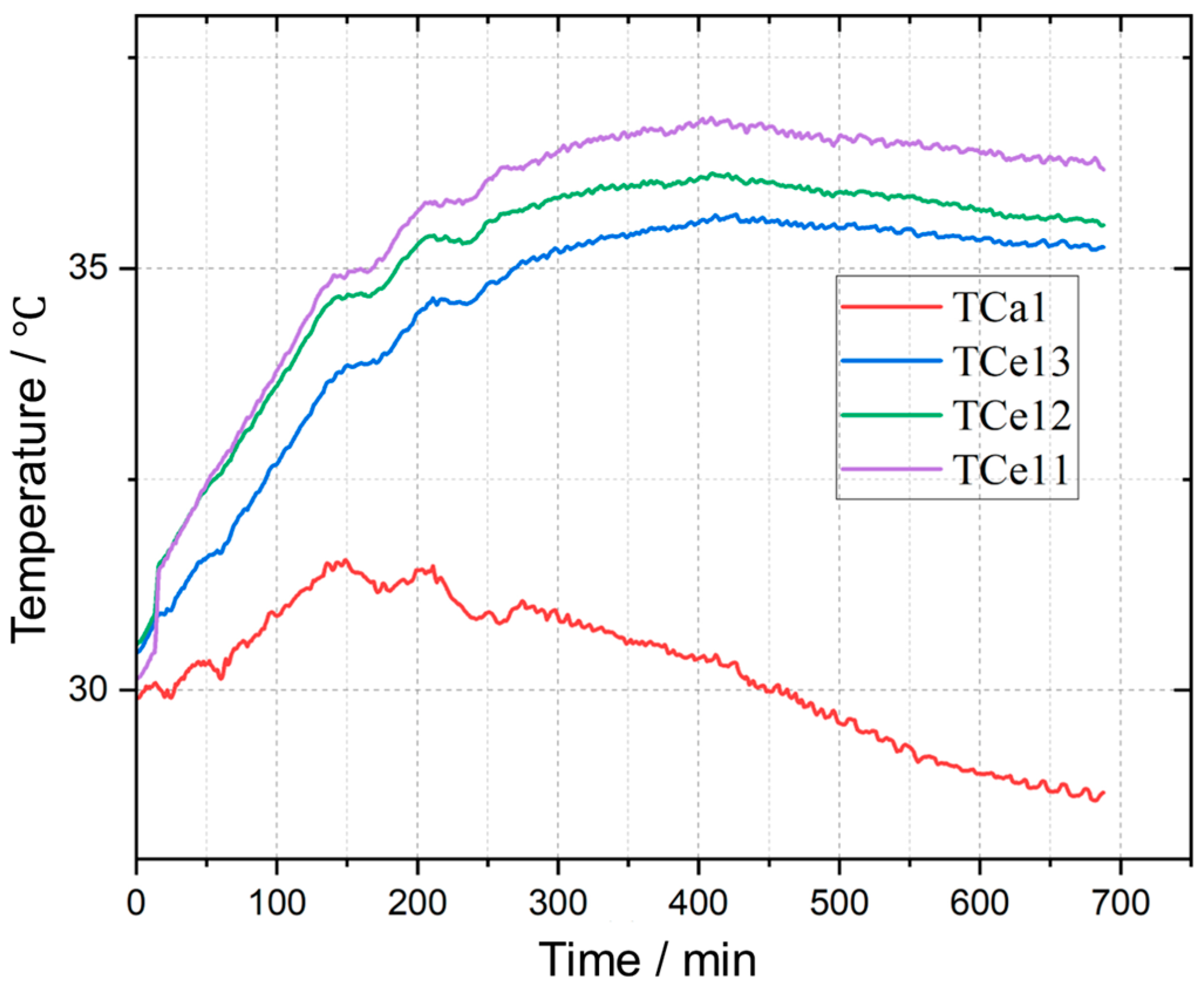
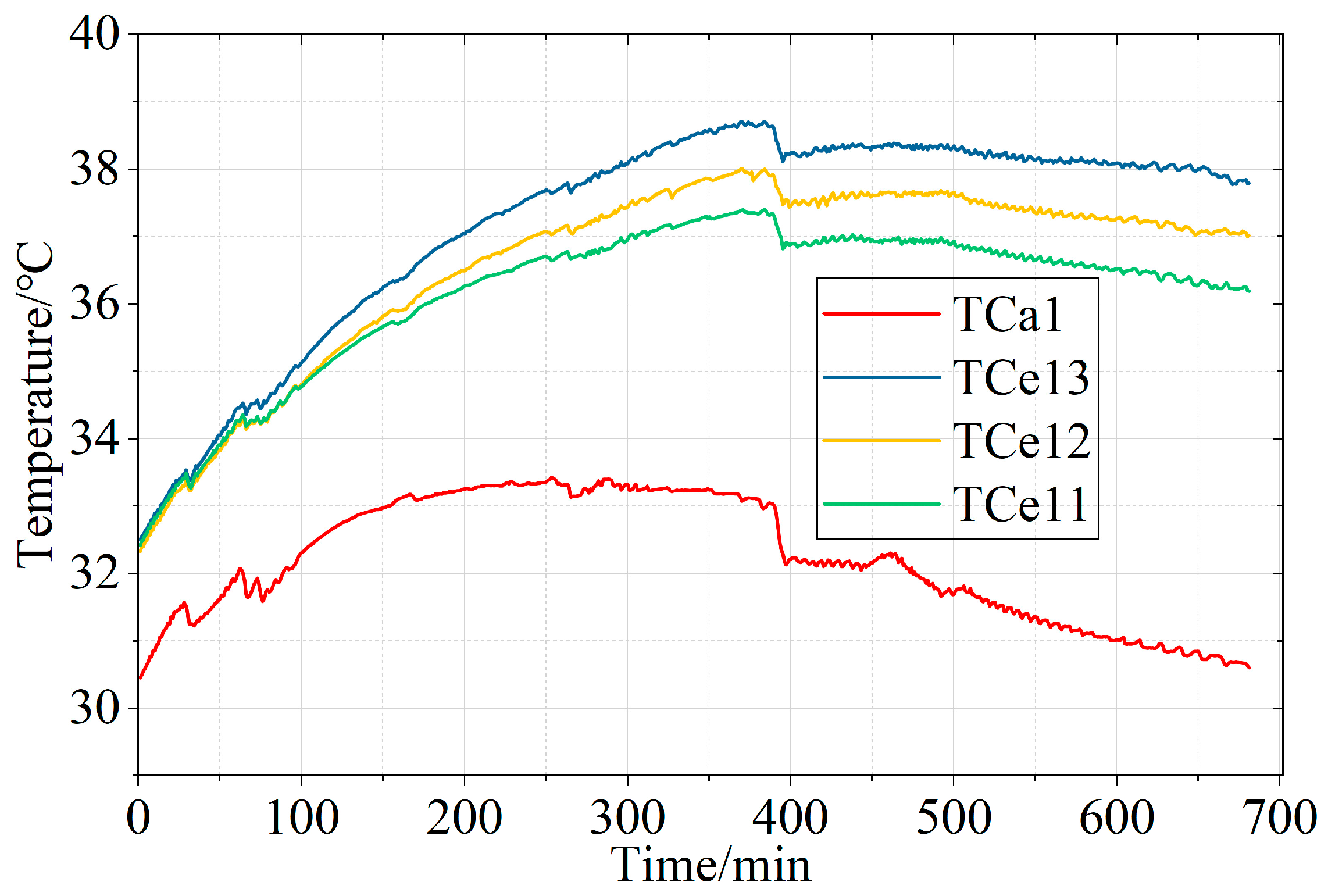
3.1. Evolution of Ambient Temperature
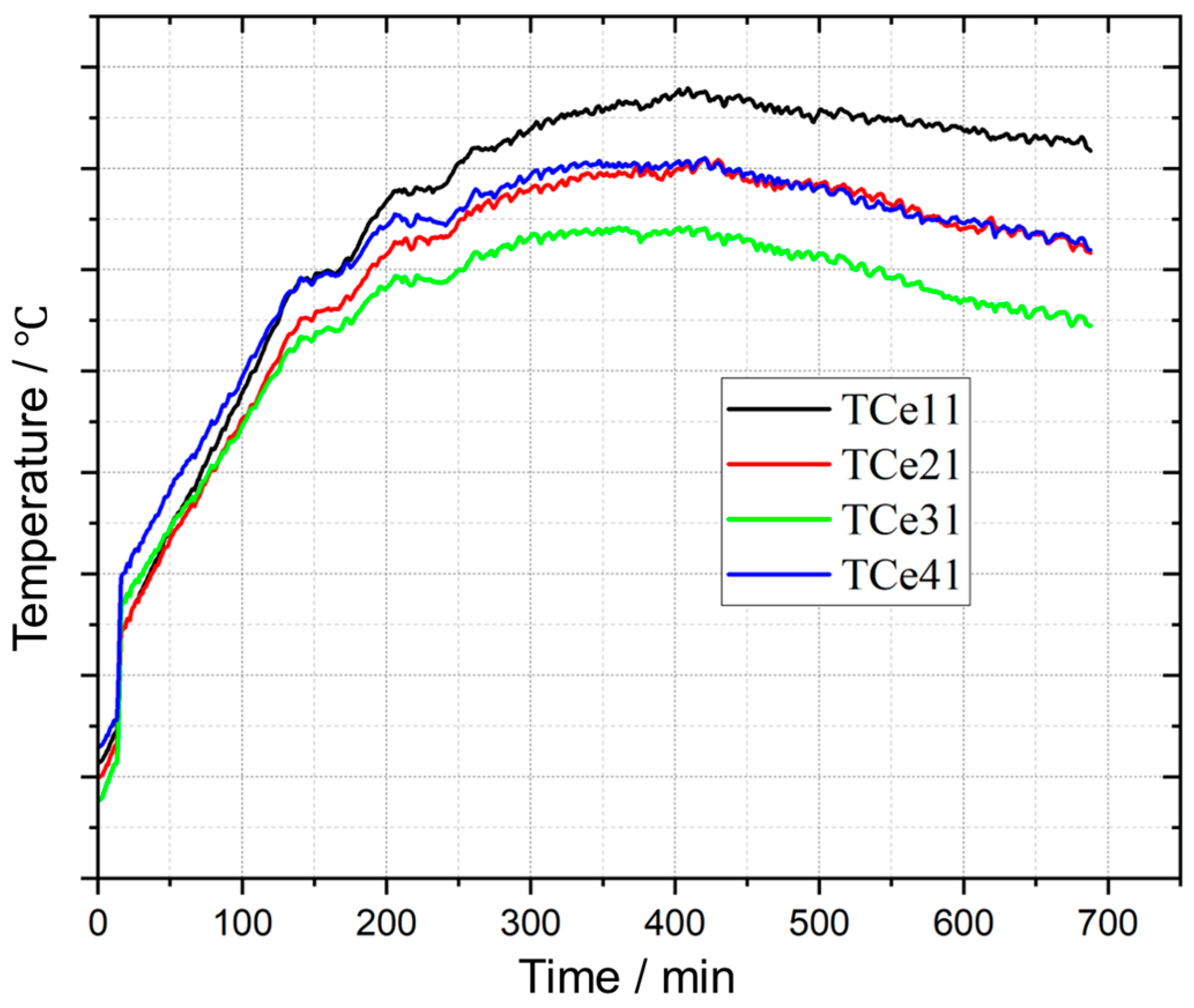
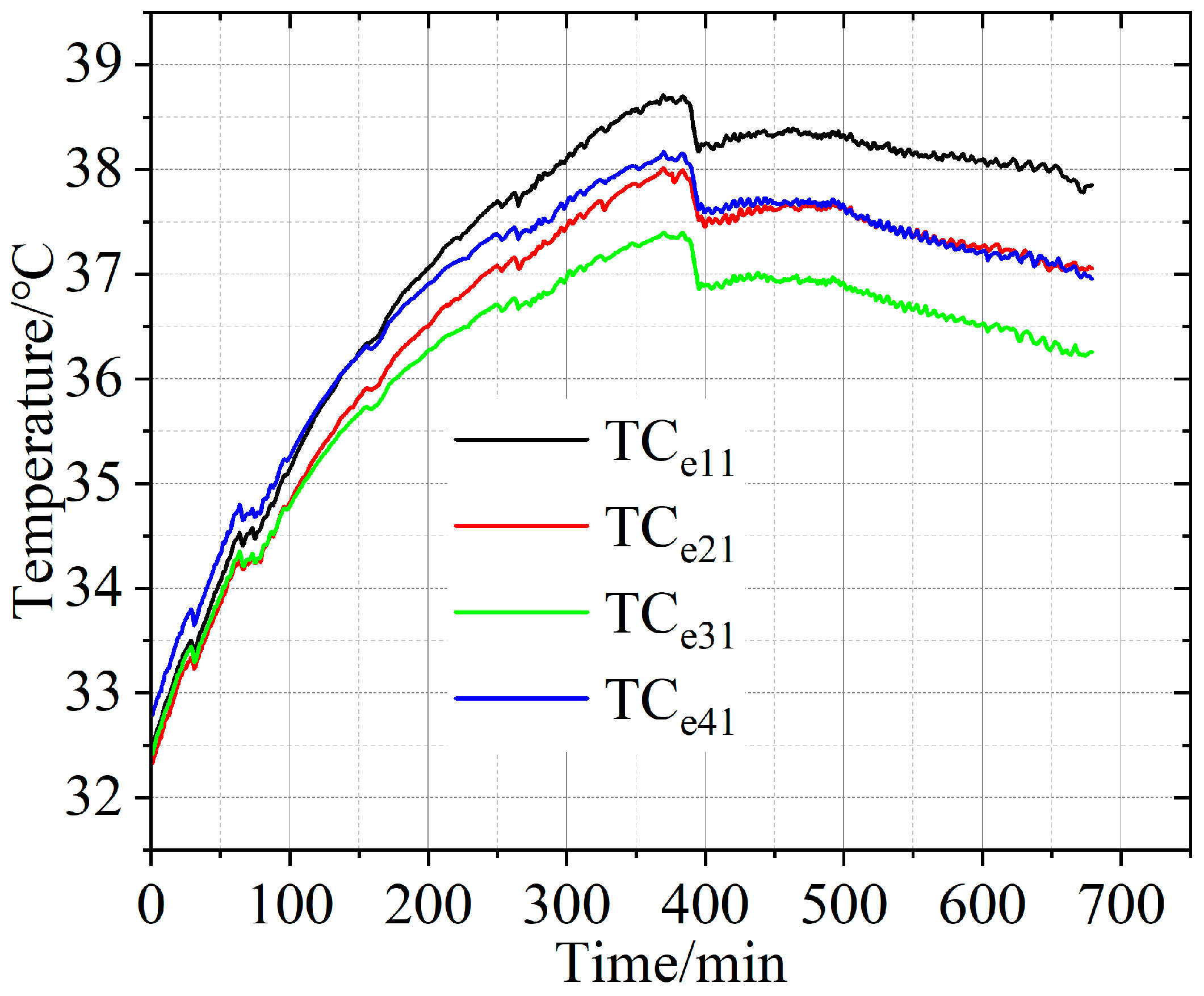
3.2. Evolution of Enclosure Temperature
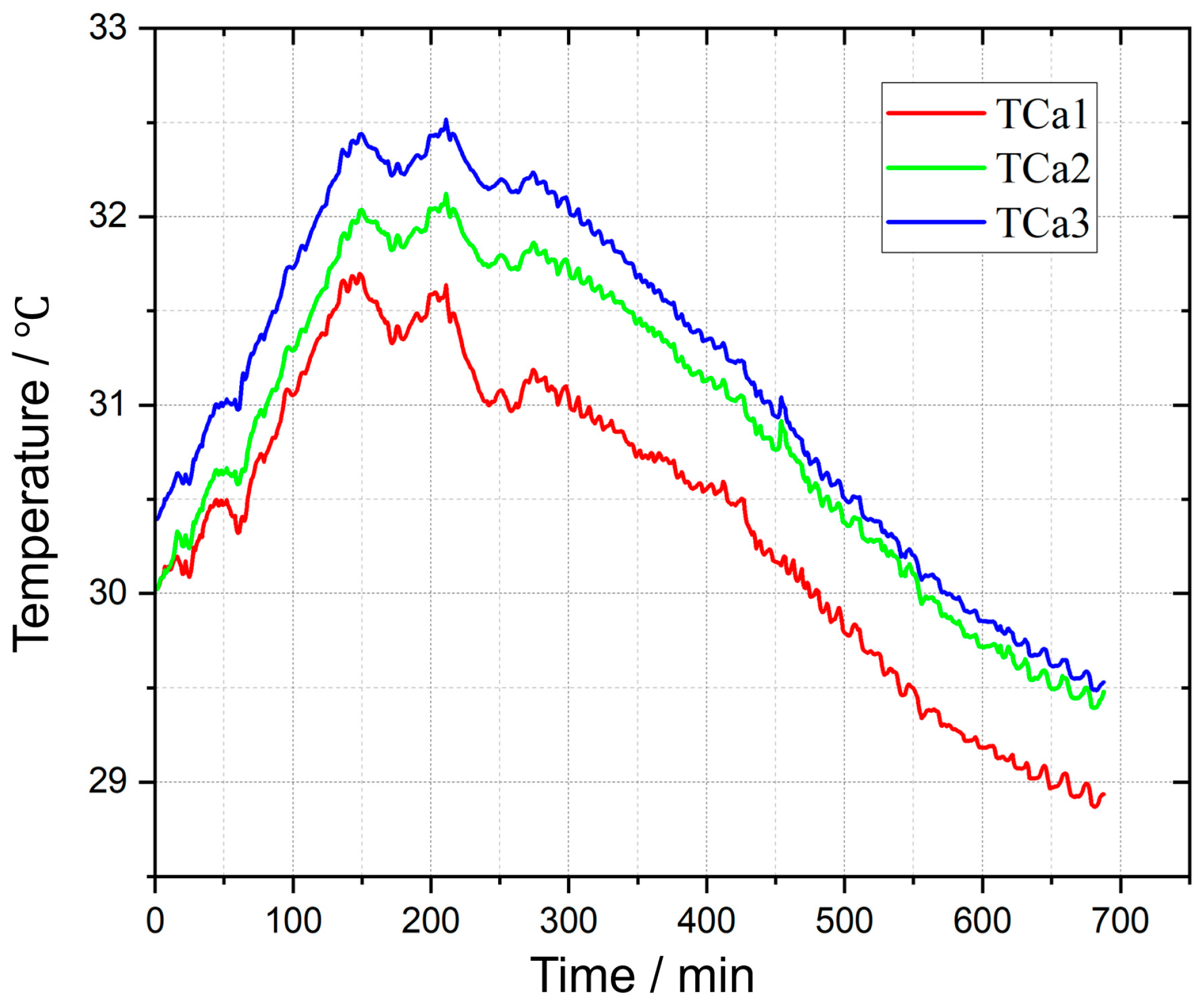
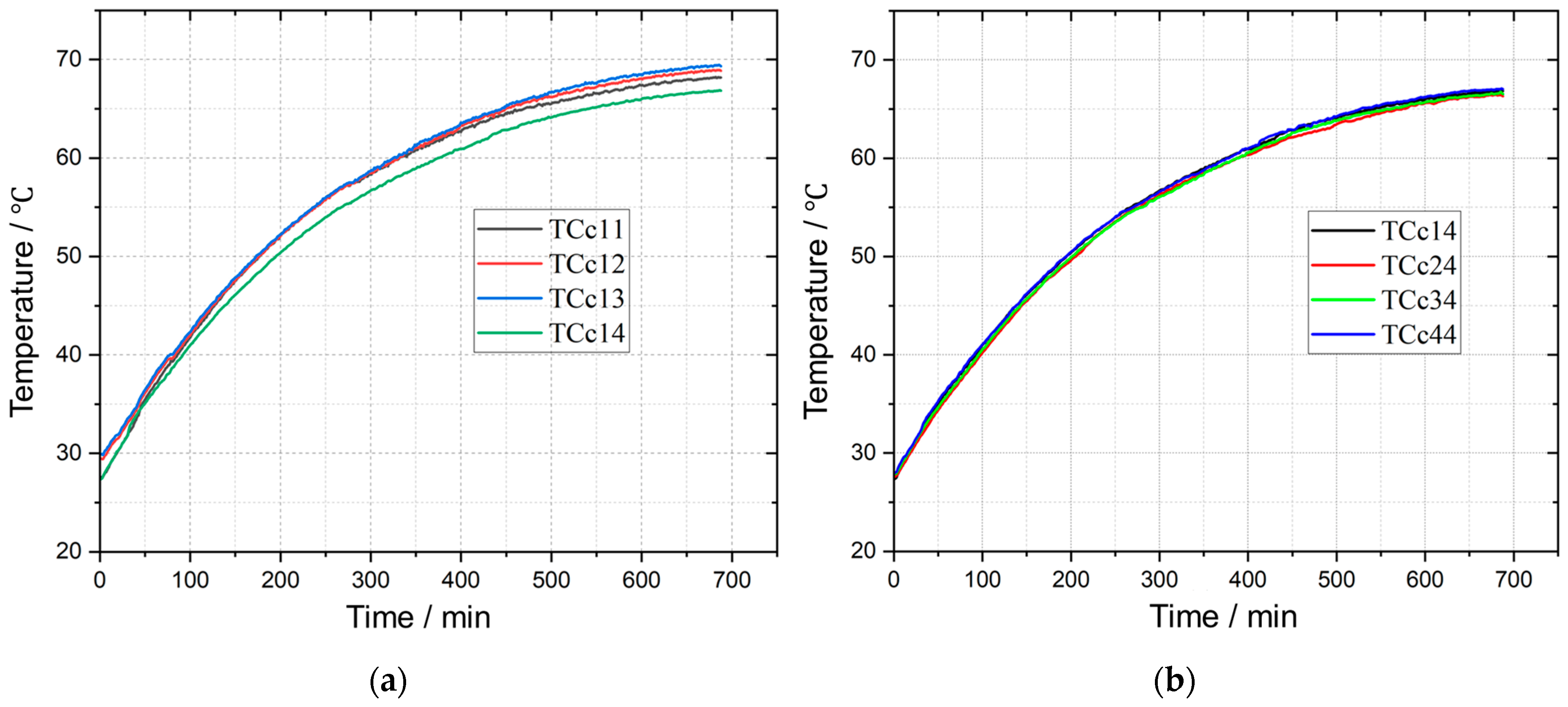
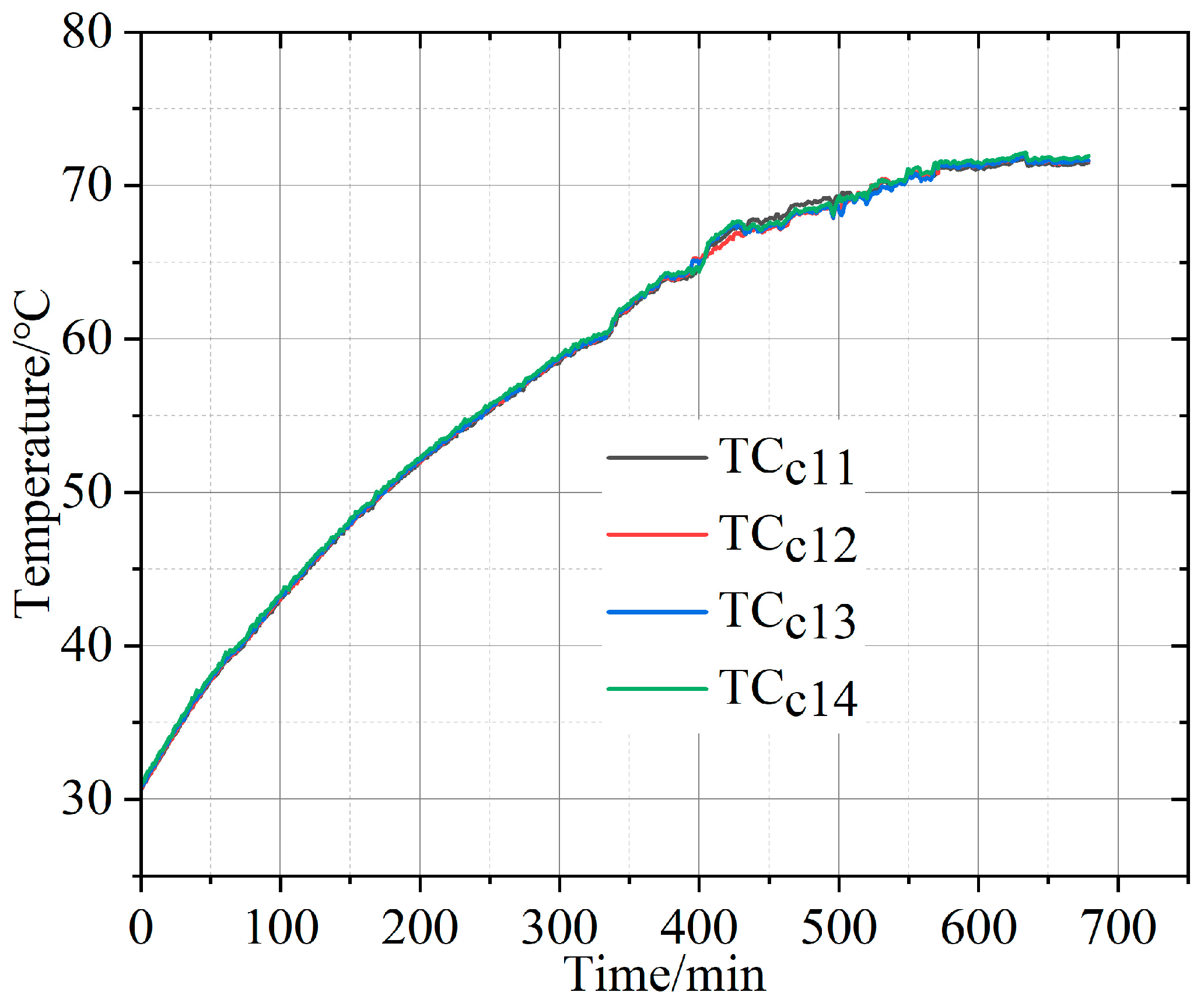
3.3. Evolution of Conductor Temperature
3.4. Characteristics Extraction Considering Transient Temperature Evolution
4. Inversion Method for Busbar Temperature Considering Transient Evolution Characteristics
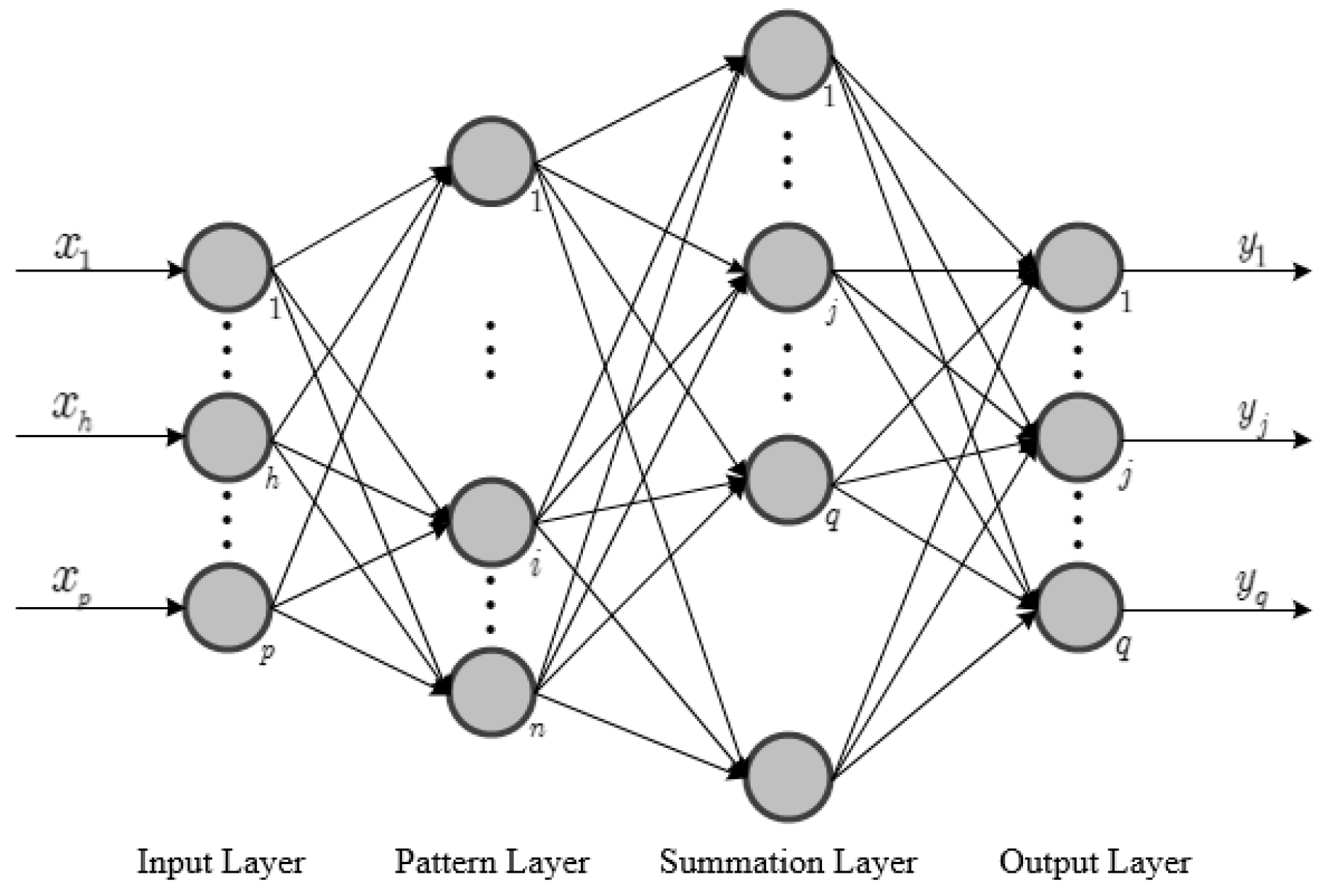
4.1. Inversion Method and Experimental Validation
4.2. Influence of Different Time Intervals for Feature Selection
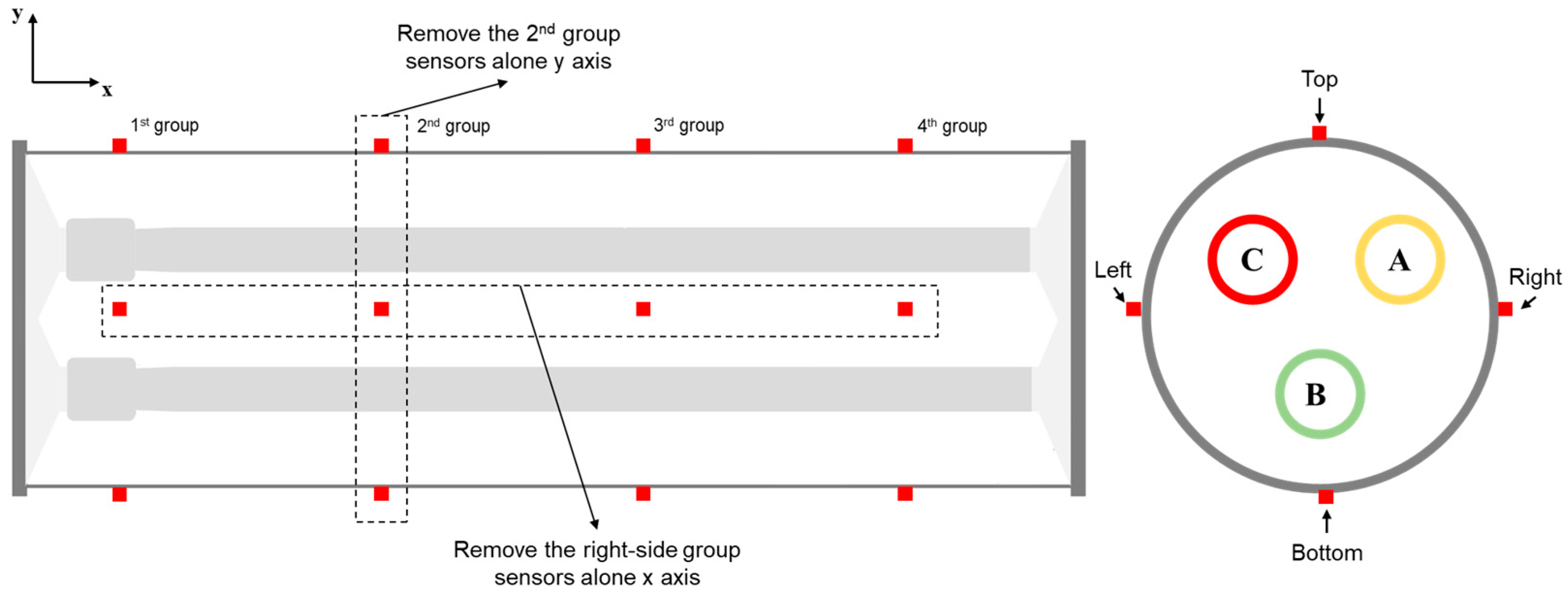
4.3. Influence of Temperature Monitoring Points
5. Conclusions
- (1)
- From the field application point of view, the temperature monitoring sensors could only be deployed on the surface of the GIS enclosure; thus, the test proved that the GIS enclosure temperature rise is influenced by both the internal conditions and the external environment, and the location of the GIS output has a more significant influence. This conclusion is important for target feature extraction for temperature inversion.
- (2)
- As presented in this paper, evenly distributed temperature measurement points within the enclosure can obtain richer information and help to assess the temperature distribution inside the GIS.
- (3)
- The proposed inversion method for the GIS busbar temperature considering transient evolution characteristics has a higher accuracy than traditional characteristic parameters, especially for the recognition of temperature increases due to mild poor contact.
- (4)
- The monitoring points along the x axis, especially at the top side of the enclosure, have a significant influence on the busbar inversion accuracy. We recommend prioritizing retaining monitoring points near hotspots, especially at the top side of the enclosure, for better performance in practical applications.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Istad, M.; Runde, M. Thirty-six years of service experience with a national population of gas-insulated substations. IEEE Trans. Power Deliv. 2010, 25, 2448–2454. [Google Scholar] [CrossRef]
- Runde, M. Failure frequencies for high-voltage circuit breakers, disconnectors, earthing switches, instrument transformers, and gas-insulated switchgear. IEEE Trans. Power Deliv. 2013, 28, 529–530. [Google Scholar] [CrossRef]
- Zhou, N.; Luo, L.; Sheng, G.; Jiang, X. Scheduling the imperfect maintenance and replacement of power substation equipment: A risk-based optimization model. IEEE Trans. Power Deliv. 2025, 40, 2154–2166. [Google Scholar] [CrossRef]
- Wu, X.W.; Shu, N.Q.; Li, L.; Li, H.T.; Peng, H. Finite element analysis of thermal problems in gas-insulated power apparatus with multiple species transport technique. IEEE Trans. Magn. 2014, 50, 321–324. [Google Scholar] [CrossRef]
- Guan, X.; Shu, N.; Peng, H. LBM simulation of heat transfer processes inside GIS capsule filled with different insulation gas mixtures. Math. Comput. Simul. 2021, 188, 212–225. [Google Scholar] [CrossRef]
- Dhotre, M.T.; Korbel, J.; Ye, X.; Ostrowski, J.; Kotilainen, S.; Kriegel, M. CFD simulation of temperature rise in high voltage circuit breakers. IEEE Trans. Power Deliv. 2017, 32, 2530–2536. [Google Scholar] [CrossRef]
- Pawar, S.; Joshi, K.; Andrews, L.; Kale, S. Application of computational fluid dynamics to reduce the new product development cycle time of the SF6 gas circuit breaker. IEEE Trans. Power Del. 2012, 27, 156–163. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, Z.; Zhu, H.; Hong, G.; Ren, J.; Long, W.; Huang, X. Study on temperature rise characteristics of GIS disconnector under different operating conditions. IEEE Trans. Power Deliv. 2021, 36, 3601–3610. [Google Scholar] [CrossRef]
- Doukas, D.I.; Papadopoulos, T.A.; Chrysochos, A.I.; Labridis, D.P.; Papagiannis, G.K. Multiphysics modeling for transient analysis of gas-insulated lines. IEEE Trans. Power Deliv. 2018, 33, 2786–2793. [Google Scholar] [CrossRef]
- Koller, L.; Novák, B. Transient heating of gas insulated switchgears. In Proceedings of the 2010 IEEE/PES Transmission & Distribution Conference & Exposition (T&D), New Orleans, LA, USA, 19–22 April 2010; pp. 1–7. [Google Scholar]
- Li, H.; Shu, N.; Wu, X.; Peng, H.; Li, Z. Scale modeling on the overheat failure of bus contacts in gas-insulated switchgears. IEEE Trans. Magn. 2014, 50, 305–308. [Google Scholar] [CrossRef]
- Minaguchi, D.; Ginno, M.; Itaka, K.; Furukawa, H.; Ninomiya, K.; Hayashi, T. Heat transfer characteristics of gas-insulated transmission lines. IEEE Trans. Power Deliv. 1986, 1, 1–9. [Google Scholar] [CrossRef]
- Han, S.; Yang, F.; Jiang, H.; Yang, G.; Zhang, N.; Wang, D. A smart thermography camera and application in the diagnosis of electrical equipment. IEEE Trans. Instrum. Meas. 2021, 70, 5012108. [Google Scholar] [CrossRef]
- Fjeld, E.; Rondeel, W.G.J.; Attar, E.; Singh, S. Estimate the temperature rise of medium voltage metal enclosed switchgear by simplified heat transfer calculations. IEEE Trans. Power Deliv. 2021, 36, 853–860. [Google Scholar] [CrossRef]
- Kim, S.W.; Kim, H.; Hahn, S.; Lee, B.; Park, K.; Shin, Y.; Song, W.; Kim, J.; Shin, I. Coupled finite-element-analytic technique for prediction of temperature rise in power apparatus. IEEE Trans. Magn. 2002, 38, 921–924. [Google Scholar] [CrossRef]
- Zhang, L.; Li, R.; Lu, Y.; Rao, X. Inversion method for contact temperature of GIS disconnect switch. IEEE Access 2024, 12, 44553–44563. [Google Scholar] [CrossRef]
- Kumar, U.; Tiwari, N.; Rao, M.M. Transient thermal analysis of gas insulated switchgear modules using thermal network approach. Int. J. Emerg. Electr. Power Syst. 2024, 25, 163–173. [Google Scholar]
- Parzen, E. On estimation of a probability density function and mode. Ann. Math. Stat. 1962, 33, 1065–1076. [Google Scholar] [CrossRef]
- Specht, D.F. A general regression neural network. IEEE Trans. Neural Netw. 1991, 2, 568–576. [Google Scholar] [CrossRef] [PubMed]

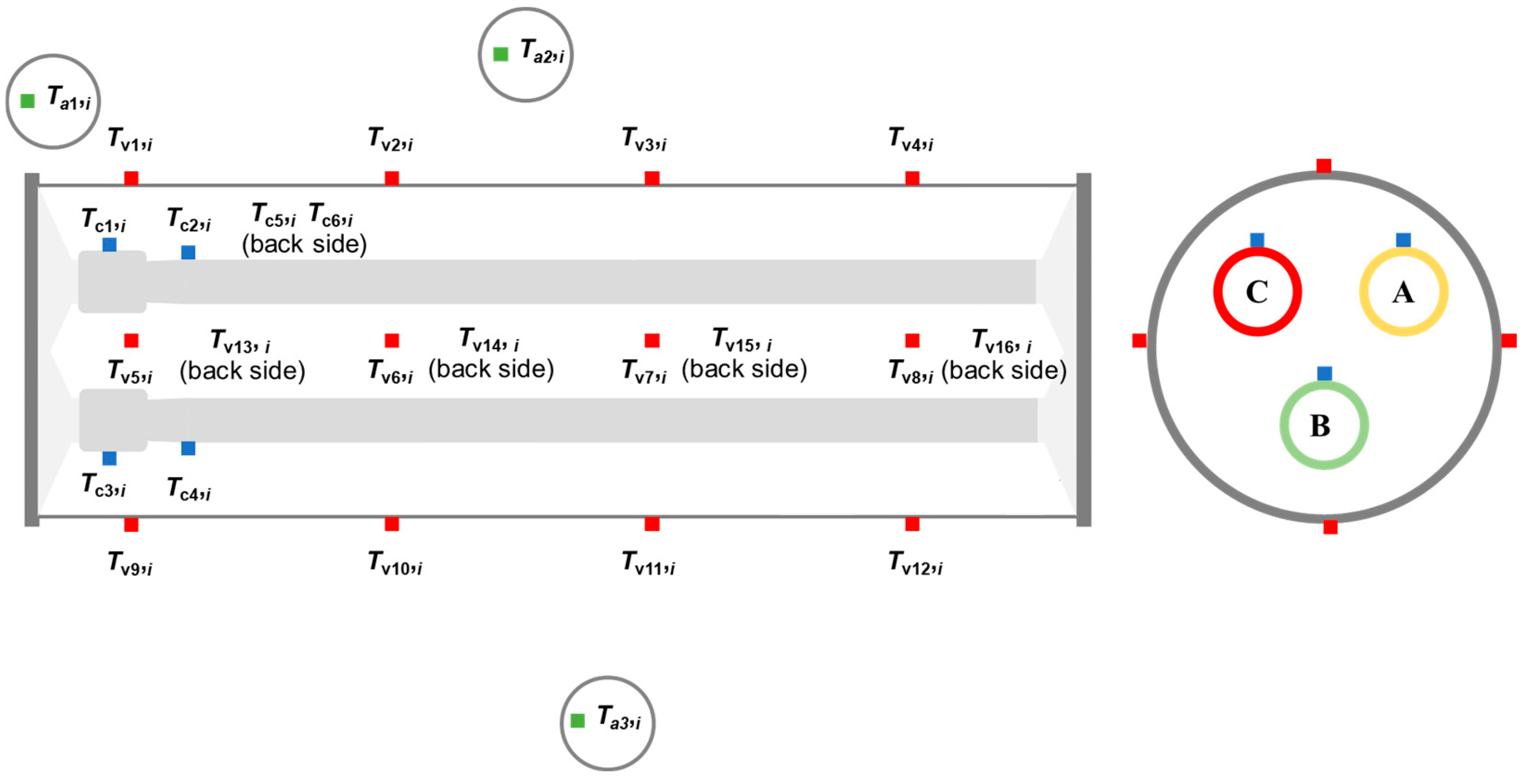
| Phase | Thermocouple Number | Starting Temperature/°C | Ending Temperature (680 min)/°C | Temperature Rise/K |
|---|---|---|---|---|
| A | TCc11 | 28.5 | 68.2 | 39.7 |
| TCc12 | 29.5 | 68.9 | 39.4 | |
| TCc13 | 29.9 | 69.4 | 39.5 | |
| TCc14 | 27.4 | 66.8 | 39.4 | |
| B | TCc12 | 29.3 | 67.9 | 36.6 |
| TCc14 | 29.1 | 65.6 | 36.5 | |
| C | TCc12 | 28.1 | 67.5 | 39.4 |
| TCc14 | 29.2 | 68.6 | 39.4 |
| Type | Ambient Temperature/°C | Proposed Method
(%) | Steady Temperature Only (%) |
|---|---|---|---|
| Normal State (20 μΩ) | 10 | 96.2/89.6 | 80.1/75.6 |
| 20 | 95.7/88.1 | 78.9/83.4 | |
| 30 | 94.3/88.6 | 77.3/76.1 | |
| Mild Poor Contact (200 μΩ) | 10 | 89.7/92.3 | 73.9/70.1 |
| 20 | 87.6/90.8 | 70.6/73.9 | |
| 30 | 86.2/89.0 | 68.4/66.8 | |
| Severe Poor Contact (300 μΩ) | 10 | 99.1/97.5 | 99.7/96.9 |
| 20 | 98.8/96.9 | 97.1/93.6 | |
| 30 | 98.4/96.3 | 95.7/91.9 | |
| (%) | 10 | 96.4 | 85.9 |
| 20 | 93.8 | 79.8 | |
| 30 | 91.5 | 77.2 |
| Type | Ambient Temperature/°C | 10 min Interval (%) | 25 min Interval (%) | 50 min Interval (%) |
|---|---|---|---|---|
| Normal State (20 μΩ) | 10 | 89.4/80.2 | 96.9/89.7 | 97.3/90.2 |
| 20 | 88.7/81.5 | 96.1/88.3 | 96.4/89.5 | |
| 30 | 87.7/80.1 | 95.2/89.1 | 95.1/89.7 | |
| Mild Poor Contact (200 μΩ) | 10 | 77.3/83.5 | 90.2/91.5 | 91.4/93.7 |
| 20 | 77.2/80.9 | 89.5/90.1 | 89.0/91.8 | |
| 30 | 76.5/79.8 | 88.3/88.9 | 88.8/90.4 | |
| Severe Poor Contact (300 μΩ) | 10 | 90.4/88.7 | 98.7/96.3 | 99.3/97.8 |
| 20 | 90.0/88.9 | 98.1/95.4 | 99.2/96.8 | |
| 30 | 89.5/87.6 | 97.8/95.1 | 98.5/97.1 | |
| (%) | 10 | 84.6 | 95.8 | 97.2 |
| 20 | 85.1 | 95.1 | 95.9 | |
| 30 | 83.7 | 91.3 | 92.3 |
| Direction | Removed Group | Accuracy Rate (%) |
|---|---|---|
| Along x axis | Top-side group | 53.68 |
| Right-side group | 88.75 | |
| Bottom-side group | 89.01 | |
| Left-side group | 83.57 | |
| Along y axis | 1st group | 93.92 |
| 2nd group | 93.34 | |
| 3rd group | 94.17 | |
| 4th group | 93.68 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Li, F.; Jiang, X.; Wang, S.; Jiang, J.; Luo, L. Study on the Transient Temperature Evolution Characteristics of Three-Phase Co-Box Type GIS and Inversion Method for Busbar Temperature. Electronics 2025, 14, 4606. https://doi.org/10.3390/electronics14234606
Chen X, Li F, Jiang X, Wang S, Jiang J, Luo L. Study on the Transient Temperature Evolution Characteristics of Three-Phase Co-Box Type GIS and Inversion Method for Busbar Temperature. Electronics. 2025; 14(23):4606. https://doi.org/10.3390/electronics14234606
Chicago/Turabian StyleChen, Xiaoxin, Feiran Li, Xiongwei Jiang, Shaoan Wang, Jiongting Jiang, and Lingen Luo. 2025. "Study on the Transient Temperature Evolution Characteristics of Three-Phase Co-Box Type GIS and Inversion Method for Busbar Temperature" Electronics 14, no. 23: 4606. https://doi.org/10.3390/electronics14234606
APA StyleChen, X., Li, F., Jiang, X., Wang, S., Jiang, J., & Luo, L. (2025). Study on the Transient Temperature Evolution Characteristics of Three-Phase Co-Box Type GIS and Inversion Method for Busbar Temperature. Electronics, 14(23), 4606. https://doi.org/10.3390/electronics14234606







