Blind Separation and Feature-Guided Modulation Recognition for Single-Channel Mixed Signals
Abstract
1. Introduction
- (1)
- We introduce an adaptive spectrum partitioning strategy based on energy detection. It dynamically divides the mixed signal band into multiple sub-bands to construct multi-dimensional virtual observations. FastICA is then applied to separate these signals effectively, thereby alleviating issues of data scarcity and feature masking;
- (2)
- A novel recognition method that synergistically combines prior knowledge with deep learning feature extraction is proposed. The framework includes a dedicated module for extracting and fusing diverse forms of prior knowledge, while the deep learning component operates directly on the original I/Q data. The final step involves the integration of these knowledge-driven and data-driven features;
- (3)
- A phased feature processing framework is designed to tackle the challenges posed by the heterogeneous nature of different prior knowledge features and the temporal dependencies within signals. Initially, various prior knowledge features are extracted independently through parallel branches to preserve information purity. Subsequently, these features are combined to exploit their correlations across the temporal dimension.
2. Materials and Methods
2.1. Received Signal Model
2.2. Fast Independent Component Analysis
2.3. Relevant Parameters
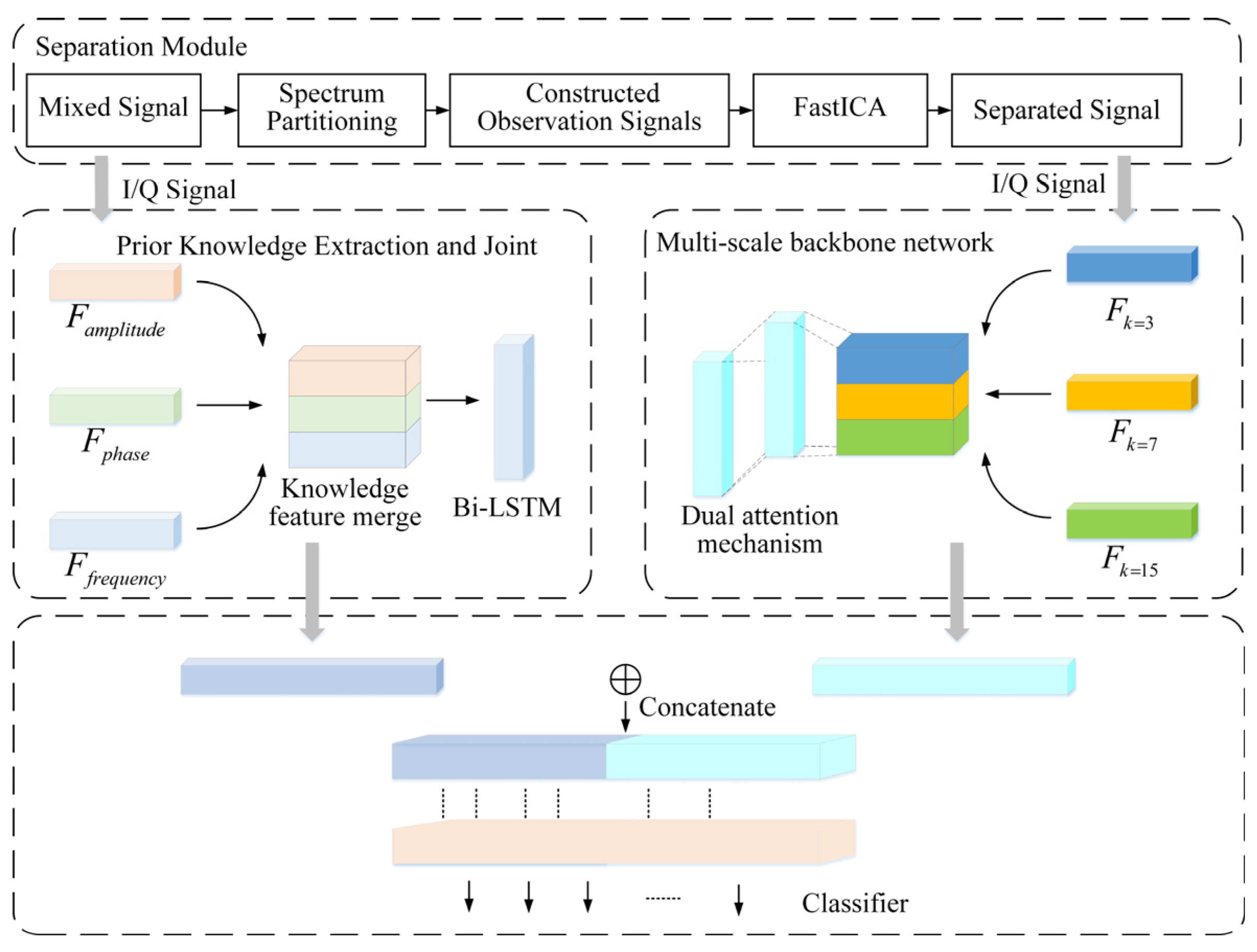
3. System Model
3.1. Signal Separation
3.1.1. Spectrum Partitioning
3.1.2. Estimation of the Number of Signal Sources
3.1.3. Waveform Separation
3.2. Prior-Guided Multiscale Network
3.2.1. Physical Feature Extraction
3.2.2. Multi-Scale Feature Extraction
3.2.3. Adaptive Feature Fusion Mechanism
3.2.4. Classification Output Layer
3.2.5. Implementation Details
4. Experiments and Results Analysis
4.1. Simulation Experiments
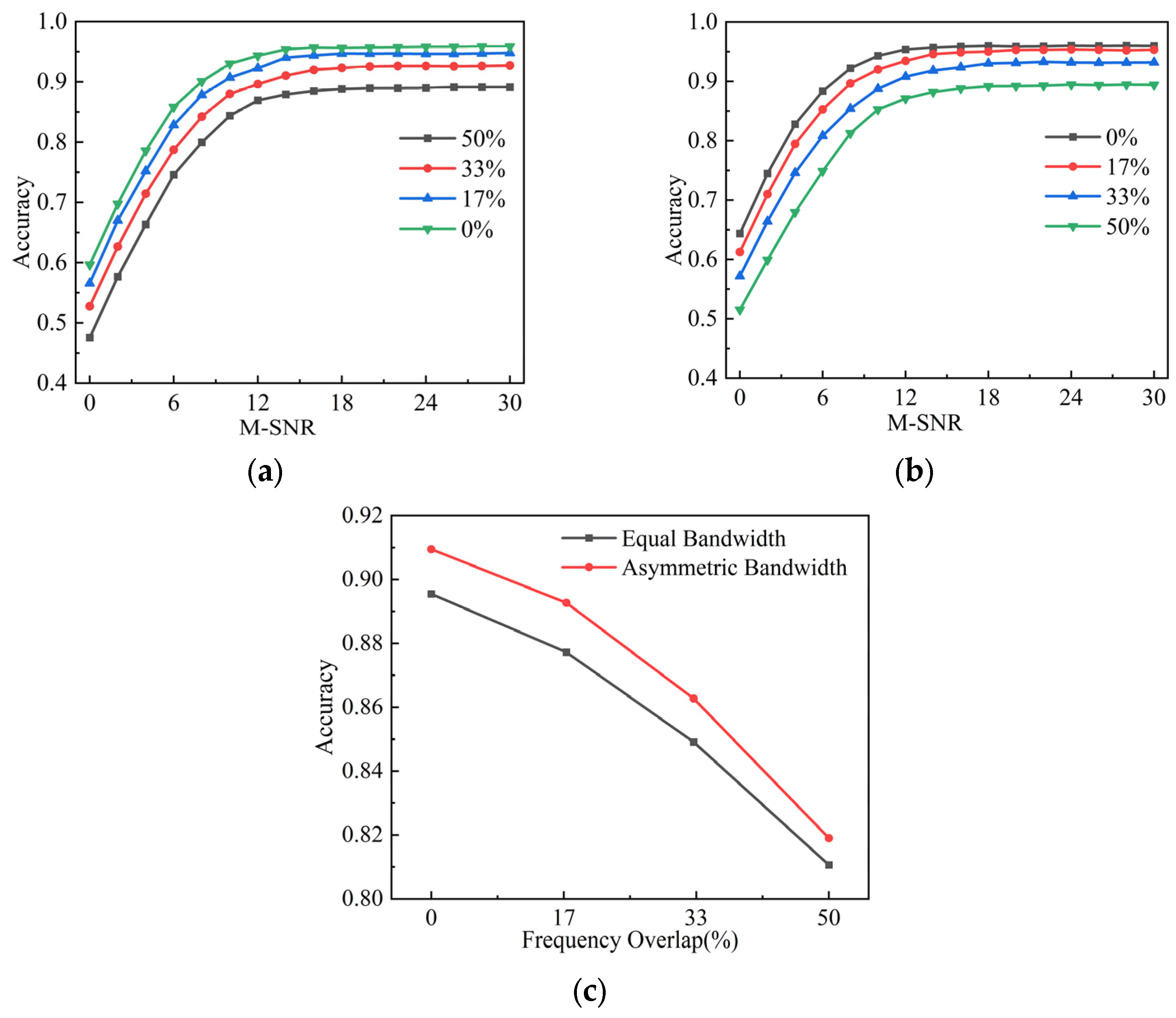
4.1.1. Separation Performance for Band-Overlapping Signals
4.1.2. Recognition After Signal Separation
4.1.3. Comparative Analysis
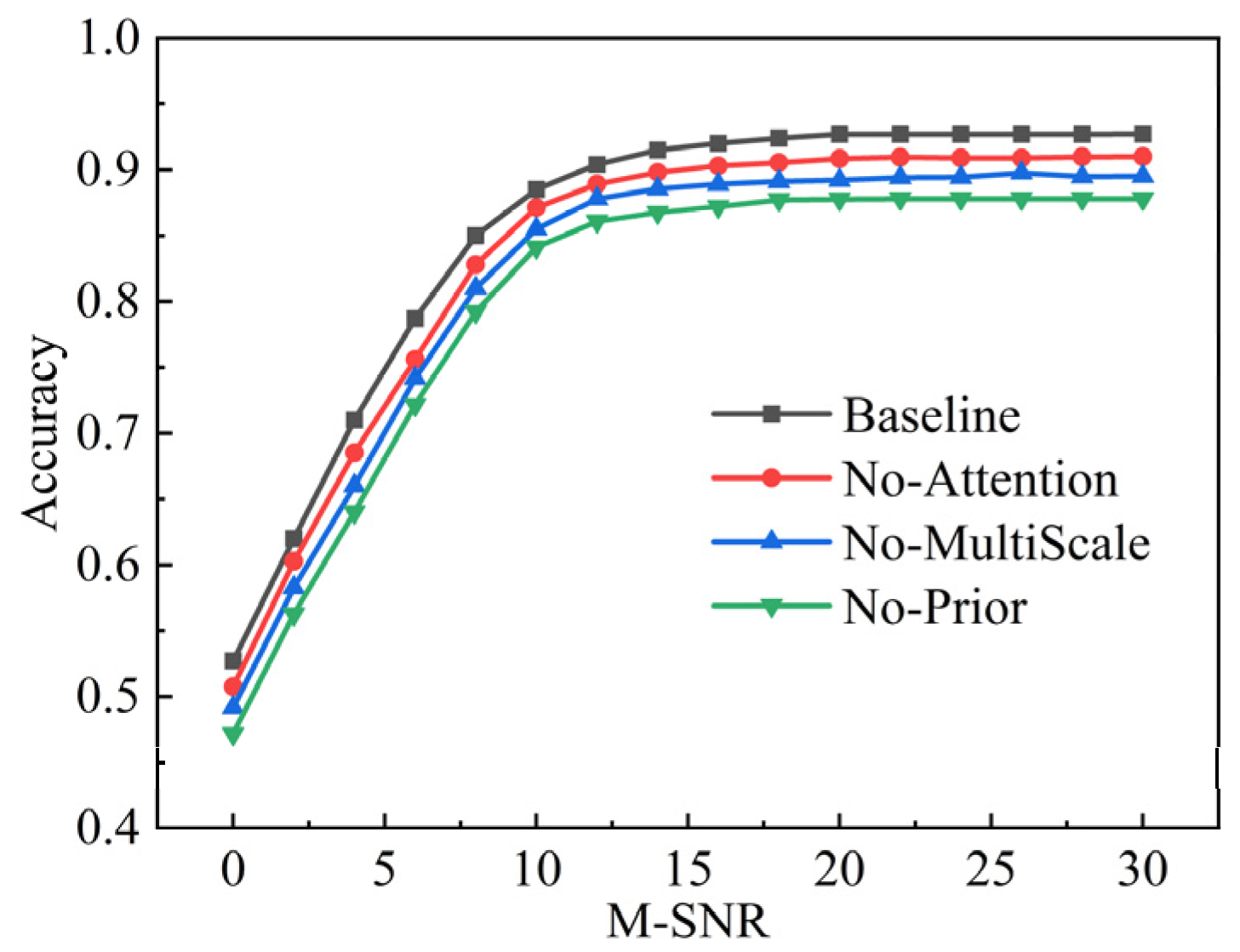
4.1.4. Ablation Study
- No-MultiScale: Replaces the multi-scale convolution with a single-scale (7 × 1) kernel to validate the importance of multi-scale temporal feature capture.
- No-Attention: Removes the channel and spatial attention modules, using direct feature propagation instead, to evaluate the role of attention in key feature selection.
- No-Prior: Discards the prior knowledge branch, using only deep learning features, to assess the contribution of physical priors to model generalization.
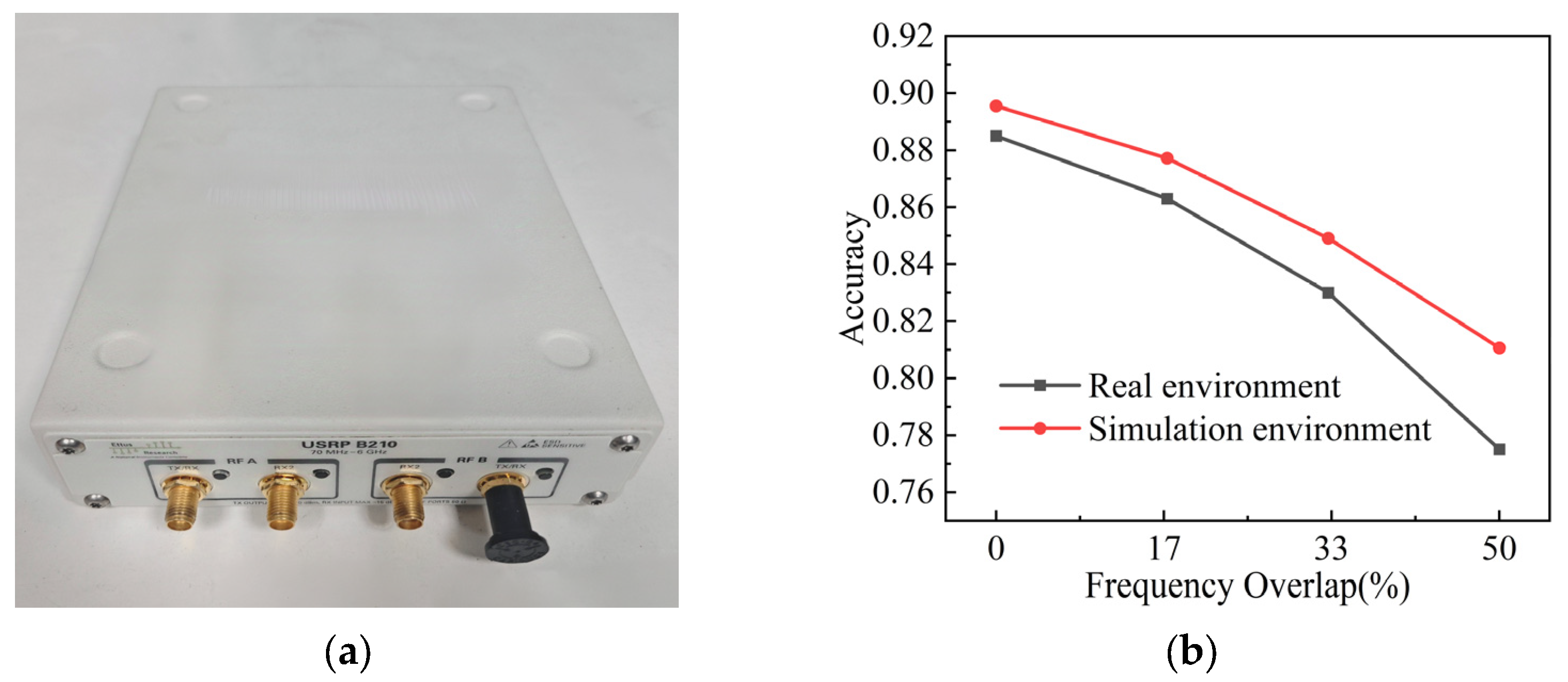
4.2. USRP-Based Real-World Experimental Validation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AMC | Automatic Modulation Classification |
| FastICA | Fast Independent Component Analysis |
| M-SNR | Mixed Signal-to-Noise Ratio |
References
- Xu, S.; Zhang, D.; Lu, Y.; Xing, Z.; Ma, W. MCCSAN: Automatic Modulation Classification via Multiscale Complex Convolution and Spatiotemporal Attention Network. Electronics 2025, 14, 3192. [Google Scholar] [CrossRef]
- Suman, P.; Qu, Y. A Lightweight Deep Learning Model for Automatic Modulation Classification Using Dual-Path Deep Residual Shrinkage Network. AI 2025, 6, 195. [Google Scholar] [CrossRef]
- Cai, J.; Guo, Y.; Cao, X. Automatic Radar Intra-Pulse Signal Modulation Classification Using the Supervised Contrastive Learning. Remote Sens. 2024, 16, 3542. [Google Scholar] [CrossRef]
- Ren, B.; Teh, K.C.; An, H.; Gunawan, E. Automatic Modulation Recognition of Dual-Component Radar Signals Using ResSwinT-SwinT Network. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 6405–6418. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhang, R.; Zhang, F.; Jing, X. An Automatic Modulation Classification Network for IoT Terminal Spectrum Monitoring under Zero-Sample Situations. EURASIP J. Wirel. Commun. Netw. 2022, 2022, 35. [Google Scholar] [CrossRef]
- Gharib, A.; Ejaz, W.; Ibnkahla, M. Distributed Spectrum Sensing for IoT Networks: Architecture, Challenges, and Learning. IEEE Internet Things Mag. 2021, 4, 66–73. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, K. Multiple Access Schemes for Cognitive Radio Networks: A Survey. Phys. Commun. 2019, 38, 100953. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, L.-L.; Hanzo, L. Joint User-Activity and Data Detection for Grant-Free Spatial-Modulated Multi-Carrier Non-Orthogonal Multiple Access. IEEE Trans. Veh. Technol. 2020, 69, 11673–11684. [Google Scholar] [CrossRef]
- Zaerin, M.; Seyfe, B. Multiuser modulation classification based on cumulants in additive white Gaussian noise channel. IET Signal Process. 2012, 6, 815–823. [Google Scholar] [CrossRef]
- Deng, W.; Wang, X.; Huang, Z. Co-Channel Multiuser Modulation Classification Using Data-Driven Blind Signal Separation. IEEE Internet Things J. 2024, 11, 14829–14843. [Google Scholar] [CrossRef]
- Yin, Z.; Zhang, R.; Wu, Z.; Zhang, X. Co-Channel Multi-Signal Modulation Classification Based on Convolution Neural Network. In Proceedings of the 2019 IEEE 89th Vehicular Technology Conference (VTC2019-Spring), Kuala Lumpur, Malaysia, 28 April–1 May 2019. [Google Scholar]
- Luo, W.; Yang, R.; Jin, H.; Li, X.; Li, H.; Liang, K. Single channel blind source separation of complex signals based on spatial-temporal fusion deep learning. IET Radar Sonar Navig. 2023, 17, 200–211. [Google Scholar] [CrossRef]
- Ma, H.; Zheng, X.; Yu, L.; Zhou, X.; Chen, Y. A Novel End-to-End Deep Separation Network Based on Attention Mechanism for Single Channel Blind Separation in Wireless Communication. IET Signal Process. 2023, 17, e12173. [Google Scholar] [CrossRef]
- Zhu, M.; Li, Y.; Pan, Z.; Yang, J. Automatic Modulation Recognition of Compound Signals Using a Deep Multi-Label Classifier: A Case Study with Radar Jamming Signals. Signal Process. 2020, 169, 107393. [Google Scholar] [CrossRef]
- Hou, X.; Gao, Y. Single-Channel Blind Separation of Co-Frequency Signals Based on Convolutional Network. Digit. Signal Process. 2022, 129, 103654. [Google Scholar] [CrossRef]
- Cai, X.; Wang, X.; Huang, Z.; Wang, F. Single-Channel Blind Source Separation of Communication Signals Using Pseudo-MIMO Observations. IEEE Commun. Lett. 2018, 22, 1616–1619. [Google Scholar] [CrossRef]
- Zhang, K.; Xu, E.L.; Feng, Z. PFS: A Novel Modulation Classification Scheme for Mixed Signals. In Proceedings of the 2017 IEEE 28th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), Montreal, QC, Canada, 8–13 October 2017. [Google Scholar]
- Cai, X.; Deng, W.; Yang, J.; Huang, Z. Recurrent Neural Network Based Single-Input/Multi-Output Demodulator for Cochannel Signals. IEEE Commun. Lett. 2023, 27, 2378–2382. [Google Scholar] [CrossRef]
- Huang, S.; Yao, Y.; Wei, Z.; Feng, Z.; Zhang, P. Automatic Modulation Classification of Overlapped Sources Using Multiple Cumulants. IEEE Trans. Veh. Technol. 2017, 66, 6089–6101. [Google Scholar] [CrossRef]
- Hyvärinen, A.; Oja, E. Independent Component Analysis: Algorithms and Applications. Neural Netw. 2000, 13, 411–430. [Google Scholar] [CrossRef]
- Yan, M.; Chen, L.; Hu, W.; Sun, Z.; Zhou, X. Secure and Intelligent Single-Channel Blind Source Separation via Adaptive Variational Mode Decomposition with Optimized Parameters. Sensors 2025, 25, 1107. [Google Scholar] [CrossRef]
- Sun, X.; Li, C.; Li, J.; Su, Q. Kernel-FastICA-Based Nonlinear Blind Source Separation for Anti-Jamming Satellite Communications. Sensors 2025, 25, 3743. [Google Scholar] [CrossRef]
- Zhu, Z.; Chen, X.; Lv, Z. Underdetermined Blind Source Separation Method Based on a Two-Stage Single-Source Point Screening. Electronics 2023, 12, 2185. [Google Scholar] [CrossRef]
- Xu, J.; Luo, C.; Parr, G.; Luo, Y. A spatiotemporal multi-channel learning framework for automatic modulation recognition. IEEE Wirel. Commun. Lett. 2020, 9, 1629–1632. [Google Scholar] [CrossRef]
- Liu, X.; Yang, D.; El Gamal, A. Deep neural network architectures for modulation classification. In Proceedings of the 2017 51st Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 29 October–1 November 2017; pp. 915–919. [Google Scholar]
- West, N.E.; O’shea, T. Deep architectures for modulation recognition. In Proceedings of the 2017 IEEE International Symposium on Dynamic Spectrum Access Networks (DySPAN), Baltimore, MD, USA, 6–9 March 2017; pp. 1–6. [Google Scholar]



| Module | Layer | Output | |
|---|---|---|---|
| Output Layer | Prior Knowledge | Amplitude Phase Frequency | (None, 1024, 1) (None, 1024, 1) (None, 1024, 1) |
| Contrast Feature | Feature | (None, 64) | |
| Prior Knowledge Extraction and Joint | Feature Extraction | Conv1D (each feature) + ReLU MaxPool1D Reshape | (None, 1024, 32) × 3 (None, 512, 32) × 3 (None, 1, 512, 32) × 3 |
| Prior Knowledge Joint | Concatenate Conv1D + ReLU Reshape BiLSTM (return sequences) BiLSTM (return last) Fully Connected | (None, 1, 512, 96) (None, 1, 508, 96) (None, 508, 96) (None, 508, 128) (None, 128) (None, 64) | |
| Multi-scale Feature Extraction | Parallel Branches | Conv1D (kernel = 3) + BN + GELU Conv1D (kernel = 7) + BN + GELU Conv1D (kernel = 15) + BN + GELU Weighted concatenation Conv1D expansion (3 × 3) Conv1D reduction (1 × 1) Adaptive average pooling Dual attention mechanism | (None, 1024, 16) (None, 1024, 16) (None, 1024, 16) (None, 1024, 48) (None, 1024, 64) (None, 1024, 48) (None, 16, 48) (None, 16, 48) |
| Feature Fusion | Feature Concatenate | Prior feature expansion Concatenate with multi-scale features | (None, 16, 64) (None, 16, 112) |
| Fusion | Conv1D (1 × 1) + BN + GELU | (None, 16, 128) | |
| Classifier | Global adaptive average pooling Dense(96) + BN + SeLU + Dropout(0.3) Dense(64) + GELU + Dropout(0.2) Dense(N_classes) | (None, 128) (None, 96) (None, 64) (None, N_classes) | |
| Total parameter | 294,992 | ||
| Scenario | Bandwidth (MHz) | Center Carrier Frequency fc2 (Overlap Ratioγ), fc1 = 5 MHz | ||||
|---|---|---|---|---|---|---|
| Equal Bandwidth | BW1 = BW2 = 0.3 | fc2(MHz) | 5.30 | 5.25 | 5.20 | 5.25 |
| γ | 0% | 16.7% | 33.3% | 50% | ||
| Asymmetric Bandwidth | fc2(MHz) | 5.45 | 5.40 | 5.35 | 5.30 | |
| BW1 = 0.3 | γ | 0% | 16.7% | 33.3% | 50% | |
| BW2 = 0.6 | γ | 0% | 8.3% | 16.7% | 25% | |
| Method | Avg. Acc. | Max. Acc | F1-Score | FLOPs | Param |
|---|---|---|---|---|---|
| IC-AMCNet [24] | 0.8037 | 0.8852 | 0.8050 | 118,746,888 | 1,260,171 |
| CLDNN2 [25] | 0.8155 | 0.8917 | 0.8120 | 235,270,852 | 513,803 |
| MCLDNN [26] | 0.8272 | 0.9064 | 0.8250 | 143,094,448 | 402,230 |
| Proposed | 0.8491 | 0.9271 | 0.8460 | 71,124,800 | 294,992 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, Z.; Fu, T.; Wu, X.; Zhu, Y. Blind Separation and Feature-Guided Modulation Recognition for Single-Channel Mixed Signals. Electronics 2025, 14, 4103. https://doi.org/10.3390/electronics14204103
Tan Z, Fu T, Wu X, Zhu Y. Blind Separation and Feature-Guided Modulation Recognition for Single-Channel Mixed Signals. Electronics. 2025; 14(20):4103. https://doi.org/10.3390/electronics14204103
Chicago/Turabian StyleTan, Zhiping, Tianhui Fu, Xi Wu, and Yixin Zhu. 2025. "Blind Separation and Feature-Guided Modulation Recognition for Single-Channel Mixed Signals" Electronics 14, no. 20: 4103. https://doi.org/10.3390/electronics14204103
APA StyleTan, Z., Fu, T., Wu, X., & Zhu, Y. (2025). Blind Separation and Feature-Guided Modulation Recognition for Single-Channel Mixed Signals. Electronics, 14(20), 4103. https://doi.org/10.3390/electronics14204103






