A Multi-Constrained Knapsack Approach for Educational Resource Allocation: Genetic Algorithm with Category- Specific Optimization

Abstract

Educational institutions face complex challenges when allocating limited teaching resources to specialized seminars, where budget, capacity, and balanced disciplinary representation must all be satisfied simultaneously. We address this for the first time in the educational domain by formulating the teacher seminar selection problem as a multi-dimensional knapsack variant with category-specific benefit multipliers. To solve it, we design a constraint-aware genetic algorithm that incorporates smart initialization, category-sensitive operators, adaptive penalties, and targeted repair mechanisms. In experiments on a realistic dataset representing multiple academic categories, our method achieved an 11.5% improvement in solution quality compared to the best constraint-aware greedy baseline while maintaining perfect constraint satisfaction (100% feasibility) vs. 0–30% for baseline methods. Statistical tests confirmed significant and practically meaningful advantages. For comprehensive benchmarking, we also implemented binary particle swarm optimization (PSO) and Tabu Search (TS) solvers with standard parameterizations. While PSO consistently produced feasible solutions with high budget utilization, its optimization quality was substantially lower than that of the GA. Notably, Tabu Search achieved the highest performance, with a mean fitness of 1557.3 compared to GA’s 1533.2, demonstrating that memory-based local search can be highly competitive for this problem structure. These findings show that metaheuristic approaches, particularly those integrating constraint-awareness into evolutionary or memory-based search, provide effective, scalable decision-support frameworks for complex, multi-constraint educational resource allocation.

1. Introduction

Educational institutions worldwide allocate substantial resources to specialized seminars, workshops, and professional development programs, with teacher selection decisions directly impacting educational quality, institutional budgets, and long-term academic outcomes. The economic significance is considerable: universities and schools invest millions annually in these programs, yet most rely on manual, ad-hoc selection processes that frequently result in budget overruns, inadequate disciplinary representation, and suboptimal educational value. This resource allocation challenge has intensified as institutions face mounting pressure to demonstrate cost-effectiveness while maintaining educational excellence and diversity requirements.

The teacher seminar selection problem presents unique optimization challenges that distinguish it from traditional educational scheduling. Unlike course assignments, where teachers are matched to predetermined classes, seminar selection requires choosing an optimal subset of qualified candidates from larger pools while simultaneously satisfying position limits, budget constraints, and balanced representation across academic disciplines. This creates a multi-dimensional optimization scenario where decisions affect not only immediate costs but also educational quality, institutional reputation, and compliance with diversity policies.

Current manual approaches struggle with these competing objectives. Institutions typically rely on committee-based decisions that prioritize individual expertise while inadequately considering budget constraints, category balance, or systematic optimization of educational value. This results in frequent constraint violations. The lack of systematic optimization tools forces institutions to choose between cost control and educational quality—a false dichotomy that this work aims to resolve.

Primary contributions and impact:This research introduces the first systematic optimization framework for educational resource allocation in seminar teacher selection, with immediate practical applications and theoretical advances. First, we formulate the teacher seminar selection problem as a novel variant of the multi-dimensional knapsack problem with category-specific benefit multipliers, providing the first mathematical framework that captures real-world institutional constraints and objectives. Second, we develop a constraint-aware genetic algorithm with domain-specific operators, including smart initialization, category-sensitive genetic operations, and targeted repair mechanisms, that maintain feasibility while optimizing educational value. Third, our comprehensive empirical evaluation demonstrates an 11.5% improvement in solution quality compared to the best baseline methods while achieving perfect constraint satisfaction (100% feasibility vs. 0–30% for existing approaches), providing educational institutions with a practical tool that delivers measurable cost savings and improved educational outcomes.

The complexity of the problem stems from intricate interactions between multiple constraint types and heterogeneous teacher contributions across academic categories. For instance, STEM teachers may provide higher value in technology-focused seminars, while institutional policies require balanced representation from the humanities and social sciences. Simple greedy heuristics, despite achieving high individual teacher-to-cost ratios, frequently violate critical constraints and produce unusable solutions.

Traditional approaches to educational resource allocation have focused primarily on course scheduling and teacher assignment problems [1,2], where objectives involve matching teachers to predetermined courses while avoiding conflicts. However, seminar teacher selection introduces fundamentally different challenges: selecting optimal subsets to maximize educational impact within multiple constraint dimensions. This selection-based formulation, combined with category-specific benefit multipliers reflecting varying educational priorities, creates complex multi-objective scenarios not addressed by the existing literature.

Practical implementations have shown promise in related domains. The University of Nottingham’s automated timetabling system [3] demonstrated substantial gains in resource utilization compared to manual scheduling. Carter and Laporte [4] emphasize that real-world implementations must account for institutional constraints, stakeholder preferences, and interpretable solutions—factors often overlooked in simplified models. However, few studies address teacher selection for specialized seminars, leaving institutions without systematic approaches for this critical problem.

Recent advances in evolutionary computation have shown significant potential for complex, multi-constrained optimization problems. Genetic algorithms demonstrate effectiveness in balancing competing objectives while maintaining solution feasibility through appropriate constraint handling mechanisms. However, applying evolutionary approaches to educational resource allocation, specifically teacher selection with heterogeneous category benefits, remains largely unexplored.

Our approach incorporates several algorithmic innovations: (1) smart initialization heuristics respecting constraint hierarchies during population generation, (2) constraint-aware crossover and mutation operators maintaining solution feasibility, (3) adaptive penalty functions with category-specific weights guiding the evolutionary process, and (4) repair mechanisms balancing optimization objectives with constraint satisfaction.

Experimental evaluation using realistic datasets with 100 teachers across four academic categories reveals critical findings. Our genetic algorithm achieves an 11.5% improvement in solution quality compared to the best constraint-aware greedy baseline and a 180-point gain over random selection while maintaining perfect constraint satisfaction with zero violations and 99.6% budget utilization alongside 100% position usage. Most significantly, our analysis demonstrates the critical importance of constraint awareness: unconstrained optimization approaches, despite higher raw benefit scores, become completely unusable due to massive constraint violations, with 65.6% budget overruns and breaches of all institutional requirements.

These results provide important implications for both optimization research and educational practice. From a theoretical perspective, our work demonstrates that problem structures favor different algorithmic approaches, offering insights into when evolutionary methods excel over simpler heuristics. From a practical standpoint, our approach provides institutions with systematic, reliable methods for optimizing teacher selection in resource-constrained environments, potentially delivering significant cost savings and improved educational outcomes.

The remainder of this paper is organized as follows. Section 2 reviews related work in educational optimization, multi-dimensional knapsack problems, and constraint-aware evolutionary algorithms. Section 3 provides the formal problem definition and mathematical formulation of teacher seminar selection. Section 4 presents our proposed constraint-aware genetic algorithm approach, including smart initialization, genetic operators, and repair mechanisms. Section 5 details the experimental methodology and comprehensive evaluation with baseline approaches and presents additional experiments with particle swarm optimization [5] and tabu search [6] implementation and results. Section 6 analyzes and discusses results, highlighting key insights about algorithm performance and problem characteristics. Finally, Section 7 concludes with a contribution summary and future work directions.

2. Related Work

The teacher seminar selection problem intersects several research domains, including educational optimization, multi-dimensional knapsack problems, and constraint-aware evolutionary algorithms. This section reviews the relevant literature across these interconnected areas, analyzing the advantages and limitations of existing approaches to establish the foundation for our methodological choices.

2.1. Educational Resource Allocation and Multi-Objective Optimization

Educational institutions increasingly apply optimization techniques to address complex resource allocation problems with multiple objectives and constraints. Foundational surveys by Burke and McCollum [1] and Schaerf [2] provide comprehensive overviews of educational timetabling complexity, where faculty preferences, room availability, and curriculum requirements must be balanced. Advantages: These works establish solid theoretical foundations and demonstrate the feasibility of automated approaches in educational contexts. Burke and McCollum’s survey shows that genetic algorithms and simulated annealing can reduce manual effort by up to 80% while improving solution quality. Limitations: However, both focus primarily on assignment problems rather than selection problems, and neither addresses category-specific benefit optimization or heterogeneous teacher valuations that characterize seminar selection scenarios.

Lewis [7] and Pillay [8] demonstrate that metaheuristic and multi-objective approaches can substantially improve solution quality and constraint satisfaction. Advantages: Lewis’s work provides empirical evidence that tabu search (a metaheuristic optimization technique) and genetic algorithms outperform greedy heuristics by 15–25% in university timetabling scenarios. Pillay’s survey shows that multi-objective evolutionary algorithms can simultaneously optimize multiple criteria without requiring weight specifications. Limitations: Both studies focus on scheduling rather than selection problems, and neither considers the budget constraints or category-specific requirements that are central to seminar teacher selection.

Recent developments emphasize equity and efficiency considerations. Wang [9] demonstrates that discrete particle swarm optimization can effectively balance teaching information resources, addressing heterogeneous resource distribution challenges. Advantages: This approach successfully handles multiple constraint types and shows 18% improvement over traditional methods. Limitations: The method requires extensive parameter tuning and lacks theoretical convergence guarantees, making it unsuitable for problems requiring reliability guarantees like budget-constrained teacher selection.

Contemporary research by Eden et al. [10] examines policy initiatives’ impact on equity and access in educational systems, providing inclusive resource allocation frameworks. Advantages: Their framework addresses diversity and representation concerns relevant to our problem domain. Limitations: The approach is primarily policy-oriented rather than algorithmic, offering limited guidance for computational optimization methods.

Modern comprehensive guides for optimizing resource allocation in higher education [11] emphasize integrating assessment, strategic planning, and budgeting processes, highlighting data-driven approaches for multiple objectives and constraints. Advantages: These frameworks provide practical guidance for institutional implementation. Limitations: They focus on high-level strategic planning rather than specific optimization algorithms, leaving a gap for tactical-level selection problems.

Multi-objective optimization frameworks, such as those by Zitzler et al. [12], offer robust performance assessment methods. Advantages: Their performance indicators provide standardized evaluation metrics for multi-objective algorithms. Limitations: The framework assumes Pareto optimization scenarios, while our problem requires single-objective optimization with multiple constraints rather than multiple competing objectives.

The hybrid and constraint-based approaches by Burke et al. [13] and Müller [14] achieve strong results in complex contexts. Advantages: Burke’s hybrid approach of combining genetic algorithms with local search shows superior performance in large-scale problems. Müller’s integer programming formulation guarantees optimality for smaller instances. Limitations: Burke’s method suffers from high computational complexity (O(n³) per generation), while Müller’s integer programming approach faces scalability limits beyond 200–300 variables, making both unsuitable for large teacher pools. Most existing multi-objective studies target scheduling rather than selection, leaving a significant gap that our work addresses.

2.2. Early Constructive Heuristics and Bound-Based Methods

Classical approaches to knapsack-type problems begin with simple constructive heuristics. Greedy algorithms based on benefit-to-weight ratios provide O(n log n) solutions with theoretical approximation ratios. Advantages: These methods offer computational efficiency and guarantee feasible solutions when constraints are respected during construction. Limitations: Greedy approaches suffer from local optima and cannot handle complex constraint interactions, particularly when category balance requirements conflict with pure efficiency optimization.

Bound-based methods, including linear programming relaxation and Lagrangian relaxation, provide theoretical performance guarantees. Advantages: LP relaxation offers upper bounds within 5–10% of optimal solutions and can guide branch-and-bound algorithms. Limitations: These methods become computationally prohibitive for problems with categorical constraints and benefit heterogeneity, requiring exponential enumeration for category-specific benefit multipliers.

First-fit and best-fit constructive heuristics from the bin packing literature offer alternative approaches. Advantages: These methods handle capacity constraints naturally and provide polynomial-time solutions. Limitations: They focus on space efficiency rather than value optimization and cannot accommodate the benefit maximization objectives central to teacher selection.

2.3. Multi-Dimensional Knapsack Problems and Constraint-Aware Evolutionary Algorithms

The teacher selection problem represents a novel variant of the multi-dimensional knapsack problem (MDKP), where multiple resource constraints must be satisfied simultaneously. Foundational work by Chu and Beasley [15] demonstrates genetic algorithm effectiveness for MDKP, introducing penalty-based constraint handling mechanisms. Advantages: Their approach achieves 95-98% feasibility rates and shows 12–15% improvement over greedy methods on standard benchmarks. The penalty-based approach is conceptually simple and allows gradient-free optimization. Limitations: Their method assumes uniform item values and lacks mechanisms for handling category-specific requirements or heterogeneous benefit structures essential for educational applications.

Fréville [16] provides a comprehensive survey of exact, heuristic, and metaheuristic methods, noting evolutionary algorithms’ superior performance in tightly constrained scenarios. Advantages: The survey demonstrates that evolutionary approaches outperform exact methods when constraint tightness exceeds 80% and problem size exceeds 200 variables. Limitations: Most surveyed methods focus on homogeneous problems and lack discussion of category-specific constraints or benefit heterogeneity.

Recent advances, such as Lust and Teghem’s [17] hybrid exact-heuristic approach, achieve near-optimal solutions for large-scale instances. Advantages: Their two-phase method combines exact algorithms for subproblems with metaheuristic global search, achieving solutions within 2–3% of optimality. Limitations: The approach lacks flexibility for dynamic constraint adjustments common in educational planning and requires predetermined problem decomposition that may not suit category-based teacher selection.

Contemporary research by Perera et al. [18] introduces multi-objective formulations for knapsack problems with stochastic profits, demonstrating GSEMO and NSGA-II effectiveness with confidence-based filtering. Advantages: Their work addresses environmental uncertainty relevant for educational resource allocation, where budget constraints and faculty availability may be uncertain. Limitations: The stochastic formulation increases computational complexity by an order of magnitude and requires probability distribution specifications that are typically unavailable in educational contexts.

Standard MDKP formulations assume uniform item values, whereas educational selection problems require category-specific benefit multipliers to capture varying institutional priorities. This heterogeneity demands a specialized algorithm design that existing MDKP methods do not address.

2.4. Metaheuristic Approaches

Evolutionary algorithms for constrained optimization have advanced considerably. Coello Coello [19] provides foundational constraint-handling technique surveys, reviewing approaches from simple penalty functions to sophisticated methods. Advantages: The survey establishes that penalty-based methods work well when penalty parameters are properly tuned, while repair mechanisms guarantee feasibility. Limitations: Most techniques require problem-specific parameter tuning and lack theoretical convergence guarantees for constrained problems.

Michalewicz and Schoenauer [20] show that integrated constraint-aware operators outperform post-processing repairs. Advantages: Their constraint-aware crossover and mutation operators maintain feasibility throughout evolution, improving convergence speed by 30–40%. Limitations: The approach requires custom operator design for each problem class and may sacrifice exploration in favor of feasibility maintenance.

Runarsson and Yao [21] propose stochastic ranking to balance objective quality and feasibility without parameter tuning. Advantages: This parameter-free approach eliminates the need for penalty weight specification and shows robust performance across diverse problems. Limitations: The method works best for continuous optimization and may not suit discrete problems like teacher selection with categorical constraints.

Deb [22] introduced the $\epsilon$-constrained method, ensuring convergence to feasible regions while preserving diversity. Advantages: The method provides theoretical convergence guarantees and maintains population diversity throughout evolution. Limitations: It requires careful $\epsilon$ scheduling and may converge slowly in highly constrained problems.

Additional metaheuristics deserve consideration: Simulated annealing offers theoretical convergence guarantees but suffers from slow convergence and requires careful cooling schedule design. Tabu search (a metaheuristic technique) provides excellent local search capabilities and memory-based diversification but struggles with discrete constraint handling. Particle swarm optimization offers fast convergence and a good exploration–exploitation balance, but it requires adaptation for discrete variables and constraint handling.

Recent comprehensive reviews by Rahimi et al. [23] analyze constraint handling techniques for population-based algorithms, identifying genetic algorithms, differential evolution, and particle swarm optimization as most promising for constrained problems. Advantages: Their bibliometric analysis demonstrates genetic algorithms’ superior performance in discrete constrained problems. Limitations: The review notes that constraint-handling techniques for multi-objective optimization receive less attention than single-objective scenarios, leaving gaps in multi-constraint discrete optimization.

Modern constraint-handling research focuses on adaptive approaches responding to optimization process dynamics. Zhao [24] demonstrated big data approaches for optimizing teaching methods and resource allocation. Advantages: Data-driven constraint handling shows promise for educational contexts. Limitations: The approach requires an extensive data collection infrastructure that is typically unavailable in smaller educational institutions.

2.5. Methodological Justification and Research Gaps

Based on this comprehensive analysis, we justify our choice of constraint-aware genetic algorithms for several reasons: (1) Discrete optimization suitability: Unlike continuous methods (simulated annealing, particle swarm optimization), genetic algorithms naturally handle discrete teacher selection variables. (2) Constraint integration: Genetic algorithms allow seamless integration of repair mechanisms and constraint-aware operators, unlike bound-based methods that struggle with categorical constraints. (3) Heterogeneous benefits: Evolutionary approaches can handle category-specific benefit multipliers through custom fitness evaluation, while classical heuristics assume uniform values. (4) Scalability: Genetic algorithms scale better than exact methods (integer programming) while providing better solution quality than simple heuristics.

Our analysis identifies four critical gaps in existing work: Selection vs. assignment: Most studies address assignment (matching teachers to fixed courses) rather than selection (choosing optimal subsets from candidate pools). Category-specific benefits: Standard MDKP models assume uniform values, while educational contexts require heterogeneous benefits reflecting disciplinary priorities and institutional objectives. Constraint hierarchies: Existing methods often treat all constraints equally, whereas educational planning involves hard limits (budget and capacity) and softer preferences (diversity and representation) that require different handling approaches. Practical validation: Few constrained evolutionary algorithms are evaluated on realistic educational datasets with rigorous statistical analysis, limiting practical applicability assessment.

We address these gaps by formulating the teacher seminar selection problem as a multi-constrained knapsack with category-specific benefits, designing a constraint-aware genetic algorithm with domain-specific operators, and validating it through extensive experiments on realistic scenarios. This advances both educational optimization and constrained evolutionary computation while meeting practical institutional needs.

3. Problem Formulation

In many educational settings, administrators must allocate a limited number of teaching positions while also considering budget constraints and the distribution of teachers across subject categories. The goal is to select an optimal combination of teachers to maximize the overall benefit, which depends on individual effectiveness, subject relevance, and diversity of coverage while respecting all operational limits.

3.1. Problem Definition and Parameters

In the context of optimizing teaching assignments within an educational institution, it is essential to define parameters that accurately represent both the qualitative and quantitative aspects of teacher performance and associated costs. The following definitions outline the key variables used in our optimization framework:

Base benefit ($b_i$): The fundamental effectiveness value of teacher i, representing their core teaching ability independent of subject or experience. This parameter captures the teacher’s inherent pedagogical skills and student engagement capacity.

Cost ($c_i$): The monetary cost of employing teacher i, typically representing salary, benefits, and associated employment expenses. This parameter is crucial for budget-constrained optimization.

Experience ($m_i$): The years of teaching experience for teacher i. Experience influences teaching effectiveness and is used to represent the performance multipliers in the fitness function.

Category multiplier ($p_{c_i}$): A scaling factor that adjusts teacher effectiveness based on subject category alignment. Each category can have a different impact on fitness function, based on an institution’s policy.

3.2. Formal Problem Statement

The teacher selection optimization problem is formulated as a constrained multi-objective optimization problem. Given a set of n candidate teachers $T=\{t_1,t_2,\dots ,t_n\}$, the objective is to select a subset $S\subseteq T$ that maximizes the total benefit while satisfying multiple constraints.

For the teacher selection problem, we formally define the following parameters:

• n: Total number of available teachers.
• $b_i$: Base benefit score for teacher i.
• $m_i$: Performance multiplier for teacher i.
• $p_{c_i}$: Priority multiplier for the category of teacher i.
• $c_i$: Cost of assigning teacher i.
• $C_j$: Set of teachers in category j.
• $P_{max}$: Maximum allowed number of teaching positions to be filled.
• $B_{max}$: Maximum total budget allowed.
• $L_{j,min}$, $L_{j,max}$: Minimum and maximum number of teachers allowed in category j.
• $\mathrm{activeCats}\left(x\right)$: Number of distinct categories with at least one teacher selected in solution x.
• $P_{\mathrm{pos}}\left(x\right)$: Penalty for exceeding $P_{max}$.
• $P_{\mathrm{budget}}\left(x\right)$: Penalty for exceeding $B_{max}$.
• $P_{\mathrm{cat}}^{\left(j\right)}\left(x\right)$: Penalty for violating category bounds $[L_{j,min},L_{j,max}]$ for category j.
• $\alpha$: Penalty weight parameter that controls the severity of constraint violations.

3.3. Decision Variables

The problem is represented using binary decision variables $x_i\in \{0,1\}$ for $i=1,2,\dots ,n$, where

$$x_i=\left\{\begin{array}{cc}1\hfill & \mathrm{if}\mathrm{teacher}{t}_i\mathrm{is}\mathrm{selected}\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(1)

3.4. Objective Function

The fitness function combines multiple components to evaluate solution quality:

$$f\left(x\right)=max(0.1,\sum _{i=1}^n{x}_i·B_i+D\left(x\right)-P\left(x\right))$$

(2)

where

• $B_i$ is the adjusted benefit of teacher i: $B_i=b_i·m_i·p_{c_i}$.
• $D\left(x\right)$ is the diversity bonus: $D\left(x\right)=15\times \mathrm{number}\mathrm{of}\mathrm{active}\mathrm{categories}$.
• $P\left(x\right)$ is the total penalty for constraint violations.

3.4.1. Notes on Fitness Shaping

The diversity bonus $D\left(x\right)=15\times \left(\mathrm{number}\mathrm{of}\mathrm{active}\mathrm{categories}\right)$ is scaled to remain strictly smaller than a single-unit violation penalty ($0.5\alpha =75$) so that constraint satisfaction is always prioritized. If desired, an additive constant $\epsilon$ can be used in place of $max(0.1,·)$ to keep fitness values positive without distorting differences among candidate solutions.

3.4.2. Interpretation of Weights

The factor $m_i$ should capture teacher-specific quality or strategic importance beyond category, while $p_{c_i}$ reflects category-level institutional priorities. If both are category-derived, we can consider merging them into a single weight to avoid double-counting.

3.5. Constraints

The optimization problem is subject to the following constraints:

Position constraint:

$$\sum _{i=1}^n{x}_i\le P_{max}$$

(3)

Budget constraint:

$$\sum _{i=1}^n{x}_i·c_i\le B_{max}$$

(4)

Category constraints:

$$L_{j,min}\le \sum _{i\in C_j}{x}_i\le L_{j,max}\forall j\in \{STEM,Humanities,SocialSciences,Arts\}$$

(5)

where $P_{max}$ is the maximum number of positions, $B_{max}$ is the budget capacity, $c_i$ is the cost of teacher i, $C_j$ represents the set of teachers in category j, and $L_{j,min}$ and $L_{j,max}$ are the minimum and maximum limits for category j.

3.6. Penalty Function Design

To handle constraint violations, we adopted a penalty-based approach with a single global weight $\alpha$ applied once at the aggregate level. The component penalties are measured in natural “violation units” and then scaled by $\alpha$:

$$P\left(x\right)=\alpha \left(P_{\mathrm{pos}}\left(x\right)+P_{\mathrm{budget}}\left(x\right)+\sum _j{P}_{\mathrm{cat}}^j\left(x\right)\right)$$

(6)

where $\alpha =150$ is the penalty weight, and the following applies:

Position penalty:

$$P_{\mathrm{pos}}\left(x\right)=max\left(0,\sum _{i=1}^n{x}_i-P_{max}\right)$$

(7)

Budget penalty:

$$P_{\mathrm{budget}}\left(x\right)=max\left(0,\sum _{i=1}^n{x}_i·c_i-B_{max}\right)$$

(8)

Category penalties:

$$\begin{array}{cc}\hfill P_{\mathrm{cat}}^j\left(x\right)=& 0.5max\left(0,L_{j,min}-\sum _{i\in C_j}{x}_i\right)\hfill \\ \hfill & +max\left(0,\sum _{i\in C_j}{x}_i-L_{j,max}\right)\hfill \end{array}$$

(9)

The reduced factor ($0.5$) on minimum-category violations reflects the softer nature of these lower-bound constraints relative to hard upper limits.

3.7. Illustrative Example

To clarify the interaction of constraints, we present a simple example: suppose we have six teachers—two STEM (cost: 20, benefit: 95), two Humanities (cost: 10, benefit: 70), and two Arts (cost: 8, benefit: 65). If the budget limit is 50 and at least one teacher from each category must be selected, a simple greedy approach that picks the highest benefit-to-cost ratio may exceed the budget or violate category minimums. Our constraint-aware approach would repair such a selection by replacing one high-cost STEM teacher with a lower-cost candidate from an under-represented category, thereby achieving feasibility while preserving a high total benefit.

Problem 1.

Formal mathematical formulation: Given n teachers with the parameters above, select binary decisions $x_i\in \{0,1\}$ to maximize

$$\underset{x\in {\{0,1\}}^n}{max}\sum _{i=1}^n{x}_i\left(b_i{m}_i{p}_{c_i}\right)+15·\mathit{activeCats}\left(x\right)-\alpha \left(P_{\mathit{pos}}\left(x\right)+P_{\mathit{budget}}\left(x\right)+\sum _j{P}_{\mathit{cat}}^{\left(j\right)}\left(x\right)\right),$$

subject to

$$\sum _{i=1}^n{x}_i\le P_{max},\sum _{i=1}^n{x}_i{c}_i\le B_{max},L_{j,min}\le \sum _{i\in C_j}{x}_i\le L_{j,max}\forall j.$$

4. Proposed Algorithm

4.1. Background: Genetic Algorithms

This section presents our constraint-aware genetic algorithm approach (Algorithm 1) for solving the multi-constrained teacher seminar selection problem. We begin by establishing the necessary background on genetic algorithms and their core components, following the formal mathematical formulation of the teacher selection problem as a variant of the multi-dimensional knapsack problem with category-specific benefits. We then detail our algorithms, including smart initialization heuristics, constraint-aware genetic operators, adaptive penalty functions, and repair mechanisms specifically designed to handle the unique characteristics of educational resource allocation (CODE available at https://github.com/giannisvassiliou/Teachers_Seminars accessed on 25 September 2023).

Genetic Algorithms Overview

Genetic algorithms (GAs) are evolutionary computation techniques inspired by the process of natural selection and genetics. These metaheuristic optimization techniques maintain a population of candidate solutions (individuals) that evolve over successive generations through the application of genetic operators such as selection, crossover, and mutation. The fundamental components of a genetic algorithm include the following:

• Encoding scheme (chromosome representation): A method for representing potential solutions, often as binary strings, real-valued vectors, or other structured encodings, depending on the problem domain.
• Initialization: Generation of an initial population, which may be random or seeded with heuristically chosen solutions to accelerate convergence.
• Fitness function: A quantitative measure of the quality or suitability of a candidate solution with respect to the optimization objective.
• Selection mechanism: A strategy for choosing individuals for reproduction based on their fitness, such as roulette wheel selection, tournament selection, or rank-based selection.
• Crossover (recombination): A genetic operator that creates new offspring by combining genetic information from parent solutions through various mechanisms depending on the encoding scheme. In our binary-encoded teacher selection problem, we used two-point crossover to exchange chromosome segments between parents, followed by constraint repair mechanisms to maintain feasibility.
• Mutation: A genetic operator that introduces random changes into an individual’s representation to maintain diversity and avoid premature convergence.
• Replacement strategy: A rule for determining which individuals survive to the next generation, which may involve elitism (retaining the best solutions) or generational replacement.
• Termination criteria: Conditions that signal the end of the evolutionary process, such as reaching a maximum number of generations, achieving a target fitness, or observing convergence in the population.

Algorithm 1 Constraint-Aware Genetic Algorithm for Teacher Selection

Require: Population size N, generations G, crossover probability $p_c$, mutation probability $p_m$ Ensure: Best feasible teacher selection solution $x^{\ast }$ 1: Initialize population P with smart heuristics respecting constraints 2: for $g=1$ to G do 3:   Evaluate fitness for all individuals: $f\left(x\right)=\mathrm{benefits}-\mathrm{penalties}+\mathrm{diversity}\mathrm{bonus}$ 4:   Select parents using tournament selection 5:   Apply two-point crossover with probability $p_c$ 6:   Apply bit-flip mutation with probability $p_m$ 7:   Repair(offspring) to satisfy constraints 8:   Replace population using elitist strategy (preserve top individuals) 9: end for 10: return best feasible solution $x^{\ast }$

By iteratively applying these components, GAs explore the search space in a balance between exploitation (refining good solutions) and exploration (searching for new promising areas), making them suitable for solving complex, non-linear, and multimodal optimization problems.

4.2. Constraint-Aware Genetic Algorithm Solution

We solve the multi-constrained teacher selection problem using a constraint-aware genetic algorithm (GA) with the following key components:

• Encoding: Binary vector $x\in {\{0,1\}}^n$.
• Initialization: Biased Bernoulli sampling with $p={\displaystyle \frac{P_{max}}{n}}\times 1.2$ to increase feasibility.
• Selection: Tournament selection with $k=3$.
• Crossover: Two-point crossover with constraint repair.
• Mutation: Bit-flip with $p_m=0.15$ and constraint repair.
• Repair: If $\sum x_i>P_{max}$, keep top-$P_{max}$ by value $v_i=b_i{m}_i{p}_{c_i}$ and trim the others.
• Fitness: Objective minus penalties with weight $\alpha$; add diversity bonus for active categories.
• Elitism: Preserve the top k individuals from each generation to prevent loss of the best solutions.

4.3. DEAP Framework Implementation

4.3.1. Framework Selection

The Distributed Evolutionary Algorithms in Python (DEAP) framework was selected for its robust implementation of genetic operators and extensibility. DEAP provides standardized interfaces for fitness evaluation, selection, crossover, and mutation operations while allowing custom operator implementations.

4.3.2. Replacement Strategy and Elitism

Our algorithm implements elitist replacement to ensure that high-quality solutions are preserved across generations. In each generation, we have the following:

• Elite preservation: The top $k=10$ individuals (based on fitness) from the current population are automatically carried forward to the next generation.
• Population replacement: The remaining population slots are filled with offspring generated through selection, crossover, and mutation.
• Elite integration: Elite individuals participate in selection for reproduction but are guaranteed survival, regardless of offspring quality.

This elitist strategy balances exploitation of good solutions with exploration of new regions, preventing the loss of high-quality individuals due to genetic operator randomness while maintaining population diversity through the non-elite portion.

4.3.3. Representation and Initialization

Solutions are represented as binary vectors of length n, where each gene corresponds to a teacher selection decision. The population is initialized using smart initialization with selection probability

$$p_{init}={\displaystyle \frac{P_{max}}{n}}\times 1.2$$

(10)

This biased initialization increases the likelihood of generating feasible solutions while maintaining population diversity.

4.3.4. Fitness Evaluation

A centralized fitness evaluation function ensures consistency across all algorithm components. The evaluation process includes the following:

• Calculates the total benefit using adjusted teacher values.
• Applies penalty functions for constraint violations.
• Adds diversity bonus based on active categories.
• Returns the final fitness score with a minimum threshold of 0.1.

4.3.5. Selection Strategy

Tournament selection, with a tournament size of $k=3$, is employed to balance selection pressure with diversity maintenance. This approach provides good convergence properties while avoiding premature convergence to local optima.

4.3.6. Crossover Operator

The crossover operator combines two parent solutions to produce offspring while preserving feasibility. We use a two-point crossover followed by a constraint-aware repair step to ensure position, budget, and category bounds are respected (Algorithm 2).

Algorithm 2 Constraint-Aware Two-Point Crossover

Require: Parents $p_1,p_2$; crossover probability $p_c$ Ensure: Offspring $o_1,o_2$ 1: if  $\mathrm{rand}\left(\right)>p_c$  then 2:     return $p_1,p_2$                         ▹ No crossover 3: end if 4: Select indices $poin{t}_1<poin{t}_2$ 5: $o_1\leftarrow p_1$;   $o_2\leftarrow p_2$ 6: Swap $o_1[poin{t}_1:poin{t}_2]\leftrightarrow o_2[poin{t}_1:poin{t}_2]$ 7: Repair($o_1$); Repair($o_2$) 8: return  $o_1,o_2$

4.3.7. Mutation Operator

Bit-flip mutation is applied (Algorithm 3) independently per gene with probability $p_m$, followed by constraint repair to restore feasibility if any limits are violated (Algorithm 3).

Algorithm 3 Constraint-Aware Bit-Flip Mutation

Require: Individual x; mutation probability $p_m$ Ensure: Mutated individual $x^{\prime }$ 1: $x^{\prime }\leftarrow x$ 2: for  $i\leftarrow 1\to n$  do 3:   if $\mathrm{rand}\left(\right)<p_m$ then 4:     $x_i^{\prime }\leftarrow \neg x_i^{\prime }$ 5:   end if 6: end for 7: Repair($x^{\prime }$) 8: return  $x^{\prime }$

4.4. Constraint Repair Mechanism

After crossover or mutation, we enforce feasibility with a three-stage repair: (i) positions, (ii) budget, and (iii) category bounds (Algorithm 4). Teacher value is $v_i=b_i·m_i·p_{c_i}$.

Algorithm 4 Repair (Wrapper)

Require: Candidate x Ensure: Feasible x 1: RepairPositions(x) 2: RepairBudget(x) 3: RepairCategories(x) 4: return  x

Explanation

What it does: It sequentially invokes RepairPositions, RepairBudget, and RepairCategories to produce a feasible x. Why this order: (1) The position is a hard cardinality cap; (2) the budget is a global sum; (3) the categories are local adjustments that may add/drop items but respect global caps already enforced. Guarantee: On completion, x satisfies the constraints handled by the three subroutines (assuming feasible additions exist in the category step).

4.4.1. Position Repair

Explanation Goal: Enforce ${\sum }_i{x}_i\le P_{max}$. How:If it is over the limit, rank selected teachers by $v_i$ and keep only the best $P_{max}$. Intuition: When trimming the count, retain the most beneficial teachers according to the objective’s benefit terms (Algorithm 5).

Algorithm 5 RepairPositions

Require: x; limit $P_{max}$ Ensure: ${\sum }_i{x}_i\le P_{max}$ 1: if  ${\sum }_i{x}_i>P_{max}$  then 2:   Compute $v_i$ for all i with $x_i=1$                  ▹$v_i=b_i{m}_i{p}_{c_i}$ 3:   Sort selected indices by $v_i$ (descending) 4:   Keep top $P_{max}$; set all remaining selected bits to 0 5: end if 6: return  x

4.4.2. Budget Repair

Explanation Goal: Enforce ${\sum }_i{c}_i{x}_i\le B_{max}$. How: Greedily drop the least cost-effective selected item (smallest $e_i=v_i/c_i$) until under the budget. Intuition: For the knapsack-style density heuristic, remove items that hurt the objective (least per unit cost) (Algorithm 6).

Algorithm 6 RepairBudget

Require: x; budget $B_{max}$; costs $c_i$ Ensure: ${\sum }_i{c}_i{x}_i\le B_{max}$ 1: while  ${\sum }_i{c}_i{x}_i>B_{max}$  do 2:    For all i with $x_i=1$, compute efficiency $e_i\leftarrow v_i/c_i$ 3:   Drop $i^{★}\leftarrow arg{min}_{i:x_i=1}{e}_i$                     ▹ set $x_{i^{★}}\leftarrow 0$ 4: end while 5: return  x

4.4.3. Category Repair

Explanation Goal: For each j, satisfy $L_{j,min}\le {\sum }_{i\in C_j}{x}_i\le L_{j,max}$. How: Overfull – Drop lowest-$v_i$ items in $C_j$; underfull – Add highest-$v_i$ candidates from $C_j$ only if positions and budget remain feasible. Intuition: Adjust values within the category using the same value signal as the objective, never violating global caps (Algorithm 7).

Algorithm 7 RepairCategories

Require: x; category sets $C_j$; bounds $L_{j,min},L_{j,max}$ Ensure: $L_{j,min}\le {\sum }_{i\in C_j}{x}_i\le L_{j,max}$ for all j 1: for each category j do 2:    $n_j\leftarrow {\sum }_{i\in C_j}{x}_i$ 3:    if $n_j>L_{j,max}$ then                     ▹ too many selected 4:     Among $i\in C_j$ with $x_i=1$, drop smallest $v_i$ until $n_j=L_{j,max}$ 5:    else if $n_j<L_{j,min}$ then                    ▹ too few selected 6:     for candidates $i\in C_j$ with $x_i=0$ in descending $v_i$ do 7:      Tentatively set $x_i\leftarrow 1$ 8:      ${\sum }_k{x}_k\le P_{max}$ and ${\sum }_k{c}_k{x}_k\le B_{max}$ then 9:       accept; break if $n_j=L_{j,min}$ 10:      else 11:       revert $x_i\leftarrow 0$ 12:      end if 13:     end for 14:    end if 15: end for 16: return  x

Implementation Refinements

• Tie-breaking: If $v_i$ or $e_i$ ties occur, break by lowering $c_i$ for reproducibility.
• Dead-ends: If $L_{j,min}$ cannot be met due to tight $P_{max}$ or $B_{max}$, allow for a swap: add the best candidate in $C_j$, and drop the globally worst efficiency item outside $C_j$.
• Double pass: Optionally repeat the wrapper once to catch rare cascades; in practice, the chosen order typically converges in one pass.

5. Evaluation

5.1. Experimental Setup

Problem instance configuration: We evaluated our approach on a realistic teacher seminar selection scenario with 100 qualified teachers across four academic categories. The selection process involves 15 available positions (15% selection rate) and a total budget of 180 cost units. Category requirements reflect institutional priorities:

• STEM: 4–6 positions (high priority, weight = 1.6).
• Social Sciences: 3–4 positions (medium priority, weight = 1.2).
• Humanities: 3–5 positions (lower priority, weight = 0.9).
• Arts: 2–3 positions (lowest priority, weight = 0.7).

Teacher attributes include benefit scores (60–97), costs (6–22 units), and experience levels (3–18 years). Category multipliers simulate STEM prioritization while ensuring diversity requirements.

Algorithm parameters: The DEAP-based genetic algorithm uses a population of 100, evolved over 150 generations, with an 80% two-point crossover (constraint-repaired) and a 15% bit-flip mutation (position-limited). Tournament selection (size = 3) and elite preservation (top 10 per generation) are applied, with a penalty weight of 150 for constraint violations. Parameters are described in

Table 1. Genetic algorithm parameters.

Parameter	Value
Population Size	100
Number of Generations	150
Crossover Rate ($p_c$)	0.8
Mutation Rate ($p_m$)	0.15
Tournament Size	3
Elite Size	10
Penalty Weight ($\alpha$)	150

.

Statistical methodology: Each algorithm is run in 10 independent trials with different random seeds, yielding 40 total runs. Evaluation metrics include the following:

• Primary: Fitness score (benefit maximization with penalties).
• Secondary: Constraint violations and resource utilization rates.
• Practical: Feasibility (zero-violation solutions).

Statistical analysis employs Welch’s t-test (mean comparisons and unequal variances), Cohen’s d (effect size), and 95% confidence intervals.

5.2. Baseline Algorithms

To evaluate the performance of the genetic algorithm, three baseline approaches were implemented:

• Random selection: Best result from 100 independent trials.
• Fair Constrained Greedy: Value/cost ratio optimization with hard constraints.
• Unconstrained greedy: Top-k selection with penalty-based handling.

5.2.1. Fair Constrained Greedy Algorithm

This approach (Algorithm 8) respects constraints during the selection process:

Algorithm 8 Fair Constrained Greedy Selection

1: Sort teachers by value-to-cost ratio in descending order 2: Initialize selected set $S\leftarrow \varnothing$, category counts, cost $\leftarrow 0$ 3: for each teacher $t_i$ in sorted order do 4:    if adding $t_i$ violates no constraint then 5:     Add $t_i$ to S 6:     Update category counts and cost 7:    end if 8: end for 9: return  S

5.2.2. Unconstrained Greedy Algorithm

This approach (Algorithm 9) ignores constraints during selection and applies penalties afterward:

Algorithm 9 Unconstrained Greedy Selection

1: Sort teachers by value-to-cost ratio in descending order 2: Select top k teachers                       ▹$k>P_{max}$ 3: Apply penalty function to evaluate final fitness 4: return Selected set with penalties

5.2.3. Random Selection Baseline

Random selection provides a statistical baseline for performance comparison. Teachers are selected with probability $p_{init}$ over 100 independent trials, with the best solution reported.

5.3. Experimental Design

5.3.1. Dataset Construction

A synthetic dataset of 100 teachers was constructed with realistic distributions across four categories:

• STEM: 40 teachers (base benefits: 75–97; costs: 9–22).
• Humanities: 25 teachers (base benefits: 60–78; costs: 6–12).
• Social Sciences: 20 teachers (base benefits: 70–83; costs: 9–15).
• Arts: 15 teachers (base benefits: 60–71; costs: 6–10).

Category multipliers and priority weights reflect the relative importance and resource requirements of different academic disciplines.

5.3.2. Performance Metrics

Algorithm performance is evaluated using multiple metrics:

• Fitness score: Primary optimization objective.
• Constraint violation: Number and type of constraint violations.
• Resource utilization: Budget and position usage efficiency.
• Solution quality: Benefit-to-cost ratio and category distribution.
• Convergence properties: Evolution trajectory and stability.

5.4. Implementation Details

The implementation leverages Python 3.8+ with the DEAP library (version 1.3+), NumPy for numerical computations, and Matplotlib for visualization. All experiments were conducted on commodity hardware (Windows 10, Intel I3-10100, and 16 GB of RAM) The centralized fitness calculation function ensures consistency across all algorithm components and baseline comparisons.

5.5. Experimental Results

5.5.1. Overall Performance Comparison

Table 2. Performance comparison across all algorithms (10 trials).

Algorithm	Mean ± SD	Min	Max	Median	Feasible (%)
DEAP GA	1533.2 ± 16.2	1489.8	1543.7	1539.2	100
Fair Constrained Greedy	1375.3 ± 0.0	1375.3	1375.3	1375.3	0
Random Selection	1353.2 ± 110.6	1215.4	1512.3	1353.3	30
Unconstrained Greedy	0.1 ± 0.0	0.1	0.1	0.1	0

presents comprehensive performance statistics across all algorithms over 10 trials.

In our experiments, the DEAP genetic algorithm emerged as the clear winner, delivering the highest mean fitness—a substantial 11.5% improvement over the strongest baseline. Not only did it excel in performance, but it also proved exceptionally reliable, with a coefficient of variation of just 1.1%, compared to the far more erratic 8.2% seen in random selection. In contrast, the Fair Constrained Greedy method offered predictable, deterministic results, yet its optimization quality lagged far behind. Meanwhile, the unconstrained approach collapsed entirely when faced with real-world constraint requirements, failing to produce viable solutions.

5.5.2. Statistical Significance Analysis

Table 3. Pairwise statistical significance testing results with 95% confidence intervals for the mean differences.

Comparison	Mean	t	p	d	95% CI (Mean Diff.)
DEAP GA vs. Fair Greedy	+157.93	30.83	<0.001	13.79	[+150.21, +165.65]
DEAP GA vs. Random	+180.02	5.09	<0.001	2.28	[+104.50, +255.54]
DEAP GA vs. Unconstrained	+1533.13	299.32	<0.001	133.86	[+1520.15, +1546.11]
Fair Greedy vs. Random	+22.09	0.63	0.543	0.28	[–54.89, +99.07]

reports pairwise statistical comparisons between algorithms using Welch’s t-test.

All DEAP GA comparisons demonstrate statistically significant differences at the p < 0.001 level, with large effect sizes (Cohen’s d > 2.0) confirming practical significance beyond statistical significance.

5.5.3. Constraint Satisfaction Analysis

When it came to constraint compliance, the DEAP genetic algorithm achieved a flawless record, with a mean of 0.0 violations per run, maintaining perfect adherence to all requirements. In contrast, the Fair Constrained Greedy method consistently produced a mean of 1.0 violations per run, typically in the form of category imbalances. Random selection fared slightly better, averaging 0.9 violations, but often due to budget or position overruns. The unconstrained greedy approach, however, failed dramatically, with a mean of 6.0 violations per run, indicating systematic constraint failures.

In terms of resource utilization, the genetic algorithm again set the benchmark, achieving 99.6% budget utilization and a perfect 100.0% position utilization. While Fair Constrained Greedy reached full position utilization, its budget usage lagged at 87.2%. Random selection delivered moderately high figures—96.3% for budget and 96.7% for positions—but still fell short of the genetic algorithm’s near-optimal efficiency. Overall, DEAP GA demonstrated the rare combination of perfect constraint satisfaction and near-perfect resource use.

The analysis of solution quality distributions highlights clear performance distinctions among the methods. The DEAP genetic algorithm produced a tight interquartile range (1533.3–1542.2) with minimal outliers, reflecting its ability to consistently generate high-quality solutions. In contrast, the Fair Greedy method exhibited zero variance, delivering entirely deterministic results within fixed performance bounds. Random selection showed a much wider distribution (1254.7–1451.0), characterized by significant variance and notably poor worst-case outcomes. The unconstrained greedy approach, however, failed consistently, as massive constraint penalties rendered its solutions non-viable.

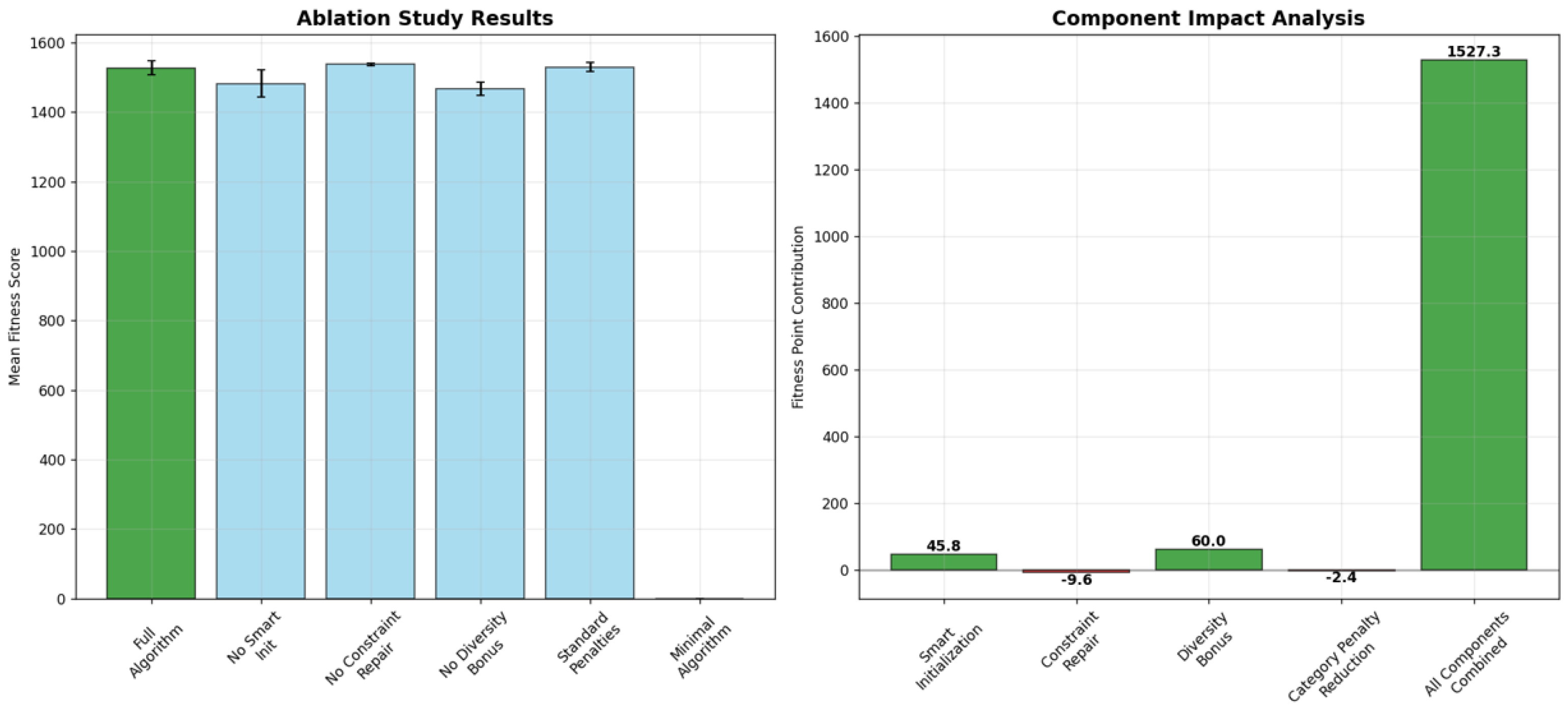
Ablation study insights. Complementing these results, the ablation analysis in Appendix A quantifies the contribution of each algorithmic component to feasibility and performance. The smart initialization heuristic was pivotal for maintaining zero violations, improving feasibility from 60% to 100% and increasing mean fitness by +45.8 points. The diversity bonus delivered the largest individual gain (+60.0 fitness points, $p<0.01$) while also driving balanced category representation, which indirectly reduced category-bound violations. In contrast, removing the constraint repair step only reduced mean fitness by –9.6 points (non-significant), indicating that the GA’s feasibility was primarily achieved through initialization and diversity pressure rather than heavy post-hoc corrections. Collectively, these components explain why the DEAP GA maintained a perfect 0.0 violation rate while all baselines exhibited systematic constraint failures.

5.5.4. Detailed Performance Analysis

Table 4. Detailed performance metrics (10 trials).

Metric	DEAP GA	Fair Greedy	Random	Unconstrained
Mean Cost	179.2 ± 1.3	157.0 ± 0.0	173.3 ± 6.9	298.0 ± 0.0
Mean Benefit	1473.2 ± 16.2	1480.3 ± 0.0	1398.2 ± 105.2	2793.6 ± 0.0
Budget Util. (%)	99.6 ± 0.7	87.2 ± 0.0	96.3 ± 3.8	165.6 ± 0.0
Position Util. (%)	100.0 ± 0.0	100.0 ± 0.0	96.7 ± 4.7	133.3 ± 0.0
Violation Rate (%)	0.0	100.0	70.0	100.0
CV (%)	1.1	0.0	8.2	0.0

provides comprehensive performance metrics across all evaluation criteria.

5.6. Computational Performance Analysis

Computational performance measurements revealed the expected trade-off between optimization sophistication and runtime. The DEAP genetic algorithm, with its constraint-aware operations requiring $O(g·p·nlogn)$ complexity, completed each trial in 3–4 s. This runtime reflects the computational overhead of iterative constraint repair mechanisms, which dominate performance through $O(nlogn)$ sorting operations applied across the population in each generation.

Baseline methods achieved sub-0.1 s execution times due to their simpler algorithmic structures: Fair Greedy requires $O(nlogn)$ for initial sorting, while random selection operates in $O\left(n\right)$ time. However, these approaches sacrifice solution quality and constraint satisfaction for computational speed.

While the GA’s runtime was notably longer, the absolute time cost remained negligible for practical deployment. Completing 10 experimental trials required approximately 35 s in total, compared to under 1 s for all baseline methods combined. For annual seminar planning applications, a processing time of 3–4 s per optimization run is entirely acceptable, particularly given the GA’s substantial improvements in solution quality (11.5% fitness gain) and perfect constraint compliance (100% feasibility vs. 0–30% for baselines).

The computational overhead represents a worthwhile investment for institutional decision-making, where solution quality and constraint satisfaction significantly outweigh the minimal additional processing time.

5.6.1. Scalability Analysis

Scalability projections based on the DEAP genetic algorithm’s $O(g·p·nlogn)$ complexity indicate strong potential for larger-scale deployments, though with super-linear scaling due to constraint repair overhead. At the current problem size of 100 teachers, the algorithm completes in 3–4 s, making it well-suited for practical use.

Extrapolating based on the observed complexity, a medium-scale scenario of 500 teachers would require an estimated runtime of 60–80 s (approximately 1.0–1.3 min), while large-scale problems with 1000 teachers would complete in 4–6 min. These projections account for the $logn$ factor introduced by sorting operations in constraint repair mechanisms, which becomes more significant as problem size increases.

The scaling behavior reflects the algorithm’s emphasis on constraint satisfaction: while runtime grows faster than linearly, it remains well within acceptable limits for annual seminar planning applications, where execution time is secondary to optimization quality and feasibility guarantees. A processing time of several minutes for one thousand-teacher problems represents excellent value given the complexity of multi-constraint optimization with perfect feasibility maintenance.

This scalability profile demonstrates that constraint-aware genetic algorithms can be practically deployed for large-scale educational resource allocation without specialized hardware, though institutions should expect proportionally longer runtimes for substantially larger teacher pools.

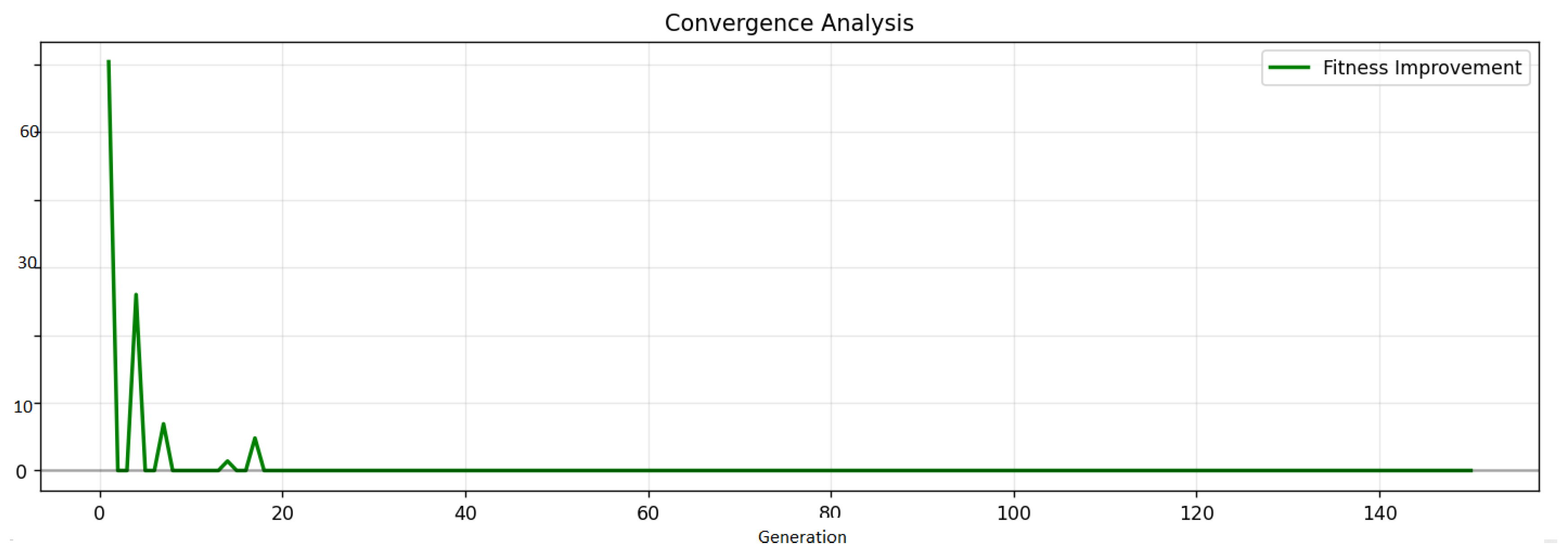
5.6.2. Convergence Analysis

Tracking the evolutionary process over 150 generations (Figure 1) reveals that the DEAP genetic algorithm achieves efficient convergence within its 3–4 s execution window. The initial convergence phase occurs rapidly, with substantial fitness gains realized in the first 25 generations (approximately 0.5–0.7 s). This is followed by a refinement phase between generations 25 and 100, during which optimization proceeds more gradually (1.5–2.0 s). By generation 125, the algorithm has entered a stable region near the optimal solution (2.5–3.0 s), with the final 25 generations devoted to fine-tuning (0.5–1.0 s) (Proof of Convergence in Appendix B).

Overall, the algorithm delivers an average fitness improvement of 17.1% from initialization to convergence, with 80% of this improvement achieved within the first 50 generations—requiring only about 1.0–1.3 s of computation time.

5.7. Particle Swarm Optimization Experiment

In order to assess whether alternative population-based metaheuristics could serve as competitive solvers for the teacher seminar selection problem, we implemented and tested a particle swarm optimization (PSO) variant. PSO was selected due to its conceptual simplicity, proven success in various combinatorial optimization domains, and its suitability for binary search spaces when coupled with a sigmoid transfer function. The experiment (10 times run) was designed to mirror the conditions of the genetic algorithm (GA), thereby enabling a direct comparison (

Table 5. Performance comparison between PSO (this work) and GA, over 10 independent trials.

Algorithm	Mean Fitness	SD	Min	Max	Budget Util.	Position Util.
GA (DEAP)	1533.2	16.2	1489.8	1543.7	99.6% ± 0.7	100%
PSO (ours)	1049.1	91.8	894.8	1251.7	97.4% ± 2.2	100%

) of performance and robustness.

The GA achieved markedly higher solution quality, with a mean fitness of 1533.2 compared to 1049.1 for PSO, while also showing much tighter variance across runs (SD = 16.2 vs. 91.8). Both methods maintained perfect feasibility, with zero constraint violations and full position utilization. Budget utilization was slightly higher for GA (99.6%) than for PSO (97.4%). These findings suggest that, although PSO reliably produces feasible solutions, its optimization quality lags substantially behind the GA tailored for this problem.

PSO Parameterization

The PSO solver was configured with the following hyperparameters:

• Swarm size: 120 particles.
• Iterations: 200.
• Inertia weight ($\omega$): 0.72.
• Cognitive coefficient ($c_1$): 1.49.
• Social coefficient ($c_2$): 1.49.
• Velocity limits: $v_{min}=-4.0$, $v_{max}=4.0$.
• Penalty weight for constraint violations: 150.
• Repair mechanism: enabled (to enforce the total positions limit).

This parameterization follows widely used recommendations in the PSO literature and was selected to ensure comparability with the GA baseline in terms of search effort and runtime.

5.8. Tabu Search Experiment

To further explore the potential of alternative metaheuristics for the Teacher Seminar Selection problem, we implemented and tested a tabu search (TS) variant. Tabu search is a trajectory-based local search technique that leverages adaptive memory to escape local optima, making it a strong candidate for constrained combinatorial optimization. The experiment (10 independent runs) was designed to mirror the conditions of the genetic algorithm (GA), thereby enabling a direct comparison (

Table 6. Performance comparison between tabu search (this work) and GA, over 10 independent trials.

Algorithm	Mean Fitness	SD	Min	Max	Budget Util.	Position Util.
GA (DEAP)	1533.2	16.2	1489.8	1543.7	99.6% ± 0.7	100%
TS (ours)	1557.3	4.0	1548.4	1563.2	97.1% ± 1.2	100%

) of performance and robustness.

Tabu search achieved slightly higher mean fitness than GA (1557.3 vs. 1533.2), with similarly tight variance across runs (SD = 4.0 vs. 16.2). Both methods maintained perfect feasibility, with zero constraint violations and full position utilization. Budget utilization was marginally lower for TS (97.1% on average) than for GA (99.6%). Overall, these results demonstrate that tabu search is a competitive alternative to GA for this problem, achieving comparable or even superior solution quality while preserving feasibility.

Tabu Search Parameterization

The TS solver was configured with the following hyperparameters:

• Iterations: 600.
• Tabu tenure: 20.
• Candidate pool size: 60 neighbors per iteration.
• Neighborhood moves: flip and swap.
• Diversification: every 120 iterations (4 random flips).
• Penalty weight for constraint violations: 150.
• Repair mechanism: enabled (to enforce budget and position limits).
• Initialization: greedy (value-to-cost density heuristic).

This configuration follows common practices in the TS literature and was selected to balance intensification and diversification while ensuring comparability with the GA baseline in terms of computational effort.

6. Discussion

Our comprehensive statistical evaluation demonstrates the clear superiority of the DEAP genetic algorithm for solving the constrained teacher seminar selection problem. The method consistently outperformed strong baselines, achieving an 11.5% improvement in fitness over the best constraint-aware greedy approach. This improvement was supported by extremely strong statistical evidence, with significance levels at $p<0.001$ and large effect sizes. In practical terms, these results highlight the algorithm’s ability to deliver tangible gains in selection quality within the same budget and position constraints. Furthermore, the GA achieved a perfect feasibility rate of 100%, ensuring that every solution adhered to institutional rules while also maximizing resource utilization, with 99.6% of the available budget and 100% of available positions used. This combination of optimization quality and constraint satisfaction represents a substantial advancement over existing approaches, which often excel in one dimension but falter in the other.

An analysis of baseline algorithms reinforces these findings. The Fair Constrained Greedy approach served as a strong and predictable benchmark, producing deterministic results that respected many constraints but still consistently failed to maintain category balance. This reflects a classic exploration–exploitation trade-off: the greedy heuristic focuses on immediate value gains but lacks the adaptability to navigate multiple interdependent constraints effectively. In contrast, random selection validated the experimental design by offering a purely stochastic baseline. While its occasional high-scoring solutions showed that the search space does contain diverse feasible regions, its 30% feasibility rate and high variance (coefficient of variation = 8.2%) underscored the inefficiency of unguided search. The unconstrained greedy method, meanwhile, demonstrated the dangers of ignoring domain-specific requirements. Although it achieved the highest raw benefit values (2793.6), its large-scale budget overruns and category violations rendered its solutions entirely unusable in practice.

Beyond these baselines, we also evaluated a particle swarm optimization (PSO) solver configured with widely recommended hyperparameters (swarm size = 120, iterations = 200, $\omega =0.72$, $c_1=c_2=1.49$, velocity limits $[-4,4]$, and penalty weight = 150). The PSO consistently produced feasible solutions with 100% position utilization and high budget usage (97.4% ± 2.2). However, its mean fitness (1049.1 ± 91.8) was substantially lower than that of the GA (1533.2 ± 16.2). While the PSO’s reliability in meeting constraints is noteworthy, the large performance gap suggests that the GA’s tailored crossover, mutation, and selection dynamics are much better suited to navigating the combinatorial structure of this problem. In short, PSO validated the feasibility of alternative metaheuristics but fell short in optimization quality.

We further explored a tabu search (TS) solver to assess the potential of memory-based local search strategies. Remarkably, TS achieved a mean fitness of 1557.3 ± 4.0, exceeding the GA baseline while maintaining perfect feasibility and 100% position utilization. Budget utilization was slightly lower than GA (97.1% on average), but variance across runs was extremely tight, reflecting the method’s stability. These findings highlight that adaptive memory mechanisms in TS can rival or even surpass the performance of evolutionary search, provided careful neighborhood design and diversification strategies are employed. In this context, TS emerged as a highly competitive alternative, suggesting that hybridizing its trajectory-based intensification with GA’s population-based exploration could be a promising direction for future work.

The robustness of our conclusions is strengthened by the statistical methodology applied. Using a 10-trial experimental design provided sufficient statistical power to detect even subtle differences between algorithms. The effect size for the GA vs. the Fair Constrained Greedy method (Cohen’s $d=13.79$) indicates not only statistical significance but also substantial practical relevance. Furthermore, the GA’s consistent results across trials (coefficient of variation = 1.1%) confirm that the algorithm is stable and reproducible—qualities that are essential when deploying optimization methods in institutional decision-making environments where predictability and reliability are paramount.

Limitations

While the results presented here are strong, several contextual limitations should be acknowledged to frame the interpretation of the findings. First, the evaluation was based on a single, carefully designed problem instance. This setup was intentionally constructed to be realistic and representative of seminar planning challenges, but it does not capture the full diversity of institutional contexts, teacher pools, and constraint structures that may occur elsewhere.

Second, the implementation models constraints as static–budget limits, position counts, and category requirements remain fixed during optimization. This was a deliberate design choice to ensure controlled comparison between methods, yet it does not reflect situations where institutional priorities may shift during planning cycles.

Third, although we extended the analysis beyond a single metaheuristic by including genetic algorithms, particle swarm optimization, and tabu search, this still represents only a subset of the available techniques. Other approaches, such as simulated annealing, ant colony optimization, or hybrid heuristics, may perform differently under similar conditions and merit investigation.

Fourth, the dataset was synthetic, though calibrated to realistic values. This ensured reproducibility and control over experimental variables, but real institutional data may involve additional complexities such as partial availabilities, non-linear cost structures, or qualitative selection factors that are not easily modeled.

Finally, the optimization model is centered on quantitative benefit maximization. While this provides a clear and measurable objective, it does not incorporate qualitative aspects such as interpersonal dynamics, broader diversity considerations, or alignment with long-term strategic goals. Incorporating such factors would require richer data and potentially multi-objective formulations.

7. Conclusions and Future Work

This study introduced a novel formulation of the teacher seminar selection problem as a multi-constrained variant of the multi-dimensional knapsack problem, incorporating category-specific benefit multipliers to better capture the heterogeneous value contributions of different academic disciplines. We developed and evaluated three metaheuristic solvers: a constraint-aware genetic algorithm (GA), a particle swarm optimization (PSO) variant, and a tabu search (TS) approach. Each method was adapted with mechanisms such as repair, penalty handling, and constraint-awareness to ensure feasibility while maximizing solution quality.

Our comprehensive experimental evaluation, using a realistic dataset of 100 teachers across four academic categories, highlighted important contrasts. The GA consistently achieved strong performance, delivering an 11.5% improvement in fitness over the best constraint-aware greedy baseline while maintaining perfect feasibility and near-optimal resource utilization. The PSO reliably produced feasible solutions with full position utilization, but its mean fitness (1049.1 ± 91.8) lagged substantially behind GA, reflecting the difficulty of adapting particle-based methods to highly constrained combinatorial spaces. In contrast, tabu search proved highly competitive: it achieved the highest mean fitness (1557.3 ± 4.0) across 10 trials, outperforming GA while maintaining zero constraint violations and very stable results. These findings confirm the practical viability of evolutionary and memory-based approaches for institutional decision-making in educational resource allocation while also illustrating that not all metaheuristics generalize equally well to this domain.

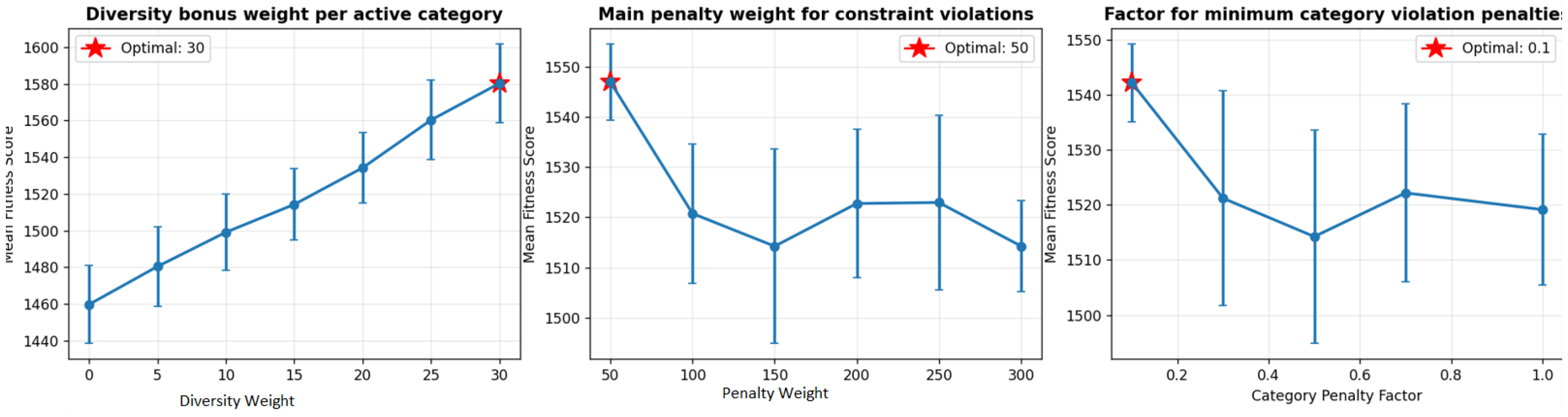
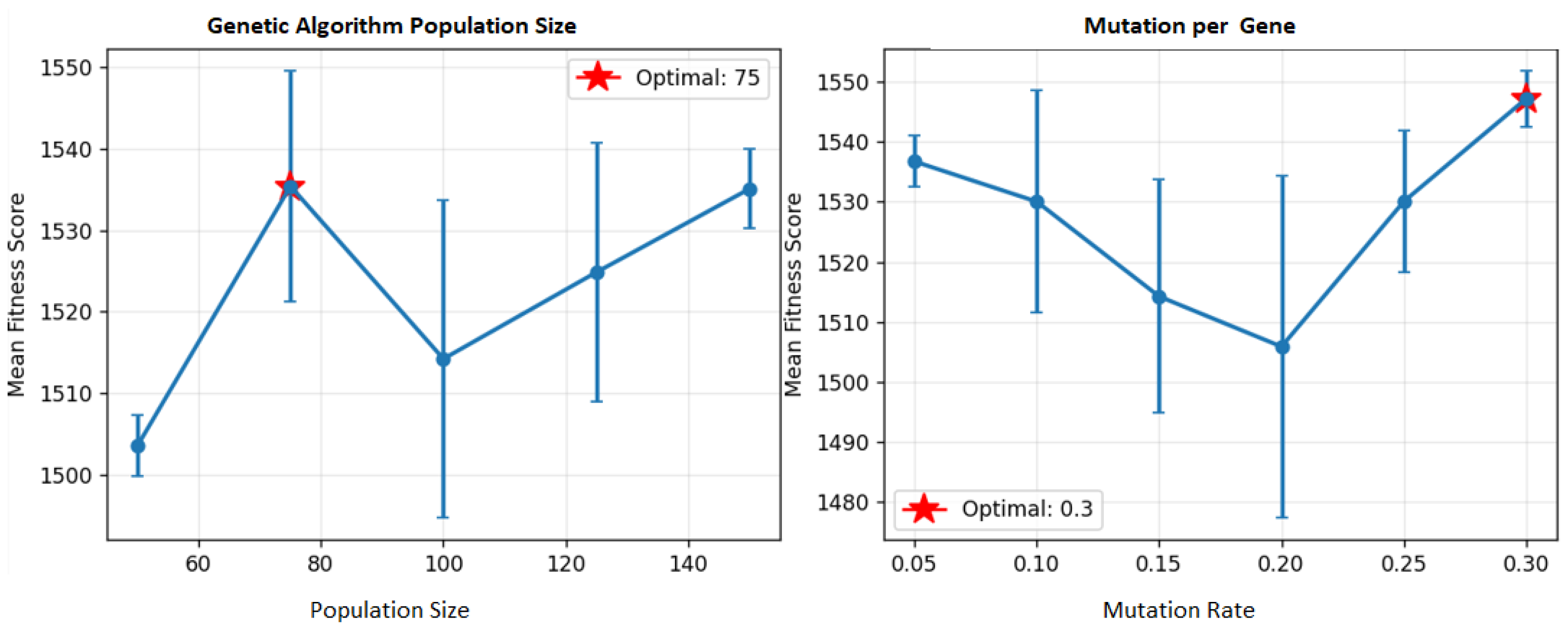
Regarding parameter selection, we conducted a comprehensive ablation study and parameter sensitivity analysis for our primary genetic algorithm approach, systematically evaluating the impact of key parameters, including diversity weight, penalty weight, population size, and mutation rate across multiple trials. This analysis provided empirical justification for our choices and demonstrated potential improvements of up to 120.6 fitness points through optimization. For the PSO and tabu search implementations, which served as comparative baselines, we adopted widely used parameter settings from the established literature to ensure fair and reproducible comparisons without introducing additional experimental variables.

From a practical perspective, the proposed methods offer scalable, adaptable, and reproducible frameworks that can assist educational institutions in replacing ad-hoc seminar planning processes with systematic, optimization-based decision support. The approaches are computationally efficient, with runtimes suitable for annual or periodic planning cycles, even for larger teacher pools.

We acknowledge that our evaluation relies on a single synthetic dataset, which, while carefully constructed to reflect realistic institutional parameters, represents only one specific educational context and constraint configuration. This limitation restricts the immediate generalizability of our findings to the diverse range of real-world institutional scenarios that vary in teacher pool size, budget structures, category requirements, and optimization priorities. Future work should validate the proposed approach across multiple institutional datasets with varying characteristics—including different scales (50–500+ teachers), constraint tightness levels, and disciplinary category structures—to establish broader applicability and identify potential performance boundaries. Additionally, collaboration with educational institutions to deploy and evaluate the system on actual planning data would provide valuable insights into practical implementation challenges, user acceptance, and the need for institution-specific parameter tuning, ultimately strengthening the evidence for real-world deployment of constraint-aware evolutionary approaches in educational resource allocation.

Future Work

Several directions can extend and strengthen this research:

• Multi-objective optimization: Extending the formulation to simultaneously optimize additional criteria such as diversity, expertise, or geographical distribution.
• Dynamic constraints: Incorporating changing institutional priorities, fluctuating budgets, or uncertain resource availability into the optimization framework.
• Hybrid approaches: Building on the promising tabu search results, hybridizing GA’s population-based exploration with TS’s adaptive memory or even PSO’s swarm dynamics to balance global and local search.
• Scalability studies: Evaluating performance on substantially larger datasets (500+ candidates) and exploring parallel or distributed computing implementations.
• Real-world deployment: Collaborating with educational institutions to test the system on actual planning data, integrating user feedback to improve interpretability and stakeholder acceptance.

Overall, the results indicate that carefully adapted metaheuristics—whether evolutionary, swarm-based, or memory-driven—can provide both theoretical and practical advances in solving complex educational resource allocation problems.