Enhancing the Sustained Capability of Continual Test-Time Adaptation with Dual Constraints
Abstract
1. Introduction
- Lack of constraints in parameter updates: The model contains a large number of domain-sensitive parameters, which tend to learn domain-specific knowledge. When the model encounters a new domain, the distribution difference between the old and new domains causes these domain-sensitive parameters to behave abnormally, leading to unstable channel representations that incorporate substantial domain-specific knowledge from previous domains, especially in the early stages of adapting to the new domain. This results in severe interference between domain-specific knowledge. More importantly, relying on domain-specific knowledge for classification significantly hinders the learning of domain-invariant knowledge.
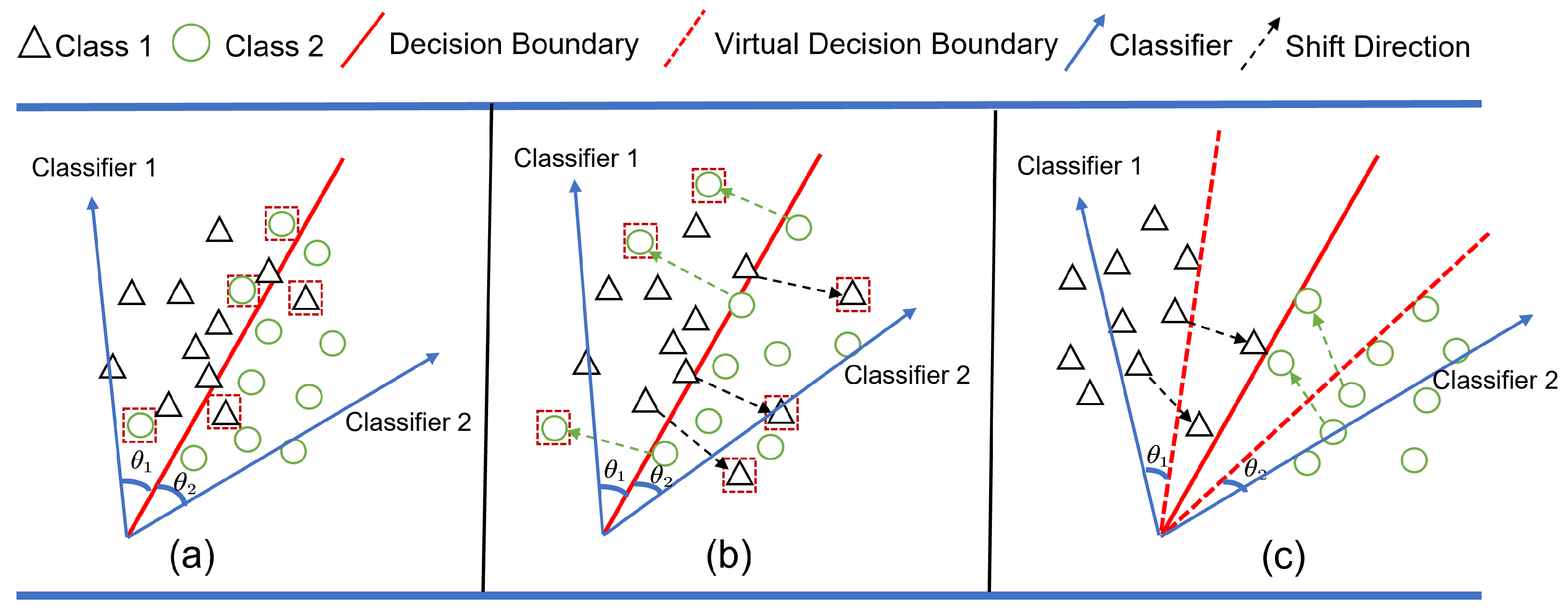
- Lack of constraints in decision boundary: Domain shifts carry a significant amount of domain-specific knowledge, causing the features generated by the model to spread out more. The lack of constraints makes these features prone to clustering near or crossing the decision boundary. Under the interference of domain-specific knowledge, features near the decision boundary are more likely to cross, particularly in the early stages of the new domain.
- We propose a novel parameter constraint method that minimizes the representation changes in domain-sensitive channels, which, respectively, enhance and suppress the learning of domain-invariant and domain-specific knowledge. In addition, we theoretically prove that it can effectively enhance the model’s generalization ability.
- We introduce a strongly constrained virtual decision boundary that creates a virtual margin, forcing features away from the original decision boundary, effectively mitigating the problem of features crossing the boundary during domain shifts.
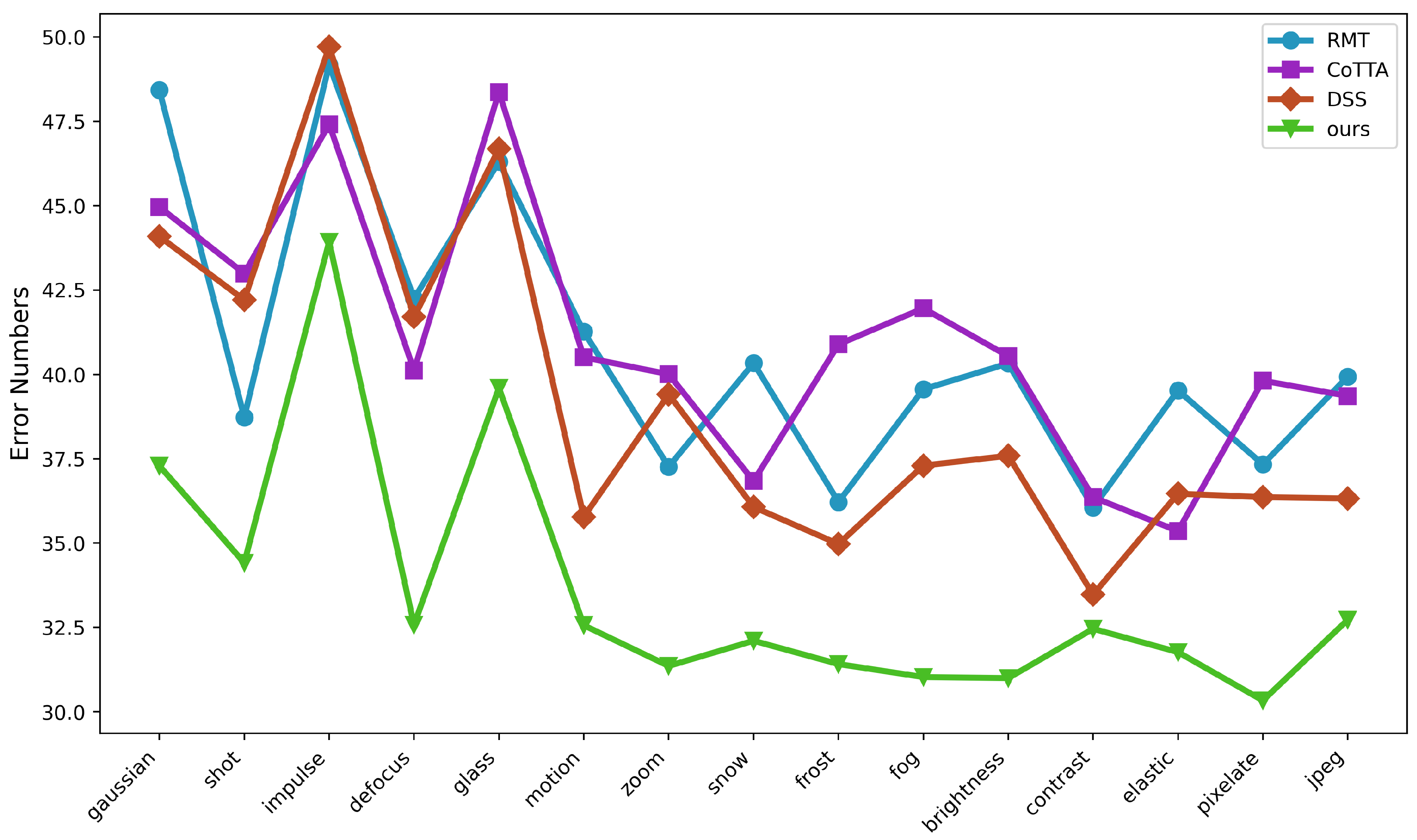
- Dual Constraints enhance the model’s sustained capability and achieve excellent performance, surpassing all existing state-of-the-art methods.
2. Related Work
2.1. Unsupervised Domain Adaptation
2.2. Domain Generalization
2.3. Continual Learning
2.4. Continual Test-Time Adaptation
3. Method
3.1. Problem Setting
3.2. Domain-Sensitive Parameter Suppression
3.2.1. Motivation of Domain-Sensitive Parameter Suppression
3.2.2. Implementation of Domain-Sensitive Parameter Suppression
3.2.3. Theoretical Analysis of Domain-Sensitive Parameter Suppression
3.3. Virtual Decision Boundary
3.3.1. Motivation of Virtual Decision Boundary
3.3.2. Implementation of Virtual Decision Boundary
3.3.3. Dynamic Virtual Margin of Virtual Decision Boundary
3.4. Loss Function
4. Experiment and Results
4.1. Experimental Setup
4.1.1. Datasets and Task Setting
4.1.2. Compared Methods and Implementation Details
4.2. Classification CTTA Tasks
4.2.1. CIFAR10-to-CIFAR10C Gradual and Continual
4.2.2. CIFAR100-to-CIFAR100C
4.2.3. ImageNet-to-ImageNetC
4.3. Semantic Segmentation CTTA Task
Cityscapes-to-ACDC
4.4. Ablation Study and Further Analysis
4.4.1. Ablation Study
4.4.2. Integration with Existing Methods
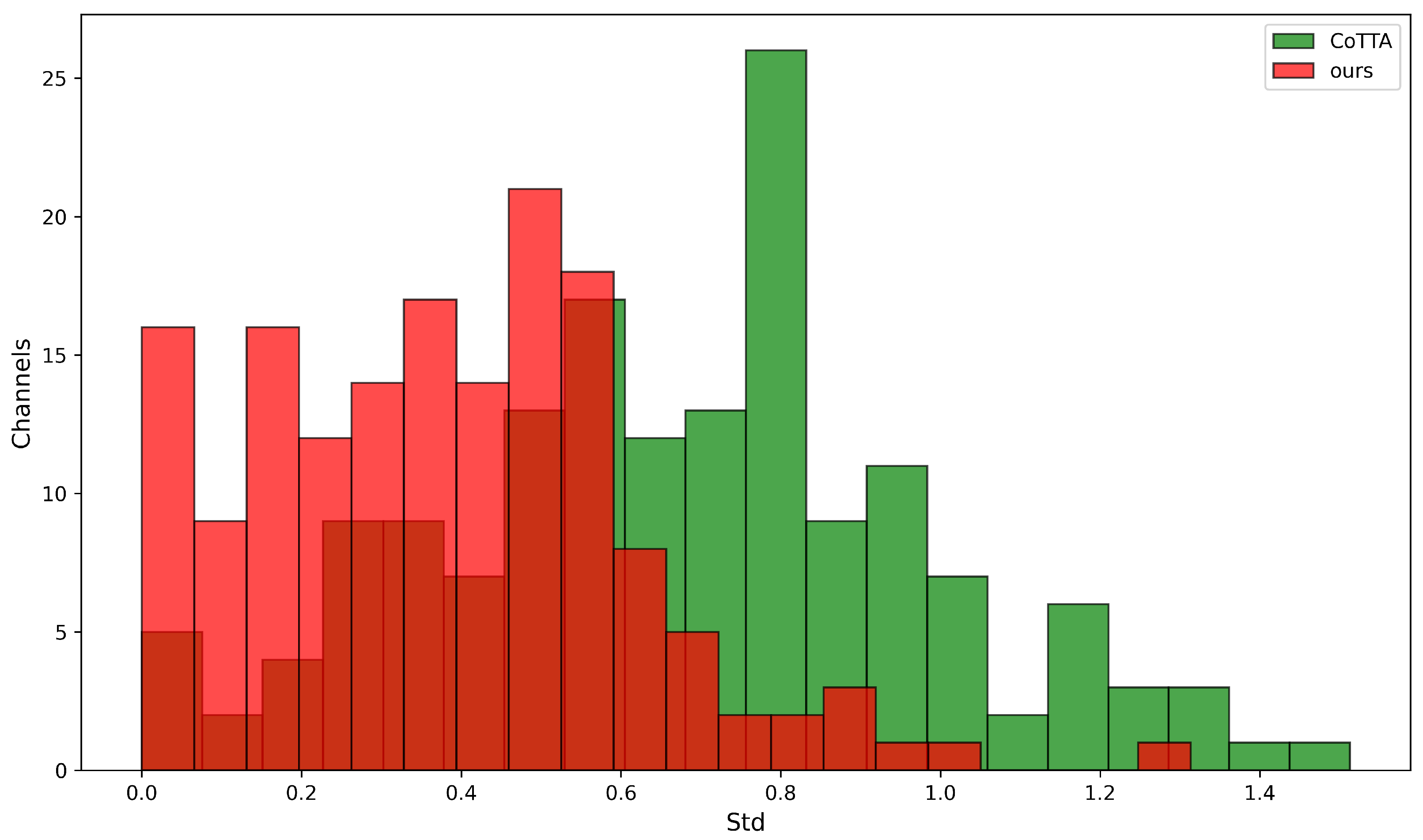
4.4.3. Analysis of Domain Sensitivity Parameter Suppression
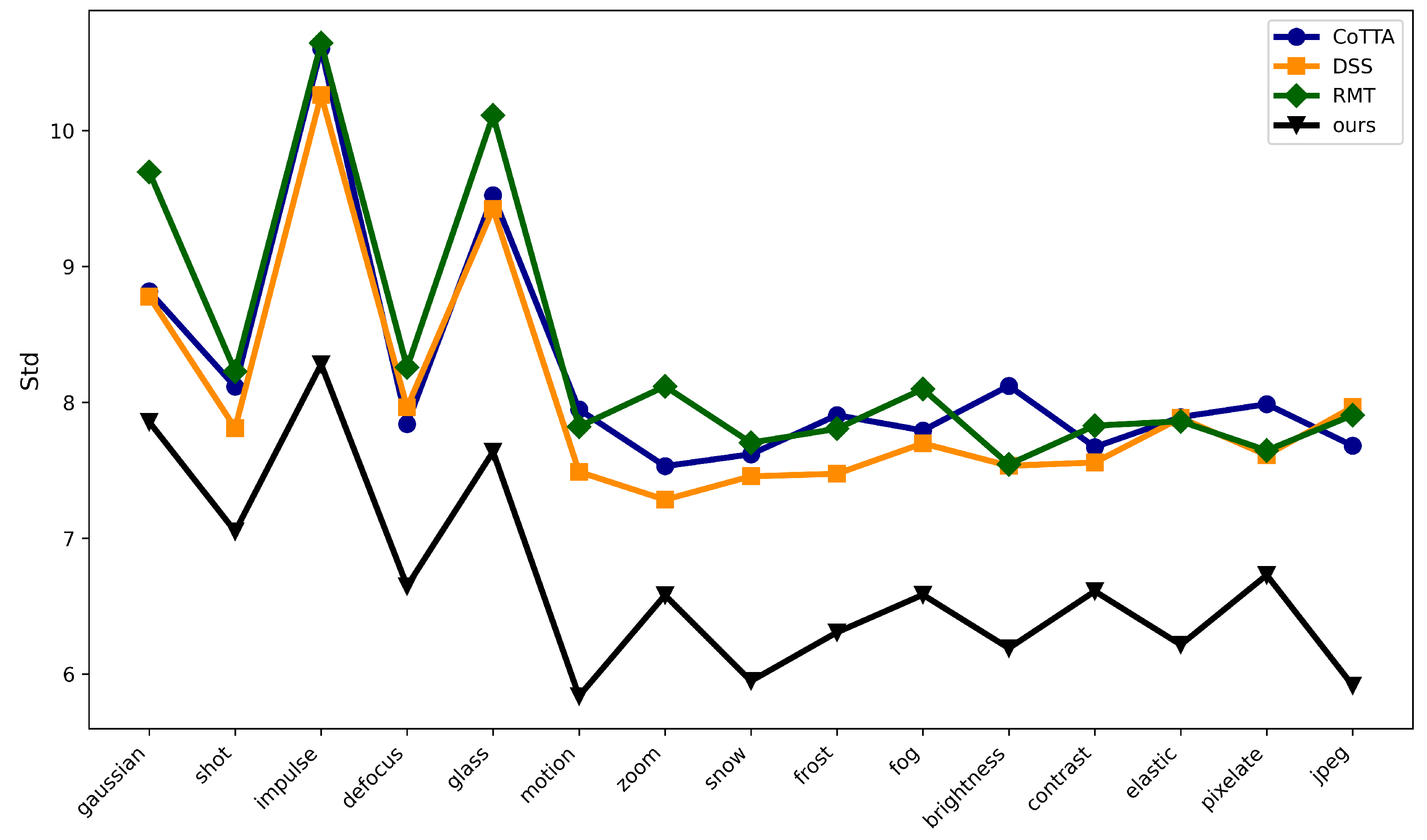
4.5. Analysis of Dynamic Virtual Margin
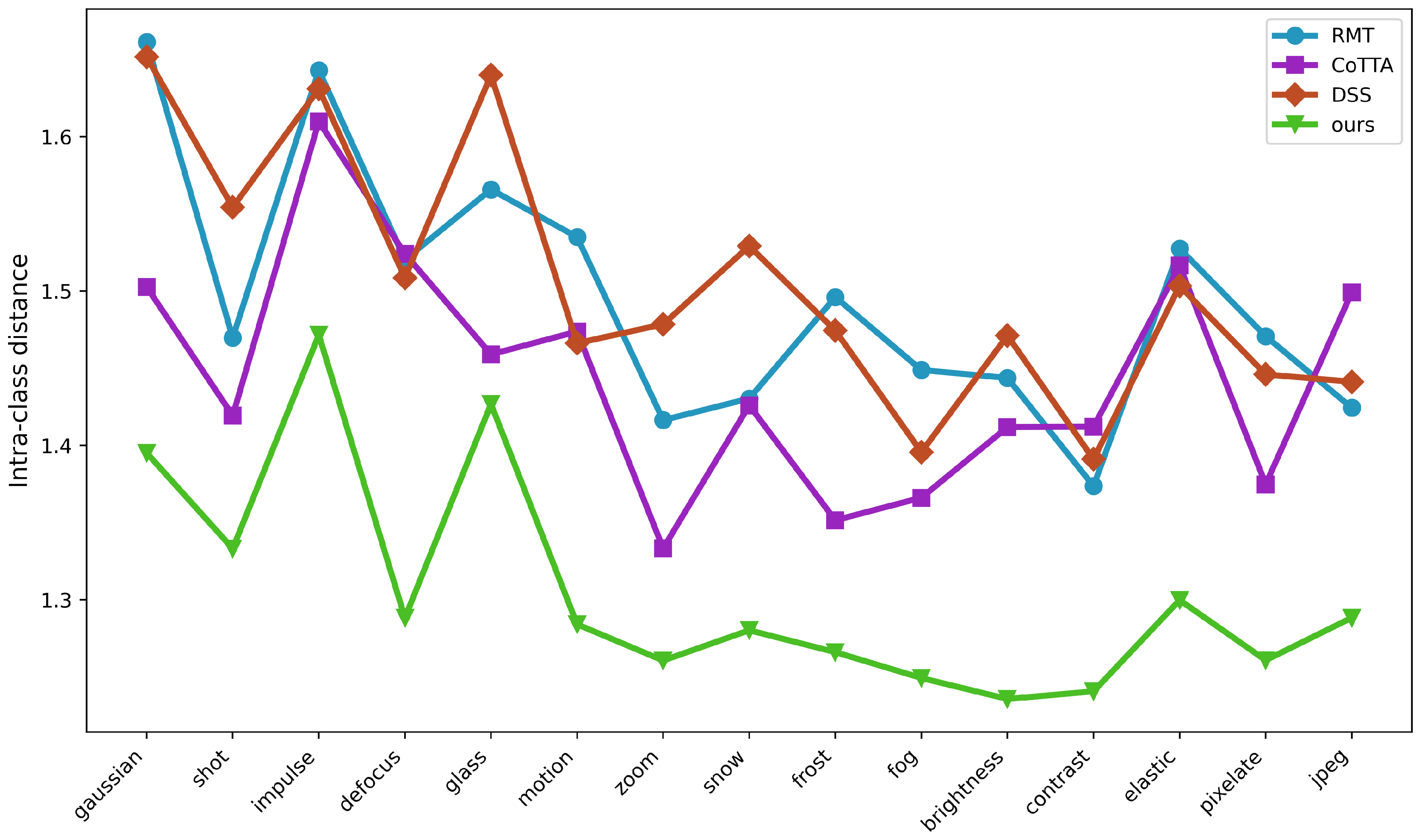
4.6. Analysis of Virtual Decision Boundary
4.7. Time and Parameter Complexity Evaluation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hu, C.; Hudson, S.; Ethier, M.; Al-Sharman, M.; Rayside, D.; Melek, W. Sim-to-real domain adaptation for lane detection and classification in autonomous driving. In Proceedings of the 2022 IEEE Intelligent Vehicles Symposium (IV), Aachen, Germany, 4–9 June 2022; IEEE: New York, NY, USA, 2022; pp. 457–463. [Google Scholar]
- Shi, Z.; Su, T.; Liu, P.; Wu, Y.; Zhang, L.; Wang, M. Learning Frequency-Aware Dynamic Transformers for All-In-One Image Restoration. arXiv 2024, arXiv:2407.01636. [Google Scholar] [CrossRef]
- Chen, W.; Miao, L.; Gui, J.; Wang, Y.; Li, Y. FLsM: Fuzzy Localization of Image Scenes Based on Large Models. Electronics 2024, 13, 2106. [Google Scholar] [CrossRef]
- Xu, E.; Zhu, J.; Zhang, L.; Wang, Y.; Lin, W. Research on Aspect-Level Sentiment Analysis Based on Adversarial Training and Dependency Parsing. Electronics 2024, 13, 1993. [Google Scholar] [CrossRef]
- Wang, Q.; Fink, O.; Van Gool, L.; Dai, D. Continual test-time domain adaptation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 7201–7211. [Google Scholar]
- Döbler, M.; Marsden, R.A.; Yang, B. Robust mean teacher for continual and gradual test-time adaptation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 7704–7714. [Google Scholar]
- Brahma, D.; Rai, P. A probabilistic framework for lifelong test-time adaptation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 3582–3591. [Google Scholar]
- Wang, Y.; Hong, J.; Cheraghian, A.; Rahman, S.; Ahmedt-Aristizabal, D.; Petersson, L.; Harandi, M. Continual test-time domain adaptation via dynamic sample selection. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2024; pp. 1701–1710. [Google Scholar]
- Liu, J.; Yang, S.; Jia, P.; Zhang, R.; Lu, M.; Guo, Y.; Xue, W.; Zhang, S. Vida: Homeostatic visual domain adapter for continual test time adaptation. arXiv 2023, arXiv:2306.04344. [Google Scholar]
- Zhu, Z.; Hong, X.; Ma, Z.; Zhuang, W.; Ma, Y.; Dai, Y.; Wang, Y. Reshaping the Online Data Buffering and Organizing Mechanism for Continual Test-Time Adaptation. In Proceedings of the European Conference on Computer Vision, Dublin, Ireland, 22–23 October 2025; Springer: Berlin/Heidelberg, Germany, 2025; pp. 415–433. [Google Scholar]
- Liu, J.; Xu, R.; Yang, S.; Zhang, R.; Zhang, Q.; Chen, Z.; Guo, Y.; Zhang, S. Continual-MAE: Adaptive Distribution Masked Autoencoders for Continual Test-Time Adaptation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 28653–28663. [Google Scholar]
- Wang, D.; Shelhamer, E.; Liu, S.; Olshausen, B.; Darrell, T. Tent: Fully test-time adaptation by entropy minimization. arXiv 2020, arXiv:2006.10726. [Google Scholar]
- DeVore, R.A.; Temlyakov, V.N. Some remarks on greedy algorithms. Adv. Comput. Math. 1996, 5, 173–187. [Google Scholar] [CrossRef]
- Knowles, J.D.; Watson, R.A.; Corne, D.W. Reducing local optima in single-objective problems by multi-objectivization. In Proceedings of the International Conference on Evolutionary Multi-Criterion Optimization, Zurich, Switzerland, 7–9 March 2001; Springer: Berlin/Heidelberg, Germany, 2001; pp. 269–283. [Google Scholar]
- Wang, D.Z.; Lo, H.K. Global optimum of the linearized network design problem with equilibrium flows. Transp. Res. Part B Methodol. 2010, 44, 482–492. [Google Scholar] [CrossRef]
- Zhou, W.; Zhou, Z. Unsupervised Domain Adaption Harnessing Vision-Language Pre-Training. IEEE Trans. Circuits Syst. Video Technol. 2024, 34, 8201–8214. [Google Scholar] [CrossRef]
- Wilson, G.; Cook, D.J. A survey of unsupervised deep domain adaptation. ACM Trans. Intell. Syst. Technol. (Tist) 2020, 11, 1–46. [Google Scholar] [CrossRef]
- Long, M.; Cao, Y.; Wang, J.; Jordan, M. Learning transferable features with deep adaptation networks. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; PMLR: San Diego, CA, USA, 2015; pp. 97–105. [Google Scholar]
- Long, M.; Zhu, H.; Wang, J.; Jordan, M.I. Unsupervised domain adaptation with residual transfer networks. Adv. Neural Inf. Process. Syst. 2016, 29. [Google Scholar]
- Long, M.; Zhu, H.; Wang, J.; Jordan, M.I. Deep transfer learning with joint adaptation networks. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; PMLR: San Diego, CA, USA, 2017; pp. 2208–2217. [Google Scholar]
- Fan, X.; Wang, Q.; Ke, J.; Yang, F.; Gong, B.; Zhou, M. Adversarially adaptive normalization for single domain generalization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 8208–8217. [Google Scholar]
- Yang, F.E.; Cheng, Y.C.; Shiau, Z.Y.; Wang, Y.C.F. Adversarial teacher-student representation learning for domain generalization. Adv. Neural Inf. Process. Syst. 2021, 34, 19448–19460. [Google Scholar]
- Zhu, W.; Lu, L.; Xiao, J.; Han, M.; Luo, J.; Harrison, A.P. Localized adversarial domain generalization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 7108–7118. [Google Scholar]
- Liang, J.; Hu, D.; Feng, J. Do we really need to access the source data? source hypothesis transfer for unsupervised domain adaptation. In Proceedings of the International Conference on Machine Learning, Virtual, 13–18 July 2020; PMLR: San Diego, CA, USA, 2020; pp. 6028–6039. [Google Scholar]
- Lowd, D.; Meek, C. Adversarial learning. In Proceedings of the Eleventh ACM SIGKDD International Conference on Knowledge Discovery in Data Mining, Chicago, IL, USA, 21–24 August 2005; pp. 641–647. [Google Scholar]
- Gopnik, A.; Glymour, C.; Sobel, D.M.; Schulz, L.E.; Kushnir, T.; Danks, D. A theory of causal learning in children: Causal maps and Bayes nets. Psychol. Rev. 2004, 111, 3. [Google Scholar] [CrossRef] [PubMed]
- Hospedales, T.; Antoniou, A.; Micaelli, P.; Storkey, A. Meta-learning in neural networks: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 5149–5169. [Google Scholar] [CrossRef] [PubMed]
- Cubuk, E.D.; Zoph, B.; Shlens, J.; Le, Q.V. Randaugment: Practical automated data augmentation with a reduced search space. In Proceedings of the IEEE/CVF conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020; pp. 702–703. [Google Scholar]
- Zhou, K.; Yang, Y.; Hospedales, T.; Xiang, T. Deep domain-adversarial image generation for domain generalisation. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 13025–13032. [Google Scholar]
- Gan, Y.; Bai, Y.; Lou, Y.; Ma, X.; Zhang, R.; Shi, N.; Luo, L. Decorate the newcomers: Visual domain prompt for continual test time adaptation. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 7595–7603. [Google Scholar]
- Wang, H.; Ge, S.; Lipton, Z.; Xing, E.P. Learning robust global representations by penalizing local predictive power. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar]
- Guo, J.; Qi, L.; Shi, Y. Domaindrop: Suppressing domain-sensitive channels for domain generalization. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–3 October 2023; pp. 19114–19124. [Google Scholar]
- Zhao, Y.; Zhang, H.; Hu, X. Penalizing gradient norm for efficiently improving generalization in deep learning. In Proceedings of the International Conference on Machine Learning, Baltimore, MD, USA, 17–23 July 2022; PMLR: San Diego, CA, USA, 2022; pp. 26982–26992. [Google Scholar]
- Cong, W.; Cong, Y.; Sun, G.; Liu, Y.; Dong, J. Self-Paced Weight Consolidation for Continual Learning. IEEE Trans. Circuits Syst. Video Technol. 2024, 34, 2209–2222. [Google Scholar] [CrossRef]
- Zhang, W.; Huang, Y.; Zhang, W.; Zhang, T.; Lao, Q.; Yu, Y.; Zheng, W.S.; Wang, R. Continual Learning of Image Classes With Language Guidance From a Vision-Language Model. IEEE Trans. Circuits Syst. Video Technol. 2024, 34, 13152–13163. [Google Scholar] [CrossRef]
- Yu, D.; Zhang, M.; Li, M.; Zha, F.; Zhang, J.; Sun, L.; Huang, K. Contrastive Correlation Preserving Replay for Online Continual Learning. IEEE Trans. Circuits Syst. Video Technol. 2024, 34, 124–139. [Google Scholar] [CrossRef]
- Li, H.; Liao, L.; Chen, C.; Fan, X.; Zuo, W.; Lin, W. Continual Learning of No-Reference Image Quality Assessment With Channel Modulation Kernel. IEEE Trans. Circuits Syst. Video Technol. 2024, 34, 13029–13043. [Google Scholar] [CrossRef]
- Li, K.; Chen, H.; Wan, J.; Yu, S. ESDB: Expand the Shrinking Decision Boundary via One-to-Many Information Matching for Continual Learning With Small Memory. IEEE Trans. Circuits Syst. Video Technol. 2024, 34, 7328–7343. [Google Scholar] [CrossRef]
- Shi, Z.; Liu, P.; Su, T.; Wu, Y.; Liu, K.; Song, Y.; Wang, M. Densely Distilling Cumulative Knowledge for Continual Learning. arXiv 2024, arXiv:2405.09820. [Google Scholar] [CrossRef]
- Wu, Y.; Chi, Z.; Wang, Y.; Plataniotis, K.N.; Feng, S. Test-time domain adaptation by learning domain-aware batch normalization. In Proceedings of the AAAI Conference on Artificial Intelligence, Philadelphia, PA, USA, 25 February–4 March; Volume 38, pp. 15961–15969.
- Zhang, J.; Qi, L.; Shi, Y.; Gao, Y. Domainadaptor: A novel approach to test-time adaptation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–3 October 2023; pp. 18971–18981. [Google Scholar]
- Chen, K.; Gong, T.; Zhang, L. Camera-Aware Recurrent Learning and Earth Mover’s Test-Time Adaption for Generalizable Person Re-Identification. IEEE Trans. Circuits Syst. Video Technol. 2024, 34, 357–370. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, H.; Heng, Q.; Hou, W.; Fan, Y.; Wu, Z.; Wang, J.; Savvides, M.; Shinozaki, T.; Raj, B.; et al. Freematch: Self-adaptive thresholding for semi-supervised learning. arXiv 2022, arXiv:2205.07246. [Google Scholar]
- Yuan, L.; Xie, B.; Li, S. Robust test-time adaptation in dynamic scenarios. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 15922–15932. [Google Scholar]
- Shi, B.; Zhang, D.; Dai, Q.; Zhu, Z.; Mu, Y.; Wang, J. Informative dropout for robust representation learning: A shape-bias perspective. In Proceedings of the International Conference on Machine Learning, Virtual, 13–18 July 2020; PMLR: San Diego, CA, USA, 2020; pp. 8828–8839. [Google Scholar]
- Klinker, F. Exponential moving average versus moving exponential average. Math. Semesterber. 2011, 58, 97–107. [Google Scholar]
- Dinh, L.; Pascanu, R.; Bengio, S.; Bengio, Y. Sharp minima can generalize for deep nets. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; PMLR: San Diego, CA, USA, 2017; pp. 1019–1028. [Google Scholar]
- Yang, S.; Wu, J.; Liu, J.; Li, X.; Zhang, Q.; Pan, M.; Zhang, S. Exploring sparse visual prompt for cross-domain semantic segmentation. arXiv 2023, arXiv:2303.09792. [Google Scholar]
- Sakaridis, C.; Dai, D.; Van Gool, L. ACDC: The adverse conditions dataset with correspondences for semantic driving scene understanding. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 10765–10775. [Google Scholar]
- Li, Y.; Wang, N.; Shi, J.; Liu, J.; Hou, X. Revisiting batch normalization for practical domain adaptation. arXiv 2016, arXiv:1603.04779. [Google Scholar] [CrossRef]
- Chakrabarty, G.; Sreenivas, M.; Biswas, S. Sata: Source anchoring and target alignment network for continual test time adaptation. arXiv 2023, arXiv:2304.10113. [Google Scholar] [CrossRef]
- Zagoruyko, S.; Komodakis, N. Wide residual networks. arXiv 2016, arXiv:1605.07146. [Google Scholar]
- Xie, S.; Girshick, R.; Dollár, P.; Tu, Z.; He, K. Aggregated residual transformations for deep neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1492–1500. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]







| Dataset | Source | BN [50] | TENT [12] | CoTTA [5] | Ours |
|---|---|---|---|---|---|
| CIFAR10C (Error %) | 24.8 | 13.7 | 30.7 | 10.4 | 8.3 |
| Gaussian | Shot | Impulse | Defocus | Glass | Motion | Zoom | Snow | Frost | Fog | Brightness | Contrast | Elastic | Pixelate | Jpeg | Mean | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Source | 72.3 | 65.7 | 72.9 | 46.9 | 54.3 | 34.8 | 42.0 | 25.1 | 41.3 | 26.0 | 9.3 | 46.7 | 26.6 | 58.5 | 30.3 | 43.5 |
| BN [50] | 28.1 | 26.1 | 36.3 | 12.8 | 35.3 | 14.2 | 12.1 | 17.3 | 17.4 | 15.3 | 8.4 | 12.6 | 23.8 | 19.7 | 27.3 | 20.4 |
| TENT [12] | 24.8 | 20.6 | 28.6 | 14.4 | 31.1 | 16.5 | 14.1 | 19.1 | 18.6 | 18.6 | 12.2 | 20.3 | 25.7 | 20.8 | 24.9 | 20.7 |
| CoTTA [5] | 24.3 | 21.3 | 26.6 | 11.6 | 27.6 | 12.2 | 10.3 | 14.8 | 14.1 | 12.4 | 7.5 | 10.6 | 18.3 | 13.4 | 17.3 | 16.2 |
| RoTTA [44] | 30.3 | 25.4 | 34.6 | 18.3 | 34.0 | 14.7 | 11.0 | 16.4 | 14.6 | 14.0 | 8.0 | 12.4 | 20.3 | 16.8 | 19.4 | 19.3 |
| RMT [6] | 24.1 | 20.2 | 25.7 | 13.2 | 25.5 | 14.7 | 12.8 | 16.2 | 15.4 | 14.6 | 10.8 | 14.0 | 18.0 | 14.1 | 16.6 | 17.0 |
| PETAL [7] | 23.7 | 21.4 | 26.3 | 11.8 | 28.8 | 12.4 | 10.4 | 14.8 | 13.9 | 12.6 | 7.4 | 10.6 | 18.3 | 13.1 | 17.1 | 16.2 |
| SATA [51] | 23.9 | 20.1 | 28.0 | 11.6 | 27.4 | 12.6 | 10.2 | 14.1 | 13.2 | 12.2 | 7.4 | 10.3 | 19.1 | 13.3 | 18.5 | 16.1 |
| DSS [8] | 24.1 | 21.3 | 25.4 | 11.7 | 26.9 | 12.2 | 10.5 | 14.5 | 14.1 | 12.5 | 7.8 | 10.8 | 18.0 | 13.1 | 17.3 | 16.0 |
| Reshaping [10] | 23.6 | 19.9 | 26.0 | 11.8 | 25.3 | 13.2 | 10.9 | 14.3 | 13.5 | 12.7 | 9.0 | 11.9 | 17.1 | 12.7 | 15.9 | 15.8 |
| Ours | 20.1 | 16.5 | 23.4 | 11.2 | 24.1 | 12.6 | 10.3 | 14.3 | 13.6 | 12.1 | 7.3 | 10.9 | 18.2 | 12.9 | 17.0 | 14.5 |
| Gaussian | Shot | Impulse | Defocus | Glass | Motion | Zoom | Snow | Frost | Fog | Brightness | Contrast | Elastic | Pixelate | Jpeg | Mean | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Source | 73.0 | 68.0 | 39.4 | 29.3 | 54.1 | 30.8 | 28.8 | 39.5 | 45.8 | 50.3 | 29.5 | 55.1 | 37.2 | 74.7 | 41.2 | 46.4 |
| BN [50] | 42.1 | 40.7 | 42.7 | 27.6 | 41.9 | 29.7 | 27.9 | 34.9 | 35.0 | 41.5 | 26.5 | 30.3 | 35.7 | 32.9 | 41.2 | 35.4 |
| TENT [12] | 37.2 | 35.8 | 41.7 | 37.9 | 51.2 | 48.3 | 48.5 | 58.4 | 63.7 | 71.1 | 70.4 | 82.3 | 88.0 | 88.5 | 90.4 | 60.9 |
| CoTTA [5] | 40.1 | 37.7 | 39.7 | 26.9 | 38.0 | 27.9 | 26.4 | 32.8 | 31.8 | 40.3 | 24.7 | 26.9 | 32.5 | 28.3 | 33.5 | 32.5 |
| RoTTA [44] | 49.1 | 44.9 | 45.5 | 30.2 | 42.7 | 29.5 | 26.1 | 32.2 | 30.7 | 37.5 | 24.7 | 29.1 | 32.6 | 30.4 | 36.7 | 34.8 |
| RMT [6] | 40.2 | 36.2 | 36.0 | 27.9 | 33.9 | 28.4 | 26.4 | 28.7 | 28.8 | 31.1 | 25.5 | 27.1 | 28.0 | 26.6 | 29.0 | 30.2 |
| PETAL [7] | 38.3 | 36.4 | 38.6 | 25.9 | 36.8 | 27.3 | 25.4 | 32.0 | 30.8 | 38.7 | 24.4 | 26.4 | 31.5 | 26.9 | 32.5 | 31.5 |
| SATA [51] | 36.5 | 33.1 | 35.1 | 25.9 | 34.9 | 27.7 | 25.4 | 29.5 | 29.9 | 33.1 | 24.1 | 26.7 | 31.9 | 27.5 | 35.2 | 30.3 |
| DSS [8] | 39.7 | 36.0 | 37.2 | 26.3 | 35.6 | 27.5 | 25.1 | 31.4 | 30.0 | 37.8 | 24.2 | 26.0 | 30.0 | 26.3 | 31.1 | 30.9 |
| Reshaping [10] | 38.8 | 35.0 | 35.4 | 26.7 | 33.2 | 27.4 | 25.0 | 27.4 | 26.8 | 29.8 | 24.1 | 25.1 | 26.9 | 24.9 | 28.0 | 29.0 |
| Ours | 33.9 | 32.6 | 31.8 | 25.4 | 30.2 | 26.7 | 24.8 | 28.9 | 24.3 | 29.7 | 23.4 | 25.1 | 26.5 | 23.3 | 30.6 | 27.8 |
| Gaussian | Shot | Impulse | Defocus | Glass | Motion | Zoom | Snow | Frost | Fog | Brightness | Contrast | Elastic | Pixelate | Jpeg | Mean | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Source | 95.3 | 95.0 | 95.3 | 86.1 | 91.9 | 87.4 | 77.9 | 85.1 | 79.9 | 79.0 | 45.4 | 96.2 | 86.6 | 77.5 | 66.1 | 83.0 |
| BN [50] | 87.7 | 87.4 | 87.8 | 88.0 | 87.7 | 78.3 | 63.9 | 67.4 | 70.3 | 54.7 | 36.4 | 88.7 | 58.0 | 56.6 | 67.0 | 72.0 |
| TENT [12] | 81.6 | 74.6 | 72.7 | 77.6 | 73.8 | 65.5 | 55.3 | 61.6 | 63.0 | 51.7 | 38.2 | 72.1 | 50.8 | 47.4 | 53.3 | 62.6 |
| CoTTA [5] | 84.7 | 82.1 | 80.6 | 81.3 | 79.0 | 68.6 | 57.5 | 60.3 | 60.5 | 48.3 | 36.6 | 66.1 | 47.2 | 41.2 | 46.0 | 62.7 |
| RoTTA [44] | 88.3 | 82.8 | 82.1 | 91.3 | 83.7 | 72.9 | 59.4 | 66.2 | 64.3 | 53.3 | 35.6 | 74.5 | 54.3 | 48.2 | 52.6 | 67.3 |
| RMT [6] | 79.9 | 76.3 | 73.1 | 75.7 | 72.9 | 64.7 | 56.8 | 56.4 | 58.3 | 49.0 | 40.6 | 58.2 | 47.8 | 43.7 | 44.8 | 59.9 |
| PETAL [7] | 87.4 | 85.8 | 84.4 | 85.0 | 83.9 | 74.4 | 63.1 | 63.5 | 64.0 | 52.4 | 40.0 | 74.0 | 51.7 | 45.2 | 51.0 | 67.1 |
| SATA [51] | 74.1 | 72.9 | 71.6 | 75.7 | 74.1 | 64.2 | 55.5 | 55.6 | 62.9 | 46.6 | 36.1 | 69.9 | 50.6 | 44.3 | 48.5 | 60.1 |
| DSS [8] | 84.6 | 80.4 | 78.7 | 83.9 | 79.8 | 74.9 | 62.9 | 62.8 | 62.9 | 49.7 | 37.4 | 71.0 | 49.5 | 42.9 | 48.2 | 64.6 |
| Reshaping [10] | 78.5 | 75.3 | 73.0 | 75.7 | 73.1 | 64.5 | 56.0 | 55.8 | 58.1 | 47.6 | 38.5 | 58.5 | 46.1 | 42.0 | 43.4 | 59.0 |
| Ours | 72.2 | 70.7 | 68.3 | 75.9 | 71.3 | 62.0 | 54.8 | 55.2 | 61.3 | 43.3 | 40.5 | 61.2 | 48.6 | 42.1 | 41.7 | 57.9 |
| Time |  | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Round | 1 | 4 | 7 | 10 | All | ||||||||||||||||
| Condition | Fog | Night | Rain | Snow | Mean | Fog | Night | Rain | Snow | Mean | Fog | Night | Rain | Snow | Mean | Fog | Night | Rain | Snow | Mean | Mean ↑ |
| Source | 69.1 | 40.3 | 59.7 | 57.8 | 56.7 | 69.1 | 40.3 | 59.7 | 57.8 | 56.7 | 69.1 | 40.3 | 59.7 | 57.8 | 56.7 | 69.1 | 40.3 | 59.7 | 57.8 | 56.7 | 56.7 |
| BN | 62.3 | 38.0 | 54.6 | 53.0 | 52.0 | 62.3 | 38.0 | 54.6 | 53.0 | 52.0 | 62.3 | 38.0 | 54.6 | 53.0 | 52.0 | 62.3 | 38.0 | 54.6 | 53.0 | 52.0 | 52.0 |
| TENT [12] | 69.0 | 40.2 | 60.1 | 57.3 | 56.7 | 66.5 | 36.3 | 58.7 | 54.0 | 53.9 | 64.2 | 32.8 | 55.3 | 50.9 | 50.8 | 61.8 | 29.8 | 51.9 | 47.8 | 47.8 | 52.3 |
| CoTTA [5] | 70.9 | 41.2 | 62.4 | 59.7 | 58.6 | 70.9 | 41.2 | 62.4 | 59.7 | 58.6 | 70.9 | 41.2 | 62.4 | 59.7 | 58.6 | 70.9 | 41.2 | 62.4 | 59.7 | 58.6 | 58.6 |
| Reshaping [10] | 71.2 | 42.3 | 65.0 | 62.0 | 60.1 | 72.8 | 43.6 | 66.7 | 63.3 | 61.6 | 72.5 | 42.5 | 66.8 | 63.3 | 61.3 | 72.5 | 42.9 | 66.7 | 63.0 | 61.3 | 61.3 |
| ours | 71.8 | 43.1 | 65.2 | 62.3 | 60.6 | 72.6 | 44.6 | 66.7 | 63.5 | 61.9 | 72.8 | 43.5 | 67.8 | 63.4 | 61.9 | 73.1 | 43.9 | 67.3 | 64.0 | 62.1 | 61.7 |
| VDB | DSP | CIFAR10C | CIFAR100C | ImageNetC | |
|---|---|---|---|---|---|
| 0 | 16.2% | 32.5% | 62.7% | ||
| 1 | ✓ | 15.4% | 30.1% | 60.3% | |
| 2 | ✓ | 15.1% | 28.3% | 59.2% | |
| 3 | ✓ | ✓ | 14.5% | 27.8% | 57.9% |
| Method | CIFAR10C | CIFAR100C | ImageNetC |
|---|---|---|---|
| TENT+ours | |||
| CoTTA+ours | |||
| RMT+ours | |||
| DSS+ours |
| m = 1 | m = 2 | m = 3 | m = 4 | m = 5 | m = 6 | m = 7 | m = 8 | |
|---|---|---|---|---|---|---|---|---|
| CIFAR10C | 14.8 | 14.5 | 14.7 | 14.9 | 15.3 | 15.5 | 16.1 | 16.8 |
| CIFAR100C | 27.9 | 27.8 | 28.2 | 28.3 | 28.4 | 28.7 | 29.5 | 30.1 |
| ImageNetC | 58.1 | 57.9 | 58.1 | 58.3 | 58.6 | 59.1 | 59.7 | 60.9 |
| m = 1 | m = 2 | m = 3 | m = 4 | m = 5 | m = 6 | m = 7 | m = 8 | m = Dynamic | |
|---|---|---|---|---|---|---|---|---|---|
| CIFAR10C | 15.3 | 15.2 | 14.9 | 15.5 | 15.9 | 16.3 | 16.7 | 17.3 | 14.5 |
| CIFAR100C | 28.2 | 28.1 | 28.5 | 28.9 | 29.3 | 29.7 | 30.2 | 31.1 | 27.8 |
| ImageNetC | 58.7 | 58.2 | 58.5 | 58.9 | 59.3 | 59.9 | 60.3 | 61.2 | 57.9 |
| TENT | CoTTA | DSS | RMT | Ours | |
|---|---|---|---|---|---|
| CIFAR10C | 7 min | 15 min | 16 min | 15 min | 19 min |
| CIFAR100C | 9 min | 17 min | 19 min | 18 min | 23 min |
| ImageNetC | 33 min | 71 min | 73 min | 72 min | 86 min |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Y.; Liu, P.; Wu, Y. Enhancing the Sustained Capability of Continual Test-Time Adaptation with Dual Constraints. Electronics 2025, 14, 3891. https://doi.org/10.3390/electronics14193891
Song Y, Liu P, Wu Y. Enhancing the Sustained Capability of Continual Test-Time Adaptation with Dual Constraints. Electronics. 2025; 14(19):3891. https://doi.org/10.3390/electronics14193891
Chicago/Turabian StyleSong, Yu, Pei Liu, and Yunpeng Wu. 2025. "Enhancing the Sustained Capability of Continual Test-Time Adaptation with Dual Constraints" Electronics 14, no. 19: 3891. https://doi.org/10.3390/electronics14193891
APA StyleSong, Y., Liu, P., & Wu, Y. (2025). Enhancing the Sustained Capability of Continual Test-Time Adaptation with Dual Constraints. Electronics, 14(19), 3891. https://doi.org/10.3390/electronics14193891





