MSBN-SPose: A Multi-Scale Bayesian Neuro-Symbolic Approach for Sitting Posture Recognition
Abstract
1. Introduction
- We present USSP, a novel, real-world sitting posture dataset that fills a critical gap in existing benchmarks by capturing diverse postural behaviors in natural educational settings.
- We propose MSBN-SPose, a hybrid neuro-symbolic framework that enhances model interpretability and generalization through rule-guided reasoning and epistemic uncertainty estimation.
- We conduct extensive experiments demonstrating that MSBN-SPose consistently outperforms baseline methods under both the USSP dataset and few-shot conditions. In addition to strong predictive performance, the model generates symbolic, interpretable outputs that align with its confidence estimates, supporting both transparency and reliability in low-resource scenarios.
2. Related Work
2.1. Dataset Challenges in Posture Recognition
2.2. Pose Classification Methods
2.3. Uncertainty Modeling with Bayesian Neural Networks
2.4. Neuro-Symbolic Systems
3. University Student Sitting Posture Dataset
3.1. Participant Recruitment and Demographic Diversity
3.2. Environmental and Contextual Variability
3.3. Camera Viewpoint and Device Diversity
3.4. Data Collection Protocol
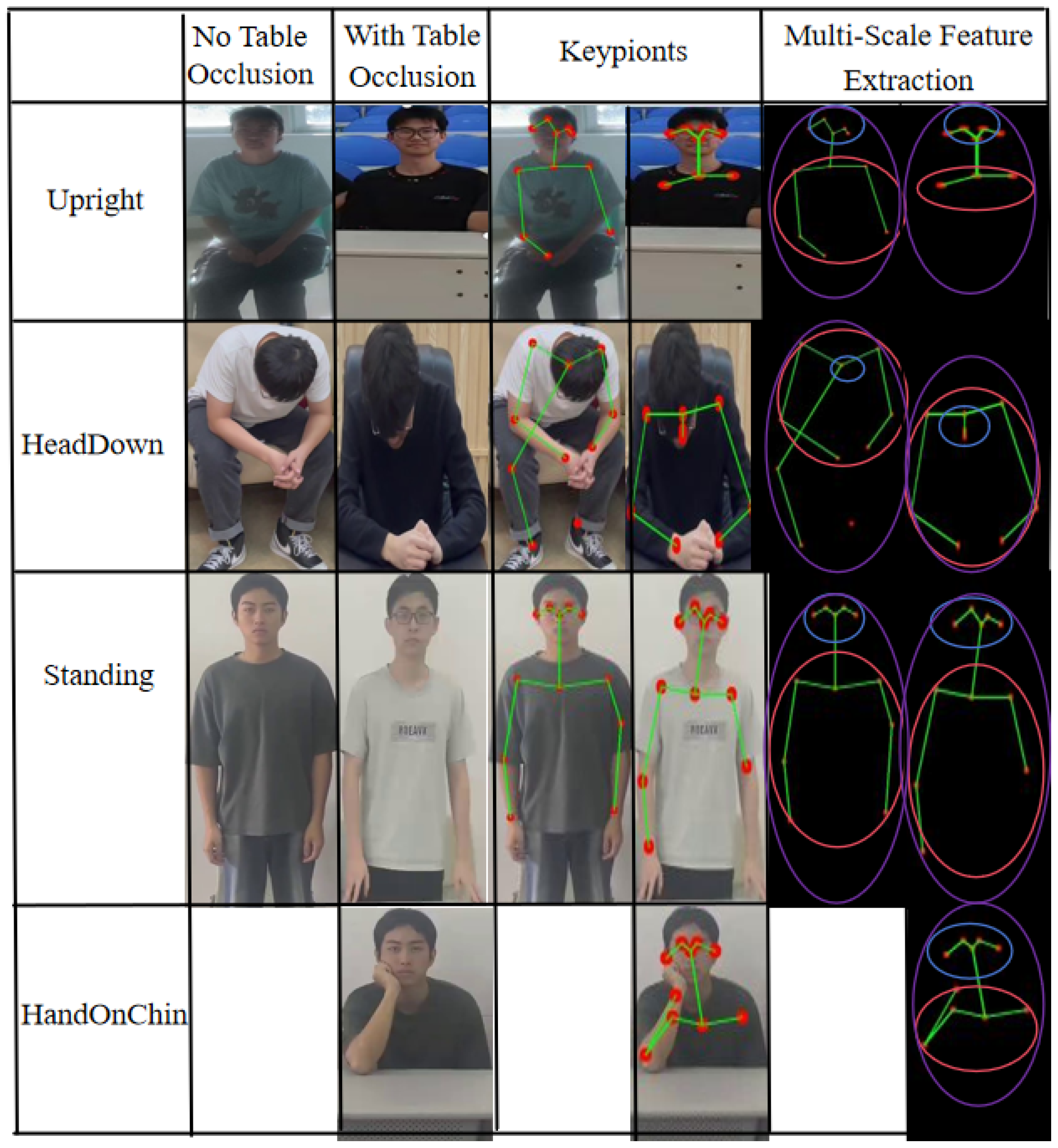
- Upright: Spine straight, head aligned with shoulders;
- HeadDown: Head tilted forward, nose below shoulder line;
- HandOnChin: One hand supporting chin or head;
- Standing: Standing upright.
3.5. Data Annotation and Quality Control
- (1)
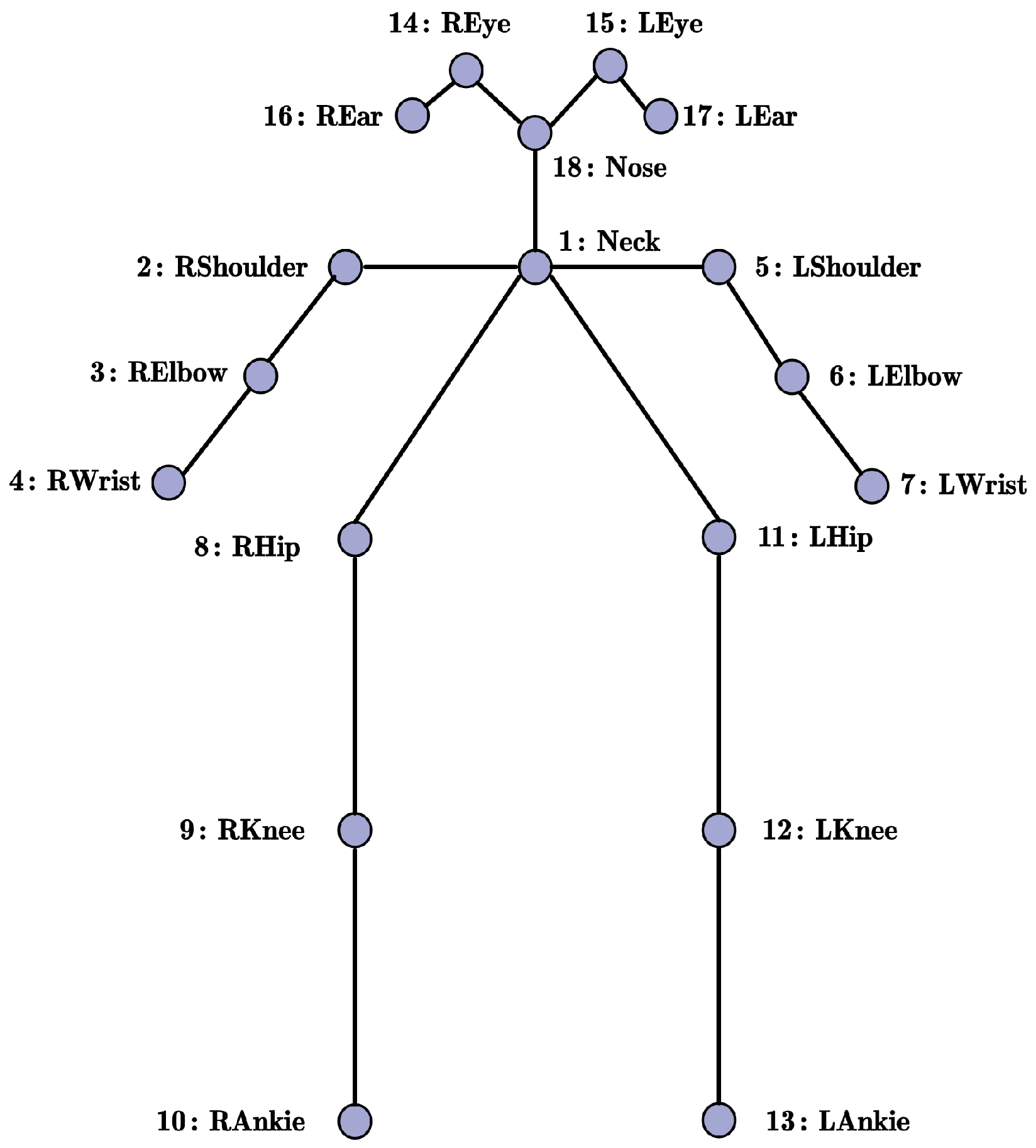
- Automated Keypoint Extraction: We used OpenPose (https://github.com/CMU-Perceptual-Computing-Lab/openpose accessed 16 August 2025) to extract 18 COCO-format 2D keypoints (including interpolated neck point) for each frame. Frames with missing or severely occluded keypoints (e.g., >4 joints undetected) were automatically discarded.
- (2)
- Manual labeling and verification: All retained frames were manually classified into four types of sitting postures; the classification was performed uniformly based on visual interpretation and geometric thresholds (if the vertical distance between the nose tip and the acromion is >15% of the torso length, it is judged as bowing the head).
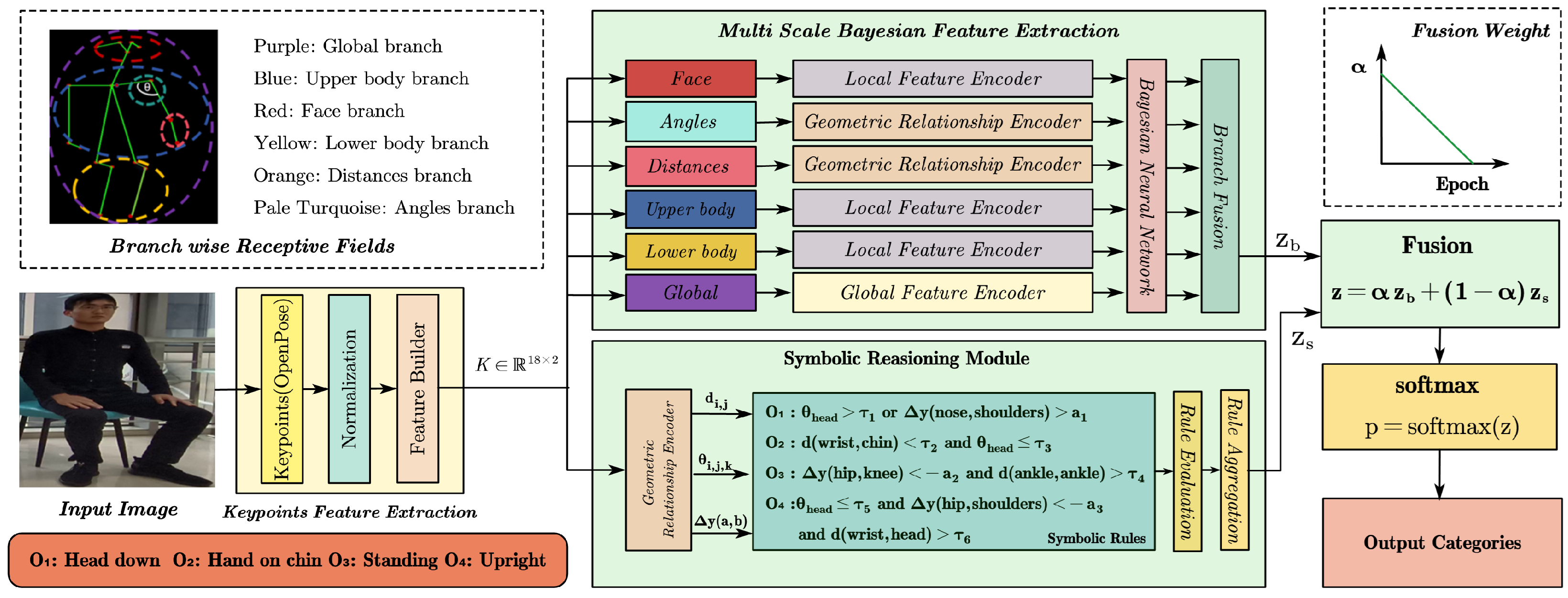
4. Method
4.1. Keypoints Feature Extraction
- (1)
- Pairwise Euclidean distances between all pairs of keypoints.
- (2)
- Joint angles formed by three consecutive keypoints.
4.2. Multi-Scale Bayesian Feature Extraction and Processing Module
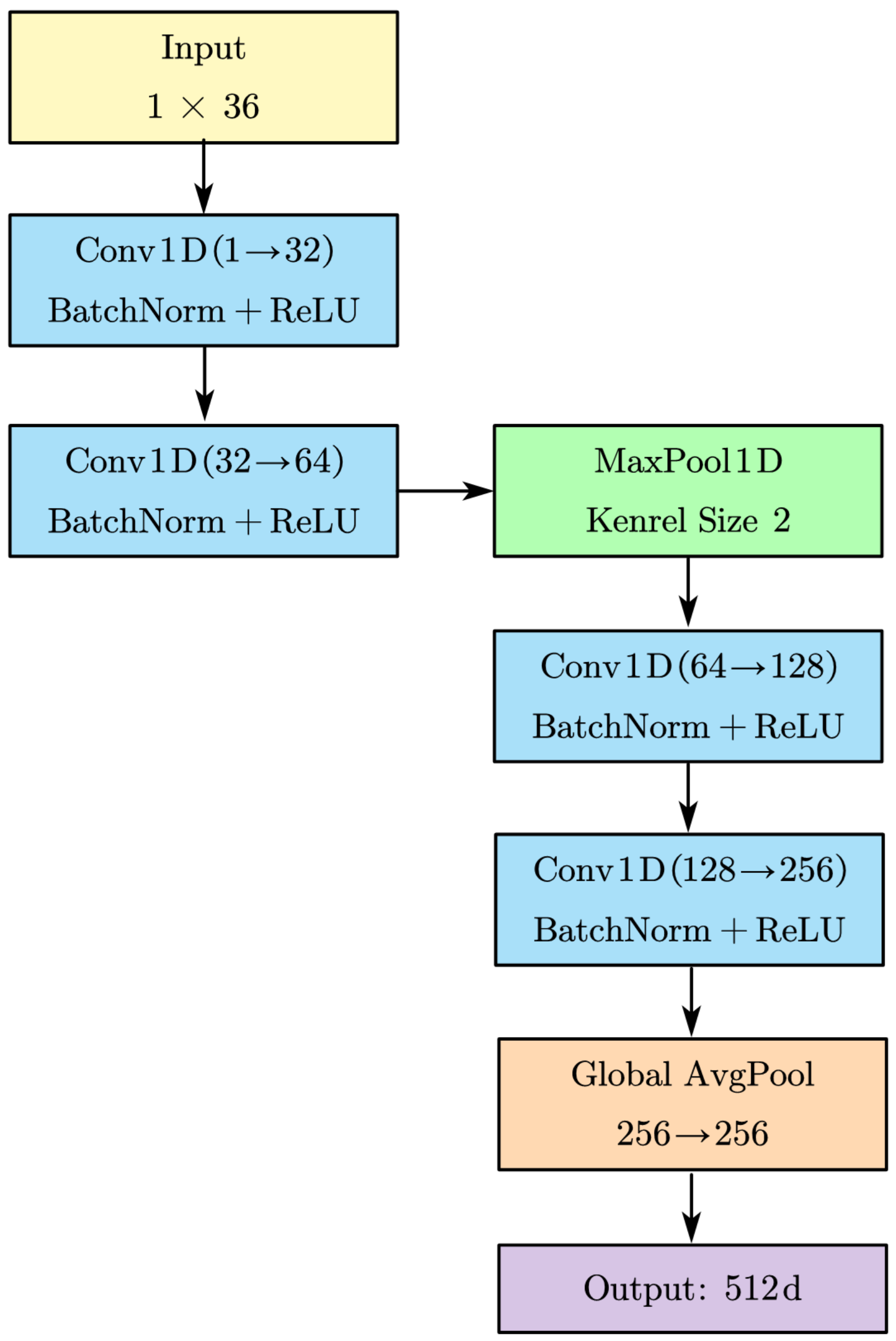
4.2.1. Multi-Scale Feature Extraction
- (1)
- Global Coordinate Features
- (2)
- Local Region Features
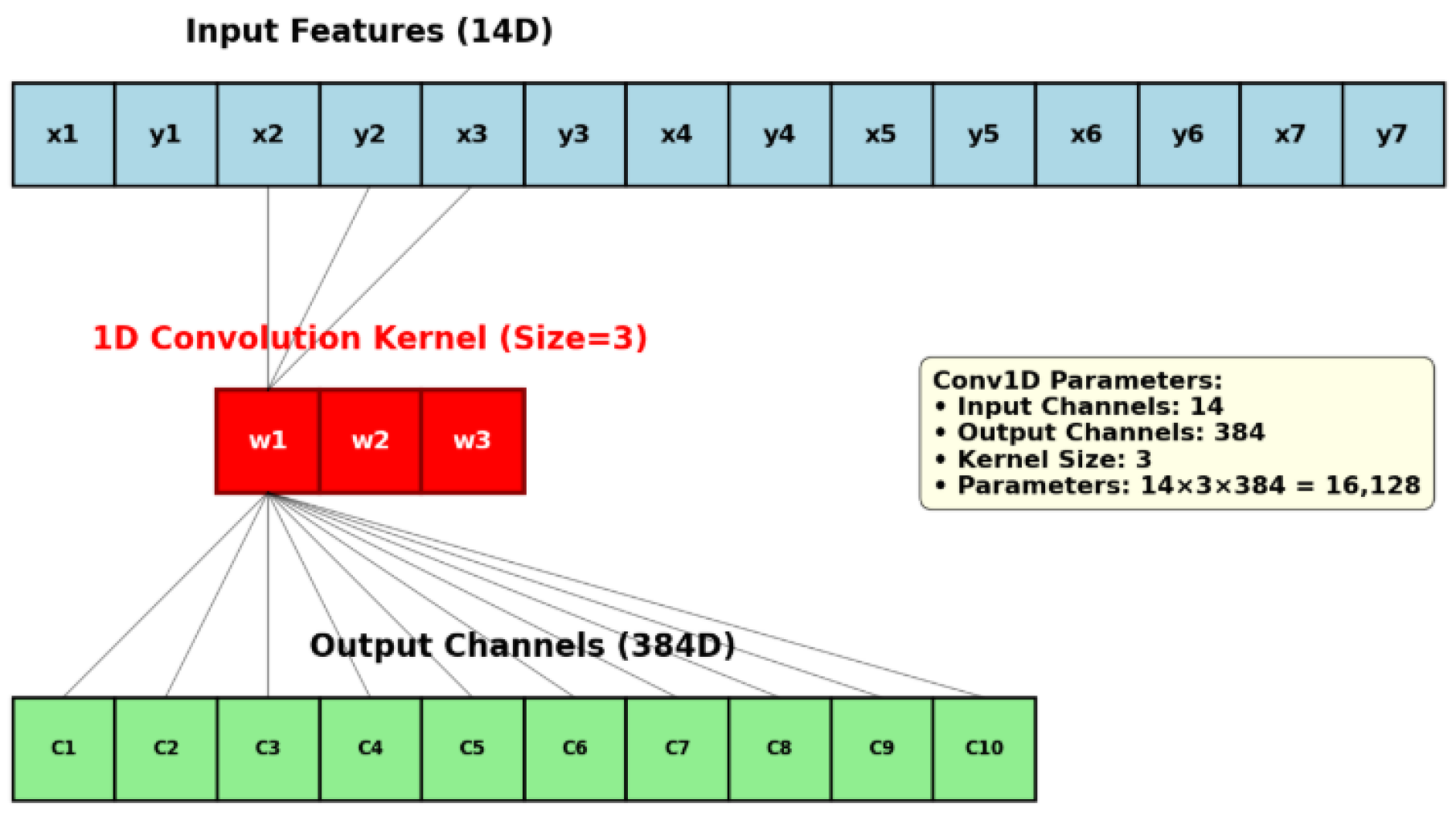
- Conv1D (, 384, kernel_size = 3) → BatchNorm → ReLU;
- MLP: 384 → 140 (with dropout ).
- (3)
- Geometric Relationship Features
- (4)
- Feature Fusion and Dimensional Harmonization
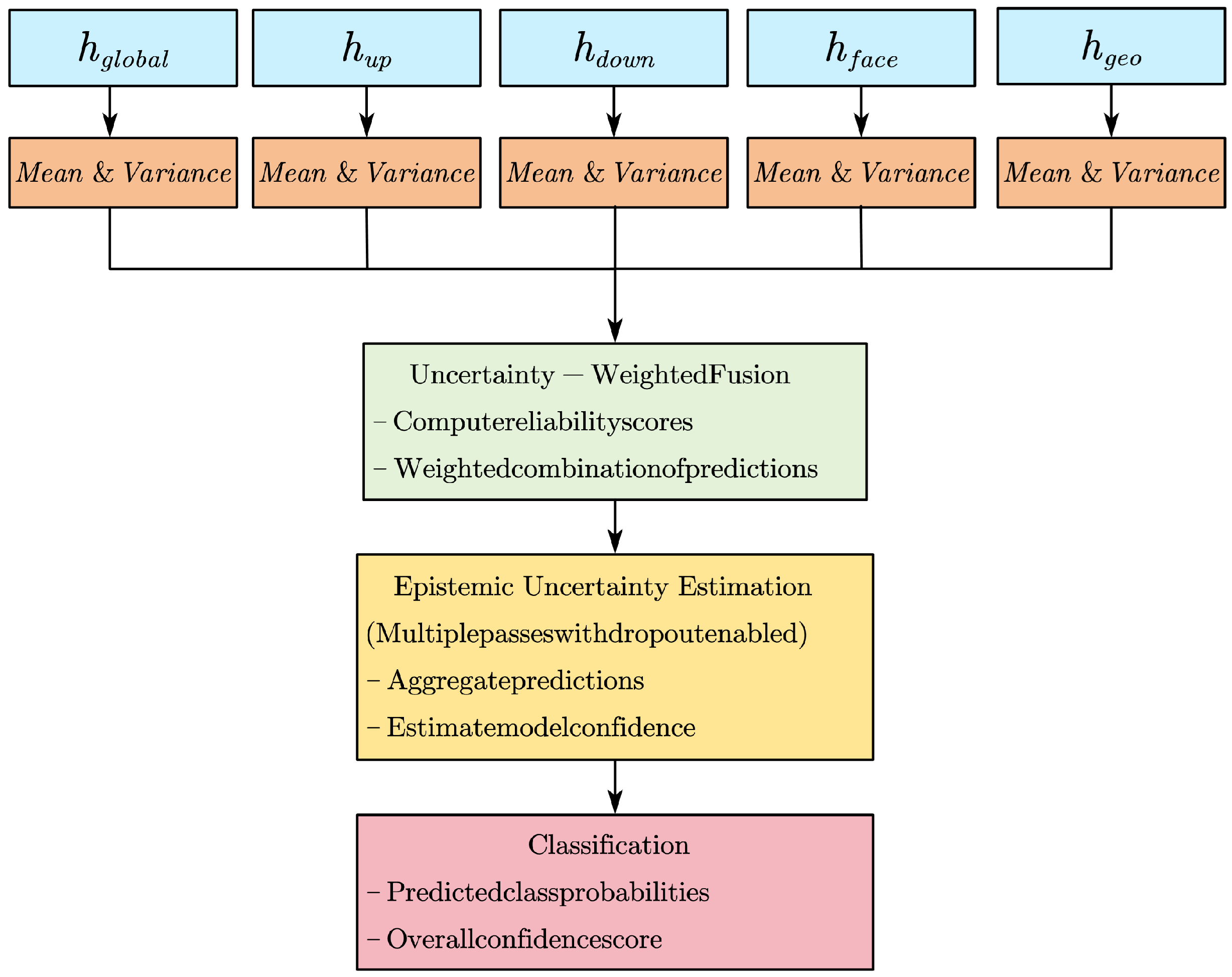
4.2.2. Uncertainty-Weighted Bayesian Fusion
- (1)
- Aleatoric uncertainty—inherent data noise captured explicitly by each branch’s predicted variance;
- (2)
- Epistemic uncertainty—uncertainty in the model parameters, estimated by MC Dropout over the fused prediction.
4.3. Symbolic Reasoning Module
4.4. Decision Fusion with Neural–Symbolic Integration
5. Experimental Section
5.1. Experimental Setup
Evaluation Metrics
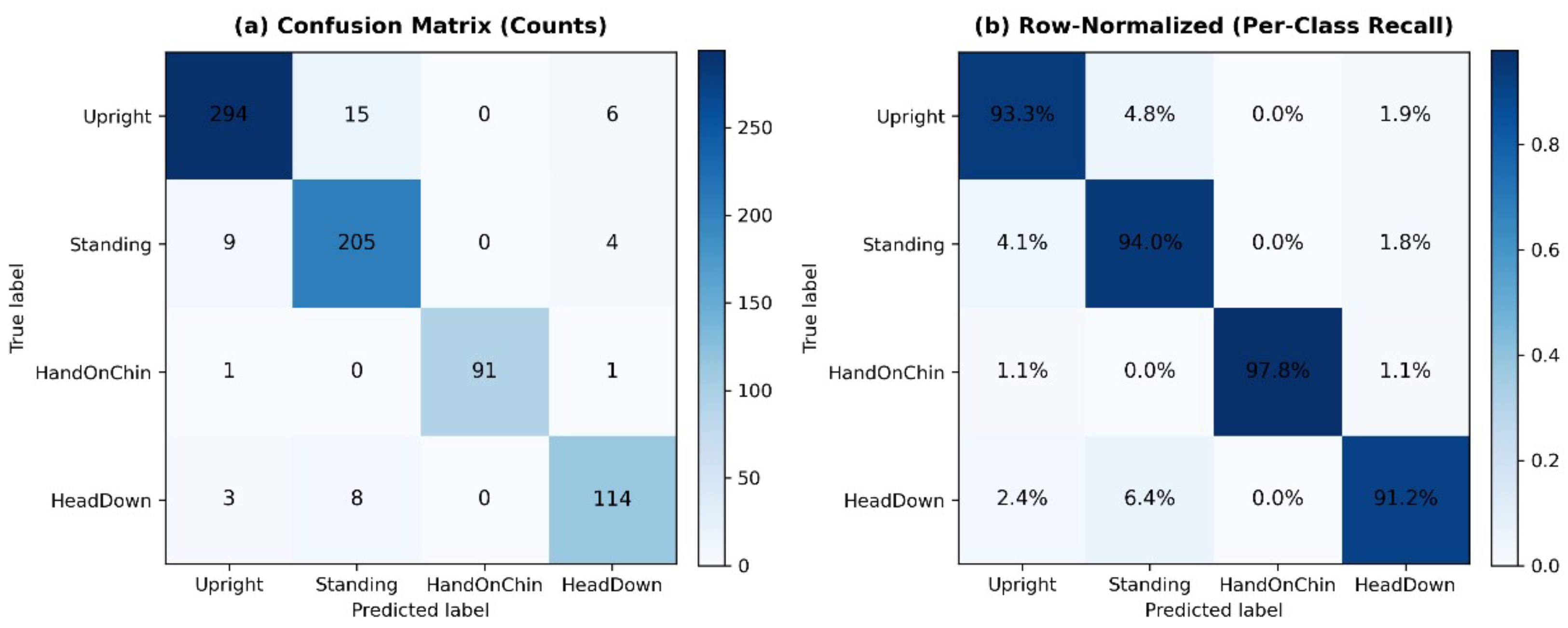
5.2. Results Analysis
5.3. Model Comparison Experiments
5.4. Ablation Study
5.4.1. Ablation of Key Components
5.4.2. Ablation on Jittered Data
5.4.3. Ablation on Feature-Stream Contributions
5.5. Hyperparameter Analysis
5.5.1. Sensitivity to the Symbolic Fusion Weight
5.5.2. Study of Hyperparameters , , s
5.6. Few-Shot Learning Experiment
5.7. Threshold Tuning Experiment
5.8. Visualization Analysis
5.9. Failure Cases
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- de Rezende, L.F.M.; Rodrigues Lopes, M.; Rey-López, J.P.; Matsudo, V.K.R.; do Carmo Luiz, O. Sedentary behavior and health outcomes: An overview of systematic reviews. PLoS ONE 2014, 9, e105620. [Google Scholar] [CrossRef]
- Casas, A.S.; Patiño, M.S.; Camargo, D.M. Association between the sitting posture and back pain in college students. Rev. Univ. Ind. Santander Salud 2016, 48, 446–454. [Google Scholar]
- Falla, D.; Jull, G.; Russell, T.; Vicenzino, B.; Hodges, P. Effect of neck exercise on sitting posture in patients with chronic neck pain. Phys. Ther. 2007, 87, 408–417. [Google Scholar] [CrossRef]
- Liu, Y.; Han, Z.; Chen, X.; Ru, S.; Yan, B. Effects of different sitting postures on back shape and hip pressure. J. Med. Biomech. 2023, 38, 756–762. [Google Scholar]
- Vlaović, Z.; Jaković, M.; Domljan, D. Smart office chairs with sensors for detecting sitting positions and sitting habits: A review. Drv. Ind. 2022, 73, 227–243. [Google Scholar] [CrossRef]
- Gupta, R.; Gupta, S.H.; Agarwal, A.; Choudhary, P.; Bansal, N.; Sen, S. A wearable multisensor posture detection system. In Proceedings of the 2020 4th International Conference on Intelligent Computing and Control Systems (ICICCS), Madurai, India, 13–15 May 2020; pp. 818–822. [Google Scholar]
- Hu, Y.; Huang, T.; Zhang, H.; Lin, H.; Zhang, Y.; Ke, L.; Cao, W.; Hu, K.; Ding, Y.; Wang, X.; et al. Ultrasensitive and wearable carbon hybrid fiber devices as robust intelligent sensors. ACS Appl. Mater. Interfaces 2021, 13, 23905–23914. [Google Scholar] [CrossRef]
- Sun, K.; Xiao, B.; Liu, D.; Wang, J. Deep high-resolution representation learning for human pose estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5693–5703. [Google Scholar]
- Wang, B.; Jin, X.; Yu, M.; Wang, G.; Chen, J. Pre-training Encoder-Decoder for Minority Language Speech Recognition. In Proceedings of the 2024 International Joint Conference on Neural Networks (IJCNN), Yokohama, Japan, 30 June–5 July 2024; pp. 1–8. [Google Scholar]
- Kamel, A.; Sheng, B.; Yang, P.; Li, P.; Shen, R.; Feng, D.D. Deep convolutional neural networks for human action recognition using depth maps and postures. IEEE Trans. Syst. Man Cybern. Syst. 2018, 49, 1806–1819. [Google Scholar] [CrossRef]
- Li, X.; Xiong, H.; Li, X.; Wu, X.; Zhang, X.; Liu, J.; Bian, J.; Dou, D. Interpretable deep learning: Interpretation, interpretability, trustworthiness, and beyond. Knowl. Inf. Syst. 2022, 64, 3197–3234. [Google Scholar] [CrossRef]
- Dindorf, C.; Ludwig, O.; Simon, S.; Becker, S.; Fröhlich, M. Machine learning and explainable artificial intelligence using counterfactual explanations for evaluating posture parameters. Bioengineering 2023, 10, 511. [Google Scholar] [CrossRef] [PubMed]
- Ding, Z.; Li, W.; Ogunbona, P.; Qin, L. A real-time webcam-based method for assessing upper-body postures. Mach. Vis. Appl. 2019, 30, 833–850. [Google Scholar] [CrossRef]
- Gal, Y.; Ghahramani, Z. Dropout as a bayesian approximation: Representing model uncertainty in deep learning. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 1050–1059. [Google Scholar]
- Kendall, A.; Gal, Y. What uncertainties do we need in bayesian deep learning for computer vision? In Proceedings of the NIPS’17: 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Abdar, M.; Pourpanah, F.; Hussain, S.; Rezazadegan, D.; Liu, L.; Ghavamzadeh, M.; Fieguth, P.; Cao, X.; Khosravi, A.; Acharya, U.R.; et al. A review of uncertainty quantification in deep learning: Techniques, applications and challenges. Inf. Fusion 2021, 76, 243–297. [Google Scholar] [CrossRef]
- Hesamian, M.H.; Jia, W.; He, X.; Kennedy, P. Deep learning techniques for medical image segmentation: Achievements and challenges. J. Digit. Imaging 2019, 32, 582–596. [Google Scholar] [CrossRef]
- Besold, T.R.; Bader, S.; Bowman, H.; Domingos, P.; Hitzler, P.; Kühnberger, K.U.; Lamb, L.C.; Lima, P.M.V.; de Penning, L.; Pinkas, G.; et al. Neural-symbolic learning and reasoning: A survey and interpretation 1. In Neuro-Symbolic Artificial Intelligence: The State of the Art; IOS Press: Amsterdam, The Netherlands, 2021; pp. 1–51. [Google Scholar]
- Lin, T.Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft coco: Common objects in context. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; Springer: Cham, Switzerland, 2014; pp. 740–755. [Google Scholar]
- Andriluka, M.; Pishchulin, L.; Gehler, P.; Schiele, B. 2d human pose estimation: New benchmark and state of the art analysis. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 3686–3693. [Google Scholar]
- Cao, Z.; Hidalgo, G.; Simon, T.; Wei, S.E.; Sheikh, Y. Openpose: Realtime multi-person 2d pose estimation using part affinity fields. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 43, 172–186. [Google Scholar] [CrossRef]
- Rhodes, J.S.; Cutler, A.; Moon, K.R. Geometry-and accuracy-preserving random forest proximities. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 10947–10959. [Google Scholar] [CrossRef] [PubMed]
- Zavala-Mondragon, L.A.; Lamichhane, B.; Zhang, L.; Haan, G.d. CNN-SkelPose: A CNN-based skeleton estimation algorithm for clinical applications. J. Ambient. Intell. Humaniz. Comput. 2020, 11, 2369–2380. [Google Scholar] [CrossRef]
- Yan, S.; Xiong, Y.; Lin, D. Spatial temporal graph convolutional networks for skeleton-based action recognition. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- Li, L.; Yang, G.; Li, Y.; Zhu, D.; He, L. Abnormal sitting posture recognition based on multi-scale spatiotemporal features of skeleton graph. Eng. Appl. Artif. Intell. 2023, 123, 106374. [Google Scholar] [CrossRef]
- Cao, Z.; Wu, X.; Wu, C.; Jiao, S.; Xiao, Y.; Zhang, Y.; Zhou, Y. KeypointNet: An Efficient Deep Learning Model with Multi-View Recognition Capability for Sitting Posture Recognition. Electronics 2025, 14, 718. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Chen, J.; Yang, L.; Zhang, Y.; Alber, M.; Chen, D.Z. Combining fully convolutional and recurrent neural networks for 3d biomedical image segmentation. In Proceedings of the NIPS’16: 30th International Conference on Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; Volume 29. [Google Scholar]
- Ovadia, Y.; Fertig, E.; Ren, J.; Nado, Z.; Sculley, D.; Nowozin, S.; Dillon, J.; Lakshminarayanan, B.; Snoek, J. Can you trust your model’s uncertainty? Evaluating predictive uncertainty under dataset shift. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Volume 32. [Google Scholar]
- Wanyan, Y.; Yang, X.; Dong, W.; Xu, C. A comprehensive review of few-shot action recognition. arXiv 2024, arXiv:2407.14744. [Google Scholar] [CrossRef]
- Chen, C.; Liang, J.; Zhu, X. Gait recognition based on improved dynamic Bayesian networks. Pattern Recognit. 2011, 44, 988–995. [Google Scholar] [CrossRef]
- Hitzler, P.; Eberhart, A.; Ebrahimi, M.; Sarker, M.K.; Zhou, L. Neuro-symbolic approaches in artificial intelligence. Natl. Sci. Rev. 2022, 9, nwac035. [Google Scholar] [CrossRef]
- Qu, M.; Tang, J. Probabilistic logic neural networks for reasoning. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Volume 32. [Google Scholar]
- Badreddine, S.; Garcez, A.D.; Serafini, L.; Spranger, M. Logic tensor networks. Artif. Intell. 2022, 303, 103649. [Google Scholar] [CrossRef]
- Johnston, P.; Nogueira, K.; Swingler, K. NS-IL: Neuro-symbolic visual question answering using incrementally learnt, independent probabilistic models for small sample sizes. IEEE Access 2023, 11, 141406–141420. [Google Scholar] [CrossRef]
- Magherini, T.; Fantechi, A.; Nugent, C.D.; Vicario, E. Using temporal logic and model checking in automated recognition of human activities for ambient-assisted living. IEEE Trans. Hum.-Mach. Syst. 2013, 43, 509–521. [Google Scholar] [CrossRef]
- Tang, J.; Wang, Z.; Hao, G.; Wang, K.; Zhang, Y.; Wang, N.; Liang, D. SAE-PPL: Self-guided attention encoder with prior knowledge-guided pseudo labels for weakly supervised video anomaly detection. J. Vis. Commun. Image Represent. 2023, 97, 103967. [Google Scholar] [CrossRef]
- Ye, Y.; Shi, S.; Zhao, T.; Qiu, K.; Lan, T. Patches Channel Attention for Human Sitting Posture Recognition. In Proceedings of the International Conference on Artificial Neural Networks, Heraklion, Crete, Greece, 26–29 September 2023; Springer: Cham, Switzerland, 2023; pp. 358–370. [Google Scholar]
- Groenesteijn, L.; Ellegast, R.P.; Keller, K.; Krause, F.; Berger, H.; de Looze, M.P. Office task effects on comfort and body dynamics in five dynamic office chairs. Appl. Ergon. 2012, 43, 320–328. [Google Scholar] [CrossRef]
- Abdullah, S.; Ahmed, S.; Choi, C.; Cho, S.H. Distance and Angle Insensitive Radar-Based Multi-Human Posture Recognition Using Deep Learning. Sensors 2024, 24, 7250. [Google Scholar] [CrossRef]
- Atvar, A.; Cinbiş, N.İ. Classification of human poses and orientations with deep learning. In Proceedings of the 2018 26th Signal Processing and Communications Applications Conference (SIU), Izmir, Turkey, 2–5 May 2018; pp. 1–4. [Google Scholar]
- Ko, K.R.; Chae, S.H.; Moon, D.; Seo, C.H.; Pan, S.B. Four-joint motion data based posture classification for immersive postural correction system. Multimed. Tools Appl. 2017, 76, 11235–11249. [Google Scholar] [CrossRef]
- Zeng, X.; Sun, B.; Wang, E.; Luo, W.; Liu, T. A Method of Learner’s Sitting Posture Recognition Based on Depth Image. In Proceedings of the 2017 2nd International Conference on Control, Automation and Artificial Intelligence (CAAI 2017), Sanya, China, 25–26 June 2017; Atlantis Press: Dordrecht, The Netherlands, 2017; pp. 558–563. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Lin, T.Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature pyramid networks for object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2117–2125. [Google Scholar]
- Loshchilov, I.; Hutter, F. Decoupled Weight Decay Regularization. arXiv 2017, arXiv:1711.05101. [Google Scholar]
- Zhao, S.; Su, Y. Sitting Posture Recognition Based on the Computer’s Camera. In Proceedings of the 2024 2nd Asia Conference on Computer Vision, Image Processing and Pattern Recognition, Xiamen, China, 26–28 April 2024; pp. 1–5. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Tan, M.; Le, Q. Efficientnetv2: Smaller models and faster training. In Proceedings of the International Conference on Machine Learning, Virtual, 18–24 July 2021; pp. 10096–10106. [Google Scholar]
- Mehta, S.; Rastegari, M. Mobilevit: Light-weight, general-purpose, and mobile-friendly vision transformer. arXiv 2021, arXiv:2110.02178. [Google Scholar]
- Jiao, S.; Xiao, Y.; Wu, X.; Liang, Y.; Liang, Y.; Zhou, Y. LMSPNet: Improved lightweight network for multi-person sitting posture recognition. In Proceedings of the 2023 IEEE 3rd International Conference on Computer Communication and Artificial Intelligence (CCAI), Taiyuan, China, 26–28 May 2023; pp. 289–295. [Google Scholar]

| Category | Sub-Factors | Sample Size |
|---|---|---|
| Gender | Male, Female | 25 females, 25 males |
| Body Shape | Slim, Average, Slightly Overweight | 8 per category |
| Clothing | Tight-fitting clothes, Loose clothes, Hat, Coat | At least 10 participants per condition |
| Individual Sitting Posture Differences | Habitual sitting posture (e.g., slouching, upright) | 8 per category |
| Factor | Scenario | Images per Condition |
|---|---|---|
| Seat Type | Hard chair, soft chair, chair with backrest, chair without backrest | 1000 |
| Desk Height | Low desk (classroom), medium desk (study room), high desk (laboratory) | 1000 |
| Lighting Conditions | Daylight, indoor lighting, low light, backlight | 1000 |
| Background Complexity | Clean background, regular indoor, crowded background | 1000 |
| Angle | Description | Images per Angle |
|---|---|---|
| Front View | The subject faces the camera directly | 1000 |
| Left 45° | Slightly side-facing from the left | 1000 |
| Right 45° | Slightly side-facing from the right | 1000 |
| Full Side View | 90° profile view from the side | 1000 |
| Device Type | Device Examples | Usage Description |
|---|---|---|
| Smartphone | iPhone, Android | Flexible and mobile; suitable for diverse environments such as classrooms and study rooms |
| Computer Webcam | Built-in or external | Suitable for fixed-position recording to ensure stable and continuous posture tracking |
| Metric | Definition |
|---|---|
| Accuracy | — Overall correctness |
| Precision | — Correctness among predicted positives |
| Recall | — Coverage of actual positives |
| F1-score | — Balance of precision and recall |
| Macro Avg | Average of per-class metrics (unweighted) |
| Weighted Avg | Average of per-class metrics (weighted by support) |
| Predictive Entropy | — Uncertainty of prediction |
| Class | Precision (%) | Recall (%) | F1-Score (%) | Support |
|---|---|---|---|---|
| Upright | 98.63 | 97.25 | 97.94 | 315 |
| Standing | 93.33 | 96.12 | 94.70 | 218 |
| Hand On Chin | 98.21 | 98.47 | 98.34 | 93 |
| Head Down | 95.23 | 94.36 | 94.79 | 125 |
| Macro Average | 96.26 | 96.55 | 96.40 | 751 |
| Weighted Average | 96.30 | 96.06 | 96.18 | 751 |
| Accuracy | 96.01 | |||
| Model | Precision (%) | Recall (%) | F1-Score (%) | Accuracy (%) | Parameters (M) |
|---|---|---|---|---|---|
| MLP [47] | 91.89 | 91.63 | 91.76 | 91.61 | 0.03 |
| ResNet-18 [48] | 91.04 | 90.76 | 90.90 | 90.55 | 11.28 |
| EfficientNet-V2 [49] | 90.17 | 89.54 | 89.85 | 89.35 | 20.29 |
| MobileViT [50] | 88.69 | 88.90 | 88.79 | 88.42 | 5.04 |
| LMSPNet [51] | 93.11 | 92.46 | 92.78 | 92.14 | 12.80 |
| KeypointNet [26] | 94.32 | 94.12 | 94.22 | 93.12 | 8.96 |
| MSBN-SPose (Ours) | 96.26 | 96.55 | 96.40 | 96.01 | 1.97 |
| Model | Bayesian Layers | Symbolic Rules | Accuracy (%) |
|---|---|---|---|
| CNN (Baseline) | × | × | 90.28 |
| + Bayesian Layers | ✓ | × | 92.75 |
| + Multi-Scale Input | ✓ | × | 94.41 |
| + Symbolic Rules (Full Model) | ✓ | ✓ | 96.01 |
| Dataset | Precision | Recall | F1-Score | Accuracy |
|---|---|---|---|---|
| Geometric | 94.83 | 94.27 | 94.55 | 94.08 |
| Photometric | 95.72 | 95.31 | 95.51 | 95.57 |
| Occlusion | 93.78 | 93.66 | 93.72 | 93.37 |
| Keypoin | 93.23 | 92.88 | 92.05 | 92.12 |
| Jitter-All | 91.68 | 91.53 | 91.60 | 91.22 |
| Clean-test | 96.26 | 96.55 | 96.40 | 96.01 |
| Setting | Feature | Precision | Recall | F1-Score | Accuracy |
|---|---|---|---|---|---|
| Single-Scale Feature Extraction | Global | 84.34 | 84.75 | 84.54 | 85.37 |
| Upper | 78.68 | 79.12 | 78.90 | 78.15 | |
| Lower | 75.34 | 75.86 | 75.60 | 75.54 | |
| Face | 77.88 | 78.16 | 78.02 | 77.53 | |
| Geometric | 79.24 | 80.17 | 79.70 | 80.16 | |
| Multi-Scale Feature Extraction | G + U | 88.31 | 88.49 | 88.40 | 87.65 |
| G + U + L | 90.12 | 90.24 | 90.18 | 89.86 | |
| G + U + L + F | 92.17 | 91.88 | 92.02 | 91.52 | |
| G + U + L + F + Geom | 96.26 | 96.55 | 96.40 | 96.01 |
| Fusion Weight | Precision | Recall | F1-Score | Accuracy (%) |
|---|---|---|---|---|
| = 0 | 94.70 | 94.81 | 94.75 | 94.60 |
| = 0.05 | 95.27 | 95.36 | 95.31 | 95.70 |
| = 0.10 | 96.26 | 96.55 | 96.40 | 96.01 |
| = 0.20 | 95.31 | 95.42 | 95.36 | 95.94 |
| Setting | Precision | Recall | F1-Score | Accuracy |
|---|---|---|---|---|
| 95.37 | 95.48 | 95.42 | 95.18 | |
| 96.26 | 96.55 | 96.40 | 96.01 | |
| 95.41 | 95.56 | 95.48 | 95.30 | |
| 95.15 | 95.31 | 95.23 | 95.08 | |
| 95.43 | 95.77 | 95.60 | 95.69 | |
| 96.26 | 96.55 | 96.40 | 96.01 | |
| 95.82 | 96.03 | 95.92 | 95.72 | |
| 95.41 | 95.36 | 95.39 | 95.29 | |
| 96.26 | 96.55 | 96.40 | 96.01 | |
| 94.88 | 95.12 | 95.00 | 94.67 | |
| Adaptive thresholds | 95.42 | 94.75 | 94.72 | 95.46 |
| Class | Precision (%) | Recall (%) | F1-Score (%) | Support |
|---|---|---|---|---|
| Upright | 69.42 | 80.00 | 74.34 | 315 |
| Standing | 74.78 | 39.45 | 51.65 | 218 |
| HandOnChin | 71.43 | 86.02 | 78.05 | 93 |
| HeadDown | 57.14 | 73.60 | 64.34 | 125 |
| Overall Accuracy | 67.91 | |||
| Model | Test Accuracy (%) |
|---|---|
| BaselineCNN | 56.46 (±0.71) |
| BaselineMultiScaleCNN | 48.87 (±0.93) |
| MSBN-SPose (w/o Symbolic) | 62.00 (±0.68) |
| MSBN-SPose (w/o Bayesian) | 60.00 (±0.85) |
| MSBN-SPose (Ours) | 67.91 (±0.82) |
| GT | Margin | Failure Mode | |
|---|---|---|---|
| Head Down | 0.63 | 0.07 | Similar-class confusion |
| Hand On Chin | 0.58 | 0.05 | Extreme head pose |
| Standing | 0.61 | 0.09 | Partial wrist occlusion |
| Upright | 0.55 | 0.06 | Strong backlight |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Tavares, A.; Lima, C.; Gomes, T.; Zhang, Y.; Liang, Y. MSBN-SPose: A Multi-Scale Bayesian Neuro-Symbolic Approach for Sitting Posture Recognition. Electronics 2025, 14, 3889. https://doi.org/10.3390/electronics14193889
Wang S, Tavares A, Lima C, Gomes T, Zhang Y, Liang Y. MSBN-SPose: A Multi-Scale Bayesian Neuro-Symbolic Approach for Sitting Posture Recognition. Electronics. 2025; 14(19):3889. https://doi.org/10.3390/electronics14193889
Chicago/Turabian StyleWang, Shu, Adriano Tavares, Carlos Lima, Tiago Gomes, Yicong Zhang, and Yanchun Liang. 2025. "MSBN-SPose: A Multi-Scale Bayesian Neuro-Symbolic Approach for Sitting Posture Recognition" Electronics 14, no. 19: 3889. https://doi.org/10.3390/electronics14193889
APA StyleWang, S., Tavares, A., Lima, C., Gomes, T., Zhang, Y., & Liang, Y. (2025). MSBN-SPose: A Multi-Scale Bayesian Neuro-Symbolic Approach for Sitting Posture Recognition. Electronics, 14(19), 3889. https://doi.org/10.3390/electronics14193889






