Surrogate-Assisted Evolutionary Multi-Objective Antenna Design

Abstract

This paper presents a multi-problem surrogate-assisted evolutionary multi-objective optimization approach for antenna design. By transforming the traditional antenna design optimization problem into expensive multi-objective optimization problems, this method employs a multi-problem surrogate (MPS) model to stack multiple antenna design problems. The MPS model is a knowledge-transfer framework that stacks multiple surrogate models (e.g., Gaussian Processes) trained on related antenna design problems (e.g., Yagi–Uda antennas with varying director configurations) to accelerate optimization. The parameters of Yagi–Uda antenna including radiation patterns and beamwidth—across various director configurations are considered as decision variables. The several surrogates are constructed based on the number of directors of Yagi–Uda antenna. The MPS algorithm identifies promising candidate solutions using an expected improvement strategy and refines them through true function evaluations, effectively balancing exploration with computational cost. Compared to benchmark algorithms assessed by hypervolume, our approach demonstrated superior average performance while requiring fewer function evaluations.

1. Introduction

In recent years, evolutionary algorithms (EAs) have found broad applications in antenna synthesis and design optimization [1]. Antenna design typically involves complex and challenging constrained optimization problems to meet specific performance metrics, such as the voltage standing wave ratio (VSWR) [2], gain [3], directional diagram [4], axial ratio [5], bandwidth [6], radiation pattern control [7], and size constraints [8]. For antenna arrays, it is necessary to generate beam patterns with desired beamwidths while maintaining a constrained peak sidelobe level. Moreover, antenna performance must be validated through electromagnetic (EM) simulations, where the computational cost grows exponentially with structural complexity. Given the high computational cost, complex multi-objective trade-offs, and resource-intensive iterative processes, antenna design is widely regarded as an expensive multi-objective optimization problem. Traditional design methods rely heavily on expert knowledge and are often -consuming and labor-intensive. EAs have proven to be effective optimization tools in the field of electromagnetics [9,10,11], especially in antenna design, where they offer clear advantages: not only do they overcome the limitations of conventional approaches, but they also enable efficient parameter tuning in response to evolving design requirements.

As a key research direction in computational intelligence and complex systems, evolutionary algorithms offer significant advantages over traditional mathematical programming and gradient-based methods, particularly in solving black-box, nonlinear, and multimodal problems. In the antenna design domain, evolutionary strategies such as Genetic Algorithms (GAs) [12], Particle Swarm Optimization (PSO) [13], and Differential Evolution (DE) [14] have been widely applied to tasks such as geometry optimization, pattern shaping, and bandwidth enhancement, often outperforming traditional heuristic methods. Despite their strong global search capabilities, EAs face a fundamental challenge when applied to expensive multi-objective problems (eMOPs): the high cost of fitness evaluations [15]. In EM simulation-driven optimization, a single structural evaluation can take from several minutes to hours, which limits both population size and iteration count during evolution [16,17].

To address this issue, researchers have proposed Surrogate-Assisted Evolutionary Algorithms (SA-EAs) in recent years. These approaches construct approximate models (surrogates) to replace the true objective functions, significantly reducing the number of actual simulations while maintaining convergence accuracy. Common surrogate models include Gaussian Processes (GPs), Support Vector Regression (SVR), Random Forests (RFs), and Neural Networks (NNs) [18,19,20], which aim to approximate the true objective function using existing data, enabling fast prediction in unexplored regions. In [21], Knowles introduced the ParEGO method, which scalarizes multi-objective optimization problems using an augmented Tchebycheff function and employs a GP model with an expected improvement (EI) criterion to guide the selection of evaluation points, thereby improving efficiency. Unlike this weighted aggregation strategy, Wang et al. selected candidate solutions based on hypervolume contribution, which performs well but incurs high computational costs in high-dimensional objective spaces [22]. Zhang et al. proposed MOEA/D-EGO [23], which decomposes the problem into sub-tasks, uses fuzzy clustering and GP modeling, and introduces an EI matrix that considers both diversity and density. However, most of these methods rely solely on the data from the current problem, ignoring transferable knowledge from related problems.

Most surrogate-assisted MOEAs focus only on the target problem and neglect useful information from other related source problems. Studies show that integrating EAs with cross-domain knowledge transfer—known as Transfer Evolutionary Multi-objective Optimization (TEMO) [24,25,26]—can improve optimization efficiency and effectiveness. In [27], Jiang et al. proposed a transfer learning-based dynamic multi-objective EA (Tr-DMOEA), which uses the Pareto-optimal set from the previous stage as source knowledge to generate the initial population for the next stage, thereby accelerating convergence. To further enhance efficiency, the HeMPS framework [28] constructs a large-scale surrogate model library, aligns feature spaces across tasks using kernel methods, and introduces Adaptive k-fold Cross-Validation (AKCV) to balance modeling cost and prediction accuracy. Similarly, the “Sparse Transfer Stacking” approach [29] incorporates L1 regularization to filter the most relevant source models, effectively mitigating the risk of negative transfer. This method also integrates the expected improvement (EI) criterion to enable cost-sensitive optimization in scenarios with non-uniform evaluation costs. In [30], the concurrent optimization of multiple multi-objective problems facilitated genetic information sharing, improving convergence speed and solution diversity. These studies suggest that knowledge transfer mechanisms under multi-task frameworks can accelerate optimization and open new pathways for solving problems in dynamic environments.

Current TEMO approaches demonstrate limited capability in effectively utilizing knowledge from source models, primarily handling only a small subset of available reference information. In practical applications, however, there exists substantial accumulated expertise derived from diverse design tasks—including both finalized projects and ongoing tasks—all of which could potentially enhance performance in specific objective optimization scenarios. Implementations such as pre-trained models in the fields of deep learning and parallel task execution frameworks in cloud computing have demonstrated practical effectiveness in knowledge transfer applications.

To address this, we integrate the Multi-Problem Surrogate-Assisted (MPS) algorithm into the expensive antenna design problem and propose an evolutionary algorithm for multi-problem surrogate-assisted antenna design. For high-cost simulation tasks, this approach uses historical data from source problems along with limited real evaluations on the target problem to collaboratively construct cross-problem surrogate models. The goal is to achieve high-accuracy, low-cost, and generalizable antenna optimization. Building on this concept, our study proposes a novel methodology that integrates multi-problem surrogate modeling, evolutionary strategies, and electromagnetic simulation feedback. The method is tailored to address the computational bottlenecks and engineering challenges present in modern antenna design. The contributions of this paper are two-fold: (1) Multi-Problem Surrogate Framework: Develops a novel meta-regression model that intelligently combines multiple surrogate models, enabling effective knowledge transfer across related optimization problems while preventing negative transfer through adaptive weighting. (2) Computationally Efficient Optimization: Achieves superior performance with fewer evaluations than benchmarks by integrating expected improvement with evolutionary search, significantly reducing simulation costs.

The rest of the study is structured as follows. Section 2 first introduces the modeling process of converting antenna design into a multi-objective problem, and then elaborates on the multi-problem surrogate model. Section 3 details the proposed MPS, including its overall framework, specific components, and parameter settings. Section 4 reports and analyzes the comprehensive experimental results. Section 5 summarises the full paper and provides an outlook on future research directions.

2. Background and Motivation

This section describes the Yagi antenna design by using an anonymous function together with the bounds and the options structure. Then the multi-problem surrogates are introduced in detail.

2.1. Yagi Antenna Design

The Yagi antenna investigated in this work consists of a driven element, a reflector, and multiple directors [31]. Its performance primarily depends on the lengths and spacings of these metallic elements. To facilitate parametric modeling and optimization, the antenna geometry is abstracted into a decision variable vector denoted by $\mathbf{x}=[rl,rs,dl,ds]$, where $rl$ represents the length of the reflector, $rs$ denotes the spacing between the reflector and the driven element, and $ds$ is the spacing between the director elements. The decision vector $\mathbf{x}$, thus, fully defines the antenna geometry, making it possible to reconstruct the structure automatically within an electromagnetic simulation environment during the optimization process.

Before carrying out the optimization process, the initial guess of the radiation pattern was plotted in 3D. Simulation results revealed that this initial Yagi–Uda antenna did not exhibit enhanced directivity in the preferred direction, namely toward the zenith (elevation = 90°), indicating that it is a poorly designed radiator. Therefore, further optimization of the antenna structure is necessary to improve its performance.

To comprehensively assess the antenna’s performance within the desired frequency range, several key metrics are considered, including the maximum directivity $D_{\max }\left(f\right)$, the reflection coefficient $\Gamma \left(f\right)$, the front-to-back ratio $FB\left(f\right)$, and the mismatch loss $T\left(f\right)$. Among these metrics, $D_{\max }\left(f\right)$ serves as a direct measure of the antenna’s ability to radiate or receive energy in a desired direction, while $T\left(f\right)$ quantifies impedance matching performance, which strongly influences signal transmission efficiency. According to established research in antenna performance optimization [32], these two factors are typically the most critical for evaluating and improving overall antenna behavior.

Considering the limited effectiveness and convergence of multi-objective optimization algorithms in high-dimensional objective spaces, we selected $D_{\max }\left(f\right)$ and $T\left(f\right)$ as the primary objective functions, as they capture the essential trade-off between radiation performance and power efficiency. Other performance-related factors, including $FB\left(f\right)$ and $\Gamma \left(f\right)$, though also important, are incorporated as constraint functions to ensure engineering feasibility while maintaining optimization tractability.

In the following, we present the mathematical formulations of the performance metrics, constraint penalties, and the overall objective function used in our optimization framework. The mismatch loss is calculated from the reflection coefficient as

$$T\left(f\right)=10{log}_{10}{(1-|\Gamma \left(f\right)|}^2)$$

(1)

where $T\left(f\right)$ denotes the mismatch loss (in decibels, dB), and $\Gamma \left(f\right)$ represents the reflection coefficient at frequency f.

Since the Yagi antenna needs to maintain satisfactory performance across the bandwidth, these metrics are evaluated at the center frequency $f_c$ as well as at the bandwidth edge frequencies  

$$\begin{array}{c}\hfill f_{min}=f_c-{\displaystyle \frac{B}{2}},f_{max}=f_c+{\displaystyle \frac{B}{2}},\end{array}$$

(2)

where B denotes the bandwidth over which the antenna performance is specified. We define the frequency set as $\mathcal{F}=\{f_{min},f_c,f_{max}\}$. At each frequency point, the composite gain is defined as  

$$\begin{array}{c}\hfill G\left(f\right)=D_{\max }\left(f\right)+T\left(f\right),\end{array}$$

(3)

which integrates both the directivity and the mismatch effects.

To ensure the designed antenna meets practical engineering requirements, several performance constraints are introduced. Firstly, a gain constraint enforces that $G\left(f\right)\ge G_{min}$. If this requirement is not met, a penalty term is added as

$$\begin{array}{c}\hfill P_{gain}=\sum _{f\in \mathcal{F}}max(0,G_{min}-G\left(f\right)).\end{array}$$

(4)

Secondly, to guarantee gain flatness across the band, a deviation constraint is imposed such that $|G\left(f\right)-G_{min}|\le \Delta G$, with the corresponding penalty expressed as

$$\begin{array}{c}\hfill P_{dev}={\displaystyle \frac{1}{3}}\sum _{f\in \mathcal{F}}max(0,|G\left(f\right)-G_{min}|-\Delta G).\end{array}$$

(5)

Additionally, to ensure adequate directional properties, the front-to-back ratio is required to satisfy $FB\left(f\right)\ge F{B}_{min}$, yielding the penalty

$$\begin{array}{c}\hfill P_{F/B}={\displaystyle \frac{1}{3}}\sum _{f\in \mathcal{F}}max(0,F{B}_{min}-FB\left(f\right)).\end{array}$$

(6)

Finally, for impedance matching, the reflection coefficient is constrained at the center frequency as $\Gamma \left(f_c\right)\le {\Gamma }^{\max }$, resulting in the penalty

$$\begin{array}{c}\hfill P_{\Gamma }=max(0,\Gamma \left(f_c\right)-{\Gamma }^{\max }).\end{array}$$

(7)

By integrating the above performance metrics and constraint penalties, the antenna optimization problem is formulated as a single-objective minimization problem. The objective function is defined as

$$\begin{array}{c}\hfill minf\left(\mathbf{x}\right)=-G\left(f_c\right)+K·P\left(\mathbf{x}\right),\end{array}$$

(8)

where K is a large penalty factor employed to heavily penalize designs that violate the constraints. The overall penalty function $P\left(\mathbf{x}\right)$ is given by

$$\begin{array}{c}\hfill P\left(\mathbf{x}\right)=max(0,P_{gain}+P_{dev}+P_{F/B}+P_{\Gamma }).\end{array}$$

(9)

This modeling approach enables the optimization process to simultaneously pursue high gain at the center frequency while effectively controlling in-band performance flatness, front-to-back ratio, and impedance matching, thereby achieving a balanced and practically viable antenna design.

2.2. Multi-Problem Surrogates

Traditionally, the development of surrogate model techniques has mainly focused on approximating a single expensive objective function or constraint function. However, many engineering and scientific applications actually involve multiple interrelated problems. To effectively handle such situations, the concept of multi-problem surrogates (MPS) has emerged, aiming to simultaneously approximate several related problems by exploiting their shared information.

Recently, combining multi-problem surrogate strategies with evolutionary algorithms has attracted widespread attention. Studies have shown that there exists useful knowledge from other problems, which can be transferred to assist in optimizing the current problem [24]. This involves extracting valuable information to optimize the target multi-objective optimization (MOO) problem of interest. This approach is known as transfer evolutionary multi-objective optimization (TEMO), which can be categorized into problem-based transfer, model-based transfer, and feature-based transfer [33].

Since single-objective problems may have significant similarity with the given MOO problems, in [34], useful features are extracted from single-objective problems to enhance the solving capability for the considered MOO problem. In [35], positive prior knowledge is transferred into existing MOEAs via probabilistic models, thereby accelerating search convergence. Zou et al. extracted stable features from past community structures [36], preserving valuable characteristic information. These features were then transferred into the current optimization process to improve EAs. Meanwhile, in [37], Jiang et al. proposed a novel individual-based transfer learning approach, which combines a pre-search strategy to identify high-quality individuals with improved diversity, effectively mitigating negative transfer caused by individual clustering.

In recent years, Alan et al. proposed a TEMO multi-problem surrogate (MPS) algorithm that extracts useful information from source surrogate models and transfers it to optimize the target problem [38]. Overall, the relevant literature highlights that multi-problem surrogate strategies can significantly reduce computational burdens and improve predictive robustness by leveraging multiple data sources and the correlations among optimization objectives.

3. Methodology

In this section, the multiobjective antenna design optimization problem is defined first. Then, the general framework of the MPS algorithm is introduced. Finally, the components of the algorithm tailored for multi-objective antenna design optimization and their computational details are discussed.

3.1. Multiobjective Antenna Design

The Yagi–Uda antenna consists of a driven half-wavelength dipole, a reflector behind it, and directors in front. The reflector length $rl$ shapes current distribution, enhancing back lobe suppression and the front-to-back ratio. The spacing $rs$ between the driven element and reflector governs interference, reducing backward radiation. The director length $dl$ sets resonance and coupling, impacting gain and frequency response, while spacing $ds$ between directors and to the driven element controls main lobe formation and impedance. Optimizing $[rl,rs,dl,ds]$ enables precise tailoring of the radiation pattern, gain, bandwidth, and matching, thus, meeting specific antenna performance requirements. As described in Section 2, the Yagi antenna design can be modeled as a constrained multiobjective optimization problem, which is defined as:

$$\begin{array}{cc}\hfill & min{\{D_{\max }\left(f\right),T\left(f\right)\}}^T\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& P_{gain}<0,P_{dev}<0,P_{F/B}<0,P_{\Gamma }<0,\hfill \end{array}$$

(10)

where $T\left(f\right)=10{log}_{10}{(1-|\Gamma \left(f\right)|}^2)$, $\Gamma \left(f\right)$ is the reflection coefficient. The design parameter vector $x=[rl,rs,dl,ds]$ includes the reflector length $rl$, the distance between the driven element and the reflector $rs$ (reflector spacing), the director length $dl$, and the spacing $ds$ between director elements as well as between the driven element and the nearest director. These parameters are subject to practical constraints, which collectively define the feasible design space $\mathcal{X}=[r{l}_{min},r{l}_{max}]\times [r{s}_{min},r{s}_{max}]\times [d{l}_{min},d{l}_{max}]\times [d{s}_{min},d{s}_{max}]$.

3.2. General Framework of MPS

The construction method of the MPS model is outlined in Algorithm 1, and its detailed process is described below. To alleviate the high computational cost associated with evaluating the objective functions through electromagnetic simulations or measurements, the multi-problem surrogate-assisted algorithm is employed in this work. By surrogate models trained on related tasks, cross-domain knowledge is effectively transferred and rapid performance estimates are provided.

Algorithm 1 MPS model construction

Require: Source model set $S=\{S_1,S_2,\dots ,S_{n_s}\}$, training set $D=\{X,y\}$, training size $n_D$ Ensure: MPS model ${\mathcal{M}}_{\mathrm{MPS}}$       1: Train target surrogate model ${\mathcal{M}}_T$ using D, and record hyperparameters $\mathit{\theta }$       2: for each $i=1$ to $n_D$ do       3:     Construct a new dataset $D_i=D-\{x_i,y_i\}$       4:     Train a temporary Gaussian Process model ${\mathcal{M}}_i$ on $D_i$       5:     Input $X_i$ into ${\mathcal{M}}_i$ to obtain the predicted target value ${\widehat{y}}_T^{\left(i\right)}$       6: end for       7: Input $x_i$ into each source model to obtain corresponding source features ${\mathit{y}}_{S1},{\mathit{y}}_{S2},\dots ,{\mathit{y}}_{Sn}$       8: Construct a regression model using Equation (14)       9: Combine source and target models through linear regression coefficients to form the final MPS model ${\mathcal{M}}_{\mathrm{MPS}}^S$

We first record all antenna optimization solutions and their function values in a database $\mathcal{D}=\{\mathit{X},\mathit{y}\}$. The database consists of values and their corresponding function values. Once a new evaluation is available, its exact function value will be stored in the database. From the pre-trained large-scale source model pool $\mathcal{S}=\{S_1,S_2,\cdots ,S_{n_{\mathcal{S}}}\}$, we aggregate population $P_{\mathrm{eval}}$ using a randomly selected weight vector ${\mathit{w}}^{\left(i\right)}$ where ${\mathit{w}}^{\left(i\right)}, i=1,2,\cdots ,m$, with m being the number of selected models.

The transfer of the evolutionary multi-objective optimization framework with MPS in a large-scale source surrogate setting is illustrated in Figure 1. MPS algorithm starts by initializing the population, then iteratively aggregates values using random weight vectors, selects a source surrogate set and build a MPS model, performs evolutionary optimization to determine and evaluates next candidate points, validates it with function value and repeats until termination conditions are met.

3.3. Multi-Problem Surrogate Algorithm for Multi-Objective Antenna Design

Multi-problem surrogate refers to a model formed by stacking multiple source surrogate models together with a target surrogate model, collectively called the MPS model. By replacing EM simulations with these surrogate models, the computational cost of antenna design evaluation is significantly reduced. This structure enables effective knowledge transfer from source surrogate models to the target surrogate model. Given a training dataset consisting of n input-output pairs: $\{(x^i,y^i)\mid i=1,2,\dots ,n\}$, where $x^i$ denotes the i-th row of the input matrix $X\in {\mathbb{R}}^{n\times d}$ representing antenna parameters, and $y^i$ is the corresponding value in the output vector y representing evaluation result. Let $x^{*}$ be an unknown input, then the predictive distribution is defined as:

$$\begin{array}{cc}\hfill \widehat{y}\left(x^{*}\right)& =A_{*}{(A+{\sigma }_n^{2}I)}^{-1}y,\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill {\widehat{\sigma }}^2\left(x^{*}\right)& =A_{\ast \ast }-A_{\ast }{(A+{\sigma }_n^{2}I)}^{-1}{A}_{*}^T,\hfill \end{array}$$

(12)

In this study, we use the Automatic Relevance Determination Squared Exponential (ARD-SE) covariance function, defined as:

$$\begin{array}{c}\hfill k(x^i,x^j)={\theta }_{f}exp\left(\sum _{D=1}^d{\displaystyle \frac{-{(x_D^i-x_D^j)}^2}{2{\theta }_D^2}}\right)\end{array}$$

(13)

where $x_D^i$ and $x_D^j$ are the values of the D-th dimension of the respective inputs; d is the total number of input dimensions; ${\theta }_f$ is the signal variance controlling the overall scale of the function; and ${\theta }_D$ is the characteristic length-scale associated with the D-th input dimension, controlling how sensitive the function is to variation along that dimension.

First, a set of source models is provided as input, denoted by $S=\{S_1,S_2,\dots ,S_{n_s}\}$. Before training begins, there are $n_D$ individuals that have already been evaluated by the true objective functions, forming the training dataset $D=\{X,y\}$, where X contains the values of the decision variables and y is the aggregated vector of all objective values. Prior to the main training phase, an initial Gaussian Process surrogate model $M_T$ for the target task is trained using the dataset D, and the hyperparameters $\mathit{\theta }$ used during training are recorded. The training process begins with a variant of the leave-one-out (LOO) cross-validation method to generate target feature vectors from $M_T$. Specifically, each data point in the training set is iteratively removed: for the i-th data pair, a temporary training set $D_i=D-\{X_i,y_i\}$ is constructed by excluding the i-th sample. Then, using $D_i$ and the previously recorded hyperparameters $\mathit{\theta }$, a temporary Gaussian Process model $M_i$ is trained. Once $M_i$ is obtained, the excluded data point $X_i$ is input into $M_i$ to obtain the i-th predicted value $y_T^{\left(i\right)}$ of the target vector, as is shown in Algorithm 2.

Algorithm 2 Surrogate-assisted

Require: $N_S$ source models Ensure: Nondominated solutions       1: Initialize the population P using the Latin hypercube sampling method.       2: Evaluate P.       3: while termination criterion is not satisfied do       4:    Aggregation: Obtain y by an appropriate aggregation method with a randomly sampled weight vector.       5:    Establish the target training set $\mathcal{D}=(X,y)$.       6:    MPS Model Construction (see Algorithm 1): Obtain the mixture coefficients $\alpha$ by solving the optimization problem (14) according to Algorithm 1.       7:    Evolutionary Search: Genetic operators are employed to generate the offspring O based on the parents P.       8:    while the number of cheap evaluations is not exceeded do       9:        $\%N_O$ is the size of O.     10:        for $i=1$ to $N_O$ do     11:            Calculate the prediction ${\widehat{y}}_T\left(x_i^{*}\right)$ by the target surrogate model.     12:            for $j=1$ to $N_S$ do     13:                 Calculate the prediction ${\widehat{y}}_{S,j}\left(x_i^{*}\right)$ by the j-th source surrogate model.     14:            end for     15:            Calculate the prediction $\widehat{y}\left(x_i^{*}\right)$ and variance ${\widehat{\sigma }}^2\left(x^{*}\right)$ by Equations (11) and (12) based on the mixture coefficients $\alpha$, respectively.     16:        end for     17:        Evaluate the expected improvement of solutions based on Equation (16).     18:        Generate the next population based on the population O.     19:    end while     20: end while     21: Acquire the best evolved solution $x_{\mathrm{new}}$.     22: Obtain $y_{\mathrm{new}}$ of solution $x_{\mathrm{new}}$ by the expensive function.     23: Update datasets: $\mathcal{D}=\mathcal{D}\cup (x_{\mathrm{new}},y_{\mathrm{new}})$.

After traversing all the training data, the final target feature predictions $y_T$ are obtained. Next, the source models and the target model are stacked together using meta-regression coefficients to construct the final MPS model $M_{\mathrm{MPS}}$. Specifically, each input X is fed into every source model to obtain the corresponding source features: $y_{S_1},y_{S_2},\dots ,y_{S_{n_s}}$ Then, the meta-regression coefficients are obtained by minimizing the following optimization problem:

$$\begin{array}{cc}\hfill \underset{\mathit{\alpha }}{min}E\left(\mathit{\alpha }\right)& =\sum _{i=1}^{n_D}{\left(\sum _{j=1}^{n_S}{\alpha }_{S,j}{y}_{S,j}^{\left(i\right)}+{\alpha }_T{y}_T^{\left(i\right)}-y^{\left(i\right)}\right)}^2,\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& \sum _{j=1}^{n_S}{\alpha }_{S,j}+{\alpha }_T=1,\hfill \\ \hfill & {\alpha }_{S,j}\ge 0,\mathrm{for}j=1,\dots ,n_S,\hfill \\ \hfill & {\alpha }_T\ge 0\hfill \end{array}$$

(14)

Let $\mathit{\alpha }=\{{\alpha }_{S,1},{\alpha }_{S,2},\dots ,{\alpha }_{S,n_s},{\alpha }_T\}$ denote the set of meta-regression coefficients. Here, $y_T^{\left(i\right)}$ represents the predicted value corresponding to the input $X^{\left(i\right)}$, and ${\alpha }_T$ is the weight assigned to the target surrogate model. After obtaining all the meta-regression coefficients, the final MPS model is constructed using the stacking formulation in Equation (5):

$${\mathcal{M}}_{\mathrm{MPS}}=y\left(X^{\prime }\right)=\sum _{j=1}^{n_s}{\alpha }_{S,j}{y}_{S,j}\left(X^{\prime }\right)+{\alpha }_T{y}_T\left(X^{\prime }\right)$$

(15)

To optimize the coefficients in surrogate model stacking, we incorporate evolutionary algorithms for the search process, as outlined in Algorithm 2. Firstly, The process starts with the initialization of a population P using the Latin hypercube sampling method to ensure a well-distributed sampling across the search space. This population is then evaluated by the true expensive objectives. In each generation, an aggregation method with a randomly sampled weight vector transforms the multi-objective optimization problem into a scalar optimization task, establishing a target training set $\mathcal{D}=(X,y)$. Subsequently, the MPS model construction Algorithm 1 is employed to derive optimal mixture coefficients $\alpha$ by solving the optimization problem formulated in Equation (14), effectively combining information from the $N_S$ source surrogate models and the target surrogate.

The evolutionary search is conducted using standard genetic operators to generate offspring O from the current population P. To reduce expensive evaluations, a surrogate-assisted selection mechanism is adopted wherein offspring are assessed using the constructed ensemble surrogate. Specifically, for each individual in O, predictions are generated by the target surrogate model and all source surrogate models. These predictions are fused according to the mixture coefficients $\alpha$ to compute the final predicted values and associated variances, as defined in Equations (11) and (12). The expected improvement is then evaluated for these solutions to guide the generation of the next population.

This process iterates until a pre-specified budget of inexpensive surrogate evaluations is reached. During each iteration, the surrogate-assisted search generates a set of offspring solutions, whose objective values and prediction uncertainties are estimated using the multi-problem surrogate model. For each candidate solution $x_i^{*}$, the predictive mean $\widehat{y}\left(x_i^{*}\right)$ and variance ${\widehat{\sigma }}^2\left(x_i^{*}\right)$ are computed according to Equation (11) and Equation (12), respectively. These are then used to evaluate the expected improvement (EI) criterion defined in Equation (16), which quantifies the potential benefit of sampling a candidate in terms of improvement over the current best-known solutions. The candidate with the highest EI score is selected as the most promising solution, denoted by $x_{\mathrm{new}}$. This solution is subsequently evaluated using the true expensive objective functions to obtain its actual performance $y_{\mathrm{new}}$. The dataset $\mathcal{D}$ is updated with this new observation, thereby enabling iterative refinement of the surrogate model. Through this mechanism, the proposed framework maintains an effective balance between exploration and exploitation under a limited evaluation budget, ultimately producing high-quality nondominated solutions.

4. Experimental Study

In this section, the antenna element model and partial parameter configurations are first introduced. Subsequently, the optimization objectives, optimization tools, and platform are presented. Finally, the performance of the proposed MPS method and other optimization algorithms is provided under varying numbers of directors, along with a comparative analysis.

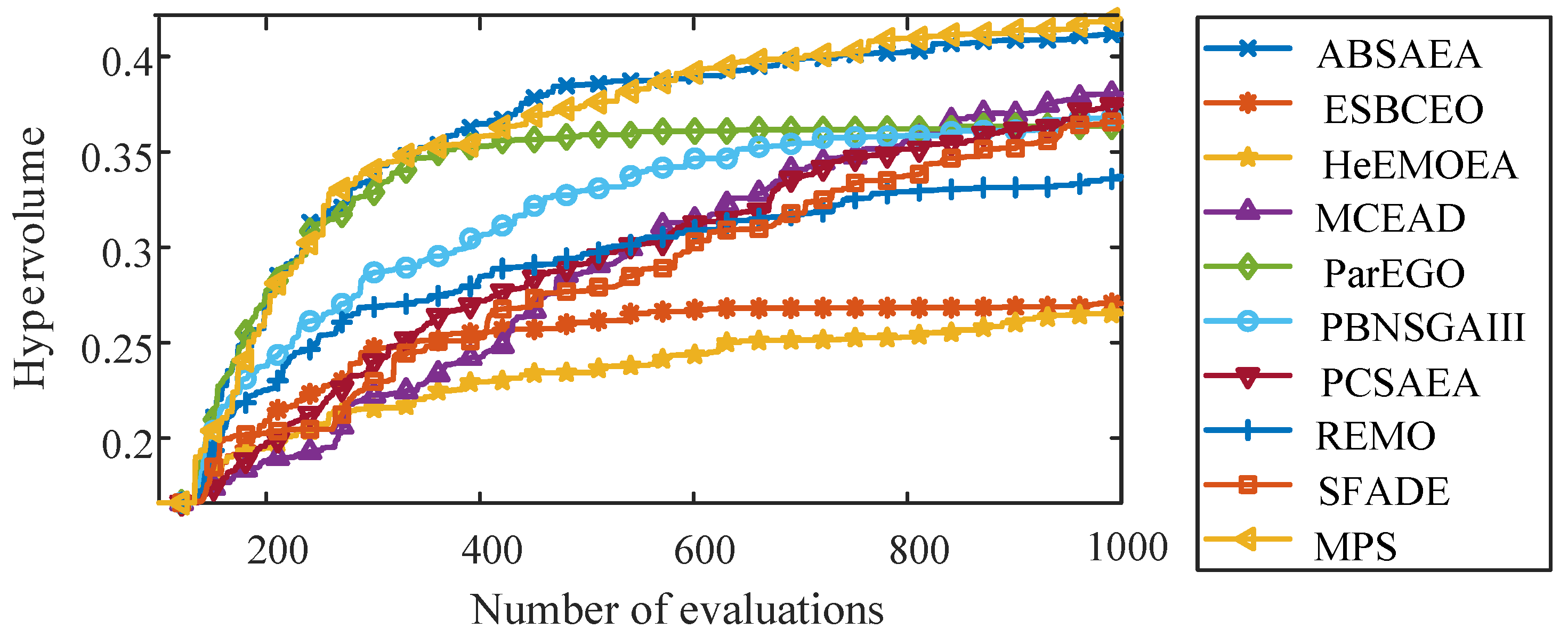
4.1. Experimental Settings

The Yagi–Uda antenna is an end-fire radiating structure comprising a driven dipole element, a passive reflector, and multiple passive directors arranged collinearly. The passive elements function as reflectors and directors, with their nomenclature determined by their spatial relationship to the driven element. The reflector dipole positions are placed behind the driven element to suppress the rearward radiation lobes, whereas the director dipoles are arranged ahead of the driven element to reinforce forward beam formation. Figure 2a displays a Yagi antenna model simulated by MATLAB R2023a, where elements with positive Z-axis coordinates operate as directors and those with negative Z-axis coordinates serve as reflectors. The product of Yagi–Uda antenna based on the simulation results is shown in Figure 2b.

Table 1. Main design parameters of antenna.

Parameter	Value	Parameter	Range
Frequency	165 MHz	RefLengthBounds	$[0.4,0.6]\times \lambda$
$Z_0$	300 $\Omega$	DirLengthBounds	$[0.35,0.5]\times \lambda$
BandWidth	8.25 MHz	RefSpacingBounds	$[0.05,0.3]\times \lambda$
$\lambda$	1.82 m	DirSpacingBounds	$[0.05,0.23]\times \lambda$

lists the main design parameters for the Yagi–Uda antenna. The left column displays the fixed parameters, while the right column shows the optimized parameters. Since a folded dipole is employed as the feed, the input impedance of the antenna is 300 $\Omega$. For Yagi–Uda antenna optimization, adjusting the physical dimensions and configuration represents the most practical and cost-effective approach. Thus, five parameters intrinsically linked to the physical structure are selected for optimization: the number of directors, the length and spacing of the reflector, and the length and spacing of the directors. The defined objective function aims to maximize the radiation pattern value at $90°$, minimize it at $270°$, and achieve a high peak power within the angular bounds of the elevation beamwidth.

In this study, we used the Antenna Toolbox in Matlab to carry out simulation experiments using a Yagi–Uda antenna [39,40]. The toolbox provides a comprehensive suite of functions and applications for designing, analyzing, and visualizing antenna elements and arrays. The toolbox enables the design of standalone antennas and the construction of antenna arrays. The Antenna Toolbox employs electromagnetic solvers, including the Method of Moments (MoM), to calculate critical electromagnetic parameters such as impedance, current distribution, radiation efficiency, near-field radiation patterns, and far-field radiation patterns. In addition, the toolbox integrates optimization algorithms to systematically refine antenna design parameters, thus enhancing operational performance through iterative computational adjustments.

4.2. Experimental Analysis

A multi-parent surrogate-assisted multi-objective optimization algorithm was applied to optimize the performance of the Yagi–Uda antenna. For comparison, several commonly used optimization algorithms were evaluated, including ABSAEA [22], ESBCEO [41], HeEMOEA [42], MCEAD [43], ParEGO, PBNSGAIII [44], PCSAEA [45], REMO [46], and SFADE [47], as illustrated in the accompanying figure.

Table 2. Comparison between MPS and other optimization algorithms across different evaluation budgets under the four directors circumstance.

Number of Evaluations Reference	Metric [22]	A1	A2	A3	A4	A5	A6	A7	A8	A9	MPS (Ours)
150	Avg.	0.2103	0.1931	0.2126	0.1976	0.2204	0.2131	0.1716	0.1912	0.1917	0.2268
	Var.	0.0214	0.0110	0.0150	0.0191	0.0269	0.0326	0.0071	0.0120	0.0235	0.2114
300	Avg.	0.3041	0.2210	0.2262	0.2351	0.3078	0.3003	0.2191	0.2547	0.2282	0.2997
	Var.	0.0449	0.0224	0.0153	0.0267	0.0194	0.0204	0.0249	0.0389	0.0365	0.0585
500	Avg.	0.3407	0.2281	0.2416	0.2930	0.3116	0.3292	0.2600	0.3063	0.2810	0.3626
	Var.	0.0421	0.0213	0.0175	0.0288	0.0193	0.0207	0.0266	0.0377	0.0350	0.0387
1000	Avg.	0.3699	0.2393	0.2699	0.3872	0.3176	0.3637	0.3394	0.3533	0.3709	0.4125
	Var.	0.0377	0.0214	0.0237	0.0187	0.0192	0.0129	0.0382	0.0344	0.0461	0.0226

A1–A9 represent the baseline optimization algorithms: ABSAEA, ESBCEO, HeEMOEA, MCEAD, ParEGO, PBNSGAIII, PCSAEA, REMO, and SFADE, respectively. MPS (ours) denotes our proposed method.

,

Table 3. Comparison between MPS and other optimization algorithms across different evaluation budgets under the five directors circumstance.

Number of Evaluations Reference	Metric [22]	A1	A2	A3	A4	A5	A6	A7	A8	A9	MPS (Ours)
150	Avg.	0.2108	0.1795	0.1838	0.1730	0.2091	0.2037	0.1739	0.1931	0.1831	0.2038
	Var.	0.0291	0.0110	0.0131	0.0070	0.0261	0.0345	0.0110	0.0159	0.0177	0.0135
300	Avg.	0.3356	0.2471	0.2153	0.2224	0.3288	0.2863	0.2396	0.2685	0.2296	0.3402
	Var.	0.0409	0.0265	0.0257	0.0329	0.0376	0.0316	0.0248	0.0270	0.0429	0.0605
500	Avg.	0.3853	0.2606	0.2342	0.2869	0.3589	0.3297	0.2913	0.2966	0.2771	0.3755
	Var.	0.0451	0.0271	0.0307	0.0517	0.0360	0.0203	0.0241	0.0162	0.0423	0.0552
1000	Avg.	0.4115	0.2705	0.2652	0.3804	0.3634	0.3676	0.3746	0.3370	0.3656	0.4197
	Var.	0.0518	0.0228	0.0312	0.0398	0.0321	0.0273	0.0374	0.0336	0.0418	0.0426

A1–A9 represent the baseline optimization algorithms: ABSAEA, ESBCEO, HeEMOEA, MCEAD, ParEGO, PBNSGAIII, PCSAEA, REMO, and SFADE, respectively. MPS (ours) denotes our proposed method.

and

Table 4. Comparison between MPS and other optimization algorithms across different evaluation budgets under the six directors circumstance.

Number of Evaluations Reference	Metric [22]	A1	A2	A3	A4	A5	A6	A7	A8	A9	MPS (Ours)
150	Avg.	0.2336	0.2028	0.2134	0.1895	0.2264	0.2022	0.1943	0.2107	0.2013	0.2538
	Var.	0.0189	0.0184	0.0115	0.0137	0.0157	0.0133	0.0097	0.0099	0.0147	0.0282
300	Avg.	0.3138	0.2523	0.2227	0.2254	0.3057	0.2491	0.2255	0.2655	0.2107	0.3300
	Var.	0.0242	0.0584	0.0132	0.0222	0.0311	0.0260	0.0155	0.0196	0.0142	0.0188
500	Avg.	0.3552	0.2807	0.2382	0.2763	0.3221	0.3213	0.2855	0.2959	0.2520	0.3801
	Var.	0.0146	0.0480	0.0165	0.0259	0.0347	0.0312	0.0171	0.0465	0.0346	0.0250
1000	Avg.	0.3923	0.2962	0.2592	0.3695	0.3309	0.3650	0.3508	0.3388	0.3355	0.4151
	Var.	0.0210	0.0447	0.0224	0.0387	0.0369	0.0257	0.0199	0.0413	0.0528	0.0224

A1–A9 represent the baseline optimization algorithms: ABSAEA, ESBCEO, HeEMOEA, MCEAD, ParEGO, PBNSGAIII, PCSAEA, REMO, and SFADE, respectively. MPS (ours) denotes our proposed method.

present a comparative analysis between the MPS method and nine alternative approaches, evaluating three director configurations (four, five, and six directors) under varying evaluation budgets. Statistical comparison results from systematic computation of mean values and variances in optimization trials. Figure 3, Figure 4 and Figure 5 quantitatively visualize the hypervolume (HV) metric distributions corresponding to these parametric conditions in the table. HV is a performance indicator that measures the hypervolume covered by the approximate front, and is widely used in MOO problems. The larger the HV value, the better the diversity and comprehensiveness of the approximate front. The specific calculation formula is as follows:

$$\begin{array}{c}\hfill HV=V\left(T\right)-\sum _{i=1}^m{\int }_{T_i}{f}_{\mathrm{i}}\left(x\right)dx,\end{array}$$

(16)

where V(T) represents the hypervolume, T represents the approximate front, m represents the number of objectives, $T_i$ represents the region formed by the line segment from the minimum value of the i-th objective to the i-th point on the approximate front, and $f_i\left(x\right)$ represents the function value of the i-th objective at point x.

The data in the analysis table show that the mean value of MPS under different evaluation times is significantly higher than that of other algorithms, and the variance is lower or close to that of other algorithms in most cases, indicating that the MPS achieves stronger optimization performance on the premise of maintaining good optimization stability.

It can be seen from the Figure 3, Figure 4 and Figure 5 that our MPS method achieves satisfactory results in all cases. For example, in the four-director case, after more than 400 evaluations, it achieves better results than other comparison algorithms, which indicates that the MPS method has faster convergence speed than other methods. After 1000 evaluations, it achieves 6% improvement over the sub-optimal MCEAD algorithm and 23% improvement over the average of other algorithms.

In five-director configurations, the MPS method matches ABSAEA’s performance at 100–300 evaluations. ABSAEA temporarily outperforms MPS between 300–600 evaluations due to faster local convergence. However, MPS achieves superior hypervolume values at 1000 evaluations, demonstrating stronger global optimization capabilities. As the number of directors increases to six, the HV value of the MPS method is higher than that of other algorithms in all evaluations, which shows that the MPS method has more obvious performance advantages than other methods in this case.

The Comparison results between the MPS model and the baseline model in different training rounds are also provided in Figure 6, Figure 7 and Figure 8. Here, the baseline refers to a model that does not leverage knowledge acquired from previous rounds to accelerate training, representing a conventional surrogate model. Data analysis and visualization reveal that within the 200-to-1000-round interval, the MPS model achieves superior performance metrics (such as the median HV value) compared to the conventional surrogate model. This shows that knowledge transfer techniques significantly enhance the efficiency of convergence.

The results with the highest HV are provided in Figure 9. Therefore, MPS proposed in this paper is superior to existing methods in accelerating convergence (less evaluations to reach a better solution), avoiding local optima (higher HV value), and improving stability (lower variance), which verifies its efficiency and practicability in expensive multi-target antenna design problems.

5. Conclusions

This paper proposes an evolutionary multi-objective antenna design method based on multi-problem surrogate-assisted optimization. By constructing simulation models of antenna specification parameters, the antenna design problem is transformed into a computationally expensive multi-objective optimization problem. To improve the evaluations efficiency, surrogate models are built for the antenna simulation process. The proposed MPS model is applied to the simulation-based optimization of a Yagi–Uda antenna. Within 1000 evaluations, it achieves significant performance advantages over existing optimization algorithms and is capable of reaching high-quality solutions with fewer evaluations. Future work will explicitly extend this framework to other antenna types, building upon the validated Yagi-Uda implementation presented in this study.