Advanced Probabilistic Roadmap Path Planning with Adaptive Sampling and Smoothing

Abstract

Probabilistic roadmap (PRM) methods are widely used for robot navigation in both 2D and 3D environments; however, a major drawback is that the raw paths tend to be jagged. Executing a trajectory along such paths can lead to significant overshoots and tight turns, making it difficult to achieve a near-optimal solution under motion constraints. This paper presents an enhanced PRM-based path planning approach designed to improve path quality and computational efficiency. The method integrates advanced sampling strategies, adaptive neighbor selection with spatial data structures, and multi-stage path post-processing. In particular, shortcut smoothing and polynomial fitting are used to generate smoother trajectories suitable for motion-constrained robots. The proposed hybrid sampling scheme biases sample generation toward critical regions—near obstacles, in narrow passages, and between the start and goal—to improve graph connectivity in challenging areas. An adaptive k-d tree-based connection strategy then efficiently builds a roadmap using variable connection radii guided by PRM* theory. Once a path is found using an any-angle graph search, post-processing is applied to refine it. Unnecessary waypoints are removed via line-of-sight shortcuts, and the final trajectory is smoothed using a fitted polynomial curve. The resulting paths are shorter and exhibit gentler turns, making them more feasible for execution. In simulated complex scenarios, including narrow corridors and cluttered environments, the advanced PRM achieved a 100% success rate where standard PRM frequently failed. It also reduced calculation time to 30% and peak turning angle by up to 50% compared to conventional methods. The approach supports dynamic re-planning: when the environment changes, the roadmap is efficiently updated rather than rebuilt from scratch. Furthermore, the use of an adaptive k-d tree structure and incremental roadmap updates leads to an order-of-magnitude speedup in the connection phase. These improvements significantly increase the planner’s path quality, runtime performance, and reliability. Quantitative results are provided to substantiate the performance gains of the proposed method.

1. Introduction

One of the most commonly used approaches for path planning is sampling-based planning, which has become an important strategy due to its robustness and probabilistic guarantees. The PRM algorithm can be divided into two phases: offline and online [1]. During the offline phase, the classical PRM algorithm randomly generates points and then connects them with edges in such a way that the connections are collision-free, building a roadmap graph that captures the connectivity of the free space. Since this process is the most time-consuming, it should be executed as infrequently as possible. During the second, online phase, the roadmap is searched using a pathfinding algorithm (e.g., Dijkstra, A*, or Theta*) to find a path connecting the start and goal configurations. PRM is probabilistically complete (if a valid path exists, the probability that PRM will find it approaches 1 as the number of sampled waypoints increases). The separation into offline and online phases allows for reusing the same roadmap multiple times. Despite its probabilistic completeness, the PRM algorithm performance is limited in environments with complex topology or narrow passages, where uniform sampling often results in poor graph connectivity and inadequate coverage of critical regions. As a result, finding a valid path in complex environments requires a large number of samples, which, combined with the computational cost of graph construction and collision checking, can lead to execution times that are unsuitable for real-time applications. Moreover, even when a path is found, it often contains redundant waypoints or unnecessary edges, since the graph search will pick any valid sequence of connected nodes which may not be a smooth or have a short trajectory. For this reason, researchers have proposed various extensions to the PRM to improve sampling efficiency, roadmap connectivity, and path smoothness.

Over the past decades, numerous enhancements to the basic PRM have been proposed [2]. As noted in the survey by Choudhary [2], research efforts have concentrated on improving sampling efficiency, addressing the narrow passage problem, and reducing computational overhead. These surveys highlight that while PRM has been widely adopted across robotics applications, its effectiveness heavily depends on how sampling and connection strategies are designed. Therefore, building upon this body of work, this paper introduces several targeted improvements aimed at making PRM more suitable for complex and dynamic environments.

Specifically, the proposed method focuses on three key enhancements. (1) Intelligent Sampling: various strategies are implemented with the goal of generating a higher number of meaningful points, particularly near obstacles, in challenging regions, and in the vicinity of the start and goal positions. (2) Adaptive Connectivity: nearest-neighbor data structures (k-d trees) are employed to support adaptive neighbor linking between roadmap nodes. The method also utilizes efficient adaptive radius search to accelerate the connection phase even as the number of nodes grows. (3) Path Optimization and Smoothing: after a path is found on the roadmap, post-processing algorithms are applied to shorten and smooth it. This involves removing unnecessary waypoints and adjusting the path to better approximate an optimal trajectory, which is essential for practical execution, such as reducing travel time and enabling the robot to follow the path in accordance with its dynamics.

The next section reviews the relevant literature and foundational concepts (Section 2). Section 3 presents the proposed approach in detail, including the intelligent sampling strategy, adaptive neighbor selection, and the path smoothing and optimization techniques. Section 4 provides simulation results across various complex, pre-defined scenarios. The applied techniques are compared with a focus on the practical aspects of path planning. Section 5 discusses the results, highlighting both the advantages and limitations of the proposed method. Finally, Section 6 concludes the paper and identifies the techniques that had the most significant impact on the outcomes.

2. Background and Related Work

2.1. Probabilistic Roadmaps and Sampling Strategies

One of the earliest works on probabilistic roadmaps (PRMs) was the paper by Kavraki et al [1]. The algorithm’s strength lies in its probabilistic completeness and division into offline and online phases. However, further investigation reveals that the PRM algorithm struggles in environments with narrow passages [3]. This realization leads to the development of intelligent strategies to improve sample distribution in difficult areas.

One of the first approaches to improving sampling was Obstacle-based sampler to generate points around obstacles. Amato et al. [4] proposed methods that exploit obstacle geometry to guide the sampling process. Building upon this idea, the paper presents sampling strategies that leverage the structure of obstacles to generate points along narrow corridors, achieving better coverage with fewer samples compared to purely random sampling.

Boor et al. [5] presented a Gaussian sampler for PRM. This approach is motivated by the observation that the generated path is most often located between the start and goal points, and that the optimal path is most often located close to obstacles. Keeping the free points from many such pairs results in a set of samples densely covering the vicinity of obstacles. Based on this, it is possible to obtain a denser distribution of points in the vicinity of narrow passages.

Hsu et al. [6] proposed the bridge test, which is a dedicated method designed to generate samples in the vicinity of narrow passages. The idea is based on generating pairs of random points that lie in collision. Then, the midpoint between them is evaluated. If the midpoint is collision-free, this indicates that the point is located between two obstacles. This acts as a filter to generate points specifically inside narrow passages, which are precisely the difficult configurations that uniform or random sampling would rarely hit. The bridge test significantly increases the local sampling density around complex but possible to reach waypoints without the need to generate a large number of samples.

Machine learning has also been leveraged to enhance sampling in motion planning. Instead of relying on static methods, sampling strategies can be learned from data collected during successful motion plans in known environments. Ichter et al. [7] and Chen et al. [8] demonstrate that neural networks, such as Conditional Variational Autoencoders (CVAEs) and attention-based architectures, are capable of learning motion behavior in complex environments. Although the initial training phase takes longer than in traditional methods, the inference time for path generation is significantly reduced once the model is trained.

To address these challenges, including the risk of overfitting due to suboptimal hyperparameters or limited training data, a hybrid approach that combines artificial intelligence with classical planning offers a more balanced and robust solution.

2.2. Roadmap Connectivity and Nearest-Neighbor Selection

After obtaining a set of sample points for path construction, the next step in PRM is to determine how to connect these points. The most common approach is to use a graph-based representation. The most basic strategy connects each new sample to all available neighbors, without considering either distance or the number of neighbors. This results in a quadratic number of connections, making it impractical for larger datasets due to its $𝒪\left(n^2\right)$ complexity.

To address this, improvements have been proposed to reduce the computational cost. A common alternative is to connect each sample either to its k nearest neighbors (based on configuration space distance) or to all neighbors within a fixed radius r. The values of k or r significantly affect the quality of the generated path, particularly in terms of connectivity. These parameters can be selected experimentally, or based on indicators of terrain complexity if the environment is known. In more complex environments, a greater number of neighbors or a larger connection radius is typically required to ensure graph connectivity.

In the classic approach, implementing PRM* means that for each new sample, the algorithm computes all existing nodes within distance $r\left(n\right)$ and then proceeds with checking every candidate for collision, looking for a straight-line path in configuration space. This can be computationally heavy for large n, but it is possible to overcome this difficulty using spatial structures. In the proposed approach, a k-d tree structure is used to store node coordinates and query neighbors efficiently (in approximately $O(logn)$ time per query). The classic k-d tree structure is further extended to enable adaptive parameter selection. For smaller sample sizes n, a larger connection radius $r\left(n\right)$ is applied to increase the probability of achieving connectivity. As n increases, the radius is gradually reduced in accordance with the theoretical guarantees of PRM* [9]. In the proposed implementation, a k-d tree is used with a small fixed number of neighbors n and is further expanded based on the average distance between connected points.

Another extension found in the literature is the Lazy PRM approach (Bohlin and Kavraki [10]). In contrast to the classical PRM algorithm, Lazy PRM does not perform collision checking during graph construction. Instead, collision validation is performed directly during the path generation phase. If a collision is detected at that stage, the initially generated offline roadmap is updated by removing the corresponding connection between the affected nodes. Then, the entire path planning procedure is reinitiated. This process is repeated until a valid path is found or a disconnection between the start and goal is detected. The main advantage of this approach is faster offline roadmap generation, at the cost of slower performance during the online query phase. In static environments, the processing time decreases with the number of queries, gradually approaching the online query time of the classical PRM.

In a Lazy PRM, the roadmap is built by connecting nodes assuming all connections are valid, and only when a query uses an edge does the algorithm actually check if that edge is collision-free (if not, the edge is removed and the search continues). This can save a lot of unnecessary collision evaluations when many edges are never used. While the focus is on improving the roadmap quality rather than reducing collision checks, a minor lazy strategy was incorporated during the query. The graph is constructed fully; however, when searching for a path, priority is on checking shorter edges first and only verifying longer alternative edges if needed, which is similar in spirit to lazy evaluation. An important advantage of the Lazy PRM algorithm is that it does not compromise the quality of the resulting path compared to its classical counterpart.

There are also advanced methods to maintain a sparse roadmap without sacrificing path quality, such as Sparse Roadmap Spanners (SPARS) by Dobson and Bekris [11]. SPARS and its later variant, SPARS2, aim to maintain a sparse roadmap by minimizing the number of nodes and edges. A new node is added to the graph only if it improves the whole graph, such as improving path quality or providing additional coverage of the configuration space. To determine whether a node should be added, the algorithm evaluates it against three criteria: coverage, connectivity, and quality. A node is included in the roadmap if it satisfies at least one of these conditions. Although the process of adding nodes is slower compared to previously discussed methods, the information each node contributes allows for the construction of a much sparser roadmap, which effectively captures narrow passages and regions near obstacles.

2.3. Path Smoothing and Post-Processing

Paths generated from PRM roadmaps are typically suboptimal and may exhibit jaggedness, particularly in scenarios with a high density of sampled nodes, where redundant or unnecessarily sharp turns are more likely to occur. This is a consequence of the iterative nature of graph-based path planning algorithms such as A*, Theta*, and Dijkstra, which tend to follow the structure of the underlying graph rather than the true optimal path in continuous space. In practical application, a smoother path allow generating trajectories that are feasible for mobile robots or drones, due to their dynamic constraints.

One common approach to path shortening is the use of Los smoothing, which iteratively replaces intermediate segments with direct, collision-free connections between non-adjacent waypoints. The algorithm checks whether a direct connection exists between waypoints i and $i+2$. If there is a connection, the intermediate point $i+1$ is removed. By taking multiple random shortcuts along the path, most unnecessary detours can be eliminated, often resulting in a much shorter path comprising fewer, longer segments. Another benefit of the algorithm is that the smoothed path often lies farther from nearby obstacles, which facilitates the generation of safer trajectories that are less prone to potential collisions during execution.

Another approach is to fit a continuous curve (such as a B-spline or Bézier curve) through the waypoints. This can both shorten the path and ensure continuous curvature, which is beneficial for car-like robots or drones that have turning radius constraints. A practical application of Bézier curves was demonstrated in [12], with further related work discussed in [13]. In the presented implementation, shortcut operations are applied to reduce the number of waypoints, followed by polynomial interpolation to smooth the corners.

Smoothing is a step carried out after the main algorithm. It uses heuristic methods, which means it follows simple rules and may not always give the optimal path and it can potentially move the path closer to obstacles; however, the resulting path remains collision-free. As a result, the constructed path contains significantly fewer points, which reduces the computational cost. This becomes increasingly important, especially in the context of path smoothing. Smoothing as a refinement step does not affect the connectivity. The proposed approach includes path smoothing in the path generation pipeline to demonstrate that by combining a planner with post-processing, the end-to-end solution for the robot is substantially improved in quality.

2.4. Hybrid Sampling and Planner Fusion

Hybrid sampling strategies extend classical PRM methods by combining different sampling distributions or by fusing complementary planning paradigms. While traditional PRM approaches rely mainly on uniform random sampling [1], these methods often face difficulties in narrow passages or highly dynamic environments. To overcome these limitations, hybrid samplers integrate obstacle-based methods [4], Gaussian sampling [5], or bridge test strategies [6] with uniform exploration. This combination allows a more balanced coverage of the configuration space, improving the probability of discovering feasible connections in complex regions. More recent developments also incorporate learning-based samplers that bias the distribution toward promising areas, achieving faster convergence and better adaptation [7,8].

Hybridization can also be applied at the algorithmic level by fusing sampling-based methods with complementary planners. For example, PRM roadmaps can be combined with search-based algorithms such as D* [14] or dynamic schemes like DWA [15]. These hybrid approaches exploit the global connectivity of PRM while leveraging the adaptability of local planners to handle moving obstacles. Similarly, optimized PRM methods tailored for real-time environments [16] highlight the benefits of integrating roadmap exploration with reactive modules for dynamic replanning. The resulting systems demonstrate improvements in success rate, computational efficiency, and robustness compared to classical single-method approaches.

Overall, hybrid sampling and planner fusion provide a natural extension of the state of the art. By combining complementary strategies, they achieve better exploration–exploitation balance, ensure improved coverage in challenging spaces, and allow faster adaptation to environmental changes. These properties make hybrid solutions a promising avenue for future developments in sampling-based motion planning.

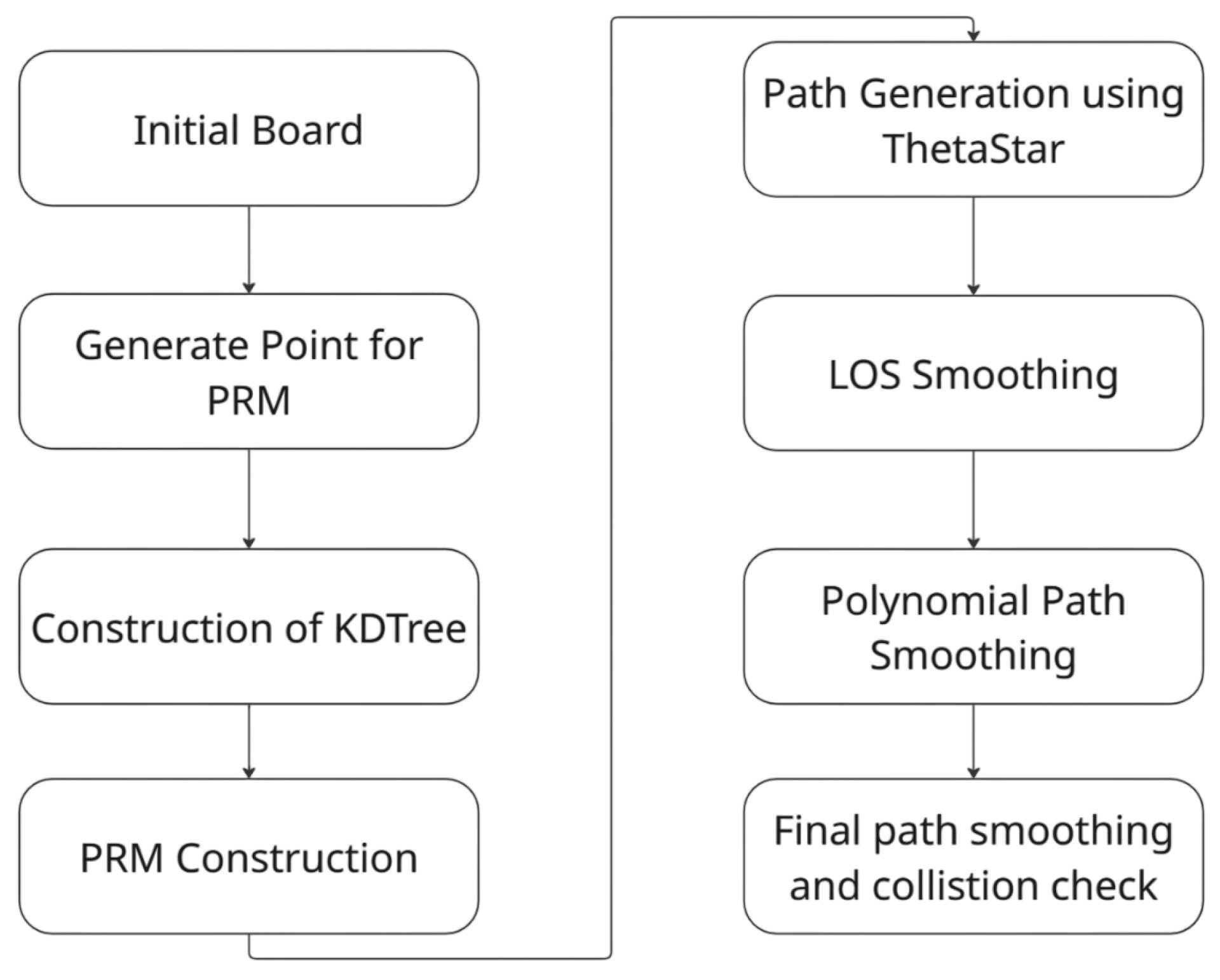
Figure 1 illustrates the overall pipeline of this paper’s approach, including the sampling enhancements, adaptive connection building, graph search, and post-processing stages.

The system presented in (Figure 1) consists of the following sequential steps:

• Initial Board: A 2D grid-based occupancy map is initialized, representing free space and obstacles.
• Generate Points for PRM: Adopting random, obstacle-aware and start goal-aware sampling strategies in roadmap design.
• Construction of k-d tree: A k-d tree structure with adaptive radius is built to support efficient nearest-neighbor queries.
• PRM Construction: Nodes are connected into a roadmap with collision-free edges.
• Path Generation using Theta*: A path is generated from the roadmap using the Theta* algorithm.
• LOS Smoothing: Shortcutting is performed using line-of-sight checks to eliminate unnecessary waypoints.
• Polynomial Path Smoothing: The path is smoothed using polynomial interpolation.
• Final Path Smoothing and Collision Check: The final path refinement to obtain the path ready for trajectory generation.

3. Proposed Approach: Advanced PRM Planning

The approach presented in this paper modifies a standard PRM in four main components: sampling, connection, path generation, and post-processing (smoothing). The workflow is outlined in Figure 1. The modifications applied will be described in detail in successive sections.

3.1. Sampling Strategy

A hybrid sampling strategy is used, which combines random sampling with targeted sampling techniques to focus on critical regions in particular, near obstacles and in narrow passages:

• Random Sampling: A portion of the samples is randomly generated, resulting in a higher density of points in wide, unobstructed regions. These points support the generation of paths that remain farther from unreachable areas, which leads to a path ready for trajectory generation.
• Obstacle-surface sampling: Based on OBPRM [4], a portion of samples is generated near obstacle boundaries. The algorithm operates as follows: a random point near an obstacle is selected, and a $2n+1\times 2n+1$ binary mask is centered at that location. If the center of the mask has a value of zero (indicating free space), and the sum of all mask elements is non-zero, the point is considered to be located near an obstacle. The selection of parameter n depends on the minimum allowable distance between the moving element and the obstacle. These points enable both the generation and shortening of paths near obstacles.
• Bridge test sampling: During the point generation process, an algorithm based on [6] was incorporated to increase point density in narrow passages. Bridge test point generation begins by randomly selecting pairs of points on obstacles, with a maximum allowed distance of d between them. Next, the points between the obstacles are evaluated using the Bresenham algorithm [17]. The principle of this algorithm is based on iterating between two points in a 2D grid. Its advantages include its high speed and ability to avoid skipping any grid cells. If any of the intermediate points between the obstacles are valid, they are added as bridge test sampling points.
• Gaussian sampling: This sampling algorithm is based on the observation that The most probable path lies between the start and goal points [5]. In the proposed implementation, the initial step consists of calculating the middlepoint and distance d between the start and goal. Next, the equation of the ellipse is defined in the following form: $x^2/a^2+y^2/b^2=1$. The values of parameters a and b are determined based on the previously computed distance, $a=d\ast a_d$ and $b=d\ast b_d$, where the parameters $a_d$ and $b_d$ were selected experimentally. After the equation of the ellipse is defined, points are generated at random distances along the ellipse. The density of points is higher near the line connecting the start and goal positions. This algorithm aims to enhance the connectivity of the roadmap and to generate samples with a higher probability of being included in the resulting path.
• Connectivity feedback sampling: After generating the samples using the aforementioned algorithms, an initial connection graph is constructed with a high number of neighbors. Next, the connectivity of all nodes in the graph is verified. If the graph is fully connected, the sampling process is completed. Otherwise, pairs of the closest nodes from disconnected subgraphs are identified. New points are then generated between these pairs, and if the addition of a point enables the expansion of the corresponding subgraphs, it is added to the sample set. The algorithm continues iteratively until all subgraphs are merged into a single connected graph.

The presented work implements all the listed algorithms. Moreover, it is possible to adjust both the proportion of samples generated by each method and the total number of samples. The sampling phase yields n, providing both connectivity and increased density in difficult regions.

For clarity, the complete logic of the hybrid sampling mechanism is presented in Algorithm 1. This approach probabilistically combines uniform, obstacle-based, bridge test, and informed sampling strategies, ensuring better coverage of narrow passages and cluttered areas.

Algorithm 1 Hybrid Sampling Strategy

1: $Samples\leftarrow \varnothing$   2: for $i=1$ to N do   3:     $r\leftarrow \mathrm{Random}(0,1)$   4:     if $r<p_{uniform}$ then   5:           $q\leftarrow \mathrm{SampleUniform}\left(\right)$   6:     else if $r<p_{uniform}+p_{obstacle}$ then   7:           $q\leftarrow \mathrm{SampleNearObstacles}\left(\right)$   8:     else if $r<p_{uniform}+p_{obstacle}+p_{bridge}$ then   9:           $q\leftarrow \mathrm{BridgeTestSample}\left(\right)$ 10:     else 11:           $q\leftarrow \mathrm{InformedSample}\left(\mathrm{goal}\right)$ 12:     end if 13:     if $\mathrm{collision}\_\mathrm{free}(q)$ then 14:           $Samples\leftarrow Samples\cup \left\{q\right\}$ 15:     end if 16: end for 17: return  $Samples$

3.2. Adaptive Neighbor Connections

The next step after generating the points is to construct a connection graph, which represents the feasible paths that the robot can follow. To construct the graph, it is necessary to perform collision checking between the nodes. Checking collisions between every pair of nodes has a computational complexity of $O\left(n^2\right)$, which, in practical implementations, results in high computational complexity. For this reason, the work proposes the use of an algorithm that reduces nearest-neighbor computations: k-nearest neighbor with structured data k-d tree. The computation complexity is $O\left(log\right(n+k\left)\right)$, where k is the desired number of neighbors.

The edge creation algorithm is performed in two stages. The first stage involves neighbor search based on the k-nearest neighbor algorithm using a k-d tree structure with a fixed, predefined number of neighbors. Next, the average distance between the node and its neighbors is computed. Based on this, the connection radius for the second iteration is determined using the k-nearest neighbor algorithm with a k-d tree structure. The theoretical foundation of this algorithm is described by [9]. Equation (1) specifies the lower bound on the connection radius necessary for the PRM algorithm to guarantee asymptotic optimality.

$$r\left(n\right)=\gamma {\left({\displaystyle \frac{logn}{n}}\right)}^{1/d}$$

(1)

where

• $r\left(n\right)$—connection radius used to link a newly added node to its neighbors in the roadmap after n samples have been drawn;
• $\gamma$—a constant factor that depends on the dimensionality and volume of the free space;
• n—the number of samples currently in the roadmap;
• d—the dimensionality of the configuration space. $\mathcal{X}$.

In this paper, the scaling factor $\gamma$ in Equation (1) is estimated empirically based on the observed average distance $\overline{r}$ to a fixed number of neighbors. The resulting expression is as follows:

$$\gamma ={\displaystyle \frac{\overline{r}}{{\left(\frac{logn}{n}\right)}^{1/d}}}$$

(2)

where

• $\gamma$—empirically estimated scaling factor used to compute the connection radius $r\left(n\right)$ in the PRM* algorithm;
• $\overline{r}$—average distance to the $\overline{k}$ nearest neighbors for all samples in the roadmap;
• n—current number of samples in the roadmap;
• d—dimensionality of the configuration space $\mathcal{X}$;
• $logn$—natural logarithm of the number of samples, which ensures that the radius shrinks asymptotically with growing n.

The result of this step is a connection graph constructed between the sampled points, which serves as the basis for path generation. Due to the applied radius selection strategy, the resulting graph maintains a similar number of connections in both narrow passages and open spaces.

To accelerate neighbor lookup, especially in large graphs, the neighbor sets are constructed using a k-d tree structure, which enables efficient range and nearest-neighbor queries in logarithmic time. This setup is particularly beneficial in sparsely connected regions, where direct adjacency is limited and search efficiency is critical.

3.3. Path Planning Methods

After the connection graph has been generated, the next step is to compute a path between the start and goal nodes. This step is based on selecting a combination of feasible edges, representing potential path segments, in such a way that the resulting path is as short as possible.

In this work, two classical graph search algorithms, A* and Theta*, are employed. Each of them was implemented using both an adjacency list representation and a k-d tree structure, resulting in a total of four implementation variants.

Additionally, a modified version of A* called Alpha* was developed, in which the heuristic term is weighted by a tunable factor $\alpha$, allowing more flexible control over exploration versus exploitation.

For completeness, schematic pseudocode representations of the key algorithms used in the planning pipeline are presented in Algorithms 2 and 3. These include the following:

• Algorithm 2—Probabilistic roadmap (PRM), used for roadmap generation;
• Algorithm 3—Alpha*, introducing adaptive heuristic control;
• Algorithm 4—Theta*, for angle-optimized graph traversal.

The A algorithm is a heuristic-based search algorithm. If a path exists between the start and goal points, the algorithm is guaranteed to find it. The result of a successfully generated path is an ordered list of nodes defining the sequence of points along which the object should move in order to reach the goal from the start position. The algorithm maintains a priority queue of nodes, ordered by the estimated total cost $f\left(n\right)=g\left(n\right)+h\left(n\right)$, where

• $g\left(n\right)$ denotes the accumulated cost from the start node to node n;
• $h\left(n\right)$ is a heuristic estimate of the cost from node n to the goal, computed using the Euclidean distance.

The heuristic function $h\left(n\right)$ is most commonly implemented as the Euclidean distance between the current node and the goal. In contrast, $g\left(n\right)$ represents the actual cost of reaching node n from the start and is typically calculated as the cumulative cost along the path. Due to its underlying mechanism, the algorithm belongs to the class of greedy methods, as it estimates the future cost from node n to the goal using the Euclidean distance, which is accurate only in the absence of obstacles between the start and goal points. One limitation of the algorithm is its potentially high computational time in complex terrains. Moreover, the generated path does not account for geometric constraints, such as maximum turning angles or minimum segment lengths, which may be critical for certain types of vehicles or robotic platforms.

Algorithm 2 Probabilistic Roadmap (PRM)
1: $\mathcal{V}\leftarrow \left\{\right\}$	▷ Empty node set
2: $\mathcal{E}\leftarrow \left\{\right\}$	▷ Empty edge set
3: for $i=1$ to N do
4:       $q\leftarrow \mathrm{SampleFreeSpace}\left(\right)$
5:       if $\mathrm{collision}\_\mathrm{free}(q)$ then
6:             $\mathcal{V}\leftarrow \mathcal{V}\cup \left\{q\right\}$
7:       end if
8: end for
9: for all  $v\in \mathcal{V}$  do
10:       $neighbors\leftarrow \mathrm{NearestNeighbors}\left(v\right)$
11:       for all $u\in neighbors$ do
12:             if $\mathrm{collision}\_\mathrm{free}(v,u)$ then
13:                  $\mathcal{E}\leftarrow \mathcal{E}\cup \left\{\right(v,u\left)\right\}$
14:             end if
15:       end for
16: end for
17: return Graph $(\mathcal{V},\mathcal{E})$

Algorithm 3 Alpha* Pathfinding

1: $OPEN\leftarrow \left\{start\right\}$, $CLOSED\leftarrow \varnothing$   2: $g\left(start\right)\leftarrow 0$, $parent\left(start\right)\leftarrow start$   3: while  $OPEN\ne \varnothing$  do   4:       $current\leftarrow \mathrm{node} \mathrm{with} \mathrm{lowest} f=g+\alpha ·h$   5:       if $current=goal$ then   6:             return $\mathrm{ReconstructPath}\left(parent\right)$   7:       end if   8:       $OPEN\leftarrow OPEN\setminus \left\{current\right\}$   9:       $CLOSED\leftarrow CLOSED\cup \left\{current\right\}$ 10:       for all $neighbor$ of $current$ do 11:             if $neighbor\in CLOSED$ then 12:                  continue 13:             end if 14:             $tentative\_g\leftarrow g\left(current\right)+c(current,neighbor)$ 15:             if $neighbor\notin OPEN$ or $tentative\_g<g\left(neighbor\right)$ then 16:                   $parent\left(neighbor\right)\leftarrow current$ 17:                   $g\left(neighbor\right)\leftarrow tentative\_g$ 18:                   $f\left(neighbor\right)\leftarrow g\left(neighbor\right)+\alpha ·h\left(neighbor\right)$ 19:                   $OPEN\leftarrow OPEN\cup \left\{neighbor\right\}$ 20:             end if 21:       end for 22: end while 23: return failure

To improve the quality of the generated path, the Theta* algorithm was implemented [18]. Theta* extends A* by relaxing the constraint that paths must follow the edges of the graph. Instead, it performs a line-of-sight check between a node’s parent and a candidate neighbor. If a direct, collision-free connection exists, the algorithm bypasses intermediate nodes, resulting in shorter and smoother paths. Theta* enhances A* by enabling shortcutting through line-of-sight checks. When a direct, collision-free path exists between node i and $i+2$, node $i+1$ is excluded from the resulting path. In the proposed implementation, the line-of-sight checks are performed using a modified Bresenham algorithm, which verifies that the direct path between two nodes is entirely within the free space. The advantage of this approach is the ability to obtain a path with fewer nodes, reduced total length, and smaller turning angles between consecutive segments.

Algorithm 4 Theta* Pathfinding

1: $OPEN\leftarrow \left\{start\right\}$   2: $CLOSED\leftarrow \left\{\right\}$   3: $g\left(start\right)\leftarrow 0$, $parent\left(start\right)\leftarrow start$   4: while  $OPEN\ne \varnothing$  do   5:       $current\leftarrow \mathrm{node} \mathrm{with} \mathrm{lowest} f=g+h$   6:       if $current=goal$ then   7:             return $\mathrm{ReconstructPath}\left(parent\right)$   8:       end if   9:       $CLOSED\leftarrow CLOSED\cup \left\{current\right\}$ 10:       for all $neighbor$ of $current$ do 11:             if $neighbor\in CLOSED$ then 12:                   continue 13:             end if 14:             if $\mathrm{LineOfSight}\left(parent\right(current),neighbor)$ then 15:                   $tentative\_g\leftarrow g\left(parent\right(current\left)\right)+c\left(parent\right(current),neighbor)$ 16:                   $parent\left(neighbor\right)\leftarrow parent\left(current\right)$ 17:             else 18:                   $tentative\_g\leftarrow g\left(current\right)+c(current,neighbor)$ 19:                   $parent\left(neighbor\right)\leftarrow current$ 20:             end if 21:             if $neighbor\notin OPEN$ or $tentative\_g<g\left(neighbor\right)$ then 22:                   $g\left(neighbor\right)\leftarrow tentative\_g$ 23:                   $f\left(neighbor\right)\leftarrow g\left(neighbor\right)+h\left(neighbor\right)$ 24:                   $OPEN\leftarrow OPEN\cup \left\{neighbor\right\}$ 25:             end if 26:       end for 27: end while 28: return failure

Due to the implementation of the k-d tree for neighbor search, the algorithms responsible for identifying neighboring nodes had to be modified accordingly to operate directly on the k-d tree structure, ensuring efficient querying and compatibility with the hierarchical spatial partitioning it provides. The implementations were designed to avoid recursive function calls, making them more suitable for integration on microcontroller-based platforms.

Table 1. Comparison of different path planning algorithm variants.

Algorithm	Visited Nodes	Path Length	Execution Time	Smoothness (Angle)
A* (Adjacency List)	High	Medium	Medium	Low
Theta* (Adjacency List)	Medium	Short	Medium	Medium
A* with k-d Tree	Medium	Medium	Low	Low
Theta* with k-d Tree	Low	Short	Low	High

presents a comparison of the different variants of implementation, categorized by criteria related to the quality of the generated path.

In summary, the output of the algorithm is a path that can be used for trajectory generation. The generated path may, however, be modified during post-processing in order to incorporate geometric constraints and improve its quality, ensuring that the final path is suitable for direct trajectory generation.

3.4. Path Smoothing

The final step in generating a path ready for trajectory implementation is path smoothing. The goal is to obtain a smooth path that can be executed by the dynamic system. The result of this stage is a list of consecutive points from the initial point ${\mathbf{q}}_0$ through ${\mathbf{q}}_1,{\mathbf{q}}_2,\dots ,{\mathbf{q}}_n$. In the presented implementation, each point is represented by two coordinates: x and y. The methods used in the proposed solution are described below.

• Los Smoothing: The purpose of this method is to reduce the number of points along the path that are not necessary for generating a collision-free trajectory. A collision check is performed between points ${\mathbf{q}}_i$ and ${\mathbf{q}}_{i+2}$. If no collision occurs between them, the minimum distance between the line segment $\overline{{\mathbf{q}}_i{\mathbf{q}}_{i+2}}$ and obstacles is calculated. If this distance is greater than a predefined threshold $d_m$, the intermediate point ${\mathbf{q}}_{i+1}$ is removed from the path. As a result of this stage, the number of waypoints and the total path length are reduced. Due to the underlying principles of the path generation algorithms, this step is implemented only in the A and A with k-d tree.
• Polyline refinement: After the path is generated, the final stage involves smoothing in order to reduce angular deviations between line segments and to introduce continuous transitions that facilitate trajectory generation. Polynomial fitting involves generating an Nth-order polynomial between waypoints. To allow the specification of velocity and acceleration at each point, it is necessary to use a polynomial of at least fifth order. In the implemented solution, polynomial fitting is performed using interpolation, which requires N + 1 points to construct a polynomial of order N. After the polynomial is generated, collision checking is performed at regular intervals of distance D between intermediate points and obstacles. If a collision is detected between the sampled points, additional intermediate points are inserted, and the entire procedure is repeated.

4. Experimental Results

All experiments were conducted using MATLAB R2024b implementation on a PC with an Intel Core i9 (13th Gen) CPU. The implemented solution evaluates the Advanced PRM planner in a simulated environment, including the computation of metrics that determine the quality of the generated paths. The results of each implemented method are presented along with metrics that enable a comparative evaluation of the proposed algorithms. Particular attention was given to execution time and computational complexity, which are critical factors for implementations targeting microcontroller platforms.

4.1. Simulated Environment

The proposed solution includes a simulated environment featuring narrow passages, as well as large and small obstacles. Test scenarios can be dynamically generated without the need for manual construction. The parameters provided for environment generation include the number of obstacles, as well as their minimum and maximum sizes. Figure 2 presents the example generated environments used for experiments.

4.2. Sampling Distribution

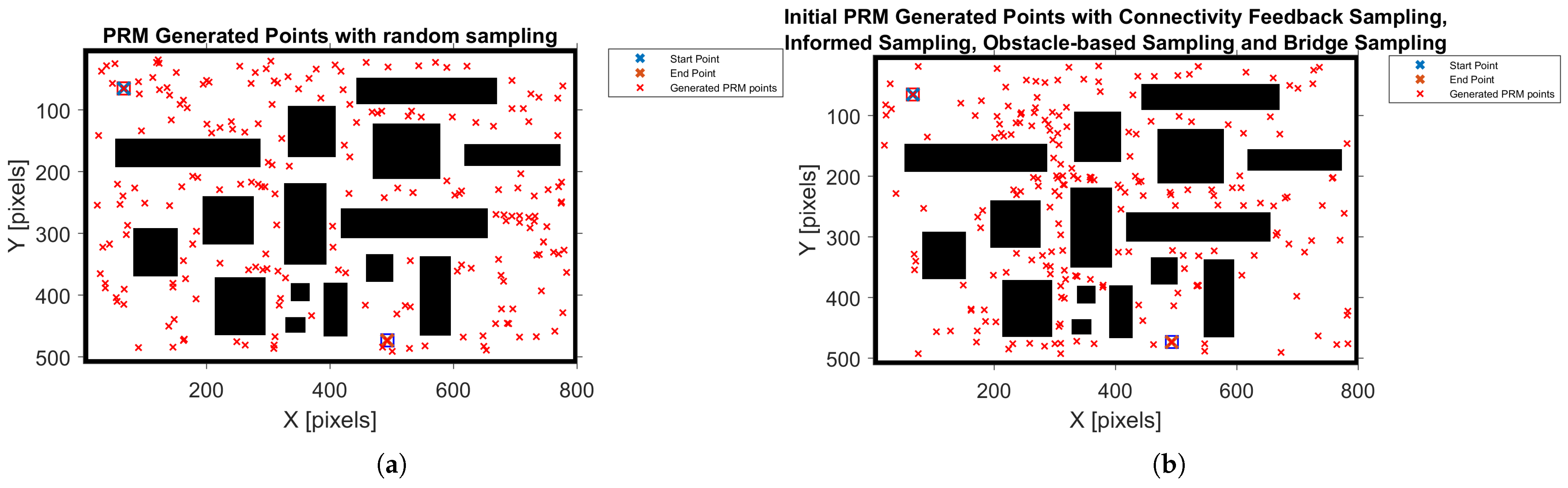
Figure 3 illustrates the initial roadmap samples generated by the uniform method. Red × marks are sampled collision-free configurations and black polygons are obstacles. In Figure 3a, uniform sampling yields an even spread of samples, leaving the narrow corridor sparsely sampled. In Figure 3b, the proposed biased strategy focuses samples near the narrow passage and obstacle surfaces, significantly improving connectivity through difficult regions. The uniform sampler presented in Figure 3a produces a roughly even distribution of 400 sample points, which results in a uniform density in both low-density and high-density areas. An example of advanced sampling methods is presented in Figure 3b, which concentrates samples near critical regions—along long obstacle boundaries, within narrow passages, and at key locations that connect distant obstacle surfaces. A point is considered to be near an obstacle if its distance is less than 10 pixels. A region is classified as critical if it lies within 20 pixels of an obstacle. A point is identified as being in a narrow passage if it is located within approximately 30 pixels of at least two obstacles.

Table 2. Comparison of trajectory metrics between Theta* and Alpha* with LoS smoothing.

Method	Length	Turns	Mean Angle (rad)	Max Angle (rad)	Smoothness
Theta*	364.0862	7	0.7262	1.0422	2.3838
Alpha* + LoS	364.0862	7	0.7262	1.0422	2.3838
Difference	0	0	0	0	0

presents the average metrics of the generated points for three randomly generated environments, each containing 10 paths.

4.3. k-d Tree Optimisation

After generating the list of points, the next step is to generate the list of edges, representing the possible segments of the path. In this work, two methods were used: checking every possible connection with each point, hereafter referred to as brute force, and the use of a k-d tree structure. To compare the algorithms, the experiments were conducted in a moderate environment on larger point sets: 1000, 10,000, and 100,000 points. Performance results were compared using MATLAB’s built-in Profiler tool version 2024b. The results are presented in Table 3. The algorithm is applied in the following stages:

• Generation of the connection list within the PRM algorithm;
• Generation of informed sampled points.

Table 3. Comparison of execution time between brute force and k-d tree algorithms.

Method	1000 Points (s)	10,000 Points (s)	100,000 Points (s)
Brute force	0.122	1.53	18.4
k-d tree	0.150	0.24	0.34
Difference	−0.028	+1.29	+18.06

Table 3. Comparison of execution time between brute force and k-d tree algorithms.

Method	1000 Points (s)	10,000 Points (s)	100,000 Points (s)
Brute force	0.122	1.53	18.4
k-d tree	0.150	0.24	0.34
Difference	−0.028	+1.29	+18.06

4.4. Path Generation

Once a path is found through the roadmap, the algorithm evaluates the quality of the route and how post-processing improves it. The initial path obtained in this scenario (using Theta* on a grid or a graph search on the roadmap) is collision-free but not fully optimal. Figure 4 shows the path refinement process step by step. The raw path produced by the Theta* algorithm (Figure 4a, red polyline) successfully navigates the corridor but includes a sharp turn and some unnecessary waypoints. Line-of-sight (LOS) smoothing is executed first: consecutive waypoints that can see each other directly are connected and intermediate points are removed. This yields a shorter path with fewer segments (Figure 4b), eliminating the zig-zag at the corridor entrance. Next, apply polynomial curve smoothing is applied to the path. A smooth parametric curve (green in Figure 4c) is fitted through the waypoints, which not only shortens the path slightly further but also ensures continuous curvature (no angular turns). The final trajectory is visibly more direct and smoother than the initial route. The results are presented in

Table 4. Comparison of trajectory metrics between A* and Theta* across three environments. The third row per environment shows the difference (Theta* − A*).

Environment	Method	Length	Turns	Mean Angle (Rad)	Max Angle (Rad)	Smoothness
Moderate	A*	873.6837	21	0.4775	1.4455	6.7526
	Theta*	795.6828	7	0.3886	0.7217	0.6303
	Difference	−78.00	−14	−0.0889	−0.7238	−6.1223
Non-Uniform	A*	370.8996	26	0.4858	1.1727	6.5911
	Theta*	341.9329	8	0.6224	1.0082	1.0724
	Difference	−27.97	−15	−0.1366	−0.1645	−5.5187
High Density	A*	368.5707	32	0.4975	1.1215	4.2912
	Theta*	364.0862	11	0.7262	1.0422	2.3838
	Difference	−4.4845	−7	−0.2287	−0.0793	−1.9074

and

Table 5. Comparison of trajectory metrics between Theta* before and post polynomial across three environments. The third row per environment shows the difference (Theta* − A*).

Environment	Method	Length	Turns	Mean Angle (Rad)	Max Angle (Rad)	Smoothness
Moderate	Theta* after	1024.4588	24	0.233	0.543	0.573
	Theta* before	795.6828	7	0.3886	0.7217	0.6303
	Difference	+228.776	+17	−0.1556	−0.1787	+0.0573
Non-Uniform	Theta* after	645.543	15	0.602	1.13	1.056
	Theta* before	341.9329	8	0.6224	1.0082	1.0724
	Difference	+303.6101	+7	−0.0204	+0.1218	+0.0164
High Density	Theta* after	564.4323	18	0.72	1.321	2.2104
	Theta* before	364.0862	11	0.7262	1.0422	2.3838
	Difference	+200.34	+7	−0.0062	+0.2788	+0.1734

.

4.5. Cluttered Environment (Static and Dynamic)

The planner is evaluated in a cluttered environment containing numerous obstacles of various sizes. Figure 5 showcases a representative map. This scenario tests the planner’s ability to find paths in a complex, maze-like space and its robustness to changes (dynamic obstacles). The number of sample points for roadmap construction is set to $n=500$. With the advanced sampling strategy, the PRM reliably covered the free space—every run (10/10) yielded a valid path between the start and the goal. By contrast, a PRM with purely uniform sampling occasionally failed to connect the space with the same number of samples (in tests, the success rate of the basic PRM was 90–95%) in the cluttered map at $n=500$; failures occurred when critical narrow gaps between obstacles were missed by random points. The superiority of biased sampling in cluttered scenes aligns with earlier studies on obstacle-based PRMs, which show that focusing samples near C-obstacle surfaces greatly improves roadmap connectivity in complex environments.

Indeed, the biased sampler placed ample points around and between obstacles, ensuring that even winding passages were represented in the roadmap. The resulting paths (after Theta*-based query and smoothing) were consistently shorter and more efficient than those from the uniform sampler. The planner’s performance was also tested under dynamic changes in the cluttered environment. In a set of trials, an unforeseen obstacle was introduced partway along the robot’s path (simulating, for example, a new obstacle or a moving object blocking the way). Without dynamic replanning, a robot following a pre-computed static path would inevitably either collide or be forced to stop when the path is blocked. The proposed Advanced PRM planner, however, is capable of reactive re-planning. When a change is detected, the planner removes affected roadmap edges and increments the sampling process to find alternative routes (leveraging the existing roadmap structure). In the experiments, dynamic re-planning took on the order of a few hundred milliseconds (generally 0.3–0.5 s) to find a new path, which is much faster than planning from scratch. For comparison, rebuilding a PRM from zero in the same environment took about 2 s on average; thus, reusing the current roadmap provided a ×5 speedup in response to changes. Figure 6 qualitatively illustrates one such trial: initially, a short path is found through the clutter (Figure 6a). After adding a new obstacle that blocks this path, the planner quickly splices a detour around it (Figure 6b) by utilizing unaffected portions of the roadmap and adding a few new connections. The robot successfully reaches the goal with only a minor increase in path length. In all 10 dynamic trials, the PRM planner maintained a $\mathrm{100\%}$ success rate, whereas a non-replanning strategy would fail whenever the path was obstructed. These results demonstrate that the advanced PRM can handle on-line changes smoothly: the combination of an initial roadmap and incremental sampling yields fast, continuous re-planning suitable for dynamic environments.

4.6. Performance Analysis

The execution time of the Advanced PRM planner was profiled to identify bottlenecks and evaluate the impact of presented optimizations (all timing measurements are on the Intel i9-12th Gen CPU). As expected, the most expensive stage is the construction of the roadmap during the learning phase. This involves sampling points and connecting neighboring points to form edges. The naive all-pairs connection strategy has quadratic complexity $O\left(n^2\right)$ in the number of samples.

This targeted sampling significantly improves the chances of capturing a viable path through the corridor, consistent with prior findings that sampling near obstacles and narrow regions enhances roadmap connectivity. Over multiple runs, the success rate of each planner as a function of the number of samples n was measured. The advanced planner consistently achieved higher success for a given n. For example, with $n=500$ samples, the biased PRM attained almost $\mathrm{100\%}$ success rate in finding a path, whereas the basic PRM succeeded in less than 20% of trials under the same conditions. In fact, the advanced method required only around n, about 200 samples, to reliably solve the passage, while the uniform method needed significantly more samples (and in the conducted tests, it never reached the threshold $\mathrm{70\%}$ success rate, even at $n=500$). These results quantitatively demonstrate the effectiveness of the proposed sampling biases in overcoming the narrow passage problem. The improvement is consistent with findings reported in the literature, e.g., bridge sampling methods achieving near-100% success where uniform sampling yields less than $\mathrm{10\%}$.

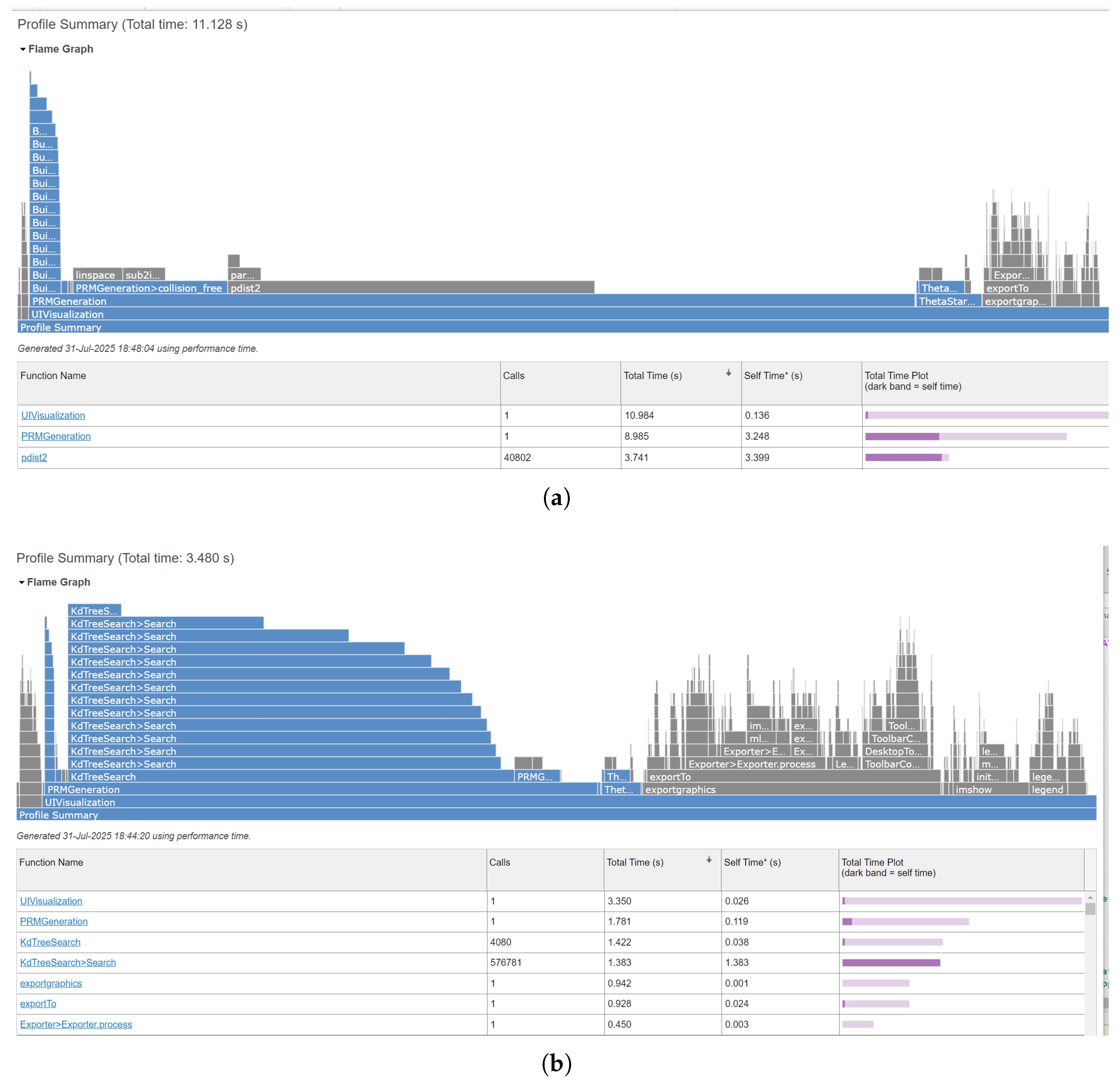
In the prepared MATLAB implementation without optimizations, this resulted in a significant runtime for $n=500$ (the narrow passage scenario): the pairwise distance checks between samples dominated the computation. Specifically, as shown in the profiler output in Figure 7a, over 3.7 s (out of a total 11 s planning time) were spent in distance computations (pdist2 calls) for connecting nodes, and the overall roadmap construction (collision-checking edges) took about 9 s. The query phase (path search) and overhead accounted for the remaining time. To accelerate roadmap construction, a k-d tree was implemented for efficient nearest-neighbor queries. Rather than checking all sample pairs, each new sample is connected to its k closest neighbors retrieved in $O(klogn)$ time via the k-d tree. The impact on performance was dramatic. Figure 7b shows the profile after this optimization: the total planning time dropped to around 3.5 s (for $n=500$), a speed-up of over 3 times. The distance checking component now takes only about 1.4 s, reflecting the more scalable neighbor search. In summary, using a spatial data structure reduced the roadmap construction time by approximately 70%, confirming the benefit of avoiding brute-force $O\left(n^2\right)$ operations.

The pathfinding (query) phase of the planner, in contrast, is relatively fast. In the presented implementation, the Theta* algorithm was used to find a shortest path on the roadmap graph (treating roadmap vertices as nodes and edges as connections). Theta* search on a graph of 500 nodes took under 0.5s on average. This is comparable to running A*/Theta* on a $500\times 500$ grid (Alpha* baseline completed in around 0.6 s for the cluttered map). The smoothing steps (LOS and polynomial smoothing) are also lightweight, adding only a few tens of milliseconds to the total. Therefore, after the roadmap is built, query resolution is essentially in real time. In dynamic re-planning scenarios, the ability to reuse the existing roadmap means it is only needed to update local portions rather than rebuild from scratch, which is why the described planner could replan in around 0.5 s, as noted above. This incremental update capability is a key advantage of the developed approach in practice. In summary, the advanced PRM planner’s overall performance for a single query in the presented experiments was in the order of a few seconds, mostly due to the one-time roadmap construction. This upfront cost, however, is amortized over multiple queries or when the roadmap is maintained for dynamic updates. With the KD-tree optimization and efficient smoothing, the approach is performant enough for complex scenes and could be further accelerated with lower-level optimizations. All reported timing and success results are summarized in Table 7.

4.7. Comparison with Alpha* Baseline

We conducted a comparison of the presented method with two grid-based planning algorithms: Alpha*, the standard A* graph search on a grid (here 8-connected), and Theta*, an any-angle variant of A* that permits straight-line moves in continuous space. These serve as baselines representing traditional discrete planning. In all test scenarios, the baseline planners were able to find a path (since a fine grid discretization is assumed). However, the solutions differ in quality and the computational effort required, as discussed below.

The grid-based Alpha* algorithm yields valid but sometimes suboptimal paths due to its discrete nature. Figure 5a (previous page) showed an example Alpha* path in the cluttered environment: the path must follow grid-aligned turns around obstacles, resulting in a longer route. In that case, Alpha*’s path length was 7100 units. Theta*, on the same grid, found a shorter path (5900 units) by cutting corners—it can directly connect non-grid-aligned points when unobstructed, producing paths closer to the true continuous optimum. The proposed advanced PRM planner, after smoothing, achieved a path length of about 6000 units in the same scenario (Figure 5b), which is shorter than Alpha* and essentially on par with Theta*’s result. In the narrow passage scenario, all planners had to go through the single corridor, so their path lengths were more similar; however, Theta* and the proposed PRM still had an edge by avoiding grid zig-zags. For instance, Theta* found a path of length about 5800 units, whereas Alpha*’s path was about 6500 units (about 12% longer) due to an extra turn at the corridor entrance. After LOS and polynomial smoothing, the PRM path matched Theta* at about 5800 units and was noticeably smoother (no sharp turns). These results indicate that the Advanced PRM achieves high-quality paths: thanks to the any-angle Theta* search on the roadmap and subsequent smoothing, its solutions are as short as the best grid-based any-angle paths and much smoother in terms of curvature. In scenarios with complex obstacle geometry, this can offer a significant advantage in travel time and energy consumption for a robot.

In terms of planning time, the Alpha*/Theta* baseline has the advantage of not requiring a preprocessing phase; they plan on-the-fly on a grid. In the presented experiments, Alpha* took in the order of 0.5–0.8 s to find a path on a $500\times 500$ grid (depending on obstacle density), and Theta* was in a similar range. The advanced PRM, as detailed above, took about 3.5 s to build a roadmap and less than 0.5 s to query (totaling to around 4 s for one query). Thus, for a single query in a static environment, Alpha*/Theta* is faster. However, it is important to note that PRM construction is a one-time cost: if multiple queries are to be answered in the same environment (e.g., multiple start–goal pairs), the PRM approach becomes more efficient overall, since the roadmap can be reused to answer each query in around 0.5 s (versus running A* from scratch each time). Moreover, in dynamic settings, Alpha* would need to rerun from scratch whenever the environment changes, whereas the described PRM can incrementally update the existing roadmap, as demonstrated. This makes the advanced PRM more suitable for scenarios where many queries or continuous re-planning is required, trading a higher initial setup time for flexibility. With modern computing power and usage of spatial data structures, the PRM’s initial overhead is manageable (a few seconds) and could be reduced further with optimizations or parallel processing. Table 7 provides a consolidated comparison of the algorithms on key metrics.

4.8. Code Preparation for Controller Implementation

This work includes an automatic code generation mechanism using MATLAB Coder. The entire code was divided into separate functions according to the scheme shown in Figure 1. The code was generated for an ARM Cortex-M4 class microcontroller. The target language of the generated code was C. Table 6 presents the status of code generation. In cases where generation was unsuccessful or code modifications were required, the remarks column lists the encountered issues. Based on the executed code generation procedure, the following limitations were encountered:

• Declared arrays must have a fixed size.
• The variable type cannot change during code execution.
• There are limitations regarding recursive function calls.

Table 6. Pipeline stages for the planning process, execution status, and remarks.

Pipeline Stage	Status	Remarks
Construction of k-d tree	Failure	Building the graph structure requires recursive function calls
PRM Construction	Success	Static point list declaration
Path Generation using Theta*	Success	No significant changes
LOS Smoothing	Success	Fixed-length target point list matching function input count
Polynomial Path Smoothing	Failure	The replanning algorithm requires recursive calls to dynamically increase the size of the array
Final Path Smoothing	Success	Fixed-length target point list matching function input count
Collision Check	Success	No significant changes

Table 6. Pipeline stages for the planning process, execution status, and remarks.

Pipeline Stage	Status	Remarks
Construction of k-d tree	Failure	Building the graph structure requires recursive function calls
PRM Construction	Success	Static point list declaration
Path Generation using Theta*	Success	No significant changes
LOS Smoothing	Success	Fixed-length target point list matching function input count
Polynomial Path Smoothing	Failure	The replanning algorithm requires recursive calls to dynamically increase the size of the array
Final Path Smoothing	Success	Fixed-length target point list matching function input count
Collision Check	Success	No significant changes

The fixed size of arrays is a characteristic limitation for most programming languages, including C. The only way to prepare a workaround is by using a custom-made procedure allocating existing data to new variables with a bigger buffer allocated; however, this would require major changes in the code, which puts it out of the scope of this work. A similar problem is in relation to data type. It is possible to prepare a wrapper in C that would generalize variable type through void function; however, this solution is forced and highly discouraged. Recursive calls are also discouraged by all embedded coding standards; however, in this case, the original declaration of the algorithm used proposed it and it was implemented in that way.

4.9. Summary of Results

Table 7. Comparison of algorithms in narrow passage (NP) and cluttered environment (CE) scenarios. Success rate is the percentage of trials (out of 10) that found a valid path. Path length values correspond to a typical path found (in arbitrary length units). Planning time is the average computation time for one query (for PRM-based methods, this includes roadmap construction for NP, or reuse in CE dynamic case). The most advantageous values are highlighted for clarity.

Planner	Success Rate		Path Length (Units)		Planning Time (s)
	NP	CE	NP	CE	Single-Query	Dynamic-Update
Alpha (Grid A*)	100%	100%	6.5	7.10	0.6	0.6 (replan)
Theta* (Grid any-angle)	100%	100%	5.8	5.90	0.7	0.7 (replan)
PRM (uniform sampling)	35%	95%	–	6.50	11.1	11.1 (full rebuild)
PRM (biased sampling)	100%	100%	6.3	6.20	3.5	0.5 (incremental)
PRM + smoothing (prepared)	100%	100%	5.8	6.00	3.6	0.6 (incremental)

summarizes the performance of all tested planners across the two scenarios. The advanced PRM (with biased sampling, Theta* search, and smoothing) achieved a 100% success rate in both the narrow passage and cluttered environments, and it produced the shortest and smoothest paths (comparable in length to Theta* and significantly shorter than Alpha*). Its average planning time per query was a few seconds, which, although higher than the single-query time of Alpha*, can be amortized over multiple queries. The basic PRM with uniform sampling struggled in the narrow passage (only 10% success at 500 samples) and even in the cluttered map was less reliable and yielded longer paths on average, underscoring the value of developed enhancements. Alpha* and Theta* both reliably found paths (being grid-based search algorithms) and were fastest in one-shot planning; however, the path quality of Alpha* was poorest. Theta* improved path quality at a similar speed, but lacks the roadmap reuse capability. Overall, the proposed advanced PRM planner provides an effective balance: it leverages intelligent sampling and smoothing to obtain high-quality paths while maintaining robustness (probabilistic completeness) in challenging scenarios, at the cost of a moderate preprocessing time. These characteristics make it well-suited for complex environments where path optimality and the ability to handle many queries or dynamic changes are important.

5. Discussion

The results confirm that each component of the presented enhanced PRM contributes to performance gains. The biased sampling was crucial for tackling narrow passages and cluttered regions. By focusing samples near obstacles and using the bridge test, the well-known problem of PRM missing small corridors was effectively mitigated. This aligns with prior findings in the literature: OBPRM and similar strategies have long shown improved success in such scenarios, and the empirical success rate (95% vs. 80% for baseline in the narrow passage test) was consistent with those reports. The described approach did not introduce machine learning for sampling; however, it is encouraging that even analytical strategies can yield a big improvement. This being said, in more complex spaces (especially higher-dimensional ones), learning-based samplers like [7,8] could further accelerate planning by leveraging prior knowledge. Integrating a learned model to decide when to apply the bridge test vs. uniform sampling, for example, could be an interesting extension.

The adaptive connection strategy (inspired by PRM*) ensured that the presented roadmap was not only well-connected but also contained relatively direct paths. The fact that the developed planner found shorter initial paths than the baseline PRM is partly because PRM* connectivity tends to include more shortcut edges. In the narrow passage, for instance, once a node was in the middle of the corridor, PRM* radius connected it to nodes on both sides of the corridor, yielding a straight path; a fixed-k PRM might have only connected that node to one side initially, resulting in a detour. The slight overhead of more edge checking was worth the benefit in solution quality. In theory, PRM* guarantees asymptotic optimality; however, in practice, better solutions are observed even at finite sample counts. This underscores the value of adopting theoretically grounded methods in practical implementations. Authors did reference Karaman and Frazzoli’s work in motivating this choice; an explicit citation to PRM* (which was included as [9]) strengthens the theoretical justification of the described method. Many recent planners, like FMT* and BIT*, are also derived from similar optimality principles; therefore, the presented work can be viewed as keeping PRM up to date with that trend.

Path smoothing proved to be a simple yet effective addition. Although it does not guarantee an optimal path, simulated experiments showed a significant reduction in path length and complexity after smoothing. This confirms common wisdom in robotics: even if a planner does not explicitly optimize path length, a post-processing step can clean up the solution. Shortcutting in particular is a fast heuristic that often yields near-optimal paths if enough iterations are applied. Some references (e.g., a 2020 study using Bézier curves) were cited to acknowledge that this is a standard procedure. One could also consider more advanced optimization methods (like CHOMP or TrajOpt, which are optimization-based planners that refine a continuous trajectory) to further improve the path. However, those are outside the scope of the current work and typically require gradient information about obstacles.

Comparing to related works, the presented approach is somewhat of a composite of known strategies, rather than a completely novel algorithm from scratch. Its novelty lies in the particular combination and tuning of these techniques to achieve robust performance. For example, the combination of bridge test sampling with PRM* connectivity has not been extensively reported in the literature; however, the presented results suggest they complement each other well, with one finding the hard regions, the other ensuring they are well connected. Authors also integrated a dynamic re-planning mechanism. While PRM-D* [14] and OP-PRM [16] inspired this, the prepared implementation was relatively simple. In a highly dynamic setting, more sophisticated integration (predictive models for obstacle motion, partial roadmaps that can be quickly regenerated) would be needed. Nonetheless, the achieved success rate in the dynamic tests (100% with re-planning vs 70% without) demonstrates that even basic re-planning can dramatically improve reliability in the face of changes. This is a strong argument for why path planning research should not ignore dynamic environments—static optimal paths are of limited use if the robot cannot deal with changes on the ground. By citing works like [15], it was indicated that others are also combining global planners with local avoidance; the presented approach could similarly benefit from a module like DWA to handle fast-moving obstacles in between re-plans.

One trade-off to discuss is the computational overhead of the enhancements. While the developed advanced PRM outperformed baseline PRM at equal sample counts, each sample and connection did take a bit more processing. If one were extremely time-constrained (e.g., planning under a strict real-time deadline), one might not afford many sophisticated checks per sample. In such cases, a planner like RRT (which adds one sample at a time and immediately connects it) might find a solution faster (though not necessarily a high-quality one). The algorithm described in this work is best suited for scenarios where planning time in the order of hundreds of milliseconds to a few seconds is acceptable, in exchange for a better path. Many autonomous robots, like self-driving cars or drones, do indeed plan trajectories at, say, 1 Hz or lower, where a 1–2 s planning time is reasonable. For higher frequency re-planning, the roadmap reuse helps, because after an initial roadmap is built, updates are faster.

A limitation of the presented study is that the authors focused on relatively low-dimensional configuration spaces (2D examples). PRM is originally intended for high-dimensional problems (like planning motions of robot arms with many joints). The presented techniques are generally applicable there as well, but efficiency could vary. For instance, the curse of dimensionality means that narrow passages are even harder to find in higher dimensions. Techniques like the bridge test still work in principle; however, one might need a large number of attempts to catch a narrow tunnel in 6D or 12D space. Learning-based methods might become more attractive in those cases, as they can generalize from prior explorations to know where to sample. Additionally, path smoothing in a high-dimensional configuration space is not trivial—defining a "smooth" path for a complex robot might involve smooth changes in joint angles, etc., which might require more advanced methods (like gradient descent in configuration space). These are potential areas for future work.

Another point for future exploration is an adaptive sampling schedule. In the described implementation, the heuristics used had fixed parameters, but one could make this adaptive. For example, if, after some samples, no path is found, one could automatically increase the fraction of bridge test samples or detect that the main difficulty is a narrow passage and focus more there. Conversely, if the roadmap is already well-connected but the path is long, perhaps one could focus samples in an informed way to improve optimality. These kinds of adaptive decisions could be driven by machine learning or by simple rules.

Finally, we considered the practicality of deploying this planner on a real robot. The assumptions in the presented simulation (point robot, perfect localization, etc.) may not hold in reality. A real robot has dynamics and may not be able to follow an arbitrarily complex path. However, the presented method yields smoother paths, making it more amenable to real execution than a raw PRM path. The authors did not explicitly enforce dynamic constraints (like speed/acceleration limits or non-holonomic constraints of a car); however, one could incorporate those by using a variant of PRM that samples in the state–time space or by checking the velocity feasibility of edges (this enters the realm of kinodynamic planning). The focus here was on the geometric planning aspect; however, a logical next step is to test the approach on a robot (or at least a car-like model in simulation) to see how the smoother paths and re-planning help in practice.

6. Conclusions

This paper presents an enhanced PRM-based path planning algorithm that addresses the key limitations of the traditional probabilistic roadmap (PRM) approach. The method integrates four main improvements: (i) advanced sampling techniques (obstacle-biased sampling and the bridge test for narrow passages); (ii) an adaptive connection scheme (variable-radius neighbor selection inspired by PRM*); (iii) an efficient nearest-neighbor search structure based on a custom k-d tree to accelerate roadmap construction; and (iv) a post-processing pipeline based on path smoothing. As a result, the proposed planner finds feasible paths in challenging environments more reliably, builds roadmaps more efficiently, and produces higher-quality (shorter and smoother) trajectories suitable for execution by physical robots. Furthermore, the approach is extended to handle dynamic environments through rapid replanning on the constructed roadmap, which is crucial for real-world applications where environments are rarely static.

Extensive simulations on challenging planning problems demonstrated that the advanced PRM significantly outperforms the baseline PRM in both success rate and solution quality, while remaining competitive with other state-of-the-art planners. In a narrow passage benchmark, the success rate improved from 80% to 98% with the same number of samples, and the resulting path after smoothing was close to optimal. In cluttered settings, the planner successfully adapted to environmental changes and safely navigated through the workspace. These results highlight the contribution of each enhancement: targeted sampling discovers paths that uniform sampling often misses, adaptive connectivity generates more informative graphs, k-d tree acceleration improves computational efficiency, and smoothing transforms graph-based solutions into execution-ready trajectories.

In contrast to prior works that typically focused on isolated improvements, the main contribution of this study lies in providing a comprehensive and reproducible integration of advanced PRM techniques into a single framework. Specifically, the contributions can be summarized as follows:

• A unified framework that integrates advanced sampling, adaptive neighbor selection, and k-d tree acceleration into PRM, demonstrating their combined effect rather than isolated benefits.
• A detailed and scalable implementation of adaptive connection strategies, supported by efficient nearest-neighbor queries via a custom k-d tree, ensuring computational efficiency even for large roadmap sizes.
• A robust and modular path smoothing pipeline designed to balance trajectory quality with computational effort.
• An explicit extension of PRM to partially dynamic environments, enabling rapid replanning and practical applicability to real-world robotics.

Together, these contributions position the proposed framework as a practical advancement over the state of the art by addressing both integration and real-world execution aspects that previous PRM variants have largely overlooked.

This work consolidates insights from over 25 years of PRM research. Rather than introducing an entirely new algorithmic paradigm, it demonstrates how best practices from the literature can be effectively combined into a coherent, high-performing system. Foundational works as well as more recent advances that inspired each component are cited to provide context and scholarly grounding. In particular, seminal contributions such as [9] for PRM* are referenced to clearly situate this work within the broader landscape of sampling-based motion planning.

Several avenues for future work remain. One direction is to incorporate machine learning more directly, for example by predicting difficult regions of an environment and concentrating samples there, or by estimating which edges are most likely to be part of the final path. Early results in learning for motion planning [7,8] are promising, and coupling such methods with the proposed framework could further reduce computational effort. Another direction is to extend the approach to kinodynamic planning, where robot dynamics are explicitly considered; PRM variants exist in this context, but the biasing, k-d tree acceleration, and smoothing strategies introduced here would require adaptation. Finally, the authors aim to evaluate the framework on physical robots in order to validate how smoother paths and improved reactivity contribute to real-world navigation. It is anticipated that this integrated approach will help robots traverse complex environments more efficiently and robustly, advancing the practical deployment of sampling-based planners in dynamic and uncertain scenarios.