Fast Intra-Coding Unit Partitioning for 3D-HEVC Depth Maps via Hierarchical Feature Fusion
Abstract
1. Introduction
- Construct external features: Designing a wavelet energy ratio for quantifying the texture complexity of depth map CUs and combining it with QP to jointly serve as external features. These are fused with network-extracted features, thereby enhancing the model’s perception of texture structure and coding quality;
- Propose the HFF-CNN: Hierarchically processes input CU features and employs a multi-scale feature fusion strategy. Combines with a channel attention mechanism (SE module) to achieve adaptive enhancement of key features, followed by integration with external features to enable accurate predictions.
2. Observations and Analysis
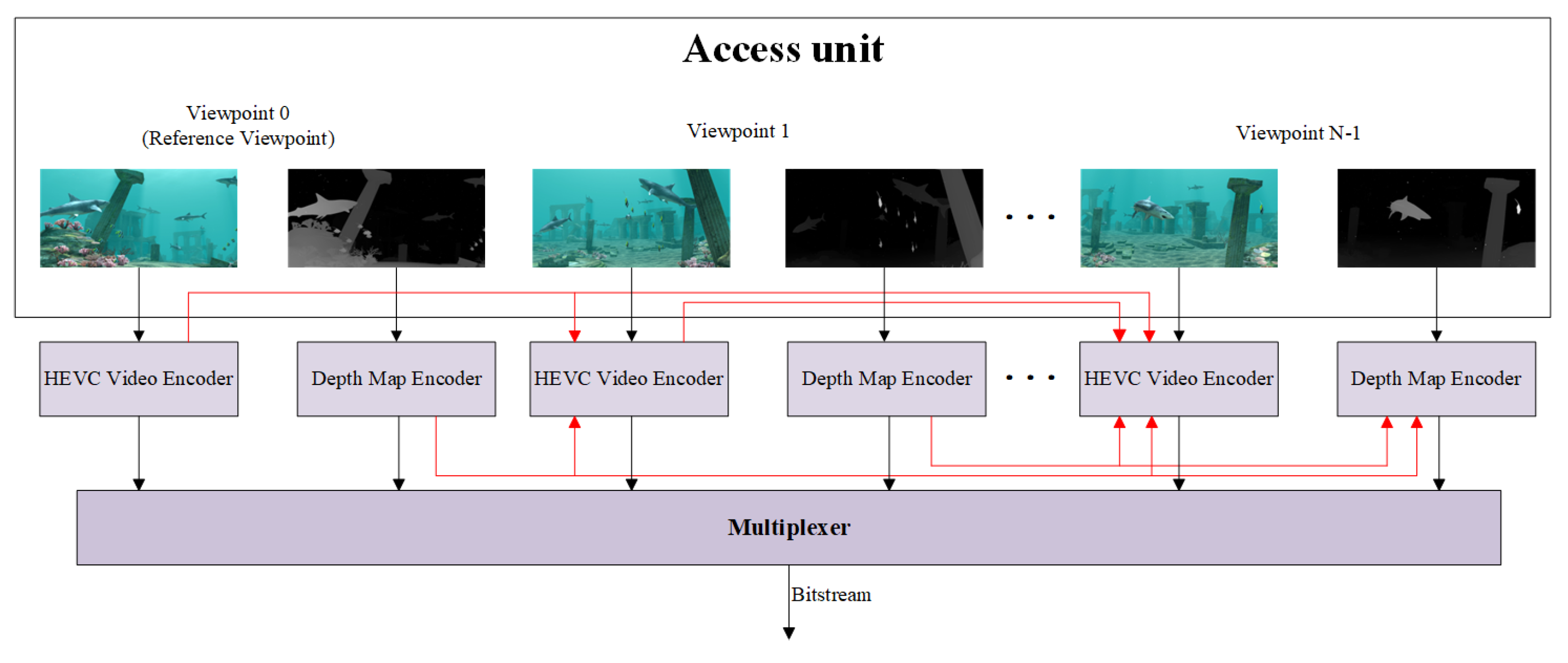
2.1. Complexity Analysis of 3D-HEVC Depth Map Coding
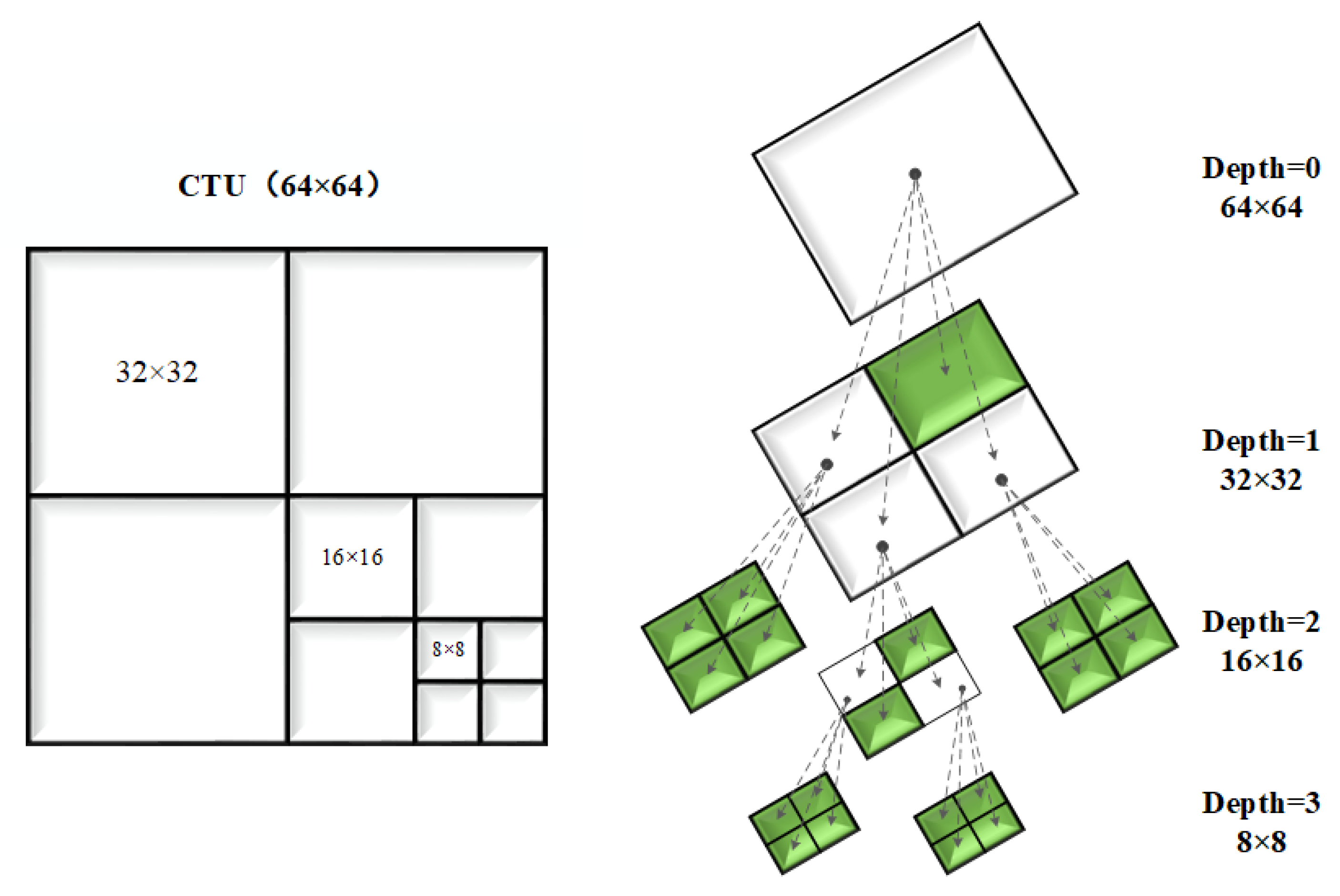
2.2. Complexity Analysis of CU Partitioning for 3D-HEVC Depth Maps
3. The Proposed Algorithm
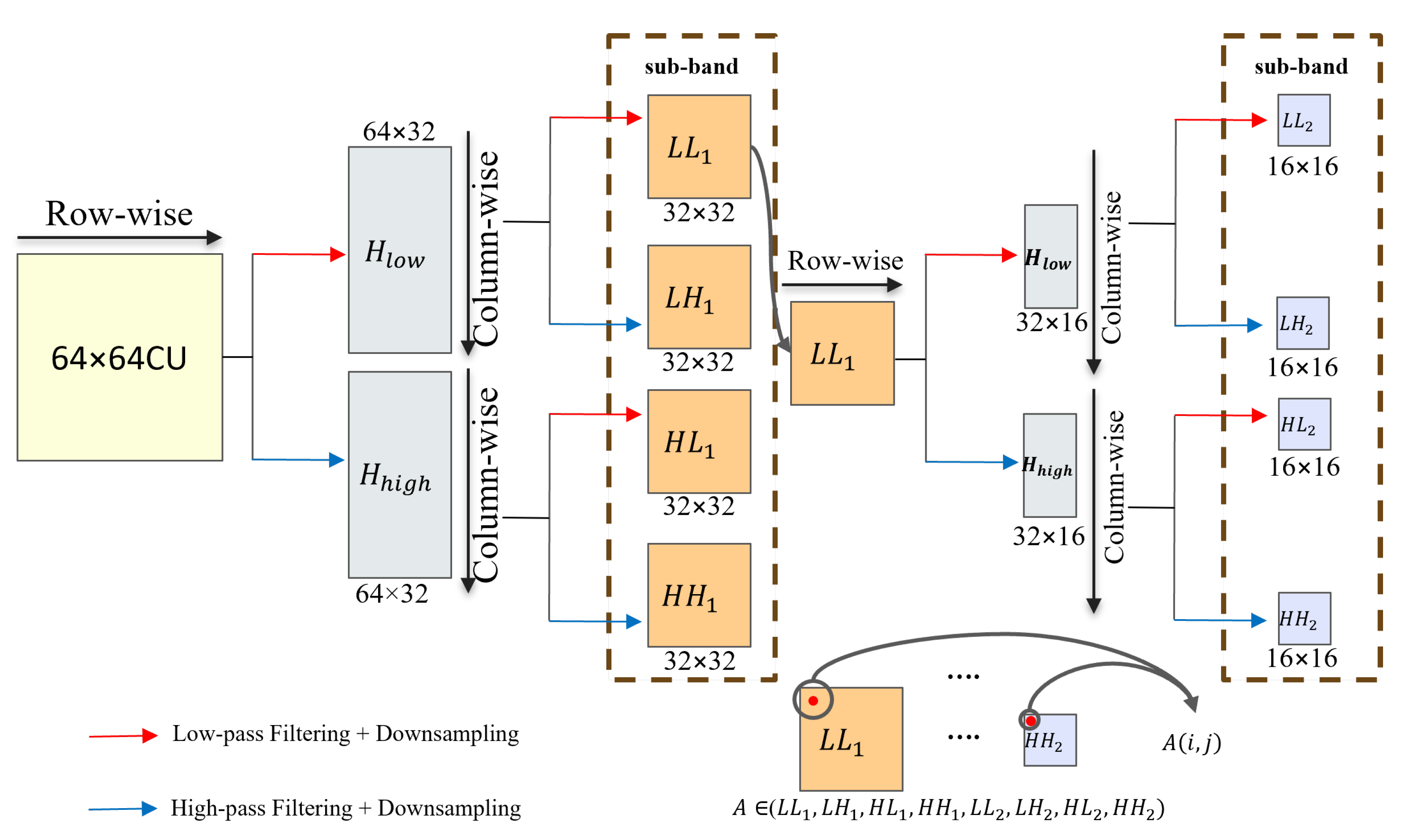
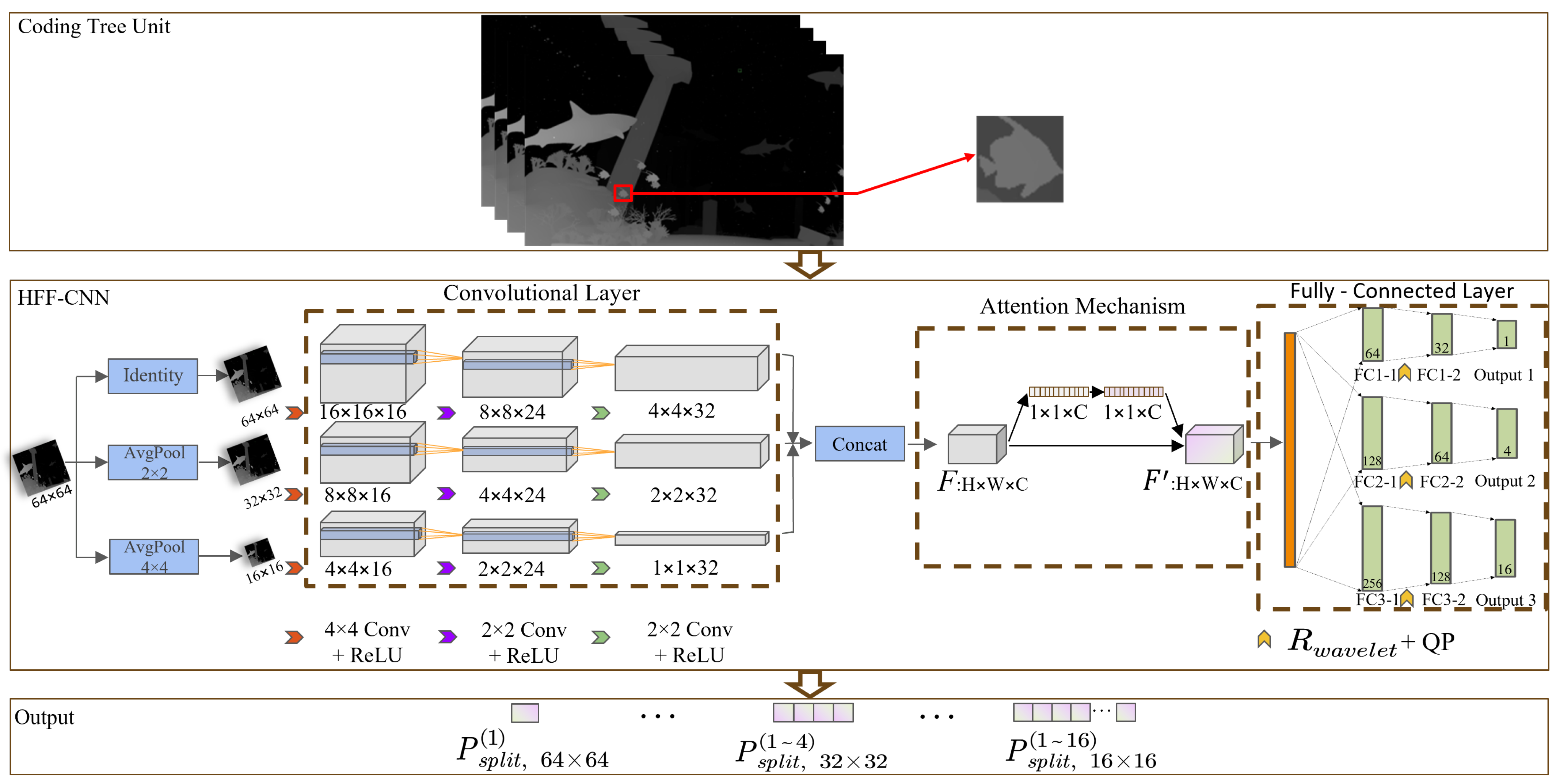
3.1. Construction of CU Complexity Features Based on Wavelet Energy Ratio and Quantization Parameter
3.2. CU Partitioning Prediction Based on HFF-CNN
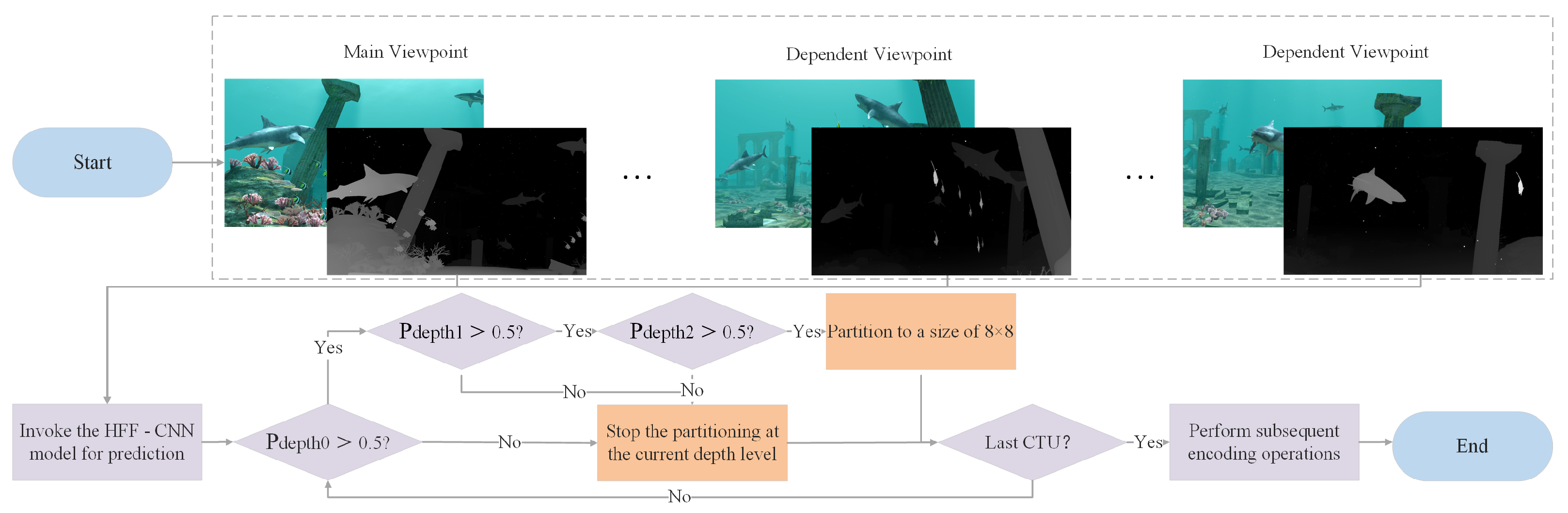
3.3. Overall Algorithm Flow
4. Experimental Results and Analyses
4.1. Dataset Construction and Experimental Setup
4.2. Analysis of Experimental Results
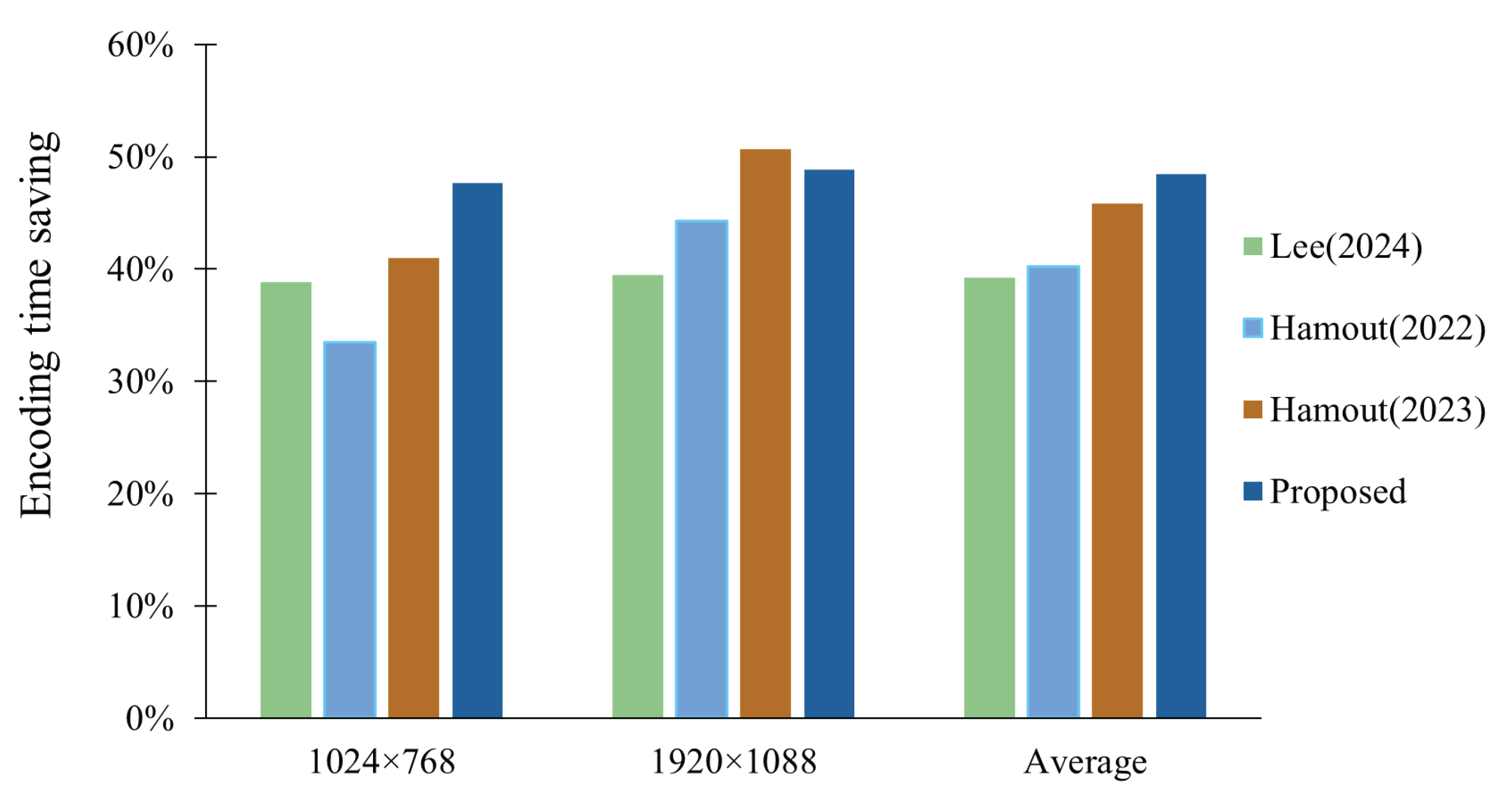
4.3. Comparison with Other Algorithms
4.4. Comparison of Synthesized Views
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Artois, J.; Van Wallendael, G.; Lambert, P. 360DIV: 360° video plus depth for fully immersive VR experiences. In Proceedings of the 2023 IEEE International Conference on Consumer Electronics (ICCE), Las Vegas, NV, USA, 6–8 January 2023; pp. 1–2. [Google Scholar]
- Li, T.; Yu, L.; Wang, H.; Kuang, Z. A bit allocation method based on inter-view dependency and spatio-temporal correlation for multi-view texture video coding. IEEE Trans. Broadcast. 2020, 67, 159–173. [Google Scholar] [CrossRef]
- Cai, Y.; Wang, R.; Gu, S.; Zhang, J.; Gao, W. An adaptive pyramid single-view depth lookup table coding method. In Proceedings of the 2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; pp. 1940–1944. [Google Scholar]
- Mallik, B.; Sheikh-Akbari, A.; Bagheri Zadeh, P.; Al-Majeed, S. HEVC based frame interleaved coding technique for stereo and multi-view videos. Information 2022, 13, 554. [Google Scholar] [CrossRef]
- Li, T.; Yu, L.; Wang, H.; Kuang, Z. An efficient rate–distortion optimization method for dependent view in MV-HEVC based on inter-view dependency. Signal Process. Image Commun. 2021, 94, 116166. [Google Scholar] [CrossRef]
- Hamout, H.; Elyousfi, A. Fast depth map intra-mode selection for 3D-HEVC intra-coding. Signal Image Video Process. 2020, 14, 1301–1308. [Google Scholar] [CrossRef]
- Khan, S.N.; Khan, K.; Muhammad, N.; Mahmood, Z. Efficient prediction mode decisions for low complexity MV-HEVC. IEEE Access 2021, 9, 150234–150251. [Google Scholar] [CrossRef]
- Jeon, G.; Lee, Y.; Lee, J.-K.; Kim, Y.-H.; Kang, J.-W. Robust spatial-temporal motion coherent priors for multi-view video coding artifact reduction. IEEE Access 2023, 11, 123104–123116. [Google Scholar] [CrossRef]
- Du, G.; Cao, Y.; Li, Z.; Zhang, D.; Wang, L.; Song, Y.; Ouyang, Y. A low-latency DMM-1 encoder for 3D-HEVC. J. Real-Time Image Process. 2020, 17, 691–702. [Google Scholar] [CrossRef]
- Zhang, H.; Yao, W.; Huang, H.; Wu, Y.; Dai, G. Adaptive coding unit size convolutional neural network for fast 3D-HEVC depth map intracoding. J. Electron. Imaging 2021, 30, 041405. [Google Scholar] [CrossRef]
- Zou, D.; Dai, P.; Zhang, Q. Fast depth map coding based on Bayesian decision theorem for 3D-HEVC. IEEE Access 2022, 10, 51120–51127. [Google Scholar] [CrossRef]
- Wang, X. A fast 3D-HEVC video encoding algorithm based on Bayesian decision. In Proceedings of the International Conference on Algorithms, High Performance Computing, and Artificial Intelligence (AHPCAI 2023), Yinchuan, China, 18–19 August 2023; Volume 12941, pp. 937–942. [Google Scholar]
- Omran, N.; Kachouri, R.; Maraoui, A.; Werda, I.; Belgacem, H. 3D-HEVC fast CCL intra partitioning algorithm for low bitrate applications. In Proceedings of the 2025 IEEE 22nd International Multi-Conference on Systems, Signals and Devices (SSD), Sousse, Tunisia, 17–20 February 2025; pp. 749–755. [Google Scholar]
- Hamout, H.; Elyousfi, A. A computation complexity reduction of the size decision algorithm in 3D-HEVC depth map intracoding. Adv. Multimed. 2022, 2022, 3507201. [Google Scholar] [CrossRef]
- Hamout, H.; Elyousfi, A. Low 3D-HEVC depth map intra modes selection complexity based on clustering algorithm and an efficient edge detection. In Proceedings of the International Conference on Artificial Intelligence and Green Computing, Hammamet, Tunisia, 15 January 2023; pp. 3–15. [Google Scholar]
- Su, X.; Liu, Y.; Zhang, Q. Fast depth map coding algorithm for 3D-HEVC based on gradient boosting machine. Electronics 2024, 13, 2586. [Google Scholar] [CrossRef]
- Li, Y.; Yang, G.; Qu, A.; Zhu, Y. Tunable early CU size decision for depth map intra coding in 3D-HEVC using unsupervised learning. Digit. Signal Process. 2022, 123, 103448. [Google Scholar] [CrossRef]
- Wang, X. Application of 3D-HEVC fast coding by Internet of Things data in intelligent decision. J. Supercomput. 2022, 78, 7489–7508. [Google Scholar] [CrossRef]
- Liu, C.; Jia, K.; Liu, P. Fast depth intra coding based on depth edge classification network in 3D-HEVC. IEEE Trans. Broadcast. 2021, 68, 97–109. [Google Scholar] [CrossRef]
- Omran, N.; Werda, I.; Maraoui, A.; Kachouri, R.; Belgacem, H. 3D-HEVC fast partitioning algorithm based on MD-CNN. In Proceedings of the 2024 IEEE International Conference on Artificial Intelligence & Green Energy (ICAIGE), Sousse, Tunisia, 10–12 October 2024; pp. 1–6. [Google Scholar]
- Hamout, H.; Hammani, A.; Elyousfi, A. Fast 3D-HEVC intra-prediction for depth map based on a self-organizing map and efficient features. Signal Image Video Process. 2024, 18, 2289–2296. [Google Scholar] [CrossRef]
- Zhang, J.; Hou, Y.; Peng, B.; Pan, Z.; Li, G. Global-context aggregated intra prediction network for depth video coding. IEEE Trans. Circuits Syst. II, Exp. Briefs 2023, 70, 3159–3163. [Google Scholar] [CrossRef]
- Zhang, J.; Hou, Y.; Zhang, Z.; Jin, D.; Zhang, P.; Li, G. Deep region segmentation-based intra prediction for depth video coding. Multimed. Tools Appl. 2022, 81, 35953–35964. [Google Scholar] [CrossRef]
- Lee, J.Y.; Park, S. Fast depth intra mode decision using intra prediction cost and probability in 3D-HEVC. Multimed. Tools Appl. 2024, 83, 80411–80424. [Google Scholar] [CrossRef]
- Song, W.; Dai, P.; Zhang, Q. Content-adaptive mode decision for low complexity 3D-HEVC. Multimed. Tools Appl. 2023, 82, 26435–26450. [Google Scholar] [CrossRef]
- Chen, M.J.; Lin, J.R.; Hsu, Y.C.; Ciou, Y.S.; Yeh, C.H.; Lin, M.H.; Kau, L.J.; Chang, C.Y. Fast 3D-HEVC depth intra coding based on boundary continuity. IEEE Access 2021, 9, 79588–79599. [Google Scholar] [CrossRef]
- Huo, J.; Zhou, X.; Yuan, H.; Wan, S.; Yang, F. Fast rate-distortion optimization for depth maps in 3-D video coding. IEEE Trans. Broadcast. 2022, 69, 21–32. [Google Scholar] [CrossRef]
- Lin, J.R.; Chen, M.J.; Yeh, C.H.; Chen, Y.C.; Kau, L.J.; Chang, C.Y.; Lin, M.H. Visual perception based algorithm for fast depth intra coding of 3D-HEVC. IEEE Trans. Multimed. 2021, 24, 1707–1720. [Google Scholar] [CrossRef]
- Pan, Z.; Yi, X.; Chen, L. Motion and disparity vectors early determination for texture video in 3D-HEVC. Multimed. Tools Appl. 2020, 79, 4297–4314. [Google Scholar] [CrossRef]
- Lin, J.R.; Chen, M.J.; Yeh, C.H.; Lin, S.D.; Sue, K.L.; Kau, L.J.; Ciou, Y.S. Vision-oriented algorithm for fast decision in 3D video coding. IET Image Process. 2022, 16, 2263–2281. [Google Scholar] [CrossRef]
- Yao, W.; Wang, X.; Yang, D.; Li, W. A fast wedgelet partitioning for depth map prediction in 3D-HEVC. In Proceedings of the Twelfth International Conference on Graphics and Image Processing (ICGIP 2020), Xi’an, China, 13–15 November 2020; Volume 11720, pp. 257–266. [Google Scholar]
- Wen, W.; Tu, R.; Zhang, Y.; Fang, Y.; Yang, Y. A multi-level approach with visual information for encrypted H.265/HEVC videos. Multimed. Syst. 2023, 29, 1073–1087. [Google Scholar] [CrossRef]
- Bakkouri, S.; Elyousfi, A. Early termination of CU partition based on boosting neural network for 3D-HEVC inter-coding. IEEE Access 2022, 10, 13870–13883. [Google Scholar] [CrossRef]
- Hamout, H.; Elyousfi, A. Fast 3D-HEVC PU size decision algorithm for depth map intra-video coding. J. Real-Time Image Process. 2020, 17, 1285–1299. [Google Scholar] [CrossRef]
- Bakkouri, S.; Elyousfi, A. Machine learning-based fast CU size decision algorithm for 3D-HEVC inter-coding. J. Real-Time Image Process. 2021, 18, 983–995. [Google Scholar] [CrossRef]
- Chen, J.; Wang, B.; Liao, J.; Cai, C. Fast 3D-HEVC inter mode decision algorithm based on the texture correlation of viewpoints. Multimed. Tools Appl. 2019, 78, 29291–29305. [Google Scholar] [CrossRef]
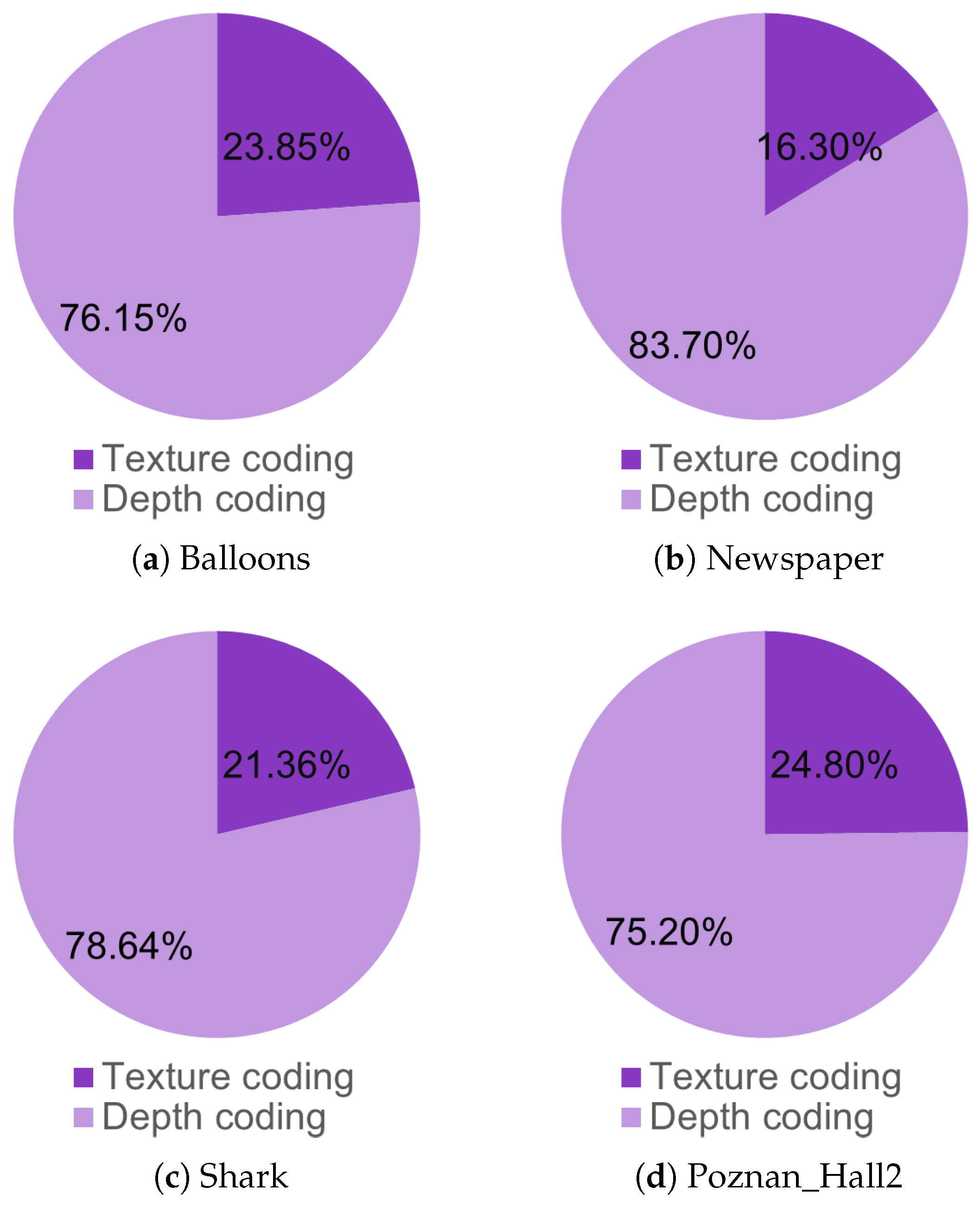
| Sequence | QP | Depth 0 (%) | Depth 1 (%) | Depth 2 (%) | Depth 3 (%) |
|---|---|---|---|---|---|
| Balloons | 34 | 33.1 | 30.9 | 23.8 | 12.2 |
| 39 | 44.3 | 36.7 | 15.1 | 3.9 | |
| 42 | 57.4 | 34.6 | 6.7 | 1.3 | |
| 45 | 73.6 | 23.9 | 2.1 | 0.4 | |
| Newspaper | 34 | 12.5 | 29.1 | 32.8 | 25.6 |
| 39 | 25.1 | 40.4 | 23.8 | 10.7 | |
| 42 | 41.7 | 39.8 | 14.8 | 3.7 | |
| 45 | 61.4 | 31.4 | 6.4 | 0.8 | |
| Shark | 34 | 30.4 | 35.4 | 19.7 | 14.5 |
| 39 | 53.0 | 30.2 | 11.3 | 5.5 | |
| 42 | 68.2 | 23.8 | 6.3 | 1.7 | |
| 45 | 80.6 | 16.4 | 2.8 | 0.2 | |
| Poznan_Hall2 | 34 | 71.4 | 20.9 | 5.8 | 1.9 |
| 39 | 83.4 | 13.3 | 2.8 | 0.5 | |
| 42 | 91.0 | 7.6 | 1.2 | 0.2 | |
| 45 | 95.8 | 3.8 | 0.4 | 0.0 | |
| Average | 57.7 | 26.1 | 11.0 | 5.2 |
| Hardware | ||
| CPU | AMD Ryzen 9 8900X3D | |
| GPU | RTX 4070Ti Super | |
| RAM | 32GB | |
| OS | windows 11 64bits | |
| Software | ||
| Reference software | HM 16.18 | |
| Configuration file | encoder_intra_main.cfg | |
| QP(depth) | 34, 39, 42, 45 |
| Sequence | Resolution | Frames | Frame Rate | 3-Views Input | Scene Characteristics |
|---|---|---|---|---|---|
| Kendo | 1024 × 768 | 300 | 30 | 1-3-5 | Multiple overlapping objects |
| Balloons | 300 | 30 | 1-3-5 | High-dynamic motion | |
| Newspaper | 300 | 30 | 2-4-6 | Static text, dynamic person | |
| GT_Fly | 1920 × 1088 | 250 | 25 | 9-5-1 | CG city geometry |
| Shark | 300 | 30 | 1-5-9 | Complex biological contours | |
| Poznan_Hall2 | 200 | 25 | 7-6-5 | Large smooth areas | |
| Poznan_Street | 250 | 25 | 5-4-3 | Complex street dynamics | |
| Undo_Dancer | 250 | 25 | 1-5-9 | Rapid complex motion |
| Sequence | Resolution | BD-PSNR (db) | Proposed (Without ) | Proposed | ||
|---|---|---|---|---|---|---|
| BDBR (%) | TS (%) | BDBR (%) | TS (%) | |||
| Kendo | 1024 × 768 | −0.01 | 0.15 | 44.32 | 0.13 | 46.68 |
| Balloons | −0.02 | 0.29 | 46.81 | 0.27 | 49.33 | |
| Newspaper | −0.03 | 0.38 | 44.12 | 0.36 | 46.97 | |
| Average (1024 × 768) | −0.02 | 0.27 | 45.08 | 0.25 | 47.66 | |
| GT_Fly | 1920 × 1088 | −0.02 | 0.42 | 46.52 | 0.39 | 48.23 |
| Shark | −0.01 | 0.61 | 49.53 | 0.58 | 52.23 | |
| Poznan_Hall2 | −0.02 | 0.46 | 43.71 | 0.44 | 45.93 | |
| Poznan_Street | −0.03 | 0.40 | 44.92 | 0.41 | 46.57 | |
| Undo_Dancer | −0.02 | 0.22 | 49.14 | 0.21 | 51.49 | |
| Average (1920 × 1088) | −0.02 | 0.42 | 46.76 | 0.41 | 48.89 | |
| Average (overall) | −0.02 | 0.37 | 46.13 | 0.35 | 48.43 | |
| Sequence | [24] | [14] | [15] | Proposed | ||||
|---|---|---|---|---|---|---|---|---|
| BDBR (%) | TS (%) | BDBR (%) | TS (%) | BDBR (%) | TS (%) | BDBR (%) | TS (%) | |
| Kendo | 0.6 | 39.5 | 0.17 | 35.2 | 0.43 | 44.6 | 0.13 | 46.68 |
| Balloons | 1.4 | 39.0 | 0.12 | 32.9 | 0.27 | 38.7 | 0.27 | 49.33 |
| Newspaper | 1.4 | 38.0 | 0.08 | 32.3 | 0.20 | 39.8 | 0.36 | 46.97 |
| GT_Fly | 0.3 | 38.3 | 0.08 | 35.0 | 0.15 | 55.7 | 0.39 | 48.23 |
| Shark | 0.5 | 39.4 | 0.26 | 44.0 | 0.14 | 42.6 | 0.58 | 52.23 |
| Poznan_Hall2 | 0.6 | 41.4 | 0.39 | 51.6 | 0.40 | 52.7 | 0.44 | 45.93 |
| Poznan_Street | 0.4 | 39.9 | 0.26 | 41.6 | 0.62 | 52.6 | 0.41 | 46.57 |
| Undo_Dancer | 0.2 | 38.6 | 0.29 | 49.3 | 0.44 | 49.9 | 0.21 | 51.49 |
| Average | 0.68 | 39.26 | 0.21 | 40.2 | 0.32 | 45.8 | 0.35 | 48.43 |
| Sequence | Resolution | Original Reference Frame | Synthesized Views (HTM16.3) | Synthesized Views (Proposed) |
|---|---|---|---|---|
| Balloons | 1024 × 768 |  |  |  |
| Newspaper | 1024 × 768 |  |  |  |
| Shark | 1920 × 1088 |  |  |  |
| GT_Fly | 1920 × 1088 |  |  |  |
| Sequence | SSIM | VMAF | ||
|---|---|---|---|---|
| HTM16.3 | Proposed | HTM16.3 | Proposed | |
| Balloons | 0.948 | 0.945 | 92.7 | 91.9 |
| Newspaper | 0.962 | 0.960 | 94.3 | 93.8 |
| Shark | 0.935 | 0.931 | 91.5 | 90.6 |
| GT_Fly | 0.956 | 0.953 | 93.8 | 93.1 |
| Average | 0.950 | 0.947 | 93.1 | 92.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, F.; Zhang, H.; Zhang, Q. Fast Intra-Coding Unit Partitioning for 3D-HEVC Depth Maps via Hierarchical Feature Fusion. Electronics 2025, 14, 3646. https://doi.org/10.3390/electronics14183646
Liu F, Zhang H, Zhang Q. Fast Intra-Coding Unit Partitioning for 3D-HEVC Depth Maps via Hierarchical Feature Fusion. Electronics. 2025; 14(18):3646. https://doi.org/10.3390/electronics14183646
Chicago/Turabian StyleLiu, Fangmei, He Zhang, and Qiuwen Zhang. 2025. "Fast Intra-Coding Unit Partitioning for 3D-HEVC Depth Maps via Hierarchical Feature Fusion" Electronics 14, no. 18: 3646. https://doi.org/10.3390/electronics14183646
APA StyleLiu, F., Zhang, H., & Zhang, Q. (2025). Fast Intra-Coding Unit Partitioning for 3D-HEVC Depth Maps via Hierarchical Feature Fusion. Electronics, 14(18), 3646. https://doi.org/10.3390/electronics14183646




