Optimal Capacity Configuration of Multi-Type Renewable Energy in Islanded LCC-HVDC Transmission Systems
Abstract
1. Introduction
- (1)
- Construction of typical wind and PV generation scenarios via a K-medoids clustering method, and development of an islanded power flow framework using a virtual balancing node.
- (2)
- Incorporation of active power droop control and quadratic programming-based reactive power optimization to enhance frequency and voltage stability.
- (3)
- A particle swarm optimization (PSO) algorithm is applied to realize the maximum capacity configuration of renewable energy in a water–wind–PV–storage-integrated islanded DC transmission system under operational constraints.
2. Topology of DC Island Transmission and New Energy Scene Clustering
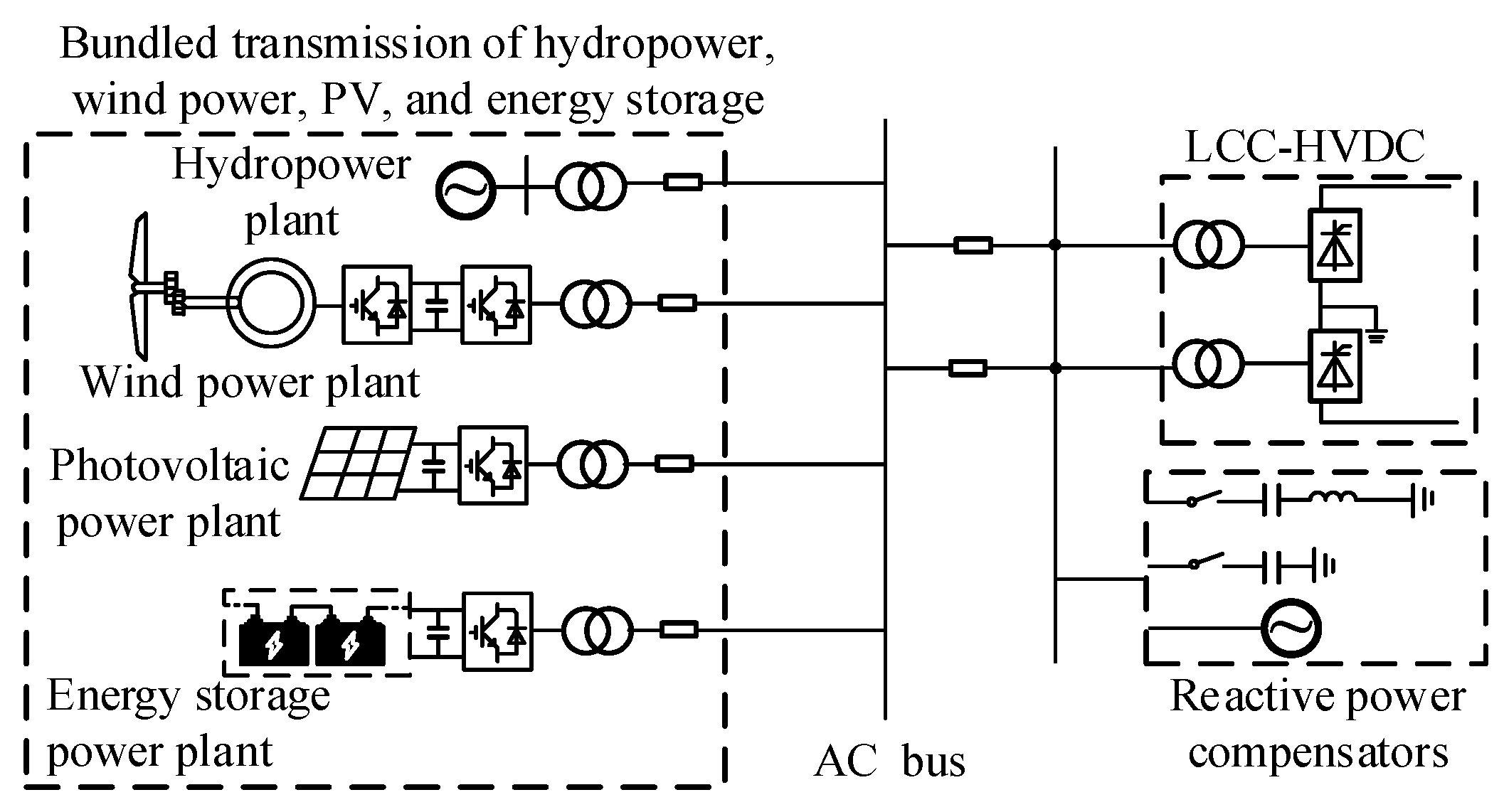
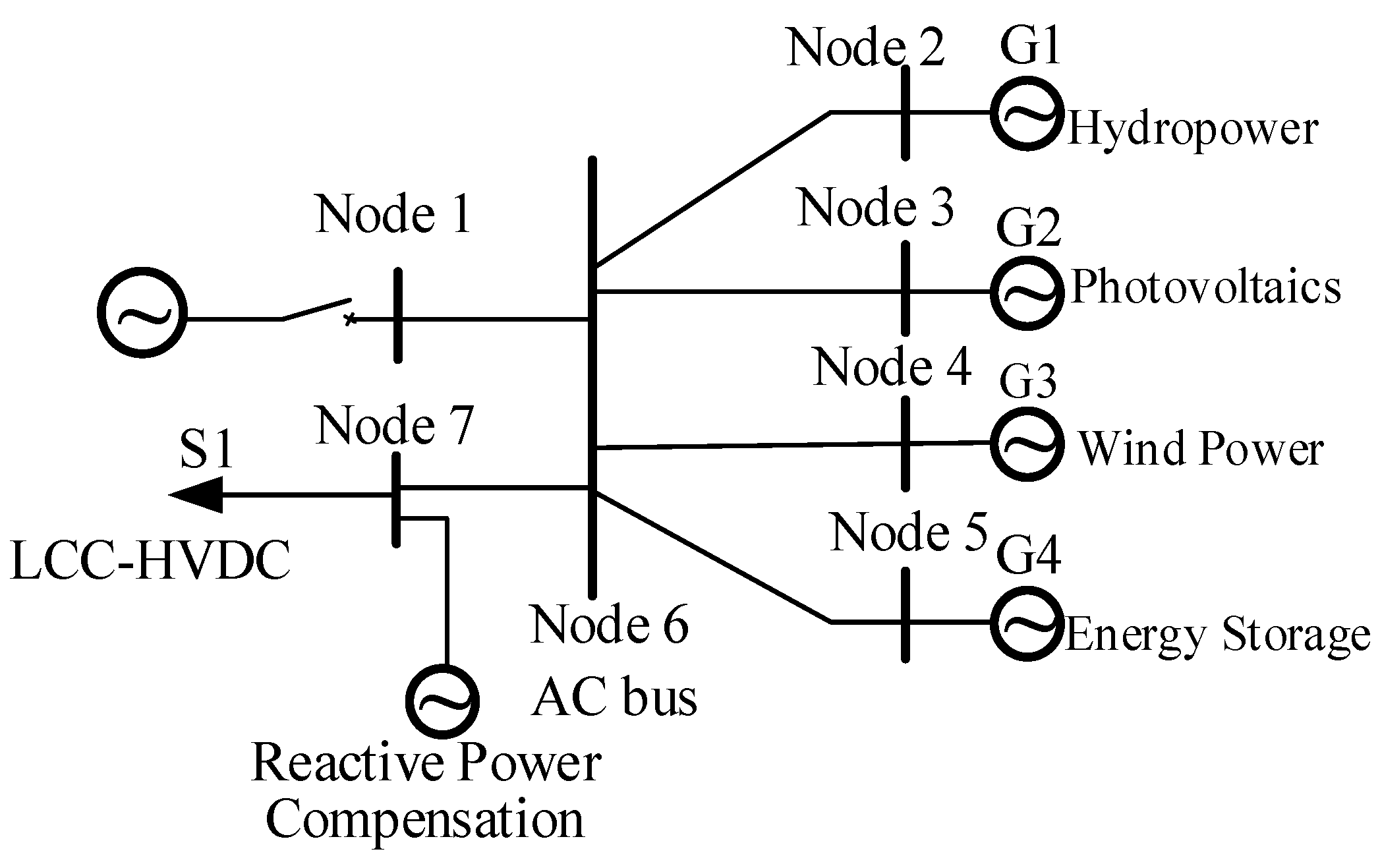
2.1. Topology of Islanded DC Transmission for Renewable Energy Integration
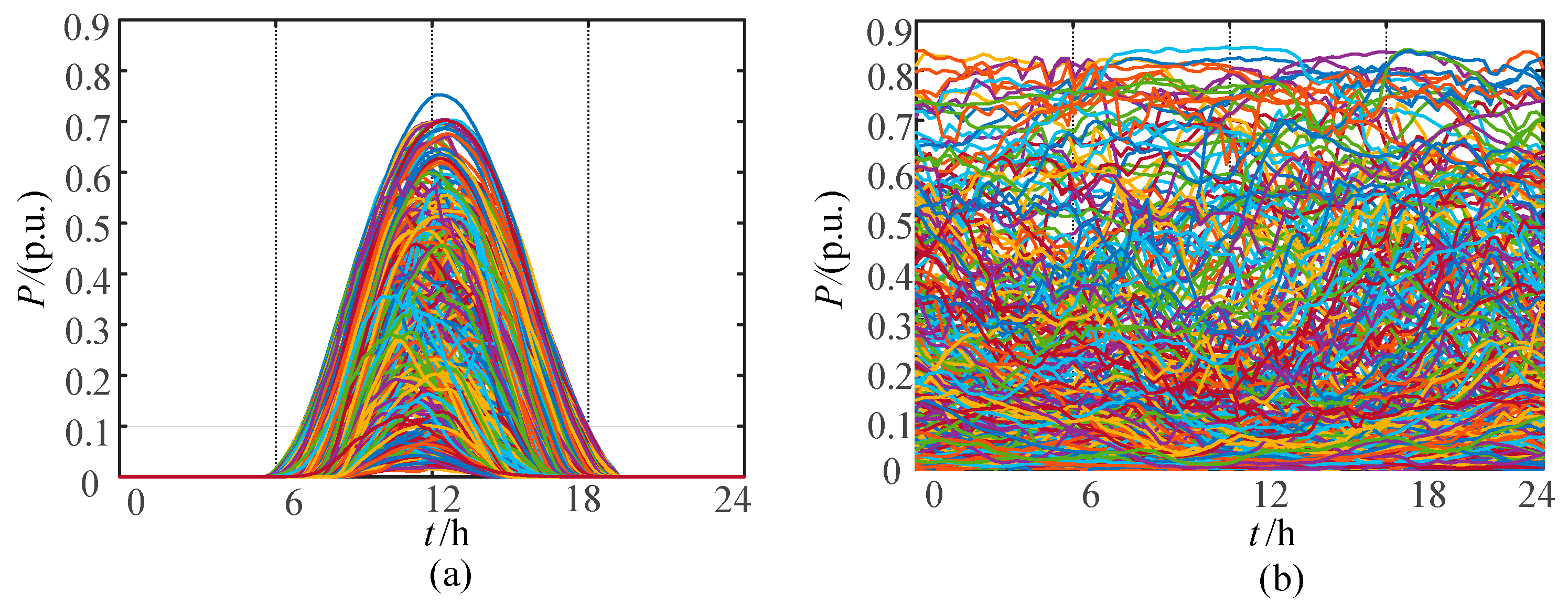
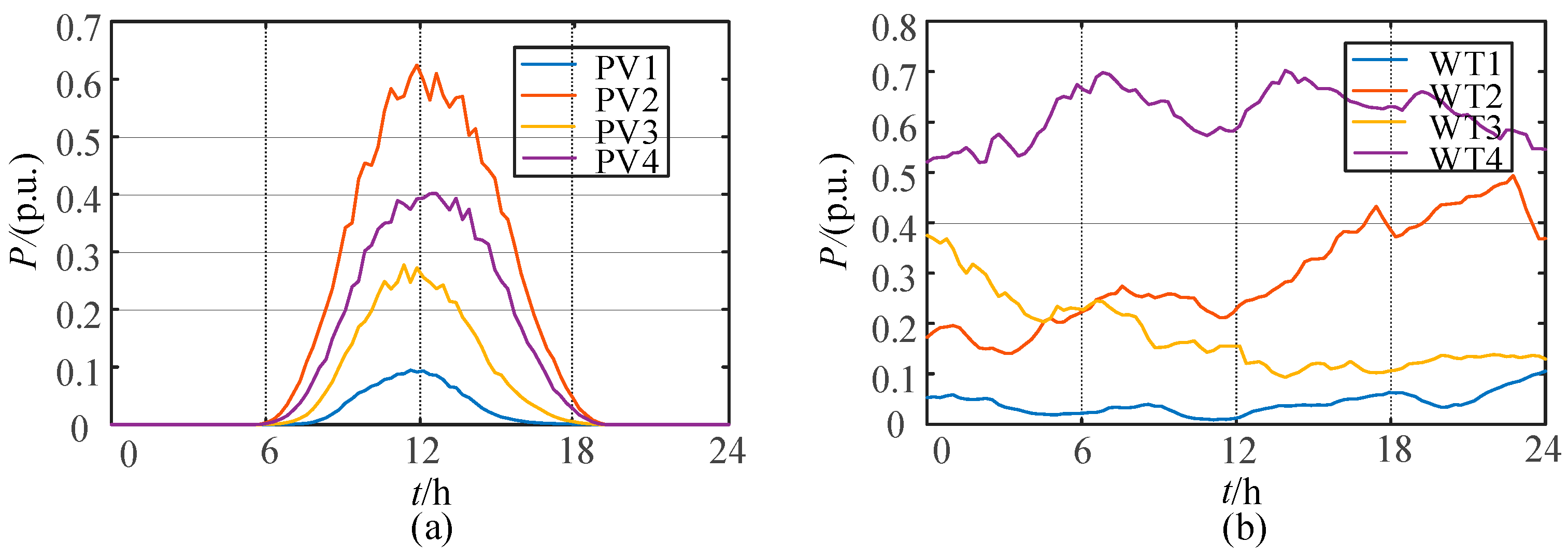
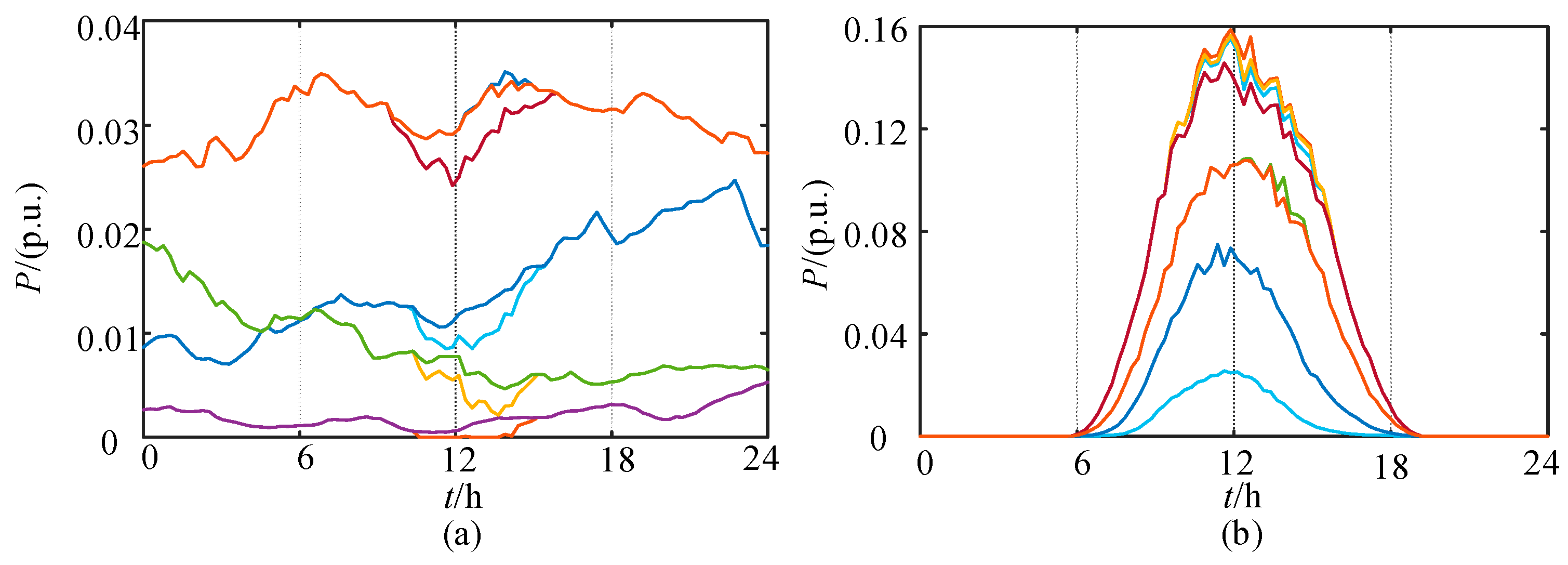
2.2. Renewable Energy Scenario Clustering
3. Power Flow Analysis of Islanded DC Transmission with Renewable Integration
3.1. Power Flow Modeling in Islanded Mode
3.2. Active Power Droop Control
3.3. Quadratic Programming-Based Reactive Power Control
3.4. Constraint Conditions
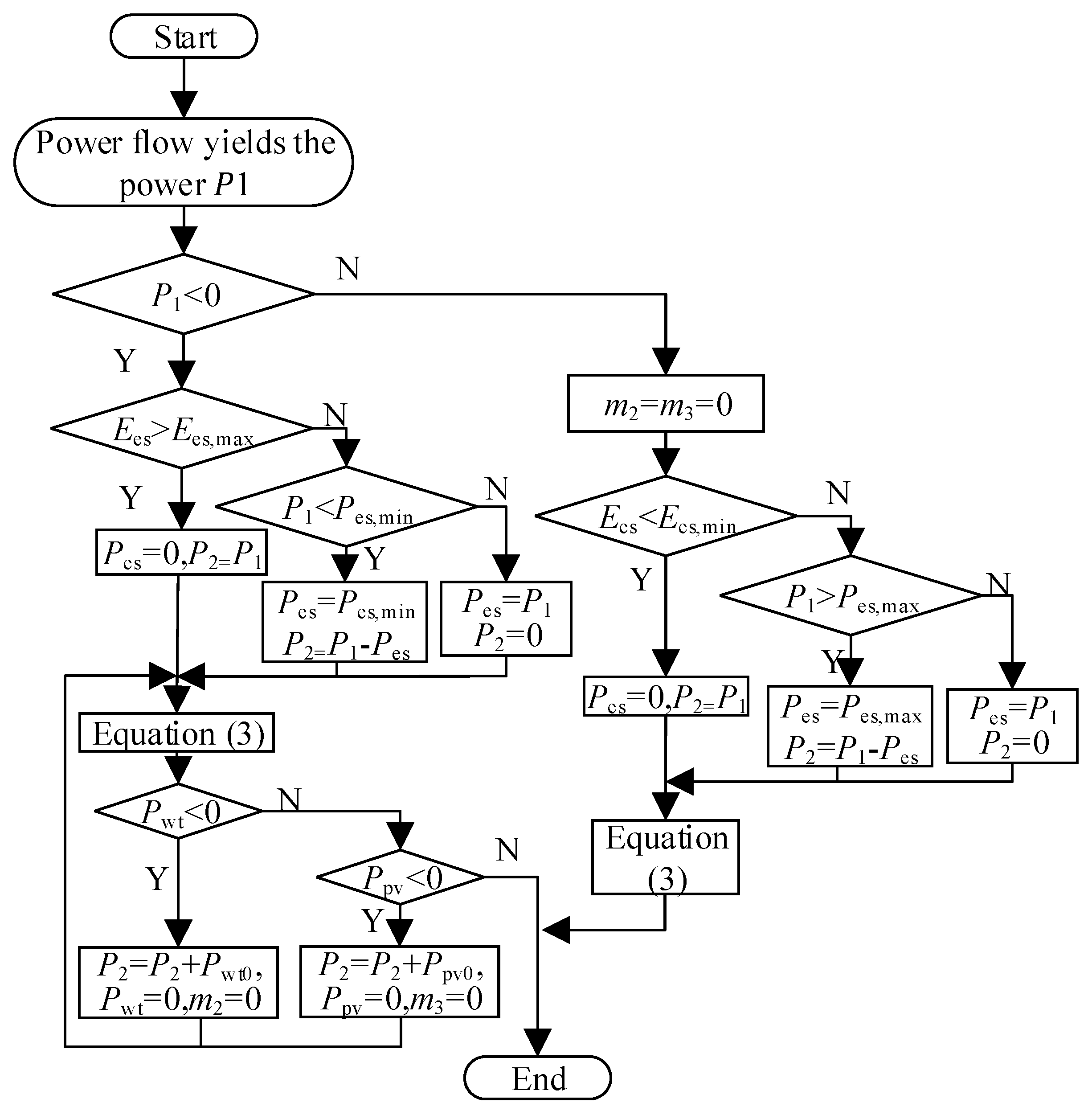
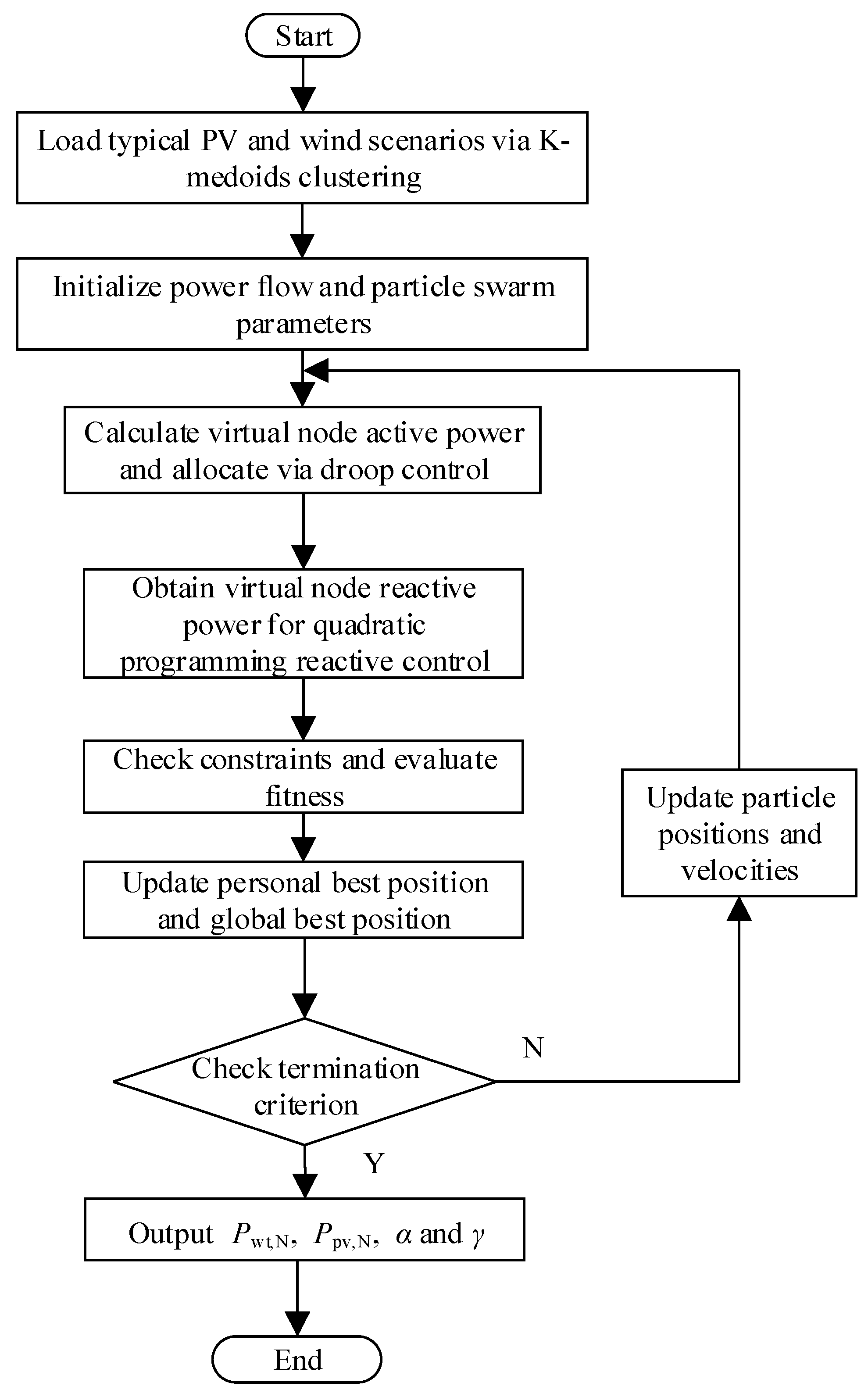
4. Optimal Sizing of Renewable Energy Integration Using PSO
- (1)
- Set the parameters of the PSO algorithm and initialize the capacity-related parameters for PV power, wind power, LCC-HVDC, and energy storage systems. Then, load the wind scenarios obtained via the K-medoids clustering algorithm.
- (2)
- The feasibility of solutions is evaluated based on active power droop control and quadratic programming-based reactive power optimization. If all constraints are satisfied, the fitness value is set to the objective function value; otherwise, penalty terms are incorporated to account for constraint violations.
- (3)
- Calculate the fitness values of individual particles and the entire swarm, reflecting how well each solution meets the optimization objectives.
- (4)
- Update the personal best and global best positions. For each particle, update its personal best position if its current fitness value is better than its historical best. Then, select the particle with the best personal fitness among all particles as the global best position.
- (5)
- Based on the current velocity and position of each particle, as well as its distances to the personal best and global best positions, the velocity and position are updated accordingly.
- (6)
- Steps 2 to 5 are iteratively repeated until either the maximum number of iterations is reached or the convergence tolerance is satisfied.
5. Simulation Verification
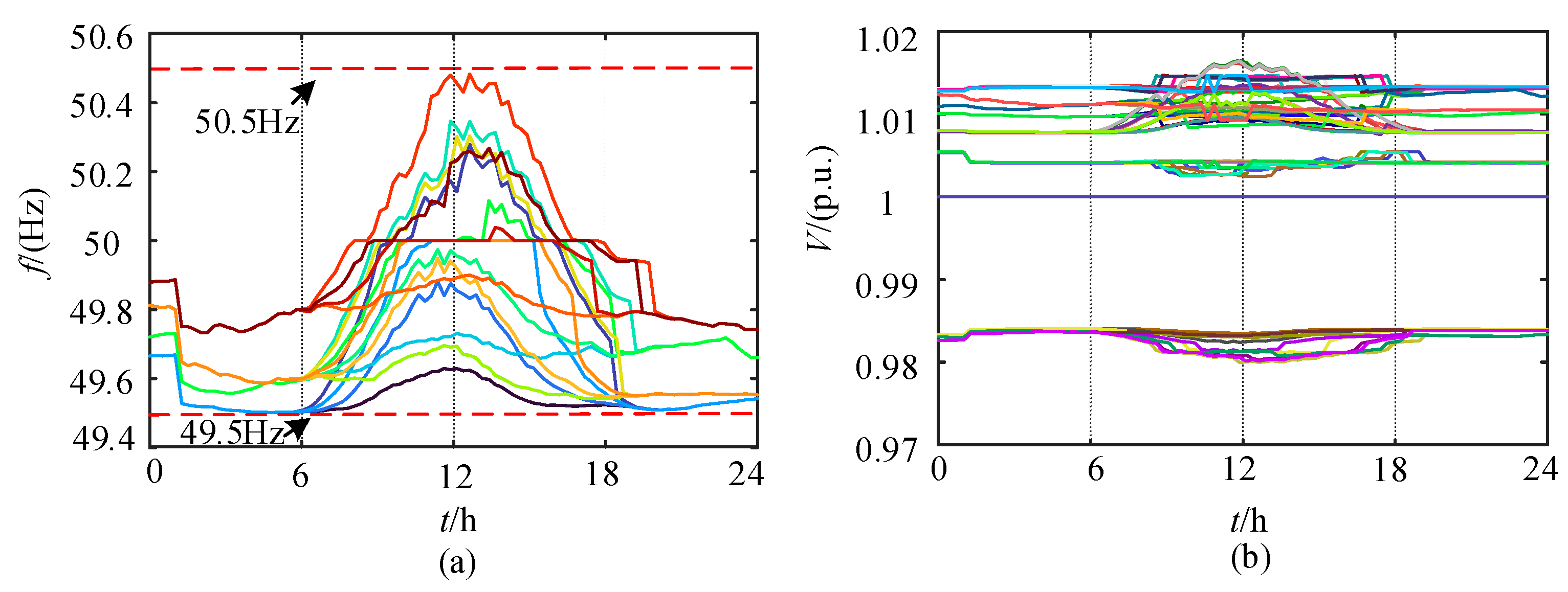
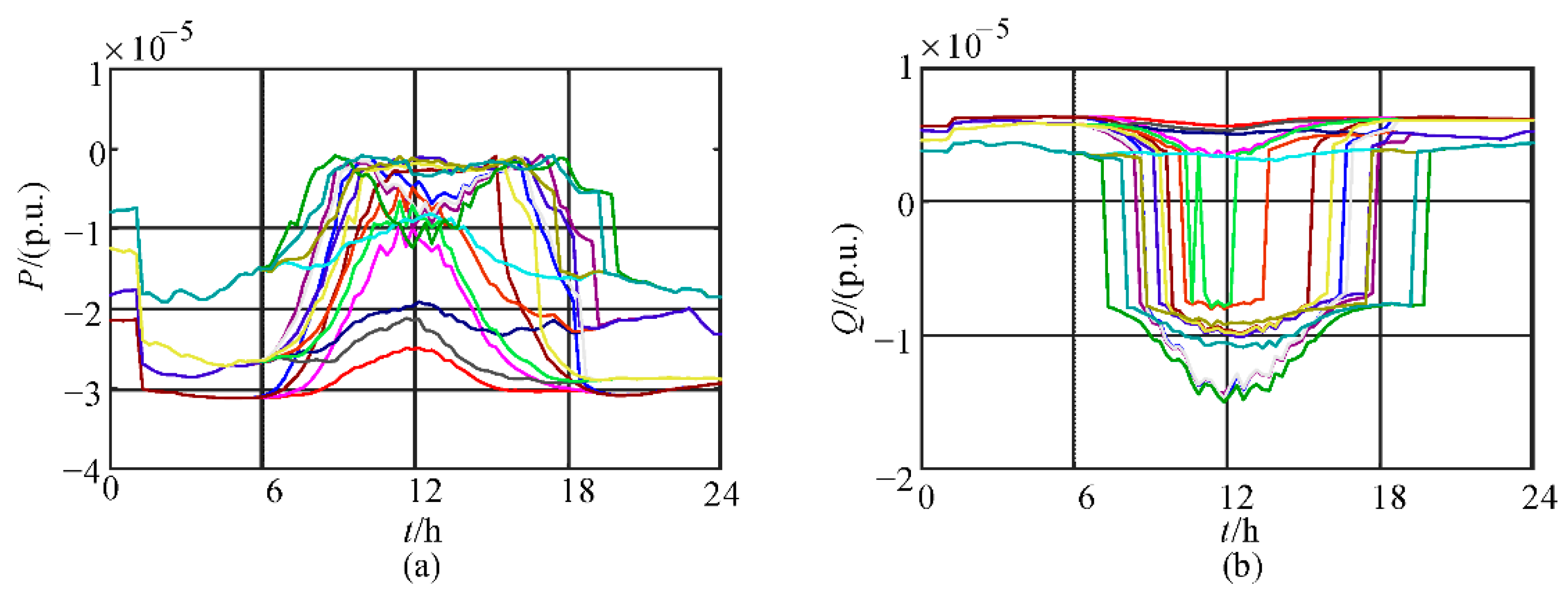
5.1. Control Performance Verification
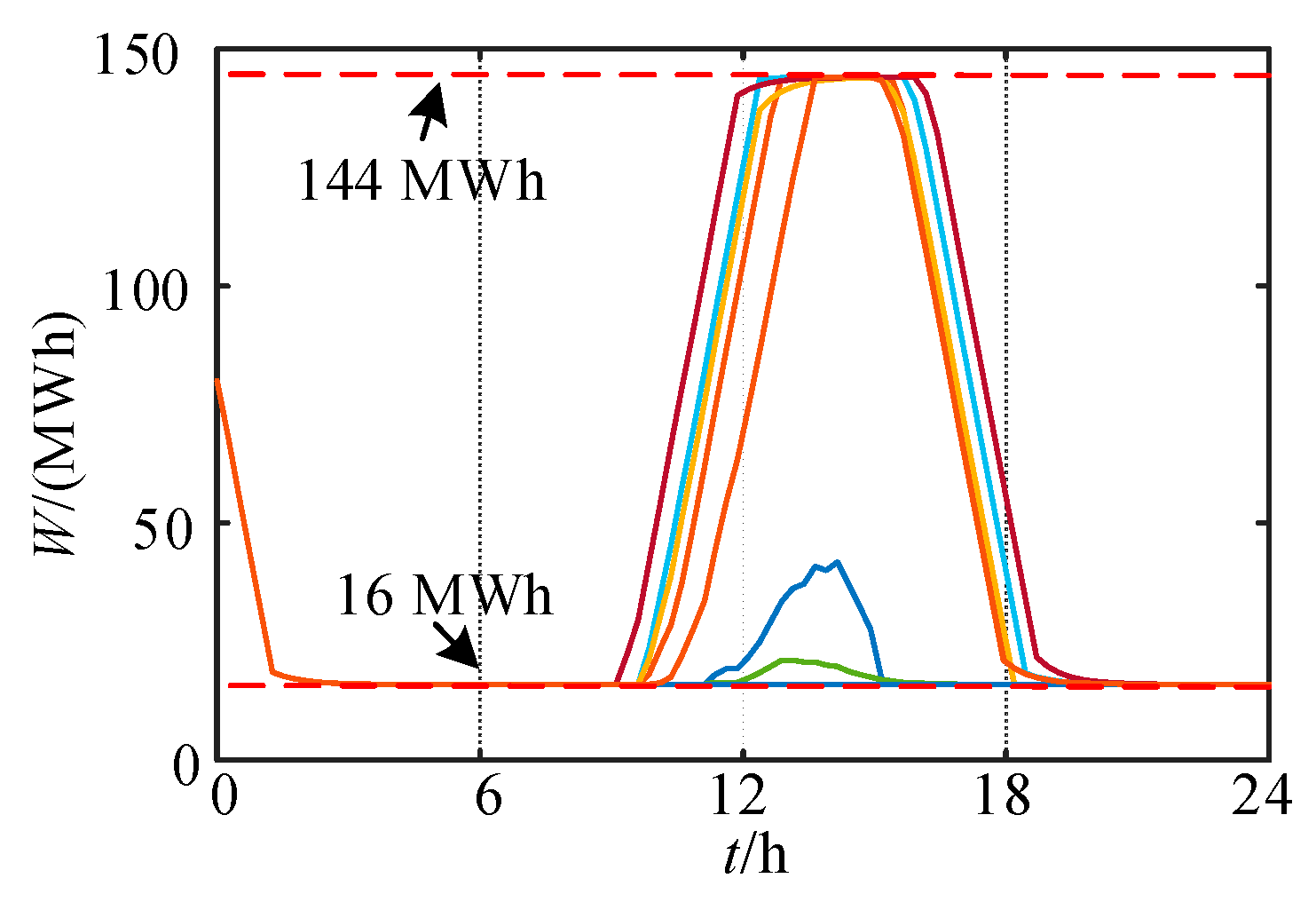
5.2. Validation of Maximum Renewable Energy Capacity Configuration
5.3. Validation of Maximum Renewable Energy Capacity Configuration Under Hydropower Secondary Frequency Regulation
6. Conclusions
- (1)
- Typical wind and PV output scenarios are extracted using the K-medoids clustering method, effectively preserving the variability and uncertainty of renewable generation.
- (2)
- Based on a virtual balancing node, an islanded power flow model is developed, incorporating droop control for active power and quadratic programming for reactive power to coordinate frequency and voltage regulation. The maximum active and reactive power at the virtual balancing node is only 3.2 × 10−5 p.u. and 1.4 × 10−5 p.u., respectively, indicating the efficient self-balancing capability of the system.
- (3)
- Under the proposed optimization model, the method achieves maximum integration capacities of 100 MW for wind power and 304 MW for PV power without secondary frequency regulation. With hydropower secondary frequency regulation, the wind capacity remains at 100 MW, while the PV capacity increases to 540 MW, significantly enhancing renewable energy accommodation. Meanwhile, the required energy storage output coefficient is only 0.10, indicating that the strategy ensures system stability while balancing renewable energy utilization and overall economic efficiency.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Mathew, E.C.; Sharma, R.; Das, A. A fault tolerant scheme for integration of remote renewable energy sources with HVDC system. IEEE Trans. Power Deliv. 2020, 35, 2876–2884. [Google Scholar] [CrossRef]
- Guo, C.; Zhang, J. Impact of grid-forming-based PV on SSTI stability of PV–thermal-bundled system transmitted by LCC-HVDC. IEEE Trans. Power Deliv. 2025, 40, 152–165. [Google Scholar] [CrossRef]
- Yang, Y.; Wen, Y.; Zhang, Z.; Dong, Y.; Shen, C.; Liu, Y. Toward 100% renewable power grids: A review. IEEE Access 2025, 13, 69690–69704. [Google Scholar] [CrossRef]
- Jiao, Y.; Li, B.; Ding, L.; Suo, Z.; Xu, D. DC/DC converter with high current capability for all DC renewable system. IEEE Trans. Power Electron. 2024, 39, 12091–12095. [Google Scholar] [CrossRef]
- Wang, W.; Li, G.; Guo, J. Large-scale renewable energy transmission by HVDC: Challenges and proposals. Engineering 2022, 19, 252–267. [Google Scholar] [CrossRef]
- Guo, H.; Zhang, Z.; Xu, Z. Parallel converter-based hybrid HVDC system for integration and delivery of large-scale renewable energy. J. Mod. Power Syst. Clean Energy 2025, 13, 688–697. [Google Scholar] [CrossRef]
- Teng, S.; Xiong, L.; Zheng, K.; Gang, M.; Wen, W.; Li, Q. Research on the full DC collection system for onshore large-scale islanded new energy. In Proceedings of the 6th International Conference on Energy Systems and Electrical Power (ICESEP), Wuhan, China, 21–23 June 2024; pp. 494–499. [Google Scholar]
- Xing, C.; Liu, M.; Peng, J.; Wang, Y.; Liao, J.; Zheng, Z.; Gao, S.; Guo, C. LCC-HVDC frequency robust control strategy based on system parameter identification in islanded operation mode. Electronics 2024, 13, 951. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, J.; Zhao, Y.; Li, G.; Li, S.; Liu, Y.; Yang, L.; Zhou, Z.; Zhao, C. Sending end frequency and voltage under islanded operation mode of HVDC transmission system. In Proceedings of the IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 26–28 November 2017; pp. 1–6. [Google Scholar]
- Wu, J.Y.; Li, H.F.; Wang, G.; Liang, Y.S. An improved traveling-wave protection scheme for LCC-HVDC transmission lines. IEEE Trans. Power Deliv. 2017, 32, 106–116. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, P.; Lu, G.; Chen, X. Influence analysis of oscillation harmonics in LCC-HVDC delivery system based on impedance modeling. IEEE Trans. Circuits Syst. I 2023, 70, 4194–4203. [Google Scholar] [CrossRef]
- Guo, C.; Liao, J.; Wang, Y.; Zhang, W.; Liu, Y.; Wang, H.; Yu, D. Fault location and protection for metallic return HVDC grid based on natural frequency extraction of modal derivative current. IEEE Trans. Instrum. Meas. 2025, 74, 3508116. [Google Scholar] [CrossRef]
- Ding, R.; Zhao, C.; Shen, X.; Liang, C.; Liao, M. Control strategy of islanded wind farms connected to LCC-HVDC. In Proceedings of the 8th International Conference on Energy, Electrical and Power Engineering (CEEPE), Wuxi, China, 25–27 April 2025; pp. 465–470. [Google Scholar]
- Meng, P.; Xiang, W.; Chi, Y.; Wang, Z.; Lin, W.; Wen, J. Resilient DC voltage control for islanded wind farms integration using cascaded hybrid HVDC system. IEEE Trans. Power Syst. 2022, 37, 1054–1066. [Google Scholar] [CrossRef]
- Wang, S.; Wang, Y.; Ma, J.; Wei, L.; Li, X.; Liu, X. Study of frequency and voltage characteristics of islanding HVDC system and the corresponding control strategy. In Proceedings of the International Conference on Power System Technology, Chengdu, China, 20–22 October 2014; pp. 2247–2251. [Google Scholar]
- Xiong, W.; Tang, Z.; Cui, X. Distributed data-driven voltage control for active distribution networks with changing grid topologies. Control Eng. Pract. 2024, 147, 105933. [Google Scholar] [CrossRef]
- Lin, K.; Lu, X.; Wu, F.; Shi, L. Evaluation of the renewable energy accommodation capacity in the regional power grid. In Proceedings of the 12th IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Nanjing, China, 20–23 September 2020; pp. 1–4. [Google Scholar]
- Xia, S.; Wu, J.; Ma, S.; Wang, Z.; Sun, C.; Tang, T.; Shao, C. Photovoltaic power generation and energy storage capacity cooperative planning method for rail transit self-consistent energy systems considering the impact of DoD. IEEE Trans. Smart Grid 2025, 16, 665–677. [Google Scholar] [CrossRef]
- Starke, A.R.; Cardemil, J.M.; Escobar, R.; Colle, S. Multi-objective optimization of hybrid CSP+PV system using genetic algorithm. Energy 2018, 147, 490–503. [Google Scholar] [CrossRef]
- Hou, H.; Xu, T.; Wu, X.; Wang, H.; Tang, A.; Chen, Y. Optimal capacity configuration of the wind–photovoltaic–storage hybrid power system based on gravity energy storage system. Appl. Energy 2020, 271, 115052. [Google Scholar] [CrossRef]
- Roy, P.; He, J.; Liao, Y. Cost optimization of battery and supercapacitor hybrid energy storage system for dispatching solar PV power. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 561–568. [Google Scholar]
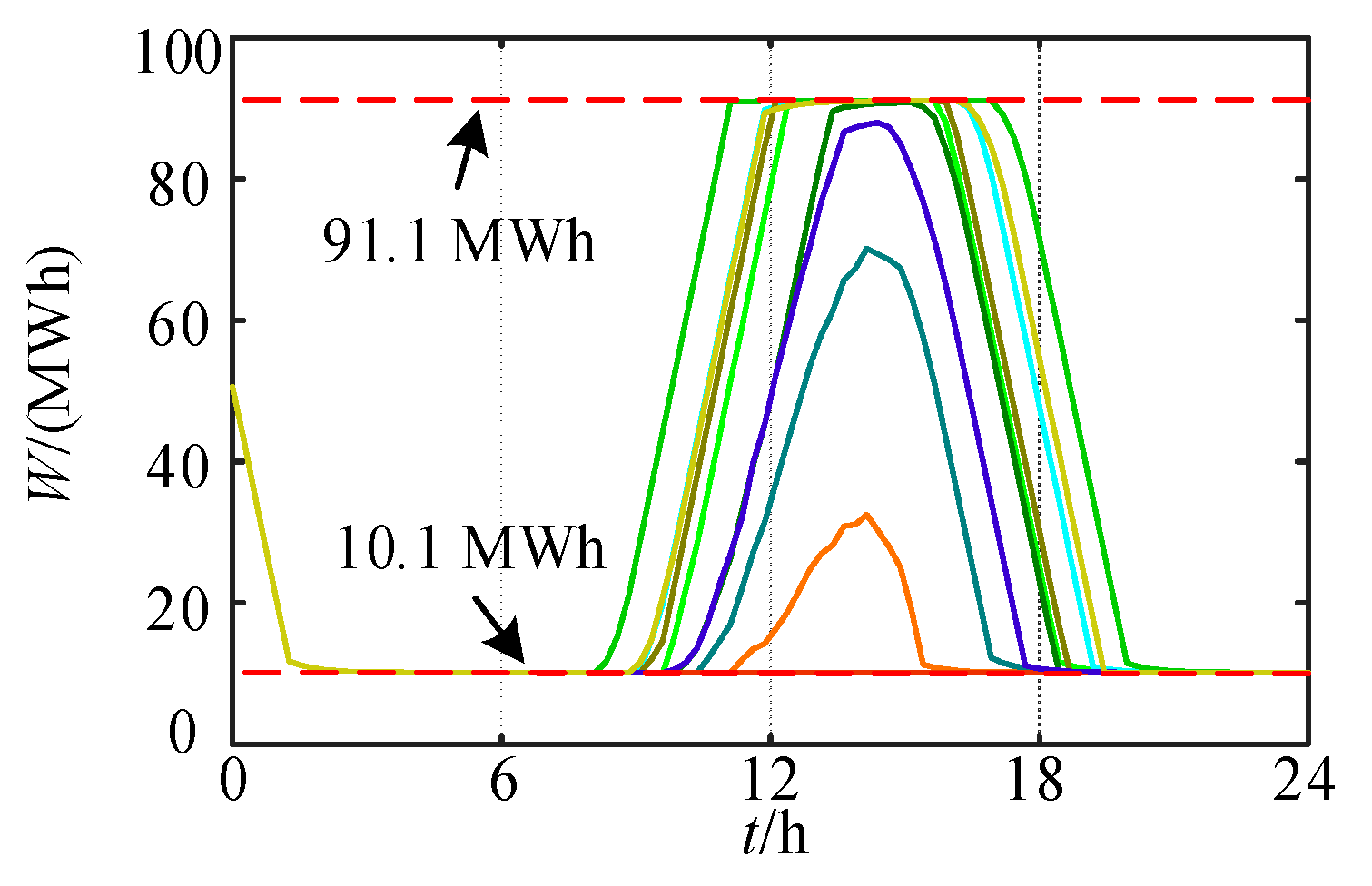
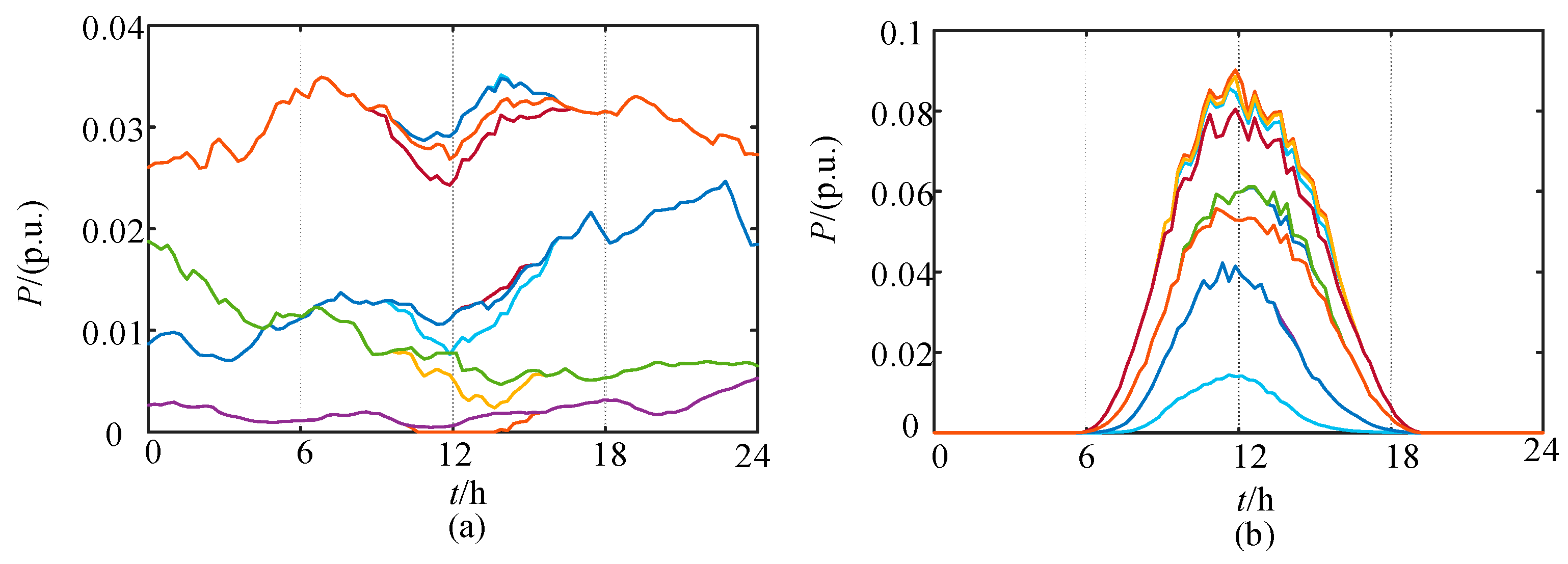
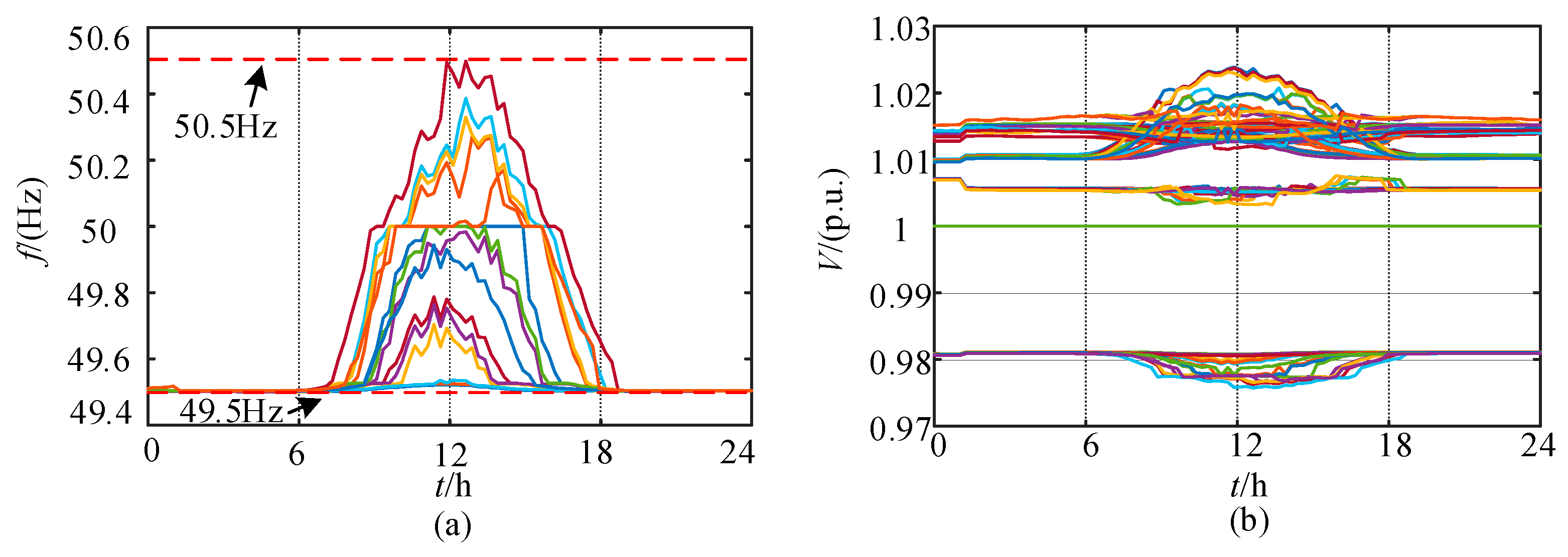
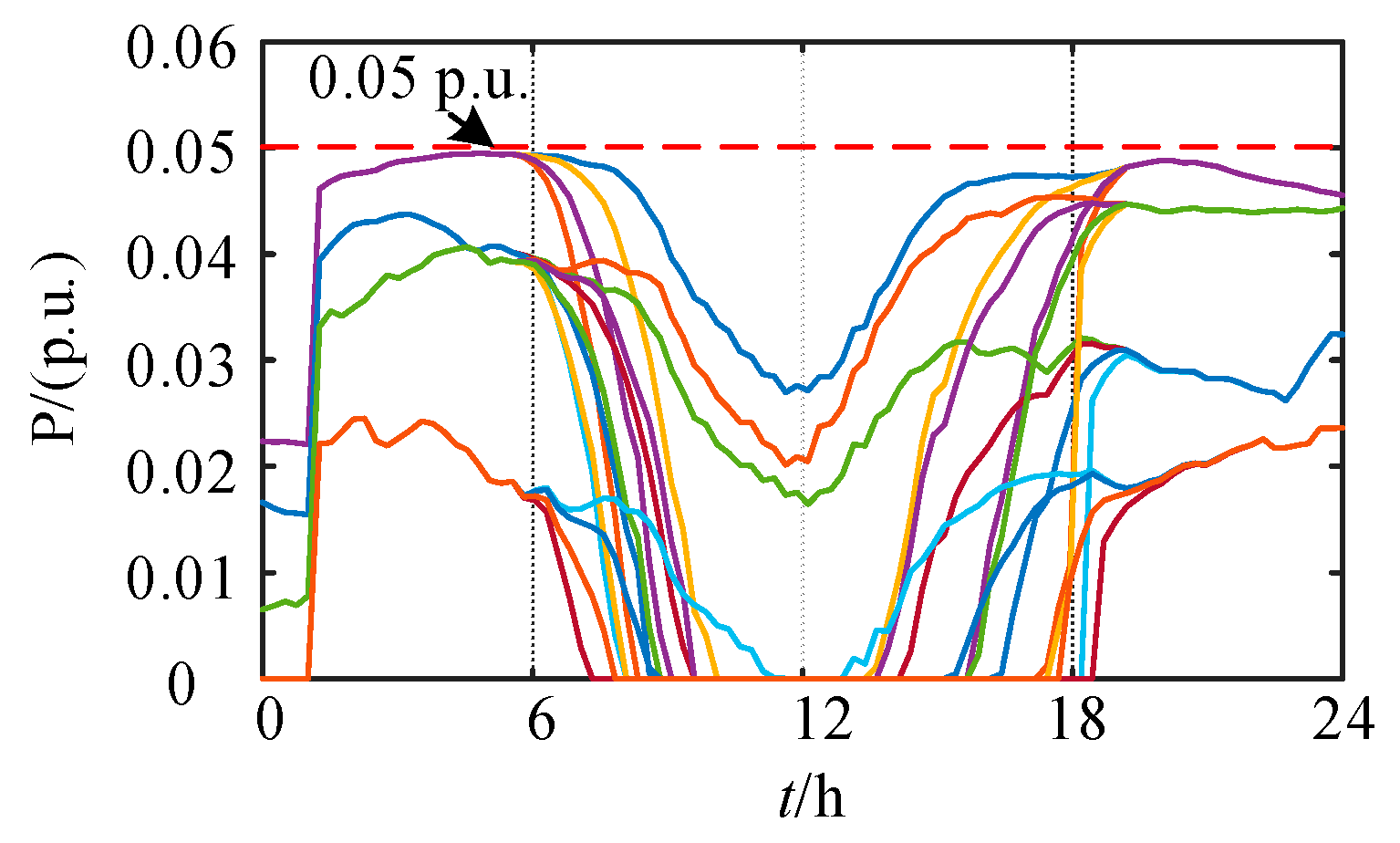
| Study/ Method | Research Objective | Storage Sizing Approach | Constraint Handling |
|---|---|---|---|
| This study (proposed) | Maximizing renewable utilization and stable power sharing in an islanded DC system | Joint sizing of wind, photovoltaic, and energy storage using PSO; droop and voltage optimization reduce storage burden | Frequency (49.5–50.5 Hz), DC voltage (0.95–1.05 p.u.), virtual-node Q = 0, converter active/reactive/apparent power limits, Energy Storage System (ESS) State of Charge (SOC) and power bounds |
| Reference [18] | Photovoltaic integration and storage lifetime optimization in urban rail systems | Co-planning of photovoltaic and hybrid ESS, considering battery Depth of Discharge (DoD) and cycle life | Power balance, SOC/DoD limits, equipment capacity boundaries, does not involve frequency stability constraints of islanded DC systems. |
| Reference [20] | Economic optimization of renewable capacity configuration | Economic optimization to minimize cost of renewable capacity configuration | Energy balance, SOC and power limits, cost and reliability indicators, does not involve frequency stability constraints of islanded DC systems. |
| Reference [21] | Photovoltaic power dispatch and storage cost minimization | Battery–supercapacitor hybrid scheduling; PSO-optimized low-pass filter (LPF) parameters; SOC fuzzy control | ESS power/voltage/current limits, SOC and temperature constraints; objective includes investment and operating cost |
| Representative Scenario | Probability | MSE |
|---|---|---|
| PV 1 | 0.22 | 0.198 |
| PV 2 | 0.30 | 0.057 |
| PV 3 | 0.29 | 0.321 |
| PV 4 | 0.19 | 0.242 |
| WT 1 | 0.15 | 2.539 |
| WT 2 | 0.20 | 1.777 |
| WT 3 | 0.41 | 0.296 |
| WT 4 | 0.24 | 1.321 |
| Parameter | Value |
|---|---|
| Upper limit of rated power for PV and wind/MVA | 1500 |
| Lower limit of rated power for PV and wind/MVA | 100 |
| Range of energy storage output coefficient (α) | [0.1, 0.2] |
| Energy storage capacity range | [0.1, 0.9] |
| Charging/discharging efficiency of energy storage | 0.96 |
| Energy storage maximum capacity (Ees,max)/MWh | 2.5 h × Pes,N |
| Initial energy storage capacity | 0.5Ees,max |
| Range of DC output coefficient (γ) | [0, 1] |
| Rated power of hydropower (Ph,N)/MW | 500 |
| System rated power/MVA | 4000 |
| System frequency range/Hz | [49.5, 50.5] |
| Node frequency range/p.u. | [0.95, 10.5] |
| Hydropower droop coefficient (m1)/(MW/Hz) | 100 |
| Wind power droop coefficient (m2)/(MW/Hz) | 0.1Pwt,N/0.5 Hz |
| PV droop coefficient (m3)/(MW/Hz) | 0.1Ppv,N/0.5 Hz |
| DC droop coefficient (m4)/(MW/Hz) | 0.2Pdc,N/1 Hz |
| number of particles | 30 |
| Maximum iterations | 100 |
| Inertia weight | 0.7 |
| Individual learning factor | 2 |
| Global learning factor | 2 |
| Wind Power/MW | PV Power /MW | Energy Storage Output Coefficient α | DC Output Coefficient γ |
|---|---|---|---|
| 100 | 304 | 0.1 | 0.23 |
| Wind Power/MW | PV Power /MW | Energy Storage Output Coefficient α | DC Output Coefficient γ |
|---|---|---|---|
| 100 | 540 | 0.1 | 0.31 |
| Scenario | Wind Power/MW | PV Power/MW | Energy Storage Output Coefficient (α) | DC Output Coefficient (γ) |
|---|---|---|---|---|
| Grid-connected | 1165 | 1091 | 0.1 | 0.5 |
| Wind-only | 355 | / | 0.2 | 0.22 |
| PV-only | / | 416 | 0.1 | 0.26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, Y.; Wang, Q.; Hu, C.; Chen, K.; Guo, C.; Liao, J. Optimal Capacity Configuration of Multi-Type Renewable Energy in Islanded LCC-HVDC Transmission Systems. Electronics 2025, 14, 3557. https://doi.org/10.3390/electronics14173557
Tao Y, Wang Q, Hu C, Chen K, Guo C, Liao J. Optimal Capacity Configuration of Multi-Type Renewable Energy in Islanded LCC-HVDC Transmission Systems. Electronics. 2025; 14(17):3557. https://doi.org/10.3390/electronics14173557
Chicago/Turabian StyleTao, Yuxuan, Qing Wang, Chengbin Hu, Kuangyu Chen, Chunsheng Guo, and Jianquan Liao. 2025. "Optimal Capacity Configuration of Multi-Type Renewable Energy in Islanded LCC-HVDC Transmission Systems" Electronics 14, no. 17: 3557. https://doi.org/10.3390/electronics14173557
APA StyleTao, Y., Wang, Q., Hu, C., Chen, K., Guo, C., & Liao, J. (2025). Optimal Capacity Configuration of Multi-Type Renewable Energy in Islanded LCC-HVDC Transmission Systems. Electronics, 14(17), 3557. https://doi.org/10.3390/electronics14173557










